OPTIMALISASI EKSEKUSI SAHAM DENGAN PENINGKATAN RISIKO PERDAGANGAN

OPTIMALISASI EKSEKUSI SAHAM

DENGAN PENINGKATAN RISIKO PERDAGANGAN

SITI MARIAM

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

ABSTRACT

SITI MARIAM. Optimal Share Execution with Enhanced Trading Risk. Supervised by RETNO BUDIARTI and DONNY CITRA LESMANA.

Generally, share transaction in capital market considers two things, i.e. transaction cost and transaction risk. The cost of share transaction consists of temporary (liquidity premium) and permanent market impact (cost information). On the other hand, the transaction risk consists of the volatility risk related to the randomization of share price and the risk of the uncertain liquidity premium. This paper discusses the trade strategies, which are able to minimize the transaction cost subject to the uncertainty risk. In order to minimize the cost of transaction, it is necessary to decide the optimal execution time, the quantity of share be sold in a certain time interval, as well as the amount of the initial traded shares. To find the optimal solutions, calculus variation is used. If the uncertainty of liquidity premium in a trade does not depend on the trading rate, so a risk averse trader accelerate his trade programs to reduce the risk. On the other hand, a risk lover trader will defer his trade in order to minimize the cost of transaction. On the contrary, if the uncertainty of liquidity premium in a trade depends on the trading rate, so the amount initial traded shares depends on the risk aversion of a trader, i.e. the risk averse investors will decrease the amount of the initial traded shares, while the risk lover investor will increase them.

ABSTRAK

SITI MARIAM. Optimalisasi Eksekusi Saham dengan Peningkatan Risiko Perdagangan. Dibimbing oleh RETNO BUDIARTI dan DONNY CITRA LESMANA .

Pada umumnya transaksi saham di pasar modal mempertimbangkan dua hal, yaitu biaya transaksi dan risiko transaksi. Adapun biaya transaksi saham dipengaruhi oleh dampak temporer (biaya likuiditas) dan dampak permanen (biaya informasi). Sedangkan risiko dari transaksi saham terdiri atas risiko volatilitas yaitu risiko yang berhubungan dengan keacakan harga saham, dan risiko ketidakpastian biaya likuiditas. Dalam karya ilmiah ini dibahas tentang strategi perdagangan yang dapat meminimumkan biaya transaksi dengan kendala adanya risiko ketidakpastian. Untuk meminimumkan biaya transaksi maka perlu dicari waktu eksekusi optimal, banyaknya saham yang akan dijual pada suatu waktu atau banyaknya saham awal yang diperdagangkan, yaitu dengan menggunakan metode kalkulus variasi. Jika ketidakpastian biaya likuiditas dalam perdagangan tidak bergantung pada rata-rata perdagangan maka seorang penjual yang menghindari risiko akan mempercepat program penjualannya dengan tujuan untuk mengurangi risiko, sedangkan penjual yang lebih berani mengambil risiko akan memperlambat perdagangannya dengan tujuan meminimumkan biaya transaksi. Jika ketidakpastian biaya likuiditas dalam perdagangan bergantung pada rata-rata perdagangan maka banyaknya saham awal optimal yang diperdagangkan bergantung pada tingkat penghindaran risiko seorang penjual, yaitu ketika seorang penjual semakin menghindari risiko maka banyaknya saham awal optimal yang diperdagangkan akan semakin sedikit, dan sebaliknya jika penjual semakin berani mengambil risiko maka banyaknya saham optimal yang diperdagangkan akan semakin banyak.

OPTIMALISASI EKSEKUSI SAHAM

DENGAN PENINGKATAN RISIKO PERDAGANGAN

Oleh :

SITI MARIAM

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMETIKA DAN ILMU PENEGATHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

Judul Skripsi : Optimalisasi Eksekusi Saham dengan Peningkatan Risiko

Perdagangan

Nama

: Ritawati

NIM

: G54051614

Disetujui

Ir. Retno Budiarti MS.

Pembimbing I

Donny Citra Lesmana S.Si, M.Fin.Math.

Pembimbing II

,

Diketahui

Dr. drh. Hasim, DEA.

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

PRAKATA

ALHAMDULILLAH, segala puji dan syukur penulis panjatkan ke hadirat illahi rabbi, yang telah memberikan kekuatan kepada penulis untuk dapat menyelesaikan halaman demi halaman sehingga menjadi skripsi ini. Selawat terbingkai salam semoga tercurah kepada junjungan alam,

qudwatuna Muhammad saw, motivator dan inspirator terhebat sepanjang zaman.

Sementara penulis menulis kalimat demi kalimat di dalam skripsi ini, memikirkan dan berharap betapa besarnya impact yang ingin penulis capai sehingga ia berguna bagi banyak orang, terbayang selalu oleh penulis wajah-wajah mereka yang terus mendukung, menyokong, memberikan inspirasi dan memotivasi kepada penulis untuk terus maju melanjutkan perjalanan panjang membangun peradaban baru nan cemerlang. Penulis sadar bahwa setiap pencapaian adalah buah dari kerja dan sokongan banyak pihak yang begitu luar biasa, oleh karena itu penulis ingin menyampaikan ucapan terima kasih dan penghargaan setinggi-tingginya kepada:

1. Ibu Retno Budiarti dan Bapak Donny Citra Lesmana selaku pembimbingI dan pembimbing II, begitu banyak ilmu, inspirasi dan motivasi yang penulis peroleh dengan penuh kesabaran membimbing penulis, serta Ibu Endar Hasafah Nugrahani selaku penguji terima kasih atas saran dan masukannya.

2. Ummi tercinta terima kasih atas semua dukungan baik moral maupun materil, doa, semangat dan kasih sayang yang tiada henti . Terima kasih juga kepada bapak tercinta yang tidak pernah lelah dan berhenti membanting tulang untuk membiayai semua anakmu, semangatmu adalah motivasi bagi ananda.

3. Saudara-saudaraku tercinta : Teh Menk, A’ade, Teh Nyai, Boyenk, Boe, Boni,Tuti dan Cumi serta sahabat kecilku Bogis, terima kasih untuk masa kecil yang luar biasa indah yang telah kita lewati dalam kebersahajaan.

4. Bu Susi, Pak Yono, dan Bu Ade, atas saran-saran dan informasi yang telah diberikan. 5. Oby, Titi dan Lela atas kesediaannya menjadi pembahas pada saat seminar.

6. Rima dan lisda serta mamah Lisda yang selalu menemani suka dan duka dalam penyusunan skripsi, ramadhan kali ini sangat berkesan.

7. Teman-teman mathe42 : Tia, Lela, Pipit, Lina, Titi, Rima, Mira, Oby, Dewi, Zil, Wiwi, Hapsari, Vino, Dian, Okta, Hikmah, Warno, Eko, Awi, Ridwan, Danu,dan semuanya yang tidak bisa disebutkan satu persatu, empat tahun begitu singkat mengukir kenangan indah ini. Begitu juga kepada kakak kelas dan adik kelas mate41 dan mate43 serta mate 44 yang telah memotivasi.

8. Imeh dan temen-temen MIPA 42 tercinta: Ulfa, Fefin, Dinar, Sari, Nisa, Dude, Lili, Fuji, Kartika, Eka, Lisma, Ami,Ncun, Puscan, Ratna, Mita, Astri, Oby, Ciciw, Gia, Darti, Amel, Aria, Listi.

9. Teman-teman “Alfarabi” yang telah memberikan bantuan, saran, semangat dan doa. 10.Seluruh mahasiswa FMIPA, kakak kelas dan adik kelas yang telah membantu dan

memberikan semangatnya.

Tentunya begitu banyak nama yang terus menerus memberikan dukungan, pengaruh dan pelajaran yang amat berharga. Namun, tentunya tidak dapat penulis sebutkan pada kesempatan kali ini tanpa mengurangi hormat dan takzim penulis kepada mereka.

Semoga skripsi ini dapat menjadi suatu kontribusi positif dan konstruktif bagi para pembaca, dan tentunya dapat menjadi ilmu yang bermanfaat bagi semuanya.

Bogor, September 2009

RIWAYAT HIDUP

SITI MARIAM, lahir di Bogor 24 Juni 1987 anak keempat dari tujuh bersaudara dari pasangan Tamri dan Sukarsih. Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1999 di SD Negeri 2 Jasinga Kab. Bogor, Sekolah Lanjutan Tingkat Pertama Negeri I Jasinga Kab. Bogor tahun 2002, Sekolah Menengah Atas Negeri I Jasinga Kab. Bogor tahun 2005 dan diterima sebagai mahasiswa Institut Pertanian Bogor melalui jalur USMI pada tahun yang sama. Masuk Departemen Matematika Fakultas Matematika dan IPA Institut Pertanian Bogor tahun 2006.

Selama mengikuti perkuliahan, penulis pernah menjadi pengajar privat mahasiswa Tingkat Persiapan Bersama dan menjadi pengajar SMP dan SMA di Pandu Madania. Selain belajar diperkuliahan banyak juga pelajaran yang didapat dari organisasi yang telah diikuti yaitu : BEM FMIPA sebagai bendahara umum, Serambi Ruhiyah Mahasiswa FMIPA (SERUM-G) sebagai sekretaris divisi relasi, Gugus Mahasiswa Matematika (GUMATIKA) sebagai staff divisi PSDM, kesatuan Aksi Mahasiswa Muslim Indonesia (KAMMI) sebagai staff divisi Pemberdayaan Masyarakat, Forum Ukhuwah Pelajar dan Remaja Jasinga (FUPRJ) sebagai staff divisi PSDM. Selain itu aktif dalam berbagai kepanitiaan yaitu: panitia seminar pekan kreativitas mahasiswa ilmiah (PKMI), panitia seminar nasional kajian ilmu pengetahuan, panitia try out SPMB, panitia G_Force 43 dan 44, panitia Welcome Ceremoni Matematika (WCM) 43 dan 44, panitia bakti sosial Serum-G FMIPA, panitia open house angkatan 43 IPB, panitia Masa Perkenalan Kampus Mahasiswa Baru (MPKMB).

DAFTAR ISI

Halaman Daftar Gambar ... ix Daftar Lampiran ... ix I PENDAHULUAN ... 1 1.1. Latar Belakang ... 1 1.2. Tujuan ... 1 1.3. Sistematika Penulisan ... 1 II LANDASAN TEORI ... 2 2.1 Istilah-istilah Keuangan ... 2

2.2 Percobaan Acak, Ruang Contoh, Medan-σ, Ukuran Peluang, Peubah Acak, Peubah Acak Diskret dan Peubah Acak Kuntinu ... 2

2.3 Nilai Harapan Peubah Acak Diskret, Nilai Harapan Peubah Acak Kontinu, Ragam dan Simpangan Baku ... 3

2.4 Proses Stokastik, Random Walk, ... 3

2.5 Kalkulus Variasi, Syarat Perlu Untuk Optimum, Deret Taylor ... 4

III PEMODELAN ... 6

3.1 Waktu Perdagangan ... 6

Model Waktu Diskret ... 6

Model Waktu Kontinu ... 7

3.2 Formulasi Lagrange ... 7

IV PEMBAHASAN ... 9

4.1 Peningkatan Risiko Perdagangan Konstan ... 10

4.2 Peningkatan Risiko Perdagangan Linear ... 10

V ILUSTRASI ... 11

5.1 Ilustrasi Solusi Peningkatan Risiko Perdagangan Konstan ... 11

5.2 Ilustrasi Solusi Peningkatan Risiko Perdagangan Linear ... 14

5.3 Contoh Penerapan Peningkatan Risiko Konstan ... 15

5.4 Contoh Penerapan Peningkatan Risiko Linear ... 17

VI SIMPULAN ... 18

DAFTAR PUSTAKA ... 19

LAMPIRAN ... 20

DAFTAR GAMBAR

Halaman

Gambar 1 Grafik Hubungan Peningkatan Biaya Likuiditas dengan Waktu Eksekusi

Optimal untuk Peningkatan Risiko Perdagangan Konstan ... 12

Gambar 2 Grafik Hubungan Risiko Volatilitas dengan Waktu Eksekusi Optimal untuk Peningkatan Risiko Perdagangan Konstan ... 12

Gambar 3 Grafik Hubungan Risk Aversion dengan Waktu Eksekusi Optimal untuk Peningkatan Risiko Perdagangan Konstan ... 13

Gambar 4 Grafik Hubungan Waktu Eksekusi dengan Expected Cost yang dipengaruhi oleh Risk Aversion pada Peningkatan Risiko Konstan ... 13

Gambar 5 Grafik Hubungan Waktu Eksekusi dengan Standar Deviasi yang dipengaruhi oleh Risk Aversion pada Peningkatan Risiko Konstan ... 13

Gambar 6 Grafik Hubungan Peningkatan Biaya Likuiditas dengan Waktu Eksekusi yang Optimal untuk Peningkatan Risiko Perdagangan Linear ... 14

Gambar 7 Grafik Hubungan antara Risk Aversion dengan Waktu Eksekusi untuk Peningkatan Risiko Perdagangan Linear ... 14

Gambar 8 Grafik Hubungan antara Risiko Volatilitas dengan Waktu Eksekusi yang Optimal untuk Peningkatan Risiko Perdagangan Linear ... 15

Gambar 9 Grafik Hubungan antara Risk Aversion dengan Banyaknya Saham Optimal untuk Peningkatan Risiko Perdagangan Linear ... 15

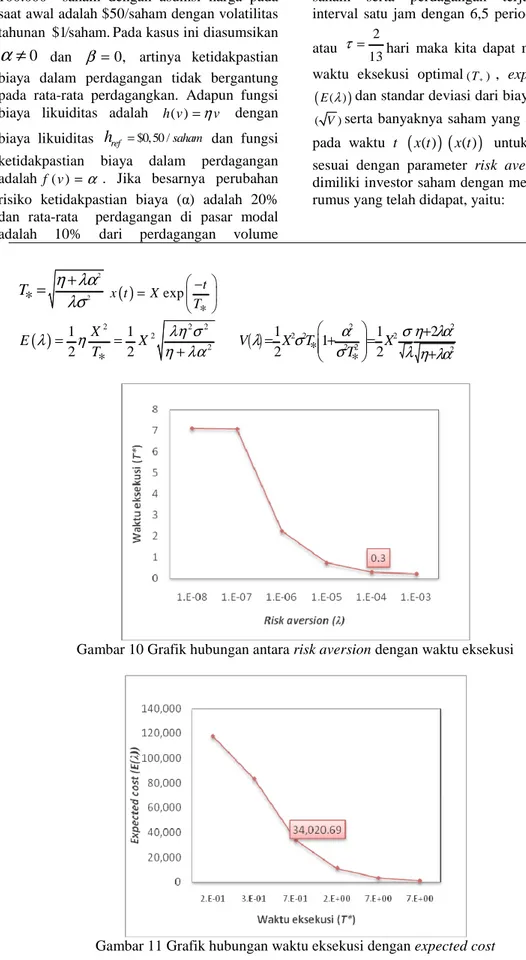
Gambar 10 Grafik Hubungan antara Risk Aversion dengan Waktu Eksekusi pada Contoh Penerapan ... 16

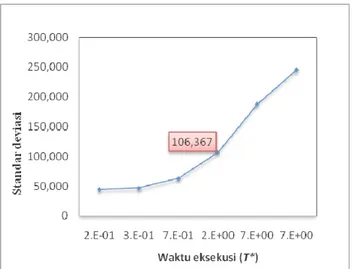
Gambar 11 Grafik Hubungan Waktu Eksekusi dengan Expected Cost pada Contoh Penerapan ... 16

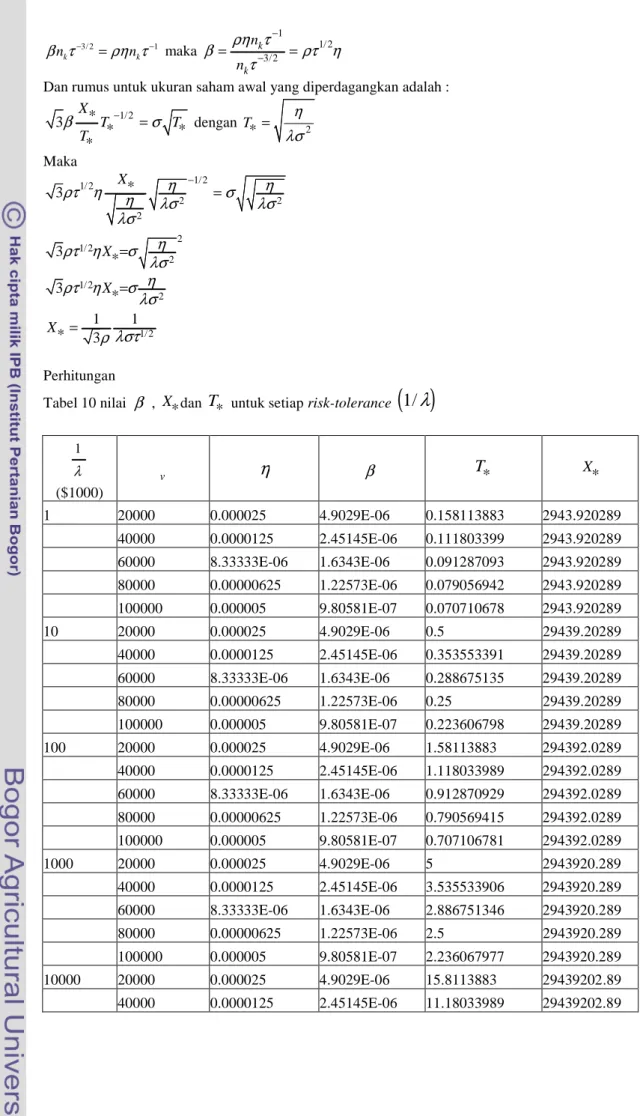
Gambar 12 Grafik Hubungan Waktu Eksekusi dengan Standar Deviasi pada Contoh Penerapan ... 17

DAFTAR LAMPIRAN

Halaman Lampiran 1 Pembuktian Harga Saham Permanen ... 20

Lampiran 2 Pembuktian Nilai Harapan dan Ragam ... 21

Lampiran 3 Pembuktian Persamaan (16) ... 22

Lampiran 4 Pembuktian Persamaan (17) ... 22

Lampiran 5 Pembuktian Persamaan (18) ... 23

Lampiran 6 Pembuktian Solusi Kuadratur ... 24

Lampiran 7 Pembuktian Persamaan (20) ... 24

Lampiran 8 Pembuktian Expected Cost dan Ragam untuk Peningkatan Risiko Perdagangan Konstan ... 25

Lampiran 9 Pembuktian Persamaan (25) ... 28

Lampiran 10 Pembuktian Persamaan (26) ... 28

Lampiran 11 Pembuktian Persamaan (27) ... 29

Lampiran 12 Hasil Penghitungan Ilustrasi ... 30

Lampiran13 Hasil Penghitungan Contoh Penerapan……….. 32

I PENDAHULUAN

1.1 Latar Belakang

Pada dasarnya, pasar modal (capital

market) merupakan pasar untuk berbagai

instrumen keuangan jangka panjang yang bisa diperjualbelikan, baik dalam bentuk utang ataupun modal sendiri. Selain itu, Pasar modal memberikan peran besar bagi perekonomian suatu negara karena pasar modal memberikan dua fungsi sekaligus, yaitu fungsi ekonomi dan fungsi keuangan. Pasar modal dikatakan memiliki fungsi ekonomi karena pasar modal menyediakan fasilitas atau wahana yang mempertemukan dua kepentingan yaitu pihak yang memiliki kelebihan dana (investor) dan pihak yang memerlukan dana (issuer). Pasar modal dikatakan memiliki fungsi keuangan karena pasar modal memberikan kemungkinan dan kesempatan memperoleh imbalan (return) bagi pemilik dana, sesuai dengan karakteristik investasi yang dipilih.

Salah satu produk yang diperjualbelikan di pasar modal adalah saham yaitu sebagai tanda penyertaan atau kepemilikan seseorang atau badan dalam suatu perusahaan. Wujud saham berupa selembar kertas yang menerangkan pemiliknya.

Para investor yang bermain di pasar modal, khususnya saham, pasti memiliki motivasi yang sama yaitu mendapatkan tingkat pengembalian (expected return) yang besar. Tetapi hukum investasi yang tidak dapat dipungkiri adalah semakin tinggi tingkat pengembalian akan semakin tinggi pula risiko yang harus diambil. Risiko adalah selisih antara tingkat pengembalian aktual dengan tingkat pengembalian yang diharapkan. Para investor dapat mengelompokkan risiko tersebut menjadi dua kelompok besar yaitu risiko sistematis dan risiko nonsistematis. Risiko sistematis merupakan sebuah risiko yang secara sistematis akan terjadi dan tidak dapat dihindari oleh para investor dan risiko ini dikenal juga dengan risiko pasar. Salah satu risiko sistematis ini yaitu risiko likuiditas. Biaya likuiditas adalah besarnya biaya yang harus dikeluarkan untuk mengubah suatu sekuritas menjadi kas atau sebaliknya. Biaya likuiditas merupakan ukuran likuiditas pasar yang mencerminkan biaya yang dihadapi oleh penjual. Sedangkan risiko nonsistematis adalah risiko yang terjadi tidak secara sistematis dan biasanya dapat dihindari. Risiko ini dapat juga disebut dengan risiko perusahaan. Risiko ini dapat dihindari oleh

perusahaan yang bersangkutan. Salah satu risiko nonsistematis adalah risiko ketidakpastian (volatility risk).

Pengelolaan risiko sangat penting supaya tidak terjadi pemusnahan terhadap apa yang diinvestasikan. Dalam menghitung risiko tersebut dikenal dengan simpangan baku (standard of deviation). Risiko tidak mungkin dihilangkan 100% tetapi hanya dapat diminimumkan atau dibuat sekecil mungkin sampai batas tertentu yaitu dengan mengelola risiko secara baik. Sehingga permasalahan yang muncul adalah bagaimana meminimumkan biaya yang dikeluarkan ke dalam kegiatan transaksi yang akan dilakukan dengan mengoptimalkan banyaknya saham yang diperdagangkan dengan kendala suatu risiko (volatility) yang harus dihadapi. Risiko yang akan dibahas adalah risiko ketidakpastian biaya eksekusi dalam tingkat perdagangan.

1.2 Tujuan

Tujuan dari penulisan karya ilmiah ini adalah untuk mempelajari strategi perdagangan saham yang optimal dengan menentukan banyaknya saham pada waktu t yang akan dijual dan banyaknya saham awal optimal yang diperdagangkan serta waktu optimal eksekusi saham dengan asumsi biaya likuiditas merupakan fungsi linear dan kendala yang dihadapi adalah risiko ketidakpastian biaya likuiditasi.

1.3 Metode dan Sistematika Penulisan

Metode Penulisan karya ilmiah ini adalah studi pustaka yang materinya diambil dari jurnal yang berjudul “Optimal Execution with

Nonlinear Impact Functions and Trading-Enhanced Risk” oleh Robert F. Almgren

tahun 2001.

Karya ilmiah ini terdiri atas tujuh bagian. Bagian pertama berisi pendahuluan yang terdiri atas latar belakang, tujuan, metode dan sistematika penulisan. Bagian kedua adalah landasan teori yang menjadi dasar penulisan karya ilmiah ini. Bagian ketiga adalah pemodelan yang akan dipakai. Bagian keempat pembahasan yang merupakan hasil analisis terhadap karya ilmiah ini. Bagian kelima adalah ilustrasi. Bagian keenam adalah kesimpulan, dan bagian ketujuh adalah daftar pustaka.

II LANDASAN TEORI

Landasan teori menyajikan hal-hal yang

menjadi dasar penulisan karya ilmiah ini, ditampilkan dalam bentuk definisi-definisi dasar, Lema dan beberapa teorema penting.

2.1.Istilah-istilah keuangan

Definisi 1 Aset Real dan Aset Keuangan

Aset real adalah aset yang menentukan kekayaan suatu perekonomian suatu perusahaan sedangkan aset keuangan adalah aset yang menunjukkan klaim atas aset real.

(Bodie, Kane, dan Marcus, 2006)

Definisi 2 Sekuritas

Sekuritas adalah surat berharga atau instrumen keuangan yang telah distandarisasi dan dijaga nilai-nilainya sehingga mempunyai kemampuan jual beli atau likuid.

(Bodie, Kane, dan Marcus, 2006)

Definisi 3 Saham

Saham adalah tanda penyertaan atau kepemilikan seseorang atau badan dalam suatu perusahaan atau perusahaan terbatas. Wujud saham berupa selembar kertas yang menerangkan siapa pemiliknya.

(Bodie, Kane, dan Marcus, 2006)

Definisi 4 Volatilitas (Volatility)

Volatilitas σ menyatakan tingkat risiko suatu aset yang ditunjukkan oleh keacakan harga saham. Semakin besar nilai volatilitas, semakin tak terduga pergerakan harga saham. Sebaliknya semakin kecil nilai volatilitas, semakin mudah untuk menduga harga saham tesebut.

(Harvey & Gretchen 2002)

Definisi 5 Risiko Perdagangan

Risiko Perdagangan merupakan besarnya penyimpangan antara tingkat pengembalian yang diharapkan (expected return) dengan tingkat pengembalian aktual (actual return)

(Widoatmodjo Sawidji. 2005)

Definisi 6 Volume Perdagangan

Volume perdagangan adalah jumlah satuan unit saham yang diperjualbelikan dalam suatu periode tertentu, biasanya harian.

(Bodie, Kane, dan Marcus, 2006)

2.2 Percobaan Acak, Ruang Contoh, Medan-σ , Ukuran Peluang, Peubah Acak,

Peubah Acak Kontinu, Peubah Acak Diskret

Definisi 7 Percobaan Acak

Dalam suatu percobaan sering kali dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul dapat diketahui, tetapi hasil pada percobaan berikutnya tidak dapat diduga dengan pasti. Percobaan yang semacam ini disebut percobaan acak.

(Grimmett dan Stirzaker, 1992)

Definisi 8 Ruang Contoh

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω. Suatu kejadian adalah himpunan bagian dari Ω.

(Grimmett dan Stirzaker, 1992

Definisi 9 Medan-σ

Medan–σ adalah suatu himpunan F yang anggotanya terdiri atas himpunan bagian ruang contoh Ω, yang memenuhi kondisi berikut: 1.

φ ∈

F

2. jika

A A

₁

,

₂

,...

∈

F

maka 1 i i A F ∞ = ∈ U 3. jika

A F

∈

maka c A∈F

(Grimmett dan Stirzaker, 1992)

Definisi 10 Ukuran Peluang

Misalkan F adalah medan-σ dari ruang contoh Ω. Ukuran peluang adalah suatu fungsi P F: →[0,1] pada ( , )Ω F yang memenuhi :

1. ( )Pφ =0 dan P(Ω =) 1

2. Jika

A A

₁

,

₂

,...

∈

F

adalah himpunan yang saling lepas yaitu Ai∩Aj =

φ

untuk setiap pasangan i≠ j, maka ). ( 1 1 P A_i P A_i i i ∞ ∞   = ∑   =  U₌ 

(Grimmett dan Stirzaker, 1992)

Definisi 11 Peubah Acak

Misalkan F adalah medan-σ dari ruang contoh Ω. Suatu peubah acak X adalah

suatu fungsi X → Ω ℜ: dengan sifat

{

ω

∈ Ω:X( )

ω

≤ x

}

∈F untuk setiap x∈ℜ. (Grimmett dan Stirzaker, 1992)

Definisi 12 Peubah Acak Diskret

Peubah acak X dikatakan peubah acak diskret jika nilainya hanya pada himpunan bagian yang terbilang dari ℜ.

Catatan:

Suatu himpunan bilangan C disebut terbilang, jika C terdiri atas bilangan terhingga atau anggota C dapat dipadankan 1-1 dengan bilangan bulat positif.

(Grimmett dan Stirzaker, 1992)

Definisi 13 Peubah Acak Kontinu

Peubah acak X dikatakan kontinu jika terdapat fungsi f_X( )x sehingga fungsi

sebaran FX( )x = P X( ≤ x) dapat dinyatakan sebagai:F_X( )x f t dt x_x( ) ,

∞ −∞

=

_∫

∈ℜ untuk suatu fungsi f :R→[0,∞) adalah fungsi yang terintegralkan. Fungsi f disebut fungsi kepekatan peluang bagi X

(Grimmett dan Stirzaker, 1992)

2.3 Nilai Harapan Peubah Acak Diskret, Nilai Harapan Peubah Acak Kontinu, Ragam dan Simpangan Baku

Definisi 14 Nilai Harapan (Expected Value) Peubah Acak Diskret

Jika X adalah peubah acak diskret dengan

fungsi massa peluang ( )

X

p x , maka nilai harapan dari X dinotasikan dengan E X( )

( )

( ) _X

x

E X =

∑

xp x

Asalkan jumlah di atas konvergen mutlak (Grimmett dan Stirzaker, 1992)

Definisi 15 Nilai Harapan Peubah Acak Kontinu

JikaX adalah peubah acak kontinu dengan fungsi kepekatan peluang

f

_X

( )

x

, maka nilai harapan dari Xadalah

( ) _X( )

E X x f x

∞ −∞

= ∫

asalkan integral di atas konvergen mutlak.

(Grimmett dan Stirzaker, 1992)

Lema 1 (Sifat Nilai Harapan)

Beberapa sifat nilai harapan, antara lain: 1) Jika k adalah suatu konstanta, maka

( )

k k.

E =

2) Jika k adalah suatu konstanta dan V adalah peubah acak, maka

( )

kV kE

( )

V

E = .

3) Jika k₁,k₂ adalah konstanta dan

2

1,V

V adalah suatu peubah acak, makaE

(

k₁V₁+k₂V₂

)

=k₁E

( )

V₁ +k₂E

( )

V₂ . (Bukti: lihat Hogg & Craig 1995)

(Hogg dan Craig, 1995)

Definisi 16 Ragam dan Simpangan Baku

Misalkan X adalah peubah acak (diskret atau kontinu). Ragam X atau var ( )X

dinotasikan dengan 2 X σ dengan

(

)

2

(

)

2 2 2 . [ ( ) ] ( ) ( ) X E X E X E X E X σ = − = −

Standar deviasi X, dinotasikan dengan σ_X, didefinisikan

2

.

X X

σ = σ

(Hogg dan Craig, 1995) Lema 2 (sifat Ragam)

Beberapa sifat dari ragam, antara lain : 1. jika k suatu konstanta, maka

2

( ) ( )

Var kX =k Var X

2. jika k suatu konstanta dan X , ₁ X ₂

adalah peubah acak, maka

(

)(

)

2 1 1 2 2 1 1 2 2 2 1 2 1 1 2 2 ( ) ( ) ( ) 2 ( ( ) ( ( ) Var k X k X k Var X k Var X k k E X E X X E X + = + + − − (Ghahramani, 2000)

2.4 Proses Stokastik, Random Walk Definisi 17 Proses Stokastik

Proses stokastik X ={ ( ),X t t∈T} adalah suatu koleksi (gugus, himpunan atau kumpulan) dari peubah acak yang memetakan suatu ruang contoh Ω ke suatu ruang state

.

S

Catatan:

Suatu proses stokastik X disebut proses stokastik diskret (discrete-time stochastic

process) jika gugus indeks T adalah gugus

tercacah (countabel set), sedangkan X disebut proses stokastik kontinu (continuous-time

stochastic process) jika T adalah suatu

interval.

(Grimmet and Stirzaker, 2001)

Definisi 18 Random Walk

Random Walk adalah suatu rantai

Markov dengan state (ruang state) adalah himpunan bilangan bulat dan mempunyai peluang transisi

, 1 1 , 1 ; 0, 1, 2,....

i i i i

P ₊ = = −P P ₋ i= ± ± , dengan 0< <P 1. Dengan kata lain setiap transisi perubahan akan bergerak satu langkah ke kanan dengan peluang P atau bergerak satu langkah ke kiri dengan peluang 1-P.

(Ross, 2000)

2.5 Kalkulus Variasi, Syarat Perlu Untuk Optimum, Deret Taylor

Kalkulus Variasi

Kalkulus variasi adalah salah satu cabang matematika yang berhubungan dengan masalah memaksimumkan atau meminimumkan fungsional (Tu 1983). Dalam masalah kalkulus variasi tujuannya adalah untuk memaksimumkan atau meminimumkan fungsi objektif:

( )

( )

(

( ) ( )

, ,

)

b a J x t =

∫

f x t x t& t dt, dengan fungsi kendala atau tanpa kendala. Fungsi kendala dapat berupa persamaan diferensial parsial atau persamaan aljabar, misalkannyax&= f x t x t t

(

( ), ( ),&

)

. Fungsional memiliki peranan penting dalam kalkulus variasi. Fungsional, misalkannya

( )

b

( )

a

J x =

∫

x t dt (1) adalah suatu aturan yang mengaitkan tiap fungsi x∈ℜ dengan J x

( )

. Terdapat analogi antara fungsi dengan fungsional. Argumen dari fungsi merupakan peubah, misalkannya

( )

x=x t . Sedangkan argumen dari fungsional merupakan fungsi. Dalam mempelajari fungsi, kita tertarik untuk menemukan titik yang memberikan ekstremum untuk fungsi, sedangkan dalam pembahasan fungsional kita tertarik untuk menemukan fungsi yang memberikan ekstremum untuk fungsional.

Variasi dari fungsional J x

( )

adalah

( ) (

) ( )

J x J x δx J x

∆ = + − . Dengan mengambil

x h

δ = sembarang fungsi, maka dengan menggunakan ekspansi deret taylor diperoleh

(

)

(

)

(

)

(

)

(

)

0 0 0 2 2 2 0 , , , , 1 2 2 T T T T x x xx xx xx J x h f x h x h t dt f x x t dt hf hf dt h f hhf h f dt h + = + + = + + + + + + Ο

∫

∫

∫

∫

&

& & &

& & & & & &

(

)

0 ( ) , , T J x =

∫

f x x t dt&

(

)

0 ( ) T x x J x h f h f dt ∂ =

_∫

+& &

(

)

2 2 2 0 1 ( ) 2 2 T xx xx xx J x h f hhf h f dt

∂ =

_∫

+ & &+ & & &

dengan:

(

, ,

)

x f x x t f x ∂ = ∂ &

(

, ,

)

x f x x t f x ∂ = ∂ & & & . dh h dt = & Maka

(

)

₂ 2 ( ) ( ) ( ) J x h+ =J x +

δ

J x +

δ

J x + Ο h sehingga diperoleh 2 2 ( ) ( ) ( ) J x δJ x δ J x h ∆ = + + Ο (2) 2 h

Ο adalah simbol yang mewakili orde lebih tinggi. Notasi δJ x( ) disebut variasi pertama dan δ2_{J x( ) disebut variasi kedua.} Variasi pertama berperan sebagai syarat perlu agar J(x) maksimum,δJ x( )=0.

(Tu, 1983)

Definisi 19 Syarat Perlu Untuk Optimum (Persamaan Euler)

Perhatikan masalah variasi dalam bentuk sederhana,

( )

(

)

0 , , T J x =

∫

f x x t dt& , (3) dengan titik ujung A

(

0, (0)x

)

dan

(

, ( )

)

B T x T adalah tetap,

(

) ( )

2

[ ]

, , , 0, f x x t& x t ∈C T , dt dx x&= _{x adalah}

fungsi bernilai scalar dan C2adalah semua fungsi yang didefinisikan di selang [0,T] dan memiliki turunan ke-2 yang kontinu. Permasalahan adalah memilih *_{( )}

x t yang memberikan nilai maksimum atau nilai minimum untuk fungsional J(x).

Syarat perlu untuk adanya ekstremum adalah δJ x( )=0. Misalkan

( )

0 ( ) ( ) , T J x g t h t dt ∂ =

_∫

(4) dengan g t( )∈C

[ ]

0,T dan h(t) fungsi sembarang dan kontinu. Untuk T dan kedua titik ujung peubah x(t) ditentukan, h(t) memiliki sifat h(0)=0=h(T).

Lema 3

Misalkan g t( ) sebarang fungsi yang kontinu pada

( )

0,T dan S merupakan himpunan dari sebarang fungsi h(t) yang kontinu dan terdiferensialkan pada

[ ]

0,T sehingga h(0)=0=h(T) dengan T ditentukan.

Jika

( )

0 ( ) 0 T g t h t dt=

∫

, (5) untuk semua h t( )∈S maka g t( )=0 untuk

semua t∈

[ ]

0,T

(Bukti: lihat Tu, 1983)

Solusi dari masalah kalkulus variasi diberikan oleh suatu bentuk persamaan Euler yang merupakan syarat perlu untuk menentukan nilai ektremum.

Teorema 2 Misalkan

( )

(

)

0 , , T J x = ∫ f x x t dt& terdefinisi pada

[ ]

0, T dan memenuhi syarat batas

0

(0)

x = x dan x T( )=x_T. Syarat perlu agar

J(x) mempunyai nilai ekstrem adalah x(t)

memenuhi persamaan berikut: 0 x x d f f dt − & = . (6) (Bukti: lihat Tu, 1983)

Definisi 20 Deret Taylor

Jika suatu fungsi

y

=

f x

( )

memiliki turunan ke-n maka fungsi tersebut memiliki ekspansi deret Taylor.

(

)

( ) ( ) 2

( )

3

( )

2! 3! h h f x h+ =f x +h f x′ + f′′ x + f′′′ x +Lya ng setara dengan

( )

1

( )

( )

2

( )

2! n n n n h f x+ = f x +hf′ x + f′′ x

( )

( )

_{( )}

( )

3 1 3! ! p p p n n h h f x f x h p + ′′′ + + +L + Ο (7) dengan

h

=

x

_n+1

−

x

_n. (Fisher, 1998)

III PEMODELAN

Suatu permasalahan dalam matematika

dapat disederhanakan dalam bentuk model. Model tersebut dapat merepresentasikan kondisi sebenarnya. Langkah awal pembentukan model adalah dengan memberikan variabel-variabel yang akan digunakan dan asumsi-asumsi awal.

Berikut adalah variabel-variabel yang akan digunakan:

t : waktu eksekusi saham dengan

t

=

0

adalah waktu awal eksekusi dan t=T adalah waktu akhir eksekusi

X : kepemilikan saham awal yang akan dieksekusi secara lengkap pada waktu t=T dengan X =x₀

*

X : _{banyaknya saham optimal yang} diperdagangkan

σ

: risiko volatilitas ( )

f v : fungsi ketidakpastian harga

( )

h v : dampak temporer (biaya

likuiditas) ( )

g v : dampak permanen (pengaruh harga

saham akibat informasi perdagangan)

k

S%

_{: harga saham sebenarnya pada} perdagangan ke-k ( ) E x : expected cost ( ) V x _{: standar deviasi} ( )

x t : banyaknya saham pada waktu t,

dengan (0)x = X dan ( )x T =0

0

τ

>

: interval perdagangan

k

k

t

=

τ

_{: waktu diskret perdagangan untuk} k=0,1, 2, 3,....N

k

n

_{: banyaknya saham yang terjual} antara waktu t_k−1 sampai t _k

Adapun asumsi-asumsi yang dipergunakan dalam pemodelan masalah ini:

1. Model karya tulis ini mengikuti kerangka dari Almgren dan Chris (2000).

2. Kasus yang dihadapi merupakan kasus penjualan, sehingga X >0. 3. Perdagangan berupa aset tunggal

(saham) bukan portofolio.

Kasus yang dihadapi adalah kasus penjualan maka pemodelan ini dibangun dari sudut sebagai penjual yang berupaya

menentukan fungsi optimal x t , ( ) X_*

,

danT_*

agar diperoleh suatu pilihan biaya fungsional yang meminimumkan biaya transaksi.

Strategi perdagangan dalam transaksi suatu saham sangat diperlukan dengan tujuan agar saham yang dimiliki atau kepemilikan saham menjadi likuid. Likuiditas dari suatu saham dapat diukur dari biaya likuiditas. Biaya likuiditas ini merupakan biaya yang akan dihadapi oleh penjual. Oleh karena itu, permasalahan yang dihadapi adalah bagaimana meminimumkan biaya likuiditas (expected cost) pada akhir perdagangan. Permasalahan tersebut dibentuk menjadi sebuah model yang melibatkan unsur waktu.

Pada karya ilmiah ini pelaksanaan optimal lebih dititikberatkan pada kepemilikan saham dan waktu akhir, sehingga permasalahannya menjadi berapa banyak kepemilikan saham yang dimiliki pada waktu t, yaitu x t( ), banyaknya saham awal yang diperdagangkan yaituX∗ dan waktu akhir yang optimal, yaitu

*

T , agar tercapai kondisi yang diinginkan yaitu biaya likuiditas yang dikeluarkan minimum pada akhir perdagangan.

3.1 Waktu Perdagangan A. Model Waktu Diskret

Dalam model waktu diskret saham diperdagangkan dalam interval waktu τ yaitu pembagian waktu per periode dengan

k

t

=

k

τ

yang menyatakan waktu pada saat periode ke-k untuk k =0,1, ...,N dengan

T N

τ

= sehingga jika X adalah banyaknya saham yang dimiliki pada t=0 maka

x

k menyatakan banyaknya saham yang dimiliki pada waktu t_k dengan x₀ = X dan

x

_N

=

0

Dalam model ini diasumsikan bahwa saham diperdagangkan dalam waktu antara

1

k

t _{− dan}

k

t sehingga n_k menyatakan banyaknya saham yang terjual dalam waktu antara t_k−₁dan tkatau nk =xk−1−xk dan

rata-rata perdagangan adalah banyaknya saham yang terjual per satuan waktu. Sehingga kita dapat memodelkan banyaknya saham pada waktu ke-k sebagai berikut:

1 1 , k N k j j k x X n_j n_j = = + = −∑ = ∑ (8)

Harga saham dari aset yang tersedia dipasar dipengaruhi oleh informasi perdagangan yang bersifat acak dengan biaya informasi yang diperoleh disebut biaya dampak permanen, sehingga untuk menentukan harga saham dari aset yang tersedia dipasar akibat pengarus dampak permanen dapat dicari dengan aritmatik

random walk, yaitu: 1 2 1 k k k k n S S στ ξ τg τ − = + −













(9)

dengan

ξ

j~N(0,1) adalah peubah acak bebas dan σ merupakan risiko volatilitas. Persamaan (9) di atas dapat ditulis dalam bentuk sebagai berikut:

( )

1 2 0 1 1 k k k j j j j S S στ ξ τ g v = = = + ∑ − ∑

(Bukti: lihat Lampiran1)

Selain informasi perdagangan, harga saham dipengaruhi juga oleh biaya dampak temporer yaitu biaya yang harus dikeluarkan untuk mengubah saham menjadi kas atau disebut biaya likuiditas, sehingga harga sebenarnya yang didapatkan pada perdagangan ke-k akibat pengaruh dari dampak temporer dapat dimodelkan sebagai berikut: 1 2 1 k k k k k n n S S h

τ

f

ξ

τ

τ

− −     = −  +       % % ₍₁₀₎

Total uang yang diterima dalam waktu

ke-k adalah penjumlahan dari perkalian banyaknya saham yang terjual dengan harga sebenarnya yang didapatkan pada perdagangan ke-k yang dimodelkan dalam bentuk:

( )

( )

( )

1 2 1 2 1 0 1 1 1 1 1 . (11) N N N k k k k k k k k k N N k k k k k k k n S XS x x g v v h v v f v στ ξ τ τ τ ξ − − = = = = = = + − ∑ ∑ ∑ − ∑ + ∑ % %

Dari persamaan (9) dan (10) di atas dapat disimpulkan bahwa biaya transaksi meliputi biaya informasi, biaya likuiditas dan ketidakpastian biaya likuiditas pada perdagangan, sehingga biaya transaksi dapat dimodelkan sebagai berikut:

0 k k XS −∑n S%

Nilai harapan dan ragam pada saat t=0 bergantung pada parameter bebas

1, 2,..., n 1

x x x₋ pada strategi perdagangan dan dapat dituliskan sebagai berikut.

(

1 2 1

)

( )

( )

1 1 , ,...n N k k N k k k k E x x x₋ x g v τ v h v τ = = =∑ +∑ (12) dan

(

)

( )

2 2 2 2 1 2 1 1 1 , ,..._n N _k N k k V x x x₋ σ x v f v_{k k} τ = = =∑ +∑ (13) (Bukti: lihat Lampiran 2)

B. Model waktu kontinu

Untuk kebutuhan analisis waktu kontinu maka persamaan-persamaan yang ada pada model waktu diskret diubah dalam model waktu kontinu dengan τ→0, x menjadi _k

( )

x t

, dan

n

_k tetap berlaku sehingga

( )

,

k

v

→

v k

τ

karena _v nk τ = dan 1 k k k n =x₋ −x maka 1 ( 1) k k k k k n x x x x x v x t τ −τ τ − − − − ∆ = = = = − = − ∆ &

maka v t

( )

= −x t&

( )

, sehingga persamaan (12) dan (13) dapat dituliskan dalam persamaan sebagai berikut:

( ) ( )

( )

( ) ( )

( )

(

)

0 ( ) T E x =∫ x t g v t +v t h v t dt (14)

( )

( )

( )

( )

(

2 2 2 2

)

0 ( ) . T V x =∫ σ x t +v t f v t dt (15) Seorang penjual yang rasional akan membuat strategi perdagangannya dengan meminimumkan E dengan kendala V.

3.2 Formulasi Lagrange

Masalah optimisasi yang akan dibahas pada karya ilmiah ini adalah mencari strategi perdagangan yang meminimumkan biaya transaksi. Biaya likuiditas merupakan biaya yang harus dikeluarkan untuk mengubah suatu saham menjadi kas atau sebaliknya. Untuk pengoptimalan strategi perdagangan, para penjual meminimumkan biaya likuiditasnya dengan mengasumsikan bahwa transaksi saham yang tidak pasti (risiko ketidakpastian) merupakan kendala yang mendukung model ini.

Suatu masalah pengoptimuman didefinisikan mempunyai bentuk sebagai berikut: Minimumkan

( )

( )

( )

( )

( )

( )

(

)

0 ( ) T E x =∫ x t g v t +v t h v t dt terhadap

( )

( )

( )

( )

(

2 2 2 2

)

0 ( ) T . V x =∫ σ x t +v t f v t dt

Salah satu metode yang dapat digunakan untuk menyelesaikan masalah di atas adalah metode pengali Lagrange. Metode ini dimulai

dengan mendefinisikan fungsi Lagrange sebagai berikut: U x( )=E x( )+λV x( )

( )

( )

( )

( ) ( )

( )

(

)

(

2

( )

2

( )

2

( )

( )

2

)

0 0 T T x t g v t v t h v t dt

λ σ

x t v t f v t dt =∫ + + ∫ +

( ) ( )

( )

( ) ( )

( )

( )

( )

( )

( )

(

₂ 2 2 2

)

0 T

x t g v t

v t h v t

λσ

x t

λ

v t

f v t

dt

=

_∫

+

+

+

dengan

λ

merupakan pengali Lagrange untuk kendala dari masalah pengoptimuman

Untuk meminimumkan U x ( ) maka digunakan metode kalkulus variasi yaitu

( )0

(

( )

( )

)

min , .

T

F x t x t dt

x t ∫ −&

Bentuk fungsional objektifnya adalah

( )

()

(

(), ()

)

. 0 dt t x t x F t x U T

∫

− = &

Formulasi fungsional objektif tersebut merupakan formulasi Lagrange, sehingga

(

( ), ( )

)

( )

( )

( )

( )

( )

( )

F x t v t

=

x t g v t

+

v t h v t

+λσ2x t

( )

2+λv t

( )

2 f v t

( )

( )

2

dan secara sederhana dapat dituliskan menjadi

( )

( ) ( )

_{2 2 2}

( )

2 , F x v =xg v +vh v +

λσ

x +

λ

v f v

(

) ( ) ( )

_{2 2 2}

( )

2

,

.

F x x

− = − − − +

&

xg x

&

xh x

&

&

λσ

x

+

λ

x f

&

−

x

&

Dalam kalkulus variasi syarat perlu fungsional objektif memiliki nilai minimum adalah

( ) 0

U x

δ = . Nilai

δ

U x( ) adalah variasi pertama yang diperoleh dengan menggunakan ekspansi Taylor sebagai berikut:

(

x h

)

F

(

x h x h

)

dt U T

∫

+ − + = + 0 , & &

(

)

(

)

0 0 , T T x x F x x dt hF hF₋ dt

=

∫

−& +

∫

−& & +

(

2 2

)

2 0 ( ) ( )( ) 1 2 2 T xx x x x x h F − hhF ₋ +h F_{− −} dt+Οh

∫

& & & & &

(

x x

)

dt F x U T

∫

− = 0 , ) ( & .

(

)

0 ( ) T x x U x hF hF₋ dt ∂ =

_∫

−& &

(

)

2 2 2 0 ( ) ( )( ) 1 ( ) 2 2 T xx x x x x U x h F hhF ₋ h F_{− −} dt

∂ =

_∫

− & & +& & &

(

)

x x x F Fx ∂ − ∂ = , &,

(

)

) ( , x x x F F_x & & & − ∂ − ∂ = − dt dh h&= maka

(

x h

)

U + =U

( ) ( ) ( )

x +φh +Qh +Οh 2

(

x h

) ( )

U x U + − =φ

( ) ( )

h +Qh +Οh 2 sehingga diperoleh

( ) ( )

2 2 2 ) ( ) ( ) ( h x U x U h h Q h x U Ο + δ + δ = Ο + + φ = ∆

dengan φ

( )

h merupakan suku-suku linear dalam deret Taylor yang kita sebut dengan variasi pertama δU(x) dan Q

( )

h adalah suku-suku kuadrat yang mengindikasikan variasi kedua 2 ( )

x U

δ dan Οh2 adalah simbol yang mewakili orde lebih tinggi. Sehingga syarat perlu agar U

( )

x minimum adalah δU x( )=0, sehingga

(

)

(

)

0 0 , , 0 T T x x F x−x hdt− F₋ x−x hdt=

∫ & ∫ & & &

0 0 T x x hF hF₋ dt  ₋  ₌ ∫  & & 0 0 0 T T x x h F dt− h F dt₋ = ∫ ∫& &

dengan metode integral parsial persamaan tersebut dapat dituliskan sebagai berikut:

0 0 0 0. T T T x x x d hF dt hF F hdt dt − −  _{ }  − −   =    

∫

&

∫

&

Karena fungsi h merupakan fungsi kontinu dan terturunkan yang bersifat

( )

0 0

( )

h = =h T 0 0 0 0 0 0 T T T x x x x d hF dt F hdt dt d F F hdt dt − −   − + = ∫ ∫       + = ∫     & &

0. x x d F F dt − + & =

Karena v= −x& , maka dapat dituliskan 0 x v d F F dt + =

(

,

)

(

,

)

0. x v d F x x F x x dt = −& + −&

Berdasarkan aturan rantai diperoleh

(

,

)

(

,

)

(

,

)

0

F_x x −x& +xF& _xv x −x& −xF&& _xv x −x& =

0.

x xv _vv

F +xF& −xF&& = (16) (Bukti: lihat Lampiran 2)

Persamaan (16) merupakan bentuk persamaan diferensial parsial orde dua, yang dapat diselesaikan dengan menggunakan nilai awal, sehingga diperoleh x t

( )

. Karena pada kasus ini, fungsi objektif tidak mengandung

t _{secara eksplisit, maka persamaan (16) dapat}

dikalikan dengan x&, sehingga diperoleh persamaan sebagai berikut:

(

)

2 0 0 x vx vv v F x x F xxF d F xF dt + − = ⇔ + =

& & &&& & dengan

( _v) ( , ) _v( , )

d d d

F xF F x x x F x x

dt +& =dt − +& &dt −&

( )

x x v vx xv

F x F₋ x xF x F x F₋ x

= &− &&&+&& +& &− & &&

x x v vx xv

F x F₋ x xF xF x xF₋ x = &− &&&+&& +& &−& & &&

2

x vx xv

F x x F xF₋ x = &+& −& & &&

Ini berarti bahwa

v

F+xF& =c, dengan c adalah suatu konstanta,

sehingga dapat dituliskan dalam persamaan berikut:

( )

( )

2 2 2

( )

2

(

( )

( ) ( )

₂ 2

( ) ( )

₂

( )

2

)

c=xg v +vh v +λσ x +λv f v +x xg v& ′ +vh v′ +h v + λv f v f′ v + λf v v

( )

( )

2 2 2

( )

2

( )

( )

( )

2

( ) ( )

( )

2

2 2 (17)

c=xg v +vh v +

λσ

x +

λ

v f v +xxg v& ′ +xvh v& ′ +xh v& +

λ

xv f v f v& ′ +

λ

xvf v&

(Bukti: lihat Lampiran 4) Persamaan (17) dapat dipisah dalam

bentuk

( ) ( )

( )

2 2

0

P − −x& P v =xg − +x& xxg& ′+λσ x

dan

( )

v v h

( )

v v

(

f

( )

v vf

( ) ( )

v f v

)

P = 2 ′ +λ 2 2+2 ′ v2 d

(

h v

( )

vf v

( )

2

)

dv λ = + (18) (Bukti: lihat Lampiran 5)

Dampak permanen merupakan fungsi linear terhadap banyaknya saham pada perdagangan awal, yaitu misalkan g v( )=γX,

dengan

γ

X adalah total biaya yang bebas

terhadap x t( )maka solusi umum dari persamaan

( ) ( )

( )

( )

2 2

0

P − −x& P v =xg − +x& xxg& ′ − +x& λσ x

adalah persamaan kuadratur yaitu:

( )

(

)

dx t v P x P X t x = +

∫

− ) ( 0 2 2 1 1 λσ (19) (Bukti: lihat Lampiran 6)

selanjutnya persamaan (19) akan digunakan untuk menentukan solusi umum dari banyaknya saham pada waktu t yang akan

dijual dan waktu eksekusi optimal.

IV PEMBAHASAN

Telah disebutkan di atas bahwa biaya transaksi terdiri atas biaya likuiditas, biaya informasi dan risiko ketidakpastian biaya likuiditas. Dalam karya ilmiah ini diasumsikan bahwa biaya informasi pada umumnya merupakan dampak yang kecil, sehingga dapat dianggap tidak berpengaruh pada strategi optimal yang akan ditentukan artinya g v( )=0. Adapun fungsi biaya

likuiditas dan risiko ketidakpastian biaya likuiditas dituliskan dalam persamaan berikut:

( )

h v

=

η

v

( )

f v

= +

α β

v

dengan v≥0 untuk rata-rata perdagangan,

( )

h v adalah dampak temporer linear yang menunjukkan fungsi biaya likuiditas dengan koefisien ηadalah perubahan biaya likuiditas

akibat perubahan rata-rata perdagangan, sedangkan fungsi f v menunjukkan fungsi ( ) risiko ketidakpastian biaya likuiditas dalam perdagangan dengan αadalah suatu konstanta yang menggambarkan ketidakpastian biaya dalam perdagangan dan tidak bergantung pada rata-rata penjualan, sedangkan βadalah koefisien yang menggambarkan perubahan ketidakpastian biaya akibat perubahan rata-rata perdagangan.

Minimumkan total risiko dengan membagi perdagangan dalam beberapa bagian yang sama, maka dengan

x

&

=− ≤

v

0

persamaan (18) menjadi:

( )

(

2

)

2 3 2 4 4 3 P v = η λα+ v + λαβv + λβ v ₍₂₀₎ (0 ) 0 , P = P v

( )

meningkat untuk v≥0_.

(Bukti: lihat Lampiran 7)

4.1Peningkatan Risiko-Perdagangan Konstan

Kasus ini diasumsikan

β

=0 artinya ketidakpastian biaya likuiditas dalam perdagangan tidak bergantung pada rata-rata perdagangan sehingga dari persamaan (20) dengan menggunakan solusi pada persamaan (19) diperoleh solusi optimal untuk banyaknya saham pada waktu t dan solusi optimal untuk waktu eksekusi saham adalah sebagai berikut:

( )

exp t x t X T ₋  =    _∗ (21) dengan 2 2

T

η λα

λσ

+

=

∗

(22) Bukti: Dari persamaan (8)

( )

(

2

)

2 ₄ 3 ₃ 2 4 P v = +η λα v + λαβv + λβ v

dengan β= 0 maka persamaan tersebut menjadi 2 2 ( ) ( ) p v = +

η λα

v Misalkan 2 2

(

)

y

= +

η λα

v

2 2

(

)

y

v

η λα

=

+

2 ( ) y v

η λα

= + 1 2 . ( ) ( ) y p y η λα − ₌ +

Jika persamaan di atas disubstitusikan ke dalam persamaan (19) maka diperoleh solusi umum untuk banyaknya saham pada waktu t yang akan dijual dan waktu eksekusi optimal sebagai berikut:

(

)

2 2 1/2 1/2 1 2 2 0 0 2 ( ) ( ) 2 _{( )} ( ) p v x p λσx p v λσ η λα η λα − _{+ =}_ _{ +}     ₊  _{ + }  

1/ 2 2 2 1/ 2 2 2 2 2 ( ) 0 ( ) ( ) v x

η λα

λσ

η λα

η λα

 ₊      = ₊  +_{ + }   _{ } 0 (karenav =0) maka

(

)

2 2 1/ 2 1 2 2 . 0 2 ( ) ( ) x p λσ x p v λσ η λα − _{+ =}    +  

Sehingga persamaan (19) menjadi

(

)

1 2 2 ( ) _{( )} 0 X x t dx t p− λσ x p v = ∫ + 1/ 2 2 2 ( ) 2 ( ) X x t dx t x

λσ

η λα

= ∫     +   1/ 2 2 2 2 ( ) ( ) X x t x dx t λσ η λα −   = ∫   +   1/ 2 2 2 ( ) 1 ( ) X x t dx t x λσ η λα −   = ∫   +   2 2 ( )

ln

X x t

x

t

η λα

λσ



+

_

₌



(

)

2 2 lnX ln ( )x t t

η λα

λσ

+ _{− =}

(

)

₂ 2 lnX ln ( )x t t

η λα

λσ

− = + 2 2 ln ( )x t lnX t η λα λσ    ₋    = +_{ } +     2 2 exp(ln ( ))x t exp lnX t

η λα

λσ

     ₋     = _ +_{ } +        2 2 ( ) exp t x t X η λα λσ    ₋    = _{ } +    

* 2 * 2 ( ) exp . t x t X T T

η λα

λσ

₋  =     + = Terbukti. Solusi optimal waktu eksekusi saham pada persamaan (22) menunjukkan bahwa dengan meningkatnya risiko volatilitas dan risk

aversion maka nilai T akan semakin kecil _*

artinya semakin tinggi risiko volatilitas dan semakin tidak berani seorang penjual mengambil risiko maka waktu eksekusi saham akan semakin cepat.

Untuk mengetahui expected cost dan ragam dari suatu saham maka diperoleh fungsi objektif sebagai berikut:

( )

2 2 2 2 2 1 1 2 2 X E X T λη σ λ η η λα = = + ∗ (23)

( )

2 2 2 2 2 2 2 2. 1 1 2 1 2 2 V X T X T α σ η λα λ σ σ λ η λα   ₊ = _∗_+ _= +  _∗ (24) (Bukti: lihat Lampiran 8)

Jika

λ

→∞

, maka diperoleh: , T α σ → ∗ (25) 2 1 , 2 X E T η → ∗ 2 V →ασX

(Bukti: lihat Lampiran 9)

Persamaan (25) menunjukkan bahwa selama dalam perdagangan terdapat risk

aversion (λ) yang semakin besar yaitu

semakin besar tingkat penghindaran risiko maka waktu eksekusi saham, expected cost, dan ragam dalam perdagangan mempunyai nilai terbatas.

4.2 Peningkatan Risiko-Perdagangan Linear

Kasus ini diasumsikan bahwa 0 dan 0

α = β ≠ , artinya ketidakpastian biaya likuiditas dalam perdagangan bergantung pada rata-rata perdagangan. Sehingga fungsi pada persamaan (18) menjadi:

2 2 4

( ) 3

P v =ηv + λβ v (26) (Bukti: lihat Lampiran 10)

Karena fungsi pada persamaan (26) adalah fungsi yang monoton naik maka persamaan (26) mempunyai invers sebagai berikut:

( )

2 2 1 2 . 12 6 w P w η λβ η λβ − ₌ + − ₍₂₇₎

(Bukti: lihat Lampiran 11)

Selanjutnya dengan menggunakan solusi persamaan (19) diperoleh solusi optimal untuk waktu eksekusi saham sebagai berikut :

2

T η

λ σ

∗ = , (28)

Persamaan (28) menunjukkan bahwa waktu eksekusi saham berbanding lurus dengan perubahan biaya likuiditas ( )η artinya semakin besar perubahan biaya likuiditas maka waktu eksekusi akan semakin lama dan sebaliknya semakin kecil perubahan biaya likuiditas maka waktu eksekusi akan semakin cepat.

Karena ketidakpastian biaya dalam perdagangan dipengaruhi oleh rata-rata perdagangan maka banyaknya saham optimal yang diperdagangkan diberikan oleh persamaan: 2 1 1 . 3 3 T X η σ λσβ β ∗ = = ∗ (29)

V ILUSTRASI

Untuk lebih memahami solusi optimal

yang diperoleh maka hal tersebut digambarkan pada ilustrasi sebagai berikut:

5.1 Ilustrasi Solusi Peningkatan Risiko Perdagangan Konstan

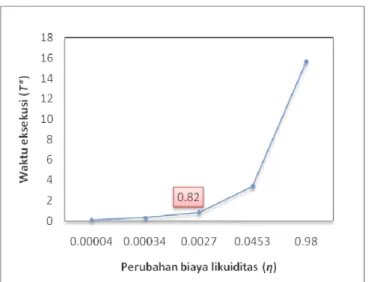
Waktu eksekusi optimal pada persamaan (22) menunjukkan bahwa semakin besar nilai η maka semakin besar pula nilaiT artinya * semakin besar perubahan biaya likuiditas

maka saham akan semakin lama dieksekusi, sebaliknya semakin kecil nilai η maka semakin kecil pula nilai T artinya semakin _*

kecil perubahan biaya likuiditas maka saham akan semakin cepat dieksekusi

Misalkan diambil λ=0.001, σ =2 dan 0.03

α = , maka waktu eksekusi optimal untuk nilai perubahan biaya likuiditas yang berbeda diilustrasikan pada grafik di bawah ini:

Gambar 1 Grafik hubungan perubahan biaya likuiditas dengan waktu eksekusi optimal untuk solusi peningkatan risiko perdagangan konstan

Selain itu pada solusi waktu eksekusi optimal persamaan (22) menunjukkan bahwa dengan meningkatnya risiko volatilitas (σ) maka nlai T akan semakin kecil artinya _*

semakin tak terduga pergerakan harga saham maka waktu eksekusi saham akan semakin cepat. Sebaliknya semakin kecil risiko volatilitas (σ) maka nilai T akan semakin _*

besar artinya semakin mudah pergerakan harga saham diduga maka waktu eksekusi saham akan semakin lama.

Misalkan diambil

η

=0.087, λ=0.001 dan α =0.03maka waktu eksekusi saham yang optimal untuk risiko volatilitas yang berbeda diilustrasikan pada grafik berikut

Gambar 2 Grafik hubungan risiko volatilitas dengan waktu eksekusi optimal untuk solusi peningkatan risiko perdagangan konstan

Solusi waktu eksekusi optimal pada persamaan (22) juga menunjukkan bahwa dengan meningkatnya risk aversion (λ) maka

nilai T akan semakin kecil artinya semakin _*

tidak berani seorang penjual mengambil risiko maka waktu eksekusi saham akan semakin cepat, sehingga nilai expected cost akan

semakin besar dengan nilai standar deviasi semakin kecil dan sebaliknya semakin kecil

risk aversion (λ) maka nilai T akan semakin _*

besar artinya semakin berani seorang penjual mengambil risiko maka waktu eksekusi saham akan semakin lama, sehingga nilai expected cost akan semakin kecil dengan nilai standar

Misalkan diambil

η

=0.087, σ =2 dan α =0.03maka waktu eksekusi saham yang optimal untuk risk aversion yang

berbeda diilustrasikan pada grafik di bawah

ini :

Gambar 3 Grafik hubungan risk aversion dengan waktu eksekusi optimal untuk solusi peningkatan

risiko perdagangan konstan

Gambar 4 Grafik hubungan waktu eksekusi dengan expected cost yang dipengaruhi oleh risk aversion pada peningkatan risiko konstan

Gambar 5Grafik hubungan waktu eksekusi dengan standar deviasi yang dipengaruhi oleh risk aversion pada peningkatan risiko konstan

5.2 Ilustrasi Solusi Peningkatan Risiko Perdagangan Linear

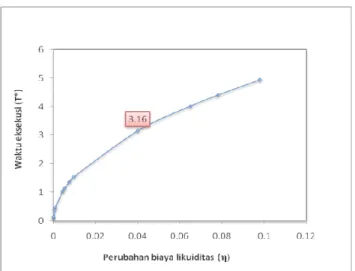
Persamaan (28) menunjukkan bahwa waktu eksekusi saham berbanding lurus dengan perubahan biaya likuiditas ( ),η artinya semakin besar perubahan biaya likuiditas maka waktu eksekusi akan semakin lama dan sebaliknya semakin kecil perubahan

biaya likuiditas maka waktu eksekusi akan semakin cepat.

Misalkan diambil risk aversion

(

λ

=0.001

)

dan risiko volatilitas

(

σ

=2

)

maka waktu eksekusi untuk perubahan biaya likuiditas yang berbeda diilustrasikan pada grafik berikut:

Gambar 6 Grafik hubungan antara perubahan biaya likuiditas dengan waktu eksekusi yang optimal untuk peningkatan risiko perdagangan linear

Selain itu, pada persamaan (28) hubungan

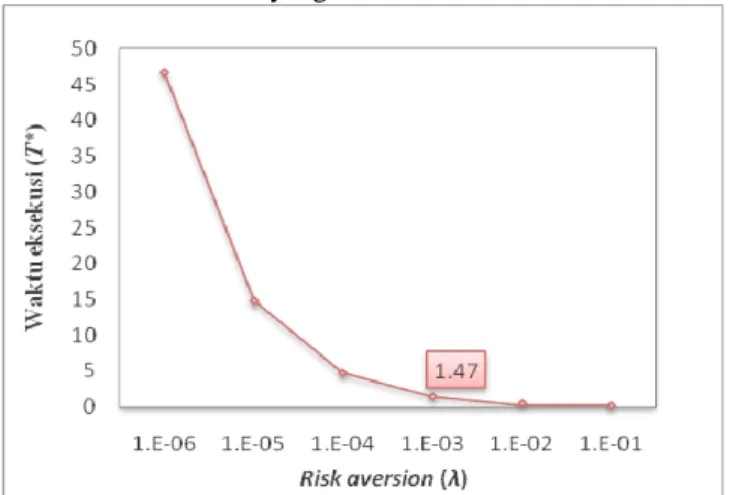
waktu eksekusi dengan risk aversion adalah berbanding terbalik yaitu semakin besar risk

aversion maka nilai T akan semakin kecil _*

artinya semakin tidak berani seorang penjual mengambil risiko maka waktu eksekusi saham akan semakin cepat dan sebaliknya semakin kecil risk aversion maka waktu eksekusi akan

semakin besar artinya semakin berani seorang penjual mengambil risiko maka waktu eksekusi saham akan semakin lambat.

Misalkan diambil

(

η=0.00435

)

dan risiko volatilitas (σ =2) maka waktu eksekusi

optimal untuk risk aversion yang berbeda diilustrasikan pada grafik berikut ini:

Gambar 7 Grafik hubungan antara risk aversion dengan waktu eksekusi untuk peningkatan risiko perdagangan linear

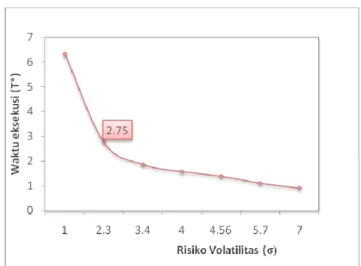
Pada persamaan (28), hubungan waktu eksekusi dengan risiko volatilitas adalah

berbanding terbalik yaitu semakin besar risiko volatilitas maka nilai T akan semakin kecil _*

artinya semakin tak terduga pergerakan harga saham maka waktu eksekusi saham akan semakin cepat dan sebaliknya semakin kecil risiko volatilitas maka nilai T akan semakin _*

besar artinya semakin mudah menduga harga saham maka waktu eksekusi saham akan semakin lambat.

Misalkan diambil peningkatan biaya likuiditas (η=0.004)dan risk aversion

(λ = 0.0001)maka waktu eksekusi saham yang optimal untuk risiko volatilitas yang berbeda diilustrasikan seperti pada grafik di berikut ini:

Gambar 8 Grafik hubungan antara risiko volatilitas dengan waktu eksekusi yang optimal untuk peningkatan risiko perdagangan linear

Persamaan (29) menunjukkan bahwa

semakin besar risk aversion maka banyaknya saham optimal yang diperdagangkan akan semakin kecil artinya semakin tidak berani seorang penjual mengambil risiko maka saham yang diperdagangkan akan semakin kecil dan sebaliknya semakin kecil risk

aversion maka banyaknya saham yang

diperdagangkan akan semakin besar artinya semakin berani seorang penjual mengambil

risiko maka saham yang diperdagangkan akan semakin besar. Hal tersebut dijelaskan dalam ilustrasi sebagai berikut.

Misalkan η=0.006, σ =2, dan 0.00035

β = maka banyaknya saham yang diperdagangkan untuk risk aversion yang

berbeda diilustrasikan seperti pada grafik di bawah ini:

Gambar 9 Grafik hubungan antara risk aversion dengan banyaknya saham optimal untuk

peningkatan risiko perdagangan linear

5.3 Contoh Penerapan Peningkatan Risiko Konstan

Misalkan volume perdagangan di pasar modal sebanyak 1.000.000 juta saham sedangkan banyaknya banyaknya saham awal