Bab 4: Sinyal dan Sistem di Domain Frekuensi

Bab 4: Sinyal dan Sistem di Domain Frekuensi

1 Konsep Spektrum Frekuensi

Suatu Sinyal dapat didekomposisi menjadi komponen-komponen sinusoidal (atau eksponensial kompleks). Dengan dekomposisi semacam itu, sebuah sinyal dikatakan direpresentasikan dalam Domain Frekuensi.

Pada sinyal periodik, dekomposisi menjadi komponen sinusoidal disebut Deret Fourier. Sedangkan pada sinyal aperiodik (finite energy) disebut sebagai Transformasi Fourier. Transformasi Fourier dan Deret Fourier adalah alat matematis yang sangat penting dalam analisis dan desain sistem LTI.

Dengan melakukan analisis frekuensi, kita dapat melihat representasi matematis komponen-komponen frekuensi yang terkandung dalam suatu sinyal. Rangkaian frekuensi yang terkandung dalam sinyal tersebut disebut spectrum.

1.1 Frekuensi Sinyal Kontinue Periodik

Tujuan Belajar 1

Peserta dapat menghitung spektrum (deret Fourier) dari sinyal kontinu yang periodik.

Representasi matematis dasar dari sinyal periodik adalah Deret Fourier, yang merupakan penjumlahan berbobot linear (linear weighted sum) dari sinyal sinusoidal atau eksponensial kompleks.

Kombinasi linear dari eksponensial kompleks harmonis dalam bentuk

∑

∞ −∞ = = k t kF j ke o c t

x( ) 2π adalah sinyal periodik dengan periode fundamental:

o p

T T = 1 . Oleh karena itu, kita dapat berpikir bahwa sinyal eksponensial {_ej2πkFot _{k = …, -2, -1, 0,}

1, 2, …} adalah “building block” dasar, yang darinya kita dapat mengkonstruksi sinyal periodik dengan berbagai tipe dengan memilih frekuensi fundamental dan koefisen-koenfisien {ck}. Fo menentukan periode fundamental dari x(t) dan koefisien {ck}

menentukan bentuk dari gelombang (waveform).

Bila diberikan sinyal periodik x(t) dengan periode Tp. Kita dapat merepresentasikan

sinyal tersebut dengan suatu deret yang disebut Deret Fourier, dimana frekuensi fundamental Fo dipilih timbal balik dengan periode Tp. Untuk menentukan ekpresi dari

koefisen-koenfisien {ck}, kita pertama-tama harus mengalikan kedua sisi dengan

eksponensial kompleks _e−j2πFolt_{, dimana l adalah integer, dan kemudian}

dt e c e dt e t x p o o o o p o o o T t t k t kF j k t lF j T t t t lF j

∫

∑

∫

+ − ₌∞_−∞ + − _      = π π π 2 2 2 ) ( ( )

(

o p

)

_{o( )o} o o p o o p o o o t l k F j T t l k F j t T t k o t l k F j k T t t t l k F j k k e e l k l k F j e c dt e c − + − + ∞ −∞ = − + − ∞ −∞ = = ≠ ↓         − =

_∑

∫

∑

π π π π π 2 2 ) ( 2 ) ( 2 karena bila 0 ) ( 2 tapi bila k=l p T t t o p o T t T t t dt p o o = + =

∫

+ Jadi p l k T t t t l k F j k e dt cT c p o o o =

∑

∞

∫

−∞ = + −) ( 2π

Karena to adalah sembarang, maka integral dapat dievaluasi dalm setiap interval Tp.

Konsekuensinya, integral untuk koefisien Deret Fourier dapat ditulis sebagai

∫

− = p o T t kF j p k x t e dt T c 1 ( ) 2π Tujuan Belajar 2

Peserta mengerti konvergensi deret Fourier melalui kondisi Dirichlet.

Hal penting yang muncul dalam merepresentasikan sinyal periodik dalam Deret Fourier adalah apakah deret tersebut konvergen untuk x(t) pada setiap nilai t, yaitu bila sinyal x(t) dan representasi Deret Fourier-nya

∑

∞

−∞ = k t kF j ke o

c 2π adalah sama untuk setiap nilai t.

Kondisi Dirichlet menjamin bahwa deret tersebut akan sama dengan x(t), kecuali pada nilai t dimana x(t) diskontinyu.

Kondisi Dirichlet adalah :

1. Sinyal x(t) memiliki discontinuitas dalam setiap perioda dalam jumlah yang terbatas.

2. Sinyal x(t) mengandung maxima dan minima dalam suatu perioda dalam jumlah yang terbatas.

∫

<

∞

p T

dt

t

x

(

)

|

|

Sebagai kesimpulan, bila sinyal x(t) adalah periodik dan memenuhi Kondisi Dirichlet, maka sinyal tersebut dapat direpresentasikan sebagai Deret Fourier

∑

∞ −∞ = = k t kF j k o e c t x( ) 2π dimana =

∫

− p o T t kF j p k x t e dt T c 1 ( ) 2π Tujuan Belajar 3

Peserta dapat menghitung variant dari deret Fourier dalam bentuk cos dan sin.

Secara umum, Ck adalah bilangan kompleks. Lebih jauh lagi, bila sinyal periodik

tersebut adalah, maka Ck dan C-k adalah complex conjugate.

k j k k c e c =| | θ k j k k c e c₋ =| | −θ maka :

(

j k j k

)

k k k c c e e c + ₋ =| | θ + − θ k k c |cosθ | 2 =

Sehingga Deret Fourier dapat direpresentaskan dalam bentuk :

∑

∞ = + + = 1 ) 2 cos( 2 ) ( k k o o kFt c t x π θ

dimana co adalah real ketika x(t) adalah real.

Persamaan tersebut dapat jabarkan menjadi :

k o k o k ot kFt kF t kF θ π θ π θ

π ) cos2 cos sin2 sin

2

cos( + = −

Sehingga kita dapat merepresentasikan Deret Fourier dalam bentuk :

∑

∞ = − + = 1 ) 2 sin 2 cos ( ) ( k o k o k o a kFt b kF t a t x π π dimana a0 = co ak = 2|ck|cosθk bk = 2|ck|sinθk

Tujuan Belajar 4

Peserta dapat menghitung Power Density Spectrum atau Power Spectrum dari sinyal kontinu yang periodik, dalam term domain waktu maupun domain Fourier (Parseval’s relation).

Suatu sinyal periodik memiliki energi tak terhingga (infinite) dan daya rata-rata yang terhingga (finite), yang diberikan sebagai

∫

= p T p x xt dt T P 1 | ()|2

Kita ingat bahwa _{x= xx}*_{, maka :}

∫

= p T p x xt x t dt T P 1 ( ) *( )

∫

∑

∞ −∞ = − = p o T k k F j k p tdt e c t x T π 2 * ) ( 1 k k T t kF j p k c dt e t x T c p o ↑           =

∑

∞

_∫

−∞ = − ) ( 1 2 * π

∑

∞ −∞ = = k k c |2 |

Ini disebut Parseval's Relation, yang dihitung dalam term ck.

Tujuan Belajar 5

Peserta dapat memplot spektrum secara alternatif berbetuk power spectrum maupun magnitude dan fasa.

Kita dapat melihat bahwa x(t) adalah deret dari harmonic :

... ...+C−2e−j2πFo2t +C−1e−j2πFot +Co +C1ej2πFot +C2ej2πFo2t +

Daya rata-rata pada masing-masing komponen frekuensi adalah : Px =

2

| |c_k

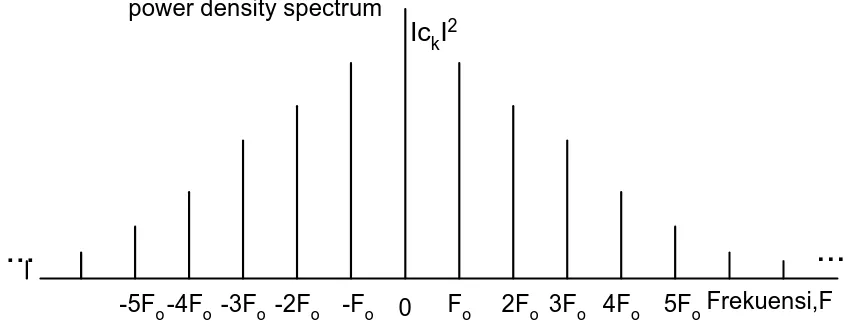
Bila kita memplot |ck |2 sebagai fungsi dari frekuensi kF0, k= …-2,-1,0,1,2, … , maka dapat dibuat suatu diagram yang disebut Power Density Spectrum, yang menggambarkan bagaimana daya dari sinyal periodik didistribusikan diantara komponen-komponen frekuensi.

power density spectrum

Ic_kI2 ... ... 0 F_o 2F_o 3F_o 4F_o 5F_oFrekuensi,F -F_o -2F_o -3F_o -4F_o -5F_o

Gambar 1. |ck|2 adalah daya dari komponen pada frekuensi kFo

Karena daya pada sinyal periodik ada hanya pada nilai diskrit frekuensi (F= … -2F0,

-F0, 0, F0,2F0 …), makanya sinyal tersebut dikatakan memiliki line spectrum. Spasi

diantara garis spectral yang bersebelahan adalah sebanding dengan periode fundamental Tp.

Sebagai alternatif dari memplot Power Density Spectrum, kita dapat memplot Magnitude Spectrum {|ck |} dan Phase spectrum {|θk |} sebagai fungsi dari frekuensi.

Koefisien Detet Fourier yang merupakan bilangan kompleks dapat direpresentasikan sebagai : k j k k c e c =| | θ dimana k k =/_c θ

Power Density Spectrum adalah kuadrat dari Magnitude Spectrum, jadi tidak mengandung info θk.

Bila sinyal periodik adalah x(t) real, maka koefisien deret Fourier-nya memenuhi kondisi

c-k =ck* sehingga |ck|2 = |ck*|2

Oleh karena itu, power spectrum adalah fungsi symetric/even dari frekuensi. Kondisi ini berrati pula bahwa Magnitude spectrum adalah fungsi symetric/even dan Phase spectrum adalah fungsi ganjil. Sebagai konsekuensi dari adanya simetri tersebut, spektrum dari fungsi real cukup dispesifikasi pada frekuensi positif saja.

∑

∞

∑

= ∞ = + + = + = 1 1 2 2 2 1 2 2 2 _{2 | | ( )} k k k k o k o x C c a a b P

Tujuan Belajar 6

Peserta dapat menghitung spektrum dari deret pulsa rektangular waktu kontinu.

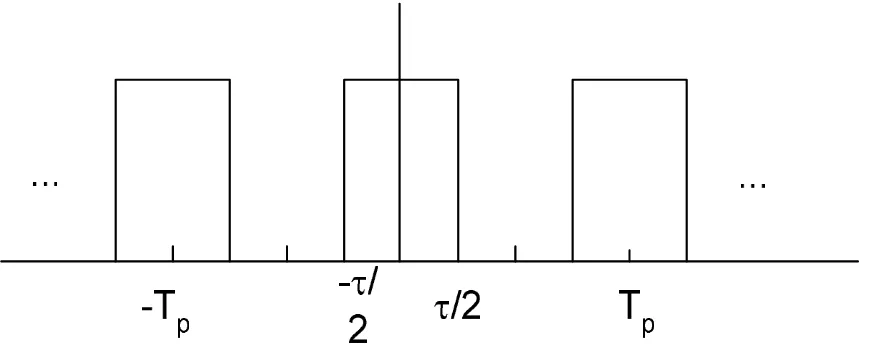
Bagaimana menentukan Deret Fourier dan Power Density Spectrum dari pulsa rectangular train?

Gambar 2. Pulsa rectangular train.

Untuk menyelesaikannya, pertama-tama kita lihat bahwa x(t) adalah periodik dengan periode dasar Tp⇒ Fo = 1/Tp, jadi kita bisa menggunakan deret Fourier. Selain itu, x(t)

adalah sinyal genap sehingga x(t) = x(-t), maka kita dapat memilih interval integrasi dari -Tp/2 s.d. Tp/2

Untuk k=0, kita dapatkan :

p p T T p T A A Adt T dt t x T Co p p τ τ τ τ τ = = = = − − −

∫

∫

/2 2 / 2 / 2 / 2 / 2 / 1 ) ( 1

Untuk k tidak sama dengan nol, kita dapatkan :

2 / 2 / 2 2 / 2 / ) ( 2 2 1 τ τ π τ τ π π ₋ − −         − = =

_∫

o kt F j p t kF j p k kF j e T A dt Ae T c o o 2j sin 2 jx jx t kF j t kF j p o k e e x j e e T kF A c o o − − − = ↓         ₋ = ⇒ π π π maka : ) sin(π τ π o p o k kF T kF A c = k = ±1, ±2, …

karena _{= Φ} Φ Φ c sin sin _{, maka}

(

)

sinc ) sin( τ π τ τ π τ π τ o p o o p k kF T A kF kF T A c = = ↓∅k

∅k bernilai diskrit karena Fo dan τ fixed bergantung k .

Tapi bila ∅kontinu

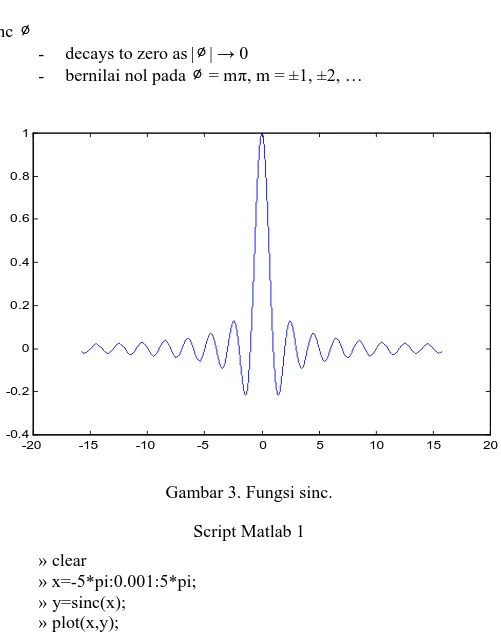
sinc ∅

- decays to zero as|∅| → 0

- bernilai nol pada ∅= mπ, m = ±1, ±2, …

-20 -15 -10 -5 0 5 10 15 20 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

Gambar 3. Fungsi sinc. Script Matlab 1 » clear

» x=-5*pi:0.001:5*pi; » y=sinc(x);

» plot(x,y);

Jadi ∅k adalah sample dari ∅ pada posisi (πFoτ)k. Jadi ck adalah sample dari sin∅

pada posisi tersebut dengan amplitudo terskala sebesar Aτ/Tp

Ctt.

0 →ck positive π→ ck negative k j k k

c

e

c

=

|

|

θ → jadi plot saja ck tanpa perlu phase dan

magnitude Akibat dari perubahan Tp dan τ pada spektrum

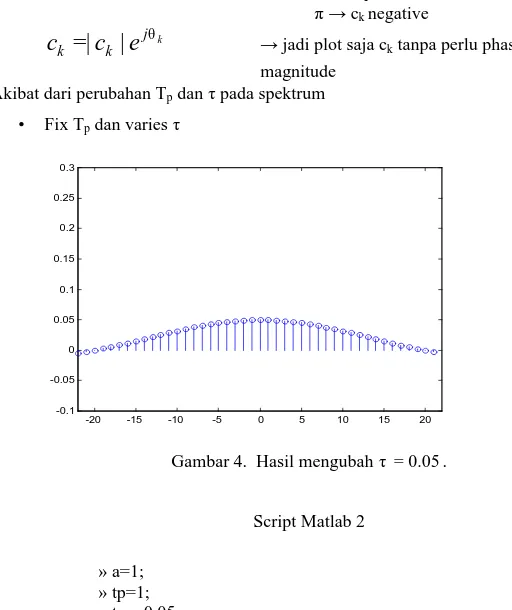
• Fix Tp dan varies τ

-20 -15 -10 -5 0 5 10 15 20 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25 0.3

Gambar 4. Hasil mengubah τ =0.05. Script Matlab 2 » a=1; » tp=1; » tau=0.05; » x=-7*pi:1:7*pi; » y=((a*tau)/tp)*sinc(x*tau); » stem(x,y); » axis([-7*pi 7*pi -0.1 0.3]);

-20 -15 -10 -5 0 5 10 15 20 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25 0.3

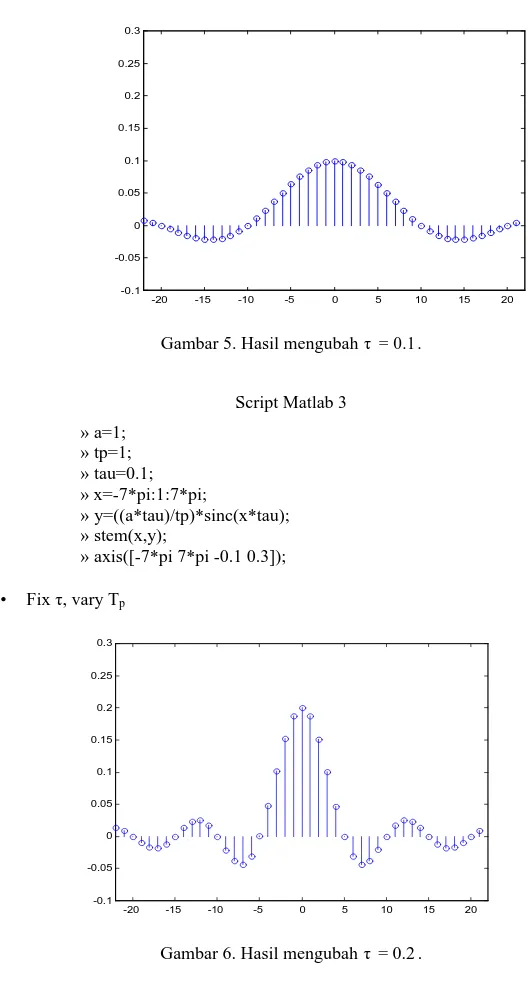
Gambar 5. Hasil mengubah τ = 0.1. Script Matlab 3 » a=1; » tp=1; » tau=0.1; » x=-7*pi:1:7*pi; » y=((a*tau)/tp)*sinc(x*tau); » stem(x,y); » axis([-7*pi 7*pi -0.1 0.3]); • Fix τ, vary Tp -20 -15 -10 -5 0 5 10 15 20 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25 0.3

Script Matlab 4 » a=1; » tp=1; » tau=0.2; » x=-7*pi:1:7*pi; » y=((a*tau)/tp)*sinc(x*tau); » stem(x,y); » axis([-7*pi 7*pi -0.1 0.3]); Perhatikan, bila k≠0 dan sin(πkFoτ), ck = 0

Padahal pada kFo tertentu

(π(kFo)τ = mπ, m= ±1, ±2, …)

⇒ sin πkFoτ = 0 ⇒ ini terjadi pada kFo = m/τ

Contoh : Bila Fo = 4 Hz dan τ=0.2Tp, (τ = 0.2/4=0.1/2) ck = 0 pada kFo = m.2/0.1 = 20m → kFo = ±20, ±40, ±60, … → pada k = ±5, ±10, ±15, … PDF:                 =         = ) ( sin 0 , | | 2 2 2 2 τ π τ τ o p p k kF c T A k T A c

1.2 Frekuensi Sinyal Kontinu Aperiodik

Tujuan Belajar 7

Peserta dapat menghitung spektrum (X(F)) dari sinyal kontinu yang aperiodik, serta mengerti hubungannya dengan kasus periodik.

Pada sinyal kontinyu periodik, kita melihat bahwa sinyal memiliki spektra garis dengan spasi yang sebanding dengan frekuensi fundamental. Bila periodenya dibuat menjadi tak terhingga (menjadi sinyal aperiodik), maka lebar spasi akan nol dan spectrum-nya menjadi kontinyu.

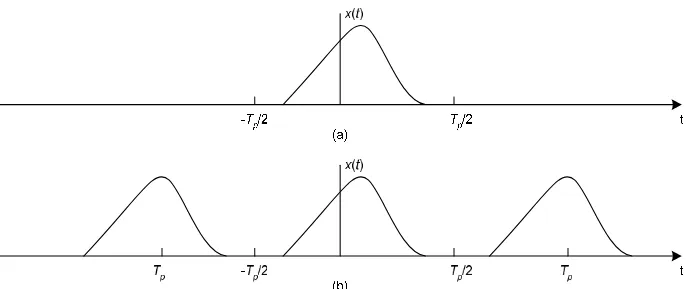
Gambar 7. Sinyal aperiodik dengan durasi terbatas dapat digunakan untuk membuat sinyal periodik.

Bila kita mengamati sinyal aperiodik dengan durasi finit pada gambar (a) diatas, maka kita dapat menyusun suatu sinyal periodik xp(t) dengan perioda Tp, seperti pada gambar

(b).

Jelas, xp(t) = x(t) dengan Tp tak terhingga, yaitu x(t)

lim

x_p(t)

Tp→∞

= .

Representasi Deret Fourier untuk sinyal periodik adalah :

∑

= j kF t k p t c k o x ( ) 2π( ) Fo =1/Tp dimana dt e t x T c j kF t T T p p k o p p ) ( 2 2 / 2 / ) ( 1 − π −

∫

= dt e t x T c j kF t p k o) ( 2 ) ( 1 ∞ _{− π} ∞ −

∫

=

Kini kita definisikan suatu fungsi, Tranformasi Fourier X(F) dari x(t), sebagai :

∫

∞ ∞ − − = x t e dt F X( ) ( ) j2πFt

X(F) adalah fungsi dengan variable kontinyu F. Koefisien Fourier dapat diekspresikan dengan term X(F) sebagai :

) ( ) ( ) ( 1 o o o o o p k X kF F X kF F X kF T c = = = maka : k p p o T c T k X kF X _=       = ) (

Dengan demikian dapat dikatakan bahwa koefisien ck adalah sampling dari X(F), yang

diambil pada setiap kelipatan Fo dan diskala sebesar Fo (dikalikan dengan 1/ Tp).

Dengan mensubstitusikan ck diperoleh : t kF j k p p p o e T k x T t x ( ) 1

∑

2π ∞ −∞ =         =

Untuk mencari x(t) dari X(F) maka didefiniskan : ) ( ) (t

_lim

x t x _p T_p→∞ = Fo= ∆F= 1/Tp sehingga :

∑

∞ −∞ = ∆ _∆ ∆ = k Ft k j p t X k F e F x ( ) ( ) 2π k∆F → F

Jelas bahwa pada Tp mendekati tak terhingga, xp(t) tereduksi menjadi x(t), juga

F

∆ menjadi differensial dF dan k∆F menjadi variabel frekuensi kontinyu F. Maka diperoleh :

∫

∞ ∞ − ∞ → = = ( ) ( ) ) ( 2

lim

x_p t X F ej FtdF x t T_p π

Dapat disimpulkan, untuk sinyal kontinyu aperiodik, berlaku :

∫

∞ ∞ − = X F e dF t x( ) ( ) j2πFt dan

∫

∞ ∞ − − = x t e dt F X( ) ( ) j2πFt Tujuan Belajar 8

Peserta dapat menghitung Power Density Spectrum atau Power Spectrum dari sinyal kontinu yang periodik, dalam term domain waktu maupun domain Fourier (Parseval’s relation).

Bila x(t) adalah sinyal energi berhingga dengan tranformasi Fourier X(f), maka energinya dapat diekpresikan sebagai:

∫

∞ ∞ − = X t dt Ex 2 | ) ( |

∫

∞ ∞ −

= |X(F)|2 dF

Ini adalah Parseval’s Relation untuk sinyal aperiodik energi berhingga dan mengekspresikan prinsip konservasi energi dalam domain waktu dan frekuensi. Sedangkan kuantitas Sxx(F) = |X(F)|2 merepresentasikan distribusi energi dari sinyal

sebagai fungsi frekuensi. Oleh karena itu Sxx(F) disebut Energy Density Spectrum dari

x(t). Intergral dari Sxx(F) sepanjang semua frekuensi menghasilkan total energi dari

sinyal tersebut.

Tujuan Belajar 9

Peserta dapat menghitung spektrum dari sebuah pulsa rektangular waktu kontinu.

Bagaimana menentukan Transformasi Fourier dan Energy Density Spectrum dari sinyal pulsa rektangular pada gambar (a) dibawah ini ?

Jelas bahwa sinyal tersebut aperiodik dan memenuhi Kondisi Dirichlet, oleh karena itu Transformasi Fourier-nya ada. Dengan mengaplikasikan persamaan transformasi fourier diperoleh :

( )

τ τ _ππ_ττ τ π F F A dt Ae F X j Ft sin 2 / 2 / 2 = =

_∫

− −

Diagramnya dapat dilihat pada gambar atas bagian (b). Energy Density Spectrum dari pulsa rektangular adalah :

( )

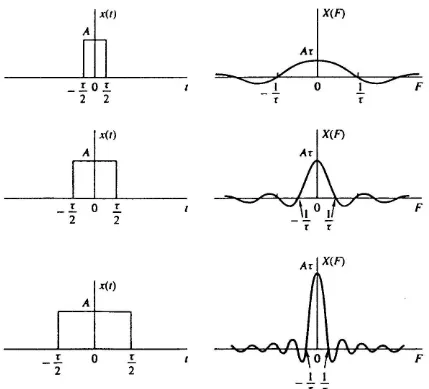
2 sin 2 ) (       = τ π τ π τ F F A F Sxx

Berikut ini beberapa gambar pulsa rektangular dalam berbagai variasi lebar berserta Transformasi Fouriernya.

Gambar 8. Beberapa gambar pulsa rektangular dalam berbagai variasi lebar berserta Transformasi Fouriernya

1.3 Frekuensi Sinyal Diskrit Periodik

Tujuan Belajar 10

Peserta dapat menghitung spektrum (deret Fourier) untuk sinyal periodik waktu diskrit.

Kita diberi skuens periodik x(n) dengan periode N, dimana x(n)=x(n+N) untuk semua n. Representasi deret fourier untuk x(n) terdiri dari N harmonic yang berhubungan dengan fungsi eksponensial

n N k j k e s       = 2π k = 0, 1, …, N-1 dan diekspresikan sebagai

∑

− = = 1 0 ) ( N k k ks c n x

dimana {ck} adalah koefisien-koefisien dalam representasi deret.

Bagaimana mencari ck ? factor scaling , * ↓ = x s G ck k

∑

−

∑∑

= − = − = −       − = = 1 0 1 0 1 0 ) ( 2 2 ), ( N n N n N k N n l k j k n n k j e c e n x π π    − = ± ± = ↓

∑ ∑

− = − = − ,else N N, , l N ,k e c N k N n N n l) p(k j k 0 2 0 1 0 1 0 2 Sehingga diperoleh : 1 1 0 2

∑

− = − = N n n n k p j k x(n)e N c

Maka untuk sinya diskrit periodik :

( ) (

n x n N

)

x n S e c n x N k k n N k j k + = ↓ = =

∑

− = relate ly harmonical ) ( ) ( 1 0 2π Ingat :

∑

− =     ≠ − − = = 1 0 , 1 1 1 1 , N n N n a a a a N a maka    = ± ± =

∑

− =       otherwise N N k N e N n n k j n , 0 2 , , 0 , 1 0 2π

( )

n j n N k j k N n N kn j k k e e n s n x e n x N c ω π π = = ↓ =       − = −

∑

2 1 0 / 2 ) ( pada fasa dan amplitudo ) ( 1

∑

∑

− = − − = + − + = = = 1 0 2 1 0 ) ( 2 ) ( 1 ) ( 1 N n k n N k j N n N n N k j N k C e n x N e n x N C π π karena

∑

− n N n k j n j e e n x N π π 2 2 ) ( 1

Berikut ini beberapa contoh pencarian spectrum untuk sinyal diskrit periodik: a.

x

(

n

)

=

cos

2

π

n

b.

x

n

n

3

cos

)

(

=

π

c.

x

(

n

)

=

x

(

n

+

4

)

, x(n) = {1, 1, 0, 0} Jawab : a. 2 1 2 → = = o o π f ω → non periodic b. fo = 1/6 → x(n) periodic N = 6

( )

( )

0 2 1 2 1 2 1 2 1 6 2 cos ingat 5 ,..., 1 , 0 6 1 4 3 2 5 1 6 / 2 6 / 2 5 0 6 / 2 = = = = = = → + = = = = − = −

∑

c c c c c c e e n n x k e n x c o n j n j n kn j k π π π π Spectrum f 2 1

c.

∑

= − = 3 0 4 2 ) ( 4 1 n n k j k x n e C π

















+

=

₁

e

−j24k

4

1

π , k = 0, 1, 2, 3, …     + = → ₁ − 2 4 1 j k k e C π Co = 1/2 C1 = 1/4(1-j) C2 = 0 C3 = 1/4(1+j) Tujuan Belajar 11

Peserta dapat menghitung power density spectrum dalam term domain waktu maupun domain Fourier (Parseval’s relation).

Daya rata-rata dari sinyal waktu-diskrit periodik dengan periode N didefiniskan sebagai:

∑

−

∑

= − = = = 1 0 1 0 2 2 | | | ) ( | 1 N n N k k x x n c N P

Skuens |c_k|2 untuk k=0,1,…,N-1 adalah distribusi daya sebagai fungsi frekuensi dan disebut Power Density Spectrum dari sinyal periodik.

Energi dari skuens x(n) pada satu perioda

∑

−

∑

= − = = = 1 0 1 0 2 2 | | | ) ( | N n N k k N x n N c E

Sebagai contoh, bagaimana mencari deret Fourier dan PDS dari sinyal waktu-diskrit kontinyu square-wave dibawah ini?

Dengan mengaplikasikan persamaan analisis, diperoleh :

c

_k 2

1 0 , 1 ) ( 1 1 0 2 1 0 / 2 _{Ae k} ,...N-N e n x N C L n n N k j N n N kn j k =

∑

=

∑

= − = − − = − π π

(

)

N k N kL e e e N A k L N A n e N A Ck N L k j L n N k j N kL j N k j / sin / sin 1 1 0 , / ) 1 ( 2 1 0 / 2 / 2 2 π π π π π π − − − = − − = ↓      − − = =     =

∑

Power Density Spectrum dari sinyal tersebut adalah :

                         = _{2 2} 2 2 sin sin | pk/N pkL/N N A N AL | C_k

1.4 Frekuensi Sinyal Diskrit Aperiodik

Tujuan Belajar 12

Peserta dapat menghitung spektrum (X

( )

ω ) untuk sinyal aperiodik waktu diskrit.

Tranformasi Fourier untuk sinyal waktu-diskrit energi berhingga x(n) didefinisikan sebagai : integer ) 2 ( ) ( , ) ( ) ( * = + = ↓ = =

∑

∞ −∞ = − k k X X s x e n x X n n j π ω ω ω ω Cari x(n) → x(n)=

∑

x,s* s

Mari kita mengevaluasi skeuens x(n) dari X(ω). Pertama-tama kita kalikan kedua sisi dengan ejωn dan mengintegralkannya dalam interval (-π,π).

∑

∫ ∑

∫

− = − ∞ → − − ∞ −∞ = − = ↓         = N N n n j N N N n j n j n n j e n x X X d e e n x d e X ω π π ω ω π π ω ω ω ω ω ω ) ( ) ( ) ( ) ( ) (

lim

Dengan asumsi konvergen

( )

m x n m d e n x d e n x n n n m j n m j π π ω ω π π π π ω ω 2 0 , 0 , 2 ) ( ) ( ( ) ( ) =    = = ↓ = =

∫ ∑

∑

∫

− ∞ −∞ = ∞ −∞ = ₋ − − − maka didapat :

∫

− = π π ω _ω ω π X e d n x ( ) j n 2 1 ) (

Maka untuk sinyal waktu-diskrit aperiodik berlaku :

∑

∞ −∞ = − = n n j e n x X(ω) ( ) ω

∑

∞ −∞ = + − ₌ = + n n k j X e n x k X(ω 2π ) ( ) (ω 2π ) (ω)

∫

− = π π ω _ω ω π X e d n x ( ) j n 2 1 ) ( Tujuan Belajar 13

Peserta dapat menghitung spektrum dari sebuah pulsa rektangular waktu diskrit.

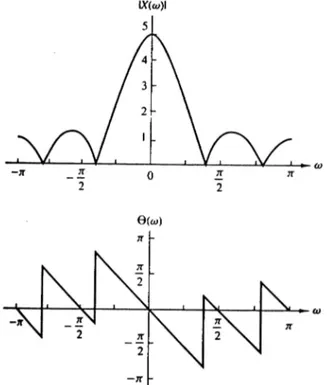
Bagaimana menghitung spektrum dari sebuah pulsa rektangular waktu diskrit dibawah ini ?

Gambar 9. Spektrum rektangular.    ≤ < ≤ = π ω ω ω ω ω c c X , 0 , 1 ) (

Invers transformasi dari X(ω) menghasilkan sekuens :

∫

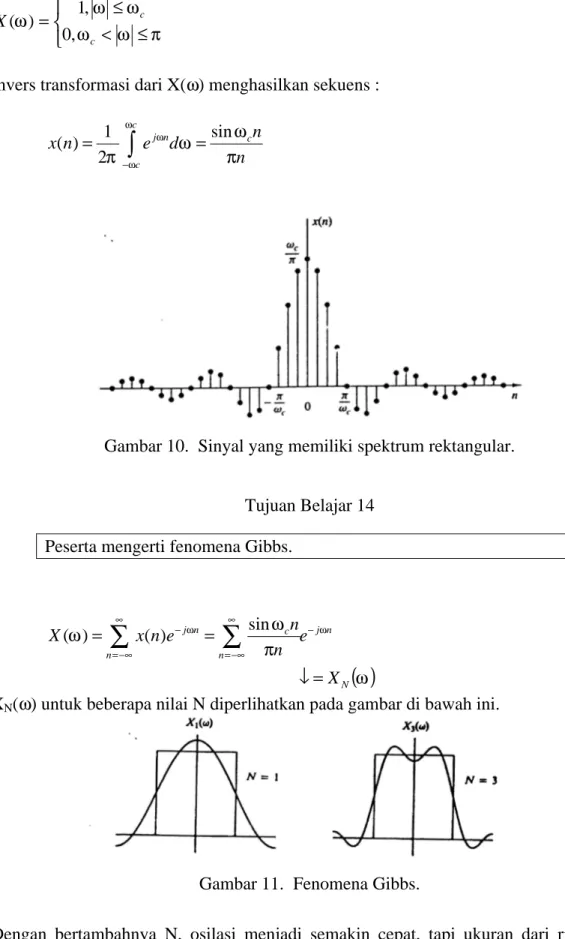
− = = c c c n j n n d e n x ω ω ω π ω ω π sin 2 1 ) (

Gambar 10. Sinyal yang memiliki spektrum rektangular. Tujuan Belajar 14

Peserta mengerti fenomena Gibbs.

( )

ω π ω ω ω ω N n j n n c n j X e n n e n x X sin ) ( ) ( = ↓ = = ∞ − −∞ = ∞ −∞ = −

∑

∑

XN(ω) untuk beberapa nilai N diperlihatkan pada gambar di bawah ini.

Gambar 11. Fenomena Gibbs.

Dengan bertambahnya N, osilasi menjadi semakin cepat, tapi ukuran dari riak tetap sama. Bila N→∝, osilasi akan konvergen pada titik diskontinyuitas pada ω=ωc, tapi

amplitudonya tidak menuju nol. Oleh karena itu, XN(ω) konvergeb menuju X(ω) dalam

sense mean-square.

Kelakuan osilatoris dari aproksimasi XN(ω) menuju funsi X(ω) pada titik

diskontinyuitas dari X(ω) disebut Fenomena Gibbs.

Tujuan Belajar 15

Peserta dapat menghitung energy density spectrum dalam term domain waktu maupun domain Fourier (Parseval’s relation).

Relasi energi antara x(n) dan X(ω) adalah :

∑

∞

_∫

−∞ = − = = n x x n X d E ω ω π π π 2 2 | ) ( | 2 1 | ) ( |

Ini adalah Relasi Paserval untuk sinyal waktu-diskrit aperiodik dengan energi berhingga.

Spektrum X(ω), secara umum, adalah bilangan kompleks dan dapat dituliskan sebagai : ) ( | ) ( | ) (ω X ω ejθ ω X =

Sebagaimana dalam sinyal kontinyu, kuantitas

2 | ) ( | ) (ω X ω S_xx =

merepresentasikan distribusi energi sebagai fungi frekuensi, dan disebut sebagai Energy Density Spectrum dari x(n).

Untuk x(n) real maka berlaku simetri, dimana

ω ω) ( ( X X − = dan ∠X(−ω)=−∠X(ω) demikian juga: ) ( ) (ω = xx −ω xx S S .

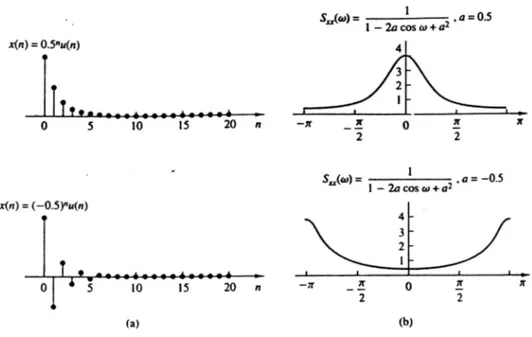
Sebagai contoh, untuk mencari Sxx(ω) dari sinyal x(n) = anu(n) -1<|a| < 1

Maka kita mengaplikasikan transformasi fourier

(

)

∑

∞

∑

= ∞ = − − ₌ = 0 0 ) ( n n j n j ne ae n a X ω ω ω bila |a| < 1 → ω _jω ae X ₋ − = 1 1 ) (

Maka Energy Density Spectrum-nya adalah

(

ω

)(

ω

)

ω ω ω _{j j} xx ae ae X X S − − = = ₋ 1 1 1 ) ( ) ( ) ( * ₂ cos 2 1 1 a a + − = ω

Gambar 12. Energy density spectrum.

Tujuan Belajar 16

Peserta mengerti hubungan spektrum antara sebuah pulsa rektangular dengan spektrum dari deret pulsa rektangular waktu diskrit.

Bila diketahui suatu skuens

   ≤ ≤ − = otherwise L n A n x , 0 1 0 , ) ( ,

bagaimana kita menentuka ni X(ω) dan Sxx(ω) nya?

Pertama-tama kita lihat bahwa

∑

∑

∞ −∞ = − = ∞ < = = n L n A L A n x 1 0 | | | | ) ( , maka Transformasi

Fourier-nya ada. Lebih lanjut, kita mencatat bahwa x(n) adalah sinyal energi berhingga dengan Ex A L

2

| |

= .

Maka Transformasi fouriernya adalah :

∑

− = − − − − − = = 1 0 1 1 ) ( L n j L j n j e e A Ae X _ω ω ω ω ) 2 / sin( ) 2 / sin( ) 1 )( 2 / ( L L Ae−jω L− ω = dengan 2 / sin 2 / sin ) 1 ( 2 ) ( ω ω ω ω A L L X =∠ − − +∠ ∠

Gambar 13. Spektrum pulsa rektangular. Perhatikan bahwa k Nck N X =     2π k=0,1,….,N-1

2 Ekstensi Transformasi Fourier

2.1 Hubungan Spektrum dengan Transformasi z

Tujuan Belajar 17

Peserta mengerti hubungan transformasi Fourier dengan z.

Transformasi Z untuk skuens x(n) didefinisikan sebagai

∑

∞ −∞ = − = n n z n x z X( ) ( ) ROC : r2 < |z| <r1

Marilah kita menuliskan variable kompleks z dalam bentuk z = rejω. Maka diperoleh :

[

]

∑

∞ −∞ = − − = = n n j n re z x n r e z X j ω ω ( ) ) (

Perlu dicatat bahwa, Transformasi Fourier ada bila

∑

∞ −∞ = ∞ < = n x x n E | ( )|2

Z transform exist bila

∑

∞ −∞ = −

_<

_∞

n n

r

n

x

(

)

|

|

- anu(n), |a| > 1 → ada daerah Z-transform exist, FT tidak -n n n x c π ω sin )

( = , ada daerah FT exist Z-transform tidak Keduaya exist bila |z| = 1 ∈ ROC

2.2 Konsep Cepstrum

Tujuan Belajar 18

Peserta dapat menghitung Cepstrum dari sinyal.

Untuk skuens {x(n)} yang mempunyai transformasi-Z X(z), diasumsikan bahwa {x(n)} adalah skuens stabil sehingga X(z) konvergen pada unit circle.

Cepstrum kompleks dari dari skuens {x(n)} didefinisikan sebagai skuens {cx(n)}

yang merupakan invers tranformasi-Z dari Cx(z), dimana

{ } {

}

( )

( )

1 ; 1 0 : ROC ln ) ( ) ( 2 1 2 1 > < < < < = ↔ r r r z r z C z X n c n x x x b b

Dalam ROC tersebut, Cx(z) dapat direpresentasikan dengan Deret Laurent :

∑

∞ −∞ = − = = n n x x z X z c n z C ( ) ln ( ) ( ) dimana

∫

− = c n x X z z dz j n c ln ( ) 1 2 1 ) ( π

Secara Transformasi Fourier, bila |z| = 1∈ ROC, maka :

∑

∞ −∞ = − = = n n j x x X c n e C (ω) ln (ω) ( ) ω

dimana {cx(n)} adalah skuens yang diperoleh dari invers tranformasi fourier dari X(ω), yaitu

∫

− = π π ω _ω ω π X e d n cx ln ( ) j n 2 1 ) (

Dalam ekpresi magnitude dan fasa,

) ( | ) ( | ) (ω X ω ejθ ω X = maka ) ( | ) ( | ln ) ( lnX ω = X ω +jθ ω

Dengan melakukan substitusi, kita peroleh Cepstrum Kompleks dalam bentuk :

[

]

∫

∞ ∞ − + = ω θ ω ω π ω _d e j X n c j n x | ( )| ( ) 2 1 ) (

2.3 Transformasi Fourier pada Sinyal dengan Pole di Unit-Circle

Tujuan Belajar 19

Peserta dapat mengekstensi transformasi Fourier agar dapat mencakup sinyal dengan pole pada unit circle.

Transformasi Fourier terdefinisi bila X

( )

z _z=1, sayangnya bila ada pole pada |z| = 1 maka Transformasi Fourier tidak eksis.

Skuens semacam itu misalnya skuens unit step yang mempunyai transformasi-Z :

1 1 1 ) ( ₋ − = z z X

atau skuens x(n)=(cos ωon)u(n) yang mempunyai transformasi-Z : 2 1 1 cos 2 1 cos 1 ) ( _{− −} − + − − = z z z z X o o ω ω

Untuk skuens semacam itu, kita dapat mengizinkan Transformasi Fourier untuk mengandung impuls pada frekuensi tertentu yang berkorespondensi dengan dengan lokasi pole dari X(z) yang terletak pada unit circle. Maka digunakan impulse δ(ω), yaitu sinyal dengan magnitude ∞, infinite angle, zero width dan unit area. Jadi "abaikan" titik-titik pole.

Kita lihat beberapa contoh skuens berikut dengan mengevaluasi Transformasi-Z-nya pada unit circle.

*Bagaimana menentukan Transformasi Fourier untuk sinyal step ? 1 1 1 ) ( ) ( ) ( 1 = − − = → = ₋ z z z z X n u n x

→ pole di z = 1

(

)

j j j j j j j j z e e e e e e z X X 2 2 1 | | . 1 ) ( ) ( 2 2 2 ω ω ω ω ω ω ω _{= −} − = − = = kecuali z=1 atau ω=0 ( )

( )

ω πδ

( )

ω π ω π ω ω ω π ω ω = = ≠ = = − 1 , 2 di 2 2 sin 2 1 2 sin 2 2 2 X k k e j e j j

*Bagaimana menentukan Transformasi Fourier untuk sinyal x(n) = (-1)nu(n) ? π j e z z z z X → =− = + = 1 1 ) ( 2 ↓ pole untuk ω≠ 2π(k+1/2)

(

)

2 2 1 | | 2 . 1 1 ) ( 2 2 2 ω ω ω ω ω ω _{j j} j j j z e e e e e z z X _{= −} + = + = + = 2 2 cos 2 1 ω ω j e =

*Bagaimana menentukan Transformasi Fourier untuk sinyal x(n) = cos ωonu(n) ? 2 1 1 cos 2 1 cos 1 ) ( _{− −} − + − − = z z z z X o o ω ω

(

j o

)(

j o

)

o j e e e X _{ω ω ω ω} ω _ω ω _{− −}− ₊ − − − = _{( (} 1 1 cos 1 ) ( ω≠±ωo + 2πk 2.4 Teorema Sampling Tujuan Belajar 20

Peserta dapat memahami teorema sampling dalam kontek domain frekuensi (hubungan antara X

( )

F dengan X

( )

ω ), termasuk konsep aliasing, dan interpolasi.

Bagianakah hubungan antara X(F) dengan X(ω) ? Xa(t) xa(nT) = x(n)

• xa(t) adalah sinyal aperiodik dengan energi berhingga, maka spektrumnya dapat

ditunjukkan oleh relasi Tranformasi Fourier : dt e t x F Xa a j Ft π 2 ) ( ) ( − ∞ ∞ −

∫

= dF e F X t x_a( )

∫

_a( ) j2πFt ∞ ∞ − =

• Sedangkan spktrum untuk sinyal diskrit x(n) dapat ditunjukkan oleh relasi Tranformasi Fourier :

∑

∞ −∞ = − = n n j e n x X(ω) ( ) ω atau

∑

∞ −∞ = − = n n j e n x f X( ) ( ) 2π/ skuens x(n) dapat dikembalikan sebagai :

∫

∫

− − = = 2 / 1 2 / 1 2 ) ( ) ( 2 1 ) (n X e d X f e df x j n j πfn π π ω _ω ω π

∫

∫

∞ ∞ − − = = =x n x nT x F e dF df e f X j πfn _{a a} j2πFnT 2 / 1 2 / 1 2 ) ( ) ( ) ( ) ( Ingat bahwa dF F df F F f s s 1 = → = , maka :

( )

∫

∫

− ∞ ∞ − =     2 / 1 2 / 1 2 2 ) ( 1 dF e F X dF e F F X F s F F s F F _{j n} a n j s s π π

( )

∑ ∫

₌∞_−∞ + − = k F k F k n j a s s s F F dF e f X ) ( ) ( 2 2 1 2 1 ) ( π

∑ ∫

₌∞_−∞ − − = k F F n j s a s s s F F dF e kF F X 2 / 2 / 2 ) ( π

∫ ∑

− − = 2 / 2 / 2 ) ( s s s F F F F k n j s a F kF e dF X π Disimpulkan bahwa :

∑

∞ −∞ = − =     k s a s s kF F X F F F X ( ) atau

[

]

∑

∞ −∞ = − = k s a s X f K F F f X( ) ( ) **)

Berikut ini gambar sampling dari suatu sinyal analog pita terbatas dan aliasaing dari komponen spectral.

)

(

ˆ

t

x

_a

_X

ˆ

₍

_F

₎

a

Gambar 14. Aliasing di domain frekuensi. Bila B < Fs/2, maka :

( )

    > ≤ = 2 2 1 0 s s s s F F F F F a F , F , X (F) X inversnya adalah

∫

− = 2 / 2 / 2 ) ( ) ( Fs Fs Ft j a a t x F e dt x π

[

]

∫ ∑

− − = /2 2 / 2 2 ) ( 1 ) ( Fs Fs Ft j n j s a x n e e dF F t x Fs F π π

∑

₌∞_−∞

∫

− − = n Fs Fs t F j s dF e n x F Fs n 2 / 2 / ) ( 2 ) ( 1 π

(

)

(

t nT

)

g nT t T nT x n a − ↓       ₋

∑

∞ −∞ = sinc ) ( π

dimana ( ) sinc t sinc(2 Bt) T t g π = π      =

Persamaan diatas yang digunakan untuk merekonstruksi sinyal analog dari sampelnya disebut sebagai formula interpolasi ideal.

Teorema Sampling : Suatu sinyal waktu-kontinyu pita terbatas, dengan frekuensi tertinggi (bandwidth) B Hz, dapat direkonstruksi secara unik dari samplenya yang memiliki sampling rate Fs≥ 2B sampel per detik.

Relasi antara variabel frekuensi F dan f dapat dilihat pada gambar dibawah ini.

Gambar 15. Gambar dibawah ini menunjukkan relasi untuk sinyal sampel pada domain waktu dan domain frekuensi.

≤

∫

−∞ ∞

=

X

f

e

df

n

x

(

)

(

)

j2πfn

∑

∞ −∞ = −

=

n fn j

e

n

x

f

X

(

)

(

)

2π

∑

∞ −∞ =

−

=

k s q s

X

f

k

F

F

f

X

(

)

(

)

∫

∞ ∞ − −

=

x

t

e

dt

F

X

_a

(

)

_a

(

)

j2πFt

∑

∞ −∞ =

−

−

=

n a

T

nT

t

T

nT

t

n

x

t

x

/

)

(

/

)

(

sin

)

(

)

(

π

π

∫

∞ ∞ −

=

X

F

e

dF

t

x

_a

(

)

_a

(

)

j2πFt

Gambar 16. Peta spektrum dari sinyal kontinue dan diskrit hasil samplingnya. Sekarang marilah kita melihat contoh soal berikut.

Jika diberikan sinyal waktu-kontinyu x_a(t)=cos2πF_ot, dengan sampling Fs, Fs/2 < Fo

Gambar 17. Hasil rekonstruksi spektrum.

2.5 Konsep Bandwidth

Tujuan Belajar 21

Peserta mengerti berbagai konsep bandwidth, termasuk LP, HP, BP, BS.

Bandwidth adalah range dari frekuensi dimana energi density spectrum terkonsentrasi. Bandwidth dikatakan berkisar pada F1 ≤ F ≤ F2 , bila 95% power of energy berada

dalam range antara F2 dan F1.

Dalam term sinyal bandpass, maka

*Sinyal narrow-band adalah sinyal yang bandwidth-nya 

     + ≈ − 2 10 1 1 2 F2 F1 F F

*Sinyal wide-band adalah sinyal yang bandwidth-nya yang lebih besar dari sinyal narrow-band.

*Sinyal bandlimited adalah sinyal yang spektrumnya nol diluar range frekuensi |f|≥B. Suatu sinyal waktu-diskrit energi berhingga x(n) dikatakan bandlimited bila :

|X(ω)| = 0 untuk ωo < |ω| <π.

*Sinyal timelimited adalah bila x(t) = 0, |t| > τ ωo < |ω| <π

Perlu dicatat bahwa secara absolut tidak ada sinyal yang time limited sekaligus dengan band limited.

Gambar 18. Filter lowpass, highpass, dan bandpass.

3 Sifat-Sifat Transformasi Fourier

Tujuan Belajar 22

Peserta mengerti dan dapat memanfaatkan sifat-sifat transformasi Fourier, seperti simetri dari sinyal real, sifat linier, time-shifting, convolution, correlation, Frequency shifting, Modulation, Parseval’s, Multiplication, dan differentiation.

Berikut ini adalah sifat-sifat Transformasi Fourier :

Gambar 19. Hubungan simetris. • Linear

( )

( )

∑

αixi n →

∑

αiXi ω Sebagai contoh :

( )

( )

( )

( )

   ≥ < =    < ≥ = < = − 0 n 0 0 n 0 n 0 0 n X cari 1 a 2 1 n n a n x a n x a n x n ω Diperoleh :

∑

∞

∑

−∞ = ∞ = − − ₌ = n n n j n n j e a e n x X 0 1( ) ( ) ω ω ω

(

)

∑

∞ = − − − = = 0 1 1 n j n j ae ae ω _ω

(

)

∑

∑

∞ = − − −∞ = − ₌ = 1 1 2( ) k K j n n j n ae e a X ω ω ω

∑

( )

∞ = − = = 0 1 k j j K j j ae ae ae ae _ω ω ω ω

2 2 cos 2 1 1 1 1 1 ) ( a a a e ae ae X _j j j − + − = − + − = ₋ ω ω _ω ω_ω

• Time Shifting dan Time reversal

( )

( )

( )

ω

( )

ω ω _{X X} e -n x n-k x k j − ↓ ↓ • Konvolusi ) ( ) ( ) ( ) ( _{2 1 2} 1 n x n X ω X ω x ∗ ↔

Sebagai contoh, hitunglah konvolusi dari x1(n) * x2(n)

Dimana

{ }

↑ = = 1 , 1 , 1 ) ( 2 1(n) x n x Maka :

( )

ω ₂

( )

ω 1 2cosω 1 = X = + X

⇒ X(ω) = (1 + cos ω)2 = 1 + 4 cos ω + cos 2ω = 3 + 2(ejω + e -jω) + (ej2ω + e -j2ω)

{

}

↑ = 5 , 4 , 3 , 2 , 1 x(n) • Korelasi

∑

∞ −∞ = − = k x x n x k x k n r_{1 2}( ) ₁( ) ₂( ) ) ( ) ( ) ( _{1 2} 2 1 ω X ω X ω S x x = ⇔ ) ( ) ( _xx ω xx l S r ↔ Auto-Korelasi • Frequency Shifting ) ( ) ( _o n j X n x e ωo ↔ ω−ω • Modulation

[

( ) ( )

]

cos ) ( 2 1 o o on X X n x ω ↔ ω+ω + ω−ω

Gambar 20. Hasil modulasi. • Parseval

∫

∑

− ∞ ∞ − ↔ π π ω ω ω π X X d n x n x ( ) ( ) 2 1 ) ( ) ( ₂* _{1 2}* 1 • Multiplication

∫

− − ↔ π π λ λ ω λ π X X d n x n x ( ) ( ) 2 1 ) ( ) ( _{2 1 2} 1 • Diferensiasi ω ω d dX j n nx( )↔ ( ) Tujuan Belajar 23

Peserta menguasai pasangan transformasi yang berguna seperti impuls, rektangular, dan fungsi sinc.

Tabel berikut memberikan pasangan Transformasi Fourier untuk sinyal waktu-diskrit aperiodik yang sering digunakan.

−π π X(ω) 1 π/2 −π/2 2_π −2π ω ω ω 0 0 _π −π/2 π/2 1 Y1(ω) 0 π/2 π −π/2 −π −π 1 1/2 Y₂(ω) = X(ω-π)

Tabel 1. Pasangan transformasi Fourier yang sering digunakan.

4 Transformasi Fourier untuk Sistem

4.1 Sistem LTI di Domain Frekuensi

Tujuan Belajar 24

Peserta menguasai konsep eigenvalue dan eigenfunction dalam konteks respons frekuensi dari sistem LTI, terutama untuk menghitung respons sistem.

Eigenfunction dari suatu sstem sistem adalah sinyal input yang menghasilkan output yang berbeda dari input karena perkalian dengan faktor konstan. Faktor pengali tersebut disebut sebagi eigenvalue dari sistem.

Aejωn y(n) H(ω)

∑

∞ −∞ = − = k k n j Ae k h n y( ) ( ) ( )

( )

ω ω ω H e e k h A j n k k j ) ( ↓     =

∑

∞ −∞ = − y(n) = AH(ω)ejωn Maka

H(ω) adalah eigen value

ejωn adalah eigen vector/ eigen function

Sebagai contoh, tentukan output dari sistem dengan respon impuls _h(_n)=

( )

₂1 n_u(_n) _dan input x₍n₎=Aejπ2n_.

Kita cari H(π₂) terlebih dahulu untuk kemudian mencari y(n), hasilnya :

( ) fasa er terges amplitudo tergeser 5 2 ) ( 2 26.6 ↑ ↑ = _{j n}− o Ae n y π Tujuan Belajar 25

Peserta dapat menghitung respons frekuensi (magnitude dan phase) dari sistem yuang diketahui h(n) nya, dan dapat memanfaatkannya untuk menghitung output dari sinyal complex exponential dan sinusoidal dengan durasi tak terhingga.

Secara umum kita dapat menulis :

) ( ) ( ) (ω H ω ejθ ω H = ↓ = ∠ H(ω)

( )

ω

( )

ω ω ω ω I R k k jH H k k h j k co k h H sin ) ( ) ( ) ( + ↓ ↓ − =

∑

∑

      − + = ( ) ) ( tan 2 2 1 ) ( ) ( ω ω ω ω R I H H j I R H e H

dengan catatan HR(ω) = HR(-ω)

HI(ω) = -HI(-ω)

Sebagai contoh, tentukan magnitude dan fasa dari h(ω) sistem three-point moving averages. y(n) = 1/3 (x(n+1) + x(n) + x(n-1)) Karena h(n) = {1/3, 1/3, 1/3} maka

(

)

(

)

( )

ω ω ω ω ω R j j H e e H cos 2 1 1 ) ( ₃1 3 1 ↑ + = + + = −

( )

0 ) cos 2 1 ( ) (ω = ₃1 + ω ω = I H H ) ( 0 ) ( ) ( ) ( tan ω ω ω ω θ R R I H H H = =

Jadi untuk input Aejωn

y(n) = A|H(ω)|ejθ(ω)ejωn = A|H(ω)|ej(ωn+θω) - input Ae-jωn n j j e e H A n y( )= (−ω) θ(−ω) −ω ) ) (ω − (ω +θ(ω) = j n e H A - input Acosωn )) ( cos( ) ( ) (n = AH ω ωn+θ ω y - input Asinωn )) ( sin( ) ( ) (n = AH ω ωn+θ ω y |H(ω)| = magnitude response θ(ω) = phase response

Sebagai contoh, tentukan respon dari sistem dengan input sinyal x(n) = 10 - 5sinπn/2 + 20 cos ωπn Frekuensi responsnya ω ω _j e H ₋ − = 2 1 1 1 ) ( - untuk 10 →ω = 0 → H(0) = 2 - untuk π/2 →ω = π/2 →

( )

_j e j o e H 26.6 2 1 2 5 2 1 1 2 − − = − = π π - untuk π→ω = π→ 3 2 1 1 ) ( 2 1 = − = _{− π} π _j e H

Maka :

(

−

)

+ ∞< <∞ − = cos - n 3 40 6 . 26 sin 5 10 20 ) (n ₂n n y π o π

[

]

∑

∑

= = + + = ⇒ + = L i i i i L i i i in y n A H n A n x 1 1 1 1cos( ) ( ) ( ) cos ( ) ) ( ω φ ω ω φ θ ω

4.2 Respons Steady State dan Transien

Tujuan Belajar 26

Peserta dapat menghitung respons steady state dan transien pada sinyal input sinusoidal, khususnya pada kasus sistem y

( )

n =ay

( ) ( )

n−1+xn .

Bagaimanakah respons steady state dan respons transient pada sinyal sinusoidal?

• bila x(n) diterapkan pada n = -∞ maka tidak ada transien

• bila x(n) diterapkan pada n = 0 maka akan muncul transient Sebagai contoh,

y(n) = ay(n-1) + x(n) dan x(n) diterapkan pada n = 0 maka condition initial 0 n ) ( ) 1 ( ) ( 0 1 ↓ ≥ − + − =

∑

= + n k k n k n x a y a n y

asumsikan x(n) = Aejωn n ≥ 0, diaplikasikan pada n=0, diperoleh :

∑

= − + _{− +} = n k k n j k n e a A y a n y 0 ) ( 1 ) 1 ( ) ( ω transient decay to 1 a karena state steady 0 n 1 1 ) 1 ( ) 1 ( 1 1 → → < ↑ ↑ ≥ − + − − − = + + −₋ + ₋ φ ω ω ω ω ω n j j n j j n j n n e ae A e ae e Aa y a

Bila menyangkut input sinudoidal, apalagi bila |a| kecil, → transient sering diabaikan → SS penting

Bagaimanakah respons steady state terhadap sinyal periodik ? 1 0 ) ( ) ( / 2 1 0 , ..., k e c n x N n x N kn j N k k = = = +

∑

− = π let

x

_k

(

n

)

=

c

_k

e

j2πkn/N ← komponen cari response

→ x(n)=

∑

xk(n)

( )

( )

N k n p j N pk k k k H e H c (n) H(? (? (n) y N k π ω ω 2 2 2 = ↓ = =

( )

n y dari series Fourier 2 ) ( ) ( 2 → ↓       = =

∑

∑

k k k n j k k d e N k H c n y n y N k π π

LTI mengubah amplitudo dan menggeser fasa, tetapi tidak mempengaruhi perioda N Tujuan Belajar 27

Peserta dapat menghitung respons sistem pada sinyal input yang aperiodik.

Untuk menghitung respons terhadap sinyal aperiodik, pertama-tama marilah kita lihat teorema konvolusi :

Y(ω) = H(ω) X(ω) Yang berarti pula :

Y(ω)| = |H(ω)||X(ω)|

∠Y(ω) = ∠X(ω) + ∠H(ω)

→ H(ω) filter

→ X(ωi) = 0 → y(ωi) = 0 sistem tidak menambah frekuensi.

Skuens output dapat ditentukan dari invers transformasi Fourier :

∫

∞ ∞ − = ω ω π ω d e Y n y ( ) j 2 1 ) ( ↑

Tapi metode ini jarang digunakan karena kalah populer dibanding Z-transform. Dari pengkuadratan magnitude, kita memperoleh :

|Y(ω)|2 = |H(ω)|2|X(ω)|2 Syy(ω) = (H(ω))2 Sxx(ω)

4.3 Hubungan Dengan Fungsi Sistem

Tujuan Belajar 28

Peserta dapat menghitung H

( )

ω dari H

( )

z atau pole-zeronya.

Kita tahu bahwa bila fungsi sistem H(z) konvergen pada unit circle, maka kita mendapatkan respons frekuensi dari sistem dengan mengevaluasinya pada unit circle. Maka kita dapatkan

(

)

(

)

∏

∏

= − = − = − − = = _N i j k M k j k o e z e p e z b z H H j 1 1 1 1 ) ( ) ( ω ω ω ω dengan

(

)

(

)

     = − − =

∏

∏

= = * * 1 * 1 * * 1 1 1 ) ( z H e p e z b H _N k j k M k j o ω ω ω Jadi H ω H ω H ω H ω H ω H z H z _z=ejω − = − = = ( ) ( ) ( ) ( ) ( ) ( ) ) ( 2 * 1

Untuk menghitung H(ω) kita lakukan

(

)

(

)

(

)

(

)

∏

∏

∏

∏

= = − = − = − = − − = − − = = _N k k j M k k j M N j o N i j k M k j k o e z p e z e e b e p e z b z H H k k j 1 1 ) ( 1 1 1 1 ) ( ) ( ω ω ω ω ω ω ω ) (

)

(

θ ω ω

_ω

j k k k j

e

v

z

e

−

=

→

) (

)

(

φ ω ω

_ω

j k k j

e

u

p

e

−

=

→

maka ) ( )... ( ) ( )... ( ) ( 1 1 ω ω ω ω ω N M o U U V V b H =

∑

∑

= = − + − + ∠ = ∠ M i N i i i o N M b H 1 1 ) ( ) ( ) ( ) (ω ω θ ω θ ω

Gambar-gambar berikut merupakan intepretasi geometris dari kontribusi pole dan zero untuk Transformasi Fourier.

Gambar 21. Ilustrasi geometris dari pengaruh pole dan zero terhadap spektrum. Sebagai contoh, evaluasilah respons frekuensi dari sistem yang dideskripsikan oleh fungsi sistem : 8 . 0 ) ( 8 . 0 8 . 1 1 ) ( ₁ − = ⇒ − ± − = ₋ ω _jω jω e e H z z z z H

Jelas, H(z) memiliki zero pada z=0 dan pole pada p=0.8, maka :

ω ω _ω ω cos 6 . 1 64 . 1 1 8 . 0 ) ( − = − = _j j e e H

dan 8 . 0 cos sin tan ) ( 1 − − = − ω ω ω ω θ dalam decible :

∑

∑

= = − + = M k N k k k dB b V U H 1 1 10 10 20 log ( ) 20 log10 ( ) log 20 ) (ω ω ω

5 Sistem LTI Sebagai Filter

5.1 Konsep Filter

Tujuan Belajar 29

Peserta memahami bahwa sistem LTI dapat dipandang sebagai filter, terutama dalam hal magnitude response nya.

Filter adalah divais yang menentukan apa yang dilewatkan dari input yang diberikan. Kelakuan fikter ditentukan oleh karakteristik respons frekuensi H(ω), yang bergantung pada parameter sistem. H(ω) berlaku sebagai weighting function atau spectral shaping function untuk komponen-komponen frekuensi yang berbeda dalam sinyal input. Dalah hal ini, setiap sistem LTI dapat dipandang sebagai filter frequency-shaping.

Y(ω) = H(ω) X(ω) → filter ↑

pembobot frekuensi/ Fungsi pengubah spektrum

Dengan mengubah-ubah ai dan bi, H(ω) dapat dibentuk dengan berbagai bentuk respons.

Gambar 22. Spektrum dari beberapa jenis filter. Tujuan Belajar 30

Peserta mengerti konsep linear phase response, dan motivasinya.

Karakteristik lain dari filter ideal adalah respon fasa linear. Untuk mendemonstrasikannya, marilah kita lihat :

   < < = − otherwise ce H o n j , 0 , ) (ω ω1 ω ω2 ω

C, no constants. Let X(ω) ada di [ω1,ω2]

Output filter mempunyai spektrum

Y(ω) = X(ω)H(ω)= CX(ω)e-jωno ω1 < ω <ω2

Dari sifat Transformasi Fourier, diperoleh y(n) = Cx(n-no)

Jadi output dari sistem ini adalah sinyal aslinya yang tergeser fasa dan terskala. Kedua perubahan ini biasanya dapat ditoleransi apabila terjadi pada sinyal seutuhnya.

Dengan demikian filter-filter ideal mempunyai karakteristik linear di daerah passband, θ(ω) = -ωno delay :

ω

ω

θ

ω

τ

d

d

g

)

(

)

(

=

−

→ envelope delay/ group delay

→τg(ω) adalah time delay dari komponen ω akibat filter.

Pada kasus fasa linear,

τg(ω) = no→ semua komponen mendapat delay yang sama, sehingga integritas

sinyal terjaga.

Tujuan Belajar 31

Peserta mengetahui definisi filter ideal, dan mengapa tidak dapat di buat secara praktis.

Dari bagian sebelumnya, dapat kita simpulkan bahwa filter passband ideal memiliki karakteristik

- magnitude yang konstan - fasa yang linear

Sayang sekali, hal ini hanya ada di dunia matematis

Sebagai contoh, filter lowpass ideal memiliki respons impuls n n n h c ep π π ω sin ) ( = -∞ < n <∞

→ non causal, not absolutely summable → unstable

→ Dalam praktek, filter ini dijadikan pedoman ideal untuk proses aproksimasi Kita akan melihat bagaimana filter-filter dapat dibuat berdasarkan penempatan pole dan zero. Prinsip utama : letakkan ke dekat unit circle. Frekuensi sekitar zero akan diredam, frekuensi sekitar pole akan diperkuat.

Selanjutnya :

- pole harus di dalam UC, zero bisa di mana saja

- pole/zero komplex harus berbentuk conjugate pairs agar koefisien real

(

)

(

)

∏

∏

∑

∑

= − = − = − = − − − = + = _N k k M k k o N k k k M k k k z p z z b z a z b z H 1 1 1 1 0 0 1 1 1 ) (

bo dipilih agar |H(ωo)| = 1di pass, N ≥ M

Tujuan Belajar 32

Peserta dapat membuat filter (LP, HP, BP, BS) dengan menempatkan pole-zero pada posisi yang sesuai.

Dalam mendesain filter digital lowpass,

- pole harus diletakkan dekat ω = 0 di dekat unit circle - zero harus diletakkan pada ω = π (high frequency)

Gambar 23. Contoh peletakan poles. Sebagai contoh,

( ) (

)

( )

? az a z H 0 , 1 H agar gain 1 1 1 1 1 1 = = ↑ − − = ₋ ω ω

Tambah zero z = -1 → atenuasi frequency response

( )

1 1 2 1 1 2 1 − − − + − = az z a z H