Masalah transportasi dan distribusi produk dalam kehidupan sehari-hari dapat dimodelkan sebagai vehicle routing problem (VRP). Model VRP akan menghasilkan sejumlah rute kendaraan untuk mengunjungi setiap konsumen. Pada umumnya, setiap rute berawal dan berakhir pada tempat yang sama, yaitu depot. Selain itu, model VRP juga memastikan agar total permintaan pada suatu rute tidak melebihi kapasitas kendaraan yang beroperasi.
Permasalahan dapat terjadi ketika perusahaan tidak memiliki kendaraan atau banyaknya kendaraan tidak dapat memenuhi permintaan konsumen, sehingga perusahaan diharuskan menyewa kendaraan lain. Kendaraan sewa akan mengunjungi konsumen dan tidak kembali ke depot. Untuk memecahkan masalah tersebut digunakanlah open vehicle routing problem (OVRP) yaitu model VRP dengan rute yang terbuka.
Model OVRP berbeda dengan model VRP karena kendaraan tidak diharuskan untuk kembali ke depot, atau jika kendaraan diperbolehkan kembali ke depot maka kendaraan akan mengunjungi kembali konsumen yang telah dikunjungi sebelumnya secara terbalik. Oleh karena itu rute kendaraan tidak tertutup tetapi terbuka.
merupakan gabungan antara masalah kapasitas dan masalah penentuan rute. Salah satu cara untuk menyelesaikannya adalah dengan menggunakan metode heuristik.
Dalam karya ilmiah ini, metode heuristik akan digunakan untuk mencari solusi dari OVRP. Solusi tersebut dapat dicari dengan bantuan software MATLAB versi 6.5.180913a.
1.2 Tujuan
Karya ilmiah ini disusun dengan tujuan menentukan himpunan rute yang meminimumkan total biaya transportasi. 1.3 Metode Penelitian
Metode yang digunakan dalam penulisan karya ilmiah ini adalah studi literatur. Materi dari karya ilmiah ini diambil dari artikel yang berjudul A Heuristic Method for the Open Vehicle Routing Problem yang ditulis oleh D Sariklis dan S Powell pada tahun 2000. Di samping itu dalam pembuatan karya ilmiah ini, penulis menggunakan beberapa bahan penunjang dari buku dan situs internet yang terkait dengan topik karya ilmiah ini.
II LANDASAN TEORI
Dalam bab ini akan dibahas mengenaiteori-teori yang berkaitan dengan pembahasan karya ilmiah ini.
2.1 Definisi Dasar Graf
Teori graf pertama kali dikenal sejak Euler (1736) meneliti tentang masalah jembatan Königsberg. Dua ratus tahun kemudian, pada tahun 1936, Dénes König telah menulis buku tentang teori graf yang pertama. Dalam periode yang relatif singkat, teori graf mengalami perkembangan yang sangat pesat. Definisi 1 (Graf)
Suatu graf G adalah pasangan terurut ( ) dengan V adalah himpunan berhingga dan takkosong dari elemen graf yang disebut simpul (node) dan E adalah himpunan pasangan takterurut (mungkin saja himpunan kosong) dari simpul-simpul berbeda di V. Misalkan G graf maka { } ( ) (dengan
( )) disebut sisi (edge). Sisi { } dapat dituliskan { } dan boleh disingkat dengan uv atau vu.
(Chartrand & Oellermann 1993)
z
v
y x w
G
:
Gambar 1 Graf G=(V,E) Pada Gambar 1 diperlihatkan graf dengan { } dan
Definisi 2 (Graf Trivial dan Taktrivial) Graf yang hanya memiliki sebuah simpul disebut graf trivial sedangkan yang lainnya adalah graf taktrivial.
(Chartrand & Oellermann 1993)
Gambar 2 Graf trivial.
Gambar 3 Graf taktrivial. Definisi 3 (Incident dan Adjacent)
Misalkan diberikan graf ( ) Jika { } ( ) dengan maka u dan v dikatakan adjacent di G dan e dikatakan incident dengan u dan v.
(Chartrand & Oellermann 1993) Ilustrasi incident dan adjacent diperlihatkan dalam Gambar 4. v u w x e1 e2 e 4 e3
D
:
Gambar 4 Graf D.Pada gambar 4, u dan v, v dan w, u dan w, dan x dan w adjacent di graf D. Sisi e1
incident dengan u dan v, sisi e2 incident
dengan u dan w, sisi e3 incident dengan x dan
w, dan sisi e4 incident dengan v dan w.
Definisi 4 (Subgraf)
Graf H adalah suatu subgraf dari graf G jika ( ) ( ) dan ( ) ( )
(Chartrand & Oellermann 1993) Pada Gambar 5, graf H adalah subgraf dari graf G pada Gambar 1.
z
y x w
H
:
Gambar 5 Graf H. Definisi 5 (Order dan Size)
Banyaknya simpul dari suatu graf G disebut order dari G, dan banyaknya sisi dari G disebut size dari G. Jadi order dari G adalah ( ) dan size dari G adalah ( ) Suatu graf dengan order p dan size q dituliskan sebagai graf ( )
(Chartrand & Oellermann 1993) v u w x e1 e2 e3 e4 e5
D
:
Gambar 6 Graf D=(p,q) dengan order 4 dan size 5.
Definisi 6 (Derajat suatu Simpul)
Derajat (degree) dari simpul v, dinyatakan dengan ( ) adalah banyaknya sisi yang incident dengan v.
Untuk suatu simpul v di G didefinisikan neighborhood ( ) atau ( ) yaitu himpunan simpul yang adjacent dengan v, yaitu:
( ) { ( ) ( )} Jadi ( ) ( ) yaitu banyaknya simpul yang adjacent dengan v.
Simpul yang berderajat 0 dinamakan simpul yang terisolasi, dan simpul berderajat 1 disebut simpul ujung (end vertex).
(Chartrand & Oellermann 1993) Pada Gambar 1, simpul v memiliki derajat satu sedangkan simpul x memiliki derajat tiga. Definisi 7 (Walk)
Walk W pada suatu graf G adalah barisan berhingga, atau yang dimulai dari suatu verteks dan berakhir pada suatu verteks juga, sehingga setiap sisi di dalam barisan harus incident dengan verteks sebelum dan sesudahnya.
Ilustrasi walk pada suatu graf bisa dilihat pada Gambar 6. adalah walk. Definisi 8 (Path)
Path adalah walk dengan setiap simpul yang berbeda.
(Chartrand & Oellermann 1993) Ilustrasi path bisa dilihat pada Gambar 6. adalah path.
Definisi 9 (Cycle)
Cycle adalah walk dengan dan semua simpulnya berbeda.
(Chartrand & Oellermann 1993) Ilustrasi cycle bisa dilihat pada Gambar 6. adalah cycle.
Definisi 10 (Digraf)
Graf berarah (digraf) adalah pasangan terurut ( ) dengan himpunan takkosong yang hingga, dan himpunan pasangan terurut yang menghubungkan elemen-elemen di . Elemen-elemen dari disebut sisi berarah (arc). Sisi berarah ( ) dinyatakan dengan garis berarah dari ke .
(Chartrand & Zhang 2009)
v u w x e1 e2 e3 e4 e5 Gambar 7 Digraf. Definisi 11 (Graf/digraf berbobot)
Suatu graf ( ) atau digraf ( ) dikatakan berbobot jika terdapat sebuah fungsi atau (dengan adalah himpunan bilangan real) yang memberikan sebuah bilangan real pada setiap sisi di atau sisi berarah di , disebut bobot. Setiap bobot ( )dengan atau dinotasikan dengan
(Foulds 1992) Definisi 12 (Adjacent ke dan Adjacent dari)
Jika ( ) adalah sebuah sisi berarah dalam graf D, maka u adjacent ke v, dan v adjacent dari u.
(Chartrand & Oellermann 1993)
Definisi 13 (Incident ke dan Incident dari) Jika ( ) adalah sebuah sisi berarah dalam graf D, maka sisi berarah ( ) incident dari v, dan incident ke v.
(Chartrand & Oellermann 1993) Definisi 14 (Derajat-masuk, derajat-keluar, dan derajat verteks dalam digraf)
Derajat-masuk id( ) dari simpul v dalam digraf D adalah banyaknya simpul yang adjacent ke v. Derajat-keluar od( ) dari simpul v dalam digraf D adalah banyaknya simpul yang adjacent dari v. Derajat dalam digraf D didefinisikan dengan
(Chartrand & Oellermann 1993) Pada Gambar 7 derajat masuk dari simpul u adalah 1 dan derajat keluar dari simpul u adalah 1.
Definisi 16 (Walk berarah)
Walk berarah pada suatu digraf D adalah walk yang sesuai dengan arah sisinya atau tidak berlawanan arah.
(Vasudev 2006) Ilustrasi walk berarah pada suatu digraf bisa dilihat pada Gambar 7. adalah walk berarah.
Definisi 17 (Path berarah)
Path berarah pada suatu digraf adalah walk berarah dengan semua verteks dalam barisannya tidak berulang.
(Vasudev 2006) Ilustrasi path bisa dilihat pada Gambar 7. adalah path berarah. Definisi 18 (Cycle berarah)
Pada graf berarah, cycle adalah path berarah yang tertutup dan takkosong.
(Chartrand & Oellermann 1993) Ilustrasi cycle berarah bisa dilihat pada Gambar 7. adalah cycle berarah.
Definisi 19 (Graf Terhubung dan takterhubung)
Misalkan u dan v adalah simpul dalam graf G. Simpul u terhubung ke v jika G mengandung sebuah path u-v. Graf G disebut graf terhubung jika u terhubung ke v untuk setiap pasangan u,v dari simpul-simpul di G.
Graf G dikatakan tak terhubung jika terdapat dua simpul u dan v yang tidak memiliki jalur u v
(Chartrand & Oellermann 1993)
(a) (b)
Gambar 8 Graf (a) terhubung dan (b) tak terhubung.
Definisi 20 (Tree)
Tree adalah suatu graf terhubung yang tidak mempunyai cycle.
(Foulds 1992) Ilustrasi tree dapat dilihat pada Gambar 9.
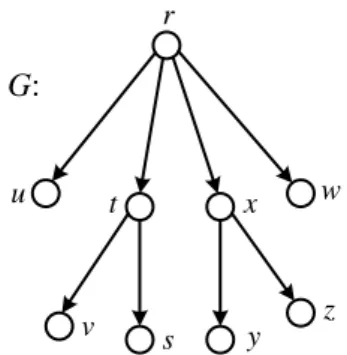
u r w t v s x y z
T
:
Gambar 9 Tree. Teorema 1Suatu tree berorder p mempunyai size
(Chartrand & Oellermann 1993) Definisi 21 (Tree pada digraf)
Suatu digraf terhubung yang tidak memiliki cycle disebut tree pada digraf.
(Chartrand & Zhang 2009) Ilustrasi tree untuk digraf dapat dilihat pada Gambar 10. u r w t v s x y z
G
:
Gambar 10 Tree pada digraf. Definisi 22 (Subtree)
Subtree adalah bagian dari tree yang jika dipisahkan dari tree tersebut, masih tetap tree.
(Chartrand & Oellermann 1993) Ilustrasi subtree dapat dilihat pada Gambar 11.
t
v s
a
Gambar 11 Subtree dari graf T. Definisi 23 (Spanning Subgraph)
Sebuah subgraf H dari graf G adalah sebuah spanning subgraph dari G jika ( ) ( )
(Chartrand & Oellermann 1993) Graf pada Gambar 8(b) merupakan spanning subgraph dari graf pada Gambar 8(a).
Definisi 24 (Spanning Tree)
Sebuah tree yang merupakan sebuah spanning subgraph dari graf terhubung G adalah sebuah spanning tree.
(Chartrand & Zhang 2009) Definisi 25 (Jarak dalam graf)
Dalam suatu graf taktrivial G dan untuk pasangan simpul di G, maka jarak antara simpul u dan v, ditulis ( ) atau ( ) adalah panjang dari path yang terpendek di G, jika path ini ada. Jika tidak, maka didefinisikan bahwa ( ) .
2.2 Algoritme Prim
Ada beberapa algoritme yang dapat digunakan untuk menentukan minimum spanning tree pada graf berbobot yang terhubung. Salah satu algoritme tersebut adalah algoritme Prim yang akan digunakan dalam karya ilmiah ini. Algoritme Prim digunakan pada graf berbobot ( ) yang taktrivial dengan p menyatakan order dari graf G dan q menyatakan size dari graf G.
Metode dari algoritme Prim adalah mengganti tree T dalam graf berbobot G yang terhubungkan dengan tree baru. Tree baru dibentuk dengan menambahkan sebuah sisi yang memiliki bobot minimum yang menghubungkan verteks dari T ke verteks yang tidak di T. Langkah-langkah algoritme Prim adalah sebagai berikut :
1. [Inisialisasi tree T]
Misalkan u sembarang simpul di G dan .
2. [Update tree T]
Jika v adalah simpul dengan jarak minimum ke u, maka
3. [Memeriksa apakah sebuah minimum spanning tree sudah terbentuk]
Jika ( ) dengan p adalah size dari graf T, maka keluarannya adalah ( ) Jika tidak, maka kembali ke Langkah 2.
(Chartrand & Oellermann 1993) Contoh pemakaian algoritme Prim
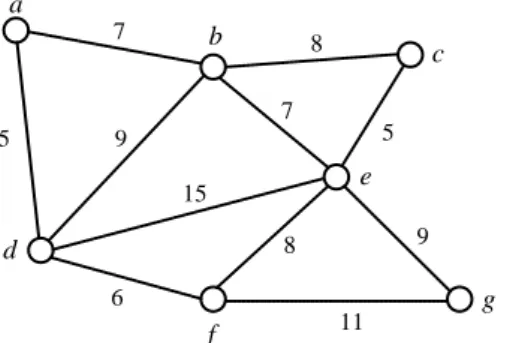
Diberikan G adalah graf berbobot seperti pada Gambar 12. a b c d e f g 5 6 7 9 8 7 15 5 8 9 11 Gambar 12 Graf berbobot G.
Jika dipilih d sebagai simpul awal, maka dengan algoritme Prim didapat minimum spanning tree dengan proses sebagai berikut : 1. a adalah simpul yang terhubung ke d
dengan bobot terkecil sehingga dipilih sisi da (lihat Gambar 13). a b c d e f g 5 6 7 9 8 7 15 5 8 9 11
Gambar 13 Sisi da hasil dari algoritme Prim tahap ke-1.
2. Simpul berikutnya yang dipilih adalah simpul dengan bobot terkecil terhadap d atau a. Sisi ab memiliki bobot 7, db berbobot 9, de berbobot 15, dan df berbobot 6, sehingga sisi df dipilih sebagai sisi yang memiliki bobot terkecil (lihat Gambar 14). a b c d e f g 5 6 7 9 8 7 15 5 8 9 11
Gambar 14 Sisi df hasil dari algoritme Prim tahap ke-2.
3. Algoritme dilanjutkan seperti tahap sebelumnya. Sisi ab dipilih sebagai sisi yang memiliki bobot terkecil terhadap sisi-sisi yang incident dengan simpul a dan d (lihat Gambar 15). a b c d e f g 5 6 7 9 8 7 15 5 8 9 11
Gambar 15 Sisi ab hasil dari algoritme Prim tahap ke-3.
4. Sisi be dipilih sebagai sisi yang memiliki bobot terkecil (lihat Gambar 16).
a b c d e f g 5 6 7 9 8 7 15 5 8 9 11
Gambar 16 Sisi be hasil dari algoritme Prim tahap ke-4.
5. Sisi ec dipilih sebagai sisi yang memiliki bobot terkecil (lihat Gambar 17).
a b c d e f g 5 6 7 9 8 7 15 5 8 9 11
Gambar 17 Sisi ec hasil dari algoritme Prim tahap ke-5.
6. Sisi eg dipilih sebagai sisi yang memiliki bobot terkecil (lihat Gambar 18).
Jadi, dihasilkan suatu minimum spanning tree dari graf G seperti pada Gambar 18.
a b c d e f g 5 6 7 7 5 9
Gambar 18 Solusi minimum spanning tree dengan bobot 39.
III PEMBAHASAN
Di dalam karya ilmiah ini akandiperkenalkan sebuah masalah manajemen distribusi, yang disebut open vehicle routing problem (OVRP). Masalah manajemen distribusi OVRP berbeda dengan vehicle routing problem (VRP). Ciri utama permasalahan yang membedakan OVRP dengan VRP adalah kendaraan tidak diharuskan kembali ke depot, namun jika kendaraan diperbolehkan kembali ke depot maka kendaraan akan mengunjungi kembali konsumen melalui rute sebelumnya secara terbalik.
OVRP bisa dijelaskan sebagai berikut. Misalkan terdapat sebuah depot dan himpunan konsumen yang memiliki permintaan terhadap barang. Pada depot terdapat sejumlah kendaraan transportasi. Setiap kendaraan memiliki kapasitas maksimum barang yang bisa dibawa dan tiap kendaraan juga memiliki biaya operasional. Biaya perjalanan antara depot dan semua konsumen, seperti juga dari konsumen ke konsumen, diketahui.
Permasalahannya adalah menentukan total biaya perjalanan yang minimum dan memenuhi tiga kriteria berikut:
i. setiap rute berawal dari depot dan berakhir pada konsumen,
ii. setiap konsumen hanya dikunjungi oleh tepat satu kendaraan dan permintaannya terpenuhi,
iii.total permintaan konsumen yang dikunjungi di setiap rute kurang dari atau sama dengan kapasitas kendaraan yang bertugas di rute tersebut.
Tujuannya adalah menentukan rute perjalanan yang meminimumkan total biaya perjalanan dan biaya pemakaian kendaraan.
Di dalam OVRP terdapat beberapa kondisi yang mungkin muncul ketika kendaraan melakukan pendistribusian barang dari depot ke konsumen, di antaranya:
i. kendaraan berangkat dari depot dan berhenti di konsumen akhir,
ii. kendaraan berangkat dari depot dan berhenti di konsumen akhir, lalu kembali lagi ke depot dengan melalui rute yang telah dilewati sebelumnya secara terbalik.