PENYELESAIAN BEDA HINGGA UNTUK PERSAMAAN PANAS DAN GELOMBANG DENGAN MENGGUNAKAN SEGITIGA PASCAL

i Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Yohanes Sulistiono

NIM: 043114016

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii Final Project

Presented as Partial Fulfillment of The Requirement to Obtain The Sarjana Sains Degree in Mathematics

By:

Yohanes Sulistiono

Student Number: 043114016

STUDY PROGRAM OF MATHEMATICS SCIENCE DEPARTEMENT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY

iii

PENYELESAIAN BEDA HINGGA UNTUK PERSAMAAN PANAS

DAN GELOMBANG DENGAN MENGGUNAKAN SEGITIGA

PASCAL

Oleh:

Yohanes Sulistiono

NIM: 043114016

Telah disetujui oleh:

Pembimbing

iv

GELOMBANG DENGAN MENGGUNAKAN SEGITIGA PASCAL

Dipersiapkan dan ditulis oleh Yohanes Sulistiono

NIM: 043114016

Telah dipertahankan di depan Panitia Penguji pada tanggal 1 September 2008

dan dinyatakan memenuhi syarat

Susunan Panitia Penguji

Ketua MV. Any Herawati, S.Si., M.Si. Sekretaris Herry Pribawanto S., S.Si., M.Si. Anggota Lusia Krismiyati B., S.Si., M.Si.

Yogyakarta, 23 September 2008 Fakultas Sains dan Teknologi

vi

memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 23 September 2008

Penulis

vii

Penyelesaian dari masalah persamaan panas dan masalah persamaan gelombang, dapat diperoleh secara eksak atau secara pendekatan. Suatu metode untuk memperoleh penyelesaian secara pendekatan adalah metode beda hingga. Dengan menggunakan metode tersebut, persamaan panas maupun persamaan gelombang diubah menjadi suatu persamaan beda hingga yang kemudian diselesaikan untuk menghasilkan penyelesaian beda hingga. Penyelesaian beda hingga tersebut akan konvergen ke penyelesaian eksaknya, jika selang letak ( x) dan selang waktu ( t) yang digunakan kecil ( x_→0 dan t_→0).

viii

equation problems can be obtained exactly or approximately. A method that can be used to obtain the approximate solution is finite difference method. By this method, heat and wave equations are changed into a finite difference equation and solved to obtain the finite difference solution. This solution would be converge to the exact solution, when the space distance ( x) and time distance ( t) that used are small ( x→0 and t→0).

ix

Nama : Yohanes Sulistiono Nomor Mahasiswa : 043114016

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:

PENYELESAIAN BEDA HINGGA UNTUK PERSAMAAN PANAS DAN GELOMBANG DENGAN MENGGUNAKAN SEGITIGA PASCAL

beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, me-ngalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini yang saya buat dengan sebenarnya. Dibuat di Yogyakarta

Pada tanggal : 23 September 2008

x

oleh penulis. Skripsi ini merupakan tugas akhir yang ditulis dalam rangka untuk mengakhiri Program S1 Matematika yang penulis ikuti di Universitas Sanata Dharma.

Selama proses penulisan skripsi ini, penulis mendapatkan bantuan, baik secara langsung atau tidak langsung, dari berbagai pihak. Oleh karena itu, penulis meng-ucapkan terimakasih kepada:

1. Ibu Lusia Krismiyati, atas koreksi, anjuran, serta masukkan yang diberikan selama membimbing penulis,

2. Romo Frans Susilo, atas anjuran yang diberikan saat kuliah Seminar Matematika,

3. Para dosen penguji: ibu Any Herawati, pak Herry Pribawanto, dan ibu Lusia Krismiyati, atas koreksi dan anjuran yang diberikan,

4. Romo Greg. Heliarko, sebagai Dekan Fakultas Sains dan Teknologi,

5. Kedua orang tua, kakak, dan adik, atas dukungan dan doa yang diberikan sehingga penulis terdorong untuk tetap bersemangat dalam mengerjakan skripsi,

6. Para karyawan Perpustakaan Sanata Dharma Paingan, atas pelayanan yang diberikan sehingga penulis tanpa kesulitan mendapatkan referensi yang dibutuhkan,

7. Para karyawan Laboratorium Komputer Dasar dan Tugas Akhir, atas pelayanan yang diberikan sehingga penulis dapat menggunakan fasilitas komputer untuk penulisan skripsi,

8. Para dosen, atas ilmu pengetahuan yang diberikan selama penulis mengikuti kuliah,

xi

11. Teman-teman seprodi, adik tingkat dan kakak tingkat, serta teman-teman seangkatan di prodi Fisika dan Ilmu Komputer, atas semua hal yang penulis alami bersama kalian,

12. Setiap pihak yang tidak dapat penulis sebutkan satu per satu.

Penulis sadar bahwa skripsi ini belum menjadi karya ilmiah yang baik dan sempurna. Oleh karena itu, setiap kritik dan saran yang pembaca berikan akan penulis terima dengan senang hati.

Yogyakarta, 22 September 2008

xii

HALAMAN PERSETUJUAN PEMBIMBING …...………... iii

HALAMAN PENGESAHAN ………. iv

HALAMAN PERSEMBAHAN ……….. v

PERNYATAAN KEASLIAN KARYA ……….. vi

ABSTRAK ………... vii

ABSTRACT ………. viii

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ……….... ix

KATA PENGANTAR ………. x

DAFTAR ISI ……… xii

BAB I PENDAHULUAN ……….... 1

A. Latar Belakang Masalah ……….. 1

B. Rumusan Masalah ……… 3

C. Batasan Masalah ……….. 4

D. Metode Penulisan ………. 4

E. Tujuan Penulisan ……….. 4

F. Manfaat Penulisan ……… 4

G. Sistematika Penulisan ……….. 4

BAB II SEGITIGA PASCAL ……….. 6

A. Permutasi dan Kombinasi ……….... 6

1. Aturan Penjumlahan (Sum Rule) ………. 6

2. Aturan Perkalian (Product Rule) ………. 8

3. Permutasi ………. 9

4. Kombinasi ………... 12

B. Bentuk Segitiga Pascal ………. 14

xiii

2. Persamaan Gelombang ……… 31

C. Penyelesaian Eksak Persamaan Panas dan Gelombang ………... 34

1. Persamaan Panas ………. 35

2. Persamaan Gelombang ……… 42

D. Pendekatan Beda Hingga ………. 46

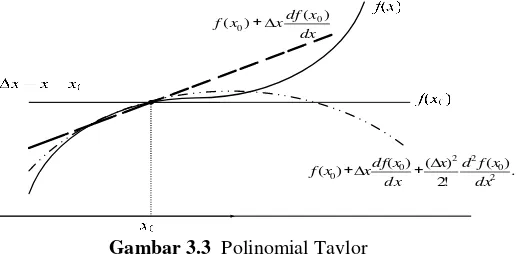
1. Pendekatan Polinomial Taylor ……… 47

2. Pendekatan Turunan Pertama dan Ke-dua ……….. 48

3. Turunan Parsial dalam Bentuk Pendekatan Beda Hingga ………….. 52

BAB IV PENYELESAIAN BEDA HINGGA UNTUK PERSAMAAN PANAS DAN GELOMBANG MENGGUNAKAN SEGITIGA PASCAL……. 54

A. Turunan Orde Tinggi dan Formulasi Segitiga Pascal untuk Persamaan Beda Hingga ………... 54

1. Pendekatan Beda Maju untuk Turunan Orde Tinggi ……….. 55

2. Pendekatan Beda Mudur untuk Turunan Orde Tinggi ……… 56

3. Pendekatan Beda Pusat untuk Turunan Orde Tinggi ……….. 57

4. Formulasi Segitiga Pascal untuk Persamaan Beda Hingga …………. 62

B. Penerapan pada Persamaan Panas dan Persamaan Gelombang ………... 65

1. Persamaan Panas (Difusi) ………... 65

2. Persamaan Gelombang ……… 90

BAB V PENUTUP ……….. 109

A. Kesimpulan ……….. 109

B. Saran ……… 110

DAFTAR PUSTAKA ……….. 111

A. Latar Belakang Masalah

Nilai dari turunan fungsi satu variabel di suatu titik, secara analitik dapat ditentukan dengan menggunakan definisi turunan suatu fungsi yang didapat dari proses limit. Turunan fungsi merupakan limit dari perbandingan selisih nilai fungsi di dua titik dengan jarak kedua titik tersebut. Secara pendekatan, nilai turunan fungsi di suatu titik dapat dicari tanpa menggunakan proses limit melainkan dengan memilih suatu nilai berhingga untuk jarak. Cara pendekatan inilah yang disebut pendekatan beda hingga. Pendekatan beda hingga dibedakan menjadi tiga metode, yaitu beda mundur, beda maju dan beda pusat.

Pendekatan beda hingga pada jangkauan yang lebih luas dapat diterapkan un-tuk mencari turunan suatu fungsi dengan orde yang lebih tinggi. Unun-tuk turunan fungsi dengan orde tinggi, formula yang digunakan sebagai pendekatan beda hingga memiliki bentuk yang lebih rumit. Sebagai contoh, turunan fungsi orde dua diperoleh dengan menurunkan turunan fungsi orde satu. Turunan fungsi orde-orde berikutnya didapatkan dengan cara yang sama.

Segitiga Pascal. Munculnya pola segitiga Pascal di dalam formula turunan fungsi dengan pendekatan beda hingga, memberikan solusi yang lebih cepat untuk memben-tuk suatu turunan fungsi. Hal ini menarik karena metode pendekatan beda hingga juga digunakan di dalam persamaan diferensial parsial.

Persamaan diferensial parsial merupakan suatu persamaan yang memuat suatu fungsi dengan dua atau lebih variabel dan beberapa turunan parsial didalamnya. Tu-runan parsial pada persamaan diferensial parsial merupakan perluasan dari tuTu-runan fungsi satu variabel pada penjelasan sebelumnya. Bentuk pendekatan beda hingga untuk persamaan diferensial parsial pada dasarnya menggunakan bentuk pendekatan beda hingga pada turunan fungsi satu variabel. Oleh karena itu, adanya hubungan antara bentuk turunan fungsi satu variabel dengan segitiga Pascal memungkinkan segitiga Pascal untuk digunakan dalam membentuk pendekatan beda hingga untuk persamaan diferensial parsial. Penyelesaian beda hingga dari suatu persamaan difer-ensial parsial diperoleh dengan cara membentuk persamaan beda hingga dari per-samaan diferensial parsial tersebut. Apabila perper-samaan diferensial parsial telah di-nyatakan dalam persamaan beda hingga maka persamaan diferensial parsial akan le-bih mudah untuk diselesaikan.

model tersebut adalah persamaan panas dan gelombang. Kedua persamaan tersebut dapat diselesaikan secara eksak maupun secara pendekatan.

Penyelesaian eksak persamaan panas dan gelombang memuat integral fungsi syarat awal yang diberikan dan juga deret tak hingga. Adanya deret tak hingga meng-akibatkan nilai penyelesaian eksak akan sulit ditentukan secara pasti. Selain itu, men-ghitung nilai integral untuk fungsi-fungsi dengan bentuk tertentu akan sulit dilaku-kan. Dengan demikian, metode numerik yang digunakan, yaitu metode beda hingga, diperlukan untuk menyelesaikan kedua masalah tersebut.

B. Rumusan Masalah

1. Bagaimana merumuskan formula persamaan beda hingga untuk turunan de-ngan menggunakan segitiga Pascal?

2. Bagaimana merumuskan formula persamaan beda hingga untuk penyelesaian persamaan panas dan persamaan gelombang dengan menggunakan segitiga Pascal?

C. Batasan Masalah

Pembahasan masalah yang ada hanya akan dibatasi pada mencari penyelesaian dari persamaan diferensial parsial orde dua yang linear homogen dengan koefisien kons-tan (persamaan panas dan persamaan gelombang).

D. Metode Penulisan

Metode penulisan yang digunakan adalah studi pustaka dari buku-buku serta jurnal.

E. Tujuan Penulisan

Memberikan gambaran yang jelas tentang bagaimana segitiga Pascal digunakan dalam menyajikan pendekatan beda hingga untuk persamaan panas dan persamaan gelombang.

F. Manfaat Penulisan

Memberikan pengetahuan tentang adanya hubungan antara segitiga Pascal dengan pendekatan beda hingga.

G. Sistematika Penulisan BAB I PENDAHULUAN

D. Metode Penulisan E. Tujuan Penulisan F. Manfaat Penulisan G. Sistematika Penulisan BAB II SEGITIGA PASCAL

A. Permutasi dan Kombinasi B. Bentuk Segitiga Pascal

BAB III PERSAMAAN PANAS DAN PERSAMAAN GELOMBANG A. Pengertian Persamaan Diferensial Parsial

B. Pembentukkan Persamaan Panas dan Gelombang C. Penyelesaian Eksak Persamaan Panas dan Gelombang D. Pendekatan Beda Hingga

BAB IV PENYELESAIAN BEDA HINGGA UNTUK PERSAMAAN PANAS DAN GELOMBANG MENGGUNAKAN SEGITIGA PASCAL

A. Turunan Orde Tinggi dan Formulasi Segitiga Pascal untuk Persamaan Beda Hingga

B. Penerapan pada Persamaan Panas dan Persamaan Gelombang BAB V PENUTUP

Segitiga Pascal dibentuk berdasar pada konsep permutasi dan kombinasi, yang menjadi konsep dalam penyusunan sejumlah objek dengan aturan tertentu. Konsep tersebut memuat sifat-sifat yang berlaku dalam penggunaannya. Pembahasan pada bab ini hanya akan difokuskan pada sifat-sifat yang bersesuaian dengan penggunaan segitiga Pascal di bab IV.

A. Permutasi dan Kombinasi

Pembahasan tentang konsep permutasi dan kombinasi diawali dengan mem-berikan aturan tentang perhitungan. Aturan tersebut adalah aturan penjumlahan dan aturan perkalian. Kedua aturan tersebut digunakan untuk menentukan banyaknya cara pemilihan sejumlah objek dari objek-objek yang tersedia. Hal yang membedakan kedua aturan tersebut dalam penggunaannya adalah prinsip pemilihan sejumlah objek yang dilakukan.

1. Aturan Penjumlahan (Sum Rule)

Aturan penjumlahan menyatakan: Misalkan terdapat dua buah kejadian. Ke-jadian pertama dapat muncul sebanyak w1 cara dan kejadian ke-dua dapat muncul

dari dua kejadian tersebut dapat muncul, namun tidak untuk muncul secara bersama-sama.

Aturan penjumlahan dapat diperluas untuk jumlah kejadian yang lebih dari dua. Misal diambil n kejadian. Kejadian pertama dapat muncul sebanyak w1 cara,

ke-jadian ke-dua dapat muncul sebanyak w2 cara yang berbeda, …, kejadian ke-n dapat

muncul sebanyak wn cara yang berbeda. Jadi, terdapat

n

w w

w1+ 2 +...+ cara (2.1.1)

untuk (hanya) salah satu kejadian dapat muncul.

Contoh 2.1.1

Sebuah perusahaan jasa membuka sebuah lowongan kerja untuk satu posisi, yang akan ditempatkan di bagian promosi. Lowongan tersebut dibuka untuk lulusan sar-jana maupun diploma. Pada hari terakhir penyeleksian pelamar, terdapat 7 orang lulu-san sarjana dan 3 orang lulululu-san diploma yang memenuhi persyaratan. Ada berapa banyak cara yang dimiliki perusahaan untuk memilih pelamar yang akan diterima se-bagai staf promosi perusahaan tersebut?

Penyelesaian: terdapat 7 + 3 = 10 cara pemilihan.

Contoh 2.1.2

Saat hari ulang tahunnya tiba, ayahnya memberi 9 topi bertuliskan ‘YOVHANA’ dan ibunya memberi 10 topi bertuliskan ‘MARIA’. Dengan demikian, Merlin memiliki cara sebanyak 9 + 10 = 19 cara untuk memilih mengenakan topi.

2. Aturan Perkalian (Product Rule)

Aturan perkalian menyatakan: Andaikan terdapat dua kejadian. Kejadian per-tama dapat terjadi dengan w1 cara dan kejadian ke-dua dapat terjadi dengan w2 cara

tanpa bergantung pada kejadian pertama. Dengan demikian, terdapat w1×w2 cara un-tuk dua kejadian tersebut terjadi (secara bersama-sama atau berurutan).

Seperti pada aturan penjumlahan, aturan perkalian juga dapat diperluas untuk lebih dari dua kejadian. Misalkan terdapat n kejadian. Kejadian pertama dapat terjadi dengan w1 cara, kejadian ke-dua dapat terjadi dengan w2 cara tanpa bergantung pada

kejadian pertama, kejadian ke-tiga dapat terjadi dengan w3 cara tanpa bergantung

pada kejadian pertama dan ke-dua, …, kejadian ke-n dapat terjadi dengan wn cara

tanpa bergantung pada kejadian pertama, ke-dua, ke-tiga, …, dan ke-(n-1). Jadi n ke-jadian tersebut dapat terjadi secara bersama-sama atau berurutan dengan

n

w w

w

w1× 2× 3×...× cara. (2.1.2)

Contoh 2.1.3

le-taknya bersebelahan. Jika seorang mahasiswa ingin mencari sebuah buku dan saat itu ia berada di Lantai Dasar, maka dengan berapa cara ia dapat naik ke ruang penyim-panan koleksi buku via lift?

Penyelesaian:

Oleh karena letak lift bersebelahan, maka mahasiswa tersebut dapat masuk lewat pintu lift manapun. Kemudian ia dapat memencet tombol penunjuk lantai untuk lantai I atau lantai II. Jadi, mahasiswa tersebut mempunyai 2 x 2 = 4 cara untuk menuju ke ruang penyimpanan koleksi buku via lift.

3. Permutasi

Misalkan terdapat suatu himpunan dengan n anggota, H, yang secara singkat disebut himpunan n-anggota. Secara umum definisi permutasi dari himpunan

n-anggota H adalah penyusunan tiap anggota himpunan tersebut dalam suatu urutan.

Contoh 2.1.4

Tiga orang kakak-beradik, yaitu NIA, ANI, dan IAN duduk bersebelahan di dalam sebuah bus yang membawa mereka menuju ke sekolah. Berapa banyakkah posisi duduk yang mungkin untuk mereka?

Penyelesaian:

un-tuk duduk di posisi sebelah kanan. Akhirnya unun-tuk tiap pilihan tersebut, terdapat 1 pilihan sisa untuk menempati posisi di sebelah kiri. Dengan demikian, dapat di-simpulkan bahwa terdapat 3 x 2 x 1 = 6 posisi duduk yang mungkin untuk NIA, ANI, dan IAN. Hasil tersebut berdasar pada aturan perkalian.

Misal diambil suatu bilangan, sebut r, dengan r∈ℤ+. Suatu r-permutasi dari himpunan n-anggota H adalah penyusunan r anggota secara berurutan dari n anggota

H. Jumlah r-permutasi dari himpunan H dinotasikan dengan P(n,r). Oleh karena

penyusunan dilakukan terhadap anggota-anggota H, maka permutasi tersebut hanya

berlaku untuk r≤n. Jika r >n, maka permutasinya bernilai nol, P(n,r)=0.

De-ngan kata lain tidak ada penyusunan yang dapat dilakukan untuk kasus tersebut.

Teorema 2.1.1

Jika n dan r adalah dua bilangan bulat positif dengan r≤n, maka

) 1 (

... ) 1 ( ) ,

(n r =n× n− × × n−r+

P . (2.1.3)

Bukti:

Menurut prinsip pemilihan objek pada aturan perkalian, terdapat n cara untuk pilihan

pertama, n−1 cara untuk pilihan ke-dua tanpa bergantung pada pilihan pertama, …,

dan n−(r−1) cara untuk pilihan ke-r tanpa bergantung pada r – 1 pilihan

sebelum-nya. Dengan demikian, r objek tersebut dapat dipilih dalam n×(n−1)×...×(n−r+1)

Secara khusus, jumlah permutasi untuk r=0 didefinisikan oleh P(n,0)=1. Hal ini

karena banyaknya cara untuk mengurutkan nol objek hanya terdapat satu cara.

Terdapat notasi yang penting untuk didefinisikan pada pembahasan di bab ini,

yakni n! yang disebut nfaktorial. Notasi tersebut didefinisikan oleh

! 1 2 ... ) 2 ( ) 1

(n n n

n× − × − × × × = , (2.1.4)

dengan n adalah bilangan bulat tak negatif. Secara khusus 0!=1.

Teorema 2.1.2

Jika r ≤n dan r, n adalah dua bilangan bulat tak negatif, maka

)! (

! )

, (

r n

n r

n P

−

= .

Bukti:

Menurut Teorema 2.1.1,

)! (

! )

1 (

... ) 1 ( ) , (

r n

n r

n n

n r n P

− = + − × × − ×

= ,

dengan 1≤r ≤n. Oleh karena 1

! ! )! 0 (

! _{= =}

− n

n n

n

untuk setiap n bilangan bulat tak

negatif, maka formula

)! (

! )

, (

r n

n r

n P

−

= juga berlaku untuk r=0. ■

Contoh 2.1.5

Sebuah perkumpulan pengendara sepeda motor besar menandai setiap sepeda motor

digunakan adalah 1, 7, 8, 4, dan 5 serta tidak ada dua sepeda motor dengan nomor

sama, maka ada berapakah jumlah sepeda motor yang ada di dalam perkumpulan

tersebut?

Penyelesaian:

Oleh karena terdapat 5 angka berbeda yang dipakai, maka perkumpulan tersebut

memiliki

20 4 5 ! 3

! 5 )! 2 5 (

! 5 ) 2 , 5

( = = × =

− =

P buah sepeda motor.

4. Kombinasi

Suatu r-kombinasi dari himpunan n-anggota H, dengan r bilangan bulat tak

negatif, menyatakan suatu penyeleksian r anggota dari n anggota H. Penyeleksian

tersebut tak berdasarkan urutan. Suatu r-kombinasi dari H juga dapat dinyatakan

se-bagai suatu himpunan bagian r-anggota dari H. Notasi yang digunakan untuk

me-nyatakan jumlah r-kombinasi dari H adalah _

    

r n

. Seperti pada permutasi, _=0

    

r n

,

untuk r >n.

Teorema 2.1.3

Jika 0≤r≤n, maka

     

=

r n r r n

Dengan demikian, )! ( ! ! r n r n r n − =       . Bukti:

Suatu r-permutasi dari himpunan n-anggota dapat diperoleh dengan membentuk

r-kombinasi dari himpunan tersebut dan kemudian mengurutkan tiap elemen dari

r-kombinasi tersebut. Jadi, menurut aturan perkalian didapat hubungan

! ) , ( ) , ( r r n r r P r n r n

P _×

     = ×       = , yang berakibat )! ( ! ! ! ) , ( r n r n r r n P r n − = =       . ■

Teorema Akibat 2.1.4

Jika r ≤n, maka

      − =       r n n r n . Bukti:

Berdasarkan pada Teorema 2.1.3,

)! ( ! ! r n r n r n − =      

, yang sama dengan

      − = − − − =

− n r

Menurut Teorema 2.1.3 dapat diperoleh hasil-hasil berikut

1 0 0

=

     

, 1

0=

   n

, n_=n

    

1 , dan =1

   

n n

.

Contoh 2.1.6

Seorang dosen memberikan 7 soal ujian kepada para mahasiswanya saat ujian akhir

semester. Jika para mahasiswa hanya diminta untuk mengerjakan 5 soal saja, maka

dengan berapa cara mereka dapat melakukannya?

Penyelesaian:

Soal yang ingin mereka kerjakan dapat dipilih dengan

21 ! 2 ! 5

! 7 )! 5 7 ( ! 5

! 7 5

7

= = − =

     

cara.

B. Bentuk segitiga Pascal

Terdapat suatu sifat yang penting dari _

    

r n

. Sifat tersebut dinyatakan oleh

teo-rema berikut.

Teorema 2.2.1 (Formula Pascal)

Jika 1≤r ≤n−1, maka

     

− − +

    

 −

=

     

1 1 1

r n

r n

r n

.

Misal terdapat himpunan n-anggota H, dan q adalah salah satu anggotanya. Suatu

himpunan, sebut K, memuat semua r-kombinasi dari H, dan ukuran (size) dari K

di-lambangkan dengan |K|. Setiap r-kombinasi dari H yang tak memuat q

dikelompok-kan ke dalam suatu himpunan, sebut T, sedangkan setiap r-kombinasi dari H yang

memuat q dikelompokkan ke dalam himpunan, sebut U. Dengan demikian, menurut

aturan penjumlahan

U T r n

+ =

     

,

dengan _

    

r n

menyatakan ukuran (size) dari K. Ukuran dari T adalah jumlah

r-kombinasi dari himpunan (n – 1)-anggota, H – {q}, yaitu

    

 −

=

r n

T 1 .

Oleh karena pada U, q berada di setiap r-kombinasi, maka hal tersebut berarti q

di-pasangkan dengan setiap (r – 1)-kombinasi dari himpunan H – {q}. Jadi, ukuran U

adalah

     

− − =

1 1

r n

U .

Berdasar pada dua hal tersebut diperoleh hasil yang diharapkan

     

− − +

    

 −

=

     

1 1 1

r n

r n

r n

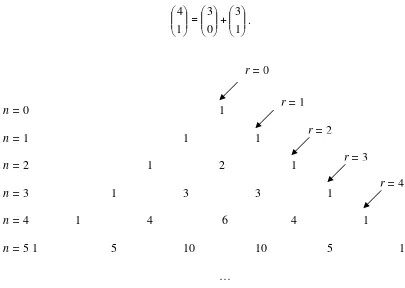
Formula Pascal tersebut menjadi dasar terbentuknya segitiga Pascal (Gambar 2.1).

Pada gambar tersebut, n menyatakan baris segitiga Pascal dan r menyatakan kolom

segitiga Pascal. Formula Pascal menunjukkan bahwa jika setiap dua bilangan yang

bersebelahan pada baris-(n – 1) dijumlahkan, maka hasil penjumlahan dua bilangan

tersebut berada tepat di bawah di antara dua bilangan itu pada baris-n.

Untuk mengilustrasikan penggunaan formula Pascal tersebut, ambil elemen

dari segitiga Pascal pada n = 4, r = 1, yaitu 4. Nilai 4 dihasilkan dari penjumlahan 1,

elemen pada n = 3, r = 0, dan 3, elemen pada n = 3, r = 1. Hubungan tersebut

diha-silkan oleh

     

+

     

=

     

1 3 0 3 1 4

.

n = 0 1

n = 1 1 1

n = 2 1 2 1

n = 3 1 3 3 1

n = 4 1 4 6 4 1

n = 5 1 5 10 10 5 1

…

Gambar 2.1 Segitiga Pascal

r = 0

r = 1

r = 2

r = 3

Sebagian besar persamaan diferensial yang termasuk dalam persamaan di-ferensial parsial merupakan persamaan didi-ferensial yang terbentuk dari proses-proses atau kejadian fisis, contohnya proses penyebaran panas dan perambatan gelombang. Pada bab ini dipaparkan juga mengenai kaitan antara deret Taylor dengan metode beda hingga yang akan digunakan untuk mendapatkan penyelesaian persamaan di-ferensial parsial.

A. Pengertian Persamaan Diferensial Parsial

Definisi dari persamaan diferensial parsial adalah suatu persamaan yang memuat suatu fungsi, sebut u, dengan dua atau lebih variabel dan beberapa turunan parsial didalamnya. Fungsi itu adalah fungsi yang tidak diketahui dan merupakan variabel tak bebas. Bentuk umum dari persamaan diferensial parsial adalah

0 ...

..., , ,

..., , , ,

1 ) ( 2

1 2 1

=

   

 

∂ ∂

∂ ∂

∂ ∂ ∂

∂ ∂

∂

k m

n x x

u x

x u x

u x

u u

F x (3.1.1)

di mana x=

(

x1,...,xn

)

adalah variabel bebas, u merupakan fungsi yang tak diketahui,

dan

j i i x x

u x

u

∂ ∂

∂ ∂

∂ 2

Suatu persamaan diferensial parsial dibentuk menurut ordenya. Orde merupakan derajat tertinggi dari turunan yang muncul. Bentuk umum persamaan diferensial

par-sial berdasar orde, dengan mengambil u =u(x,y), antara lain:

1. Bentuk umum persamaan diferensial parsial orde-satu adalah:

0 ,

, ,

, _=

  

 

∂ ∂ ∂ ∂

y u x u u y x F

(3.1.2)

2. Bentuk umum persamaan diferensial parsial orde-dua adalah:

0 ,

, , , , ,

, ₂

2 2 2 2

=

   

 

∂ ∂ ∂ ∂

∂ ∂ ∂ ∂ ∂ ∂ ∂

y u y x

u x

u y u x u u y x

F .

(3.1.3)

Definisi 3.1.1

Penyelesaian persamaan diferensial parsial adalah fungsi u(x,y) yang memenuhi persamaan diferensial parsial yang dibentuknya.

Misalkan L menyatakan suatu operator. Jika L diterapkan pada suatu persamaan

diferensial parsial, misal =2

∂ ∂ + ∂ ∂

y u x u

, maka diperoleh bentuk

y u x u u

∂ ∂ + ∂ ∂ =

) (

L . Jadi

persamaan diferensial tersebut dapat ditulis dalam bentuk L(u)=2.

Definisi 3.1.2

Suatu persamaan diferensial parsial, yaitu L(u)= f , f suatu fungsi yang diberikan,

) L( ) ( L ) (

L u+w = u + w , _(3.1.4)

) ( L ) (

L cu =c u _(3.1.5)

dengan u dan w merupakan fungsi yang memiliki turunan parsial, sedangkan c adalah

suatu konstanta. Sebaliknya, suatu persamaan dikatakan non-linear jika tidak

me-menuhi (3.1.4) dan (3.1.5).

Kelinearan dalam persamaan diferensial parsial dapat dijelaskan dalam be-berapa hal berikut:

1. Fungsi yang tidak diketahui, u, dan turunan parsialnya muncul dengan

pang-kat satu. Tidak boleh muncul bentuk, misalnya: 2 , 1 ,

( )

2 ,dan

( )

−1.

∂ ∂ ∂

∂ −

y u x

u

u

u

2. Fungsi u dan turunan parsialnya tidak menjadi variabel dari suatu fungsi lain.

Bentuk-bentuk, misalnya: u

x u

e

u ,cos ,dan

sin 2

2

∂ ∂

tidak diperbolehkan.

Contoh 3.1.3

Periksa apakah persamaan diferensial parsial berikut linear:

2 2

) , ( )

, (

x t x u t

t x u

∂ ∂ = ∂ ∂

.

(3.1.6)

Penyelesaian:

Pertama ubah persamaan tersebut menjadi

0 ) , ( )

, (

2 2

= ∂ ∂ − ∂ ∂

x t x u t

t x u

.

(3.1.7)

). L( ) , ( ) , ( 2 2 u x t x u t t x u ₌ ∂ ∂ − ∂ ∂ (3.1.8)

Berikutnya adalah dengan menerapkan (3.1.4) dan (3.1.5), sehingga diperoleh:

), ( L ) ( L ) , ( ) , ( ) , ( ) , ( ) , ( ) , ( ) , ( ) , ( ) , )( ( ) , )( ( ) ( L 2 2 2 2 2 2 2 2 2 2 w u x t x w t t x w x t x u t t x u x t x w x t x u t t x w t t x u x t x w u t t x w u w u + = ∂ ∂ − ∂ ∂ + ∂ ∂ − ∂ ∂ = ∂ ∂ − ∂ ∂ − ∂ ∂ + ∂ ∂ = ∂ + ∂ − ∂ + ∂ = + (3.1.9)

[

]

[

]

). ( L ) , ( ) , ( ) , ( ) , ( ) , ( ) , ( ) ( L 2 2 2 2 2 2 u c x t x u t t x u c x t x u c t t x u c x t x cu t t x cu cu =       ∂ ∂ − ∂ ∂ = ∂ ∂ − ∂ ∂ = ∂ ∂ − ∂ ∂ = (3.1.10)

Dengan demikian, persamaan (3.1.6) adalah persamaan diferensial parsial linear.

Contoh 3.1.4

Tunjukkan bahwa persamaan berikut adalah persamaan diferensial parsial non-linear:

. 2 u x u = ∂ ∂ (3.1.11) Penyelesaian:

Jika (3.1.4) diterapkan pada ruas kanan dari persamaan tersebut, maka didapatkan:

2 2

2

2 )

(u+w =u + uw+w _(3.1.12)

Hasil tersebut tidak memenuhi (3.1.4) karena

2 2 2

)

(u+w ≠u +w , _(3.1.13)

Definisi 3.1.5

Persamaan diferensial parsial, L(u)= f , dikatakan homogen jika fungsi f bernilai

nol, misalkan:

. 0

2 2

= ∂ ∂ − ∂ ∂

x u t u

(3.1.14)

Jika f tidak nol, maka persamaan tersebut dikatakan tidak homogen.

Definisi 3.1.6

Jika koefisien-koefisien pada persamaan diferensial parsial merupakan suatu nilai

ter-tentu, maka persamaan itu disebut persamaan diferensial parsial dengan koefisien

konstan. Contohnya adalah persamaan:

0

3 ₂

2 = ∂ ∂ − ∂ ∂

t u x u

.

(3.1.15)

Namun, jika koefisiennya berupa variabel, maka persamaan itu merupakan persamaan

diferensial parsial dengan koefisien variabel. Contohnya adalah persamaan:

0

2 2

2 ₌

∂ ∂ − ∂ ∂

t u t x u

.

(3.1.16)

Berikut ini merupakan bentuk-bentuk dari persamaan diferensial parsial,

antara lain:

2 2

x u k t u

∂ ∂ = ∂ ∂

2 2 2 2 2

x u k t

u

∂ ∂ = ∂ ∂

(3.1.18)

0

2 2 2 2

= ∂ ∂ + ∂ ∂

y u x

u

(3.1.19)

x t u x

u t

u 3 3

2 2 2 2

= + ∂ ∂ − ∂ ∂

(3.1.20)

0

4 4 2 2

= ∂ ∂ + ∂ ∂

x u t

u

(3.1.21)

0 )

( 2 2 =

∂ ∂ + + ∂ ∂

x u t x t u

(3.1.22)

0

3 3

= ∂ ∂ + ∂ ∂ + ∂ ∂

x u x u u t u

x (3.1.23)

Persamaan (3.1.17) sampai (3.1.20) adalah persamaan diferensial parsial orde-dua,

persamaan (3.1.22) adalah persamaan diferensial parsial orde-satu, sedangkan

per-samaan (3.1.21) dan (3.1.23) secara berturut-turut adalah perper-samaan diferensial

par-sial orde-empat dan orde-tiga. Persamaan (3.1.17), (3.1.18), (3.1.19), (3.1.21), dan

(3.1.22) adalah persamaan linear homogen, persamaan (3.1.20) adalah persamaan

non-linear yang tidak homogen, sedangkan persamaan (3.1.23) adalah persamaan

non-linear homogen. Persamaan diferensial dengan koefisien variabel ditunjukkan

oleh persamaan (3.1.22) dan (3.1.23) sementara lainnya adalah persamaan diferensial

dengan koefisien konstan.

Umumnya variabel bebas yang muncul pada sebagian besar persamaan

dife-rensial parsial yang terkait dengan proses atau kejadian fisis merupakan variabel yang

menyatakan jarak dan waktu. Variabel tersebut sering dinotasikan dengan x untuk

Persamaan diferensial parsial yang sering muncul dan digunakan untuk

memodelkan kejadian atau proses fisis adalah persamaan diferensial parsial

orde-dua. Bentuk umum dari persamaan diferensial parsial linear orde-dua dapat dituliskan

dalam bentuk, yaitu:

). , ( )

, ( )

, (

) , ( )

, ( )

, ( )

,

( ₂

2 2

2 2

y x w u y x f y u y x e

x u y x d y

u y x c y x

u y x b x

u y x a

= +

∂ ∂ +

∂ ∂ +

∂ ∂ +

∂ ∂

∂ +

∂ ∂

(3.1.24)

Pada bentuk umum tersebut a, b, c, d, e, f, dan w adalah fungsi yang diketahui yang

memuat variabel bebas x dan y, sedangkan fungsi u=u(x,y) adalah fungsi yang tak

diketahui. Variabel bebas y dalam masalah persamaan diferensial parsial yang

ber-hubungan dengan proses fisis akan digantikan dengan variabel t. Penggolongan yang

paling umum dari persamaan diferensial parsial orde-dua ini adalah penggolongan

berdasarkan nilai-nilai dari fungsi a(x,y), b(x,y), dan c(x,y). Ketiga fungsi itu dianggap

sebagai fungsi konstan.

Nilai yang mendasari penggolongan ini adalah nilai D=b2 −4ac.

Karak-teristik dari nilai D itulah yang menjadi dasar dari penggolongan berikut:

1. Jika D=b2 −4ac=0, maka persamaan (3.1.24) disebut persamaan

parabolik. Contoh persamaan ini adalah:

Persamaan panas, ₂

2

x u k t u

∂ ∂ = ∂ ∂

(3.1.25)

dengan nilai-nilai a = k, b = c = 0, yang berakibat = 2 −4 =0

ac b

2. Jika = 2 −4 >0

ac b

D , maka persamaan (3.1.24) disebut persamaan

hiper-bolik. Contohnya adalah:

Persamaan gelombang, ₂

2 2 2 2

x u k t

u

∂ ∂ = ∂ ∂

(3.1.26)

yang memiliki nilai-nilai a = k2, b = 0, c = -1 yang menghasilkan

. 0 4 4

2_{− = >}

=b ac

D

3. Jika D=b2 −4ac<0, maka persamaan (3.1.24) disebut persamaan eliptik.

Contohnya adalah:

Persamaan Laplace, ₂ 0

2 2 2

2 ₌

∂ ∂ + ∂ ∂ = ∇

y u x

u

u (3.1.27)

secara berturut-turut nilai a, b, c adalah 1, 0, 1 sehingga nilai D yang dihasil

kan, yaitu D=b2 −4ac=−4<0.

Ketiga contoh persamaan diferensial parsial tersebut merupakan persamaan

diferensial parsial yang linear homogen dengan koefisien konstan. Penjelasan umum

dari ketiga jenis persamaan tersebut adalah bahwa persamaan eliptik menggambarkan

proses fisis yang berada pada keadaan steady-state sehingga tidak bergantung

terha-dap waktu, persamaan parabolik menggambarkan proses fisis yang menuju pada

keadaan steady-state, sedangkan persamaan hiperbolik menggambarkan proses fisis

yang bergantung terhadap waktu yang tidak menuju pada keadaan steady-state.

Syarat awal menyatakan fungsi yang diterapkan pada waktu tertentu. Contoh syarat

awal adalah:

) ( ) , ,

(x y t0 =

ν

x

u , _(3.1.28)

fungsi ν(x)=ν(x,y) adalah fungsi tertentu yang diberikan.

Definisi 3.1.8

Syarat batas menyatakan fungsi yang diterapkan pada nilai batas dari domain untuk

persamaan diferensial parsial yang diberikan.

Domain yang dimaksud adalah suatu daerah di mana persamaan diferensial parsial itu

dapat dievaluasi dengan baik. Pada dimensi satu, contohnya adalah senar yang

dige-tarkan. Domainnya adalah nilai-nilai, sebut x, yang berada pada suatu interval [0,d], d

adalah panjang senar. Batas dari domain itu adalah titik-titik ujungnya, sehingga

kondisi batas hanya berlaku pada titik awal, sebut x = 0 dan titik akhir x = d.

Sedang-kan, untuk dimensi dua contohnya adalah bahan tipis untuk kepala gendang.

Do-mainnya berupa bidang datar yang titik-titik batasnya membentuk kurva tertutup.

Ada tiga jenis syarat batas yang sering dipakai, yaitu:

1. syarat Dirichlet, yaitu jika nilai penyelesaian u diberikan secara khusus.

Contohnya:

, ) , 1 ( , ) , 0

( t q u t r

u = = _(3.1.29)

2. syarat Neumann, yaitu jika nilai turunan parsial dari u diberikan secara

khusus. Contohnya:

, ) , 1 ( , ) , 0 (

r x

t u q

x t

u ₌

∂ ∂ =

∂ ∂

(3.1.30)

nilai q dan r diberikan.

3. syarat Robin, yaitu kombinasi dari syarat Dirichlet dan syarat Neumann.

Con-tohnya:

, ) , 1 ( ) , 1 ( , ) , 0 ( ) , 0

( _{φ κ +λ =ϕ}

∂ ∂ =

+ ∂ ∂

t u x

t u t

u r x

t u q

(3.1.31)

nilai q ,r ,φ ,κ ,λ ,dan ϕ diberikan.

Syarat-syarat batas dan awal dalam masalah persamaan diferensial parsial

berpengaruh terhadap penyelesaian dari masalah tersebut. Penyelesaian yang

di-harapkan adalah penyelesaian yang baik sehingga masalah yang muncul beserta

syarat-syarat yang diberikan akan menjadi well-posed. Kriteria-kriteria dari

well-posed adalah bahwa penyelesaian dari suatu persamaan diferensial parsial yang

meli-batkan syarat-syarat awal dan batas memenuhi:

1. Eksistensi, artinya terdapat sedikitnya satu penyelesaian yang memenuhi

se-mua syarat yang terlibat.

2. Ketunggalan, artinya terdapat sebanyak-banyaknya satu penyelesaian.

3. Kestabilan, artinya penyelesaian tunggal yang didapat tersebut stabil terhadap

bahwa perubahan kecil pada nilai-nilai yang diberikan, akan mengakibatkan

perubahan yang kecil juga pada penyelesaian yang terkait.

Contoh dari masalah persamaan diferensial parsial yang well-posed dapat dilihat pada

bab selanjutnya. Andaikan salah satu dari syarat-syarat tersebut tidak terpenuhi, maka

masalah persamaan diferensial parsial yang berkaitan menjadi ill-posed.

B. Pembentukan Persamaan Panas dan Gelombang

Subbab ini akan menjelaskan tentang bagaimana suatu proses penghantaran

panas dapat dimodelkan dengan sebuah persamaan panas dan bagaimana proses

pe-rambatan gelombang dapat dinyatakan dalam sebuah persamaan gelombang. Proses

pembentukan persamaan panas dan persamaan gelombang ini akan dijelaskan secara

garis besarnya saja tanpa penjelasan yang mendalam tentang proses fisisnya.

1. Persamaan Panas

Elemen yang ditinjau sebagai medium penghantar panas adalah sebuah batang

logam lurus dengan panjang L yang ditempatkan di sepanjang sumbu-x. Pada batang

tersebut diasumsikan selubung permukaannya terisolasi sehingga energi panas yang

dimiliki tidak dapat keluar. Asumsi lain adalah bahwa batang tersebut sangat tipis

bernilai konstan untuk waktu tertentu. Temperatur tersebut dinyatakan dalam fungsi

dari waktu t dan letak x yakni u(x,t).

Misalkan luas irisan adalah A, yang bernilai konstan sepanjang batang dan ρ

menyatakan kepadatan batang. Bahan pembuat batang mempunyai suatu konstanta

yang menyatakan besarnya energi panas yang dibutuhkan untuk menaikkan 1

unit temperatur per 1 unit massa batang. Konstanta tersebut adalah konstanta

panas yang dilambangkan dengan µ. Terdapat sebuah persamaan, yaitu: µρAu(x,t),

yang menyatakan total energi thermal di sembarang potongan tipis sebuah bahan

konduktor. Andaikan diambil sebuah segmen dari batang di antara x=

α

dan

β =

x , dengan α < β, maka total energi panas di sepanjang segmen tersebut

pada saatt adalah

∫

=

= β

α β

α t

µρ

Au x t dx

Q t

Q( ) [ , ]( ) ( , ) . (3.2.1)

Persamaan (3.2.1) dapat diturunkan terhadap t, untuk mendapatkan laju perubahan

energi panas saat waktu t pada segmen tersebut, yaitu:

∫

∫

= ∂ _∂

  

 

= β

α β

α µρ µρ _t dx

t x u A dx

t x u A dt

d dt

dQ ( , )

) ,

( , (3.2.2)

dengan syarat u dan turunan-turunan parsialnya kontinu.

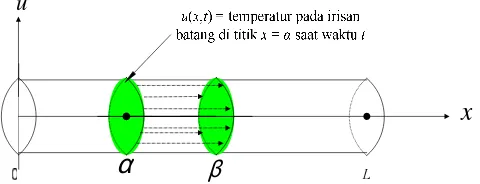
Selanjutnya diperkenalkan sebuah fungsi fluks panas,

) ,

(x t

F = energi panas yang melewati suatu irisan di posisi x

α

β

u

x

Gambar 3.1 Penampang sebuah batang dengan pengamatan pada segmen α-β.

Oleh karena fungsi fluks panas dinyatakan dalam tiap unit luas, maka aliran energi

panas pada segmen (α,β) adalah F(α,t)A−F(β,t)A. Menurut hukum Newton

ten-tang pendinginan, aliran energi panas dalam segmen tersebut dari sisi yang lebih

panas ke sisi yang lebih dingin sama dengan K kali negatif dari gradien temperatur.

Gradien temperatur merupakan nilai selisih temperatur antara kedua sisi ujung pada

segmen tersebut. Hukum tersebut dapat dinyatakan sebagai

x t x u K t x F

∂ ∂ −

= ( , )

) ,

( , (3.2.3)

dengan K > 0 merupakan konduktivitas panas dari bahan batang.

Oleh karena itu, didapatkan persamaan untuk kecepatan energi panas

me-masuki segmen tersebut, yaitu:

. ) , ( )

, (

) , ( )

, ( )

, ( ) , (

x t u KA x

t u KA

A x

t u K A

x t u K A t F A t F

fluks

∂ ∂ − ∂ ∂ =

   

 

∂ ∂ − − ∂

∂ − = −

= Γ

α β

β α

β α

(3.2.4)

sumber fluks

dt

dQ _{=Γ +Ε}

, (3.2.5)

di mana Εsumber menyatakan energi yang dihasilkan/bersumber dari dalam segmen,

maka didapatkan rumusan

sumber x t u KA x t u KA dx t t x u

A _ _+Ε

∂ ∂ − ∂ ∂ = ∂ ∂

∫

_αβµρ ( , ) (β, ) (α, ) . (3.2.6)

Sumber energi itu dapat muncul, misalnya dalam kasus adanya reaksi kimia yang

ter-jadi di dalam segmen yang menimbulkan suatu radiasi.

Jika diasumsikan tidak ada energi yang dihasilkan, maka laju perubahan

ener-gi panas dalam segmen harus seimbang dengan kecepatan masuknya enerener-gi panas

dalam segmen, yaitu:

∫

∫

∂ ∂ =       ∂ ∂ − ∂ ∂ = ∂ ∂ − ∂ ∂ = ∂ ∂ β α β α α β α β µρ . ) , ( ) , ( ) , ( ) , ( ) , ( ) , ( 2 2 dx x t x u KA x t u x t u KA x t u KA x t u KA dx t t x u A (3.2.7) Kemudian didapatkan

∫

∫

= ∂ ∂ − ∂ ∂ β α β α

µρ ( , ) (₂, ) 0

2 dx x t x u K dx t t x u

. (3.2.8)

Persamaan (3.2.8) haruslah berlaku untuk 0≤α <β ≤L. Oleh karena kedua integral

dievaluasi di selang

[ ]

α

,

β

yang sama terhadap x, maka kedua hasil integral tersebut

haruslah menghasilkan dua nilai yang identik. Dengan demikian, agar persamaan

∫

_ =

  

 

∂ ∂ − ∂ ∂

β

α

µρ

0

) , ( )

, (

2 2

dx x

t x u K t

t x u

. (3.2.9)

Oleh karena f(x) kontinu dan untuk setiap α, β, 0≤α <β ≤ L berlaku persamaan

(3.2.9), maka.fungsi di dalam tanda kurung haruslah nol (Kaczor, 2003). Jadi,

diperoleh persamaan

0 ) , ( )

, (

2 2

= ∂

∂ − ∂ ∂

x t x u K t

t x u

µρ , (3.2.10)

untuk 0<x< L dan t >0.

Persamaan (3.2.10) dinamakan persamaan panas dimensi satu atau juga

dikenal sebagai persamaan difusi dimensi satu. Hal tersebut dikarenakan oleh

penggunaan model yang sama untuk menentukan besarnya konsentrasi suatu zat

ki-mia yang mengalir (diffuse) dari daerah berkonsentrasi tinggi ke daerah

berkonsen-trasi rendah pada sebuah pipa. Secara lebih sederhana persamaan (3.2.10) ditulis

) , ( ,

2 2

t x u u x

u k t

u ₌

∂ ∂ = ∂ ∂

(3.2.11)

dengan

µρ

K

k = yang disebut difusitas dari bahan batang.

2. Persamaan Gelombang

Medium yang menjadi fokus untuk pembahasan adalah senar pada gitar.

Ang-gap senar yang sedang berada dalam keadaan diam menyatakan sumbu-x dengan titik

bidang-xu. Gelombang yang terbentuk saat senar dipetik akan dianggap sebagai

se-buah lintasan, di mana lintasan tersebut dinyatakan dalam sese-buah fungsi, yaitu

) ,

(x t

u . Fungsi u(x,t) berlaku untuk t>0, dengan demikian lintasan/kurva dari

fungsi tersebut merupakan kumpulan titik-titik posisi pada senar untuk letak x dan

waktu t tertentu. Oleh karena itu, fungsi u(x,t) disebut fungsi posisi untuk senar

tersebut. Fungsi u(x,t) juga dapat dinyatakan sebagai tinggi suatu titik pada senar

saat waktu t dan letak x.

Asumsi yang digunakan adalah tidak adanya gaya gesek udara terhadap senar

dan tidak diperhitungkannya berat senar. Vektor tegangan pada senar, T(x,t),

diang-gap selalu membentuk garis singgung terhadap senar di suatu posisi (x,t). Asumsi

lain adalah bahwa setiap titik pada kurva u(x,t) hanya bergerak secara vertikal saja

serta adanya suatu konstanta, ρ, yang menyatakan massa per unit panjang.

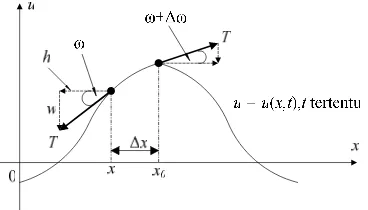
Gambar 3.2 Tegangan pada senar dan komponen-komponennya saat waktu t.

Misal diambil sebuah segmen pada senar yang berada di antara x dan

x x

gaya yang dihasilkan berdasar tegangan = percepatan pusat massa pada segmen

dikali massanya.

Besarnya tegangan dinotasikan T(x,t) =T(x,t). Oleh karena pada pendekatan gaya

horisontal tidak ada gerak yang terjadi, T(x0,t)cos(ω+∆ω)−T(x,t)cos(ω)=0,

maka vektor tegangan diasumsikan bernilai konstan, T(x,t)=T. Untuk ∆x kecil

berlaku pendekatan untuk gaya vertikal, yaitu

2 2

) , ˆ ( )

sin( )

sin(

t t x u x T

T

∂ ∂ ∆ = −

∆

+ ω ω ρ

ω , (3.2.12)

di mana xˆ menyatakan pusat massa segmen. Dari persamaan (3.2.12) didapat

2 2

) , ˆ ( )

sin( )

sin(

t t x u x

T T

∂ ∂ = ∆

− ∆

+ ω ω _ρ

ω

. (3.2.13)

Komponen vertikal dari tegangan T pada titik x ditulis dalam bentuk

) sin( )

,

(x t T ω

w = , sehingga dihasilkan persamaan

2 2 0, ) ( , ) (ˆ, )

(

t t x u x

t x w t x w

∂ ∂ = ∆

− _ρ

. (3.2.14)

Saat ∆x→0, maka nilai xˆ→x. Oleh karena itu,

2 2

) , ( )

, (

t t x u x

t x w

∂ ∂ = ∂

∂ _ρ

. (3.2.15)

Pandang komponen horisontal dari T di titik x, yaitu: h=Tcos(ω), dengan demikian

x u h h

h T

t x w

∂ ∂ = =

   

  =

= sin( ) tan( )

) cos( )

sin( )

,

( ω ω

ω

Pada pembentukkan persamaan (3.2.16), nilai tan(ω) digantikan dengan

x t x u

∂ ∂ ( ,)

. Hal ini dapat dilakukan berdasar pada pengetahuan tentang turunan. Turunan

dapat dinyatakan sebagai nilai kemiringan dari garis singgung, dalam hal ini adalah

kemiringan dari T. Nilai kemiringan itu adalah perbandingan dari w(x,t)/h=tan(ω).

Oleh karena kemiringan garis singgung hanya bergantung pada nilai x, maka turunan

dari fungsi u(x,t) adalah turunan parsial terhadap x, yakni

x t x u

∂

∂ ( ,)_{. Jika persamaan}

(3.2.16) disubtitusikan ke persamaan (3.2.15), maka diperoleh

2 2

) , ( )

, (

t t x u x

t x u h

x ∂

∂ =

  



∂ ∂ ∂

∂

ρ

. (3.2.17)

Dengan demikian, dihasilkan persamaan

2 2 2

2

) , ( )

, (

t t x u x

t x u h

∂ ∂ = ∂

∂ _ρ

. (3.2.18)

Secara lebih sederhana persamaan tersebut dapat ditulis

2 2 2 2

2

) , ( )

, (

x t x u k t

t x u

∂ ∂ = ∂ ∂

, u=u(x,t) (3.2.19)

dengan k2 = _ρh yang merupakan kecepatan gelombang. Persamaan (3.2.19) disebut

persamaan gelombang dimensi satu.

C. Penyelesaian Eksak Persamaan Panas dan Gelombang

Subbab ini akan membahas tentang bagaimana menghasilkan suatu

batas dan syarat awal. Metode yang digunakan adalah pemisahan variabel atau

dise-but juga metode Fourier. Metode tersebut dapat diterapkan, karena persamaan panas

dan gelombang merupakan persamaan diferensial parsial yang linear dan homogen.

1. Persamaan Panas

Masalah persamaan panas yang akan dicari penyelesaian eksaknya adalah:

persamaan panas: ( , ) (₂, ), 0 , 0

2

> < < ∂

∂ = ∂ ∂

t L x x

t x u k t

t x u

(3.3.1)

dengan syarat batas: u(0,t)=0 dan u(L,t)=0, (3.3.2)

dan syarat awal: u(x,0)= f(x). (3.3.3)

Masalah tersebut menggambarkan penyebaran temperatur di suatu batang konduktor

tipis yang homogen (kepadatannya konstan), dengan panjang L. Ujung-ujung batang

tersebut dikondisikan bertemperatur nol, untuk sembarang waktu. Kondisi lainnya

adalah temperatur mula-mula suatu irisan di suatu titik x saat t=0 adalah f(x).

Metode pemisahan variabel diterapkan pada bentuk penyelesaian berikut:

) ( ) ( ) ,

(x t ψ x S t

u = . (3.3.4)

Fungsi ψ(x) adalah fungsi terhadap variabel tunggal x, sedangkan S(t) merupakan

fungsi yang hanya bergantung terhadap t. Jika bentuk penyelesaian tersebut

disubsti-tusikan ke persamaan panas (3.3.1), maka dihasilkan

2 2

) ( )

(

dx

ψ

d t S k dt dS x

ψ = . (3.3.5)

2 2

) ( 1 )

( 1

dx

ψ

d x

ψ

dt dS t S

k = . (3.3.6)

Jika persamaan (3.3.6) diamati, maka terlihat bahwa ruas kirinya hanya bergantung

terhadap waktu, sedangkan ruas kanannya hanya bergantung terhadap letak. Oleh

karena itu, dapat dipilih suatu nilai konstan yang mewakili kedua ruas, yaitu:

λ

dx

ψ

d x

ψ

dt dS t S

k = 2 =−

2

) ( 1 )

( 1

. (3.3.7)

Berdasarkan persamaan (3.3.7), dapat dihasilkan dua persamaan diferensial, yaitu:

ψ λ

dx

ψ

d

2 2

−

= , (3.3.8)

S k

λ

dt dS

−

= . (3.3.9)

Sekarang ditinjau syarat batas u(0,t)=0. Syarat tersebut haruslah dipenuhi

oleh bentuk penyelesaian (3.3.4), yakni

0 ) ( ) 0

( S t =

ψ .

Terdapat dua kemungkinan untuk itu, yaitu

0 ) 0

( =

ψ atau S(t)=0.

Jika S(t)=0 untuk setiap t, maka nilai u(x,t) akan selalu bernilai nol. Hal tersebut

muncul, jika temperatur mula-mula dikondisikan f(x)=0, untuk 0≤x≤L. Oleh

karena itu, penyelesaian yang didapat hanyalah penyelesaian trivial (u(x,t)≡0),

0 ) 0

( =

ψ , yang menjadi pilihan untuk kasus ini. Berdasar syarat batas lainnya,

0 ) , (L t =

u , maka berlaku

0 ) ( ) ( ) ,

(L t =ψ L S t =

u ,

dengan demikian menurut analisis yang sama, dipilih ψ(L)=0.

Bentuk penyelesaian (3.3.4), merupakan hasil kali dari fungsi S(t) dan ψ(x),

sehingga untuk mendapatkan hasil yang diinginkan, terlebih dahulu persamaan

(3.3.8) dan (3.3.9) diselesaikan. Pertama tinjau persamaan

S k

λ

dt dS

−

= . (3.3.10)

Persamaan tersebut adalah persamaan diferensial biasa orde pertama linear homogen

dengan koefisien konstan. Penyelesaian umum dari persamaan (3.3.10) adalah

k

e c t

S( )= ₀ −λ . (3.3.11)

Oleh karena k>0, maka nilai λ dipilih λ≥0, sehingga fungsi S(t) digambarkan

me-luruh secara eksponensial (λ>0) atau bernilai konstan (λ=0) saat t bergerak naik.

Persamaan yang ditinjau selanjutnya adalah

ψ λ

dx

ψ

d

2 2

−

= , dengan ψ(0)=0 dan ψ(L)=0. (3.3.12)

Persamaan beserta syarat batas tersebut dinamakan masalah nilai batas dari

per-samaan diferensial biasa. Masalah nilai batas tersebut akan diselesaikan

mengguna-kan pencarian suatu nilai λ, yang disebut nilai eigen. Nilai eigen tersebut akan

Langkah awal yang harus ditempuh sebelum mendapatkan nilai eigen adalah

menyelesaikan persamaan diferensial biasa orde dua linear homogen dengan

koe-fisien konstan (3.3.12). Dua penyelesaian khusus persamaan (3.3.12), umumnya

di-nyatakan dalam bentuk eksponensial, rx

e x)= (

ψ . Jika penyelesaian tersebut

di-substitusikan ke persamaan (3.3.12), maka dihasilkan

( )

_{=−λ ⇒} 2 _{=−λ ⇔} 2 _=−λ 2

2

r e e

r e dx

e

d rx rx rx

rx

.

Terdapat empat kemungkinan nilai akar-akar yang dapat dihasilkan dengan berdasar

pada nilai λ, yaitu:

a. λ>0, dua akar yang dihasilkan merupakan akar kompleks imajiner murni,

yang salah satunya adalah konjugat dari yang lain, r_1,2 =±i λ .

b. λ=0, dua akarnya bernilai nol, r1,2=0.

c. λ<0, dua akarnya real berbeda, r1,2 =± −λ.

d. λ kompleks.

Dari ke-empat kemungkinan tersebut yang menjadi fokus pembahasan adalah nilai

0

>

λ , karena nilai eigen ini akan menghasilkan penyelesaian non-trivial (Haberman,

2004).

Tinjau kembali masalah nilai batas (3.3.12). Jika λ>0, maka penyelesaiannya

berupa i x

e± λ . Penyelesaian tersebut dapat dinyatakan dalam bentuk lain, yakni

x

λ

c x

λ

c x

ψ( )= ₁cos + ₂sin , (3.3.13)

Selanjutnya dengan menerapkan syarat batas ψ(0)=0, menghasilkan

1 2

1cos(0) sin(0) 0

) 0

( = =c +c =c

ψ

. (3.3.14)

Akibat yang muncul dari hasil tersebut adalah nilai-nilai cos( λx), untuk 0< x< L,

tidak memiliki pengaruh apapun. Oleh karena itu, fungsi ψ(x) sekarang hanya

ber-gantung pada sin( λx), yaitu:

) sin( )

(x c₂ λx

ψ = . (3.3.15)

Selanjutnya untuk syarat batas ψ(L)=0, berakibat

) sin( 0

)

(L c₂ λL

ψ = = . (3.3.16)

Terdapat dua kemungkinan penyelesaian untuk persamaan tersebut, yakni c₂ =0 atau

0 )

sin( λL = . Jika diambil c₂ =0, maka nilai ψ(x) menjadi identik nol, ψ(x)≡0.

Hal ini terjadi, karena dengan didapatkannya nilai c₂ =0 dan sebelumnya telah

diha-silkan c₁ =0, maka persamaan penyelesaian (3.3.13) akan selalu bernilai nol untuk

tiap x. Dengan kata lain, jika c₁ =c₂ =0, maka hanyalah penyelesaian trivial yang

dihasilkan. Oleh karena itu, nilai eigen, λ, yang diharapkan harus memenuhi

0 )

sin( λL = .

Persamaan tersebut terpenuhi saat nilai λL=nπ. Oleh karena λ >0, maka nilai n

dipilih bilangan bulat positif. Jadi nilai eigen yang dihasilkan adalah

. ... 2, , 1 ,

2

= 

    

= n

L nπ

Jika nilai tersebut disubstitusikan ke persamaan (3.3.15), maka akan diperoleh fungsi

eigen yang berkaitan, yaitu:

x L n c x       = π

ψ( ) 2sin , (3.3.18)

dengan c2 adalah konstanta sembarang. Untuk mendapatkan persamaan yang

seder-hana dan memudahkan, seringkali dipilih c₂ =1.

Menurut nilai eigen yang telah dihasilkan, maka penyelesaian umum (3.3.11)

dapat dituliskan kembali sebagai berikut

t L n k e c t S 2 0 ) (      − = π

, untuk n =1 ,2,.... (3.3.19)

Jika bentuk nilai eigen, λ, fungsi eigen, ψ(x), dan penyelesaian umum S(t) diamati,

maka terlihat bahwa ketiga bentuk tersebut akan berbeda untuk tiap n berbeda. Jadi,

nilai eigen tersebut dapat dinotasikan dengan

... 2, , 1 , 2 =       = n L n n π

λ . (3.3.20)

Setelah didapatkan penyelesaian dari dua persamaan diferensial biasa (3.3.10)

dan (3.3.12), maka secara langsung bentuk penyelesaian dari persamaan panas (3.3.1)

dengan syarat (3.3.2) dan (3.3.3), dapat ditulis

dengan C =c₂c₀ sembarang konstanta. Nilai u(x,t) akan berbeda untuk n berbeda.

Jika penyelesaian (3.3.21) diamati, maka terlihat bahwa saat t naik, u(x,t) akan

me-luruh secara eksponensial. Menurut analisa limit, lim ( , )=0.

∞ → u x t

t

Sekarang tinjau suatu prinsip yang berkaitan dengan penyelesaian persamaan

panas. Prinsip tersebut adalah prinsip superposisi yang diperluas, yang secara

umum menyatakan bahwa jika u1,u2 ,..., uM merupakan penyelesaian dari suatu

ma-salah persamaan linear homogen, maka setiap kombinasi linear dari penyelesaian

tersebut, yaitu:

∑

=

= +

+

+ M

n n n M

Mu cu

c u

c u c

1 2

2 1

1 ... ,

dengan cn konstanta sembarang untuk n=1 ,2,..., M , adalah juga penyelesaian.

Menurut prinsip tersebut, setiap penyelesaian dari persamaan panas (3.3.1), yaitu

( )

, 1 ,2,... sin

2 =

     

−

n e

x

t L n k L n

π π

, dapat dikombinasikan secara linear untuk menghasilkan

penyelesaian lain. Oleh karena itu, didapatkan

, sin

) , (

1

2

∑

=

     

−

     

= M

n

t L n k

n x e

L n C

t x u

π

π

_(3.3.22)

dengan M berhingga. Pada saat t =0, persamaan (3.3.22) menjadi

∑

=

      =

= M

n

n x