PROS Hanna A Parhusip Tinjauan ulang ekspansi asimtotik Full text

655

TINJAUAN ULANG EKSPANSI ASIMTOTIK

UNTUK MASALAH BOUNDARY LAYER

Hanna.A. Parhusip

Center of Applied Mathematics

Program Studi Matematika Industri dan Statistika Fakultas Sains dan Matematika

Universitas Kristen Satya Wacana Jl. Diponegoro 52-60 Salatiga

ABSTRAK

Pada makalah ini akan ditunjukkan pengantar Ekspansi Asimtotik yang diindikasikan adanya parameter positif kecil (sebut ε) sebagai parameter asimtotik. Parameter ini muncul karena model memuat 2 besaran yang sangat berbeda sehingga diperlukan penyekalaan dimensi.

Langkah awal adalah mengasumsikan bahwa penyelesaian dari masalah yang dikaji merupakan deret dari

ε

. Hal ini ditunjukkan terutama pada Persamaan Diferensial Biasa Orde 2 nonlinear yang mempunyai singularitas (masalah boundary layer) . Pada makalah ini ditunjukkan pula baik tidaknya ekspansi tersebut.

Kata kunci : ekspansi

ε

, operator integral, penyelesaian luar, penyelesaian dalam, boundary layer

PENDAHULUAN

Pada masalah aplikasi banyak dijumpai adanya besaran fisis yang mempunyai beberapa skala yang jauh berbeda antara 2 parameter atau lebih. Misal pada kasus penyusunan hukum Darcy sebagai aliran fluida minyak antara pipa injeksi dan pipa reservoar mempunyai jarak sekitar 100m-1000m. Sedangkan besarnya jari-jari pori-pori pada media bebatuan berorde 10−4m (Parhusip, 2005, (a)). Untuk menyatakan permiabilitas media yang muncul pada hukum Darcy, diperlukan rasio kedua besaran tersebut. Aliran panas dengan konduktivitas yang merupakan fungsi posisi menyebabkan perlu adanya transformasi variabel sehingga masalah transfer panas dapat disusun sebagai masalah transfer panas pada media homogen . Rasio antara konsentrasi enzim yang digunakan dan konsentrasi substansi pada reaksi kinetik Michelis Menten juga menunjukkan bilangan kecil yang menyebabkan model kinetik dalam persamaan diferensial merupakan masalah gangguan singular singular (singular perturbation problem) (Parhusip, 2006). Ketiga kasus tersebut diselesaikan dengan ekspansi terhadap parameter kecil (sebut

ε

) dengan menganggap solusi sebagai ekspansi terhadap parameter tersebut.

Ekspansi asimtotik dapat mendekati masalah nonlinear menjadi masalah linear. Akan tetapi diperlukan studi lebih lanjut ketepatan solusi masalah linear (berkaitan dengan masalah uniformity

penyelesaian) . Hasil ekspansi untuk hukum Carreau untuk fluida polimer merupakan salah satu contoh tentang hal ini (Parhusip, 2005, (b)). Demikian pula ekspansi asimtotik tergantung pula pada masalah yang dikaji khususnya sifat penyelesaian pada batas-batas domain. Orde persamaan diferensial dapat berubah. Hal inilah yang akan ditunjukkan pada makalah ini yaitu tata cara ekspansi asimtotik pada persamaan diferensial yang demikian yang disebut masalah boundary layer.

656

Pada Bagian III akan ditunjukkan langkah-langkah ekspansi asimtotik pada masalah boundary layer. Selanjutnya tata cara dan hasil asimtotik dan analisanya ditunjukkan pada Bagian IV dan disimpulkan pada Bagian akhir makalah ini.

DASAR TEORI

Dapat diketahui salah satu penyelesaian persamaan diferensial biasa (PDB) orde 1 yang berbentuk

) ( ) (x y Qx P

dx dy

=

+ secara umum adalah

dx

e

x

Q

e

x

y

(

)

=

−

∫

P(x)dx

∫

(

)

∫

P(x)dx . (a) Kita akan mengembangkan penggunaan (a) pada penyelesaian PDB order 2 linear tak homogen dengan contoh.

Contoh. Misal perlu diselesaikan (Holmes, 1995. hal.31)

1

2 2

=

−

+

y

dx

dy

dx

y

d

ε

dengan y(0) = y(1) =1. (c.1.1)

Kita susun bentuk PD yang difaktorkan dengan menggunakan notasi D = d/dx maka (c.1.1) dapat ditulis sebagai

(

D

2

+

ε

D

−

1

)

y

=

1

. Persamaan karakteristik adalah

m

2

+

ε

m

−

1

=

0

. Menggunakan rumus abc diperoleh :

Sebut 4 1 2 2 . 1 ε ε _{+ +} − =

m dan

4 1 2 2 2 ε ε _{− +} − =

m . (c.1.2)

Dengan (c.1.2) maka persamaan (c.1.1) dapat ditulis dalam bentuk 1 ) )(

(D−m₁ D−m₂ y = . (c.1.3)

Sebut u =

(

D

−

m

₂

)

y

maka dapat disusun

(

D

−

m

₁

)

u

=

1

atau

Du

+

(

−

m

₁

)

u

=

1

.

Sehingga mx mx mx

x m x m x m dx m dx m e C m e C e m e dx e e dx e e x

u 1 1 1

1 1 1 1 1 1 1 1 1 1 1 ) ( + =− + − = = ∫ ∫ = − − − − −

∫

∫

.

Untuk mendapatkan y(x) maka digunakan

(

D

−

m

₂

)

y

= u atau Dy + (-

m

₂)y = u = Cemx m 1 1 1 1 ₊ − .

Lagi , kita menggunakan persamaan (a) sehingga dapat diperoleh :

dx e x u e dx e x Q e x

y = −∫P xdx

∫

∫Pxdx = −∫−m2dx

∫

∫−m2dx

) ( ) ( ) ( () ( ) = 2 1 1 m m

+ _Cemx

m m 1 1 2 1 1 − + x m

e

C

2

2 .

Jadi dengan menggunakan persamaan (c.1.2) dapat ditulis penyelesaian eksak yaitu

y(x)=

2 1 1 m m + x m e C m m 1 1 2 1 1 − + x m

e

C

2

2 = mx mx

e C e

C 1 2

2 1 2 4 1 2 1 1 + + + − ε

= mx mx

e C e

C 1 2

2 3

1+ +

− .(c.1.4) dengan 4 1 2 2 . 1 ε ε _{+ +} − =

m dan

4 1 2 2 2 ε ε_{− +} − =

m . (Ingat bahwa

m

1

m

2 adalah perkalian akar-akar

dari persamaan kuadrat m2 +

ε

m−1=0). Syarat batas yaitu y(0) = y(1) = 1 digunakan untuk mencari

C

₃ dan

C

₂. Untuk y(0) =1 maka y(0) =

−

1

+

C

₃

+

C

₂ =1 sehingga

C

₃

+

C

₂

=

2

. Dengan menggunakan syarat batas y(1) = 1 diperoleh

2 2 1

2

3 + =

m m

e C e

657

Oleh karena itu mencari

C

₃dan

C

₂ dapat dilakukan denngan menyelesaikan sistem persamaan linear atau dengan substitusi. Diperoleh













−

−

−

=

2 1

2

1

2

3 m m

m

e

e

e

C

dan













−

−

=

2 1

1

1

2

2 m m

m

e

e

e

C

. (c.1.6)

Diperoleh penyelesaian eksak yaitu

x m x

m

e C e C x

y 1 2

2 3

1 )

( =− + + (s.1)

dengan

C

₃ dan

C

₂ dinyatakan pada persamaan (c.1.6). Pada Gambar (1a) ditunjukkan penyelesaian eksak untuk berbagai

ε

→

0

.

Gambar 1. Penyelesaian eksak untuk soal contoh ₁ 2

2

= − + y

dx dy dx

y

d _{ε dengan y(0) = y(1) =1.}

untuk nilai

ε

=

0

.

001

,

ε

=

0

.

01

dan

ε

=

0

.

1

.

Dari hasil ditunjukkan bahwa pada Gambar 1a untuk nilai

ε

=

0

.

001

,

ε

=

0

.

01

dan

ε

=

0

.

1

penyelesaian tidak menunjukkan perbedaan. Untuk selanjutnya ditunjukkan cara mendapatkan penyelesaian asimtotik.

Tahap 1. Kita akan menggunakan asumsi bahwa penyelesaian berbentuk deret asimtotik terhadap

ε

yaitu

...

)

(

)

(

)

(

x

=

y

₀

x

+

y

₁

x

+

y

ε

. (c.4.1)

Dengan mengelompokkan tiap orde

ε

maka dapat disusun PDB tiap kasus misal pada O(1) dan

) (

ε

O yaitu

: ) 1 (

O

y

₀

′′

−

y

₀

=

1

,

y

₀

(

0

)

=

y

₀

(

1

)

=

1

. (c.4.1)

: ) (

ε

O

y

₁

′′

+

y

₀

′

+

y

₁

′

−

y

₁

=

0

. (c.4.2)

Tampak bahwa penyelesaian pada O(1) diperlukan untuk mendapatkan penyelesaian pada O(

ε

). Penyelesaian diperoleh sebagai berikut.

PD pada persamaan (c.4.1) merupakan PDB biasa tak homogen. dengan akar-akar karakteristik adalah

m

1

=

1

dan

m

2

=

−

1

. Disusun PDB dengan operator D= d/dx yaitu

1 ) 1 )( 1

(D− D+ y0 = dan tulis

u

=

(

D

+

1

)

y

0 sehingga PDB menjadi (D−1)u =1 atau 1

) 1 (− =

+ u

Du .

Gunakan operator persamaan (a) diperoleh x x x

dx dx

e

C

dx

e

e

dx

e

e

x

658 x x x x x e C e C dx e C e e x

y = −

∫

− + 2 =− + 1 + ₂ −

1 0 2 1 ) ( )

( . Karena konstanta masih bebas maka

penyelesaian dapat ditulis sebagai y₀(x)=−1+C₃ex +C₂e−x. Dengan syarat batas maka penyelesaian

O

(

ε

0

)

dapat ditulis sebagai

1

=

y

₀

(

0

)

=

−

1

+

C

₃

+

C

₂ atau

C

₃

+

C

₂

=

2

. Menggunakan y₀(1)=1=−1+C₃e1 +C₂e−1 atau C₃e+C₂e−1 =2. Dengan menyelesaikan sistem persamaan linear, diperoleh

C

₃

=

0.5379 dan

C

₂

=

1.4621. Jadi penyelesaian O(1): adalah

x x

e e

x

y0( )=−1+0.5379 +1.4621 − .

Untuk selanjutnya akan diselesaikan PDB pada O(

ε

): yaitu

y

₁

′′

+

y

′

₀

+

y

₁

′

−

y

₁

=

0

dan karena

x x

e e

x

y0( )=−1+0.5379 +1.4621 − maka masalah menjadi

y

1

′′

+

y

1

′

−

y

1

=

x x

e

e + −

−0.5379 1.4621 . Sebagaimana pada contoh, sebut

m

₁= _{( 1 5)}

2

1 _{− + dan}

2

m

= ( 1 5) 2

1 _{− −}

adalah akar-akar karakteristik PD homogen sehingga

y

₁

′′

+

y

₁

′

−

y

₁

=

−

y

₀

′

dapat ditulis sebagai

)

(

)

)(

(

D

−

m

₁

D

−

m

₂

y

=

Q

x

dengan Q(x) = − y₀′ =−0.5379ex +1.4621e−x. Secara sama pula dimisalkan u =

(

D

−

m

₂

)

y

sehingga diperoleh

(

D

−

m

₁

)

u

=

Q

(

x

)

. Operator integral pada persamaan (a) dapat digunakan yaitu

∫

∫

∫

=

e

− −

Q

x

e

−

dx

x

u

m1dx m1dx

)

(

)

(

( ) = x mx

x e C e m m e ₁ 1 1 1 1 4621 . 1 1 5379 . 0 ₊ + − − − − _.

Selanjutnya perlu diselesaikan u =

(

D

−

m

₂

)

y

₁ atau

Dy

₁+

(

−

m

₂

)

y

₁= u. Yaitu

dx e e C m e m e e

y mx mdx

x x dx m ∫ + + − − − ∫

= − −

∫

− − 2

1 2 ) 1 4621 . 1 1 5379 . 0 ( 1 1 1 ) ( 1 .

Kita dapat menyederhanakan menjadi

x m x m x x e C e m m C e m m e m m m

y 1 2

2 2 1 1 2 1 2 1 2 1 ) 1 )( 1 ( 4621 . 1 ) 1 )( 1 ( ) 1 ( 5379 . 0 + − + + + + − − − − = − _.

Selama ini kita langsung menggunakan syarat batas pada O(1). Karena

y

₀

(

0

)

=

1

, dan

y

₀

(

1

)

=

1

kita dapat memilih bahwa

y

₁

(

0

)

=

y

₁

(

1

)

=

0

. Sehingga syarat batas untuk

y

₁

(

x

)

haruslah

)

0

(

0

=

y

₁ dan

0

=

y

₁

(

1

)

. Jadi kita dapat mencari

C

₁dan

C

₂ dengan syarat batas tersebut. Yaitu untuk

0

=

y

₁

(

0

)

diperoleh

2 2 1 1 2 1 2 1 2 1 ) 1 )( 1 ( 4621 . 1 ) 1 )( 1 ( ) 1 ( 5379 . 0 0 ) 0 ( C m m C m m m m m y + − + + + + − − − − = =

dan 1 2

2 2 1 1 1 2 1 2 1 2 1 ) 1 )( 1 ( 4621 . 1 ) 1 )( 1 ( ) 1 ( 5379 . 0 0 ) 1

( m m

e C e m m C e m m e m m m y + − + + + + − − − − = = − _.

Diperoleh sistem persamaan linear yaitu

            + + − − − − + + − − − − =                   − − −1 2 1 2 1 2 2 1 2 1 2 2 1 2 1 2 1 ) 1 )( 1 ( 4621 . 1 ) 1 )( 1 ( ) 1 ( 5379 . 0 ) 1 )( 1 ( 4621 . 1 ) 1 )( 1 ( ) 1 ( 5379 . 0 1 1 1 2 1 _e m m e m m m m m m m m C C e e m m m m m m .

Diperoleh

C

₁

=

5.1236 dan

C

₂

=

0.5790. Sehingga penyelesaian pada O(

ε

) pada masalah (c.4.2) diperoleh x m x m x x e e m m e m m e m m m

y 5.1236 1 _0.5790 2

) 1 )( 1 ( 4621 . 1 ) 1 )( 1 ( ) 1 ( 5379 . 0 2 1 2 1 2 1 2

1 _{− −} + _{+ +} + ₋ +

− −

659

dengan

m

₁= _{( 1 5)}

2

1 _{− + dan}

2

m

= ( 1 5) 2

1 _{− − . Jadi penyelesaian eksak untuk masalah (c.1.1) dengan}

pendekatan asimtotik adalah

)

(

)

(

)

(

x

y

₀

x

y

₁

x

y

=

+

ε

=−1+0.5379ex+1.4621e−x+

   

 

+ −

+ +

+ + −

−

−

− x −x mx mx

e e

m m e m m

e m m

m _{1 2}

5790 . 0 1236

. 5 )

1 )( 1 (

4621 . 1 )

1 )( 1 (

) 1 ( 5379 . 0

2 1 2

1 2

1

2

ε . (s.2)

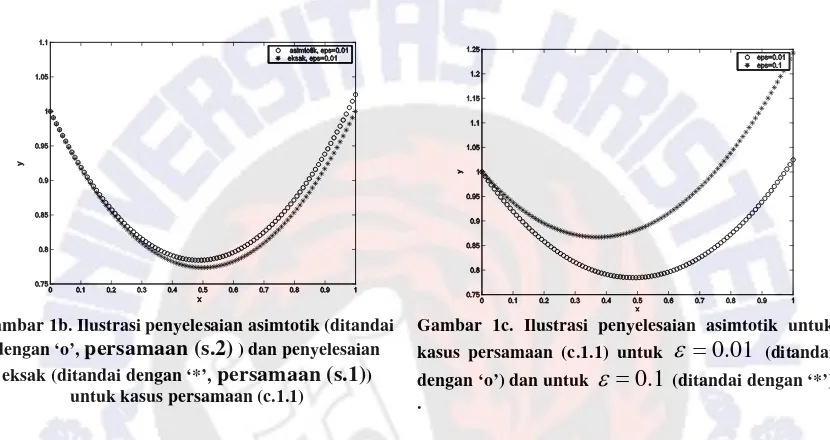
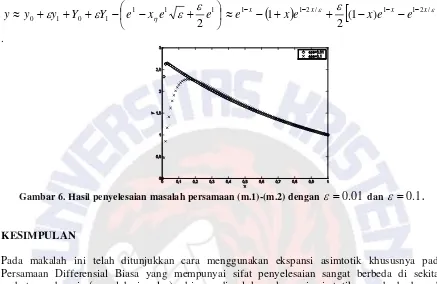
Jadi penyelesaian asimtotik telah diperoleh untuk 2 suku pertama yang akan dibandingkan dengan penyelesaian eksak (persamaan (s.1)). Hal ini diilustrasikan pada Gambar 1b. Demikian pula untuk penyelesaian dengan

ε

=

0

.

01

dan

ε

=

0

.

1

yang digambarkan pada Gambar 1c.

Gambar 1b. Ilustrasi penyelesaian asimtotik (ditandai dengan ‘o’, persamaan (s.2) ) dan penyelesaian

eksak(ditandai dengan ‘*’,persamaan (s.1)) untuk kasus persamaan (c.1.1)

Gambar 1c. Ilustrasi penyelesaian asimtotik untuk kasus persamaan (c.1.1) untuk

ε

=

0

.

01

(ditandai dengan ‘o’) dan untuk

ε

=

0

.

1

(ditandai dengan ‘*’) .

Kita dapat pula menyelesaikan masalah persamaan (c.1.1) dengan cara numerik. Hal ini diperlukan bila problem secara umum tidak dapat diselesaikan secara analitik maka penyelesaian numerik dianggap sebagai penyelesaian eksak. Untuk menunjukkan metode ini maka kasus (c.1.1) dikerjakan dengan cara numerik pula yaitu dengan metode Runge Kutta.

Pada masalah nonlinear seperti gerak roket meninggalkan bumi (Holmes, 1995, hal.1) ditunjukkan cara penyelesaian dengan ekspansi asimtotik. Parameter kecil

ε

menyatakan rasio jarak yang ditempuh terhadap jari-jari bumi. Akan tetapi sejauh ini dapat disimpulkan secara sederhana bahwa ketika ketaklinearan cukup dominan maka pendekatan asimtotik tidak cukup baik. Demikian pula pendekatan asimtotik berkembang ketika terdapat sifat transisi pada batas- batas domain. Hal ini ditunjukkan pada Bagian Analisa dan Pembahasan untuk masalah singular perturbation problem

pada PDB. Kesingularan problem terjadi karena jika dipilih

ε

=

0

maka problem berubah derajat PDB-nya. Masalah khusus sebagai materi pembelajaran tentang hal ini adalah menentukan penyelesaian (Holmes, 1995, hal 48 )

0 2 2 ′+ =

+

′′ y y

y

ε

untuk

0

<

x

<

1

, (m.1)

660

METODE PENELITIAN

Langkah-langkah penelitian pada makalah ini ditunjukkan sebagai berikut

1.1 Menyusun penyelesaian PDB Orde 1 Linear dengan operator integral sebagai penyelesaian eksak.

1.2 Jika penyelesaian analitik tidak dimungkinkan, maka dicari penyelesaian numerik dengan metode Runge Kutta dan dianggap sebagai penyelesaian eksak.

1.3 Mencari penyelesaian asimtotik.

1.4 Mengilustrasikan penyelesaian eksak dan penyelesaian asimtotik serta membandingkan. 1.5 Menganalisa penyelesaian untuk berbagai nilai

ε

.

HASIL DAN PEMBAHASAN MASALAH BOUNDARY LAYER (m.1)-(m.2)

Perhatikan bahwa problem (m.1)-(m.2) menjadi PD orde 1 untuk

ε

=

0

. Hal ini merupakan salah satu penciri PDB merupakan masalah boundary layer. Tahapan penyelesaian berbeda dengan sebelumnya. Hal ini ditunjukkan sebagai berikut. Dengan asumsi ekspansi yang standart yaitu

....

)

(

)

(

)

(

x

≈

y

₀

x

+

y

₁

x

+

y

ε

(m.3)

dan disubstitusikan pada (m.1) diperoleh

ε

(

y

₀

′′

+

...

) (

+

2

y

₀

′

+

ε

y

₁

′

+

...

) (

+

2

y

₀

+

ε

y

₁

+

...

)

=

0

. Sehingga

) 1 (

O :

0

0 0

′

+

y

=

y

(m.4a)

dan penyelesaian umumnya adalah

x

ae x

y0( )= − . (m.4b)

Penyelesaian ini hanya memuat 1 konstan sembarang, padahal ada 2 syarat yang batas pada (m.2) yang perlu digunakan. Hal ini berarti bahwa penyelesaian (m.4) dengan ekspansi (m.3) tidak dapat menjelaskan penyelesaian problem (m.1)-(m.2) pada interval

0

≤

x

≤

1

. Demikian pula kita tidak tahu syarat batas mana yang harus digunakan. Cara mengatasi ditunjukkan pada tahap berikutnya.

Mencari penyelesaian (m.1)-(m.2) untuk O(1)

Step 1. Outer Solution

Dianggap bahwa terdapat boundary layer pada x = 0 atau x = 1 sehingga perlu pendekatan asimtotik yang berbeda. Penyelesaian pada hasil asimtotik pada sekitar batas-batas interval disebut outer solution.

Step 2.Boundary layer (inner layer)

Akan tetapi dapat pula terjadi singularitas pada suatu x= a dengan 0 <a <1. Dengan asumsi ada

boundary layer pada x = 0 , diperkenalkan koordinat boundary layer yaitu

α

ε

x

x = , (m.5)

dengan

α

>

0

. Perhatikan bahwa hal ini seperti transformasi yang meregangkan (stretching transformation) variabel x jika

ε

→

0

. Dengan transformasi (m.5) maka model (m.1) perlu diubah dalam variabel yang baru, demikian pula diferensial juga berubah. Dengan aturan rantai maka

x d

d x

d d dx

x d dx

d

α

ε

1

=

661

Selanjutnya kita perlu menggunakan notasi baru untuk penyelesaian, sebutlah Y(x) sehingga masalah (m.1) menjadi

0 2 2

2 2 2

1− ₊ − _{+ =}

Y x d dY x

d Y

d α

α _ε

ε (m.7)

dan

0 ) 0 ( =

Y . (m.8)

Penyelesaian Y(x) juga perlu diekspansi , misal dipilih

... ) ( )

( )

(x ≈Y₀ x + Y₁ x +

Y

ε

γ ,

γ

>0. (m.9)

Jika parameter

ε

divariasi mendekati 0, maka variabel xdibuat tetap. Dengan mensubstitusikan (m.9) pada persamaan (m.7) diperoleh

(

₀ ...

)

2

(

₀ ...

) (

2 ₀ ...

)

0 2

2 2

1− + + − _Y + + _Y + =

x d

d Y

x d

d α

α _ε

ε . (m.10)

Kita akan menyesuaian tiap suku berdasarkan order epsilon. Ada beberapa kemungkinan.

(i). Suku kesatu dan ketiga pada (m.10) pada order yang sama sehingga dipilih

1

−

2

α

=

0

sehingga α =1/2. Hal ini berakibat suku kedua menjadi

O

(

ε

−1/2

)

. Hal ini melanggar pada masalah awal (m.1) bahwa suku kedua berorde epsilon lebih tinggi. Oleh karena itu kemungkinan penyesuaian ini tidak tepat.

(ii). Suku kesatu dan suku kedua berorde sama sedangkan suku ketiga pada orde yang lebih tinggi. Sehingga berlaku

1

−

2

α

=

−

α

. Jadi

α

=

1

. Jadi suku pertama dan suku kedua berorde

O

(

ε

−1

)

sehingga suku ketiga menjadi

O

(

ε

0

)

=

O

(

1

)

_{. Hal ini sesuai dengan masalah mula-mula sehingga}

penyesuaian ini dianggap tepat. Oleh karena itu untuk proses selanjutnya kita akan menyelesaikan masalah (m.1) dengan pendekatan asimtotik sebagaimana biasanya sebagai berikut.

)

(

ε

−1

O

:Y₀′′+2Y₀′=0, untuk 0<x<∞, Y(0)=0. (m.11)

Penyelesaian umum berbentuk

) 1 ( )

( 2

0

x

e A x

Y = − − (m.12)

dengan A konstan sembarang. Ekspansi (m.9) diharapkan memuat paling sedikit 1 penyelesaian

outer layer pada persamaan (m.4a). Yang berarti outer solution harus memenuhi syarat batas x = 1.

Dari (m.4a) dan (m.4b) harus memenuhi syarat batas x = 1. Diperoleh

x

e x

y0( )= 1− . (m.13)

Langkah selanjutnya adalah menentukan konstan A pada (m.12).

Step 3. Pencocokan (matching)

Outer solution and inner solution adalah pendekatan untuk fungsi yang sama. Oleh karena itu pada daerah transisi antara outer solution dan inner solution harus memberikan penyelesaian yang sama. Hal ini diatur dengan cara bahwa nilai

Y

₀ pada boundary layer (untuk

x

→

0

) sama dengan nilai

0

y

yang muncul (untuk

x

→

0

). Hal ini berarti

Y

₀

(

∞

)

=

y

₀

(

0

)

. Sehingga diperoleh A = e. Sehingga (m.12) menjadi

x

e e x

Y₀( )= − 1−2 . (m.14)

662

Gambar 2. Ilustrasi penyelesaian inner dan outer.

Gambar 2 menunjukkan bahwa untuk penyelesaian outer memenuhi syarat batas y(0) = 0 sedangkan syarat batas y(1) = 1 tidak dipenuhi. Sedangkan sebaliknya penyelesaian outer tidak memenuhi syarat batas pada y(0) = 0, tetapi memenuhi syarat batas pada y(1) = 1. Oleh karena itu kedua penyelesaian perlu digabungkan. Langkah selanjutnya adalah melakukan penggabungan ekspansi asimtotik. Masalah pencocokan dapat diilustrasikan pada Gambar 3 .

Ide dari pencocokan dan penggabungan ekspansi sebagai berikut. Kita perlu memperkenalkan variabel antara yaitu x_η = x/

η

(

ε

) yang diposisikan diantara koordinat yang O(1) yaitu koordinat pada outer layer dan O(

ε

) koordinat pada inner layer. Variabel antara ini ditempatkan pada daerah transisi atau domain yang tercampur (overlap) sebagaimana ditunjukkan pada Gambar 3. Untuk itu diharapkan

η

(

ε

) memenuhi

ε

<<

η

<<1. Kondisi yang tepat secara eksplisit untuk prosedur pencocokan sebagai berikut :

Gambar 3. Skema daerah validitas ekspansi dalam dan luar pada proses pencocokan

(i) Ubah variabel pada ekspansi Outer (dari x menjadi x_η) untuk memperoleh

y

outer.

Diasumsikan bahwa terdapat

η

₁

(

ε

)

<<

η

(

ε

)

≤

1

.

(ii) Ubah variabel pada ekspansi Inner (dari xke x_η) untuk memperoleh

y

_inner. Dianggap terdapat

η

(

ε

) sehingga dipenuhi

ε

≤

η

(

ε

)

<<

η

₂.

(iii) Diasumsikan bahwa domain validitas ekspansi

y

outerdan

y

inner overlap sehingga 2

1

η

η

<<

. Pada domain overlap ini ekspansi dicocokkan dan perlu bahwa suku pertama

outer

y

dan

y

_inner sama.

Untuk menggunakan prosedur tersebut, maka perlu diperkenalkan variabel antara yaitu

)

(

ε

η

η

x

x

=

= _β

ε

x

663

dengan 0<

β

<1. Interval ini ada karena perlunya penyekalaan untuk variabel antara berada pada skala outer yaitu pada O(1) dan pada skala inner yaitu O(

ε

). Dari (m.9) dan (m.12)

menjadi

(

1

)

...

1

/ 2

+

−

≈

− xη ε−β

inner

A

e

y

= A + ... .Penyelesaian outer dari persamaan (m.3) dan

(m.13) dapat disusun y_outer ≈e1−xηεβ +... = e + ... . Karena suku pertama harus cocok maka

dipilih A = e. Untuk tahap selanjutnya kita perlu menggabungkan penyelesaian.

Step 4. Ekspansi gabungan (Composite Expansion) Penggabungan dilakukan dengan memilih

) 0 ( ) ( )

( 0 0

0 y

x Y x y

y≈ + −

ε

ε / 2 1 1 x x

e

e

y

≈

−

+

− . (m.16)

yang merupakan penyelesaian O(1) pada masalah (m.1)-(m.2) dengan ekspansi asimtotik. Hasil penggabungan ditunjukkan pada Gambar 4.

Gambar 4. Hasil penggabungan ekspansi untuk masalah (m.1)-(m.2) dengan sumbu vertikal memenuhi persamaan (m.16)

Hasil penggabungan menunjukkan adanya hasil yang tepat untuk penyelesaian pada syarat batas

y(0) = 0 sedangkan pada syarat batas y(1) = 1 dipenuhi secara asimtotik (tidak tepat benar). Kita akan mencari suku kedua hasil ekspansi terhadap epsilon yaitu O(

ε

).

Mencari penyelesaian O(

ε

) untuk masalah (m.1)-(m.2)

Problem yang diperoleh sbb.

) (

ε

O : _{1 1 0}

2 1

y y

y′+ =− ′′ dengan

y

₁

(

1

)

=

0

. (m.17a)

Penyelesaian masalah ini dapat diperoleh dengan menggunakan penyelesaian (m.13) dan differensialkan 2 kali serta melakukan prosedur yang sama sebagaimana pada cara menyelesaikan PDB orde 1 linear tak homogen (lihat persamaan (a)). Diperoleh

x

e y

y₁′+ ₁ =− 1−

2 1

dengan

y

₁

(

1

)

=

0

. (m.17b)

Syarat batas

y

₁

(

1

)

=

0

karena pada masalah mula-mula y(1)=1 sedangkan y(1)=1

...

)

1

(

)

1

(

₁

0

+

+

≈

y

ε

y

. Padahal telah digunakan

y

₀

(

1

)

= 1 sehingga haruslah

y(1)=1. Dengan

persamaan (a) diperoleh

∫

 ∫

  

 − ∫

= − −

dx e e e

x

y1 (1)dx 1 x (1)dx

2 1 )

664

Penyelesaian umum berbentuk

∫

 =−

∫

=−

(

+

)

    − = − − − − C ex e edx e dx e e e x

y x x x x x

2 1 2 1 2 1 ) ( 1 1 .

Dengan kata lain yaituy x =− xe−x − Ce−x

2 1 2 1 ) ( 1

1 . Dengan syarat batas

y

1

(

1

)

=

0

diperoleh

0 2 1 ) 1 ( 2 1 ) 1 ( 1

1 =− − =

−

Ce

y . Sehingga −Ce−1 =1 atau C = -e. Diperolehy₁ x =

(

1−x

)

e1−x

2 1 )

( .

Penyelesaian masalah boudary layer dengan cara menggunakan ekspansi (m.9) pada (m.7) dan karena harus pada O(

ε

) maka dipilih

γ

=1. Masalah boundary layer berbentuk

0 1

1

2

Y

2

Y

Y

″

+

′

=

−

with

Y

₁

(

0

)

=

0

.

Dengan operator integral (persamaan a), penyelesaian umum dapat diperoleh dengan terlebih menyusun persamaan karakteristik yaitu m2 +2m=0. Sehingga

m

₁

=

0

dan

m

₂

=

−

2

. Ambil

(

D

m

2

)

Y

1

u

=

−

sehingga PDB dapat ditulis menjadi

D

(

D

−

m

₂

)

Y

₁

=

−

2

Y

₀ atau

Du

=

−

2

Y

₀ =

)

(

2

e

−

e

1−2x

−

. Sehingga

(

1 2

)

1 2 ₁

2 1 2

2 e e dx ex e C

u x x+

     ₊ − = − − = − −

∫

. Karena

u

=

(

D

−

m

₂

)

Y

₁

atau 1

2 1 1 2 1 2 1 2 )

( m Y ex e C

DY x+

     ₊ − = − + −

. Dengan operator integral kita dapat memperoleh

x d C e x e e

Y m dx x

∫

_− _ + _+ _ ∫ = − − − 1 2 1 ) ( 1 2 1 2 2

= = e 2x x 2 e1 4x C₁xe 2x C₂e 2x

2 1 ) ( − − − − _{+ + +} −

.

Dengan syarat batas

Y

₁

(

0

)

=

0

diperoleh

₁ 0 ₂ 2 1 0 0 ) 0

( e C

Y = = + + +

, sehingga

C e

2 1 2 =−

.

Sehingga

Y

₁

=

B

(

1

−

e

−2x

) (

−

x

e

1

+

e

−2x

)

dengan B adalah konstan sembarang. Untuk melakukan pencocokan, kita pergunakan variabel antara yaitu menggunakan persamaan (m.15)

x

η= _β

ε

x

sehingga penyelesaian outer berbentuk

(

1

)

...

2

1

1

+

−

+

≈

− η β β − ηεβ

η

ε

ε

ε

x

x

outer

e

x

e

y

(m.18)

Dengan menetapkan

ξ

=

−

2

x

_η

/

ε

1−β ekspansi boundary layer menjadi

(

1

)

(1 ) ₁

(

1

)

... 1 1 ₊         + − − + − ≈ ₋ ξ β η ξ ξ

ε

ε

B e x e e

e e y_inner

(

1

)

(1 ) ₁

(

1

)

... 1 1 +         + − − + − ≈ ₋ ξ β η ξ ξ

ε

ε

B e x e e

e

e

≈

e

1

−

ε

β

x

_η

e

1

+

B

ε

. (m.19)

Dengan mencocokkan antara persamaan (m.18) dan (m.19) diperoleh 1

2 1

e

B= (perhatikan bahwa

B berada pada O(

ε

).) Akan tetapi perhatikan pada persamaan (m.18) bahwa O(

ε

) adalah e

x

e1 2

2

2 η

ε

ε

+ . Suku kedua tidak terdapat pada persamaan (m.19). Mengapa hal ini terjadi ?.

665

outer, suku yang

O

(

ε

β

)

muncul pada O(1) dan pada masalah boundary layer (inner solution) muncul pada dari penyelesaian O(

ε

).

Pada akhirnya kita dapat menggabungkan hasil ekspansi yaitu dengan menambahkan dan mengurangkan hasil ekspansi yang sama. Yaitu

   



 _{− +}

− + + +

≈ 1 1 1

1 0 1 0

2e

e x e Y Y y y

y

ε

ε

_η

ε

ε

1

(

)

1 2 /ε

ε

[

1 1 2 /ε

]

) 1 ( 2

1 x x x

x

e e x e

x

e− − + − + − − − −

≈

.

Gambar 6. Hasil penyelesaian masalah persamaan (m.1)-(m.2) dengan

ε

=

0

.

01

dan

ε

=

0

.

1

.

KESIMPULAN

Pada makalah ini telah ditunjukkan cara menggunakan ekspansi asimtotik khususnya pada Persamaan Differensial Biasa yang mempunyai sifat penyelesaian sangat berbeda di sekitar perbatasan domain (masalah singular) sehingga diperlukan ekspansi asimtotik yang berbeda pada sekitar batas interval domain.

DAFTAR PUSTAKA

[1] Holmes, M. H. 1995. Introduction to Perturbation Methods, Springer Verlag.

[2] Parhusip, H. A. 2005. (a). Darcy's law and Permeability for Non-Newtonian Fluids in Porous Media with Two Scale Asymptotic Expansion, dissertation, Institut Teknologi Bandung, Indonesia.

[3] Parhusip, H. A., 2005. (b). Uniformity of the asymptotic expansion of Carreau's law for

polymer flows, Prosiding Seminar Nasional Matematika Jurusan Matematika, FMIPA

-UNDIP, ISBN,979-704-338-X, E15, hal.100-105.