PENGEMBANGAN ALGORITMA BARIS UNTUK PEWARNAAN GRAF DEVELOPMENT OF SEQUENTIAL ALGORITHM FOR GRAPH COLORING

PENGEMBANGAN ALGORITMA BARIS UNTUK PEWARNAAN GRAF DEVELOPMENT OF SEQUENTIAL ALGORITHM FOR GRAPH COLORING

Ramlah1, Hasmawati2, Armin Lawi3 1

Bagian Matematika Terapan, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Hasanuddin,

2

Bagian Graf, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Hasanuddin, 3

Bagian Pemrograman, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Hasanuddin,

Alamat Korespondensi:

Ramlah S.Si

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin

Makassar,

HP: 085394246049

Abstrak

Salah satu algoritma yang dapat digunakan untuk pewarnaan graf adalah algoritma baris. Pada tahun 2012, Rahmat Januar Noor membuat program algoritma baris dengan software matlab, yang menghasilkan jumlah warna sama dengan bilangan kromatik pada beberapa graf sederhana. Oleh karena itu, pada peneltian ini dilakukan penganalisaan dan pengembangan algoritma baris. Metode yang digunakan yaitu: merubah urutan label graf, menerapkan algoritma baris pada graf tersebut, mengubah urutan label graf berdasarkan derajat terbesar, selanjutnya menerapkan dan menganalisa dampak dari label berdasarkan derajat terbesar pada algoritma baris. Jumlah warna yang dihasilkan oleh algoritma baris pada graf sederhana yang sama dengan label yang berbeda menghasilkan jumlah warna yang ambigu (berbeda). Jumlah warna yang dihasilkan oleh algoritma baris berdasarkan derajat terbesar pada graf sederhana dengan derajat simpul berbeda, menghasilkan jumlah warna yang sama dengan bilangan kromatik graf tersebut. Jumlah warna yang dihasilkan oleh algoritma baris berdasarkan derajat terbesar pada graf sederhana dengan derajat simpulnya sama, menghasilkan jumlah warna yang ambigu. Adapun kompleksitas pengembangan algoritma baris diperoleh batas atas dan batas bawahnya ( ), dimana algoritma asalnya memiliki batas atas ( ). Disimpulkan bahwa algoritma baris berdasarkan derajat terbesar optimal pada graf dengan derajat simpul yang berbeda dan belum optimal pada graf dengan derajat simpul yang sama. Dan kompleksitas algoritma baris berdasarkan derajat terbesar mampu memperbaiki kompleksitas algoritma baris.

Kata Kunci: Pewarnaan graf, bilangan kromatik, algoritma baris, derajat terbesar, kompleksitas waktu asimptotik.

Abstract

One of algoritma that can be used for graf colouring is sequential algorithm. In 2012, Rahmat Januar Noor made sequential algoritma program with matlab software, which result the sum of colours equal with chromatic number at some simple graph. Therefore, in this research conducted analysis and development of sequential algorithm. The methods are: change the label sequence graph, applying the sequential algorithm to the graph, change the order of the graph labeled by the greatest degree, and then implement and analyze the impact of the label based on the greatest degree sequential algorithm. The amount of color produced by sequential sequential algorithm on simple graph are the same as the number of different labels produced ambiguous colors (different). The number of colors generated by an sequential algorithm based on the degree of the largest in graphs with different vertex degrees, producing the same amount of color chromatic number graph. The number of colors generated by an sequential algorithm based on the degree of the largest in simple graphs with the same degree of knots, resulting in a number of colors ambiguous. The complexity of developing sequential algorithms derived of the upper and lower limit of ( ), where the original algorithm has an upper limit of ( ). It is concluded that the sequential algorithm is based on the largest degree optimal on a graph with vertices of different degrees and not optimal for graphs with vertices of the same degree. And the complexity of the sequential algorithm by the largest degree of complexity of the algorithm is able to the repair.

PENDAHULUAN

Awal mula dikenal pewarnaan graf adalah pada tahun 1852 oleh seorang ahli matematika Francis Guthrie lulusan Universitas Perguruan tinggi London. Francis Guthrie mengamati bahwa daerah Inggris dapat diwarnai dengan empat warna sedemikian sehingga daerah yang bertetangga mempunyai warna yang berbeda. Dia menyatakan bahwa untuk mewarnai semua peta dibutuhkan empat warna dan dia mencoba untuk membuktikan hal ini. Banyak ilmuan matematik yang juga mencoba membuktikan masalah ini, diantaranya Joseph Sylvester (1838- 1841), Arthur Cayley (1841- 1878), Alfred Bray Kempe (1849- 1922), Peter Guthrie Tait (1831- 1901). Dan pada tahun 1976 Wolfgang Haken dan Kenneth Appel berhasil membuktikan teorema ini dengan menggunakan komputer dalam waktu yang cukup lama yaitu 1200 jam. Berkat usaha mereka, maka dikenal salah satu submateri dalam graf yaitu pewarnaan graf. (Chartrand, dkk., 2005)

Terdapat tiga macam pewarnaan graf yaitu pewarnaan simpul (vertex colouring), pewarnaan sisi (edge colouring) dan pewarnaan wilayah (face colouring). Pewarnaan sisi dan pewarnaan wilayah merupakan bentuk lain dari pewarnaan simpul dan dapat diubah kembali menjadi model pewarnaan simpul.

Algoritma yang dapat digunakan untuk menyelesaikan pewarnaan simpul antara lain: First Fit (FF), Largest Degree Ordering (LDO), Satureted Degree Ordering (SDO), Incident Degree Ordering (IDO) dan baris (sequential). Pada tahun 2006, Dr. Hussein Al- Omari dan Khair Eddin Sabri menemukan dua algoritma baru dengan menggabungkan LDO- IDO dan SDO- LDO, dan dari penelitian mereka diketahui bahwa gabungan algoritma SDO- LDO menggunakan warna yang lebih sedikit dari FF, LDO, SDO, IDO dan LDO- IDO. (Al- Omari, dkk., 2006). Pada tahun 2010, Akhlak Mansuri, Vijay Gupta dan R.S. Chandel berhasil membuat program untuk algoritma SDO-LDO dan LDO- SDO. (Mansuri, dkk., 2010). Pada tahun 2012, Rahmat Januar Noor membuat program algoritma baris yang menghasilkan jumlah warna sama dengan bilangan kromatik pada beberapa graf sederhana. (Noor, 2012). Dan pada tahun yang sama pula, Suh, Y., Cho, M. dan Lee, K.M, menggunakan metode sequential monte carlo dimana target yang dicapai ditentukan (Suh, dkk., 2012). Berdasarkan uraian diatas, maka penulis tertarik untuk merancang dan mengembangkan algoritma baris.

BAHAN DAN METODE

Lokasi dan Rancangan Penelitian

Pelaksanaan penelitian di jurusan matematika Universitas Hasanuddin, pada bulan agustus- desember 2012. Adapun rancangan penelian menggunakan metode algoritma baris dengan memperhatikan pelabelan simpul pada graf sederhana.

Desain dan Variabel Penelitian

Secara umum desain penelitian yang dilakukan adalah: merubah urutan label graf, menerapkan algoritma baris pada graf, mengubah urutan label graf berdasarkan derajat terbesar, selanjutnya menerapkan dan menganalisa dampak dari label berdasarkan derajat terbesar pada algoritma baris. Adapun variabel penelitian adalah seberapa dekat hasil yang diperoleh dengan bilangan kromatik graf tersebut dan waktu asimptotik dari program yang dihasilkan.

Populasi dan Sampel

Populasi adalah pewarnaan graf dengan menggunakan algoritma baris dan sofware matlab. Sampel adalah beberapa graf sederhana dengan derajat ≤ 50.

HASIL

Definisi 1

Misalkan adalah suatu graf. Simpul , ∈ ( ) dan sisi ∈ ( ). Jika = , , maka dikatakan bahwa:

Simpul bertetangga (adjacent) dengan simpul dan sebaliknya sisi terkait (incident) dengan simpul maupun simpul .

Misalkan , _dan adalah sisi dan adalah simpul. Jika , _dan terkait pada simpul , maka rusuk , _dan dikatakan bertetangga. (Chartrand, dkk., 1996).

Definisi 2

Derajat simpul pada graf dinotasikan ( ), adalah banyaknya sisi ∈ ( ) yang terkait dengan simpul . (Hasmawati. 1989).

Untuk memperoleh suatu pewarnaan simpul dengan menggunakan algoritma baris pada graf dimana ( )= { , , ⋯ , } mengikuti langkah- langkah sebagai berikut (Nurwahyu, dkk., 2009):

(Langkah ini mengawali simpul , untuk mewarnai simpul ); = 1……… (2)

Susun warna simpul yang bertetangga dengan dengan urutan orde naik dan sebut itu sebagai ……… (3.1)

Jika tidak muncul dalam , maka tandai simpul dengan , kemudian ke langkah 5, jika tidak lanjutkan……… (3.2)

(Warna dinaikkan atau ditambahkan); = + 1, kembali ke langkah (3.2)……….. (4)

(Parameter dinaikkan); jika < , maka = + 1 dan kembali ke langkah 2, jika tidak berhenti………. (5)

Gambar 1 pada lampiran merupakan graf sederhana dengan jumlah simpul 6 dan label berbeda. Dengan menggunakan algoritma baris untuk Gambar. 1(a) diperoleh , , berwarna 1, berwarna 2, berwarna 3 dan berwarna 4. Jadi banyaknya warna 4. Gambar. 1(b) diperoleh , , berwarna 1, berwarna 2, berwarna 3 dan berwarna 4. Jadi banyaknya warna 4. Gambar. 1(c) diperoleh berwarna 1, , , berwarna 2, berwarna 3 dan berwarna 4. Jadi banyaknya warna 4. Gambar. 1(d) diperoleh berwarna 1, , , berwarna 2, dan , berwarna 3. Jadi banyaknya warna 3. Gambar. 1(e) diperoleh , , berwarna 1,

berwarna 2, , berwarna 3. Jadi banyaknya warna 3.

Solusi yang diperoleh menunjukkan bahwa jumlah warna yang dihasilkan oleh algoritma baris pada graf sederhana yang sama dengan label yang berbeda menghasilkan jumlah warna yang berbeda.

Teorema 1

Kompleksitas sebuah algoritma dikatakan ( ( )) jika dan hanya jika Ω( ( )) = ( ( )). Kompleksitas waktu asimptotik pada kasus terbaik graf lintasan yaitu Ω( ) dan pada kasus terburuk graf lengkap yaitu ( ). (Noor, R.J. 2012).

PEMBAHASAN

Dalam penelitian ini terlihat bahwa hasil implementasi algoritma baris dengan label berbeda pada graf sederhana yang sama ambigu, dengan kata lain banyaknya warna yang digunakan berbeda pada graf yang sama dengan label berbeda. Dengan demikian, perlu adanya

syarat awal pada algoritma baris sehingga jumlah warna yang dihasilkan sama dan pengaturan pewarnaan graf lebih terstruktur.

Berdasarkan penjelasan diatas, berikut penulis ajukan pengembangan algoritma baris: Urutkan derajat semua simpul dalam graf sedemikian diperoleh barisan simpul = ( , , … , ), dimana ( ) ≥ ( )……… (1)

(Langkah ini mengawali parameter , digunakan untuk mewarnai simpul pada ); = 1... (2)

(Langkah ini mengawali simpul pada , untuk mewarnai simpul ); = 1……….. (3)

Susun warna simpul yang bertetangga dengan dengan urutan orde naik dan sebut itu sebagai ………. (4.1)

Jika tidak muncul dalam , maka tandai simpul dengan , kemudian ke langkah 6, jika tidak lanjutkan………. (4.2)

(Warna dinaikkan atau ditambahkan); = + 1, kembali ke langkah (4.2)……… (5)

(Parameter dinaikkan); jika < , maka = + 1 dan kembali ke langkah 3. Jika tidak berhenti………... (6)

Program Algoritma Baris Baru clear all; clc;

n= input ('jumlah simpul = '); disp (' '); for i= 1:n for j= 1:n fprintf ('r%d,%d',i,j); r(i,j)=input(' = '); end end p=sum(r); for i=1:n j=n+1; h=n+2;

r(i,j)=p(1,i); r(i,h)=i; end b=sortrows(r,n+1); for k=1:n v(k)=0; end for m=1:n p=n+1; if r(1,n+1)~= r(n,n+1) i=b(p-m,n+2); else i=1:n; end for i=i c=1; for j=1:n if r(i,j)==1 L(i,j)=v(j); else L(i,j)=0; end end t=L(i,1:n); s=sort(t); for j=1:n while c==s(1,j); c=c+1; end end v(i)=c;

end end for i=1:n; s(1,i)=i; s(2,i)=v(i); end

fprintf ('\nsimpul dan warnanya'); V=s

y=sort(v); M=y(1,n);

fprintf ('\nbanyaknya warna = %d\n\n', M)

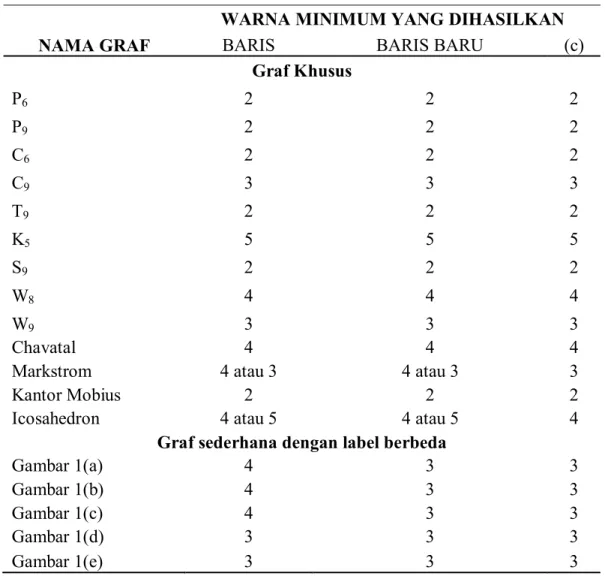
Tampak dari lampiran tabel 1, bahwa pada graf makrstrom dan graf icosahedron, pengembangan algoritma baris masih mengasilkan ambigu. Hal ini dikarenakan derajat dari graf tersebut sama, sehingga urutan berdasarkan derajat terbesar tidak merubah label awal yang diberikan.

Kompleksitas Revisi Algoritma Baris

Berikut akan ditunjukkan kompleksitas waktu asimptotik graf sederhana dengan kasus terbaik (best case) dan kasus terburuk (worst case). Untuk kasus terbaik akan ditunjukkan dengan graf lintasan, karena kepadatannya paling minimal diantara graf yang ada. Adapun, untuk kasus terburuk akan ditunjukkan dengan menggunakan graf lengkap, karena kepadatannya paling optimal diantara graf lainnya.

Berikut ini perhitungannya:

Kasus Terbaik (Best Case)

1. clear all; clc; 1

2. n= input ('jumlah simpul = '); 1

3. disp (' '); 1 4. d= [0 1 0 0 0 0; 1 0 1 0 0 0; 0 1 0 1 0 0; 0 0 1 0 1 0; 1 0 0 0 1 0 1; 0 0 0 0 1 0]

5. p=sum(d); 1 6. for i=1:n 7. j=n+1; n 8. h=n+2; n 9. d(i,j)=p(1,i); n 10. d(i,h)=i; n 11. end 12. b=sortrows(d,n+1); 1 13. for k=1:n 14. v(k)=0; n 15. End 16. If r(1,n+1)~=r 17. i=b(p-m,n+2); 1 18. else 19. i=1:n; 20. end 21. for m=1:n 22. p=n+1; n 23. for i=i 24. c=1; 25. for j=1:n 26. if d(i,j)==1 27. L(i,j)=v(j); n.n 28. else 29. L(i,j)=0; 30. end 31. end 32. t=L(i,1:n); n 33. s=sort(t); n 34. for j=1:n 35. while c==s(1,j) 36. c=c+1; n/2 37. end 38. end 39. v(i)=c; n 40. end 41. end 42. for i=1:n; 43. s(1,i)=i; n 44. s(2,i)=v(i); n 45. end 46. fprintf ('\nsimpul dan warnanya'); 1

47. V=s 1

48. y=sort(v); 1

49. M=y(1,n); 1 50. fprintf ('\nbanyaknya warna = %d\n\n', M); 1

( ) = 1 + 1 + 1 + 1 + 1 + + + + + 1 + + 1 + + + + + + + _{2 +} + + + 1 + 1 + 1 + 1 + 1

_{= 12 + 27 2 +}

( ) = 12 + 27 2 + = ( ) Karena

12 + 27 2 + ≤ 11 _{+ 27 2} + _{= 51 2 untuk semua n≥1 (C=}53 _{2 dan} = 1). Jadi kompleksitas waktu asimptotik pada kasus terbaik graf lintasan adalah Ω(n2).

Kasus Terburuk (Worst Case)

1. clear all; clc; 1

2. n= input ('jumlah simpul = '); 1

3. disp (' '); 1 4. r= [0 1 1 1 1 1; 1 0 1 1 1 1; 1 1 0 1 1 1; 1 1 1 0 1 1; 1 1 1 1 1 0 1; 1 1 1 1 1 0] 5. p=sum(r); 1 6. for i=1:n 7. j=n+1; n 8. h=n+2; n 9. r(i,j)=p(1,i); n 10. r(i,h)=i; n 11. end 12. b=sortrows(r,n+1); 1 13. for k=1:n 14. v(k)=0; n 15. End 16. If r(1,n+1)~=r 17. i=b(p-m,n+2); 1 18. else 19. i=1:n; 20. end 21. for m=1:n 22. p=n+1; n 23. for i=i 24. c=1; n 25. for j=1:n 26. if r(i,j)==1 27. L(i,j)=v(j); n.n 28. else

29. L(i,j)=0; 30. end 31. end 32. t=L(i,1:n); n 33. s=sort(t); n 34. for j=1:n 35. while c==s(1,j) 36. c=c+1; 1/2(n-1)n 37. end 38. end 39. v(i)=c; n 40. end 41. end 42. for i=1:n; 43. s(1,i)=i; n 44. s(2,i)=v(i); n 45. end

46. fprintf ('\nsimpul dan warnanya'); 1

47. V=s 1

48. y=sort(v); 1

49. M=y(1,n); 1 50. fprintf ('\nbanyaknya warna = %d\n\n', M); 1

( ) = 1 + 1 + 1 + 1 + 1 + + + + + 1 + + 1 + + + + + + + 1 2 ( − 1) + + + + 1 + 1 + 1 + 1 + 1

_{= 12 + 25 2 +}3 ₂

( ) = 12 + 25 2 +3 2 = ( ) Karena

12 + 25 2 +3 2 ≤ 11 + 25 2 + 3 2 = 25 untuk semua n≥1 (C=25 dan = 1).

Jadi kompleksitas waktu asimptotik pada kasus terburuk graf lengkap adalah O(n2).

Berdasarkan teorema 1, maka diperoleh kompleksitas pengembangan algoritma baris adalah Θ(n2), dimana diketahui kompleksitas algoritma baris untuk kasus waktu terburuk adalah O(n3) dan untuk kasus terbaik Ω(n2). Sehingga dapat disimpulkan bahwa pengembangan algoritma baris mampu memperbaiki kompleksitas algoritma baris.

KESIMPULAN DAN SARAN

Dengan menggunakan pengembangan algoritma baris pada graf sederhana dengan mengurutkan label berasarkan derajat terbesarnya, maka banyaknya warna yang dihasilkan sama dengan bilangan kromatik dari graf tersebut. Namun pada graf sederhana khususnya graf markstrom dan graf icosahedron banyaknya warna yang dihasilkan masih ambigu. hal ini dikarenakan derajat dari graf tersebut sama, sehingga urutan berdasarkan derajat terbesar tidak merubah label awal yang diberikan. Sedangkan kompleksitas dari pengembangan algoritma baris diperoleh batas atas dan batas bawahnya ( ), dimana algoritma asalnya memiliki batas atas

( ).

DAFTAR PUSTAKA

Al-Omari, Dr. Hussei, Sabri, Khair Eddin. (2006). New Graph Coloring Algorithms. American Journal of Mathematics and Statistics 2 (4): 739-741.

Chartrand, G. dan Zhang, P. (2005). Introduction to Graph Theory. Mc Graw Hill International Edition.

Chartrand, G. dan Lesniak, L. (1996). Graphs and Digraphs, 3 th. Chapman and Hall.

Hasmawati. (1989). Perentangan dan Enumerasi Graph Pohon. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin.

Irawan, F.A. (2012). Buku Pintar Pemrograman Matlab. Mediakom.

Mansuri, A., Gupta, V. dan Chandel, R. S. (2010). Coloring Programs in Graph Theory. Int Journal of Math. Analysis, 4, 2473 – 2479

Nurwahyu, B., Hasmawati, Hendra, Anisa, Abd. Haris Jalante. (2009). Pengembangan Metode Pewarnaan Graf dan Aplikasinya pada Penentuan Lampu Lalu Lintas. Fakultas Matematika dan Ilmu Pengetahuan Alam. Universitas Hasanuddin.

Noor, R.J. (2012). Implementasi Algoritma Baris dalam Pewarnaan Titik pada Graf Sederhana. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin.

Suh, Y., Cho, M. dan Lee, K.M. (2012). Graph Matching via Sequential Monte Carlo. Department of EECS, ASRI, Seoul National University, Seoul, Korea. INRIA- WILLOW/ Ecole Normale Superieure, Paris, France, 1- 14.

Sukrawan. (2011). Implementasi Algoritma Welch- Powell pada Pewarnaan Graf. Fakultas Matematika dan Ilmu Pengetahuan Alam.

LAMPIRAN

Tabel 1. Validasi Algoritma

NAMA GRAF

WARNA MINIMUM YANG DIHASILKAN

BARIS BARIS BARU (c)

Graf Khusus P6 2 2 2 P9 2 2 2 C6 2 2 2 C9 3 3 3 T9 2 2 2 K5 5 5 5 S9 2 2 2 W8 4 4 4 W9 3 3 3 Chavatal 4 4 4

Markstrom 4 atau 3 4 atau 3 3

Kantor Mobius 2 2 2

Icosahedron 4 atau 5 4 atau 5 4

Graf sederhana dengan label berbeda

Gambar 1(a) 4 3 3

Gambar 1(b) 4 3 3

Gambar 1(c) 4 3 3

Gambar 1(d) 3 3 3