2. METODE ELEMEN HINGGA BERBASIS KRIGING

(1)

2. METODE ELEMEN HINGGA BERBASIS KRIGING

2.1. Interpolasi Kriging

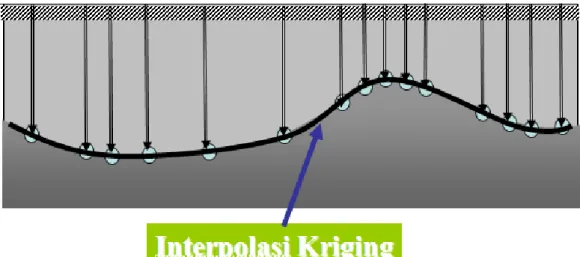
Interpolasi Kriging adalah teknik geostatistik untuk interpolasi ruang yang banyak digunakan dalam ilmu geologi dan pertambangan, dimana nama Kriging diambil dari nama seorang insiyur pertambangan Afrika Selatan bernama Danie G. Krige (Tongsuk and Kanok-Nukulchai, 2004a, Gu, 2003, Olea, 1999, p.8). Dengan menggunakan interpolasi ini maka semua titik yang tidak diketahui nilainya dapat di interpolasi dari nilai – nilai yang telah diketahui di sekitar titik tersebut. Untuk lebih jelasnya dapat dilihat pada Gambar 2.1.

Gambar 2.1. Interpolasi Kriging yang dilakukan dengan cara setiap nilai yang tidak diketahui pada suatu titik diinterpolasikan dari nilai yang diketahui pada titik-titik yang tersebar pada daerah tertentu di sekitarnya

Sumber: Syamsoeyadi (2009), dikutip dari Kanok-Nukulchai (2008)

2.2. Perumusan Interpolasi Kriging

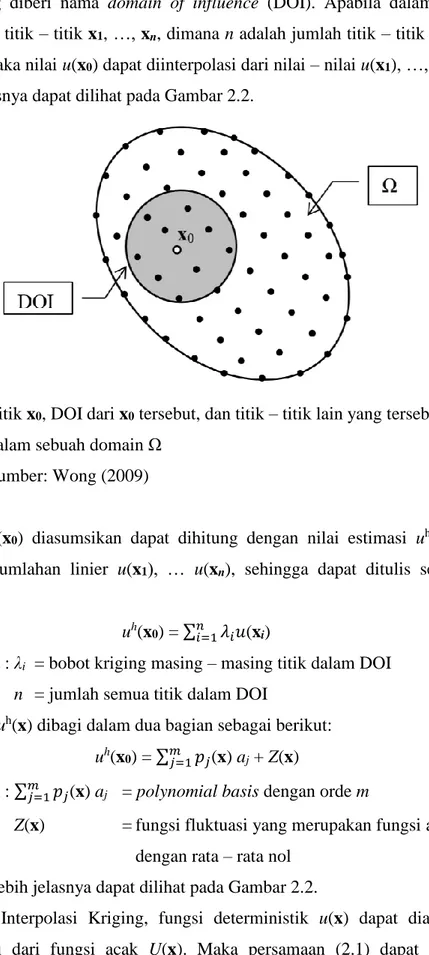
Dalam sebuah domain Ω, terdapat sejumlah titik – titik xi,i=1, 2, …, N, dimana N merupakan jumlah dari titik – titik tersebut dan fungsi dari nilai x tersebut dapat dinyatakan sebagai u(x). Untuk sebuah titik sembarang x0, nilai dari

(2)

subdomain yang diberi nama domain of influence (DOI). Apabila dalam DOI tersebut terdapat titik – titik x1, …, xn, dimana n adalah jumlah titik – titik dalam DOI tersebut, maka nilai u(x0) dapat diinterpolasi dari nilai – nilai u(x1), …, u(xn). Untuk lebih jelasnya dapat dilihat pada Gambar 2.2.

Gambar 2.2. Titik x0, DOI dari x0 tersebut, dan titik – titik lain yang tersebar

dalam sebuah domain Ω Sumber: Wong (2009)

Nilai u(x0) diasumsikan dapat dihitung dengan nilai estimasi uh yang

merupakan penjumlahan linier u(x1), … u(xn), sehingga dapat ditulis sebagai berikut:

uh(x0) = ∑𝑛_𝑖=1𝜆_𝑖𝑢(xi) (2.1) di mana : λi = bobot kriging masing – masing titik dalam DOI

n = jumlah semua titik dalam DOI

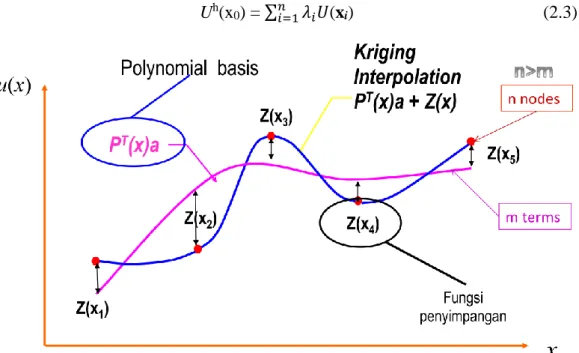
Fungsi uh(x) dibagi dalam dua bagian sebagai berikut:

uh(x0) = ∑𝑚_𝑗=1𝑝_𝑗(x) aj + Z(x) (2.2) di mana : ∑𝑚_𝑗=1𝑝_𝑗(x) aj = polynomial basis dengan orde m

Z(x) = fungsi fluktuasi yang merupakan fungsi acak dengan rata – rata nol

Untuk lebih jelasnya dapat dilihat pada Gambar 2.2.

Dalam Interpolasi Kriging, fungsi deterministik u(x) dapat dianggap sebagai realisasi dari fungsi acak U(x). Maka persamaan (2.1) dapat ditulis sebagai berikut :

(3)

Uh(x0) = ∑𝑛𝑖=1𝜆𝑖𝑈(xi) (2.3)

Gambar 2.3. Nilai estimasi uh(x) yang dibagi dalam dua bagian, yaitu polynomial basis dan fungsi penyimpangan (departure). Sumber: Syamsoeyadi (2009), dikutip dari Kanok-Nukulchai (2008)

Bobot Kriging pada persamaan (2.1) dan (2.3) ditentukan dengan syarat nilai estimasi Uh(x0) tidak bias, atau dapat pula ditulis sebagai berikut :

E [Uh(x0) – U (x0)] = 0 (2.4)

Selain tidak bias, varians nilai kesalahan dari nilai estimasi harus minimum. Nilai varians ini dapat ditulis sebagai berikut:

var [Uh_(x

0) – U (x0)] = 0 (2.5)

Menggunakan metode pengali Lagrange untuk permasalahan constrained optimization, persyaratan – persyaratan Bobot Kriging, maka dapat dirumuskan sistem persamaan Kriging. Penurunan perumusan sistem persamaan Kriging yang lengkap dan jelas dapat dilihat pada F.T. Wong (2009). Perumusan sistem persamaan Kriging adalah sebagai berikut:

Rλ + Pμ = r(x0) (2.6a)

PT_{λ = p(x}

(4)

di mana: 11 1 1 ( ) ... ( ) ... ... ... ( ) ... ( ) n n nn C C C C            h h R h h ; 1 1 1 1 ( ) ... ( ) ... ... ... ( ) ... ( ) m n m n p p p p            x x P x x (2.6c)





T 1 ... n



 λ ; μ





1 ...



m



T (2.6d)





T 0 10 20 0 ( ) C( ) C( ) ... C( _n ) r x h h h ; (2.6e) p x( ₀)



p₁(x₀) ... p_m(x₀)



T (2.6f) di mana: R = matriks kovarians berdimensi nn;

P = matriks nilai polinomial pada titik - titik, berdimensi m

n ;

λ = vektor bobot Kriging berdimensi n1; μ = vektor pengali Lagrange berdimensi m1;, r(xo)= vektor kovarians antara titik - titik dan titik yang dicari

berdimensi n1;

p(xo) = vektor polynomial basis pada titik x0, berdimensi

1



m ;

( _ij) cov ( ), (_i _j) C h  _U x U x _

= nilai fungsi kovarians antara variabel acak pada titik - titik i dan j.

𝐡𝒊𝒋= 𝐡𝒋− 𝐡𝒊 = jarak antara titik xi dengan xj

Selanjutnya nilai λ dapat diperoleh dari penyelesaian persamaan Kriging pada persamaan (2.6a) dan (2.6b), sehingga kemudian nilainya dapat dimasukkan kedalam persamaan (2.1). Adapun karena λ merupakan vektor yang berdimensi

1



n maka persamaan (2.1) dapat ditulis menjadi:

u(x0) = λT d (2.7)

di mana: d



u( ) ...x₁ u(x_n)



Tmerupakan vektor dari titik-titik nodal. Titik x0 dapat berupa sembarang titik dalam DOI, maka dapat ditulis sebagai x.

Dalam MEH, persamaan (2.7) identik dengan persamaan hubungan antara shape function dan perpindahan pada titik nodal, sebagai berikut:

(5)

 

_

 

   n i i i h u N u 1 x d x N (x) (2.8)

di mana N

 

x λT

 

x = shape function dari interpolasi Kriging.

Dengan menggunakan persamaan (2.8), nilai dari suatu titik yang tidak diketahui, x, dapat dicari.

2.3. Metode Elemen Hingga Berbasis Kriging (MEH-K)

Dalam MEH-K, yang berbeda dengan MEH standar hanyalah shape function-nya saja. Adapun definisi dari shape function adalah suatu fungsi di dalam sebuah elemen apabila derajat kebebasan ke-i elemen bernilai satu dan derajat kebebasan lainnya bernilai nol (Cook, 1989). Pada MEH-K, shape function didapatkan dari hasil interpolasi Kriging, yaitu nilai λT yang didapatkan dari persamaan (2.6a) dan (2.6b). Ilustrasi mengenai shape function untuk elemen satu dimensi dapat dilihat pada Gambar 2.4.

(a) (b)

Gambar 2.4. Shape function pada elemen balok satu dimensi (a) shape function pada MEH standar, (b) shape function pada MEH-K. Dalam gambar ini, DOF adalah “domain of influence” dan E adalah elemen yang ditinjau.

Sumber: Syamsoeyadi (2009), dikutip dari Kanok-Nukulchai (2008)

Pada MEH-K, DOI yang digunakan adalah DOI elemen berlapis. DOI pada MEH standar hanya satu lapis saja, yakni hanya mencakup elemen itu sendiri. Sedangkan pada MEH-K, DOI ditentukan sesuai dengan kebutuhan, dan tentunya semakin banyak DOI yang ditinjau, maka akan semakin akurat hasil yang didapatkan, namun pekerjaan yang dilakukan menjadi semakin lama. Oleh karena itu biasanya hanya menggunakan satu sampai tiga lapis saja. Titik – titik nodal yang berada dalam DOI, namun bukan merupakan titik yang ditinjau

(6)

dinamakan titik nodal satelit. Untuk lebih jelasnya dapat dilihat ilustrasi untuk elemen satu dimensi pada Gambar 2.5, dan untuk elemen dua dimensi dapat dilihat pada Gambar 2.6.

Gambar 2.5. Elemen satu dimensi dengan DOI dua dan tiga lapis.

Gambar 2.6. Elemen dua dimensi dengan DOI satu sampai empat lapis. Sumber: Wong (2009)

Polynomial Basis yang berperan dalam pembentukan shape function Kriging merupakan fungsi – fungsi basis pembentuk polinomial. Semakin tinggi derajat polinomial m yang digunakan maka semakin banyak juga DOI yang diperlukan, karena jumlah titik nodal dalam DOI (n) harus lebih besar atau sama dengan derajat polinomial yang digunakan (m) agar interpolasi Kriging dapat dijalankan. Tabel jumlah DOI minimum berdasarkan Polynomial Basis serta

(7)

fungsi basis pada elemen satu dimensi dapat dilihat pada tabel 2.1. Adapun dalam penelitian ini polynomial basis yang digunakan maksimum berderajat tiga.

Tabel 2.1. Polynomial basis pada elemen 1D beserta jumlah lapisan DOI minimum yang diperlukan

Sumber: Syamsoeyadi (2009)

No. Jenis Polynomial Basis Lapisan DOI Minimum Fungsi Basis

1 Linear 1 1 x

2 Quadratic 2 1 x x2

3 Cubic 3 1 x x2_x3

Dalam membentuk shape function berbasis Kriging juga diperlukan fungsi korelasi dan parameter korelasi. Fungsi korelasi didefinisikan sebagai berikut:

𝜌(𝐡) = 𝐶(𝐡) 𝜎⁄ 2 (2.9)

𝜎2 = var[𝑈(𝐱)] (2.10)

Menurut Gu, 2003, nilai 𝜎2 tidak memiliki pengaruh pada hasil akhir sehingga dalam tugas akhir ini dipakai nilai satu.

Dalam MEH-K dikenal dua macam fungsi korelasi, yaitu Gaussian dan Quartic Spline. Perumusan untuk fungsi korelasi Gaussian adalah sebagai berikut:

𝜌(ℎ) = 𝑒−(𝜃ℎ𝑑) 2

(2.11)

Perumusan untuk fungsi korelasi Quartic Spline adalah sebagai berikut:

𝜌(ℎ) = {1 − 6 (𝜃 ℎ 𝑑) 2 + 8 (𝜃ℎ 𝑑) 3 − 3 (𝜃ℎ 𝑑) 4 : untuk 0 < 𝜃ℎ 𝑑 < 1 0 ∶ untuk 𝜃ℎ 𝑑 > 1 (2.12) di mana: θ>0 merupakan parameter korelasi

h = jarak antara kedua titik nodal

d = jarak maksimum antara pasangan titik-titik nodal pada DOI

Parameter korelasi ditentukan sedemikian sehingga memenuhi batas bawah: 10 1 1 1 10 n _a i i N      



(2.13a)

(8)

dan memenuhi batas atas:

det( )R  1 10b (2.13b)

di mana: a = orde dari fungsi basis (linear1, quadratic 2, cubic 3)

b = dimensi permasalahan (1, 2, atau 3)

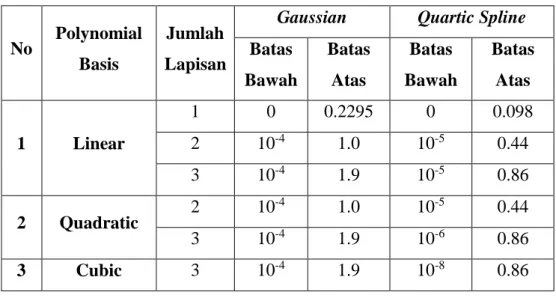
Untuk permasalahan analisa elemen satu dimensi, Syamsoeyadi (2009) telah meneliti batas atas dan batas bawah parameter korelasinya. Tabel batas atas dan batas bawah parameter korelasi dapat dilihat pada tabel 2.2. Untuk menjamin hasil interpolasi Kriging, sebaiknya diambil parameter korelasi yang berada di tengah – tengah batas atas dan batas bawahnya. Batas tengah parameter korelasi dapat dilihat pada tabel 2.3.

Tabel 2.2. Tabel batas atas dan batas bawah pada fungsi korelasi Gaussian dan Quartic Spline untuk analisis permasalahan satu dimensi.

Sumber: Syamsoeyadi (2009)

No Polynomial

Basis

Jumlah Lapisan

Gaussian Quartic Spline

Batas Bawah Batas Atas Batas Bawah Batas Atas 1 Linear 1 0 0.2295 0 0.098 2 10-4 1.0 10-5 0.44 3 10-4 1.9 10-5 0.86 2 Quadratic 2 10-4 _1.0 ₁₀-5 _0.44 3 10-4 1.9 10-6 0.86 3 Cubic 3 10-4 1.9 10-8 0.86