MODEL AMMI TERAMPAT UNTUK DATA BERDISTRIBUSI BUKAN NORMAL ALFIAN FUTUHUL HADI

MODEL AMMI TERAMPAT UNTUK

DATA BERDISTRIBUSI BUKAN NORMAL

ALFIAN FUTUHUL HADI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2006

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Model AMMI Terampat untuk

Data Berdistribusi Bukan Normal adalah karya saya sendiri dan belum pernah

diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya penulis lain baik yang diterbitkan maupun yang tidak diterbitkan telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Januari 2006

Alfian Futuhul Hadi NIM G151020011

ABSTRAK

ALFIAN FUTUHUL HADI. Model AMMI Terampat untuk Data

Berdistribusi Bukan Normal. Dibimbing oleh AHMAD ANSORI MATTJIK

dan I MADE SUMERTAJAYA.

Model AMMI (Additive Main Effect Multiplicative Interaction) untuk interaksi tabel dua arah memberikan manfaat besar pada kajian stabilitas dan adaptabilitas melalui pemodelan interaksi genotipe lingkungan secara multiplikatif. Kesahihan model AMMI bergantung pada kenormalan dan kehomogenan ragam galat.

Pada kajian ketahanan genotipe terhadap hama/penyakit, kejadian serangan hama/penyakit pada tanaman misalnya, kelayakan model AMMI diragukan. Upaya transformasi kenormalan dengan transformasi pangkat metode Box-Cox mampu mengatasi ketidaknormalan. Sehingga model AMMI dengan metode kuadrat terkecil pada pendugaan parameternya dapat secara sah digunakan pada data hasil transformasi .

Pendekaan lain untuk menangani ketaknormalan ini adalah pemodelan suku multiplikatif interaksi pada kelas pemodelan yang lebih luas, yaitu Model Linier Terampat (MLT/GLM). Pendugaan parameter secara iteratif melalui regresi GLM bolak-balik pada baris dan kolom. Model ini dikenal dengan model GAMMI (Generalized Additive Main Effect Multiplicative Interaction) atau GBMs (Generalized Bilinear Models). Suku multiplikatif model GAMMI dapat disajikan secara visual melalui Biplot, sebagaimana pada model AMMI. Pendekatan ini dapat digunakan untuk berbagai sebaran data termasuk sebaran Normal.

Aplikasi kedua pendekatan dilakukan pada data cacahan (berdistribusi Poisson) dari suatu studi hama daun genotipe kedelai dan data persentase/proporsi (berdistribusi Binomial) gabah isi varietas padi. Perbandingan matriks interaksi dugaan hasil dekomposisi kedua pendekatan ini memberikan informasi bahwa AMMI pada pendekatan transfomasi Box-Cox proporsi gabah isi padi memberikan matriks interaksi dugaan yang berbeda dari model GAMMI logit-link (nilai R-kuadrat procrostes kurang dari 25 persen). Sementara pada data rataan populasi hama daun kedelai, model AMMI dengan transformasi Box-Cox tidak banyak berbeda dengan model GAMMI log-link (nilai R-kuadrat lebih dari 98 persen). Eksplorasi data ini menunjukkan bahwa karakter sebaran data ini sangat mirip dengan sebaran Normal. Bila sebaran data simetrik, sangat mirip dengan sebaran Normal, maka hasil AMMI dengan pendekatan transformasi kenormalan tidak jauh berbeda dengan penggunan GAMMI. Sebaiknya pada data yang berdistribusi bukan Normal hasil kedua pendekatan ini sangat berbeda.

Informasi tambahan pada model log-biliner yang tidak dapat diperoleh pada model AMMI yaitu rasio odds. Ini menjadi kelebihan model GAMMI log-link dibandingkan dengan model AMMI dengan transformasi kenormalan pada data berdistribusi Poisson.

ABSTRACT

ALFIAN FUTUHUL HADI. Generalized AMMI for Non-Normal Data. Under supervision of AHMAD ANSORI MATTJIK and I MADE SUMERTAJAYA.

AMMI (Additive Main Effect Multiplicative Interaction) model for interactions in two-way table provide the major mean for studying stability and adaptability through genotype × environment interaction (GEI), which modeled by full interaction model. Eligibility of AMMI models depends on that assumption of normally independent distributed error with a constant variance.

In the study of genotypes’ resistance, disease and pest (insect) incidence on a plant for example, the appropriateness of AMMI model is being doubtful. Transform the observation by power family of Box-Cox transformation is an effort to handle the non-normality. AMMI model then can be applied to the transformed data appropriately following by the use of ordinary least square for estimating parameters.

There is another way to handle this non-normality, i.e. by introducing multiplicative terms for interaction in wider class of modeling, Generalized Linear Models. An algorithm of iterative alternating generalized regression of row and column estimates its parameters. This model is known as GAMMI (Generalized Additive Main Effect Multiplicative Interaction) or GBMs (Generalized Bilinear Models). The multiplicative terms of GAMMI models can be visualized through Biplot, as in AMMI.

A comparison of the two approaches above is investigated by applying them to a count data of pest population of Poisson distribution, which came from a study of leave pest in soybean genotype, and to study of rice genotype stability of filled grain per panicle (Binomial data). For data averages of filled grain per panicle, AMMI model for transformed data gives interaction matrix estimator slightly difference from of the one given by GAMMI logit-link model. R-square of Procrustes Rotation is less than 20 percent. On the other hand, for transformed data average of pest population, the two approaches do not give significant differences. Data exploration for the last case (the transformed data average of pest population) shows that its distribution character is very similar to Normal distribution. Therefore, it can be concluded that: (1) when the data distribution is close to Normal distribution, results of transformed AMMI and GAMMI are not significantly different; (2) when the data distribution is non Normal, results of the two approaches are quite different.

Additional information on log-bilinear, which cannot be obtained from the transformed AMMI model, is odd ratio. This makes the GAMMI model superior compared to effort of transforming normality on Poisson distributed data.

MODEL AMMI TERAMPAT UNTUK

DATA BERDISTRIBUSI BUKAN NORMAL

ALFIAN FUTUHUL HADI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Statistika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2006

Judul Tesis : Model AMMI Terampat untuk Data Berdistribusi

Bukan Normal

Nama : Alfian Futuhul Hadi

NIM : G151020011

Disetujui Komisi Pembimbing

Prof. Dr. Ir. A. A. Mattjik, MSc. Dr. Ir. I Made Sumertajaya, MSi.

Ketua Anggota

Diketahui, Ketua Program Studi

Statistika

Dekan Sekolah Pascasarjana

Dr. Ir. Budi Susetyo, M.S Prof. Dr. Ir. Syafrida Manuwoto, MSc.

dedicated to

PRAKATA

Alhamdulillah hirabbil ‘alamin. Penulis bersyukur kepada Allah SWT atas karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian ini adalah penangan data berdistribusi bukan selain Normal (selain distribusi Normal) pada pemodelan bilinier dengan judul Model AMMI Terampat untuk Data Berdistribusi Bukan Normal. Sebagian dari tesis ini, Bab 3 Model AMMI Terampat untuk Data Berdistribusi Bukan Normal, telah diterbitkan dalam prosiding Seminar Nasional Statistika ke-7 Institut Teknologi Sepuluh November Surabaya.

Penulis mengucapkan terima kasih kepada Bapak Prof. Dr. Ir. Ahmad Ansori Mattjik, MSc. dan Bapak Dr. Ir. I Made Sumertajaya, MS. selaku pembimbing. Disamping itu, penghargaan penulis sampaikan kepada Fred van Eeuwijk (Wageningen University, The Netherland) dan Paul Keizer (DLO-Centre for Plant Breeding and Reproduction Research Wageningen, The Netherland), atas prosedur GAMMI pada GENSTAT 7.1 dan diskusinya, serta Dr. Suharsono dari Malang, atas saran dan motivasinya. Kepada Balitpa Sukamandi dan Balitkabi Malang untuk data percobaannya. Kepada Bagus Sartono. MSi., Anang Kurnia, MSi., dan Utami Diyah, MSi., atas diskusinya, serta Sri Winarni atas koreksi ejaannya. Dr. Ir. Hari Wijayanto, Ir. Achmad Djauhari, MS. dan Ir. Arif Musaddad atas dukungan tempat tinggal di Bogor selama menempuh studi S2. Dr. Sudarko dan Dr I Made Tirta di Universitas Jember atas dukungan dan pinjaman fasilitasnya.

Terima kasih juga penulis ucapkan kepada istri dan anak-anak tercinta, bapak dan ibu di Jember, serta seluruh keluarga khususnya kepada ”kembaranku” Dani, atas segala do’a dan dukungannya.

Penulis berharap karya ilmiah ini bermanfaat. Semoga.

Bogor, Januari 2006

RIWAYAT HIDUP

Penulis dilahirkan di Jember pada tanggal 19 Juli 1974 dari ayah Abdul Muchith Muzadi dan ibu Siti Faridah. Penulis dilahirkan kembar, anak ke delapan dari delapan bersaudara.

Tahun 1993 penulis lulus dari SMA Negeri 1 Jember dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB pada Jurusan Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam, lulus tahun 1998. Kesempatan melanjutkan studi ke program magister diperoleh pada tahun 2002. Beasiswa pendidikan pascasarjana ini diperoleh dari Departemen Pendidikan Nasional Republik Indonesia.

Penulis bekerja sebagai Staf Pengajar di Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember, sejak tahun 1999. Penulis mengajar mata kuliah Statistika dan menekuni bidang Statistika Terapan utamanya pada bidang Pertanian. Di Jember, penulis membina sebuah kelompok

studi mahasiswa bernama Lingkar studi Statistika Terapan (eLStat).

Pada tahun 2001 penulis menikah dengan Halimatus Sa’diyah, dan kini dikaruniai Allah seorang putri bernama Hasna Adibah Qotrunnada dan seorang putra bernama Azzam Muzadi Al-Afief.

Karya ilmiah berjudul Model AMMI Terampat untuk Data Berdistribusi Bukan Normal dan Penerapannya Pada Kajian Stabilitas dan Ketahanan Genotipe telah disajikan pada Seminar Nasional Statistika ke-7 Institut Teknologi Sepuluh November Surabaya pada Bulan November 2005. Artikel lain berjudul Model AMMI untuk Analisis Interaksi Genotipe × Lokasi, telah diterbitkan pada Jurnal Ilmu Dasar, FMIPA Universitas Jember volume 5 nomor 1 Januari 2004. Karya-karya ilmiah tersebut merupakan bagian dari program S2.

i

DAFTAR ISI

Halaman

DAFTAR TABEL... iii

DAFTAR GAMBAR ... iv DAFTAR LAMPIRAN...v I. PENDAHULUAN ...1 1.1 Latar Belakang ...1 1.2 Tujuan Penelitian ...3 1.3 Kerangka Pemikiran...3

II. MODEL AMMI PADA DATA BERDISTRIBUSI BUKAN NORMAL: TRANSFORMASI KENORMALAN...5

2.1 Pendahuluan ...5

2.2 Model AMMI dan Asumsi Kenormalan Galat ...5

2.3 Langkah Pemodelan AMMI ...7

2.3.1 Perhitungan Jumlah Kuadrat...8

2.3.2 Penguraian Derajat Kebebasan ...8

2.3.2 Penguraian Nilai Singular ...8

2.3.4 Nilai Komponen AMMI ...9

2.3.5 Penentuan Banyaknya Komponen AMMI...9

2.3.6 Interpretasi Biplot AMMI ...10

2.4 Transfomasi Data ...11

2.4.1 Transformasi Box-Cox...12

2.5 Metodologi Penelitian ...14

2.5.1 Data ...14

2.5.2 Tahapan Penelitian...14

2.6 Hasil dan Pembahasan ...15

2.6.1 Kestabilan Gabah Isi Varietas Padi: Data Persentase/Proporsi ...15

2.6.2 Ketahanan Kedelai Terhadap Hama Daun: Data Frekuensi/Populasi Hama ...18

2.7 Simpulan ...20

III. MODEL AMMI TERAMPAT UNTUK DATA BERDISTRIBUSI BUKAN NORMAL...22

3.1 Pendahuluan ...22

3.2 Model Linier Terampat (Generalized Linear Models) ...23

ii

3.3.1 Algoritma Pengepasan Model AMMI Terampat ...26

3.3.2 Penentuan Banyaknya Suku Multiplikatif ...28

3.3.3 Diagnostik Sisaan...29

3.4 Penyajian Interaksi melalui Biplot Model GAMMI ...30

3.4.1 Model GAMMI Log-Bilinier ...31

3.5 Metodologi Penelitian ...34

3.5.1 Data ...34

3.5.2 Tahapan Penelitian...35

3.6 Hasil dan Pembahasan ...37

3.6.1 Ketahanan Kedelai Terhadap Hama Daun: Model Log-Bilinier ...37

3.6.2 Kestabilan Gabah Isi Varietas Padi: Model Logit-Bilinier...39

3.7 Simpulan ...40

IV. PERBANDINGAN KONFIGURASI MATRIKS INTERAKSI: METODE PROCRUSTES...42

4.1 Pendahuluan ...42

4.2 Kesesuaian Dua Konfigurasi Matriks: Metode Procrustes ...43

4.3 Metodologi ...46

4.4 Hasil Perbandingan Matriks Interaksi...47

4.4.1 Matriks Interaksi Ketahanan Kedelai Terhadap Hama Daun ...47

4.4.2 Matriks Interaksi Kestabilan Gabah Isi Varietas Padi ...48

4.3 Simpulan ...49

V. KESIMPULAN DAN SARAN ...50

5.1 Kesimpulan ...50

5.2 Saran ...51

DAFTAR PUSTAKA ...52

iii

DAFTAR TABEL

Halaman

Tabel 2.1 Analisis ragam untuk data gabah isi yang ditransformasi ...16 Tabel 2.2 Analisis ragam untuk populasi hama daun yang ditransformasi ...19 Tabel 3.1 Fungsi Penghubung (kanonik) dalam Model Linier Terampat...24 Tabel 3.2 Rataan populasi lima jenis hama daun pada empat genotipe kedelai ..37 Tabel 3.3 Analisis devians untuk data populasi hama daun ...38 Tabel 3.4 Analisis devians untuk data gabah isi ...39

iv

DAFTAR GAMBAR

Halaman

Gambar 1.1 Kerangka Pemikiran ...4

Gambar 2.1 Langkah penggunaan transformasi kenormalan pada AMMI...14

Gambar 2.2 Plot log-likelihood transformasi Box-Cox data proporsi gabah isi..15

Gambar 2.3 Uji kenormalan data proporsi gabah isi sebelum transformasi (kiri) dan sesudah transformasi Box-Cox (kanan) ...16

Gambar 2.4 Plot sisaan model AMMI data gabah isi yang ditransformasi: (a) Plot kenormalan sisaan; (b) Plot sisaan vs fitted value ...17

Gambar 2.5 Bilpot AMMI 2 data gabah isi hasil transformasi Box-Cox ...18

Gambar 2.6 Plot log-likelihood transformasi Box-Cox data populasi hama daun ...18

Gambar 2.7 Plot uji kenormalan hasil transformasi Box-Cox data populasi hama daun...19

Gambar 2.8 Biplot AMMI 2 data populas hama daun yang ditransformasi ...20

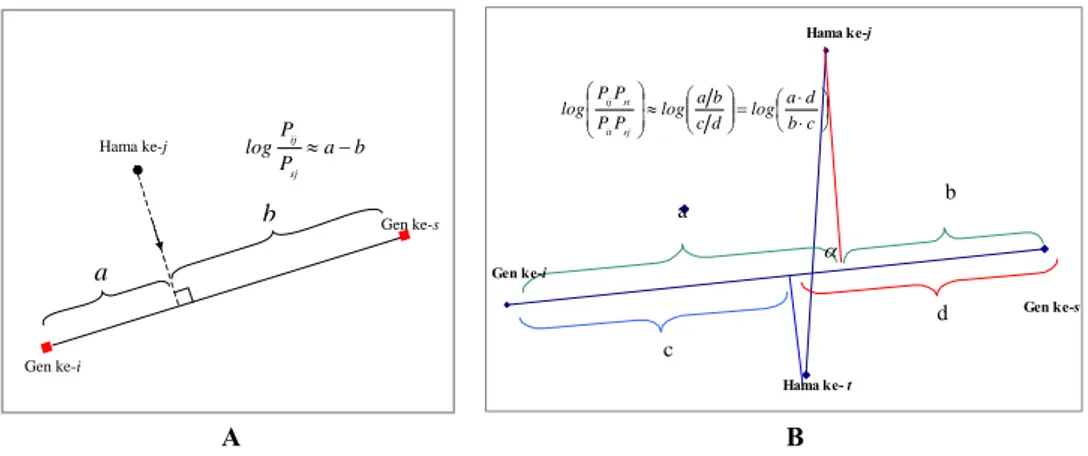
Gambar 3.1 Tinjauan geometris tentang Odds (A) dan Rasio Odds (B)...34

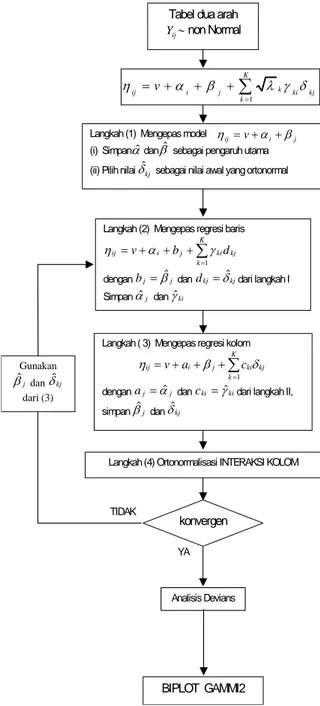
Gambar 3.2 Algoritma pengepasan model GAMMI...36

Gambar 3.3 Plot residual untuk data hama kedelai: Plot residual terstadardi-sasi terhadap nilai dugaan model GAMMI-2 log-link (kiri); Plot working variate terhadap prediktor linier (kanan). ...38

Gambar 3.4 Biplot GAMMI-2 untuk interaksi hama daun dengan fungsi hubung logaritma...39

Gambar 3.5 Biplot interaksi data gabah isi model GAMMI-2 logit-link. Lokasi ditunjukkan dengan kotak, verietas padi dengan garis. ...40

v

DAFTAR LAMPIRAN

Halaman

Lampiran 1. Data pengamatan populasi hama daun kedelai pada umur 14 hari

setelah tanam ...55

Lampiran 2. Nilai lambda dugaan dan log-likelihood transformasi Box-Cox data populasi hama daun ...55

Lampiran 3. Plot sisaan model AMMI 2 data populasi hama daun ternormalkan...56

Lampiran 4. Nilai lambda dugaan dan log-likelihood transformasi Box-Cox data proporsi gabah isi...56

Lampiran 5. Diagnostik sisaan AMMI data gabah isi ternormalkan ...57

Lampiran 6. Biplot AMMI1: KUI1 vs rataan proporsi gabah isi ternormalkan ...57

Lampiran 7. Biplot AMMI1: KUI1 vs rataan populasi hama daun ternormalkan...58

Lampiran 8. Karakteristik distribusi data hama daun ...58

Lampiran 9. Contoh perintah GENSTAT untuk transformasi Box-Cox ...58

Lampiran 10. Prosedur GAMMI pada GENSTAT 7...59

Lampiran 11. Contoh Perintah GENSTAT untuk GAMMI ...70

I. PENDAHULUAN

1.1 Latar Belakang

Interaksi antara genotipe dan lingkungan telah diketahui sejak lama, yang merupakan fenomena umum pada seluruh organisme hidup. Genotipe dan lingkungan berinteraksi untuk menghasilkan fenotipe. IGL (Interaksi Genotipe × Lingkungan) didefinisikan sebagai perbedaan antara nilai fenotipe dengan nilai yang diharapkan dari hubungan genotipe dan lingkungan. Jika respons dari dua genotipe terhadap perbedaan derajat cekaman lingkungan dibandingkan, suatu interaksi dapat dijelaskan secara statistika sebagai simpangan dari dua kurva respons secara paralel. Interaksi genotipe dan lingkungan adalah variasi yang disebabkan oleh pengaruh bersama dari genotipe dan lingkungan (Matjik, 2005).

Model AMMI (Additive Main Effect Multiplicative Interaction) telah memberikan sumbangan yang sangat berarti bagi penelitian terapan, terutama pada bidang pemuliaan yaitu analisis stabilitas dengan dekomosisi IGL. Model AMMI mampu menjelaskan interaksi secara lebih baik (Sumertajaya, 1998). Struktur interaksi diuraikan dengan memanfaatkan sifat-sifat matematis penguraian nilai singular (Singular Value Decomposition, SVD). Struktur interaksi ini didekomposisi dari matriks sisaan komponen aditif. SVD merupakan pendekatan kuadrat terkecil dengan reduksi dimensi (pangkat matriks) data yang terbaik dan menyediakan penyajian secara grafis.

Dalam konteks pemuliaan tanaman, komponen acak pada model ini seringkali diasumsikan menyebar Normal dengan ragam konstan. Kajian stabilitas genetik pada data-data pengukuran seperti tinggi tanaman, produktifitas, umur dapat menggunakan model AMMI. Model ini telah berhasil memberikan informasi tentang stabilitas dan adaptasi spesifik suatu genotipe terhadap lingkungan, karena ia dilengkapi dengan visualisasi matriks IGL pada dimensi rendah (dua atau tiga dimensi) melalui reduksi dimensi, yang dikenal secara luas dengan nama biplot.

Analisis stabilitas dapat digunakan untuk mengidentifikasi ketahanan terhadap hama dan penyakit. Jika ada interaksi antara kultivar dan patogen, maka perlu untuk mengidentifikasi suatu kultivar yang memiliki resistensi umum dan

resistensi spesifik (Mattjik, 2005). Namun untuk kajian ini (ketahanan terhadap penyakit dan kejadian serangan hama pada tanaman misalnya), kelayakan model AMMI dengan galat yang Normal dan ragam konstan tidak selalu dapat dipenuhi. Jika matriks data bebas, bersebaran Normal dengan ragam konstan, penduga kemungkinan maksimum tereduksi menjadi SVD, namun tidak demikian bila tidak menyebar Normal.

Pencatatan data serangan hama/penyakit dalam bentuk cacahan (counting) merupakan salah satu contoh fenomena ini. Sebagian peneliti melakukan pencatatan menggunakan counting kemudian menganlisisnya sebagai intensitas serangan dalam persentase. Dengan data persentase ini kemudian ia melakukan transformasi sehingga asumsi-asumsi yang diperlukan (kenormalan dan kehomogenan ragam) terpenuhi. Selama tranformasi berhasil mengatasinya cukuplah bagi kita untuk memilih cara ini. Sayangnya menemukan transformasi yang sesuai tidaklah mudah.

Sementara itu, pada pemodelan aditif telah dikenal luas apa yang disebut dengan Generalized Linear Models (GLM) atau Model Linier Terampat (MLT) sebuah kelas pemodelan yang menangani data-data berdistribusi bukan Normal. Model multiplikatif (bilinear) menjembatani kesenjangan antara model pengaruh utama (pada ANOVA ataupun GLM) dan model interaksi lengkap dengan sebuah parameter interaksi untuk setiap sel dalam tabel dua arah. Model ini pun memberikan visualisasi corak utama interaksi melalui biplot. Karenanya pengembangan teori model linier terampat dengan mengakomodasi komponen multiplikatif untuk interaksi sangat diperlukan.

Kekuatan eksplorasi model multiplikatif AMMI terletak pada visualisasi interaksi melalui biplot. Van Eeuwijk, 1995, memperkenalkan model multiplikatif dalam konteks model linier terampat sebagai perluasan dari model AMMI yang disebut dengan Generalized AMMI atau disingkat GAMMI. Pada pemodelan GAMMI, visualisasi interaksi ini masih dimungkinkan.

Permasalahan yang muncul kemudian adalah bagaimana pengepasan model GAMMI ini dilakukan? Bagaimana dengan penggunaan transformasi sebagai upaya pemenuhan asumsi kenormalan pada model AMMI? Pendekatan manakah

yang lebih menguntungkan? Penelitian ini ingin membandingkan kedua pendekatan tersebut, disertai penerapannya pada penelitian pemuliaan tanaman.

1.2 Tujuan Penelitian

Tujuan penelitian ini adalah:

1. Mempelajari bagaimana pengepasan (fiting) model bilinear dalam konsep model linier terampat, yaitu model GAMMI. Khususnya untuk pengamatan berupa cacahan (distribusi Poisson dan Binomial)

2. Mempelajari penggunaan transformasi kenormalan data pada model AMMI

3. Membandingkan hasil pendekatan pertama dan kedua dalam menguraikan interaksi.

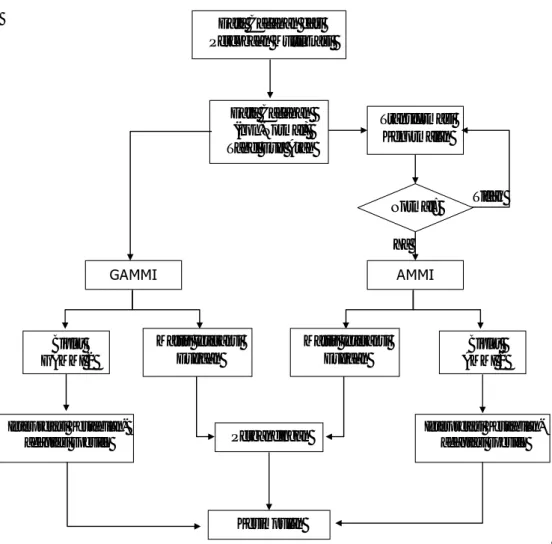
1.3 Kerangka Pemikiran

Upaya penyelesaiannya permasalahan dalam penelitian ini dilalukan melalui kerangka pemikiran pada Gambar 1.1. Interaksi direpresentasi oleh data dalam bentuk tabel dua arah. Transformasi kenormalan dimaksudkan agar dekomposisi interaksi melalui metode AMMI dapat dilakukan secara sahih.

Pembandingan hasil kedua pendekatan ini dilakukan dengan membandingkan matriks interaksi antara hasil model AMMI dari data tertrasformasi dan hasil model GAMMI dari data asal. Matriks interaksi dugaan dapat diperoleh dari model penuh ataupun model terbaik. Perbandingan ini dimaksudkan untuk membandingkan hasil dekomposisi interaksi oleh kedua model.

Pada bagian berikutnya akan disajikan penggunaan transformasi kenormalan menggunakan transformasi pangkat Box-Cox dalam model AMMI (Bab 2), Penanganan data berdistribusi bukan Normal menggunakan model GAMMI (Bab 3). Sedangkan perbandingan kedua pendekatan penanganan data bukan Normal tersebut akan dibicarakan pada Bab 4, dan kesimpulan disajikan pada Bab 5.

Data Cacahan (non-Normal) Tabel Dua Arah

Transformasi Kenormalan GAMMI AMMI Biplot GAMMI 2 Perbandingan Kesimpulan Interpretasi Kestabilan-

adaptasi spesifik Interpretasi Kestabilan-adaptasi spesifik Data Cacahan dari

Percobaan Multilokasi

Normal? Tidak

Matris Interaksi

Dugaan AMMI 2 Biplot

Matris Interaksi Dugaan

Ya

II. MODEL AMMI PADA DATA BERDISTRIBUSI BUKAN

NORMAL: TRANSFORMASI KENORMALAN

2.1 Pendahuluan

Analisis AMMI adalah suatu teknik analisis data percobaan dua faktor perlakuan dengan pengaruh utama perlakuan bersifat aditif sedangkan pengaruh interaksi dimodelkan dengan model bilinier. Model AMMI merepresentasikan observasi ke dalam komponen sistematik yang terdiri dari pengaruh utama (main effect) dan pengaruh interaksi melalui suku-suku multiplikatif (multiplicative interactions), di samping komponen acak sisaan atau galat. Komponen acak pada model ini diasumsikan menyebar Normal dengan ragam konstan.

Pada dasarnya analisis AMMI menggabungkan analisis ragam aditif bagi pengaruh utama perlakuan dengan analisis komponen utama ganda dengan pemodelan bilinier bagi pengaruh interaksi yang memanfaatkan peguraian nilai singular (SVD) pada matriks interaksi (Mattjik A. A, & Sumertajaya, I. M., 2002). Kelayakan model AMMI dengan galat yang Normal dan ragam konstan ada kalanya tidak terpenuhi. Transformasi data pengamatan mungkin menjadi salah satu teknik untuk mengatasi masalah ketidaknormalan ini.

Bab ini bertujuan mendiskusikan penggunanan transformasi kenormalan untuk mendapatkan data yang menekati Normal (setidaknya simetrik) dan kemudian memodelkannya dengan AMMI.

2.2 Model AMMI dan Asumsi Kenormalan Galat

Model AMMI dikenal luas pada bidang terapan, terutama pada bidang pemuliaan yaitu kajian interaksi genotipe × lingkungan (IGL). Sebutan lain seperti model bilinear, atau model biaditif lebih menunjuk pada struktur model

tersebut. Secara umum model AMMI untuk peubah acak y dari baris ke-i dan ij

kolom ke-j adalah:

∑

= + + + = K k kj ki k j i ij ) y ( E 1

δ

γ

λ

β

α

μ

dengan μ adalah rataan umum, αi pengaruh aditif (utama) baris ke-i(i=1,...,I),

pengaruh utama ini diidentifikasi dengan kendala berupa jumlah yang sama dengan nol. (Mattjik A. A. & Sumertajaya, I. M., 2002; Van Eeuwijk, 1995)

Pengaruh interaksi dimodelkan sebagai jumlah dari suku multiplikatif, yang banyaknya sama atau kurang dari pangkat matriks sisa dari pengaruh aditif (utama). Parameter suku multiplikatif pengaruh interaksi untuk baris dinotasikan

dengan γ_ki adalah juga skor baris sumbu ke-k dan kolom ke-i. Skor kolom ke-j

pada sumbu ke- k dinotasi dengan δki. Nilai singular yang berpadanan dengan

sumbu ke-k yang direpresentasi oleh

λ

k adalah ukuran asosiasi antara skor

baris dan kolom. Nilai yang diperoleh dari penguraian nilai singular (SVD) ini mengindikasikan tingkat kepentingan sumbu. Kuadrat dari nilai singular, yaitu nilai akarciri sama dengan jumlah kuadrat sumbu yang bersangkutan. Kendala untuk parameter suku multiplikatif meliputi jumlah yang sama dengan nol (terpusatkan) dan perkalian silangnya sama dengan nol (ortonormal).

Dalam kasus data tidak menyebar Normal, kelayakan model AMMI menjadi tidak terpenuhi. Jika matriks data bebas, berdistribusi Normal dengan ragam konstan, penduga kemungkinan maksimum tereduksi menjadi SVD. Manakala sebarannya bukan Normal –Binomal, Poisson, invers Gaussian, misalnya– kesamaan ini tidak lagi berlaku (Falguerolles, 1996).

Data yang berdistribusi bukan Normal cenderung tidak homogen, dan bila dimodelkan dengan AMMI ketakhomogenan ragam dapat berakibat buruk, sedangkan skala dugaannya mungkin juga tidak memuaskan. Kedua fenomena ini bisa jadi membutuhkan dimasukkannya suku interaksi tambahan (Van Eeuwijk, 1995). Kadangkala ada alasan kuat untuk tetap memodelkan data pada skala pengamatan. Kehomogenan ragam dapat diatasi dengan menambahkan satu atau lebih suku multiplikatif interaksi. Ketika tidak ada alasan untuk memaksa pemodelan tetap pada skala pengamatan, maka transformasi terhadap peubah respon dapat dilakukan untuk mengurangi masalah ini. Model linier atau bilinier dikenakan pada data yang telah ditransformasi, dan sifat sebaran sisaan diasumsikan memenuhi sebaran Normal.

2.3 Langkah Pemodelan AMMI

Pemodelan bilinier bagi pengaruh interaksi genotipe dengan lokasi

( )

γ_ge

pada analisis ini adalah sebagai berikut :

1. Langkah pertama menyusun pengaruh interaksi dalam bentuk matriks dimana genotipe (baris) × lokasi (kolom), sehingga matriks ini berorde a×b. ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ab a b ... ... ... ... ...

υ

υ

υ

υ

1 1 11 υ

2. Langkah selanjutnya dilakukan penguraian bilinier terhadap matriks pengaruh interaksi

∑

= + = n j ge ej gj j ge 1

δ

ρ

ϕ

λ

υ

= λ₁ϕ_g1ρ_e1+ λ₂ϕ_g2ρ_e2 +....+ λ_nϕ_gnρ_en +δ_ge

sehingga model AMMI secara lengkap dapat dituliskan sebagai berikut : ger ge n en gn n e g ger =

μ

+

α

+

β

+

λ

ϕ

ρ

+

δ

+

ε

Υ

∑

= μ+α_g +β_e + λ₁ϕ_g1ρ_e1+ λ₁ϕ_g2ρ_e1+....+ λ_nϕ_gnρ_en +δ_ge +ε_ger

keterangan : g = 1,2,….,a ; e = 1,2,…., b ; n = 1, 2, …,m dengan λ_n nilai

singular untuk komponen bilinier ke-n (λnadalah akarciri Z’Z)

1

λ ≥λ₂ ≥....≥λ_1b.

ϕ

_gn adalah pengaruh ganda genotipe ke-g melalui

komponen bilinier ke-n, ρ_en pengaruh ganda lokasi ke-e melalui komponen

bilinier ke-n. Dengan kendala (identification constrains) :

(1).

∑

_g

ϕ

_gn2

=

∑

_g

ρ

_en2

=

1, untuk n=1,2,…,m, dan

(2).

∑

_g

ϕ

_gn

ϕ

_gn'

=

∑

_e

ρ

_en

ρ

_en'

=

0

, untuk n≠n’,δ_ge simpangan dari

pemodelan bilinier (Crossa 1990 diacu dalam Mattjik A. A. & Sumertajaya, I. M., 2002).

2.3.1 Perhitungan Jumlah Kuadrat

Pada pemodelan ini pengaruh aditif genotipe dan lingkungan serta jumlah kuadrat dan kuadrat tengahnya dihitung sebagaimana umumnya pada analisis ragam, tetapi berdasarkan pada data rataan per genotipe × lokasi.

Pengaruh ganda genotipe dan lingkungan pada interaksi diduga dengan ..

.

. y y

y y

zge = ge − g − e+ sehingga jumlah kuadrat interaksi dapat diturunkan

sebagai berikut :

( )

( . . ..)2

( )

' . 2 zz teras r y y y y r z r GE JK ge g e e g ge = − − + = =

∑

∑

Berdasarkan teorema pada aljabar matriks bahwa teras dari suatu matriks sama dengan jumlah seluruh akar ciri matriks tersebut:

( )

=

_∑

i i

A

tr

λ

maka jumlah kuadrat untuk pengaruh interaksi komponen ke-n adalah akar ciri

ke-n pada pemodelan bilinier tersebut (λ_n), jika analisis ragam dilakukan

terhadap data rataan per genotipe × lingkungan.

Jika analisis ragam dilakukan terhadap data sebenarnya maka jumlah

kuadratnya adalah banyaknya ulangan dikalikan akar ciri ke-n (rλ_n). Pengujian

masing-masing komponen ini dilakukan dengan membandingkannya terhadap kuadrat tengah galat gabungan.

2.3.2 Penguraian Derajat Kebebasan

Derajat bebas untuk setiap komponen tersebut adalah a+b-1-2n. Besaran derajat bebas ini diperoleh dari jumlah p parameter yang diduga dikurangi dengan

jumlah n kendala. Banyaknya parameter yang diduga adalah a+b-1 sedangkan

banyak kendala untuk komponen ke-n adalah 2n. Kendala yang dipertimbangakan adalah kenormalan dan keortogonalan.

2.3.2 Penguraian Nilai Singular

Penguraian Nilai Singular (Singular Value Decomposition) untuk matriks pengaruh interaksi Z sebagaimana dikemukakan oleh Greenacre (1984) adalah memodelkan matriks tersebut sebagai berikut:

Dengan Z adalah matriks data terpusat, n x p, L adalah matriks diagonal

akar dari akarcirri positif bukan nol dari Z’Z, D

( )

λ

n _m×mselanjutnya disebut

nilai singular, A dan U adalah matriks ortonormal (A’A=U’U=Ir). Kolom-kolom

matriks A={a1,a2, …,an} adalah vektor-vektor ciri Z’Z sedangkan U diperoleh

dengan: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = = − n n λ λ λ Za Za Za ZAL U L 2 2 1 1 1

2.3.4 Nilai Komponen AMMI

Secara umum nilai komponen ke-n untuk genotipe ke-g adalah

l

_nk

ϕ

_gn

sedangkan nilai komponen utama untuk lokasi ke-e adalah l_n1−kρ_en. Dengan

mendefinisikan Lk (0≤ k ≤1) sebagai matrik diagonal yang elemen-elemen

diagonalnya adalah elemen-elemen matriks L dipangkatkan k demikian juga

dengan matrik L1-k, dan G=ULk serta H=AL1-k maka penguraian nilai singular

tersebut dapat ditulis:

Z=GH’

Dengan demikian skor komponen untuk genotipe adalah kolom-kolom matriks G sedangkan skor komponen untuk lingkungan adalah kolom-kolom matriks H. Nilai k yang digunakan pada analisis AMMI adalah ½ .

2.3.5 Penentuan Banyaknya Komponen AMMI

Jika beberapa kolom pertama matriks G dan H telah dapat menghasilkan penduga Z dengan baik maka banyak kolom matriks G dan H dapat dikurangi.

Gauch pada tahun 1988 dan kemudian Crossa 1990 mengemukakan dua metode penentuan banyaknya sumbu komponen utama yang sudah cukup untuk penduga, yaitu Postdictive Success dan Predictive Success..

Postdictive success berhubungan dengan kemampuan suatu model yang tereduksi untuk menduga data yang digunakan dalam membangun model tersebut. Salah satu penentuan banyaknya komponen berdasarkan Postdictive success adalah berdasarkan banyaknya sumbu tersebut yang nyata pada uji F analisis

ragam. Metode ini diusulkan oleh Gollob pada 1968 dan direkomendasikan oleh Gauch pada 1988 (Sumertajaya ,1998).

Predictive success berhubungan dengan kemampuan suatu model dugaan untuk memprediksi data lain yang sejenis tetapi tidak digunakan dalam membangun model tersebut (data validasi). Penentuan banyak sumbu komponen utama berdasarkan predictive success ini dilakukan dengan validasi silang, yaitu membagi data menjadi dua kelompok, satu kelompok untuk membangun model dan kelompok lain digunakan untuk validasi (menentukan jumlah kuadrat sisaan). Hal ini dilakukan berulang-ulang, pada setiap ulangan dibangun model dengan berbagai sumbu komponen utama. Banyaknya komponen utama yang terbaik adalah rataan akar kuadrat tengah sisa (RMSPD=Root Mean Square Predictive Different) dari data validasi paling kecil.

2.3.6 Interpretasi Biplot AMMI

Alat yang digunakan untuk menginterpretasi hasil dari metode AMMI adalah biplot. Pada dasarnya metode ini merupakan upaya untuk memberikan peragaan grafik dari suatu matriks dalam suatu plot dengan menumpangtindihkan vektor-vektor dalam ruang berdimensi dua. Vektor-vektor yang dimaksud yaitu vektor yang mewakili nilai skor komponen lingkungan.

Biplot adalah plot antara satu kolom G dengan kolom G yang lain yang ditampilkan secara bersama-sama dengan plot kolom H dengan kolom H yang lain yang bersesuaian dengan kolom G yang diplot (Jolliffe, 1986). Sebagian statistikawan membuat plot antar kolom U dan antar kolom H secara bersamaan. Sebagian peneliti pertanian (pemuliaan tanaman) bahkan membuat plot antara kolom-kolom tersebut dengan nilai rataan data asli per peubah amatan yang sesuai.

Biplot pada analisis AMMI biasanya berupa biplot antara nilai komponen utama pertama dengan rataan respon (biplot AMMI1). Biplot antara komponen utama kedua dan nilai komponen pertama (biplot AMMI2) bisa ditambahkan jika komponen utama kedua ini nyata

Interpretasi biplot AMMI1 adalah bagi titik yang sejenis. Jarak titik-titik amatan berdasarkan sumbu datar (rataan respon) menunjukkan perbedaan pengaruh utama amatan-amatan tersebut. Sedangkan jarak titik-titik amatan

berdasarkan sumbu tegak (KUI1) menunjukkan perbedaan pengaruh interaksinya atau perbedaan kesensitifannya terhadap lokasi. Biplot AMMI1 menunjukkan bahwa genotipe dikatakan mempunyai daya adaptasi baik pada suatu lingkungan jika genotipe dan lingkungan bertanda sama (berinteraksi positif).

Biplot AMMI2 menggambarkan pengaruh interaksi antara genotipe dan lingkungan. Titik-titik amatan yang mempunyai arah yang sama berarti titik-titik amatan tersebut berinteraksi positif (saling menunjang), sedangkan titik-titik yang berbeda arah menunjukkan bahwa titik-titik tersebut berinteraksi negatif.

2.4 Transfomasi Data

Akibat ketaknormalan dan ketakhomogenan ragam pada model linier atau biliner telah disinggung pada sub bab 2.1. Transformasi pada peubah respon ditengarai merupakan upaya perbaikan atas kedua hal tersebut. Model linier atau bilinier dapat dikenakan pada data yang telah ditransformasi, dan sifat sebaran sisaan diasumsikan memenuhi sebaran Normal. Berikut ini akan dibahas tentang metode transformasi.

Transformasi data pada hakekatnya adalah suatu usaha untuk mungubah data dari suatu skala ke skala yang lain. Model linier yang klasik (analisis ragam atau regresi) telah dikembangkan berdasarkan pada beberapa asumsi pokok yaitu keaditifan (model pengaruh utama), ragam perlakuan yang homogen (keragaman data bersifat bebas dari rataan dan banyaknya ulangan), dan kenormalan data.

Asumsi pertama berkaitan dengan struktur data yang pada akhirnya menyangkut penafsiran data, asumsi kedua berperan dalam menyederhanakan metode pendugaan parameter. Sedangkan yang terakhir sangat erat kaitannya dengan pengujian hipotesis. Metode pengujian hipotesis yang telah berkembang sangat lanjut adalah yang didasarkan pada kenormalan data, oleh karena itu patokan-patokannya dapat dengan mudah diperoleh dalam tabel-tabel sebaran statistik, seperti tabel t, F atau Khi-kuadrat (Aunuddin, 2005).

Dalam hal ini, transformasi bertujuan untuk mengatasi tiga masalah utama yaitu keheterogenan ragam, ketaknormalan galat, dan ketakaditifan/ketaklinieran pengaruh sistematik. Diakui bahwa bagaimanapun, tidak mudah mengatasi ketiga hal tersebut dengan satu langkah tunggal transformasi. Transformasi tunggal

biasanya manjur untuk mengatasi satu masalah tertentu tetapi tidak ketiganya. Keberhasilan transformasi untuk memperoleh kesederhanaan model (aditifitas/linieritas) mungkin mengakibatkan ketaknormalan dan ketakhomogenan ragam bila sebelumnya dua asumsi ini terpenuhi. Ada kalanya transformasi yang dilakukan untuk memperoleh ragam yang statbil membawa kita pada ketaknormalan (Rawling, J.O. et al., 1998) .

Beruntunglah, bahwa transformasi untuk memperoleh kehomogenan ragam dan ketaknormalan mempunyai kecenderugan diperoleh secara bersamaan (hand-in-hand), sehingga tidak jarang kedua asumsi dapat terpenuhi oleh suatu transformasi yang tepat (Bartlet, 1947 diacu dalam Rawling, J.O.et al.,1998)

Transformasi untuk kehomogenan ragam seringkali juga memenuhi kenormalan. Transformasi logit, arcsinus, dan probit yang digunakan untuk menstabilkan ragam dan menyederhanakan model juga membuat distribusi mendekati kenormalan. Transformasi tersebut umumnya menarik (streching) ekor distribusi untuk memberikan bentuk distribusi yang mendekati bentuk genta.

Demikian halnya dengan transformsi keluarga pangkat juga berguna untuk membuat distribusi menjadi semakin simetrik (mengurangi kemenjuluran). Harapannya adalah diperoleh distribusi data yang semakin mendekati Normal. Kriteria yang berbeda untuk menentukan tranformasi apa yang akan digunakan tidak harus munuju pada pilihan yang sama, tetapi sering terjadi transformasi yang optimum untuk suatu masalah juga memperbaiki masalah yang lain. Pada keluarga transformasi ini telah dikenal luas suatu metode perhitungan untuk menentukan transformasi optimum, yaitu transformasi Box-Cox.

2.4.1 Transformasi Box-Cox

Transformasi ini bertujuan memenuhi ketiga asumsi model linier, yaitu keheterogenan ragam, ketaknormalan galat, dan keaditifan/ketaklinieran pengaruh sistematik. Box-Cox menggunakan kriteria yang menggabungkan tujuan memperoleh model yang sederhana dan ragam yang homogen pada satu sisi serta tujuan kenormalan data pada sisi lain .

Metode transformasi Box-Cox menggunakan keluarga transformasi parametrik yang didefinisikan dalam bentuk terbakukan sebagai berikut:

( )

( )

⎪ ⎩ ⎪ ⎨ ⎧ = ≠ − = − 0 0 1 1 λ λ λ λ λ λ untuk , Y ln Y untuk , Y Y Y i i ) ( i & &

dengan Y& adalah rataan geometrik dari peubah asal yaitu =

∑

_∀

[

( )

]

i Yi n

Y& exp ln

(Rawling, J.O.et al.,1998; Box, Hunter, & Hunter, 1978)

Parameter λ diperoleh secara empirik melalui penduga kemungkinan

maksimum untuk beberapa nilai λ yang dipilih. Tahapan perhitungan sebagai berikut:

1. Nilai λ dipilih dari selang tertentu, umumnya λ ∈ [-2,2], katakanlah

λ =[ -2, -1.5,-1, -0.5, -0.25, 0, 0.25, 0.5, 1, 1.5, dan 2]

2. Jumlah kuadrat sisaan dari model Y_i(λ) dituliskan sebagai JKS(λ), dan

ragam bagi λ didefinisikan sebagai σ2

( )

λ = JKS

( )

λ n.

3. Untuk masing-masing λ dihitung fungsi kemungkinan

( )

λ

[

σ2

( )

λ

]

2 1 ˆ ln L =−

4. Memaksimumkan fungsi kemungkinan sama artinya dengan meminimumkan jumlah kuadrat sisaan. Dengan membuat plot antara λ

dan L

( )

λ dan memperhatikan titik kritis λ pada L

( )

λ maksimum, maka

λmaks ini adalah penduga titik bagi λ.

Catatlah bahwa λ dapat pula diperoleh dari plot atau antara λ dan

( )

n

JKS λ dengan memperhatikan λ pada JKS

( )

λ nminimum.

Dengan transformasi ini kita akan memperoleh sebaran yang simetrik mendekati Normal. Ketakhomogenan ragam pun dapat dikurangi dengan transformasi ini.

2.5 Metodologi Penelitian

2.5.1 Data

Terdapat dua gugus data yang digunakan dalam penelitian ini. Data pertama dari Balai Penelitian Padi (Balitpa) Departemen Pertanian RI di Sukamandi, Jawa Barat, merupakan data uji daya hasil percobaan multilokasi yang melibatkan 12 varietas padi pada 5 lokasi. Penelitian akan memodelkan data persentase gabah isi, yang diamati saat panen. Data kedua adalah data percobaan pengendalian terhadap hama daun pada galur kedelai tahan hasil persilangan oleh Balai Penelitian Kacang-kacangan dan Umbi-umbian (Balitkabi) Departemen Pertanian RI di Malang, Jawa Timur. Percobaan ini melibatkan empat galur/varietas kedelai tahan hasil persilangan (Wilis, IAC-100, IAC-80-596-2 dan W/80-2-4-20). Penelitian ini memanfaatkan data populasi hama daun pada umur 14 hari setelah tanam.

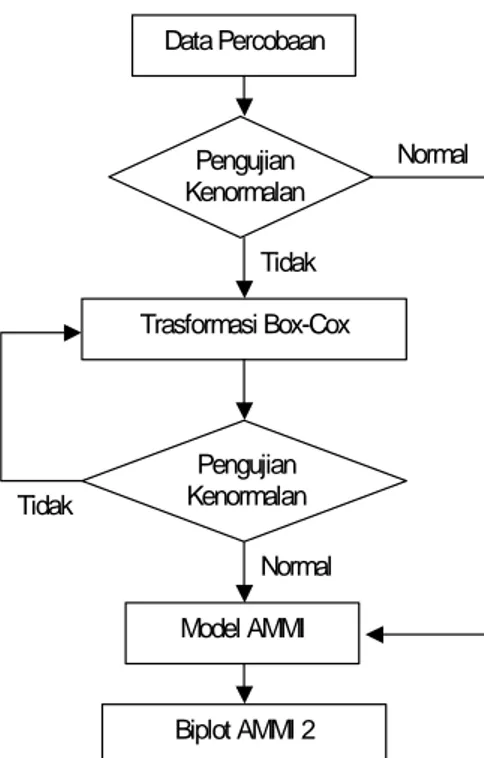
2.5.2 Tahapan Penelitian

Pada bagian ini akan disajikan secara ringkas tahapan penelitian, sebagaimana dalam Gambar 2.1.

Data Percobaan Tidak Trasformasi Box-Cox Pengujian Kenormalan Tidak Normal Pengujian Kenormalan Model AMMI Biplot AMMI 2 Normal

Langkah langkah pekerjaan penelitian adalah sebagai berikut:

1. Pengujian Kenormalan dilakukan dengan metode Anderson Darling atau Kolmogorov-Smirnov

2. Transformasi Box-Cox akan memperolah nilai lambda bagi peubah baru hasil transformasi. Transformasi Box-Cox dilakukan dengan bantuan GENSTAT (Lampiran 9).

3. Pengepasan model AMMI dilakukan dengan GENSTAT prosedur GAMMI dengan sebaran Normal dan fungsi hubung Identitas (Lampiran 10 & 11).

2.6 Hasil dan Pembahasan

2.6.1 Kestabilan Gabah Isi Varietas Padi: Data Persentase/Proporsi

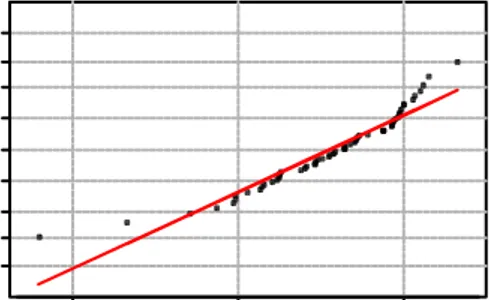
Data dalam bentuk proporsi biasanya tidak berdistribusi Normal. Hal ini ditunjukkan oleh uji kenormalan pada Gambar 2.3.

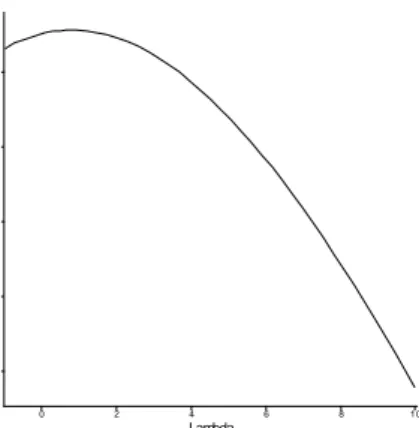
Metode transformasi Box-Cox pada data proporsi gabah isi menghasilkan nilai dugaan lambda sebesar 7.80 pada nilai maksimum log-likelihood sebesar 160.79. Plot log-likelihood disajikan pada Gambar 2.2 sedangkan nilai lambda untuk beberapa nilai log-likehood disajikan pada Lampiran 2.

Dengan demikian diperoleh transformasi pangkat 7.8. Katakanlah yp

adalah peubah populasi hama daun maka peubah transformasinya adalah 80

7.

yp

yz = . Uji kenormalan menunjukkan peubah yz ini menyebar mengikuti

distribusi Normal (Gambar 2.3 kanan).

Lambda 2 0 60 20 10 40 80 0 8 6 4 L o g lik e lih o o d

Analisis AMMI pada peubah yz menghasilkan nilai singular sebagai berikut 0.4041, 0.3483, 0.2100, dan 0.1199. Kontribusi keragaman yang mampu diterangkan oleh masing-masing komponen adalah 37.34%, 32.18%, 19.40%, 11.08% menunjukkan bahwa tiga komponen pertama memiliki peran dominan dala menerangkan keragaman pengaruh interaksi.

Gambar 2.3

Uji kenormalan data proporsi gabah isi sebelum transformasi (kiri) dan sesudah transformasi Box-Cox (kanan)

Berdasakan metode postdictive success diperoleh dua komponen pertama yang nyata dengan nilai F sebesar 3.59 dan 3.11 pada p< 0.015 dan nilai-p<0.015 (Tabel 2.1). Hal ini berarti proporsi gabah isi melalui transformasi pangkat 7.80 dapat diterangkan menggunakan model AMMI2 dengan kemampuan menerangkan keragaman pengaruh interaksi sebesar 69.51%.

Tabel 2.1. Analisis ragam untuk data gabah isi yang ditransformasi

Pengujian 1 Suku

Multiplikatif Pengujian 2 Suku Multiplikatif

Sumber _Bebas Derjat _Kuadrat Jumlah Kuadrat _Tengah

Nilai F Nilai-p Nilai F Nilai-p

Lingkungan 4 1.0277 0.2569 79.12 <0.000 143.06 0.0000 Genotipe 11 0.2240 0.0204 6.27 <0.001 11.34 0.0010 AMMI 1 14 0.1633 0.0117 3.59 <0.007 6.49 0.0061 AMMI 2 12 0.1213 0.0101 3.11 <0.015 5.63 0.0103 AMMI 3 10 0.0441 0.0044 2.45 0.1086 Residual 8 0.0144 0.0018 Total 59 1.5948 0.0270

Diagnosis sisaan menunjukkan kelayakan model ini, tidak ada penyimpangan yang serius pada plot sisaan (Gambar 2.4)

P-Value (approx): > 0.1000 R: 0.9940 W-test for Normality N: 60 StDev: 0.164410 Average: 0.487487 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 .999 .99 .95 .80 .50 .20 .05 .01 .001 P rob ab ili ty Yz P-Value (approx): < 0.0100 R: 0.9572 W-test for Normality N: 60 StDev: 0.0463283 Average: 0.904975 0.95 0.85 0.75 .999 .99 .95 .80 .50 .20 .05 .01 .001 P ro b ab ilit y p

Gambar 2.4 Plot sisaan model AMMI data gabah isi yang ditransformasi: (a) Plot kenormalan sisaan; (b) Plot sisaan vs fitted value

Biplot AMMI1 memunjukkan varietas C (B19154F-PN-1-1-4) mempunyai nilai rataan gabah isi ternormalkan yang paling rendah diantara varietas yang laun, sedangkan varietas L (IR 64) mempunyai nilai rataan yang tertinggi (Lampiran 6). Vaietas K (OBS 1658) dan E (Bio-Xa-5) mempunyai nilai rataan gabah isi yang sama namun interaksi dengan lingkungan yang berbeda, demikian pula dengan varietas G (Bio-Xa-7) dan F (S3383-1D-PN-41-3-1). Interaksi genotpie dan lingkungan lebih jelas dan detail digambarkan oleh biplot AMMI2

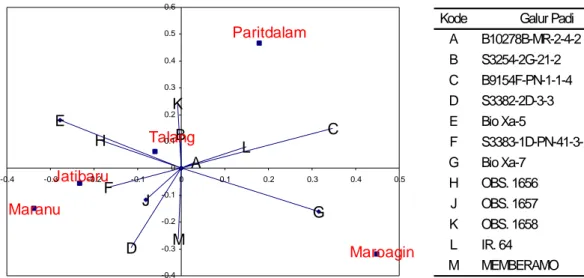
Biplot AMM2 hasil transformasi Box-Cox (Gambar 2.5) memperlihatkan varietas A (B10278-B-MR-2-4-2) relatif stabil pada seluruh lokasi, varietas lain beradaptasi secara spesifik pada lokasi tertentu. Varietas E (Bio-Xa-5) dan H (OBS. 1656) beradaptasi dengan baik di lokasi Talang sedangkan varietas G (Bio-Xa-7) di Maroangin. Varietas F (S3383-1D-PN-41-3-1) sangat baik di Jatibaru dan Maranu namun masih mungkin tumbuh dengan baik di Talang. Varietas J (OBS. 1657) dan D (S3382-2d-3-3) mampu beradaptasi di Jatibaru dan Maranu. Varietas L (IR 64) dan C (B19154F-PN-1-1-4) mampu beradaptasi di Paritdalam dan Maroangin, varietas K (OBS 1658) beradaptasi baik di Talang namun masih mungkin berkembang di Paritdalam. Varietas M (Memberamo) tidak secara spesifik beradaptasi dengan salah satu lokasi namun diperkirakan tidak mampu beradaptasi di Talang dan Paritdalam.

P -Value: 0.146 A -Squared: 0.555 And erson-Darlin g Normalit y Test N: 60 StD ev : 0. 015 6053 Aver ag e: 0. 000 0002 0.04 0.02 0.00 - 0.02 - 0.04 .999 .99 .95 .80 .50 .20 .05 .01 .001 P ro babi lit y r esidual AMMI y 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 3 2 1 0 -1 -2 -3 fit st d re s (a) (b)

E J H G A F C K M B D Jatibaru L Paritdalam Maranu Talang Maroagin -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5

Gambar 2.5 Bilpot AMMI 2 data gabah isi hasil transformasi Box-Cox

2.6.2 Ketahanan Kedelai Terhadap Hama Daun: Data Frekuensi/Populasi Hama

Metode transformasi Box-Cox pada data populasi hama daun menghasilkan nilai dugaan lambda sebesar 0.66 pada nilai maksimum log-likelihood sebesar -11.76. Plot log-likelihood disajikan pada Gambar 2.6 sedangkan nilai lambda untuk beberapa nilai log-likehood disajikan pada Lampiran 4.

Lambda 2 0 -40 -80 10 -60 -20 -100 8 6 4 L o g l ik e lih o o d Pow er : Box-Cox Gambar 2.6

Plot log-likelihood transformasi Box-Cox data populasi hama daun

Dengan demikian transformasi yang diperoleh adalah transformasi

pangkat 0.66. Katakanlah a adalah peubah populasi hama daun maka peubah

transformasinya adalah az =a0.66. Uji kenormalan menunjukkan peubah az ini

menyebar mengikuti distribusi Normal (Gambar 2.7).

Kode Galur Padi A B10278B-MR-2-4-2 B S3254-2G-21-2 C B9154F-PN-1-1-4 D S3382-2D-3-3 E Bio Xa-5 F S3383-1D-PN-41-3-1 G Bio Xa-7 H OBS. 1656 J OBS. 1657 K OBS. 1658 L IR. 64 M MEMBERAMO

P-Value (approx): > 0.1000 R: 0.9958 W-test for Normality N: 20 StDev: 0.589420 Average: 1.65575 2.5 2.0 1.5 1.0 .999 .99 .95 .80 .50 .20 .05 .01 .001 P rob ab ilit y az

Normal Probability Plot

Gambar 2.7

Plot uji kenormalan hasil transformasi Box-Cox data populasi hama daun

Analisis AMMI pada peubah az menghasilkan nilai singular sebagai

berikut 1.451, 0.7614, 0.1505. Kontribusi keragaman yang mampu diterangkan oleh masing-masing komponen adalah 61.41%, 32.22%, dan 6.37%, menunjukkan bahwa dua komponen pertama memiliki peran dominan dalam menerangkan keragaman pengaruh interaksi.

Tabel 2.2 Analisis ragam untuk populasi hama daun yang ditransformasi

Pengujian 1 Suku

Multiplikatif Pengujian 2 Suku Multiplikatif

Sumber _Bebas Derjat _Kuadrat Jumlah Kuadrat _Tengah

Nilai F Nilai-p Nilai F Nilai-p

Hama Daun 4 2.2659 0.5665 5.64 0.032 50.02 0.0197 Genotipe 3 1.6252 0.5417 5.40 0.039 47.83 0.0205 AMMI 1 6 2.1065 0.3511 3.50 0.077 31.00 0.0316 AMMI 2 4 0.5797 0.1449 12.80 0.0738 Residual 2 0.0227 0.0113 Total 19 6.5999 0.3474

Berdasakan metode postdictive success diperoleh komponen pertama yang nyata dengan nilai F sebesar 31.00 pada nilai-p<0.04, sedangkan komponen kedua nyata nilai-p=0.074 (Tabel 2.2). Sekalipun nilai-p komponen kedua cukup besar namun dua komponen pertama sangat dominan, kemampuan menerangkan keragaman pengaruh interaksi sebesar 93.63%. Hal ini berarti populasi hama daun melalui transformasi pangkat 0.66 dapat diterangkan menggunakan model AMMI2. Diagnosis sisaan juga memperkuat hal ini, tidak ada penyimpangan yang serius pada plot sisaan (Lampiran 3).

Biplot AMMI1 menunjukkan genotipe IAC-100 merupakan genotipe dengan nilai rataan populasi hama (ternormalkan) paling rendah, sedangkan Wilis

yang paling tinggi (Lampiran 7). Selengkapnya, interaksi ini digambarkan oleh Biplot AMMI2 dengan lebih baik.

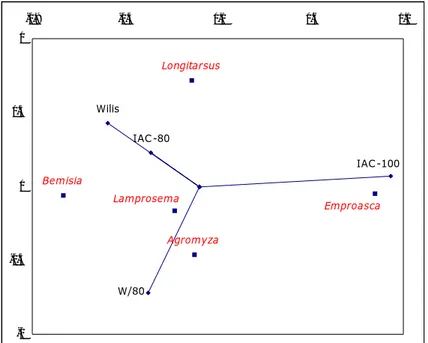
Gambar 2.8 menunjukkan biplot AMMI 2 data populasi hama daun tanaman kedelai yang ternormalkan. Pada fase ini, populasi Lamprosema hampir sama pada semua genotipe. Genotipe IAC 80 paling tahan terhadap keseluruhan hama daun pada fase ini (14 HST) dibanding yang lain. Sementara genotipe lain secara spesifik rentan terhadap hama tertentu. W/80 relatif rentan terhadap Lalat Kacang (Agromyza), IAC 100 relatif rentan terhadap Emproasca.

W/80 Longitarsus IAC-100 Lamprosema Wilis IAC-80 Bemisia Agromyza Emproasca -1 -0.5 0 0.5 1 -0.9 -0.4 0.1 0.6 1.1

Gambar 2.8 Biplot AMMI 2 data populas hama daun yang ditransformasi

2.7 Simpulan

Transformasi pangkat Box-Cox mampu mengatasi ketaknormalan data. Dengan transformasi Box-Cox dapat dilakukan pemodelan interaksi menggunakan model AMMI secara sahih pada data ternormalkan.

Studi kestabilan gabah isi varietas padi melalui transformasi memberikan informasi bahwa varietas A (B10278-B-MR-2-4-2) relatif stabil pada seluruh lokasi, varietas lain beradaptasi secara spesifik pada lokasi tertentu. Varietas E (Bio-Xa-5) dan H (OBS. 1656) beradaptasi dengan baik pada di Talang sedangkan varietas G (Bio-Xa-7) di Maroangin. Varietas F (S3383-1D-PN-41-3-1) sangat baik di Jatibaru dan Maranu namun masih mungkin tumbuh dengan baik di

Talang. Varietas J (OBS. 1657) dan D (S3382-2d-3-3) mampu beradaptasi di Jatibaru dan Maranu. Varietas L (IR 64) dan C (B19154F-PN-1-1-4) mampu beradaptasi di Paritdalam dan Maroangin, varietas K (OBS 1658) beradaptasi baik di Talang namun masih mungkin berkembang di Paritdalam. Varietas M (Memberamo) tidak secara spesifik beradaptasi dengan salah satu lokasi namun diperkirakan tidak mampu beradaptasi di Talang dan Paritdalam.

Studi ketahanan hama daun kedelai pada data ternormalkan memberikan genotipe Wilis dan IAC 80 memiliki kesamaan, sama-sama relatif tahan terhadap keseluruhan hama daun pada fase ini (14 HST) dibanding yang lain. Sementara genotipe lain secara spesifik rentan terhadap hama tertentu. W/80 relatif rentan terhadap Lalat Kacang (Agromyza), IAC 100 relatif rentan terhadap Emproasca.

III. MODEL AMMI TERAMPAT UNTUK DATA

BERDISTRIBUSI BUKAN NORMAL

3.1 Pendahuluan

Arti penting pemodelan statistika adalah meyediakan interpretasi atas fenomena yang dipelajari, dan menyatakannya dengan bahasa yang sesuai dengan bidang aplikasi. Transformasi dapat dihindari manakala kehomogenan ragam dapat dimodelkan oleh suku-suku multiplikatif pengaruh interaksi pada struktur sistematik model. Bagaimanapun, untuk data bukan Normal yang dimodelkan pada skala observasi, interaksi multiplikatif kemungkinan besar merefleksikan dua hal, kehomogenan ragam dan interaksi multiplikatif yang sebenarnya. Tidak ada jaminan penuh bahwa transformasi data pada skala pengamatan dapat memisahkan kedua hal di atas.

Transformasi, dalam kasus analisis regresi ataupun analisis ragam, bertujuan untuk memperoleh kehomogenan ragam, mendekati kenormalan galat, dan keaditifan pengaruh sistematik. Tidaklah mudah medapatkan sebuah transformasi yang memenuhi semua kebutuhan itu. Sebagai contoh, untuk data cacahan yang berdistribusi Poisson dan pengaruh sistematiknya multiplikatif, transformasi akar akan berhasil memperoleh ragam yang konstan, transformasi pangkat dengan pangkat dua per tiga akan menghasilkan distribusi yang mendekati simetrik atau Normal, sedangkan tranformasi logaritma menghasilkan aditifitas pengaruh sistematik. Jadi, setelah transfomasi pun, suku multiplikatif kemungkinan (masih) mencerminkan campuran keheterogenan ragam dan pengaruh multiplikatif.

Sementara itu, pada pemodelan aditif telah dikenal luas apa yang disebut dengan Generalized Linear Models (GLM) atau Model Linier Terampat (MLT) sebuah kelas pemodelan yang menangani data-data bukan Normal. Pada MLT, keaditifan pengaruh sistematik ditentukan pada skala ternormalkan. Kenormalan (dan kehomogenan) ragam tidak lagi diperlukan, karena dengan (quasi) likelihood hanya relasi antara nilai tengah dan ragam yang perlu ditetapkan.

Model multiplikatif (bilinear) menjembatani kesenjangan antara model pengaruh utama (pada ANOVA ataupun GLM) dan model interaksi lengkap dengan parameter interaksi untuk tiap-tiap sel dalam tabel dua arah. Model ini pun memberikan visualisasi corak utama interaksi melalui biplot. Karenanya pengembangan teori GLM dengan mengakomodasi komponen multiplikatif untuk interaksi sangat diperlukan.

Kekuatan eksplorasi model multiplikatif AMMI terletak pada visualisasi interaksi melalui biplot. Van Eeuwijk, 1995, memperkenalkan model multiplikatif dalam konteks MLT sebagai perluasan dari model AMMI yang disebut dengan Generallized AMMI atau disingkat GAMMI. Pada pemodelan GAMMI, visualisasi interaksi ini masih dimungkinkan. Namun seperti disebutkan Van Eeuwijk interpretasinya masih harus diinvestigasi karena sangat tergantung pada fungsi hubung yang digunakan. Walaupun jarak antar titik masih merepresentasikan ketakaditifan atau ketakbebasan.

Bab ini bertujuan membicarakan bagaimana pengepasan (fiting) model bilinear GAMMI dalam konsep MLT. Khususnya untuk pengamatan berupa cacahan, distribusi poisson dan binomial.

3.2 Model Linier Terampat (Generalized Linear Models)

Model linear klasik mempunyai karakteristik: galat atau peubah respon mengikuti sebaran Normal dengan ragam konstan, ragam bebas dari rataan, dan galat atau peubah respon saling bebas. Pada kelas pemodelan yang lebih luas tidak lagi terikat dengan asumsi ini. Nelder dan Wedderburn pada tahun 1972 mengenalkan model linear terampat (MLT, generalized linear model) yang tidak bergantung pada karakteristik atau asumsi model linear klasik, tetapi bergantung

hanya sifat fungsi penghubung (link function) yang menghubungkan antara μi

(rataan) dan ηi (prediktor linear [linear predictor]) dari model sebaran peluang

yang digunakan (McChullagh & Nedler, 1989).

Peubah respon yi(i=1,K,n) merupakan nilai-nilai pengamatan peubah

acak Y yang diasumsikan menyebar mengikuti sebaran tertentu (keluarga _i

ragam dari nilai tengah,V(μ), yang mungkin menyertakan parameter dispersi,

memenuhi asumsi distribusi. Var(yi)=φ V(μi) dengan φ parameter dispersi

(faktor skala) dan V(⋅)adalah fungsi ragam. Nilai tengahμi berhubungan dengan

prediktor linear (ηi =

∑

n_j−1βjxij atau η=Xβ dimana xij peubah penjelas yang

diketahui, sedang βj adalah parameter, yang nilainya tidak diketahui) melalui

suatu fungsi hubung: g_i(μ_i)=η_i. Walaupun setiap pengamatan mungkin

mempunyai fungsi penghubung yang berbeda, tetapi hal ini sangatlah jarang sehingga indeks i dalam fungsi gi dapat dihilangkan atau gi(μi)tereduksi menjadi

) ( _i

g μ . Pendugaan parameter βjdalam vektor β dilakukan melalui prosedur

iterasi regresi linier terboboti dari fungsi hubung yang terlinierisasi dan dikenakan

kepada pengamatan (y pada peubah penjelas) (x . Fungsi hubung terlinierisasi )

atau fungsi hubung yang disesuaikan atau dalam GLIM dikenal dengan

sebutan working variate, z, mempunyai bentuk z=η+(y−μ)δη δμ atau

) )]( ( [ 1 _{i i i} i i g y

z =η + ′ − η −μ (McChullagh & Nedler, 1989; Van Eeuwijk, 1995;

Falguerolles,1996). Setiap pengamatan juga mempunyai pembobot awal (prior weight) w_i =[Var(z_i)]−1, atau w=(δμ δη)2 V(μ). Pada setiap putaran iterasi nilai x dan z akan di-update. Metode ini dikenal dengan Iterative Reweighted Least Square disingkat IRLS.

Tabel 3.1. Fungsi Penghubung (kanonik) dalam Model Linier Terampat

SEBARAN RESPON NAMA SIFAT HUBUNGAN

Normal Identitas η=g(μ)=μ

Poisson Log η= g(μ)=log(μ)

Binomial Logit _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = = μ μ μ η 1 log ) ( g

Binomial Negatif Log _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = k g μ μ μ η ( ) log Gamma Kebalikan μ μ η= g( )= −1

Secara umum, model linier terampat mempunyai karakteristik:

1. Peubah respon, Y, mempunyai sebaran dalam keluarga sebaran eksponensial.

2. Komponen linear atau sistematik yang menghubungkan prediktor linear η ke

perkalian antara matrik rancangan Xdan parameter β, η= Xβ.

3. Fungsi penghubung (link function) g(⋅) –yang mengaitkan prediktor linear

dengan nilai-nilai dugaan model (fitted values)– mempunyai sifat monotonik

dan diferensiabel. g(⋅) ini mendeskripsikan bagaimana rataan respon yang

diharapkan dihubungkan dengan η, misalnya η=Xβ dan μ=g−1(η)=E(Y). 4. Peubah respon boleh mempunyai ragam tidak konstan yang nilainya berubah

dengan berubahnya nilai rataannya, σi2= f(μi).

3.3 Model AMMI Terampat (Generalized AMMI Model/GAMMI)

Dalam suatu percobaan, respon yang diamati terkadang berupa data kategorik. Hal ini mengakibatkan pendekatan model AMMI menjadi tidak relevan sehingga perlu dilakukan analisis dengan menggunakan pendekatan lain. Untuk kasus ini, metode AMMI juga telah dikembangkan untuk menangani kasus-kasus yang lebih general. Model pendekatannya dikenal dengan nama model Generalized AMMI disingkat GAMMI (Van Eeuwijk, 1995) atau Generalized Bilinear Models disingkat GBMs (Falguerolles, 1996, & Gabriel, 1998). Model GAMMI dapat dituliskan sebagai berikut:

∑

= + + + = K k kj ki k j i ij 1

δ

γ

λ

β

α

ν

η

Suatu model AMMI adalah model GAMMI dengan link identitas dan ragam

konstan. Dengan menetapkan nilai βj dan δkj mereduksi model menjadi GLM

sepanjang baris, sedang menetapkan nilai αi dan δik menjadi GLM sepanjang

kolom. Karakteristik dari model GAMMI ini dapat menjadi dasar untuk menentukan prosedur pendugaan parameter. Prosedur pendugaan parameter pada GLM lainnya, biasanya menggunakan metode kuadrat terkecil terboboti secara iteratif.

3.3.1 Algoritma Pengepasan Model AMMI Terampat

Pengepasan Model AMMI Terampat dilakukan secara iteratif dengan beberapa tahapan sebagai berikut (Van Eeuwijk, 1995; Falguerolles, 1996):

Tahapan pendugaan parameter pada model GAMMI dapat dilakukan sebagai berikut:

(i) Menentukan nilai awal untuk pengaruh utama dan interaksi kolom

Ketika suatu model GAMMI dengan poros K akan disesuaikan dan tidak ada hasil yang didapat dari penyesuaian dengan poros M < K

1. Modelkan pengaruh utama sebagai berikut: ηij = v + αi + βj

2. Simpan pendugaan βˆ_{j dari efek utama kolom}

3. Pilih skor kolom, δˆ , untuk poros 1 sampai K (skor-skor ini tidak _kj

harus sama semua, dan sebaiknya telah distandarisasi dan diortonormalisasi; , ˆ , ˆ _{0 1} 1 2 1 = =

∑

∑

= = J j kj J j kj δ δ untuk k = 1, ..., K, , ˆ ˆ ' = 0

∑

δkjδk j untuk k ≠ k’)

Ketika pendugaan parameter dapat digunakan untuk model GAMMI dengan poros M < K, nilai dari βˆ_j dan δˆ_kj, sekarang dengan k mulai dari 1, ..., M, dapat digunakan sebagai nilai awal untuk GLM pada tahap selanjutnya.

Untuk nilai δˆ_{kj yang dimiliki poros M + 1, M + 2, ..., K, nilai dapat dipilih}

lagi.

(ii) Pendugaan pengaruh utama dan interaksi baris

Tentukan b_j = βˆ_j dan d_kj =δˆ_kj, dan modelkan regresi baris

∑

= + + + = K k kj ki j i ij v b d 1 γ α η keterangan:

bj diharapkan telah diketahui dan tidak harus diduga

dkj menggambarkan variabel concomitant pada faktor kolom.

Parameter αi dan γ1i, γ2i, ..., γKi adalah intersep dan slop untuk regresi dari

perlu dipusatkan dalam proses iterasi, ini mungkin sebaiknya hanya dilakukan setelah konvergen.

(iii) Pemusatan dan pengortogonalan pengaruh interaksi baris

∑

= = I i ki ˆ 1 0

γ

, untuk k = 1, ..., K

∑

= = I i i ' k kiˆ ˆ 1 0

γ

γ

, untuk k ≠ k’

(iv) Pendugaan efek utama dan interaksi kolom

Tentukan ai =αˆi dan cki =γˆki, dan modelkan regresi kolom

∑

= + + + = K k kj ki j i ij v a c 1 δ β η keterangan: i

a membentuk offset, ketika nilai cki menunjukkan variabel concomitant

pada faktor baris.

Parameter βj dan δ1j, δ2j, ..., δKj adalah intersep dan slop untuk regresi pada

entri kolom j pada variabel c1, c2, ..., cK. Tidak perlu memusatkan efek

utama kolom, βj, dalam prosedur.

(v) Standarisasi dan pengortonormalan pengaruh interaksi kolom

Standarisasi dan ortonormalisasi: , ˆ , ˆ _{0 1} 1 2 1 = =

∑

∑

= = J j kj J j kj δ δ untuk k = 1, ..., K , ˆ ˆ ' =0

∑

δkjδkj untuk k ≠ k’

Jika tidak terpenuhi maka lanjutkan prosesnya, b_j = βˆ_j dan d_kj =δˆ_kj, dan

fitkan regresi baris,

∑

= + + + = K k kj ki j i ij v b d 1 γ α η

Perubahan dari deviansi dari salah satu atau kedua regresi baris dan kolom dapat digunakan sebagai kriteria konvergen, atau perubahan dalam pendugaan dari salah satu atau keduanya parameter baris dan kolom. Jika kriteria kekonvergenan terpenuhi maka deviansi sisaan dari regresi baris akan menjadi

sama dengan deviansi sisaan dari regresi kolom. Metode ini sering juga disebut metode pendugaan maksimum quasi-likelihood. Pada saat konvergen maka

K I i ki ˆ λ γ =

∑

=1 2

Parameter

λ

_K menunjukkan suatu parameter asosiasi general, suatu nilai

singular general. Kecuali untuk kasus model AMMI, tidak akan ada hubungan sederhana antara banyaknya deviansi yang bersesuaian dengan poros k dan kuadrat dari nilai singular:

( )

λ

_k 2 =

λ

_k.

3.3.2 Penentuan Banyaknya Suku Multiplikatif

Banyaknya unsur multiplikatif dalam model GAMMI dapat ditetapkan melalui generalisasi uji pada model AMMI, yaitu:

1) Uji rasio likelihood untuk akar ciri pertama, untuk akar ciri kedua jika diketahui yang pertama, dan untuk akar ciri berikutnya. Uji ini membandingkan persentase yang diterangkan oleh suku tertentu dengan jumlah total yang tetap akan diterangkan, dan tidak memerlukan suatu pendugaan untuk galat.

2) Uji F tidak membutuhkan tabel khusus dan mudah dalam perhitungannya. Suatu pendugaan bebas dari galat (over/under dispersi) diperlukan dan mungkin akan menyebabkan masalah.

3) Uji sederhana dengan atribut derajat bebas (I – 1) + (J – 1) – (2k – 1) kepada akar ciri bersesuaian dengan poros k, menjadi perbedaan antara banyaknya parameter yang akan diduga dan banyaknya konstrain identifikasi yang dikenakan. Kuadrat tengah yang bersesuaian kemudian diuji melawan suatu pendugaan galat (over/under dispersi). Uji ini diusulkan oleh Golob pada 1968 (Van Eeuwijk, 1995). Ketika akar ciri pertama relatif cukup besar terhadap akar ciri selanjutnya, atribut derajat bebas aman untuk mengikuti Gollob dan mengumpulkan suku berikutnya untuk suatu pendugaan galat (over/under dispersi). Aplikasi sekuensial dari prosedur ini, menguji akar ciri suksesif melawan pendugaan galat terkumpul.

Penambahan komponen multiplikatif lainnya untuk model GAMMI membutuhkan perhitungan kembali pada suku yang telah dimasukkan. Karena perbedaan bobot sel, dimensionalitas suksesif tidak disarangkan sebagaimana biasanya untuk model AMMI dengan bobot sel yang sama.

3.3.3 Diagnostik Sisaan

Sisaan untuk tujuan diagnostik, setelah konvergen, dapat diperoleh dari regresi baris sebaik regresi kolom. Sisaan regresi baris dan kolom akan menyimpang sedikit dari sesamanya, karena perhitungan dari sisaan regresi baris mengasumsikan bahwa parameter kolom lebih diketahui daripada yang diduga, sedangkan untuk sisaan regresi kolom pendugaan dari parameter baris tidak perlu diketahui juga. Kemungkinan lainnya adalah untuk membuat peregresi dari hasil parameter interaksi baris dan kolom dalam jalan yang sama dengan uji satu-derajat bebas untuk ketakaditifan yang dapat memberikan suatu interpretasi regresi, dan mencocokkan suatu model dengan efek utama dan peregresi-peregresinya. Sisaan dari model ini adalah suatu kompromi antara sisaan dari regresi baris dan regresi kolom.

Diagnostik sisaan yang dilakukan untuk menilai kelayakan model, diadopsi dari kelas GLM/MLT. Kelayakan model dapat diperiksa secara informal melalui plot sisaan terhadap suatu fungsi dari nilai dugaan model (fitted value). Untuk penilaian kelayakan model secara umum pemeriksaan disarankan menggunakan sisaan devians terbakukan (standardized deviance residual) untuk diplot terhadap prediktor linier (linear predictor) ataupun terhadap nilai dugaan model (fitted value) yang ditransformasi menjadi konstanta skala informasi bagi sebaran galat. Transformasi fitted value untuk beberapa sebaran galat antara lain:

μ

ˆ untuk galat berdistribusi Normal

μ

ˆ

2 untuk galat Poisson

μˆ

sin 1

2 − untuk galat Binomial

μˆ log

2 untuk galat Gamma

2 1

2 −