PENYELESAIAN PERSAMAAN SCHRÖDINGER POTENSIAL SHAPE - INVARIANCE DENGAN FAKTOR SENTRIFUGAL MENGGUNAKAN METODE SUPERSIMETRI MEKANIKA KUANTUM (SUSYQM)

(1)

perpustakaan.uns.ac.id digilib.uns.ac.id

commit to user

i

PENYELESAIAN PERSAMAAN SCHRÖDINGER POTENSIAL SHAPE

-INVARIANCE DENGAN FAKTOR SENTRIFUGAL MENGGUNAKAN

METODE SUPERSIMETRI MEKANIKA KUANTUM (SUSYQM)

TESIS

Untuk Memenuhi Sebagian Persyaratan untuk Mencapai Derajat Magister

Program Studi Ilmu Fisika

Oleh HETI MARINI

S911008004

PROGRAM PASCASARJANA UNIVERSITAS SEBELAS MARET

SURAKARTA 2012

(2)

commit to user

ii

PENYELESAIAN PERSAMAAN SCHRÖDINGER

POTENSIAL SHAPE INVARIANCE DENGAN FAKTOR SENTRIFUGAL MENGGUNAKAN METODE SUPERSIMETRI MEKANIKAKUANTUM

(SUSYQM)

TESIS

Oleh Heti Marini S911008004

Komisi Nama TandaTangan Tanggal

Pembimbing

Pembimbing I Dra. Suparmi, M.A., Ph.D ... 30 Juli 2012 NIP. 19520915 197603 2 001

Pembimbing II Drs. Cari, M.Sc., M.A., Ph.D ... 30 Juli 2012 NIP : 19610306 198503 1 002

Telah dinyatakan memenuhi syarat Pada tanggal 30 Juli 2012

Ketua Program Studi IlmuFisika Program Pascasarjana UNS

Drs.Cari, M.Sc., M.A., Ph.D NIP : 19610306 198503 1 002

(3)

commit to user

iii

PENYELESAIAN PERSAMAAN SCHRÖDINGER

POTENSIAL SHAPE INVARIANCE DENGAN FAKTOR SENTRIFUGAL MENGGUNAKAN METODE SUPERSIMETRI MEKANIKAKUANTUM

(SUSYQM) TESIS Oleh Heti Marini S911008004 Tim Penguji

Jabatan Nama TandaTangan Tanggal

Ketua Dr. Agus Supriyanto, S.Si.,M.Si ... Agustus 2012 NIP.19690826 199903 1 001

Sekretaris Dr. Eng. Risa Suryana, S.Si.,M.Si ... Agustus 2012 NIP. 19710831 200003 1 005

Anggota Dra. Suparmi, M.A., Ph.D ... Agustus 2012 Penguji NIP. 19520915 197603 2 001

Drs. Cari, M.Sc., M.A., Ph.D ... Agustus 2012 NIP . 19610306 198503 1 002

Telah dipertahankan di depan penguji Dinyatakan memenuhi syarat Pada tanggal 15 Agustus 2012

Program Pascasarjana UNS Ketua Program Studi IlmuFisika

Prof. Dr. Ir. Ahmad Yunus, M.S Drs.Cari, M.Sc., M.A., Ph.D NIP. 19610717198601 1 001 NIP : 19610306 198503 1 002

(4)

commit to user

iv

PERNYATAAN ORISINALITAS DAN PUBLIKASI ISI TESIS

Saya menyatakan dengan sebenarnya bahwa:

1. Tesis yang berjudul “Penyelesaian Persamaan Schrödinger Potensial

Shape Invariance dengan Faktor Sentrifugal Menggunakan Metode

Supersimetri Mekanika Kuantum (susyqm)”. ini adalah karya penelitian saya sendiri, tidak terdapat karya ilmiah yang pernah diajukan oleh orang lain untuk memperoleh gelar akademik, serta tidak terdapat karya atau pendapat yang pernah ditulis atau diterbitkan oleh orang lain kecuali secara tertulis digunakan sebagai acuan dalam naskah dan disbutkan dalam sumber acuan serta daftar pustaka. Apabila dikemudian hari terbukti pernyataan saya ini tidak benar, maka saya bersedia menerima sanksi sesuai ketentuan peraturan perundang-undangan (Permendiknas No. 17, Tahun 2010)

2. Publikasi sebagian atau keseluruhan dari isi tesis ini pada jurnal atau forum ilmiah lain harus seizin dan menyertakan tim pembimbing sebagai author dan PPs-UNS sebagai institusinya. Apabila dalam waktu sekurang-kurangnya satu semester (enam bulan sejak pengesahan tesis) saya tidak melakukan publikasi dari sebagian atau keseluruhan tesis ini, maka PPs-UNS berhak mempublikasikannya pada jurnal ilmiah yang diterbitkan oleh Prodi Ilmu Fisika PPs-UNS. Apabila saya melakukan pelanggaran dari ketentuan publikasi ini, maka saya bersedia mendapatkan sanksi akademik yang berlaku.

Surakarta, 13 Agustus 2012

Mahasiswa

Heti Marini S911008004

(5)

commit to user

v

KATA PENGANTAR

Puji syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan

hidayah-Nya sehingga penulis dapat menyelesaikan tesis dengan judul,

“Penyelesaian Persaaan Schrödinger Potensial Shape Invariance dengan Faktor Sentrifugal Menggunakan Metode Supersimetri Mekanika Kuantum (SUSYQM)” ini. Penyusunan tesis ini bertujuan untuk memenuhi sebagian persyaratan guna

memperoleh gelar Magister pada Program Studi Ilmu Fisika Program

Pascasarjana Universitas Sebelas Maret Surakarta.

Penulis menyadari bahwa tanpa bantuan dari berbagai pihak, tesis ini tidak

akan terwujud. Oleh karena itu, penulis mengucapkan terima kasih yang

sebesar-besarnya kepada:

1. Bapak Prof. Dr. Ir. Ahmad Yunus, M.S, selaku Direktur Program

Pascasarjana Universitas Sebelas Maret Surakarta.

2. Bapak Drs. Cari, M.Sc., M.A., Ph.D, selaku Ketua Program Studi Ilmu Fisika

Pascasarjana Universitas Sebelas Maret Surakarta, sekaligus sebagai

Pembimbing II yang telah banyak memberikan banyak bimbingan dan arahan

serta motivasi kepada penulis sehingga mampu menyelesaikan tesis ini.

3. Ibu Dra. Suparmi, M.A., Ph.D, selaku pembimbing I yang telah dengan sabar

membimbing dan mengajari penulis, serta memberikan semangat kepada

penulis untuk dapat menyelesaikan tesis ini.

4. Bapak/Ibu Dosen Program Studi Ilmu Fisika Pascasarjana Universitas

(6)

commit to user

vi

5. Bapak Drs. Sunarno, selaku Kepala Sekolah SMP Muhammadiyah 04 Sambi,

yang telah memberikan izin kepada penulis untuk melanjutkan studi ini.

6. Semua pihak yang telah membantu penulis dalam menyelesaikan tesis ini.

Penelitian ini didanai oleh Program Hibah Penelitian Tim Pascasarjana

(HPTP) Universitas Sebelas Maret tahun 2012 dengan nomer kontrak

2345/UN27.16/PN/2012.

Surakarta, 2012

(7)

commit to user

vii ABSTRAK

Heti Marini. S911008004. “Penyelesaian Persamaan Schrödinger Potensial

Shape Invariance dengan Faktor SentrifugalMenggunakan Metode Supersimetri Mekanika Kuantum(susyqm)”. Tesis: Program Pascasarjana Ilmu Fisika Universitas Sebelas Maret Surakarta. Pembimbing: (1). Dra. Suparmi, M.A., Ph.D, (2). Drs. Cari, M.Sc., M.A., Ph.D

Penelitian ini bertujuan untuk menentukan spektrum energi dan fungsi gelombang beberapa potensial shape invariance dengan faktor sentrifugal, yaitu potensial Kratzer, potensial Morse, dan potensial Manning Rosen menggunakan metode Supersimetri Mekanika Kuantum (SUSYQM).

Penelitian ini merupakan studi literatur untuk menyelesaikan persamaan Schrödinger potensial Kratzer, potensial Morse, dan potensial Manning Rosen dengan faktor sentrifugal secara analitik. Spektrum energi dan fungsi gelombang diperoleh melalui penyelesaian persamaan Schrödinger menggunakan metode Supersimetri Mekanika Kuantum (SUSYQM), dimana spektrum energi ditentukan dengan menggunakan metode Operator Supersimetri dan metode Kuantisasi Supersimetri-WKB (SWKB), sedangkan Fungsi gelombang ditentukan dengan menggunakan metode Operator Supersimetri. Penentuan spektrum energi dengan metode operator supersimetri dilakukan dengan menggunakan sifat shape

invariance, dan penentuan spektrum energi dengan metode kuantisasi SWKB

dilakukan dengan menggunakan formula kuantisasi SWKB untuk kondisi simetri yang baik (unbroken symetry). Sedangkan persamaan fungsi gelombang tingkat dasar ditentukan menggunakan sifat dari operator penurun, dan untuk fungsi gelombang tingkat ke-n ditentukan dengan mengoperasikan operator penaik terhadap gelombang dasar.

Spektrum energi dari potensial Kratzer, potensial Morse, dan potensial Manning Rosen dengan faktor sentrifugal yang ditentukan dengan menggunakan metode operator supersimetri hasilnya sama dengan spektrum energi dari potensial-potensial tersebut yang ditentukan dengan menggunakan metode SWKB. Spektrum energi dan fungsi gelombang untuk potensial Kratzer dapat ditentukan secara eksak untuk setiap bilangan kuantum orbital l, sedangkan untuk potensial Morse dan potensial Manning Rosen hanya dapat ditentukan secara eksak pada bilangan kuantum orbital l=0, sedangkan untuk bilangan kuantum 𝑙 ≠ 0 baik spektrum energi maupun fungsi gelombangnya hanya dapat ditentukan dengan cara pendekatan.

Kata Kunci: Persamaan Schrodinger, Potential Shape invariance, Faktor Sentrifugal, Supersimetri Mekanika Kuantum

(8)

commit to user

viii ABSTRACT

Heti Marini. S911008004. “Solution of Schrödinger Equation For Some Shape Invariance Potentials with The Centrifugal Term Using Supersymetry of Quantum Mechanics (susyqm)”. Thesis: Physics Department of Postgraduate Study Sebelas Maret University Surakarta. Advisor: (1). Dra. Suparmi, M.A., Ph.D, (2). Drs. Cari, M.Sc., M.A., Ph.D

The purposes of the research were to determine the energy spectrum and wave function of someshape invariance potentials with centrifugal term, Kratzer Potential, Morse Potential, and Manning Rosen Potential using supersymetry of quantum mechanics (SUSYQM).

The research was a literature study to solve Schrödinger equation for Kratzer Potential, Morse Potential, and Manning Rosen Potentialwith centrifugal term analytically. the energy spectrum and wave functionwere obtained by solving Schrödinger equation usingSupersymetry of Quantum Mechanics method, the energy spectrum was obtained using Supersymetry Operator and Supersymetry – WKB (SWKB) quantization method, while the wave function was obtained using Supersymetry Operator Method.Using Operator Supersymetry, the spectrum energy was obtained by applying concept of shape invariance, while using SWKB quantization method, the spectrum energy was obtainedby SWKB quantizationformula for unbroken symetry. By applying the lowering operator on ground state wave function we get the ground state wave function, and the first excited wave function was obtained by applying raising operator on the ground state wave function, and so on.

The energy spectrum obtained using SWKB quantization formula was equal to the result obtained using Supersymetry Operator. For Kratzer Potential, both the energy spectrum and the wave function can be solvedexactly for all values of orbital quantum numberl. But for both Morse and Manning potential only exactly solvable for orbital quantum number𝑙=0, while for 𝑙≠0, both energy spectrum and the wave function obtained was only treated by approximation methods.

Key words: Schrödinger Equation,Shape invariance Potential, Centrifugal Term, Supersymetryof Quantum Mechanics

(9)

perpustakaan.uns.ac.id digilib.uns.ac.id commit to user ix DAFTAR ISI HALAMAN JUDUL ... i HALAMAN PERSETUJUAN ... ii

HALAMAN PENGESAHAN ………. iii

HALAMAN PERNYATAAN ... iv

KATA PENGANTAR ... v

ABSTRAK ... vii

ABSTRACT ... viii

DAFTAR ISI ... ix

DAFTAR GAMBAR ... xii

DAFTAR TABEL ... xiii

DAFTAR LAMPIRAN ... xiv

BAB I. PENDAHULUAN ... 1 A. Latar belakang ... 1 B. Rumusan Masalah ... 7 C. Tujuan Penelitian ... 8 D. Batasan Masalah ... 8 E. Manfaat Penelitian ... 9

BAB II. DASAR TEORI ... 10

A. Persamaan Schrödinger ... 10

B. Persamaan Schrödinger dalam ruang Tiga Dimensi ... 12

C. Supersimetri Mekanika Kuantum (SUSYQM) ... 18

(10)

commit to user

x

E. Formula Kuantisasi Supersimetri – WKB (SWKB) ... 23

F. Potensial Kratzer dengan Faktor Sentrifugal ... 25

G. Potensial Morse dengan Faktor Sentrifugal ... 26

H. Potensial Manning Rosen dengan Faktor Sentrifugal ... 28

BAB III. METODE PENELITIAN ... 30

A. Waktu Dan Tempat Penelitian ... 30

B. Objek Penelitian ... 30

C. Instrumen Penelitian ... 31

D. Prosedur Penelitian ... 32

E. Diagram Penelitian ... 33

BAB IV. HASIL PENELITIAN DAN PEMBAHASAN ... 34

A. Hasil Penelitian ... 34

1. Persamaan Tingkat Energi dan Fungsi Gelombang untuk Potensial Kratzer dengan Faktor Sentrifugal ... 34

2. Persamaan Tingkat Energi dan Fungsi Gelombang untuk Potensial Morse dengan Faktor Sentrifugal ... 48

3. Persamaan Tingkat Energi dan Fungsi Gelombang untuk Potensial Manning Rosen dengan Faktor Sentrifugal ... 58

B. Pembahasan ... 70

BAB V. KESIMPULAN, IMPLIKASI, DAN SARAN ... 76

A. Kesimpulan ... 76

(11)

commit to user

xi

C. Saran ... 78

(12)

commit to user

xii

DAFTAR GAMBAR

Gambar 2.1.Koordinat Bola ... 13

Gambar 3.1. Diagram Penelitian ... 33

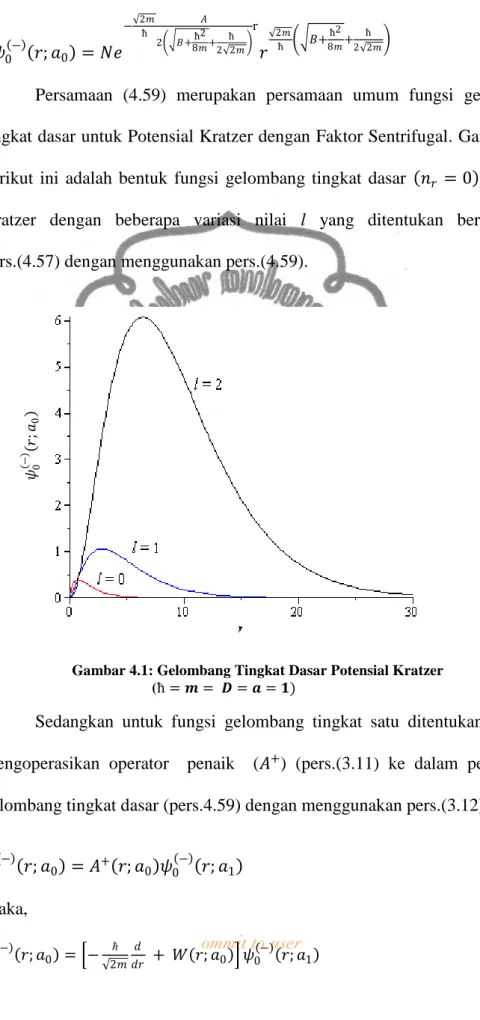
Gambar 4.1: Gelombang Tingkat Dasar Potensial Kratzer ... 47

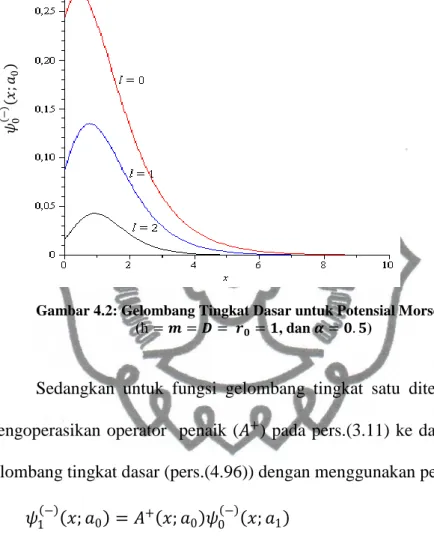
Gambar 4.2: Gelombang Tingkat Dasar untuk Potensial Morse ... 57

(13)

commit to user

xiii

DAFTAR TABEL

Tabel 4.1: Spektrum Energi Potensial Kratzer Molekul HCl... 46

Tabel 4.2: Spektrum Energi Potensial Morse Molekul HCl ... 56

(14)

commit to user

xiv

DAFTAR LAMPIRAN

Lampiran 1. Uraian Lengkap Penentuan Spektrum Energi Dan Fungsi Gelombang

Potensial Kratzer ... 81

Potensial Morse ... 95

(15)

commit to user

BAB I PENDAHULUAN

A. Latar Belakang

Persamaan Schrödinger dalam mekanika kuantum adalah persamaan

yang mendeskripsikan bagaimana keadaan kuantum (quantum state) suatu

sistem fisika yang berubah terhadap waktu. Persamaan ini merupakan hal

pokok dalam mekanika kuantum, sebagaimana hukum Newton dalam

mekanika klasik. Dalam mekanika kuantum, keadaan suatu sistem fisika

(partikel) diinterpretasikan melalui sebuah fungsi gelombang dan spektrum

energi (Griffiths, 1994). Berdasarkan kedua hal ini dapat diprediksikan

perilaku suatu sistem partikel dalam alam semesta.

Persamaan Schrödinger merupakan pilar penting dalam sistem

mekanika kuantum.Oleh karenanya teknik penyelesaian pada persamaan ini

perlu mendapatkan perhatian yang cukup serius, mengingat – meskipun

rumusan matematis dari persamaan ini relatif sederhana yang hanya berupa

persamaaan diferensial, namun pemecahan persamaan ini tetap membutuhkan

pengetahuan matematika lanjut yang rumit.

Terdapat beberapa jenis potensial dalam teori kuantum. Persamaan

dari potensial – potensial ini biasanya disajikan atau dinyatakan dalam bentuk

umum, artinya potensial terkait dalam keadaan normal, atau tanpa dipengaruhi

faktor lain, misalnya faktor gaya sentrifugal. Dalam keadaan kuantum tertentu,

(16)

commit to user

gaya sentrifugal ini tidak berpengaruh. Namun pada keadaan kuantum dengan

momentum angular 𝑙≠0, faktor ini tidak dapat diabaikan. Permasalahan yang muncul adalah bahwa penyelesaian eksak dari pesamaan Schrödinger untuk

beberapa jenis potensial dengan faktor sentrifugal hanya mungkin untuk

momentum angular 𝑙=0. Akan tetapi untuk𝑙≠0, penyelesaian hanya dapat dilakukan melalui sebuah metode pendekatan yang sesuai (Sameer, 2011).

Beberapa metode yang dapat digunakan diantaranya adalah metode klasik

WKB(Gallas, 1983), AIM (asymptotic iteration method) (Al-Dossary, 2007;

Aygun,et al., 2007); Bayrak, 2006; Bayrak, 2007), Nikivorov-Uvarov

(NU)(Sameer, 2011; Antia,et al, 2010), Ekspansi 1/N (Hammed, 2011),

Faktorisasi (Dong, 2007; Sadeghi, 2007), Supersimetri (SUSY) Mekanika

Kuantum (Cooper, et al, 2001) dan lain-lain.

Di antara metode-metode tersebut, metode SUSY Mekanika Kuantum

merupakan salah satu metode “layak” menjadi pilihan, karena selain – dengan menggunakan metode ini penyelesaian persamaan Schrödinger menjadi lebih

sederhana karena persamaan Schrödinger yang merupakan persamaan

differensial orde dua dapat difaktorkan menjadi persamaan differesial orde satu

– melalui sifat degenerasinya, dengan metode ini dapat diketahui spektrum energi terendah dan tertinggi dari suatu partikel dengan lebih akurat, yang tidak

semua metode dapat melakukannya, misalnya metode kuantisasi semiklasik

WKB. Sebagaimana diungkapkan oleh Anjana Sinha dan Rajumar

Roychoudhurydalam artikel mereka yaitu bahwa metode ini dapat memberikan

(17)

commit to user

cukup baik pada bilangan kuantum kecil. (Sinha, A and Roychoudhury,

R,2000).

Metode SUSY mekanika kuantum merupakan sebuah metode yang

dikembangkan seiring diperkenalkannya konsep simetri “baru” dalam fisika yaitu Supersimetri.Konsep ini telah mulai dikembangkan oleh para fisika

teoritis baru dalam rangka mendukung perkembangan riset di bidang fisika

pada saat ini yaitu mencari teori terpadu yang dapat menjelaskan perilaku

partikel dan interaksinya di alam semesta. Supersimetri merupakan sebuah

simetri yang dapat mempertukarkan antara boson dengan fermion atau

sebaliknya. Dimana boson adalah partikel yang dideskripsikan dengan sebuah

fungsi gelombang yang memiliki sifat simetri, sedangkan fermion merupakan

partikel yang dideskripsikan oleh sebuah fungsi gelombang yang memiliki sifat

antisimetri. Secara fisik, kedua jenis partikel ini sangat berbeda, dimana boson

memiki spin berupa kelipatan bilangan bulat, sedangkan fermion memiliki spin

berupa kelipatan setengah dari bilangan bulat. (Greiner, 1989)

SUSY merupakan simetri tingkat tinggi yang tak lazim mengingat

boson dan fermion memiliki perbedaan sifat yang mendasar. Misalnya, ketika

fermion mengikuti prinsip larangan pauli, yang menyatakan bahwa dua buah

atau lebih fermion identik tidak dapat menempati satu keadaan yang sama,

sebaliknya dua buah atau lebih boson identik dapat menempati keadaan yang

sama. Sehingga kecil kemungkinan untuk mempertukarkan keduanya.

(18)

commit to user

Pada awalnya, diyakini bahwa jika memang (partikel) supersimetri ini

terbukti ada di alam, maka simetri ini pasti sudah rusak secara spontan. Dalam

papernya, Edward Witten memaparkan secara khusus mekanisme perusakan

supersimetri (supersymetry breaking) ini. (Witten, 1981). Namun seiring

dengan perkembangan penelitian-penelitian yang telah dilakukan

terus-menerus oleh para ilmuwan fisika, akhirnya pada hari Rabu, 4 Juli 2012,

Ilmuwan CERN secara resmi melaporkan hasil sementara dari data tahun 2011

tentang keberadaan Higgs boson alias Partikel Tuhan, dalam sebuah konferensi

pers di Jenewa. Partikel baru dengan massa sekitar 125-126 gigaelectronvolts

(GeV) ini ditemukan lewat eksperimen ATLAS dan CMS menggunakan

akselerator partikel terbesar, Large Hadron Collider, di Jenewa, Swiss.(

tempo.co, 2012).

Higgs boson adalah istilah untuk suatu subatomik (Boson/partikel)

yang mengisi massa melalui interaksinya dengan kehadiran “medan lain” yang tersebar di jagat raya ini. Semakin berinteraksi, maka boson itu akan semakin

masif dan menjadi berisi dan berat. Oleh karena perannya sebagai pembentuk

materi, maka partikel dianggap sebagai perantara yang memungkinkan

terbentuknya bintang, planet dan juga kehidupan. Caranya adalah dengan

memberi massa untuk sejumlah partikel dasar. Pada mekanisme Higgs, massa

merupakan konsekuensi perusakan simetri di alam semesta yang dipicu

keberadaan partikel Higgs. Hal ini lalu berperan menimbulkan fenomena

(19)

commit to user

Konfirmasi eksistensi Higgs boson juga akan membantu menjelaskan

bagaimana menyatunya dua interaksi dasar semesta, yaitu gaya

elektromagnetik yang menguasai interaksi antara partikel bermuatan dan gaya

nuklir lemah yang bertanggung jawab dalam penguraian

radioaktif.Sebagaimana diketahui bahwa setiap gaya di alam semesta

berhubungan dengan sebuah partikel. Partikel yang terikat dengan gaya

elektromagnetik adalah photon. Sementara gaya nuklir lemah diasosiasikan

dengan partikel boson W dan Z. Mekanisme Higgs diperkirakan sebagai alasan

bisa terjadinya hal tersebut. (tempo.co, 2012)

Dampak lain dari penemuan Partikel Tuhan ini adalah supersimetri.

Dalam supersimetri, setiap partikel memiliki partikel “superpartner” dengan

sedikit perbedaan karakterstik. Supersimetri ini menarik karena dapat

membantu menyatukan beberapa gaya lain di alam semesta. Bahkan,

menawarkan kandidat partikel yang membentuk materi gelap (dark matter).

Sementara itu, partikel yang diumumkan para ilmuwan di CERN memiliki

rentang massa rendah pada 125.3 Gev. Ini merupakan tanda menuju

supersimetri. Jika partikel Higgs boson ditemukan pada massa rendah, ini akan

membuat supersimetri menjadi sebuah teori yang layak.

Meskipun temuan ini masih bersifat sementara, namun layaklah

kiranya jika konsep supersimetri menjadi mendapat perhatian “kembali” dari

para fisikawan untuk terus mengembangkan teori fisika yang terkait dengan

SUSY, termasuk juga dalam teori mekanika kuantum. Berbagai masalah dalam

(20)

commit to user

Sebagaimana dipaparkan oleh Cooper, et al., dalam bukunya (Cooper, et al,

2001) bahwa beberapa aplikasi konsep supersimetri dalam mekanika kuantum,

salah satunya adalah pemecahan masalah potensial shape invariance. Secara

spesifik Metin Aktas dalam tesisnya (Aktas, 2005) memaparkan aplikasi

supersimetri dalam mekanika kuantum yaitu dalam penyelelesaian persamaan

Schrödinger untuk beberapa potensial.

Dalam sistem SUSY mekanika kuantum terdapat beberapa metode

menentukan spektrum energi diantaranya adalah metode operator supersimetri

(operator tangga), metode pendekatan variasi, 𝛿-ekspansi, teknik 1/N ekspansi, serta metode pengembangan dari WKB yaitu Supersimetri WKB atau SWKB,

dan lain-lain (Aktas, 2005). Metode-metode ini memiliki tingkat kerumitan

masing-masing.

Sampai saat ini sudah ada beberapa artikel atau makalah yang

membahas mengenai penerapan masing-masing metode supersimetri tersebut

di atas, namun lebih sering digunakan secara terpisah. Umumnya, para peneliti

sebelumnya menggunakan satu metode untuk menyelesaikan beberapa

potensial, seperti – Anjana Sinha dan Rajumar Roychoudhury, mereka

menyelesaikan persamaan Schrödinger untuk jenis potensial Potensial

Poschl-Teller dan potensial Dua Trigonometri dengan menggunakan metode SWKB

saja (Sinha, Aand Roychoudhury, R, 2000). Atau, Metin Aktas, menyelesaikan

persamaan Schrödinger untuk jenis potensial Woods-Saxon, Morse, Hulthen,

dan lain-lain dengan menggunakan metode Operator Supesimetri (Aktas,

(21)

commit to user

memberikan hasil yang sama, ataukah berbeda. Selain itu, belum banyak juga

artikel yang membahas secara khusus mengenai cara menyelesaikan

masing-masing jenis potensial – mengingat terdapat beberapa bentuk persamaan

potensial dalam mekanika kuantum, misalnya bentuk radial biasa, bentuk

eksponensial, trigonometri, hiperbolik, dan lain-lain, maka perlu adanya contoh

khusus langkah-langkah dalam menyelesaikan persamaan Schrödinger untuk

masing-masing jenis potensial tersebut.

B. Rumusan Masalah

Berdasarkan uraian dari latar belakang masalah di atas, maka dapat

dituliskan rumusan masalahnya sebagai berikut:

1. Bagaimana persamaan spektrum energi dari beberapa jenis potensial

shape invariance yang ditentukan dengan menggunakan metode

Supersimetri Mekanika Kuantum (SUSYQM)

2. Bagaimana persamaan fungsi gelombang dari beberapa jenis potensial

shape invariance yang ditentukan dengan menggunakan metode

Supersimetri Mekanika Kuantum (SUSYQM)

C. Tujuan Penelitian

(22)

commit to user

1. Menentukan persamaan spektrum energi dari beberapa jenis potensial

shape invariance dengan menggunakan metode Supersimetri Mekanika

Kuantum (SUSYQM)

2. Menentukan persamaan fungsi gelombang dari beberapa jenis potensial

shape invariance dengan menggunakan metode Supersimetri Mekanika

Kuantum (SUSYQM)

D. Batasan Masalah

Pembahasan pada penelitian ini dibatasi pada:

1. Persamaan spektrum energi ditentukan dengan menggunakan metode

Operator Supersimetri (operator tangga) dan Metode Kuantisasi

Supersimetri – WKB (SWKB). Sedangkan fungsi gelombang ditentukan

dengan menggunakan metode operator supersimetri (operator tangga).

2. Jenis potensial shape invariance yang dibahas adalah Potensial Kratzer

untuk tipe radial biasa, Potensial Morse untuk tipe eksponensial, dan

Potensial Manning Rosen untuk tipe Hiperbolik.

3. Semua fungsi gelombang yang ditentukan dalam penelitian ini belum

ternormalisasi (N=1).

E. Manfaat Penelitian 1. Manfaat Teoritis

(23)

commit to user

Langkah-langkah penyelesaian persamaan Schrödingerdengan

menggunakan Metode Supersimetri Mekanika Kuantum (SUSYQM),

khususnya metode Operator Supersimetri dan Metode kuantisasi

SWKB untuk jenis potensial dengan bentuk persamaan radial biasa

(Potensial Kratzer), bentuk persamaan eksponensial (Potensial Morse),

dan bentuk persamaan hiperbolik (Potensial Manning Rosen) dapat

digunakan sebagai alternatif contoh untuk menyelesaikan persamaan

Schrödinger untuk jenis potensial yang lain yang bertipe sama.

2. Manfaat Praktis

Solusi dari persamaan Schrödinger untuk jenis potensial

terkait yang berupa spektrum energi dan fungsi gelombang dapat

digunakan untuk meramalkan perilaku sistem dan interaksinya dengan

sistem lain sehinggadapat memberikan struktur sistem fisika yang utuh

(24)

commit to user

BAB II DASAR TEORI

A. Persamaan Schrödinger

Persamaan Schrödinger dalam mekanika kuantum adalah persamaan

yang mendeskripsikan bagaimana keadaan kuantum (quantum state) suatu

sistem fisika yang berubah terhadap waktu. Dalam mekanika kuantum,

keadaan suatu sistem fisika (partikel) diinterpretasikan melalui sebuah fungsi

gelombang dan spektrum energi (Griffiths, 1994). Pada prinsipnya, energi

partikel dalam mekanika kuantum adalah sama dengan energi mekanik atau

energi total dalam mekanika klasik, hanya saja variabel-variabel dalam

mekanika klasik berperan sebagai operator (Suparmi, 2011).

Apabila sebuah partikel yang memiliki massa m yang bergerak

sepanjang sumbu x dan mengalami gaya konservatif F (x,t), dimana F (x,t)

dapat dituliskan sebagai gradient dari energi potensial V (x,t). Secara klasik,

energi total yang dimiliki partikel tersebut dapat dituliskan sebagai, (Griffiths,

1994)

𝐸 = 𝑝2

2𝑚+ 𝑉 𝑥, 𝑡 (2.1)

dimana 𝑝 2

2𝑚 merupakan energi kinetik partikel, dan p adalah momentum

partikel.

Dalam pendekatan mekanika kuantum, variabel-variabel pada

pers.(2.1) diubah menjadi operator dimana, 𝐸 = 𝑖ћ 𝜕

𝜕𝑡 dan 𝑝 = −𝑖ћ 𝜕 𝜕𝑥.

(25)

commit to user

11

Selanjutnya operator-operator ini dioperasikan terhadap fungsi gelombang

𝜓(𝑥, 𝑡), sehingga pers. (2.1) dapat ditulis, (Suparmi, 2011) 𝑖ћ∂𝜓 𝑥,𝑡 ∂𝑡 = − ћ 2𝑚 𝜕2 𝜕𝑥2𝜓 𝑥, 𝑡 + 𝑉 𝑥, 𝑡 𝜓 𝑥, 𝑡 (2.2) Pers.(2.2) merupakan persamaan Schrödinger satu dimensi fungsi

posisi dan waktu. Persamaan ini dapat diuraikan menjadi fungsi posisi saja

atau fungsi waktu saja dengan cara menyelesaikan persamaan differensial

orde dua tersebut dengan menggunakan metode pemisahan variabel. Dengan

memisalkan 𝜓 𝑥, 𝑡 = 𝜓 𝑥 𝑇 𝑡 , maka pers.(2.2) dapat ditulis, 𝜓(𝑥)𝑖ћ ∂ ∂𝑡𝑇 𝑡 = − ћ 2𝑚𝑇 𝑡 𝜕2 𝜕𝑥2𝜓(𝑥) + 𝑉 𝑥, 𝑡 𝜓(𝑥)𝑇 𝑡 (2.3) jika masing-masing ruas dibagi dengan 𝜓 𝑥 𝑇 𝑡 , maka

1 𝑇 𝑡 𝑖ћ ∂ ∂𝑡𝑇 𝑡 = − ћ 2𝑚 1 𝜓 𝑥 𝜕2 𝜕𝑥2𝜓 𝑥 + 𝑉 𝑥 = 𝐸 (2.4) Berdasarkan pers.(2.4) dapat diperoleh,

𝑇 𝑡 = 𝑁𝑒ћ𝑖𝐸𝑡 _(2.5a)

dengan N adalah konstanta normalisasi. Dan,

− ћ

2𝑚 𝜕2

𝜕𝑥2𝜓 𝑥 + 𝑉 𝑥 𝜓 𝑥 = 𝐸𝜓 𝑥 (2.5b)

Pers.(2.5b) merupakan persamaan Schrödinger stasioner satu dimensi

bebas waktu. Persamaan ini juga dapat dinyatakan dalam bentuk,

𝐻𝜓 𝑥 = 𝐸𝜓 𝑥 (2.6)

dengan H adalah operator Hamiltonian[Griffiths, 1994].

Pers.(2.6) ini sering disebut sebagai persamaan nilai eigen

(eigenvalue), dimana E disebut eigen nilai (eigen value) dan 𝜓 merupakan eigen fungsi (eigen function) (Greiner, 1989). Persamaan ini dapat diartikan

(26)

commit to user

bahwa jika operator hamiltonian dioperasikan/ bekerja pada suatu fungsi

gelombang tertentu maka akan menghasilkan kembali fungsi gelombang

tersebut yang dikalikan suatu konstanta E.

Berdasarkan pers. (2.5b) dan (2.6) Operator Hamiltonian (H) yang

merupakan energi total partikel untuk sistem satu dimensi dapat dituliskan

sebagai,

𝐻 = − ћ

2𝑚 𝜕2

𝜕𝑥2+ 𝑉 𝑥 (2.7)

Dengan membandingkan pers.(2.1) dan pers.(2.7) dapat dilihat bahwa

persamaan energi total (E) diubah menjadi Operator Hamiltonian (H) dalam

mekanika kuantum. Prinsip ini sering disebut prinsip korespondensi.

(Suparmi, 2011)

B. Persamaan Schrödinger dalam Ruang Tiga Dimensi

Persamaan Schrödinger untuk sistem satu dimensi yang dinyatakan

dalam pers.(2.5b) dapat diperluas ke dalam sistem tiga dimensi yang dapat

dituliskan sebagai berikut,(Griffiths, 1994).

− ћ2

2𝑚

2_{𝜓 + 𝑉𝜓 = 𝐸𝜓} _(2.8)

Dimana  adalah Laplasian dalam koordinat kartesian.

Ruang tiga dimensi umumnya digambarkan sebagai ruang pada

permukaan bola. Dalam koordinat bola (𝑟, 𝜃, 𝜑), Laplasian () dinyatakan sebagai, 2 ₌ 1 𝑟2 𝜕 𝜕𝑟 𝑟 2 𝜕 𝜕𝑟 + 1 𝑟2_{sin 𝜃} 𝜕 𝜕𝜃 sin 𝜃 𝜕 𝜕𝜃 + 1 𝑟2_sin2_𝜃 𝜕2 𝜕𝜑2 (2.9)

(27)

commit to user

13

Sehingga pers.(2.8) dapat ditulis kembali menjadi,

− ћ2 2𝑚 1 𝑟2 𝜕 𝜕𝑟 𝑟 2 𝜕𝜓 𝜕𝑟 + 1 𝑟2_{sin 𝜃} 𝜕 𝜕𝜃 sin 𝜃 𝜕𝜓 𝜕𝜃 + 1 𝑟2_sin2_𝜃 𝜕2𝜓 𝜕2 + 𝑉𝜓 = 𝐸𝜓 (2.10) Pers. (2.10) ini merupakan persamaan Schrödinger sistem tiga dimensi

bebas waktu. Umumnya energi potensial adalah fungsi yang hanya tergantung

pada jarak partikel terhadap titik pusat (r) saja, sedangkan bagian sudut

biasanya sama (tidak berubah) untuk semua potensial yang bersimetri bola.

Oleh sebab itu, untuk menyederhanakan penyelesaian, maka terlebih dahulu

persamaan dipisahkan menjadi dua, yaitu bagian radial dan bagian sudut

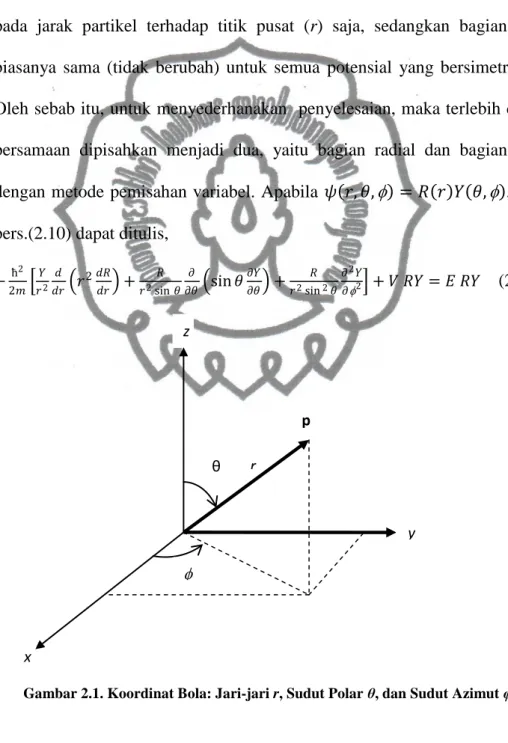
dengan metode pemisahan variabel. Apabila 𝜓 𝑟, 𝜃, = 𝑅 𝑟 𝑌 𝜃, , maka pers.(2.10) dapat ditulis,

−_2𝑚ћ2 _𝑟𝑌₂_𝑑𝑟𝑑 𝑟2 𝑑𝑅_𝑑𝑟 +_𝑟₂_{sin 𝜃}𝑅 _𝜕𝜃𝜕 sin 𝜃𝜕𝑌_𝜕𝜃 +_𝑟₂_sin𝑅₂_𝜃𝜕2𝑌

𝜕2 + 𝑉 𝑅𝑌 = 𝐸 𝑅𝑌 (2.11)

z

Gambar 2.1. Koordinat Bola: Jari-jari r, Sudut Polar θ, dan Sudut Azimut φ x p r θ y 

(28)

commit to user

Jika masing-masing ruas dibagi dengan YR, dan mengalikannya

dengan −2𝑚 𝑟2 ћ2 maka diperoleh, 1 𝑅 𝑑 𝑑𝑟 𝑟 2 𝑑𝑅 𝑑𝑟 − 2𝑚 𝑟2 ћ2 𝑉 𝑟 − 𝐸 + 1 𝑌 1 sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕𝑌 𝜕𝜃 + 1 sin2_𝜃 𝜕2_𝑌 𝜕2 = 0 (2.12)

Dapat dilihat pada pers.(2.12) bahwa suku pertama hanya bergantung

pada r, dan suku kedua hanya bergantung pada sudut 𝜃 dan . Dapat terlihat juga bahwa kedua suku identik, sehingga keduanya harus sama dengan

konstanta. Dalam kasus ini konstanta pemisahan variabel ini definisikan

sebagai faktor momentum anguler, yaitu 𝑙 𝑙 + 1 , Sehingga apabila kedua suku pada pers. (2.12) dipisahkan, maka diperoleh dua persamaan

differensial orde dua, yaitu fungsi radial dan fungsi sudut. Dimana fungsi

radial dituliskan sebagai,

1 𝑅 𝑑 𝑑𝑟 𝑟 2 𝑑𝑅 𝑑𝑟 − 2𝑚 𝑟2 ћ2 𝑉 𝑟 − 𝐸 = 𝑙 𝑙 + 1 (2.13)

Dan fungsi sudut dituliskan sebagai,

1 𝑌 1 sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕𝑌 𝜕𝜃 + 1 sin2𝜃 𝜕2_𝑌 𝜕2 = −𝑙 𝑙 + 1 (2.14)

a. Persamaan Schrödinger Pada Bagian Radial

Pers.(2.13), yaitu persamaan Schrödinger untuk sistem tiga dimensi

pada bagian radial dapat disederhanakan dengan memisalkan fungsi

gelombang baru,(Suparmi, 2011) 𝑅 =𝜓 𝑟 (2.15) Sehingga diperoleh, 𝑑𝑅 𝑑𝑟 = 1 𝑟 𝑑𝜓 𝑑𝑟 − 𝜓 𝑟2 dan 1 𝑅 𝑑 𝑑𝑟 𝑟 2 1 𝑟 𝑑𝜓 𝑑𝑟 − 𝜓 𝑟2 = 𝑟 𝑅 𝑑2𝜓 𝑑𝑟2. (2.16)

(29)

commit to user

15

Jika pers.(2.16) disubtitusikan ke pers.(2.13) dan dengan penjabaran

sederhana maka persamaan Scrhödinger bagian radial dapat ditulis kembali

menjadi 𝑟 𝑅 𝑑2𝜓 𝑑𝑟2 − 2𝑚 𝑟2 ћ2 𝑉 𝑟 − 𝐸 = 𝑙 𝑙 + 1 (2.17) Atau, 𝑟 𝑅 𝑑2𝜓 𝑑𝑟2 + 2𝑚 𝑟2 ћ2 𝐸 − 2𝑚 𝑟2 ћ2 𝑉 𝑟 = 𝑙 𝑙 + 1 (2.18)

Jika masing-masing ruas pada pers.(2.18) dikalikan dengan ћ 2_𝑅

2𝑚 𝑟2 , dengan

𝑅 =𝜓

𝑟 maka persamaan menjadi,

ћ2 2𝑚𝑟 𝑑2𝜓 𝑑𝑟2 + 𝜓 𝑟 𝐸 − 𝜓 𝑟 𝑉 𝑟 = ћ2 2𝑚 𝑟2 𝜓 𝑟 𝑙 𝑙 + 1 (2.19) Sehingga diperoleh, ћ2 2𝑚 𝑑2𝜓 𝑑𝑟2 + 𝐸𝜓 − 𝑉 𝑟 𝜓 = 𝑙 𝑙 + 1 ћ2 2𝑚 𝑟2𝜓 (2.20)

Atau dapat ditulis,

− ћ2 2𝑚 𝑑2𝜓 𝑑𝑟2 + 𝑉 𝑟 + ћ2 2𝑚 𝑙 𝑙+1 𝑟2 𝜓 = 𝐸𝜓 (2.21) Dimana, 𝑉𝑒𝑓𝑓 = 𝑉 𝑟 + ћ2 2𝑚 𝑙 𝑙+1 𝑟2 (2.22)

𝑉_𝑒𝑓𝑓 didefinisikan sebagai potensial efektif, dan ћ 2

2𝑚 𝑙 𝑙+1

𝑟2 sebagai faktor gaya

sentrifugal. Dengan ћ = ℎ

2𝜋 = 1,054573 × 10

−34_{𝐽𝑠, dan} _𝑙 _merupakan

bilangan kuantum orbital (𝑙 = 0, 1, 2, … ), sedangkan m adalah massa atom tereduksi. (Griffiths, 1994).

(30)

commit to user

Dapat dilihat bahwa pers.(2.21) ini identik dengan persamaan

Scrhödinger untuk sistem satu dimensi (2.5b).

b. Persamaan Schrödinger Pada Bagian Sudut

Pers.(2.14) merupakan persamaan Schrödinger bagian sudut

(angular). Pada bagian ini fungsi gelombang 𝜓 hanya tergantung pada sudut 𝜃 dan  saja. Jika masing-masing ruas dikalikan dengan 𝑌 sin2𝜃 diperoleh,

sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕𝑌 𝜕𝜃 + 𝜕2𝑌 𝜕2 = −𝑙 𝑙 + 1 𝑌sin2𝜃 (2.23) Dapat dilihat pada pers.(2.23) persamaan masih tergantung pada dua

variabel yaitu 𝜃 dan . Sebagaimana sebelumnya, maka dilakukan pemisahan

variabel,

𝑌 𝜃, = 𝜃   (2.24)

Jika persamaan ini dimasukkan ke pers.(2.23) dan dengan membagi

masing-masing ruas dengan  diperoleh,

1  sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕 𝜕𝜃 + 𝑙 𝑙 + 1 sin 2_{𝜃 +}1  𝜕2_ 𝜕2 = 0 (2.25)

Dapat dilihat pada pers.(2.25) persamaan terbagi menjadi dua, fungsi

yang pertama hanya bergantung pada variabel 𝜃, dan fungsi yang kedua hanya tergantung pada  saja. Sehingga keduanya harus sama dengan konstanta. Konstanta pemisahan ini didefinisikan sebagai bilangan kuantum

magnetik, 𝑚2_{; sehingga diperoleh,} 1  sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕 𝜕𝜃 + 𝑙 𝑙 + 1 sin 2_{𝜃 = 𝑚}2 _(2.26)

(31)

perpustakaan.uns.ac.id digilib.uns.ac.id commit to user 17 Atau, sin 𝜃  𝑑 𝑑𝜃 sin 𝜃 𝑑 𝑑𝜃 + 𝑙 𝑙 + 1 sin 2_{𝜃 − 𝑚}2 _{= 0} _(2.27) Dan 1  𝜕2 𝜕2 = −𝑚2 atau 1  𝜕2 𝜕2 + 𝑚2 = 0 (2.28)

Pers.(2.27) merupakan persamaan polar, dan pers.(2.28) merupakan

persamaan azimut. (Griffiths, 1994).

Apabila pers.(2.27) dikalikan dengan 

sin2_𝜃 maka diperoleh,

1 sin 𝜃 𝑑 𝑑𝜃 sin 𝜃 𝑑 𝑑𝜃 + 𝑙 𝑙 + 1 − 𝑚2 sin2_𝜃  = 0 (2.29) Jika dimisalkan  = 𝑄 sin 𝜃 , dan 𝑑 𝑑𝜃 = 1 𝑠𝑖𝑛𝜃 𝑑𝑄 𝑑𝜃 − 1 2 𝑐𝑜𝑠𝜃 sin3_𝜃𝑄, maka, 1 𝑠𝑖𝑛𝜃 𝜕 𝜕𝜃 𝑠𝑖𝑛𝜃 𝑑 𝑑𝜃 = 1 sin 𝜃 𝜕 𝜕𝜃 𝑠𝑖𝑛𝜃 𝑑𝑄 𝑑𝜃 − 1 2 𝑐𝑜𝑠𝜃 𝑠𝑖𝑛𝜃 𝑄 = 1 𝑠𝑖𝑛𝜃 𝑑2𝑄 𝑑𝜃2+ 1 2 𝑄 𝑠𝑖𝑛𝜃 + 1 4 𝑐𝑜 𝑠2𝜃 𝑠𝑖𝑛𝜃 5𝑄 (2.30) Jika pers. (2.30) ini disubtitusikan ke pers.(2.29) maka diperoleh,

1 𝑠𝑖𝑛𝜃 𝑑2𝑄 𝑑𝜃2+ 1 2 𝑄 𝑠𝑖𝑛𝜃 + 1 4 𝑐𝑜 𝑠2𝜃 𝑠𝑖𝑛𝜃 5𝑄 + 𝑙 𝑙 + 1 𝑄 𝑠𝑖𝑛𝜃 − 𝑚2 𝑠𝑖𝑛2_𝜃 𝑄 𝑠𝑖𝑛𝜃 = 0 (2.31) Atau, 𝑑2𝑄 𝑑𝜃2+ 𝑄 2 + 1 4 𝑐𝑜 𝑠2𝜃 𝑠𝑖𝑛2_𝜃𝑄 + 𝑙 𝑙 + 1 𝑄 − 𝑚2 𝑠𝑖𝑛2_𝜃𝑄 = 0 (2.32) Karena 𝑐𝑜𝑠2𝜃 = 1 − 𝑠𝑖𝑛2𝜃 , maka melaui penjabaran sederhana diperoleh,

𝑑2𝑄 𝑑𝜃2+ 1 4 𝑠𝑖𝑛2_𝜃𝑄 − 𝑚2 𝑠𝑖𝑛2_𝜃𝑄 + 𝑙 + 1 2 2 𝑄 = 0 (2.33)

Jika masing-masing dikalikan − ћ 2 2𝑚 maka, − ћ2 2𝑚 𝑑2𝑄 𝑑𝜃2− ћ2 2𝑚 1 4 𝑠𝑖𝑛2_𝜃𝑄 − ћ2 2𝑚 𝑙 + 1 2 2 𝑄 + ћ2 2𝑚 𝑚2 𝑠𝑖𝑛2_𝜃𝑄 = 0 (2.34)

(32)

commit to user

Atau dapat ditulis sebagai berikut,

− ћ2 2𝑚 𝑑2_𝑄 𝑑𝜃2+ ћ2 2𝑚 𝑚2− 1 4 𝑠𝑖𝑛2_𝜃 𝑄 = ћ2 2𝑚 𝑙 + 1 2 2 𝑄 (2.35)

Dimana 𝑄 merupakan fungsi gelombang bagian polar.

Dengan demikian persamaan Schödinger untuk sistem tiga dimensi

yang merupakan koordinat bola yang dinyatakan dalam pers.(2.10) dapat

dipisahkan menjadi tiga persamaan diferensial orde dua yang masing-masing

hanya bergantung pada satu variabel saja.

C. Supersimetri Mekanika Kuantum (SUSYQM)

Pemeran utama supersimetri mekanika kuantum adalah

operator-operator supermuatan. Witten mendefinisikan sistem supersimetri mekanika

kuantum sebagai sistem yang terdiri dari operator supermuatan 𝑄𝑖 yang

komut dengan Hamiltonian Supersimetri (𝐻_𝑆𝑆),(Witten, 1981)

𝑄_𝑖, 𝐻_𝑆𝑆 = 0 dan i = 1, 2, …,N (2.36) dimana N adalah banyaknya generator dan memenuhi hubungan anti

komutasi,

𝑄𝑖,𝑄𝑗 = 𝛿𝑖𝑗𝐻𝑠𝑠 (2.37)

Hamiltonian supersimetri (𝐻_𝑠𝑠) didefinisikan sebagai jumlah kuadrat dari operator supermuatan (𝑄_𝑖)

𝐻_𝑠𝑠 = 2𝑄₁2 = 2 𝑄₂2 (2.38)

Untuk sistem SUSY yang paling sederhana, N=2, dengan operator

(33)

commit to user

19

mempunyai spin 1

2 yang bergerak pada garis lurus. Dalam sistem yang

sederhana ini, 𝑄₁ dan 𝑄₂ didefinisikan sebagai 𝑄₁= 1 2 𝜎1 𝑝 2𝑚+ 𝜎2W 𝑥 dan, 𝑄2 = 1 2 𝜎2 𝑝 2𝑚− 𝜎1𝑊 𝑥 (2.39)

dimana σ1 dan σ2 adalah matriks dari Pauli.[Suparmi, 2011]

Hss adalah supersimetri Hamiltonian, 𝑝 = −𝑖ℏ 𝑑

𝑑𝑥, adalah

momentum linear (momentum bosonik), x adalah koordinat bosonik, W(x)

adalah superpotensial bosonik. Dengan menggunakan pers.(2.37) dapat

ditunjukkan bahwa 𝐻_𝑠𝑠 = − ℏ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑊 2_{(𝑥) +} ℏ 2𝑚 𝑑𝑊 (𝑥) 𝑑𝑥 0 0 − ℏ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑊2(𝑥) − ℏ 2𝑚 𝑑𝑊 (𝑥) 𝑑𝑥 = 𝐻+ 0 0 𝐻₋ (2.40) dimana, 𝐻₋= −ℏ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑊2(𝑥) − ℏ 2𝑚 𝑑𝑊 (𝑥) 𝑑𝑥 , dan (2.40a) 𝐻₊= − ℏ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑊 2_{(𝑥) +} ℏ 2𝑚 𝑑𝑊 (𝑥) 𝑑𝑥 (2.40b)

Sehingga dapat dikatakan Persamaan (2.36) menyebabkan timbulnya

energi terdegenerasi 𝐻−dan 𝐻+, yang merupakan SUSY partner Hamiltonian

Fermionik (penurun) dan Bosonik (penaik),dan keduanya juga dituliskan

sebagai 𝐻_𝑠𝑠. Dengan demikian persamaan Schrodinger standard dapat dinyatakan dalam Hamiltonian SUSY sebagai berikut,

𝐻₋= −ℏ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑉−(𝑥) , dengan 𝑉− 𝑥 = 𝑊2 𝑥 − ћ 2𝑚𝑊 ′_𝑥 _(2.41) Dan,

(34)

commit to user 𝐻₊= −ℏ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑉+(𝑥) ,dengan 𝑉+ (𝑥) = 𝑊2 𝑥 + ћ 2𝑚𝑊 ′_𝑥 _(2.42)

Dimana 𝑉₋ 𝑥 dan𝑉+ 𝑥 disebutpasangan potensial supersimetri, dan 𝑊 𝑥

adalah Superpotensial. Sedangkan 𝑊′ 𝑥 merupakan turunan pertama dari 𝑊 𝑥 .

Berdasarkan pers.(2.40a) dan (2.40b) masing-masing persamaan

Hamiltonian SUSY dapat difaktorkan sebagai berikut, untuk Hamiltonian

penurun dan Hamiltonian penaik berturut-turut dinyatakan sebagai berikut,

𝐻₋= 𝐴+_{𝐴, dan 𝐻} += 𝐴𝐴+ (2.43) Dimana, 𝐴+_{= −} ћ 2𝑚 𝑑 𝑑𝑥 + 𝑊 𝑥 dan 𝐴 = ћ 2𝑚 𝑑 𝑑𝑥 + 𝑊 𝑥 (2.44)

Dengan, 𝐴+ disebut operator penaik (raising operator) , dan 𝐴 sebagai operator penurun (lowering operator). (Witten, 1981; Rodrigues, 2002; Fabre

and Odelin, 2010)

Berdasarkan sifat dari operator penurun (A), yaitu apabila operator

penurun (A) dioperasikan fungsi gelombang tingkat dasar 𝜓₀ − , maka akan sama dengan nol (karena sudah tidak ada lagi fungsi gelombang di bawah fungsi gelombang tingkat dasar) (Cooper,et al., 2001),

𝐴𝜓₀ − = 0 (2.45) Atau, ћ 2𝑚 𝑑 𝑑𝑥 + 𝑊 𝑥 𝜓0 − = 0 (2.46) Sehingga diperoleh, 𝜓₀ − 𝑥 = 𝑁 exp − 2𝑚 ћ 𝑊 𝑥 𝑑𝑥 x (2.47)

(35)

commit to user

21

dengan N adalah faktor normalisasi. Dan,

𝑊 𝑥 = − ћ 2𝑚 𝑑𝜓₀ − 𝜓₀ − = − ћ 2𝑚𝑙𝑛𝜓0 − (2.48)

D. Potensial Shape Invariance

Sepasang potensial supersimetri (SUSY), yaitu 𝑉₋ 𝑥 dan 𝑉₊ 𝑥 dapat dikatakan shape invariance jika kedua potensial tersebut memiliki

bentuk yang sama, hanya dibedakan oleh sebuah parameter yang ada pada

mereka. Ditinjau pasangan potensial 𝑉_± (𝑥; 𝑎_𝑗) dimana 𝑎_𝑗 adalah sebuah set dari parameter, sepasang potensial dikatakan shape invariance bila sepasang

potensial ini memenuhi syarat berikut: (Cooper, et al., 2001)

𝑉₊ 𝑥; 𝑎_𝑗 = 𝑉₋ 𝑥; 𝑎_{𝑗 +1} + 𝑅 𝑎_{𝑗 +1} (2.49) Dengan, 𝑉₊ 𝑥; 𝑎_𝑗 = 𝑊2 𝑥, 𝑎_𝑗 + ħ 2𝑚𝑊 ′_{𝑥, 𝑎} 𝑗 (2.49a) 𝑉− 𝑥; 𝑎𝑗 = 𝑊2 𝑥, 𝑎𝑗 − ħ 2𝑚𝑊 ′_{𝑥, 𝑎} 𝑗 (2.49b)

Dimana j = 0,1,2,…, sedangkan parameter a ditentukan secara

rekursif (berturutan), 𝑎_{𝑗 +1} = 𝑓(𝑎_𝑗) dan 𝑅(𝑎_𝑗) adalah konstanta yang tidak bergantung dengan x.

Hubungan antara Hamiltonian Standard (pers.2.7) dan Hamiltonian

SUSY (2.41) dinyatakan sebagai, (Anjos, et. al., (2008), Suparmi, (2011)

𝐻 = 𝐻₋+ 𝐸₀ = − ħ2

2𝑚 𝑑2

𝑑𝑥2+ 𝑉− 𝑥; 𝑎0 + 𝐸0 (2.50) Maka berdasarkan persamaan eigen nilai (pers.2.6) diperoleh,

(36)

commit to user

Dimana 𝐸₀ merupakan energi tingkat dasar pada pasangan Hamiltonian penurun.

Dengan membandingkan pers.(2.7) dan(2.50) diperoleh hubungan

antara 𝑉 𝑥 dan 𝑉− 𝑥 sebagai berikut,

𝑉 𝑥 = 𝑉₋ 𝑥; 𝑎0 + 𝐸0 = 𝑊2 𝑥, 𝑎0 − ħ 2𝑚𝑊

′_{𝑥, 𝑎}

0 + 𝐸0 (2.52)

Dimana 𝑉 𝑥 sering dinyatakan sebagai Potensial Efektif (𝑉𝑒𝑓𝑓). Sedangkan

𝑊 𝑥 ditentukan dengan dugaan/ perkiraan secara intelektual berdasarkan bentuk potensial efektif sistem terkait.

Berdasarkan sifat shape invariance, dapat ditentukan spektrum

energi dari pasangan potensial. Untuk tujuan tersebut, berikut akan di

konstruksi sederet Hamiltonian yaitu 𝐻_𝑘, dimana k = 0, 1, 2,… Dengan mengulang prosedur sifat shape invariance, diperoleh,

𝐻_𝑘 = − ħ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑉− 𝑥; 𝑎𝑘 + 𝑅(𝑎𝑖) 𝑘 𝑖=1 (2.53)

Dimana 𝑎_𝑘 = 𝑓𝑘−1 𝑎₁ , 𝑓𝑘−1_{berarti fungsi tersebut diaplikasikan}_{𝑘 − 1}

kali. Jika diambil 𝑘  𝑘 + 1 pada pers. (2.53), maka diperoleh 𝐻_𝑘 = − ħ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑉− 𝑥; 𝑎𝑘+1 + 𝑅(𝑎𝑖) 𝑘 𝑖=1 = −ħ2 2𝑚 𝑑2 𝑑𝑥2+ 𝑉+ 𝑥; 𝑎𝑘 + 𝑅(𝑎𝑖) 𝑘−1 𝑖=1 (2.54)

Di sini 𝐻𝑘 dan 𝐻𝑘+1 merupakan pasangan Hamiltonian SUSY

dimana keduanya memiliki spektrum energi yang sama kecuali untuk

spektrum tingkat dasar, yang hanya dimiliki oleh Hamiltonian penurun saja.

Berdasarkan pers.(2.50) dan (2.54), dapat diketahui bahwa spektrum

(37)

commit to user

23

𝐸_𝑛(−) = 𝑛_𝑘=1𝑅(𝑎_𝑘) (2.55) Maka spektrum energi dari Hamiltonian dengan potensial 𝑉 𝑥

adalah

𝐸𝑛 = 𝐸𝑛 (−)

+ 𝐸0 = 𝑛𝑘=1𝑅(𝑎𝑘) + 𝐸0 (2.56)

Fungsi gelombang 𝜓_𝑛−_{𝑥; 𝑎}

0 dapat dijabarkan dari fungsi

gelombang keadaan dasar 𝜓₀−_{𝑥; 𝑎}

0 dengan metode operator yang diperoleh

dari operasi berantai operator penaik 𝐴+terhadap gelombang tingkat dasar, 𝜓𝑛− 𝑥; 𝑎0 ~ 𝐴+ 𝑥; 𝑎0 𝐴+ 𝑥; 𝑎1 … 𝐴+ 𝑥; 𝑎𝑛−1 𝜓0− 𝑥; 𝑎𝑛 (2.57)

atau

𝜓_𝑛−_{𝑥; 𝑎}

0 ~𝐴+ 𝑥; 𝑎0 𝜓𝑛−1− 𝑥; 𝑎1 (2.58)

Dengan analog diperoleh

𝜓_{𝑛 +1}− 𝑥; 𝑎₀ ~𝐴+_{𝑥; 𝑎}

0 𝜓𝑛− 𝑥; 𝑎1 (2.59)

E. Formula Kuantisasi Supersimetri – WKB (SWKB)

Metode SWKB ini merupakan pengembangan dari metode

semiklasik WKB. Nama WKB ini diambil dari singkatan nama para

penemunya, yaitu Wentzel, Kramers, dan Brillouin. (Sinha, A and

Roychoudhury, R., 2000). Seperti telah diketahui bahwa metode WKB

memiliki kelemahan dalam hal pendekatan matematik yang digunakan, yaitu

adanya koreksi Langer. Berikut adalah ulasan singkat mengenai konversi

matematis metode semiklasik WKB menjadi SWKB. Kuantisasi pendekatan

semiklasik WKB pada orde terendah untuk potensial satu dimensi 𝑉 𝑥 adalah, (Cooper et al., 2001)

(38)

commit to user

𝐸 − 𝑉 𝑥 𝑑𝑥 = 𝑛 +_𝑎𝑏 1₂ 𝜋ћ (2.60)

Sebagaimana telah disebutkan sebelumnya bahwa fungsi energi E

dapat dinyatakan dengan Hamiltonian (H). Dalam SUSY, Hamiltonian

dipisahkan menjadi dua macam yaitu, Hamiltonian Penaik (𝐻+ ) dan

Hamiltonian Penurun (𝐻₋). Demikian juga potensialnya, berturut-turut (𝑉₊) dan (𝑉₋). Sehingga persamaan Hamiltonian Penurun (𝐻_) Supersimetri-WKB (SWKB) diperoleh,

𝐸_𝑛 − − 𝑉₋(𝑥) 𝑑𝑥 = 𝑛 +1

2 𝑏

𝑎 𝜋ћ (2.61)

Dengan memasukkan nilai 𝑉− (𝑥) pada pers.(2.41) ke pers.(2.61)

diperoleh 2𝑚 (𝐸_𝑛(−)− (𝑊2_{𝑥 −} ћ 2𝑚𝑊 ′_{𝑥 ) 𝑑𝑥 = (𝑛 +}1 2)𝜋ћ 𝑏 𝑎 (2.62)

Dimana n = 0, 1, 2, ....dan a, b adalah titik balik. Jika a dan b,

dimasukkan ke persamaan diperoleh, 𝑊2 𝑎 − ћ

2𝑚𝑊 ′_{𝑎 = 𝑊}2_{𝑏 −} ћ 2𝑚𝑊 ′_{𝑏 = 𝐸} 𝑛 (−)

. Dengan mengekspansikan ruas kiri pada pers.(2.62) pada

pangkat ћ diperoleh, 2𝑚 (𝐸𝑏 _𝑛(−)− 𝑊2_{𝑥 𝑑𝑥 +} 𝑎 ћ 2 𝑊′ 𝑥 𝑑𝑥 𝐸𝑛−−𝑊2 𝑥 𝑏 𝑎 = (𝑛 + 1 2)𝜋ћ (2.63) Dimana, 𝑊2 𝑎 = 𝑊2_{𝑏 = 𝐸} 𝑛 (−) , sehingga ћ 2 𝑊′ 𝑥 𝑑𝑥 𝐸_𝑛(−)−𝑊2_𝑥 𝑏 𝑎 = ћ 2 sin −1 𝑊(𝑏) 𝐸_𝑛(−) − sin−1 𝑊(𝑎) 𝐸_𝑛(−) =1 2 𝜋ћ (2.64)

(39)

commit to user

25

Dengan mensubtitusikan hasil dari pers.(2.64) ke pers.(2.63) maka

pers.(2.62) dapat dituliskan menjadi,

2𝑚 (𝐸𝑏 _𝑛 − − 𝑊2_𝑥

𝑎 𝑑𝑥 = 𝑛𝜋ћ (2.65)

Persamaan (2.65) merupakan persamaan umum tingkat energi

SWKB untuk simetri baik (unbroken symetry). Sedangkan persamaan umum

tingkat energi SWKB untuk kondisi simetri rusak (broken symetry) dituliskan

sebagai, 2𝑚 (𝐸𝑏 _𝑛 − − 𝑊2_𝑥 𝑎 𝑑𝑥 = 𝑛 + 1 2 𝜋ћ (2.66) Faktor 1

2 𝜋ћ pada pendekatan WKB standar dapat dipandang

sebagai energi tingkat nol pada boson, yang didalam teori SUSY untuk

konsisi yang baik secara eksak dapat dihilangkan dengan bentuk fermion.

F. Potensial Kratzer Dengan Faktor Sentrifugal

Potensial Kratzer dinyatakan sebagai, (Flügge, 1971)

𝑉 𝑟 = −2𝐷 𝑎 𝑟 − 1 2 𝑎2 𝑟2 (2.67)

Dimana D merupakan Energi Disosiasi (peruraian), a adalah jarak

keseimbangan/ kestabilan antar inti atom, dan r adalah jarak antar inti atom

pada posisi tertentu. Jika 𝑎 <<< 𝑟, maka potensial ini dapat dipresentasikan dalam bentuk potensial Coulomb 𝑉 𝑟 = −𝑍𝑒′ 2

𝑟2 , dengan 𝐷𝑎

2 _{= −𝑍𝑒′}2_.

Model potensial ini umumnya digunakan untuk menyelidiki

spektrum rotasi-vibrasi dari molekul beratom dua, dimana salah satu atom

(40)

commit to user

sebagai koordinat, sedangkan atom yang lain bergerak mengelilinginya

dalam kulit bola. Dalam keadaan stabil, yaitu ketika 𝑟 = 𝑎, maka 𝑉 𝑎 = −𝐷

minimum.

Berdasarkan pers.(2.22) dan pers.(2.67), maka persamaan potensial

efektif dari Potensial Kratzer untuk 𝑙 ≠ 0dapat ditulis sebagai 𝑉_𝑒𝑓𝑓 = −2𝐷 𝑎 𝑟 − 1 2 𝑎2 𝑟2 + ћ2 2𝑚 𝑙 𝑙+1 𝑟2 (2.68)

G. Potensial Morse dengan Faktor Sentrifugal

Potensial Morse digunakan untuk mendeskripsikan interaksi antara

dua atom di dalam molekul yang beratom duayang dinyatakan sebagai,

(Flügge, 1971)

𝑉 𝑥 = 𝐷 𝑒−2𝛼𝑥 _{− 2𝑒}−𝛼𝑥_{; 𝑥 =}𝑟−𝑟0

𝑟0 (2.69)

dimana, D merupakan Energi Disosiasi (peruraian), r adalah jarak orbital

elektron terhadap inti dari molekul beratom dua, dan 𝑟₀ adalah jarak keseimbangan antar inti atom. Sedangkan dan 𝛼 adalah konstanta penyesuaian.

Berdasarkan pers.(2.22) dan pers.(2.69) maka persamaan potensial

efektif dari Potensial Morse untuk 𝑙 ≠ 0 dapat ditulis sebagai 𝑉_𝑒𝑓𝑓 = 𝐷 𝑒−2𝛼𝑥 _{− 2𝑒}−𝛼𝑥₊ ћ2

2𝑚 𝑙 𝑙+1

𝑟2 (2.70)

Dengan 𝑙 merupakan bilangan kuantum dan m adalah massa atom tereduksi. Karena 𝑥 =𝑟−𝑟0

𝑟0 , maka 𝑟 = 𝑟0 𝑥 + 1 . Sehingga pers.(2.71) dapat ditulis sebagai,

(41)

perpustakaan.uns.ac.id digilib.uns.ac.id commit to user 27 𝑉_𝑒𝑓𝑓 = 𝐷 𝑒−2𝛼𝑥 _{− 2𝑒}−𝛼𝑥₊ ћ2 2𝑚 𝑙 𝑙+1 𝑟02 𝑥 + 1 −2 _(2.72)

Dengan mengekspansikan faktor 𝑥 + 1 −2 diperoleh,

𝑥 + 1 −2 _{= 1 − 2𝑥 + 3𝑥}2_{+ ⋯} _(2.73)

Persamaan ini dirubah dalam bentuk eksponensial. Dengan asumsi

bahwa suku ke-4 dan seterusnya sangat kecil, maka penyelesaian ini diambil

sampai suku ke-3 saja. Dimisalkan suatu persamaan eksponensial sebagai

berikut, 1 − 2𝑥 + 3𝑥2 = 𝐶0+ 𝐶1𝑒−𝛼𝑥 + 𝐶2𝑒−2𝛼𝑥 (2.74) Dimana, e−αx _{= 1 − αx +}α2x2 2! + ⋯ , dan e −2αx _{= 1 − 2αx +}4α2x2 2! + ⋯ (2.75)

Jika pers. (2.75) disubtitusikan ke dalam pers. (2.74) diperoleh,

1 − 2𝑥 + 3𝑥2 _{= 𝐶} 0 + 𝐶1 1 − αx + α2x2 2! + 𝐶2 1 − 2αx + 4α2x2 2! (2.76) Atau, 1 − 2𝑥 + 3𝑥2_{= 𝐶} 0+ 𝐶1+ 𝐶2− 𝐶1+ 2𝐶2 αx + 𝐶1 2 + 4𝐶2 2 α 2_x2 _(2.77)

Dengan membandingkan komponen ruas kiridan ruas kanan dari

pers.(2.77) dapat diperoleh,

𝐶₀+ 𝐶₁+ 𝐶₂ = 1; (2.78a) 𝐶₁+ 2𝐶₂ = 2 𝛼 (2.78b) 𝐶1+ 4𝐶2 = 6 α2 (2.78c)

Dengan metode subtitusi diperoleh,

𝐶0 = 1 − 3 𝛼+ 3 α2 ; 𝐶1 = 4 𝛼− 6 α2 ; dan 𝐶2 = − 1 𝛼+ 3 α2 (2.78d)

(42)

commit to user

Dengan mensubtitusikan pers. (2.78d) ke dalam pers.(2.74), maka

pers.(2.73) dapat dituliskan sebagai berikut,

𝑥 + 1 −2 _{= 1 −}3 𝛼+ 3 α2 + 4 𝛼− 6 α2 𝑒 −𝛼𝑥 _{+ −}1 𝛼+ 3 α2 𝑒 −2𝛼𝑥 _(2.79)

Sehingga secara lengkap persamaan potensial efektif untuk potensial

Morse dapat dituliskan kembali sebagai,

𝑉𝑒𝑓𝑓= 𝐷 𝑒−2𝛼𝑥− 2𝑒−𝛼𝑥 +ћ 2 2𝑚 𝑙 𝑙+1 𝑟02 1 − 3 𝛼+ 3 α2 + 4 𝛼− 6 α2 𝑒−𝛼𝑥+ − 1 𝛼+ 3 α2 𝑒−2𝛼𝑥 (2.80) Atau, 𝑉_𝑒𝑓𝑓 = 𝐴₀− 𝐴₁𝑒−𝛼𝑥 + 𝐴₂𝑒−2𝛼𝑥 (2.81) Dengan, 𝐴0 = ћ2 2𝑚 𝑙 𝑙+1 𝑟02 1 − 3 𝛼+ 3 α2 (2.81a) 𝐴1 = 2𝐷 − ћ2 2𝑚 𝑙 𝑙+1 𝑟02 4 𝛼− 6 α2 (2.81b) 𝐴₂ = 𝐷 + ћ2 2𝑚 𝑙 𝑙+1 𝑟02 − 1 𝛼+ 3 α2 (2.81c)

H. Potensial Manning Rosen dengan Faktor Sentrifugal

Potensial Manning Rosen merupakan salah satu potensial yang

digunakan sebagai model matematika untuk mendeskripsikan vibrasi dari

molekul beratom dua. Persamaan potensial ini dinyatakan sebagai,

𝑉 𝑟 = ћ2 2𝑚 𝛼2 𝜐 𝜐−1 sinh2 𝑟 𝛼 − ћ2𝑞 𝑚 𝛼2 coth 𝑟 𝛼 (2.82)

Dimana 𝜐 dan 𝑞 merupakan dua parameter yang tak berdimensi, sedangkan 𝛼 merupakan dimensi dari panjang, dan 𝑟 adalah jarak antar inti dari kedua atom. (Sameer, 2011; Antia, AD,et al.,2010; Hammed, 2011). Untuk 𝜐 = 0 atau 𝜐 = 1, Potensial Manning Rosen potential berubah menjadi Potensial Hulthen Potential (Sameer, 2011; Antia, AD,et al.,2010).

(43)

commit to user

29

Berdasarkan pers.(2.22) dan pers.(2.82) maka persamaan potensial

efektif dari Potensial Manning Rosen untuk 𝑙 ≠ 0 dapat ditulis sebagai 𝑉𝑒𝑓𝑓 = ћ2 2𝑚 𝛼2 𝜐 𝜐−1 sinh2 𝑟 𝛼 − ћ2𝑞 𝑚 𝛼2 coth 𝑟 𝛼 + ћ2 2𝑚 𝑙 𝑙+1 𝑟2 (2.83) Jika 𝑒 𝛼𝑟 − 𝑒 – 𝑟 𝛼 = 2 sinh 𝑟 𝛼 , dimana, 𝑒 𝑟 𝛼 = 1 +𝑟 𝛼+ 𝑟 𝛼 2 2! + ⋯ (2.84)

Dengan mengambil dua suku pertama, maka diperoleh

𝑒 𝛼𝑟 − 𝑒 – 𝑟 𝛼 ≈ 1 + 𝑟 𝛼 − 1 − 𝑟 𝛼 = 2 𝑟 𝛼 (2.85) Sehingga, 2𝑟 𝛼 = 2 sinh 𝑟 𝛼 , dan sinh 𝑟 𝛼 = 𝑟 𝛼 . Jika 𝑟 𝛼 <<< 1, maka sinh 𝑟 𝛼 ≈ 𝑟 𝛼 dan sinh 2 𝑟 𝛼 = 𝑟2 𝛼2, maka diperoleh 𝑟 2 _{= 𝛼}2_sinh2 𝑟 𝛼 . Sehingga persamaan potensial efektif dari potensial Manning Rosen (pers.(2.83)) secara

lengkap dapat dituliskan kembali sebagai berikut,

𝑉_𝑒𝑓𝑓 = ћ2 2𝑚 𝛼2 𝜐 𝜐−1 sinh2 𝑟 𝛼 − 2𝑞 coth 𝑟 𝛼 + ћ2 2𝑚 𝑙 𝑙+1 𝛼2_sinh2 𝑟 𝛼 (2.86) Atau, 𝑉_𝑒𝑓𝑓 = ћ2 2𝑚 𝛼2 𝜐′ 𝜐′−1 sinh2 𝑟 𝛼 − ћ2𝑞 𝑚 𝛼2 coth 𝑟 𝛼 (2.87) Dengan, 𝜐′ = 𝜐 −1 2 2 + 𝑙 𝑙 + 1 +1 2

(44)

commit to user

BAB III

METODOLOGI PENELITIAN

A. Waktu dan Tempat Penelitian

Penelitian ini dilaksanakan mulai bulan September 2011 sampai bulan

Juli 2012 di Fakultas Pascasarjana Universitas Sebelas Maret Surakarta.

B. Objek Penelitian

Objek dalam penelitian ini adalah persamaan potensial efektif dari

beberapa jenis potensial shape invariance, diantaranya yaitu:

1. Potensial Kratzer 𝑉_𝑒𝑓𝑓 = −2𝐷 𝑎 𝑟− 1 2 𝑎2 𝑟2 + ћ2 2𝑚 𝑟2𝑙 𝑙 + 1 (3.1) 2. Potensial Morse 𝑉𝑒𝑓𝑓 = 𝐴0− 𝐴1𝑒−𝛼𝑥 + 𝐴2𝑒−2𝛼𝑥 (3.2) Dengan, 𝐴0 = ћ2 2𝑚 𝑙 𝑙+1 𝑟02 1 − 3 𝛼+ 3 α2 (3.2a) 𝐴1 = 2𝐷 − ћ2 2𝑚 𝑙 𝑙+1 𝑟02 4 𝛼− 6 α2 (3.2b) 𝐴₂ = 𝐷 + ћ2 2𝑚 𝑙 𝑙+1 𝑟02 − 1 𝛼+ 3 α2 (3.2c)

3. Potensial Manning Rosen

𝑉_𝑒𝑓𝑓 = ћ2 2𝑚 𝛼2 𝜐′ 𝜐′−1 sinh2 𝑟 𝛼 − ћ2𝑞 𝑚 𝛼2 coth 𝑟 𝛼 (3.3) Dengan, 𝜐′ = 𝜐 −1₂ 2+ 𝑙 𝑙 + 1 +1₂

(45)

commit to user

31

C. Instrumen Penelitian

Instrumen yang digunakan dalam penelitian ini berupa

persamaan-persamaan dalam metode Supersimetri Mekanika Kuantum, diantara yaitu:

1. Persamaan umum hubungan antara potensial efektif (potensial standard)

dan potensial supersimetri

𝑉_𝑒𝑓𝑓 = 𝑉₋ 𝑥; 𝑎₀ + 𝐸₀ (3.4)

2. Persamaan pasangan potensial supersimetri shape invariance

𝑉₊ 𝑥; 𝑎_𝑗 = 𝑉₋ 𝑥; 𝑎_{𝑗 +1} + 𝑅 𝑎_{𝑗 +1} (3.5) Dengan, 𝑉₋ 𝑥; 𝑎_𝑗 = 𝑊2_{𝑥, 𝑎} 𝑗 − ħ 2𝑚𝑊 ′_{𝑥, 𝑎} 𝑗 (3.5a) 𝑉+ 𝑥; 𝑎𝑗 = 𝑊2 𝑥, 𝑎𝑗 + ħ 2𝑚𝑊 ′_{𝑥, 𝑎} 𝑗 (3.5b)

3. Persamaan umum tingkat energi ke-n untuk Hamiltonian Penurun

𝐸_𝑛(−)dengan metode operator SUSY

𝐸_𝑛(−) = 𝑛𝑘=1𝑅(𝑎𝑘), (3.6)

Dimana 𝑅 𝑎_𝑘 = 𝑉₊ 𝑥; 𝑎_𝑘−1 − 𝑉₋ 𝑥; 𝑎_𝑘 (3.7) 4. Persamaan umum tingkat energi ke-n SWKB untuk Hamiltonian Penurun

𝐸_𝑛(−)

2𝑚 (𝐸𝑏 _𝑛 − − 𝑊2_𝑥

𝑎 𝑑𝑥 = 𝑛𝜋ћ (3.8)

5. Persamaan umum spektrum energi tingkat ke-n dengan metode SUSY

(46)

commit to user

6. Persamaan fungsi gelombang tingkat dasar

𝜓₀ − 𝑥 = 𝑁 exp − 2𝑚_ћ 𝑊 𝑥 𝑑𝑥x (3.10) 7. Persamaan Operator Penaik

𝐴+_{= −} ћ 2𝑚

𝑑

𝑑𝑥 + 𝑊 𝑥 (3.11)

8. Persamaan fungsi gelombang tingkat ke-n

𝜓_𝑛−_{𝑥; 𝑎}

0 ~𝐴+ 𝑥; 𝑎0 𝜓𝑛−1− 𝑥; 𝑎1 (3.12)

D. Prosedur Penelitian

Tujuan dari penelitian ini adalah menentukan persamaan spektrum

energi dan fungsi gelombang dengan menggunakan metode Supersimetri

Mekanika Kuantum dengan langkah – langkah sebagai berikut:

1. Menentukan persamaan superpotensial 𝑊(𝑥) berdasarkan potensial efektif terkait dan energi tingkat dasar (𝐸₀) dengan menggunakan persamaan (3.5) dan persamaan potensial efektif dari potensial terkait

(pers. (3.1), (3.2), atau (3.3))

2. Menentukan persamaan pasangan potensial supersimetri 𝑉_± 𝑥; 𝑎_𝑗 dan 𝑅 𝑎_𝑗 dengan menggunakan persamaan (3.4), (3.4a), dan (3.4b)

3. Menentukan persamaan umum tingkat energi ke-n dengan Metode

Operator Supersimetrimenggunakan persamaan (3.6), (3.7) dan (3.9)

4. Menentukan persamaan umum tingkat energi ke-ndengan metode

SWKByaitu dengan menggunakan persaman (3.8) dan (3.9)

5. Menentukan persamaan fungsi gelombang tingkat dasar 𝜓₀ − dengan menggunakan persamaan (3.10)

(47)

commit to user

33

6. Menentukan persamaan fungsi gelombang tingkat ke-n(𝜓_𝑛−)dengan menggunakan persamaan (3.11) dan (3.12)

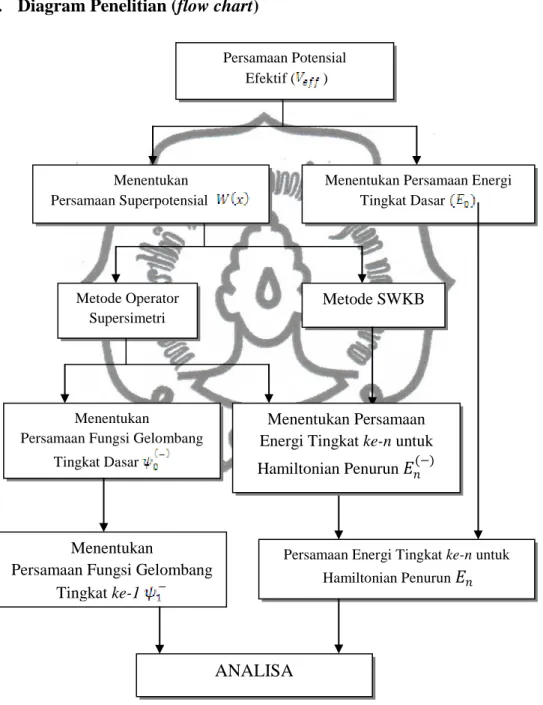
E. Diagram Penelitian (flow chart)

Persamaan Potensial Efektif ( )

Menentukan Persamaan Superpotensial

Menentukan Persamaan Energi Tingkat Dasar

Menentukan

Persamaan Fungsi Gelombang Tingkat Dasar

Persamaan Energi Tingkat ke-n untuk Hamiltonian Penurun 𝐸_𝑛 Menentukan

Persamaan Fungsi Gelombang Tingkat ke-1

Metode Operator Supersimetri

Metode SWKB

Menentukan Persamaan Energi Tingkat ke-n untuk Hamiltonian Penurun 𝐸_𝑛(−)

ANALISA

(48)

commit to user

BAB IV

HASIL PENELITIAN DAN PEMBAHASAN

A. Hasil Penelitian

1. Persamaan Tingkat Energi dan Fungsi Gelombang untuk Potensial Kratzer dengan Faktor Sentrifugal

Berdasarkan pers.(2.17), persamaan Schrödinger untuk potensial

Kratzer dengan faktor sentrifugal dapat dituliskan sebagai berikut;

− ћ2 2𝑚 𝑑2𝜓 𝑑𝑟2 + −2𝐷 𝑎 𝑟 − 1 2 𝑎2 𝑟2 + ћ2 2𝑚 𝑙 𝑙+1 𝑟2 𝜓 = 𝐸𝜓 (4.1) Atau, − ћ2 2𝑚 𝑑2𝜓 𝑑𝑟2 + − 𝐴 𝑟 + 𝐵 𝑟2 𝜓 = 𝐸𝜓 (4.2) dengan 𝐴 = 2𝐷𝑎, dan 𝐵 = 𝐷𝑎2+ ћ2 2𝑚𝑙 𝑙 + 1 .

Penyelesaian persamaan Schrödinger yang berupa persamaan fungsi

gelombang 𝜓 dan spektrum energi 𝐸untuk potensial Kratzer dengan faktor sentrifugal ini dapat dilakukan dengan menggunakan metode Supersimetri

Mekanikan Kuantum (SUSYQM) dengan langkah-langkah seperti pada

prosedur penelitian.

Berdasarkan bentuk persamaan potensial efektif potensial Kratzer

pada pers.(4.2), dapat dimisalkan persamaan superpotensialnya sebagai

berikut,

𝑊 𝑟 = 𝐹 +𝐺

𝑟 (4.3)

(49)

perpustakaan.uns.ac.id digilib.uns.ac.id commit to user 35 𝑉_𝑒𝑓𝑓 = 𝑉₋ 𝑥; 𝑎₀ + 𝐸₀ Atau, 𝑉_𝑒𝑓𝑓 − 𝐸₀ = 𝑊2 𝑟 − ћ 2𝑚𝑊 ′_𝑟 _(4.4) maka diperoleh, −𝐴 𝑟 + 𝐵 𝑟2− 𝐸0 = 𝐹 2_{+ 2}𝐹𝐺 𝑟 + 𝐺2 𝑟2+ ћ 2𝑚 𝐺 𝑟2 (4.5)

Dengan menyamakan ruas kiri dan kanan, diperoleh

𝐺 = − 𝐵 + ћ2 8𝑚+ ћ 2 2𝑚 (4.6) 𝐹 = 𝐴 2 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 (4.7)

Dan diperoleh persamaan spektrum energi tingkat dasar sebagai

berikut,

𝐸₀ = − 𝐴2

4 𝐵+_8𝑚ћ2+ ћ

2 2𝑚

2 (4.8)

Dengan mensubtitusikan pers.(4.6) dan (4.7) ke pers.(4.3), maka

persamaan superpotensial untuk potensial kratzer dapat ditulis kembali

sebagai, 𝑊 𝑟 = 𝐴 2 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 − 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 𝑟 (4.9) Sehingga, 𝑊2 𝑟 = 𝐴2 4 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 2+ 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 2 𝑟2 − 𝐴 𝑟 (4.10)

(50)

commit to user Dan, 𝑊′(𝑟) = 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 𝑟2 (4.11)

Berdasarkan persamaan superpotensial ini dapat ditentukan pasangan

potensial supersimetri 𝑉₋ 𝑥; 𝑎_𝑗 dan 𝑉₊ 𝑟; 𝑎_𝑗 . Dimana 𝑉₋ 𝑥; 𝑎_𝑗 ditentukan dengan menggunakan pers.(3.4a), sedangkan 𝑉₊ 𝑟; 𝑎_𝑗 ditentukan dengan menggunakan pers.(3.4b). Dengan mensubtitusikan pers.(4.10) dan (4.11) ke

dalam pers.(3.4a) diperoleh,

𝑉− 𝑟; 𝑎0 = − 𝐴 𝑟+ 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 2 𝑟2 + 𝐴2 4 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 2− ћ 2𝑚 𝐵+_8𝑚ћ2+ ћ 2 2𝑚 𝑟2 Atau, 𝑉− 𝑟; 𝑎0 = − 𝐴 𝑟+ 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 𝐵+ ћ2 8𝑚+ ћ 2 2𝑚− ћ 2𝑚 𝑟2 + 𝐴2 4 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 2 (4.12)

Sedangkandengan mensubtitusikan pers.(4.10) dan (4.11) ke dalam

pers.(3.4b) diperoleh, 𝑉+ 𝑟; 𝑎0 = − 𝐴 𝑟+ 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 2 𝑟2 + 𝐴2 4 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 2+ ћ 2𝑚 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 𝑟2 Atau, 𝑉+ 𝑟; 𝑎0 = − 𝐴 𝑟+ 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 𝐵+ ћ2 8𝑚+ ћ 2 2𝑚+ ћ 2𝑚 𝑟2 + 𝐴2 4 𝐵+ћ2 8𝑚+ ћ 2 2𝑚 2 (4.13)