i
SMP KANISIUS MUNTILAN TAHUN AJARAN 2009/2010
DALAM MENGERJAKAN SOAL-SOAL PERSAMAAN
LINEAR SATU VARIABEL
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Oleh: Ria Naswantari NIM. 041414045
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
ANALISIS KESALAHAN SISWA KELAS VIIA
SMP KANISIUS MUNTILAN TAHUN AJARAN 2009/2010
DALAM MENGERJAKAN SOAL-SOAL PERSAMAAN
LINEAR SATU VARIABEL
Oleh:
Ria Naswantari
NIM: 041414045
Telah disetujui oleh:
Pembimbing
iii
ANALISIS KESALAHAN SISWA KELAS VIIA
SMP KANISIUS MUNTILAN TAHUN AJARAN 2009/2010
DALAM MENGERJAKAN SOAL-SOAL PERSAMAAN
LINEAR SATU VARIABEL
Dipersiapkan dan ditulis oleh: Ria Naswantari NIM: 041414045
Telah dipertahankan di depan Panitia Penguji pada tanggal 1 Februari 2011
dan dinyatakan memenuhi syarat.
Susunan Panitia Penguji
Nama Lengkap Tanda tangan
Ketua Drs. Domi Severinus, M.Si. ... Sekretaris Prof. Dr. St. Suwarsono ... Anggota Dr. Y. Marpaung ... Anggota Drs. Sukardjono, M.Pd. ... Anggota Drs. A. Sardjana, M.Pd. ...
Yogyakarta, 1 Februari 2011
Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma
Dekan,
iv
“Sebab it u janganlah kamu kuat ir akan hari besok,
karena hari besok mempunyai kesusahannya sendiri. K esusahan sehari cukuplah
hanya unt uk sehari.”
(Matius 6:34)
“Segala perkara dapat kutanggung di
dalam D ia yang memberi kekuat an
kepadaku.”
(Filipi 4:13)
D engan penuh syukur kupersembahkan skripsiku untuk:
Tuhan Yesus Sang Juru Selamatku dan Bunda M aria
Bapak dan I buku
Adikku I rvan
v
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 5 Desember 2010
Penulis,
vi
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Ria Naswantari
Nomor Induk Mahasiswa : 041414045
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
”ANALISIS KESALAHAN SISWA KELAS VIIA SMP KANISIUS MUNTILAN TAHUN AJARAN 2009/2010 DALAM MENGERJAKAN SOAL-SOAL PERSAMAAN LINEAR SATU VARIABEL”.
Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, untuk mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis, tanpa perlu minta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian ini pernyataan yang saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada tanggal: Februari 2011 Yang menyatakan
vii
ANALISIS KESALAHAN SISWA KELAS VIIA SMP KANISIUS MUNTILAN TAHUN AJARAN 2009/2010 DALAM MENYELESAIKAN
SOAL-SOAL TOPIK PERSAMAAN LINEAR SATU VARIABEL
Ria Naswantari Universitas Sanata Dharma
2011
Penelitian ini bertujuan untuk mengetahui jenis kesalahan yang dibuat beberapa siswa Kelas VIIA SMP Kanisius Muntilan tahun ajaran 2009/2010 dalam menyelesaikan soal-soal tentang topik Persamaan Linear Satu Variabel. Subyek penelitian ini adalah 6 siswa kelas VIIA SMP Kanisius Muntilan tahun ajaran 2009/2010, yang memiliki ragam kesalahan paling banyak ketika menyelesaikan soal tes Matematika uji coba. Keenam siswa tersebut adalah Mella, Ita, Niken, Rita, Shella, dan Eko (nama samaran).
Penelitian ini menggunakan metode deskriptif kualitatif. Data dikumpulkan melalui dua tahap yaitu, tahap pertama dengan memberikan tes Matematika penelitian yang terdiri dari 10 butir soal dan tahap kedua dengan wawancara. Jenis data yang dianalisis adalah data kualitatif berupa angka, kata atau kalimat hasil tes Matematika dan hasil wawancara. Analisis data kualitatif dalam penelitian ini menggunakan metode analisis kesalahan, yaitu dengan mengidentifikasi kesalahan yang pertama kali muncul dan tampak dalam langkah-langkah penyelesaian pada jawaban tertulis siswa. Kesalahan-kesalahan tersebut kemudian digolongkan berdasarkan rumusan kategori jenis kesalahan.
viii
AN ERROR ANALYSIS OF STUDENTS IN 7THA GRADE OF KANISIUS MUNTILAN JUNIOR HIGH SCHOOL ACADEMIC YEAR 2009/2010 IN SOLVING PROBLEMS OF SIMPLE LINEAR EQUATIONS
Ria Naswantari Sanata Dharma University
2011
This research is aimed to know the kinds of mistakes made by some students in 7th A grade of Kanisius Muntilan Junior High School academic year 2009/2010 in solving the problems about Simple Linear Equations. The subjects of this research are six students in 7th A grade of Kanisius Muntilan Junior High School academic year 2009/2010, who have the most various number of errors in doing the mathematics test try out. The six students are Mella, Ita, Niken, Rita, Shella, and Eko (pseudonyms).
This research uses the qualitative descriptive method. The data are collected by two steps. The first step is by giving 10 numbers of mathematics tests and the second step is by interviewing the students. The result of Mathematics test and the interview which are in the form of numbers and sentences are analysed using errors method by identifying the errors which appear in the first time they answer the questions in written form. Those errors are grouped based on the category of kinds of errors.
ix
Puji syukur kepada Allah Bapa Yang Maha Kasih karena atas rahmat dan kasih-Nya, penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi ini diajukan sebagai salah satu syarat untuk memperoleh gelar Sarjana Pendidikan Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Banyak hambatan serta rintangan yang penulis alami dalam proses penyusunan skripsi ini. Namun karena kuasa Tuhan, keterlibatan, serta bantuan dari berbagai pihak, penulis dapat melalui semua dengan baik. Oleh karena itu, dalam kesempatan ini dengan penuh rasa syukur penulis mengucapkan terima kasih atas segala bantuan, dorongan, perhatian, kasih dan dukungan baik secara moril, materiil maupun spirituil kepada semua pihak, antara lain:
1. Allah Bapa di Surga atas segala kuasa, kasih, karunia, rahmat serta mukjizat yang sungguh luar biasa. Terima kasih atas segala karunia yang diberikan; 2. Bapak Dr. Yansen Marpaung selaku dosen pembimbing, yang telah bersedia
menyediakan waktu, tenaga, dan pikiran untuk memberikan bimbingan kepada penulis. Terima kasih atas segala motivasi, saran, dan kritik selama penyusunan skripsi ini, pengetahuan tentang cara mengajar, dan pelatihan tentang PMRI;
x dosen penguji;
5. Segenap dosen dan seluruh staf Sekretariat JPMIPA Universitas Sanata Dharma, atas segala bantuan dan kerja samanya selama penulis menempuh kuliah hingga penyelesaian skripsi ini;
6. Ibu Linda selaku Guru Bidang Studi Matematika kelas VII SMP Kanisius Muntilan. Terima kasih atas kesempatan dan bantuan yang diberikan;
7. Ibu Sumiyati selaku Kepala Sekolah SMP Kanisius Muntilan yang telah mendukung dan mengijinkan penulis melaksanakan penelitian di SMP Kanisius Muntilan;
8. Siswa-siswi kelas VII SMP Kanisius Muntilan tahun ajaran 2009/2010. Terima kasih atas kerja sama dan dukungannya selama penelitian;
9. Keluargaku tercinta, Bapak Sarmuji, Ibu Margaretha Sri Utari, dan adikku Bonaventura Irvan Prakoso Aji. Terima kasih atas doa, kesabaran, kebersamaan, penghiburan, dukungan, fasilitas, serta dorongan untuk segera menyelesaikan skripsi;
10.Keluarga besar Kartowiharjo, terima kasih atas doa, dukungan, serta dorongannya dalam penyelesaian skripsi ini. Simbah kakung yang ada di surga, terima kasih atas doa-doanya;
xi
dukungan dan dorongannya selama penelitian maupun dalam penyusunan skripsi, bantuan mempersiapkan ujian, pinjaman komputer, camera digital, serta buku-buku;
13.Lucia Niken Tyas Utami, terima kasih telah meminjamkan laptop dan mp3,
serta membantu menerjemahkan abstraknya. Bapak Muhadi, terima kasih laptopnya. Bli Ngurah dan Beny Wijaya yang telah bersedia meminjamkan
mp3 dan printer;
14.Para sahabat: Th. Veni, Kadek Ritta, Aristanika, Dina May, Dina Kurniawati, Ch. Yudi, Putu Mella, Ani Susanti D., Berta Ika, dan Embi. Terima kasih atas bantuan, dukungan, dorongan, kebersamaan, kritik, dan saran dalam penyusunan skripsi ini. Raka Setiaji sahabat baru dalam hidupku, terimakasih atas kasih, kebersamaan, dukungan, dan doa yang telah diberikan;
15.Semua pihak yang tidak dapat disebutkan satu per satu yang telah membantu penyusunan skripsi ini.
Penulis menyadari bahwa masih banyak kekurangan dalam skripsi ini. Oleh karena itu, penulis saran dan kritik dari pembaca demi perbaikan skripsi ini. Akhir kata, penulis berharap semoga skripsi yang jauh dari sempurna ini bermanfaat bagi kemajuan pendidikan dan pembaca pada umumnya.
Yogyakarta, 28 Desember 2010 Penulis,
xii
HALAMAN JUDUL i
HALAMAN PERSETUJUAN PEMBIMBING ii
HALAMAN PENGESAHAN iii
HALAMAN PERSEMBAHAN iv
PERNYATAAN KEASLIAN KARYA v
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA vi
ABSTRAK vii
ABSTRACT viii
KATA PENGANTAR ix
DAFTAR ISI xii
DAFTAR TABEL xvi
DAFTAR GAMBAR xix
DAFTAR LAMPIRAN xxi
BAB I PENDAHULUAN 1
A. Latar Belakang Masalah 1
B. Perumusan Masalah 4
C. Tujuan Penelitian 4
D. Pembatasan Istilah 4
E. Manfaat Penelitian 17
BAB II LANDASAN TEORI 18
A. Persamaan Linear Satu Variabel 18
1. Pengertian Persamaan Linear Satu Variabel 18 2. Menentukan Penyelesaian dan Himpunan Penyelesaian
Persamaan Linear Satu Variabel 19
3. Menyelesaikan Persamaan Linear Satu Variabel dengan
Metode “Pindah Ruas-Ganti Tanda” 23
4. Menyelesaikan Persamaan Linear Satu Variabel yang
xiii
B. Metode Penyelesaian Masalah Menurut George Polya
(1957) 28
C. Kategori Jenis Kesalahan Menurut Hadar, Zaslavsky, dan
Inbar 30
D. Kategori Jenis Kesalahan Menurut R. D. G. Hall 34 E. Kategori Jenis Kesalahan Menurut Cipriano dan McCoy 42 F. Kesalahan-kesalahan yang Sering Dilakukan Siswa dalam
Menyelesaikan Soal-soal Aljabar 45
BAB III METODE PENELITIAN 58
A. Jenis Penelitian 58
B. Tempat dan Waktu Penelitian 58
C. Subyek Penelitian 58
D. Bentuk Data dan Metode Pengumpulan Data 60
E. Instrumen Penelitian 61
F. Rencana Analisis Data 65
G. Keabsahan Data 77
BAB IV DESKRIPSI DATA DAN ANALISIS DATA 79
A. Deskripsi Pelaksanaan Penelitian 79
B. Analisis Hasil Uji Coba 80
1. Jenis Kesalahan Perhitungan 83
2. Kesalahan Penyederhanaan Bentuk Aljabar 85
3. Kesalahan Aturan Distributif 87
4. Kesalahan dalam Mengubah Suatu Persamaan ke
Persamaan Lain yang Ekuivalen 88
5. Jenis Kesalahan Data 92
6. Jenis Kesalahan yang Berkaitan dengan Pemahaman
Maksud/Makna Lambang/Notasi Matematika 93
xiv
D. Analisis Data penelitian 101
1. Jenis Kesalahan Hitung 103
2. Jenis Kesalahan Penyederhanaan Bentuk Aljabar 116 3. Jenis Kesalahan Aturan Distributif 121 4. Kesalahan dalam Mengubah Suatu Persamaan ke
Persamaan Lain yang Ekuivalen 125
5. Jenis Kesalahan Data 140
6. Jenis Kesalahan yang Berkaitan dengan Pemahaman
Maksud/Makna Lambang/Notasi Matematika 143 7. Kesalahan Tipe 10 (Kesalahan Kecerobohan) 154 8. Kesalahan Tipe 11 (Kesalahan Menginterpretasikan
Bahasa) 173
9. Kesalahan Tipe 12 (Kesalahan Menghapus Pembilang atau Penyebut untuk Menghilangkan Bentuk Bilangan
Pecahan pada Persamaan) 179
BAB V PEMBAHASAN, KESIMPULAN DAN SARAN 182
A. Pembahasan 182
1. Jenis Kesalahan Hitung 183
2. Jenis Kesalahan Penyederhanaan Bentuk Aljabar 189 3. Jenis Kesalahan Aturan Distributif 192 4. Kesalahan dalam Mencari Persamaan-persamaan yang
Ekuivalen pada Penyelesaian Persamaan 192
5. Kesalahan Data 197
6. Kesalahan yang Berkaitan dengan Lambang/Notasi
dalam Matematika 197
7. Kesalahan Kecerobohan 199
8. Kesalahan Pemodelan Matematika 204
xv
DAFTAR PUSTAKA 212
xvi
Tabel 2.1 Contoh Kesalahan Penyederhanaan yang Ditemukan Cipriano dan
McCoy (2008) 43
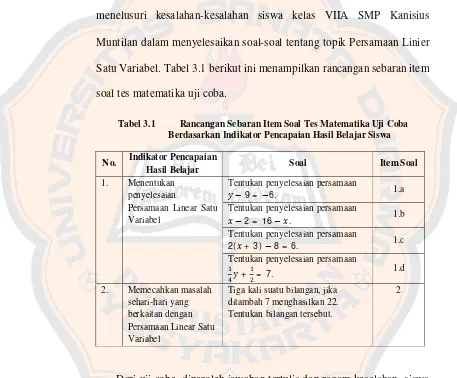
Tabel 3.1 Rancangan Sebaran Item Soal Tes Matematika Uji Coba
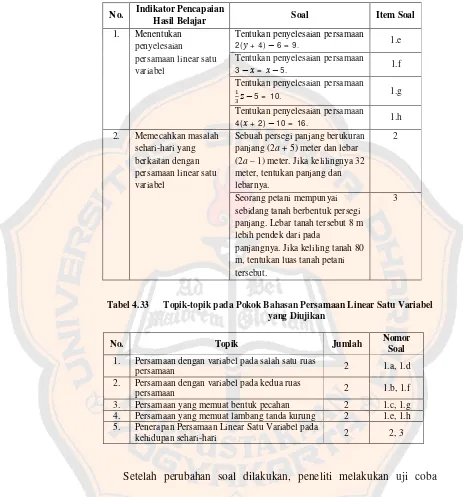
Berdasarkan Indikator Pencapaian Hasil Belajar Siswa 62 Tabel 3.2 Rancangan Sebaran Item Soal Tes Matematika Penelitian 63 Tabel 3.3 Topik-topik pada Pokok Bahasan Persamaan Linear Satu Variabel
Yang Diujikan 64
Tabel 3.4 Rangkuman Kategori Jenis Kesalahan dan Contoh
Kesalahannya 74
Tabel 4.1 Kegiatan Penelitian 79
Tabel 4.2 Kesalahan Tipe 1.a.1 dalam Uji Coba 84
Tabel 4.3 Kesalahan tipe 1.a.2 dalam Uji Coba 84
Tabel 4.4 Kesalahan Tipe 1.b dalam Uji Coba 85
Tabel 4.5 Kesalahan Tipe 2.a dalam Uji Coba 86
Tabel 4.6 Kesalahan Tipe 2.b dalam Uji Coba 86
Tabel 4.7 Kesalahan Tipe 3.a dalam Uji Coba 87
Tabel 4.8 Kesalahan Tipe 3.b dalam Uji Coba 88
Tabel 4.9 Kesalahan Tipe 3.c dalam Uji Coba 88
Tabel 4.10 Kesalahan Tipe 4.a dalam Uji Coba 89
Tabel 4.11 Kesalahan Tipe 4.b dalam Uji Coba 90
Tabel 4.12 Kesalahan Tipe 4.c dalam Uji Coba 90
Tabel 4.13 Kesalahan Tipe 4.d dalam Uji Coba 91
Tabel 4.14 Kesalahan Tipe 4.e dalam Uji Coba 92
Tabel 4.15 Kesalahan Tipe 5 dalam Uji Coba 92
Tabel 4.16 Kesalahan Tipe 6.a dalam Uji Coba 93
Tabel 4.17 Kesalahan Tipe 6.b dalam Uji Coba 94
Tabel 4.18 Kesalahan Tipe 7 dalam Uji Coba 95
Tabel 4.19 Kesalahan Tipe 9.a dalam Uji Coba 96
xvii
Tabel 4.22 Banyaknya Siswa yang Melakukan Kesalahan Penyederhanaan
Bentuk Aljabar (Kesalahan Tipe 2) 97
Tabel 4.23 Banyaknya Siswa yang Melakukan Kesalahan aturan Distributif
(Kesalahan Tipe 3) 97
Tabel 4.24 Banyaknya Siswa yang Melakukan Kesalahan dalam Mengubah Suatu Persamaan ke Persamaan Lain yang Ekuivalen (Kesalahan
Tipe 4) 97
Tabel 4.25 Banyaknya Siswa yang Melakukan Kesalahan Data (Kesalahan
Tipe 5) 98
Tabel 4.26 Banyaknya Siswa yang Melakukan Kesalahan Pemakaian
Lambang (Kesalahan Tipe 6) 98
Tabel 4.27 Banyaknya Siswa yang Melakukan Kesalahan Tidak Testruktur
(Kesalahan Tipe 7) 98
Tabel 4.28 Banyaknya Siswa yang Melakukan Kesalahan Menuliskan
Kesamaan (Kesalahan Tipe 8) 98
xviii
xix
Gambar 1.1 Soal Topik Garis dan Sudut dalam Observasi 3 Gambar 2.1 Contoh Kesalahan Penyederhanaan yang Ditemukan Cipriano
dan McCoy (2008) 43
Gambar 4.1 Jawaban Ita untuk Soal No. 1.a 104
Gambar 4.2 Jawaban Eko untuk Soal No. 1.d 106
Gambar 4.3 Jawaban Niken untuk Tes Matematika Uji Coba No. 1.d 108 Gambar 4.4 Jawaban Niken untuk Soal Tes Matematika Penelitian No. 1.b 108
Gambar 4.5 Jawaban Rita untuk Soal No. 1.e 111
Gambar 4.6 Jawaban Rita untuk Soal Tes Matematika Uji Coba No. 1.c 112 Gambar 4.7 Jawaban Rita untuk Soal Tes Matematika Penelitian No. 2 113
Gambar 4.8 Jawaban Ita untuk Soal No. 1.c 114
Gambar 4.9 Jawaban Tes Matematika Ita untuk Soal Tes Matematika
No. 2 117
Gambar 4.10 Jawaban Shella untu Soal Tes Matematika Penelitian
No. 1.f 119
Gambar 4.11 Jawaban Mella untuk Soal No. 1.e 122 Gambar 4.12 Jawaban Mella untuk Soal No. 1.h 122 Gambar 4.13 Jawaban Niken untuk Soal Tes Matematika Penelitian
No. 1.f 126
Gambar 4.14 Jawaban Shella untuk Soal Tes Matematika Penelitian
No. 1.c 129
Gambar 4.15 Jawaban Shella untuk Soal Tes Matematika Penelitian
No. 1.e 129
Gambar 4.16 Jawaban Niken untuk Soal Tes Matematika Penelitian
No. 1.g 132
xx
Gambar 4.23 Jawaban Tes Matematika Penelitian Mella untuk No. 1.f 149 Gambar 4.25a Jawaban Tes Matematika Penelitian Rita untuk Soal No. 1.a 151 Gambar 4.26b Jawaban Mella untuk Soal Tes Matematika Penelitian
No. 1.c 153
Gambar 4.26 Jawaban Ita untuk Soal Tes Matematika Penelitian No. 1.a 155 Gambar 4.27 Jawaban Tes Matematika Penelitian Niken untuk Soal
No. 1.c 157
Gambar 4.28 Jawaban Niken untuk Soal Tes Matematika Penelitian No.
1.h 160
Gambar 4.29 Jawaban Tes Matematika Penelitian Rita untuk Soal No. 1.c 163 Gambar 4.30 Jawaban Mella untuk Soal Tes Matematika penelitian No. 1.c 165 Gambar 4.31 Jawaban Ita untuk Soal No. 1.a 168 Gambar 4.32 Jawaban Ita untuk Soal Tes Matematika Uji Coba untuk Soal
No. 1.a 169
Gambar 4.33 Jawaban Shella untuk Soal No. 1.d (Penelitian) 170 Gambar 4.34 Jawaban Tes Matematika Penelitian Rita untuk soal no. 1.d 172 Gambar 4.35 Jawaban Niken untuk Soal Tes Matematika Penelitian
No. 2 174
xxi LAMPIRAN A
A.1 Tabel Jawaban Tes Matematika Siswa Kelas VIIA dalam Hasil
Uji Coba 216
A.2 Tabel Ragam Kesalahan Siswa VIIA dalam Mengerjakan Soal Tes
Matematika Uji Coba 230
LAMPIRAN B
B.1 Tabel Jawaban Tes Matematika 6 Siswa Subyek Penelitian dalam Hasil
Penelitian 236
B.2 Tabel Ragam Kesalahan 6 Siswa Subyek Penelitian 240
B.3 Transkrip Hasil Wawancara 246
B.3.1 Mella 246
B.3.2 Ita 249
B.3.3 Niken 251
B.3.4 Rita 254
B.3.5 Shella 256
B.3.6 Eko 257
LAMPIRAN C
C.1 Soal Tes Esai Matematika Uji Coba dan Kunci Jawaban 261 C.2 Soal Tes Esai Matematika Penelitian dan Kunci Jawaban 263 C.3 Jawaban Tes Matematika Uji Coba Beberapa Siswa Kelas VIIA 266 C.4 Jawaban Tes Matematika Siswa Subyek Penelitian 271
LAMPIRAN D
1
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Matematika sebagai salah satu mata pelajaran yang diajarkan di sekolah, mempunyai posisi yang sangat penting. Seperti yang diungkapkan oleh Suherman et al. (2002), siswa memerlukan Matematika untuk memenuhi kebutuhan praktis dan memecahkan masalah dalam kehidupan sehari-hari. Misalnya dapat berhitung, dapat menghitung berat, dapat mengumpulkan, mengolah, menyajikan dan menafsirkan data. Selain itu, siswa juga memerlukan matematika agar mampu mengikuti mata pelajaran Matematika lebih lanjut, untuk membantu memahami bidang studi lain (seperti: Fisika, Kimia, Geografi, Ekonomi, dan sebagainya), dan agar siswa dapat berpikir logis, kritis, praktis, sistematis, serta kreatif.
Namun ironisnya, penguasaan Matematika yang kuat sejak dini masih belum tercapai. Hal tersebut terlihat dari pencapaian hasil belajar siswa yang masih rendah. Dalam event internasional, seperti The Third Mathematics and
Science Study Repeat (TIMSS-R) pada tahun 1999 disebutkan bahwa di antara
38 negara, prestasi siswa SMP Indonesia berada pada urutan 34 untuk Matematika, sedangkan pada PISA berada pada urutan ke-39 dari 41 peserta (Marpaung, 1992).
mustahil jika siswa mengalami kesulitan dalam mempelajari Matematika, karena bila ditinjau dari segi obyeknya, obyek Matematika bukanlah obyek yang konkret. Sumardyono (2004:30) mengemukakan beberapa karakteristik umum Matematika yaitu: (1) memiliki obyek kajian yang abstrak, berupa fakta, operasi (atau relasi), konsep, dan prinsip, (2) bertumpu pada kesepakatan atau konvensi, baik berupa simbol-simbol dan istilah maupun aturan-aturan dasar (aksioma), (3) berpola pikir deduktif, (4) konsisten dalam sistemnya, (5) memiliki simbol yang kosong dari arti, serta (6) memperhatikan semesta pembicaraan.
Persamaan Linear Satu Variabel merupakan pokok bahasan yang termasuk dalam aspek Aljabar yang diajarkan di kelas VII semester I. Dalam mempelajari Persamaan Linear Satu Variabel di kelas VII, kompetensi dasar yang harus dikuasai seperti yang tercantum dalam KTSP yaitu, menyelesaikan Persamaan Linear Satu Variabel dan membuat model Matematika dari masalah yang berkaitan dengan Persamaan Linear Satu Variabel. Penguasaan kompetensi dasar tersebut sangat penting, karena akan menjadi prasyarat ketika siswa akan belajar pada tahap-tahap selanjutnya misalnya, Pertidaksamaan Linear Satu Variabel, Persamaan Linear Dua Variabel, Pertidaksamaan Linear Dua Variabel, Fungsi Linear, Persamaan Kuadrat, dan Fungsi Kuadrat.
kesalahan-kesalahan yang siswa lakukan dalam menyelesaikan soal-soal tentang topik Garis dan Sudut yang menggunakan Persamaan Linear Satu Variabel dalam proses penyelesaian soal. Berikut ini adalah salah satu contoh kesalahan siswa yang ditemukan peneliti dalam observasi tersebut:
Soal:
Pada gambar berikut ini, AOD adalah garis lurus, ∠ = ∠ = 2 °, dan ∠ = °. Tentukanlah nilai x.
Jawaban siswa:
2 + 2 + = 180
4 = 180 = 180∶4 = 45°
Jawaban siswa di atas menunjukkan bahwa ia melakukan dua kesalahan pada langkah penyelesaiannya, yaitu kesalahan hitung dalam menjumlahkan suku-suku aljabar yang sejenis dan kesalahan dalam mencantumkan satuan
derajat pada penyelesaian akhir. Dari kesalahan yang dilakukan siswa, dapat
diketahui kesulitan belajar yang dialami siswa. Seperti yang diungkapkan oleh Davis, Cooney, Hart dan Quintero (dalam Hadar et al., 1987) bahwa kesalahan siswa dalam menyelesaikan soal dapat menjadi sumber utama informasi untuk mempelajari kesulitan belajar siswa dalam Matematika.
Oleh karena itu, peneliti tertarik untuk meneliti kesalahan-kesalahan yang dilakukan siswa kelas VIIA SMP Kanisius Muntilan tahun ajaran 2009/2010
2 °
dalam mengerjakan soal-soal Persamaan Linear Satu Variabel. Kesalahan-kesalahan siswa tersebut selanjutnya akan dianalisis dan dikelompokkan berdasarkan rumusan kategori kesalahan yang telah dibuat oleh peneliti.
Dengan mengetahui letak kesulitan belajar siswa, guru dapat membantu siswa yang mengalami kesulitan belajar Matematika, khususnya pada pokok bahasan Persamaan Linear Satu Variabel, dengan cara memperbaiki metode mengajarnya atau dapat juga dengan merencanakan pengajaran remidi terutama bagi siswa yang mengalami kesulitan belajar. Oleh karena itu, penelitian analisis kesalahan siswa dalam mengerjakan soal-soal pada Persamaan Linear Satu Variabel dirasa perlu dilakukan.
B. Perumusan Masalah
Jenis kesalahan apa saja yang dibuat siswa kelas VIIA SMP Kanisius Muntilan pada tahun ajaran 2009/2010 dalam mengerjakan soal-soal Persamaan Linear Satu Variabel?
C. Tujuan Penelitian
Tujuan penelitian ini adalah untuk mengetahui jenis kesalahan yang dibuat siswa kelas VIIA SMP Kanisius Muntilan pada tahun ajaran 2008/2009 dalam mengerjakan soal-soal Persamaan Linear Satu Variabel.
D. Batasan Istilah
1. Kesalahan
Kesalahan adalah hasil tindakan yang tidak tepat atau menyimpang dari aturan atau norma-norma tertentu. Kesalahan yang dianalisis dalam penelitian ini hanyalah kesalahan yang muncul pertama kali dan tertulis/ terlihat pada hasil pekerjaan tertulis siswa, dalam menyelesaikan soal-soal Persamaan Linear Satu Variabel.
Kesalahan yang dimaksud pada penelitian ini yaitu: a. kesalahan dalam langkah-langkah penyelesaian
b. langkah-langkah penyelesaian benar, namun jawaban akhir atau penarikan kesimpulan tidak tepat.
2. Persamaan Linear Satu Variabel yang Dipelajari di SMP Kelas VII
Menyelesaikan Persamaan yang Memuat Bentuk Pecahan, dan Penerapan Persamaan dalam Kehidupan.
3. Istilah-istilah Matematika yang Digunakan
a. Bentuk Aljabar, Variabel, Konstanta, dan Koefisien
Sebuah bentuk aljabar adalah suatu kombinasi variabel atau angka (konstanta) atau keduanya, dengan lambang-lambang operasi yang sesuai (Edgerton et al., 1967).
Contoh: "2 ", " 5 ", " 2 + 3 "," ".
Variabel adalah nama, lambang atau simbol anggota sembarang suatu himpunan dari semesta pembicaraan. Bila himpunan itu berupa himpunan bilangan, maka variabel merupakan lambang dari bilangan sembarang dalam himpunan bilangan. Variabel biasanya dilambangkan dengan huruf kecil “a, b, c, ..., z”.
Konstanta adalah nama, lambang atau simbol yang mewakili bilangan tertentu dalam suatu himpunan bilangan.
Contoh: 2 + 3
Pada contoh di atas, yang dimaksud dengan variabel adalah “x”,
sedangkan konstanta adalah “2” dan “3”. Konstanta “2” disebut koefisien dari “x”.
b. Suku Bentuk Aljabar, Suku Sejenis, dan Suku Tak Sejenis
Contoh : Persamaan 2 + 3 , “2x” dan “3y” merupakan bentuk suku-suku aljabar.
Bentuk suku-suku aljabar dikatakan sejenis, bila memuat variabel dan pangkat variabel yang sama. Bentuk suku-suku aljabar dikatakan tak sejenis, bila memuat variabel atau pangkat variabel yang tidak sama.
Contoh bentuk suku sejenis: “5 ” dan “−2 ” “3 ” dan “ ”
Contoh bentuk suku tak sejenis: “2 ” dan “3 ”
“3 ” dan “−2 ”
Suatu bentuk aljabar yang mengandung suku-suku sejenis dapat disederhanakan dengan cara menjumlahkan atau mengurangkan suku-suku sejenis yang ada. Misalnya, 3 −2 + 6 + 4 − dapat disederhanakanmenjadi 9 + .
c. Kalimat Tertutup
Contoh kalimat bernilai benar:
Jumlah dari dua dan tiga adalah lima. Hasil kali lima dan enam adalah tiga puluh. Semarang adalah ibu kota propinsi Jawa Tengah. Contoh kalimat bernilai salah:
Selisih antara tujuh belas dan tujuh adalah sembilan. 15 adalah bilangan prima.
Tugu monas terletak di Yogyakarta. d. Kalimat Terbuka
Kalimat terbuka merupakan kalimat yang belum dapat ditentukan nilai benar atau salahnya.
Contoh kalimat terbuka: 1) P adalah faktor dari 4 2) 2x420
Pada contoh (1) dan (2) di atas, lambang-lambang seperti “P” dan “x” disebut variabel. Angka “2”, “4” dan “20” pada persamaan “2 + 4 = 20” disebut konstanta. Lambang dari suatu bilangan disebut angka, misalnya angka “4” menyatakan lambang dari bilangan 4.
e. Kesamaan
Relasi kesamaan adalah suatu relasi yang menyatakan bahwa dua besaran atau ekspresi adalah sama. Relasi kesamaan dilambangkan dengan lambang “=” (sama dengan).
Contoh:
6 + 1 = 7
18−5 = 13
f. Persamaan
Persamaan adalah kalimat terbuka yang memuat tanda sama dengan, yaitu “=”. Karena persamaan merupakan kalimat terbuka, maka persamaan belum dapat diketahui bernilai benar atau salah.
Contoh:
2 + 6 = 10
−3 = 9
jika siswa SMP kelas VII diajarkan dan diwajibkan untuk menulis dengan kaidah tersebut, maka akan terlalu rumit bagi siswa dan membuat siswa bingung. Oleh karena itu, dalam pembelajaran Matematika di sekolah, siswa tidak diajarkan untuk menulis persamaan dengan menggunakan tanda petik. Begitu pula dalam penulisan laporan penelitian ini, agar tidak rumit dalam penulisan, peneliti tidak menggunakan tanda petik ketika menggunakan kalimat untuk membicarakan suatu persamaan. Dalam penulisan soal tes yang merupakan instrumen penelitian, peneliti juga tidak mencantumkan
tanda petik dalam menulis persamaan.
Contoh :
Penulisan kalimat yang tepat:
Tentukan penyelesaian persamaan “2 + 4 = 5”. Penulisan kalimat dalam laporan ini:
Tentukan penyelesaian persamaan 2 + 4 = 5.
Ekspresi/pernyataan/lambang yang mewakili suatu bilangan di sebelah kiri tanda sama dengan pada suatu persamaan disebut ruas kiri persamaan, sedangkan ekspresi/pernyataan/lambang yang mewakili suatu bilangan di sebelah kanan tanda sama dengan disebut ruas kanan persamaan.
g. Penyelesaian dan Himpunan Penyelesaian Persamaan
persamaan dan menyebabkan persamaan berubah menjadi kalimat bernilai benar, maka bilangan tersebut merupakan penyelesaian dari persamaan. Himpunan penyelesaian dari suatu persamaan adalah himpunan dari semua bilangan yang diwakili oleh variabel dalam suatu persamaan, yang menyebabkan persamaan berubah menjadi kalimat bernilai benar. Himpunan penyelesaian biasanya disingkat HP.
Contoh:
−2 = 6
Bila “x” diganti dengan “8”, maka persamaan bernilai benar. Bila “x” diganti dengan angka selain “8”, maka persamaan bernilai salah, sehingga bilangan 8 merupakan penyelesaian dari persamaan −2 = 6 dan himpunan penyelesaiannya adalah {8}.
Persamaan −2 = 6 merupakan salah satu contoh persamaan kondisional. Persamaan kondisional merupakan suatu persamaan yang akan berubah menjadi kalimat bernilai benar untuk satu atau beberapa angka pengganti variabel, tetapi tidak bernilai benar untuk angka pengganti variabel yang lainnya.
himpunan penyelesaiannya adalah himpunan kosong. Menurut Aufman (1990), suatu persamaan yang tidak mempunyai penyelesaian disebut kontradiksi, misalnya = + 1. Tidak ada bilangan yang akan sama dengan bilangan itu sendiri yang ditambah dengan 1. Persamaan identitas adalah suatu persamaan yang akan menjadi kalimat bernilai benar untuk setiap bilangan real untuk semua bentuk persamaan yang terdefinisi. Misalnya, + = 2 , dan ( + 3) =
+ 6 = 9.
h. Persamaan yang Ekuivalen
Dua persamaan dengan variabel yang sama disebut ekuivalen bila kedua persamaan itu mempunyai himpunan penyelesaian yang sama. Notasi ekuivalen adalah “⟺”.
Contoh:
1) + 5 = 12
Jika x = 7, maka persamaan tersebut menjadi 7 + 5 = 12 yang bernilai benar. Maka penyelesaiannya adalah x = 7.
2) 2 + 10 = 24
Jika x = 7, maka persamaan tersebut menjadi 2 × 7 + 10 = 24, yang bernilai benar. Maka penyelesaiannya adalah x = 7.
Sifat penjumlahan dan perkalian terhadap persamaan
Untuk bilangan real a, b, dan c, = dan + = +
merupakan persamaan yang ekuivalen.
Jika , , dan ≠0, kemudian = dan = merupakan persamaan yang ekuivalen.
Pada dasarnya, sifat tersebut menyatakan bahwa suatu persamaan yang ekuivalen dapat tercipta dengan menambahkan ekspresi/pernyataan pada masing-masing ruas persamaan, atau mengalikan masing-masing ruas persamaan dengan ekspresi/pernyataan bukan nol yang sama (Durbin, 1985). Dalam penelitian ini yang dimaksud dengan “masing-masing ruas” adalah bilangan yang diwakili oleh lambang/nama/simbol pada ruas kiri maupun ruas kanan pada suatu persamaan.
Dalam laporan ini akan sering dijumpai istilah “menambah/mengurangi atau membagi/mengalikan kedua ruas persamaan”. Yang dimaksud dengan “menambah/mengurangi atau membagi/mengalikan kedua ruas persamaan” adalah menambah/mengurangi atau membagi/mengalikan bilangan yang diwakili oleh lambang/nama/simbol pada ruas kiri persamaan maupun ruas kanan persamaan.
i. Operasi Hitung Dasar
1) Operasi Penjumlahan
Operasi penjumlahan dinyatakan dengan lambang “+” (baca: tambah). Penjumlahan dua bilangan a dan b dinyatakan dengan “a+b”. Bilangan a disebut “yang dijumlahkan”, sedangkan b disebut “penjumlah”.
Contoh:
Jumlah dari 2 dan 3 dinyatakan dengan “2 + 3” dan jumlahnya sama dengan 5, sehingga dapat ditulis “2 + 3 = 5”. Bilangan 2 adalah yang dijumlahkan, sedangkan 3 adalah penjumlah.
Suatu penjumlahan disebut operasi biner apabila penjumlahan tersebut hanya melibatkan dua bilangan. Urutan penjumlahan pada bilangan yang bersangkutan dapat diubah tanpa mempengaruhi hasil. Sifat penjumlahan tersebut disebut aturan komutatif pada penjumlahan.
Aturan komutatif pada penjumlahan: Jika , ∈ maka berlaku + = +
Contoh: 5 + 7 = 7 + 5.
2) Operasi Perkalian
Perkalian merupakan penjumlahan berulang suatu bilangan. Lambang “×” atau “ ∙ ” (baca: kali) digunakan untuk menunjukkan operasi perkalian. Perkalian terhadap dua bilangan a dan b
kali. Dalam proses perkalian, lambang operasi perkalian dapat diabaikan, sehingga cukup ditulis “ab”.
Tanda kurung juga dapat digunakan untuk menunjukkan suatu perkalian a dan b seperti, (a)(b), a(b), dan (a)b. Lambang ”×” tidak banyak digunakan dalam aljabar untuk menunjukkan perkalian, karena dapat keliru dengan huruf ”x”.
Perkalian juga seperti penjumlahan dalam suatu operasi biner, di mana urutan bilangan-bilangan pada perkalian dapat diubah tanpa mempengaruhi hasil. Sifat perkalian ini disebut aturan komutatif pada perkalian.
Aturan komutatif pada perkalian: Jika , ∈ maka berlaku × = × . Contoh: 5 × 7 = 7 × 5.
3) Operasi Pengurangan
Operasi pengurangan adalah proses menemukan bilangan yang dijumlahkan lainnya ketika salah satu bilangan yang dijumlahkan dan hasil penjumlahan diketahui. Lambang “ – “ (baca: kurang) digunakan untuk menunjukkan operasi pengurangan. Terdapat suatu hubungan antara operasi penjumlahan dan pengurangan yang disebut operasi berlawanan (invers), yaitu jika , , ∈ maka − = atau
Operasi pembagian adalah proses menemukan faktor lain ketika salah satu faktor atau hasil kali faktor-faktor yang diketahui. Lambang “ ÷ ” atau “ : ” digunakan untuk menunjukkan pembagian yang ditulis “ ÷ ” atau “ : ” (baca: a dibagi b) untuk menunjukkan pembagian
a oleh b.
Seperti halnya penjumlahan dan pengurangan, ada suatu relasi antara perkalian dan pembagian. Pembagian dan perkalian merupakan operasi berkebalikan (operasi invers), yaitu jika , , ∈ dan ≠0
maka ÷ = jika dan hanya jika = .
Pembagian dapat dinyatakan dengan suatu pecahan. Hasil bagi oleh b dapat diwakili oleh pecahan , di mana a disebut pembilang dan b disebut penyebut pecahan.
5) Aturan Distributif Terhadap Penjumlahan Jika , , ∈ , maka berlaku:
a( b + c) = ab + ac
atau
( b + c) a = ba+
Contoh:
3( 6 + 4) = 3( 6) + 3( 4)
3( 10) = 18 + 12
30 = 30
Jika , , ∈ , maka berlaku
( − ) = ∙ − ∙
atau
( − ) = ∙ − ∙
Contoh:
3( 6−4) = 3( 6)−3( 4)
3( 2) = 18−12
7) Aturan Asosiatif untuk Penjumlahan
Jika , , ∈ , maka berlaku ( + ) + = + ( + ). Contoh:
( 3 + 5) + 7 = 3 + ( 5 + 7)
8 + 7 = 3 + 12
15 = 15
8) Aturan Asosiatif untuk Perkalian
Jika , , ∈ , maka berlaku ( ∙ )∙ = ∙( ∙ ). Contoh:
( 3∙5)∙7 = 3∙( 5∙7)
15∙7 = 3∙35
105 = 105
E. Manfaat Penelitian
Manfaat penelitian ini antara lain: 1. Bagi Peneliti
penelitian ini peneliti juga memperoleh pengetahuan dan gambaran tentang kesalahan-kesalahan yang dilakukan siswa dalam menyelesaikan soal-soal Persamaan Linear Satu Variabel.
2. Bagi Guru
18
BAB II
LANDASAN TEORI
A. Persamaan Linear Satu Variabel
Pokok bahasan Persamaan Linear Satu Variabel merupakan pokok bahasan yang baru bagi siswa SMP kelas VII, karena belum pernah dipelajari di tingkat pendidikan sebelumnya (Sekolah Dasar). Dalam mempelajari pokok bahasan Persamaan Linear dengan Satu Variabel, siswa dituntut untuk benar-benar menguasai pengetahuan-pengetahuan prasyarat seperti, operasi hitung pada bilangan bulat dan pecahan, unsur-usur pada bentuk aljabar, dan operasi hitung pada suku-suku aljabar.
1. Pengertian Persamaan Linear Satu Variabel
Persamaan linear satu variabel adalah persamaan yang hanya memuat satu variabel berpangkat satu.
Bentuk umum persamaan linear satu variabel adalah:
+ = 0, dengan a, b, x ∈ R dan ≠0.
Contoh:
+ 5 = 17
“x” adalah variabel, “5” dan “17” adalah konstanta, sedangkan koefisien “x” adalah “1”. Koefisien “1” biasanya tidak perlu ditulis.
6 + 2 = 3 + 1
“y” adalah variabel, “6”, “2”, “3” dan “1” adalah konstanta, sedangkan “2” dan “3” adalah koefisien “y”.
2. Menentukan Penyelesaian dan Himpunan Penyelesaian Persamaan Linear Satu Variabel
Menyelesaikan suatu persamaan adalah menemukan bilangan-bilangan yang diwakili oleh variabel-variabel, yang menyebabkan persamaan tersebut menjadi kalimat bernilai benar. Ada dua cara untuk menentukan penyelesaian atau himpunan penyelesaian dari suatu persamaan linear satu variabel, yaitu:
a. Substitusi
Menyelesaikan persamaan linear satu variabel dengan cara substitusi yaitu, menyelesaikan persamaan dengan cara mengganti variabel dengan angka, sehingga persamaan tersebut bernilai benar. Contoh: Tentukan penyelesaian dari persamaan 2 −1 = 5, “x”
bilangan asli. Jawab:
Untuk = 2, maka 2 × 2−1 = 3 (kalimat bernilai salah). Untuk = 3, maka 2 × 3−1 = 5 (kalimat bernilai benar). Untuk = 4, maka 2 × 4−1 = 7 (kalimat bernilai salah).
Jadi penyelesaiannya adalah = 3, sedangkan = 1, = 2, dan = 3 bukan penyelesaian dari persamaan 2 −1 = 5.
b. Mengubah Persamaan ke Persamaan Lain yang Ekuivalen.
Dua persamaan atau lebih adalah ekuivalen bila persamaan-persamaan tersebut mempunyai penyelesaian yang sama. Cara paling sederhana untuk menyelesaikan suatu persamaan adalah dengan mengubah persamaan menjadi persamaan lain yang ekuivalen dan lebih sederhana, sehingga diperoleh variabel terisolasi di salah satu ruas persamaan, serta sebuah konstanta di ruas yang lain (mencapai persamaan dengan bentuk “variabel=konstanta”). Cara tersebut menggunakan sifat-sifat berikut:
Jika = , maka + = + dan = untuk semua bilangan real a, b dan c.
Jika + = + , maka = untuk semua bilangan real a, b
dan c.
Jika = dan ≠0, maka = untuk semua bilangan real a
dan b.
Selain itu, persamaan yang ekuivalen juga dapat terbentuk dengan membagi kedua ruas persamaan dengan bilangan bukan nol yang sama. Yang dimaksud dengan “masing-masing ruas persamaan” adalah bilangan yang diwakili oleh lambang/nama/simbol pada ruas kiri maupun ruas kanan pada suatu persamaan. Dalam laporan penelitian ini akan sering dijumpai istilah “menambah/mengurangi atau membagi/mengalikan kedua ruas persamaan”. Dalam mengubah persamaan menjadi persamaan lain yang ekuivalen, juga digunakan sifat komutatif, asosiatif, atau distributif.
Berikut ini adalah contoh-contoh penyelesaian persamaan: Contoh 1:
Tentukan penyelesaian persamaan + 2 = 6.
Untuk mengisolasi “x” pada salah satu ruas persamaan, harus menghilangkan “2” dari ruas kiri persamaan. Hal tersebut dapat dilakukan dengan menambah bilangan -2 pada kedua ruas persamaan.
+ 2 = 6
+ 2 + (−2) = 6 + (−2)
+ 0 = 4
= 4
Penyelesaiannya adalah 4.
Penyelesaian tersebut dapat dicek hanya dengan mensubstitusikannya pada variabel.
CEK 4 + 2 ?6
Pada contoh di atas, bilangan 2 dihilangkan dari ruas kiri dengan menambahkan -2 pada masing-masing ruas persamaan. Perhatikan penyelesaian persamaan + 2 = 6berikut ini:
+ 2 = 6 + 2−2 = 6−2
= 4
Pada penyelesaian persamaan di atas, tampak bahwa hasil yang sama juga dapat diperoleh dengan mengurangkan 2 dari masing-masing ruas persamaan, karena + (− ) adalah sama dengan − . Dengan demikian dapat dikatakan bahwa ditambah – ekuivalen dengan dikurangi b.
Contoh 2:
Tentukan penyelesaian persamaan 5 = 10.
Untuk membuat koefisien “x” menjadi “1”, maka kedua ruas persamaan dikalikan dengan atau dibagi 5.
5 = 10
1
5∙5 = 10∙ 1 5
1 = 10
5
= 2
Penyelesaiannya adalah 2.
CEK 5∙2 ? 10
3. Menyelesaikan Persamaan Linear Satu Variabel dengan Metode “Pindah Ruas-Ganti Tanda”
Perhatikan contoh berikut:
5 −3 = + 9
5 −3 + 3 = + 9 + 3
5 = + 9 + 3
5 = + 12
5 − = − + 12
5 − = 12
4 = 12
4
4 =
12 4
= 12 4
= 3
Contoh di atas merupakan contoh penyelesaian persamaan linear satu variabel dengan mengubah persamaan ke persamaan lain yang ekuivalen. Pada langkah 1, tampak bahwa untuk menghilangkan “3” pada ruas kiri persamaan, maka ruas kiri persamaan ditambah 3. Agar persamaan pada langkah 1 tetap ekuivalen dengan persamaan awal, maka ruas kanan persamaan juga ditambah 3 sehingga diperoleh 5 = + 9 + 3. Pada langkah 4, juga tampak bahwa untuk menghilangkan “x” pada ruas kanan persamaan, maka ruas kanan persamaan dikurangi dengan x. Agar persamaan pada langkah 4 tetap ekuivalen dengan persamaan-persamaan sebelumnya, maka ruas kiri persamaan juga dikurangi x sehingga diperoleh
5 − = 12.
Langkah 2
Langkah 4
Langkah 5 Langkah 1
Langkah 3
Langkah 6
Langkah 7
Langkah 8
Langkah 9
Lihat perubahan bentuk persamaan pada langkah 1 ke langkah 3 dan langkah 4 ke langkah 6 berikut ini:
a. 5 −3 = + 9
5 = + 9 + 3
b. 5 = + 12
5 − = 12
Pada langkah 1 ke langkah 3, tampak bahwa “3” pada ruas kiri persamaan seolah-olah pindah ke ruas kanan persamaan dan ganti tanda. “3” yang semula di ruas kiri persamaan sebagai pengurang (bertanda “–“), ketika pindah ke ruas kanan menjadi penjumlah (bertanda “+”). Dari langkah 4 ke langkah 6 juga tampak bahwa “x” pada ruas kanan persamaan seolah-olah pindah ke ruas kiri persamaan dan ganti tanda. Koefisien dari “x” yaitu 1 yang semula bernilai positif di ruas kanan persamaan (bertanda “+”), ketika pindah ke ruas kiri berubah menjadi bernilai negatif (bertanda “–“). Oleh karena itu dapat disimpulkan bahwa mengubah suatu persamaan ke persamaan lain yang ekuivalen dapat dilakukan dengan cara memindahkan suatu suku bentuk aljabar ke ruas lain dan mengganti tandanya. Yang dimaksud dengan “mengganti tanda” adalah mengganti tanda konstanta atau koefisien pada suku bentuk aljabar yang dipindah ruas, jika semula bertanda “+” (bernilai positif), maka ketika pindah ke ruas lain menjadi bertanda “–“ (bernilai negatif), begitu juga sebaliknya. Cara tersebut disebut dengan metode “pindah ruas-ganti tanda”. Cara ini adalah cara yang sering digunakan siswa untuk menyelesaikan persamaan.
Langkah 1
Langkah 3
Langkah 4
4. Menyelesaikan Persamaan Linear Satu Variabel yang Memuat Bilangan Pecahan
Persamaan linear satu variabel yang memuat bilangan pecahan diselesaikan menggunakan cara yang sama dengan persamaan linear satu variabel yang memuat bilangan bulat. Perbedaannya hanya terletak pada fakta bahwa persamaan yang memuat bilangan pecahan lebih sulit untuk dikerjakan dari pada persamaan yang memuat bilangan bulat. Oleh karena itu, kemungkinan terjadi kesalahan dalam proses penyelesaian pada persamaan yang memuat bilangan pecahan pun cenderung lebih besar. Pada langkah pertama penyelesaian persamaan yang memuat bilangan pecahan, disarankan untuk mengubah bilangan pecahan menjadi bilangan bulat. Hal tersebut dapat dilakukan dengan mengalikan kedua ruas persamaan dengan KPK (Kelipatan Persekutuan Terkecil) dari penyebut-penyebut bilangan pecahan yang ada. KPK yang dimaksud adalah bilangan asli terkecil yang dapat dibagi oleh bilangan asli dari penyebut-penyebut bilangan pecahan pada persamaan. Setelah persamaan tidak lagi memuat bilangan pecahan, persamaan dapat diselesaikan dengan cara substitusi, atau mengubah persamaan ke persamaan lain yang ekuivalen.
Contoh : Tentukan himpunan penyelesaian dari + = 10, x anggota himpunan bilangan asli.
Jawab : + = 10
6 + = 6( 10) (kedua ruas dikalikan dengan KPK dari
2 dan 3)
6 + 6 = 6(10) (sifat distribusi perkalian terhadap
3 + 2 = 60 5 = 60
( 5 ) = (60) (kedua ruas dikalikan )
= 12
Jadi himpunan penyelesaiannya adalah {12}.
5. Penerapan Persamaan Linear Satu Variabel dalam Soal Cerita
Menurut Swokowski dan Cole (2001), untuk menyelesaikan soal-soal dalam kehidupan sehari-hari (berbentuk soal cerita), maka langkah-langkah berikut dapat membantu mempermudah penyelesaian:
a. Baca soal beberapa kali dengan hati-hati dan pikirkan fakta yang diberikan, bersama dengan besaran yang tidak diketahui yang dicari. b. Gunakan sebuah huruf untuk melambangkan besaran yang belum
diketahui. Hal ini merupakan langkah yang paling penting dalam penyelesaian.
c. Jika memerlukan diagram (sketsa), misalnya untuk soal yang berhubungan dengan geometri, buat (sketsa) berdasarkan kalimat cerita itu.
d. Mendata fakta yang diketahui, bersama dengan suatu relasi yang melibatkan besaran yang belum diketahui. Suatu relasi mungkin dideskripsikan oleh sebuah persamaan yang merupakan pernyataan tertulis, memuat huruf atau angka pada salah satu atau kedua ruas persamaan.
f. Menyelesaikan persamaan pada langkah (e).
g. Mengecek penyelesaian yang diperoleh dari langkah (f) dengan mengembalikannya ke pernyataan permasalahan awal.
Contoh penggunaan langkah-langkah tersebut dijelaskan pada contoh berikut: Soal:
Jumlah dua bilangan ganjil berurutan adalah 36. Tentukan kedua bilangan tersebut.
Penyelesaian:
Langkah 1 Baca permasalahan lebih dari sekali
Langkah 2 Besaran yang tidak diketahui adalah dua buah bilangan ganjil
yang berurutan, sehingga misalkan (2n – 1): bilangan ganjil pertama (2n + 1): bilangan ganjil kedua.
Langkah 3 Suatu sketsa atau diagram tidak diperlukan dalam masalah ini.
Langkah 4 Diketahui fakta ada dua bilangan ganjil yang berurutan. Suatu
relasi yang melibatkan bilangan ganjil yang belum diketahui yaitu jumlah dua bilangan ganjil tersebut adalah 36. Sehingga, Bilangan I + bilangan II = 36.
Langkah 5 Ketika jumlah bilangan ganjil yang belum diketahui tersebut
adalah 36 (pada langkah 4), persamaan yang terbentuk yaitu, (2n – 1) + (2n + 1) = 36.
Langkah 6 Menyelesaikan persamaan yang telah dirumuskan pada
(2n – 1) + (2n + 1) = 36 2n + 2n – 1 + 1 = 36
4n + 0 = 36 4n = 36 n = n = 9
Bilangan I : (2n – 1) = 2∙9−1 = 17
Bilangan II : (2n + 1) = 2∙9 + 1 = 19
Jadi bilangan ganjil berurutan tersebut adalah 17 dan 19.
Langkah 7 Pengecekan
Jika dua bilangan ganjil berurutannya adalah 17 dan 19, maka jumlahnya 17 + 19 = 36,
terbukti.
B. Metode Penyelesaian Masalah Menurut George Polya (1957)
Dalam bukunya yang berjudul “How to Solve It”, Polya (1957) menjelaskan langkah-langkah yang perlu dilakukan dalam menyelesaikan suatu masalah. Ada 4 langkah yang perlu dilakukan yaitu, memahami masalah, memikirkan suatu rencana, melaksanakan rencana, dan mengecek jawaban. Keempat langkah tersebut mempunyai penjelasan sebagai berikut: 1. Memahami masalah (understanding the problem)
Langkah pertama ini meliputi:
a. Membaca soal dengan teliti sehingga dapat memahami apa yang ditanyakan, data yang diketahui, dan memahami apa saja syaratnya. b. Merencanakan apa yang akan dilakukan.
2. Memikirkan suatu rencana (devising a plan)
Langkah kedua ini meliputi:
a. Mengumpulkan semua data yang ada.
b. Memikirkan beberapa tindakan yang mungkin, antara lain: mencari pola,
menggambar sketsa,
membuat sebuah daftar yang terorganisir, menyederhanakan masalah,
guess and check,
membuat tabel,
menulis beberapa kalimat, dan
mengecek kebenaran data yang diberikan. 3. Melaksanakan rencana (carrying out the plan)
Langkah ketiga ini meliputi:
Melaksanakan rencana penyelesaian masalah. Mengecek tiap-tiap langkah apakah sudah tepat.
Meninjau kembali atau mengubah rencana jika diperlukan. Membuat rencana baru jika perlu.
4. Melihat kembali (looking back)
Pada langkah ini, dilakukan pengecekan kembali penyelesaian yang diperoleh, antara lain:
Mengecek apakah semua syarat yang diberikan soal telah dipenuhi. Masing-masing langkah tersebut sangat penting untuk menentukan suatu penyelesaian. Namun, yang biasanya terjadi adalah siswa memperoleh suatu penyelesaian dengan tanpa berpikir, atau mengabaikan keempat langkah tersebut. Hal yang paling buruk juga terjadi ketika siswa memulai perhitungan, atau penafsiran tanpa memahami masalah. Banyak kesalahan yang dapat dihindari jika siswa melaksanakan rencana dan mengecek masing-masing langkah.
C. Kategori Jenis Kesalahan Menurut Hadar, Zaslavsky, dan Inbar
Hadar et al. (1987) mengklasifikasikan kesalahan siswa dalam mengerjakan soal-soal matematika dalam enam tipe kesalahan sebagai berikut:
1. Penyalahgunaan data.
2. Kesalahan menginterpretasikan bahasa. 3. Kesimpulan yang tidak tepat secara logika. 4. Penyimpangan teorema atau definisi.
5. Penyelesaian yang tidak diteliti kebenarannya. 6. Kesalahan teknis.
Adapun penjelasan dari tiap-tiap kategori kesalahan tersebut adalah sebagai berikut:
1. Penyalahgunaan Data
Kategori ini meliputi kesalahan-kesalahan yang dapat dihubungkan dengan ketidaksesuaian antara data yang diberikan dalam soal dengan data yang dikutip oleh siswa yang meliputi kesalahan-kesalahan berikut:
a. Menambah data yang tidak ada hubungannya dengan soal.
b. Mengabaikan data penting yang sudah ada dan menggantinya dengan data yang tidak relevan.
c. Menguraikan syarat-syarat (dalam pembuktian, perhitungan, penemuan) yang sebenarnya tidak dikehendaki soal.
e. Menggunakan syarat yang tidak sesuai dengan informasi yang diberikan.
f. Menggunakan angka pengganti suatu variabel untuk variabel yang lain.
g. Kesalahan menyalin soal dari lembar soal ke lembar jawab. 2. Kesalahan Menginterpretasikan Data
Kategori ini meliputi kesalahan-kesalahan matematika yang berkaitan dengan ketidaktepatan menerjemahkan suatu pernyataan matematika yang dideskripsikan dalam suatu bahasa ke bahasa yang lain.
Kategori kesalahan ini meliputi kesalahan-kesalahan sebagai berikut: a. Menerjemahkan pernyataan dalam bahasa sehari-hari ke dalam bahasa
atau persamaan matematika dengan arti yang berbeda.
b. Menuliskan simbol dari suatu konsep dengan simbol lain yang artinya berbeda.
c. Kesalahan mengartikan grafik.
3. Kesalahan Menggunakan Logika dalam Menarik Kesimpulan
Pada umumnya yang termasuk kategori ini adalah kesalahan-kesalahan dalam menarik kesimpulan dari suatu informasi yang diberikan atau dari kesimpulan sebelumnya, yaitu:
a. Dari pernyataan implikasi pq, siswa menarik kesimpulan sebagai berikut:
b. Mengambil kesimpulan tidak benar, misalnya memberikan q sebagai akibat dari p tanpa dapat menjelaskan urutan pembuktian yang betul. 4. Kesalahan Menggunakan Definisi atau Teorema
Kesalahan ini merupakan penyimpangan dari prinsip, aturan, teorema atau definisi pokok yang khas. Kategori ini meliputi kesalahan-kesalahan sebagai berikut:
1) Menerapkan suatu teorema pada kondisi yang tidak sesuai, misalnya
menerapkan aturan sinus ,
sin sin
b a
; di mana unsur-unsur a dan α
terdapat pada segitiga yang memuat unsur-unsur b dan .
2) Menerapkan sifat distributif untuk fungsi atau operasi yang bukan distributif. Misalnya:
sin (α + ) = sin α + sin
(a + b)n = an + bn
3) Tidak teliti atau tidak tepat dalam mengutip definisi, rumus, atau teorema. Misalnya:
dalam parabola Xmin = a b
sebagai pengganti Xmin = a b
2
(a-b)2 = a2 + 2ab – b2
5. Penyelesaian Tidak Diperiksa Kembali
Kesalahan dalam memanipulasi simbol aljabar dasar, contohnya: menulis 4
4
b
D. Kategori Jenis Kesalahan Menurut R. D. G. Hall
Untuk mendukung penelitian ini, peneliti akan membahas kesalahan yang dilakukan siswa dalam mengerjakan soal-soal Persamaan Linear Satu Variabel berdasarkan penelitian Hall (2002), serta model klasifikasinya. Penelitian yang dilakukan Hall (2002) dengan judul “An Analysis of Errors
Made in the Solution of Simple Linear Equation”, merupakan penelitian
tentang kesalahan yang dibuat siswa dalam menyelesaikan persamaan linear sederhana. Tujuan penelitian ini adalah untuk mengidentifikasi dan mengklasifikasikan dengan frekuensi relatif, kesalahan yang secara umum dibuat siswa dalam usaha untuk menyelesaikan persamaan linear sederhana. Data diambil dari 246 jawaban ujian siswa yang berusia 12 – 16 tahun yang mengikuti seleksi akademik di sekolah menengah di Bermuda. Penelitian ini murni penelitian survei, yaitu berdasarkan jawaban siswa dalam ujian, tanpa pemberian pengajaran khusus atau tekanan. Pertanyaan yang digunakan sebanyak 6 butir soal. Penentuan pengkategorian jenis kesalahan dalam penelitian ini berdasarkan literatur dan hasil analisis data uji coba.
Sebelum melakukan penelitian dalam skala besar, Hall (2002) melakukan uji coba penelitian. Uji coba penelitian ini melibatkan 87 siswa tahun pertama yang bukan merupakan sampel penelitian. Jawaban siswa tersebut kemudian dianalisis sehingga menghasilkan beberapa kategori jenis kesalahan dalam uji coba, yaitu:
1. Kesalahan penghapusan (deletion error)
3. Kesalahan penukaran penjumlahan (switching addends error) 4. Kesalahan karena kelelahan (exhaustion error)
5. Kesalahan karena kelalaian (omission error)
6. Kesalahan penyalahgunaan invers penjumlahan (misuse of additive
inverse error)
7. Kesalahan ketidak mampuan mengisolasi variabel (inability to isolate
variable error)
8. Kesalahan pembagian (division error)
9. Kesalahan ketiadaan struktur (absence of stricture error).
Tiga tipe kesalahan yaitu kesalahan penghapusan, kesalahan pengulangan distribusi, dan kesalahan penukaran penjumlahan merupakan jenis kesalahan yang ditemukan oleh para peneliti sebelumnya. Kesalahan penghapusan sebelumnya ditemukan oleh Carry et al. (dalam Hall, 2002), sedangkan kesalahan pengulangan distribusi dan kesalahan penukaran penjumlahan ditemukan oleh Kieran (dalam Hall, 2002). Jenis-jenis kesalahan tersebut digunakan dalam pengkategorian jenis kesalahan pada penelitian ini, karena ditemukan dalam uji coba. Keenam jenis kesalahan yang lain merupakan jenis kesalahan baru yang ditemukan Hall (2002) dalam uji coba.
ketidakmampuan mengisolasi variabel). Kesalahan ketiadaan struktur merupakan jenis kesalahan yang tidak dapat digabungkan dengan jenis kesalahan lain, dan dirasa penting seperti kemungkinan untuk menghubungkannya dengan beberapa bentuk kebingungan struktural, baik dari penggunaan tanda sama dengan atau penerapan algoritma.Kesalahan karena kelelahan tidak bertahan di penelitian skala besar karena hanya ditemukan 2 di antara 246 jawaban siswa. Jenis kesalahan Invers yang lain dan kesalahan menghitung juga ikut melengkapi daftar jenis kesalahan. Sehingga diperoleh sembilan jenis kesalahan yang digunakan Hall (2002) untuk mengklasifikasikan kesalahan pada penelitian skala besar. Sembilan jenis kesalahan tersebut adalah:
1. Kesalahan penghapusan (deletion error)
2. Kesalahan pengulangan distribusi (redistribution error)
3. Kesalahan penukaran penjumlahan (switching addends error)
4. Kesalahan transpose (transposing errror)
5. Kesalahan karena kelalaian mencantumkan (omission error)
6. Kesalahan invers yang lain (the other inverse error)
7. Kesalahan menghitung (number line error)
8. Kesalahan pembagian (division error)
Adapun penjelasan dari tiap jenis kesalahan di atas yaitu sebagai berikut: 1. Kesalahan Penghapusan (Deletion Error)
Kesalahan jenis ini biasanya dibuat oleh siswa ketika menyederhanakan pernyataan dalam penyelesaian persamaan. Matz (dalam Hall, 2002), memberikan contoh kesalahan penghapusan yaitu, 3 + 5 = + 3 menjadi + 5 = (di mana 3x – 3 sehingga menjadi x). Contoh kesalahan penghapusan yang ditemukan oleh Hall (2002) :
3 −3 + 2 = 12−3
+ 2 = 9
Kesalahan pada contoh di atas adalah 3x – 3 dengan tidak tepat disederhanakan menjadi x. Kesalahan tersebut tidak banyak ditemukan pada penelitian Hall (2002). Hanya ditemukan 5 kesalahan dari 149 kesalahan yang dibuat siswa ketika menyelesaikan persamaan.
2. Kesalahan Pengulangan Distribusi (Redistribution Error)
Menurut Hall (2002), kesalahan ini mungkin terjadi ketika siswa melakukan proses yang sama pada kedua ruas persamaan. Seperti yang ditemukan oleh Kieran (dalam Hall, 2002), kesalahan pengulangan distribusi terjadi ketika x + 37 = 150 dianggap mempunyai penyelesaian yang sama dengan x + 37 – 10 = 150 + 10.
Contoh kesalahan pengulangan distribusi yang ditemukan oleh Hall (2002):
5 + 2−2 = 2 + 12−2
3. Kesalahan Penukaran Penjumlahan (Switching Addends Error)
Salah satu contoh kesalahan tipe ini yang ditemukan oleh Kieran (dalam Hall, 2002) yaitu x + 37 = 150 dianggap mempunyai penyelesaian yang sama dengan x = 37 + 150. Kesalahan penyalahgunaan invers penjumlahan merupakan bagian dari kategori ini. Hall (2002), mengemukakan bahwa kesalahan penukaran yang dijumlahkan dapat terjadi karena kurangnya pemahaman aspek struktural dalam menyelesaikan persamaan linear.
Contoh kesalahan penukaran penjumlahan yang ditemukan Hall (2002):
6 + 2 = 3 + 12
9 = 14
4 −2 = −1
4 + = −1−2
+ 3 = 5
= 5 + 3
Hall (2002) berpendapat bahwa siswa mungkin hanya mengikuti anjuran guru (dalam usaha mencegah siswa dari kesalahan mentranspose) yaitu, “Jangan hanya mengubah ruas-mengubah tanda”, tetapi bingung bagaimana melakukannya. Siswa justru mengubah ruas namun tidak mengubah tanda.
4. Kesalahan Transpose (Transposing Errror)
dilakukan Hall (2002), kesalahan ini merupakan kesalahan yang paling banyak ditemukan. Ada beberapa fakta yang menunjukkan bahwa kesalahan ini terjadi karena penerapan pendekatan “perubahan ruas-perubahan tanda” tanpa pemahaman. Dengan transposing siswa dengan mudah memindahkan bilangan atau huruf yang ada.
Contoh kesalahan yang ditemukan Hall (2002):
5 + 2 = 2
5 + = 4
5. Kesalahan Kelalaian Mencantumkan (Omission Error)
Kesalahan ini biasanya terjadi di tengah-tengah proses penyelesaian masalah. Kerumitan soal maupun tekanan situasi ketika ujian dapat menjadi penyebab untuk melalaikan huruf atau bilangan.
Contoh kesalahan yang ditemukan Hall (2002):
5 + + 2 = 3 + 12
6 + 2−2 = 3 + 12
6. Kesalahan Invers yang Lain (Other Inverse Error)
Hall (2002) menemukan suatu contoh kesalahan, di mana 4 = 1
Menurut Hall (2002) kesalahan tersebut mungkin disebabkan oleh beberapa faktor. Pertama, kesalahan tersebut karena ketidakmampuan memahami maksud pernyataan 4 = 1. Kedua, mungkin karena tidak memahami invers pembagian atau invers perkalian. Siswa mungkin kenal dengan konsep invers, namun belum tentu memahaminya secara tepat. Ketiga, berdasarkan pernyataan tegas Greeno (dalam Hall, 2002), bahwa siswa sering tidak mengetahui pentingnya untuk mengecek atau mengetahui kebenaran dari penyelesaian yang telah diperolehnya. Keempat, mungkin karena salah menafsirkan 4x. Seperti pada penafsiran 3 yang berarti 3+ , sehingga siswa menafsirkan 4x sebagai 4+x.
7. Kesalahan Perhitungan (Number Line Error)
Dalam mempelajari penyelesaian pokok bahasan Persamaan Linear Satu Variabel, membutuhkan banyak kemampuan prasyarat. Salah satunya adalah kemampuan untuk menyederhanakan pernyataan, seperti -3 + 1. Siswa mungkin bingung dengan −3 + 1 dan −( 3 + 1), atau mungkin salah mengaplikasikan aturan untuk sistem operasi penjumlah bilangan dengan berpikir bahwa penjumlahan 3 + 1 harus dilakukan terlebih dahulu, kemudian tanda negatif dicantumkan di depan 4 yang tadi telah diperoleh. Kesalahan ini disebut sebagai kesalahan aturan penjumlahan.
8. Kesalahan Pembagian
pada operasi pembagian itu sendiri. Kesalahan karena ketidakmampuan mengisolasi variabel tampak ketika siswa dengan benar mencapai langkah 3 = 10, namun berhenti sampai di situ. Kesalahan ini merupakan indikasi bahwa siswa tidak melihat bahwa tidak hanya bisa menambah atau mengurangi kedua ruas dengan bilangan yang sama, tetapi juga bisa dengan membagi atau mengalikan kedua ruas dengan bilangan yang sama. Hal tersebut bisa terjadi ketika siswa tidak memahami bahwa 3x berarti “3 kali x”. Alasan ketiga, siswa tahu bahwa 3x berarti “3 kali x”, tetapi tidak tahu bahwa untuk memperoleh nilai x
dapat dilakukan dengan membagi kedua ruas persamaan dengan 3. Alasan keempat, siswa takut membuat kesalahan pembagian, sehingga meninggalkan persamaan tidak terselesaikan.
Contoh kesalahan ketidakmampuan mengisolasi variabel yang ditemukan Hall (2002):
3x = 10
Tidak ada lanjutannya
Contoh kesalahan pembagian yang ditemukan Hall (2002):
3x = 10
= 3,1
9. Kesalahan Tidak Terstruktur
merupakan sebuah kategori kesalahan untuk kesalahan-kesalahan yang tidak dapat terkategorisasikan di kategori kesalahan lainnya karena struktur atau pola kesalahan yang tidak jelas.
Contoh kesalahan ketiadaan struktur yang ditemukan oleh Hall (2002):
4 −2 = −1
2x−4 = −1
−12x−4 = −1−1
x = 2x−3
E. Kategori Kesalahan Menurut Cipriano dan McCoy
Cipriano dan McCoy (2008), mendeskripsikan tiga tipe kesalahan yang paling sering dilakukan oleh 14 siswa Sekolah Menengah Pertama di wilayah Carolina Utara, dalam mengerjakan soal Persamaan Linear Satu Variabel. Tiga tipe kesalahan tersebut adalah sebagai berikut:
1. Kesalahan Aturan Distributif
menunjukkan kurangnya pemahaman siswa dalam menggunakan aturan distributif dengan tepat.
2. Kesalahan Penyederhanaan
Kesalahan penyederhanaan merupakan kesalahan yang paling sering dilakukan oleh siswa. Kesalahan tersebut sebagian besar berhubungan dengan pengelompokkan suku-suku sejenis. Gambar 2.1 adalah hasil pekerjaan siswa A dalam menyelesaikan soal no. 1, yang memperlihatkan kesalahan karena dengan tidak tepat mengkombinasikan suku sejenis dengan melakukan operasi kebalikan pada ruas persamaan yang sama. Pada baris 3, siswa salah menambahkan 5 untuk menghilangkan -5, ketika seharusnya cukup dengan menggabungkan -5 dan 14 yang terdapat pada ruas kanan persamaan. Kesalahan ini juga dilakukan oleh tiga siswa lainnya. Hal tersebut menunjukkan bahwa siswa kebingungan mengenai menggabungkan suku yang sejenis dan overgeneralisasi aturan yang memindahkan suatu suku ke ruas yang lain pada suatu persamaan, memerlukan dilakukannya operasi yang berlawanan pada kedua ruas persamaan.
Gambar 2.1 Contoh Kesalahan Penyederhanaan yang Ditemukan Cipriano dan
Kesalahan penyederhanaan lainnya adalah melakukan kesalahan perhitungan menggunakan operasi hitung dasar pada suku aljabar yang sejenis. Sebagai contohnya, pada soal 2 dan 3, kedua ruas persamaan memuat bentuk “12x”. Untuk mengumpulkan bentuk yang sama, siswa harus mengurangkan 12x dari kedua ruas. Akan tetapi, tiga siswa menambahkan 12x pada kedua ruas menghasilkan 24x yang seharusnya 0x. Kesalahan ini juga dilakukan oleh dua siswa ketika berusaha memindahkan semua bilangan real dalam suatu soal dan mengumpulkannya pada ruas yang sama dalam persamaan. Lima siswa menyimpulkan bahwa jika mereka mengurangkan 12 dari kedua ruas, bentuk “x” pada ruas kanan akan hilang, namun bentuk “x” pada ruas kiri akan sederhana menjadi “x”. Terutama, mereka menyimpulkan bahwa
12 – 12 = 0 pada ruas kanan, sedangkan 12 – 12 = pada ruas kiri. Sementara kesalahan ini dapat diklasifikasikan sebagai kesalahan penyederhanaan, kesalahan tersebut juga menunjukkan kurangnya pemahaman kemungkinan suatu persamaan tidak mempunyai penyelesaian atau penyelesaian yang tidak terbatas banyaknya.
3. Kesalahan Aritmetika
menggunakan operasi hitung dasar pada bilangan yang dapat menghambat keberhasilan siswa dalam matematika.
Kesalahan pemahaman dengan konsep dasar juga mengakibatkan siswa melakukan kesalahan fatal dalam penyelesaian persamaan. Siswa seringkali tidak memahami bahwa tanda sama digunakan untuk menunjukkan suatu relasi. Kieran (dalam Cipriano dan McCoy, 2008) menemukan bahwa siswa cenderung melihat tanda sama dengan sebagai tanda untuk menuliskan suatu jawaban, dan sering menggunakan tanda sama dengan sebagai penghubung antara langkah tanpa perlu mempertahankan kesamaan pada kedua ruas.
F. Kesalahan-kesalahan yang Sering Dilakukan Siswa dalam Menyelesaikan Soal-soal Aljabar
Perso (1992) dalam penelitiannya juga menemukan kesalahan perhitungan yang dilakukan siswa dalam operasi penjumlahan pada himpunan bilangan pecahan.
Contoh: 2
3+ 1 4=
3 7
Kesalahan tersebut biasanya terjadi ketika siswa belajar penjumlahan pada bilangan pecahan setelah belajar perkalian pada bilangan pecahan. Metode penyelesaian pada contoh di atas salah, namun sistematis. Siswa mempunyai gagasan penyelesaian tersebut berawal dari apa yang telah ia ketahui.