Bab II Tinjauan Pustaka

II.1 Proses Stokastik dan Sifat-Sifatnya

Suatu himpunan peubah acak

{

Z

( ) ( )

t Z t ∈E,t∈T

}

disebut proses stokastik, yaitu koleksi peubah acak Z

( )

t dimana untuk setiap t dalam himpunan indeks T. Dalam proses stokastik ada dua himpunan yang terlibat yaitu: (1) Ruang keadaan (E), yaitu himpunan yang mengandung semua nilai Z yang mungkin, dan (2) himpunan indeks parameter (T) adalah himpunan barisan dimana peubah acakZ dibangun. Biasanya indeks parameter adalah waktu.

Data spasial dapat dinyatakan sebagai hasil observasi dari proses stokastik

( ) ( )

{

Z t Z t ∈E,t∈T

}

dimana indeks parameternya adalah lokasi. Untuk membedakannya dapat ditulis dengan

{

Z

( )

s s∈D

}

dimana D adalah himpunan random di Rd. Nilai data di lokasi s yaitu z

( )

s disebut realisasi dari peubah acak

( )

s

Z . Z

( )

s disebut juga peubah teregional, yaitu peubah yang terdistribusi di dalam ruang dan menunjukkan adanya korelasi spasial. D koleksi dari peubah-peubah acak disebut fungsi acak.

Berdasarkan kestasionerannya, proses stokastik dibagi menjadi dua, yaitu strictly stationary processes (kestasioneran kuat) dan weakly stationary processes (kestasioneran lemah) atau disebut juga stasioner orde dua. Z

( )

s dikatakan stasioner kuat, yaitu jika untuk setiap h,n,s₁,...,s_n distribusi dari Z

( )

s₁ ,..,Z

( )

s_n dan Z

(

s₁ +h

)

,..,Z

(

s_n +h

)

mempunyai distribusi gabungan yang sama. Dengan kata lain Z

( )

s dikatakan stasioner kuat jika distribusi gabungannya tidak berubah karena pertambahan h. Akan tetapi karena keterbatasan data, kondisi ini seringkali tidak dipenuhi, maka biasanya hanya dua momen pertama dari Z

( )

s yang diharapkan memenuhi sifat ini yaitu rataan dan variansi. Kondisi ini dinamakan stasioner lemah.

Menurut Armstrong (1998), proses stokastik

{

Z

( )

s s∈D

}

dimana D adalah himpunan random di Rd akan memenuhi stasioner lemah jika:

1. Rataan dari Z

( )

s konstan untuk setiap s∈D, tidak bergantung lokasi, maka, E

[

Z

( )

s

]

=µ

( )

s ,∀s∈D

2. Fungsi kovariansi antara dua titik lokasi s dan s+h hanya bergantung pada vektor h.

( )

[

( )

]

(

) (

(

)

[

(

)

]

)

[

Z s E Z s Z s h E Z s h

]

E − + − + =Cov

[

Z

( ) (

s ,Z s+h

)

]

=C

( )

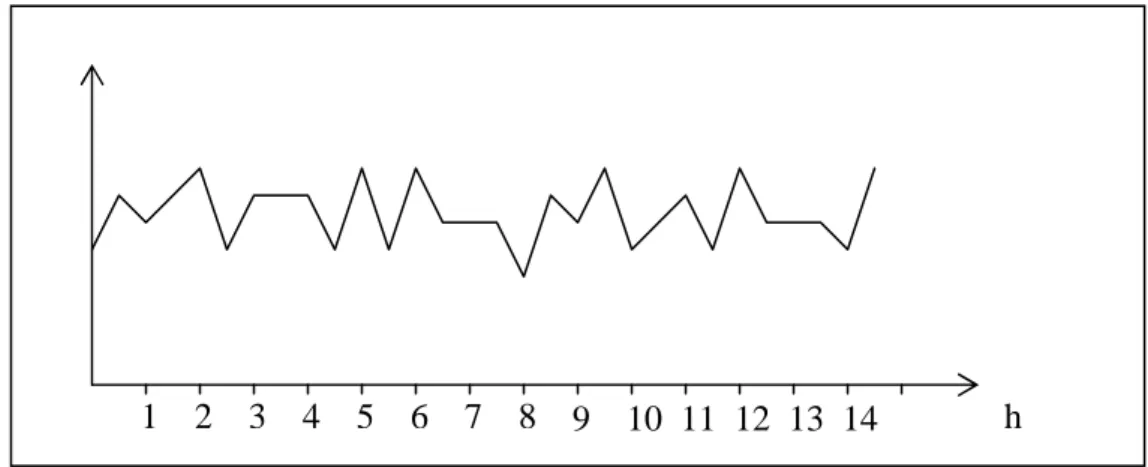
h

Gambar II.1. Rata-rata berfluktuasi pada nilai yang konstan pada jarak h, sehingga memenuhi stasioner

II.2 Semivariogram

Sebelum membicarakan semivariogram kita kemukakan 3 hal penting yang merupakan bagian dasar kovariansi dan hubungannya dengan semivariogram untuk peubah acak stasioner, yaitu:

1. C

( )

0 =σ2, artinya kovariansi pada jarak nol adalah variansi. Maksudnya adalah karena jarak h=0, maka hanya ada satu peubah acak Z

( )

s yang diamati.

2. C

( )

h =C

( )

−h , artinya kovariansi adalah fungsi genap.

3. C

( )

h ≤C

( )

0 , artinya kovariansi adalah fungsi terbatas dan kovariansi bisa juga bernilai negatif. Hal ini terjadi apabila nilai Z

( )

s yang besar berkaitan dengan nilai Z

(

s+h

)

yang kecil.

Dalam geostatistika, untuk mengukur hubungan spasial antara peubah acak di suatu titik lokasi s dan s+h masing-masing Z

( )

s dan Z

(

s+h

)

, dengan h jarak antara dua lokasi digunakan semivariogram.

Variogram antara Z

( )

s dan Z

(

s+h

)

, dimanaZ

( )

s adalah peubah acak Z di D

s∈ dan Z

(

s+h

)

adalah peubah acak Z di s+h∈D, dengan d

R D∈ didefinisikan,

( ) (

)

(

Z s Z s h

)

Var − + =E_⎣⎡

(

Z s

( )

−Z s h

(

+

)

)

2 ⎤_⎦−

(

E Z s⎡_⎣

( )

−Z s

(

+h

)

⎤_⎦

)

2

Variansi dapat dinyatakan sebagai kovariansi pada jarak nol

(

C

( )

0

)

. Apabila kovariansi tidak ada, peubah acak diasumsikan memenuhi hipotesis stasioner intrinsik. Proses spasial

{

Z

( )

s s∈D

}

memenuhi stasioner intrinsik jika:

1. E

[

Z

( ) (

s −Z s+h

)

]

=0

2. Var

(

Z

( ) (

s −Z s+h

)

)

=E_⎣⎡

(

Z s

( ) (

−Z s h+

)

)

2 ⎤_⎦=2γ

( )

h

Artinya rataan dan variansi Z

( ) (

s −Z s+h

)

ada dan tidak bergantung pada lokasi s. 2γ

( )

h disebut fungsi variogram. Setengah dari variogram disebut semivariogram, dinotasikan γ

( )

h .

Secara geometri, h adalah suatu vektor yang nilainya tergantung pada arah dan panjang vektor tersebut. Dalam praktek biasanya arah hanya ditentukan oleh mata angin saja, yaitu Utara, Timur, Selatan dan Barat. Jika semivariogram hanya tergantung pada panjang h saja disebut isotropik. Sedangkan semivariogram tergantung pada arahnya maka disebut anisotropik.

Menurut Armstrong (1998) apabila semivariogram yang cocok dengan semivariogram eksperimental sudah diperoleh, maka model ini dapat digunakan untuk memprediksi di lokasi-lokasi yang tidak tersampel melalui kriging.

Selanjutnya menurut Armstrong (1998) hubungan antara semivariogram dan kovariansi:

( )

[

(

( ) (

)

)

]

2 2γ h =E Z s −Z s+h ( )

(

(

( )

)

(

( )

)

)

2 2γ h =E_⎢⎡ Z s −µ − Z s+h −µ ⎤_⎥ ⎣ ⎦ ( )

(

(

( )

)

2

(

( )

)

(

( )

)

(

( )

)

2

)

2γ h =E_⎢⎡ Z s −µ −2 Z s −µ Z s+h −µ + Z s+h −µ ⎤_⎥ ⎣ ⎦

( )

[

(

( )

)

2

]

[

(

( )

) (

(

)

)

]

[

(

(

)

)

2

]

2 2γ h =E Z s −µ −E Z s −µ Z s+h −µ +E Z s+h −µ

( )

h 2C

( )

0 2C

( )

h 2γ = −

( )

h =C

( ) ( )

0 −C h γ (2.1)

Hubungan tersebut dapat diilustrasikan sebagai berikut,

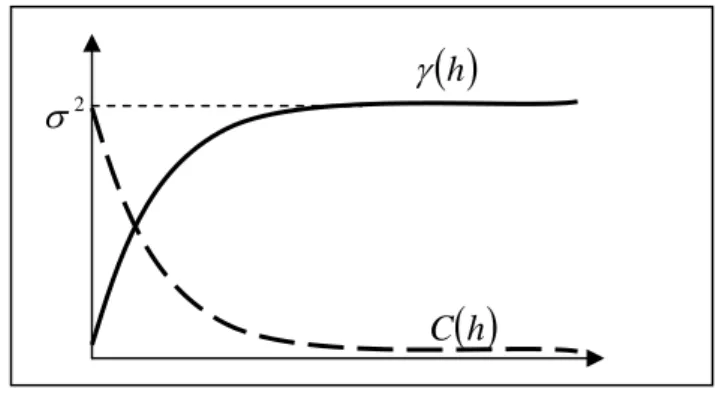
Gambar II.2. Hubungan antara variogram dan kovariansi

Berdasarkan gambar di atas, variogram mulai dari nol dan naik menuju nilai tertentu, sedang kovariansi mulai dari variansi dan monoton turun.

( )

h γ

( )

h C 2 σ

II.2.1 Model Semivariogram

Menurut Cressie (1993) ada beberapa model yang dapat dicocokkan, yaitu: 1. Model Linier (Linear Model)

⎩ ⎨ ⎧ + = h C C h 0 0 ) ( γ 0 0 ≠ = h h

Model ini berhubungan dengan fenomena yang murni acak dengan tanpa-korelasi antar nilai-nilainya.

2. Model Bola (Spherical Model)

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + = , , 2 2 3 , 0 ) ( 0 3 3 0 C C a h a h C C h γ a h a h h ≥ ≤ < = 0 0

Model ini mengikuti model pertumbuhan yang hampir linier sampai pada jarak tertentu, kemudian tercapai stabilitas.

3. Model Eksponensial (Exponential Model)

⎪ ⎩ ⎪ ⎨ ⎧ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + = , exp 1 , 0 ) ( 0 a h C C h γ 0 0 ≠ = h h

Model ini pada awalanya meningkat lebih cepat tetapi hanya mengarah pada sill dan tidak betul-betul mencapai nilai tersebut.

4. Model Kuadratik Rasional (Rational Quadratic Model)

⎪ ⎩ ⎪ ⎨ ⎧ + + = , / 1 , 0 ) ( 2 2 0 a h h C C h γ 0 0 ≠ = h h

5. Model Gelombang ( Hole-Effect Model)

, sin 1 , 0 ) ( 0 ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + = h a h a C C h γ 0 0 ≠ = h h

Model ini termasuk model yang langka dengan sebuah efek lubang dan berhubungan dengan struktur yang kontinyu.

6. Model Kuasa (Power Model) ⎩ ⎨ ⎧ + = , , 0 ) ( 0 α γ h C C h 0 0 ≠ = h h dengan 0<α ≤2

Model ini cocok untuk semivariogram dalam Rd, d ≥1

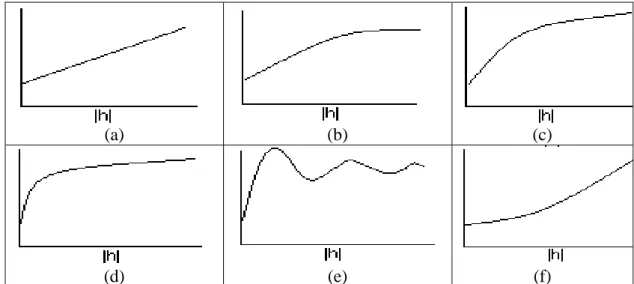
(a) (b) (c)

(d) (e) (f)

Gambar II.3. (1) Model Linier, (2) Model Bola, (3) Model Eksponensial,(4) Model Kuadratik Rasional, (5) Model Gelombang, (6) Model Kuasa

Keterangan

a : Range (Jangkauan), merupakan jarak maksimum dimana masih terdapat korelasi spasial antar data.

0

C : Efect Nugget (Efek Gumpal), merupakan diskontinu disekitar titik asal dimana semivariogram pada jarak sama dengan nol (pada lokasi itu sendiri) tidak sama dengan nol.

C

C₀ + : Sill (ambang), merupakan nilai semivariogram yang konstan untuk h yang tidak terbatas. Biasanya nilainya mendekati variansi data. (Armstrong; 1998)

Dalam tulisan ini akan digunakan semivariogram model bola. Menurut Setyadji (2005), model bola merupakan model yang paling umum dipakai. Model ini menggunakan ekspresi polinomial yang sederhana dan bentuknya sesuai dengan berbagai jenis fenomena yang diamati. Model bola mempunyai kelakuan linier

disekitar titik (0,0). Pada model bola, kenaikan semivariogram pada awalnya tidak terlalu cepat atau landai. Satu pertumbuhan yang hampir linier sampai pada jarak tertentu, kemudian tercapai stabilitas.

Gambar. II.4. Ilustrasi Semivariogram Model Bola dan Eksperimental

Berdasarkan gambar di atas, diilustrasikan bahwa semivariogram eksperimental dapat naik maupun turun sesuai dengan data yang diperoleh. Sedangkan model bola mengikuti sebuah model linier. Untuk lebih jelasnya dapat dilihat pada perhitungan semivariogram eksperimental dari penelitian ini, yang akan dijelaskan pada bab III.

Ada beberapa sifat plot semivariogram, yaitu:

1. γ

( )

h selalu berawal di titik nol (untuk h= 0), Z

( )

s =Z

(

s+h

)

mungkin terjadi diskontinu disekitar titik pangkal γ

( )

h ≠0.

2. γ

( )

h bertambah besar jika h membesar. Hal ini menunjukkan nilai pada dua data akan sangat bergantung pada jarak kedua data tersebut.

3. γ

( )

h naik menuju nilai tertentu setelah itu cenderung konstan. Kenaikan nilai

( )

h

γ akan berlangsung selama data masih berkorelasi.(Armstrong; 1998). II.2.2 Semivariogram Eksperimental

Selanjutnya dikenal semivariogram eksperimental yang merupakan semivariogram yang diperoleh dari data yang diketahui. Menurut Armstrong (1998) semivariogram eksperimental didefinisikan sebagai,

teoritis eksperimen semivarogram

( )

_{( )}

_∑

( )

(

( ) (

)

)

= + − = N h i i i Z s h s Z h N h 1 2 2 1 ˆ γ (2.2)

dengan si : lokasi sampel

Z

( )

si : nilai data pada lokasi si.

N

( )

h : banyaknya pasangan

(

si,si +h

)

yang mempunyai jarak h. II.3 Taksiran Model Semivariogram

Pada dasarnya taksiran model semivariogram pada semivariogram eksperimental merupakan pencarian dua nilai parameter utama pada model semivariogram teoritis yaitu C dan a.

Pedoman penting dalam melakukan penaksiran model semivariogram adalah: 1. Efek nugget (C₀) didapat dari perpotongan garis tangensial dari dua titik

pertama semivariogram dengan sumbu vertikal.

2. Sill kira-kira sama dengan atau mendekati variansi populasi. Garis tangensial di atas akan memotong garis sill pada jarak a

3

2 _{, sehingga selanjutnya}

dapat dihitung harga a. jarak ini disebut practical range.

3. Interpretasi efek nugget untuk semivariogram dengan sudut toleransi 1800 akan sangat membantu untuk memperkirakan besarnya efek nugget. (Darijanto, 1999).

II.4 Validasi Model

Menurut Kitanidis (1997), yang dimaksud dengan validasi model adalah melakukan uji terhadap model. Setiap model empiris harus diuji terlebih dahulu sebelum digunakan untuk melakukan prediksi.

Sebuah uji statistik adalah memadankan sebuah eksperimen yang dihubungkan pada validasi teoritis. Untuk melihat apakah model spherikal dengan parameter yang diperoleh merupakan model semivariogram yang sesuai, akan dilakukan uji galat hasil taksiran.

Prosedur yang digunakan dalam validasi model semivariogram adalah dengan mengevaluasi kecocokan model tersebut terhadap data dengan melihat galat taksirannya, yaitu selisih antara data dengan nilai penaksirnya. Untuk menaksir nilai data dilakukan dengan menggunakan metode kriging, yaitu dengan mengeliminasi salah satu nilai data pada masing-masing lokasi, kemudian ditaksir nilainya pada lokasi tersebut dengan kriging. Namun sebelumnya, galat hasil taksirannya dibakukan terlebih dahulu, yaitu dibagi dengan standar deviasinya. Standar deviasi galat dapat diperoleh dari akar variansi kriging masing-masing lokasi.

Uji statistik yang digunakan adalah statistik Q1, yaitu

∑

= − = n s s n Q 2 1 1 1 _ε , (2.3) dimana s s s z s z σ

ε = ( )− ∗( ) adalah galat taksiran kriging yang telah distandarkan.

1

Q adalah variabel acak dengan rataan E

[ ]

Q₁ =0 0 ] [ 1 1 1 1 ] [ 2 2 1 = − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − =

∑

∑

= = n k k n k k E n n E Q E ε ε dan variansi

[ ]

1 1 2 1 = ₋ n Q E

∑∑

∑∑

∑

= = = = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = n k l n l k n k l n l k n k k E n n E n E Q E 2 2 2 2 2 2 2 2 2 1 [ ] 1 1 1 1 1 1 ] [ ε ε ε ε ε 1 1 ) 1 ( 1 1 2 − = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = n n n Sehingga diperoleh Q₁~ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −1 1 , 0 n N .

Model semivariogram ditolak jika

1 2 1 − > n Q .

Staistik uji lainnya yang digunakan adalah statistik Q₂, yaitu

∑

= − = n s s n Q 2 2 2 1 1 _ε . (2.4)

2

Q adalah variabel acak dengan rataan E

[ ]

Q₂ =1

1 ) 1 ( 1 1 1 1 1 1 ] [ 2 2 2 2 2 − = − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − =

∑

∑

= = n n n E n E Q E n k k n k k ε ε dan variansi

[

(

)

]

1 2 12 2 − = − n Q E , Sehingga diperoleh (n−1)Q2~ 1 2 − n χ .

Model semivariogram ditolak jika Q2 >U atau Q2 <L.

II.5 Prediksi Kriging

Kriging adalah sebuah algoritma interpolasi untuk memprediksi suatu titik atau rata-rata blok yang tidak diambil sampelnya. Metode kriging merupakan sebuah metode yang memberikan estimasi linier terbaik dari suatu titik atau rata-rata blok, yaitu memberikan nilai variansi minimum. Metode ini dikenal dengan istilah BLUE (Best Linier Unbiased Estimation). Dalam hal ini, estimator adalah sebuah fungsi linier dari data dengan bobot dihitung sesuai pada syarat ketakbiasan dan variansi minimum. Bobot ditentukan dengan menyelesaikan sebuah sistem persamaan linier dengan koefisien yang tergantung hanya pada variogram yang menggambarkan struktur sebuah keluarga fungsi.

Gambar II.5. Kriging

Menurut Kitanidis (1997), dalam kriging nilai estimasi pada titik s0 akan

dihampiri oleh sejumlah n titik data dari Z(s_i)dengan i =1,2,...,n Estimator merupakan kombinasi linier nilai fungsi pada titik data dengan bobot λi,

( )

=

_∑

n₌

( )

i iZ si s Z 1 0 ˆ λ _(2.5)

dengan λ_i, i=1,_K,n adalah koefisien atau bobot.. s1

s2

s3

s4

Estimasi galat adalah selisih antara estimasi Zˆ

( )

s₀ dengan nilai sebenarnya

( )

s0 Z ,

( ) ( )

0 0 ₁

( ) ( )

0 ˆ _{s Z s Z s Z s} Z n i i i − = −

∑

₌λ

Dalam kriging, estimator memenuhi tak bias, artinya rata-rata estimasi galat adalah nol.

( )

0

( )

0

ˆ ₀

E⎡_⎣ Z s −Z s ⎤_⎦= , atau E

[

Zˆ

( )

s₀

]

=E

[

Z

( )

s₀

]

Selanjutnya adalah variansinya minimum, artinya rata-rata kuadrat estimasi galat adalah sekecil mungkin.

( ) ( )

(

Zˆ s0 Z s0

)

Var −

(

( ) ( )

)

(

[

(

( ) ( )

0 0

)

]

)

2 2 0 0 ˆ ˆ _{s Z s E Z s Z s} Z E_⎢⎣⎡ − _⎥⎦⎤− − = (2.6)

Karena tak bias, maka persamaan (2.6) menjadi

( ) ( )

(

Zˆ s0 Z s0

)

Var − =E_⎢⎣⎡

(

Zˆ

( ) ( )

s₀ −Z s₀

)

2⎤_⎥⎦ Perdefinisi diperoleh

( ) ( )

(

)

_⎥⎦⎤ ⎢⎣ ⎡ ₋ 2 0 0 ˆ _{s Z s} Z

E _{1 1} Cov

(

s ,s

)

2 ₁ iCov

(

si,s0

)

Cov

(

s0,s0

)

n i j i j i n j n i − + =

∑

₋

∑

₌ λλ

∑

₌ λ (2.7)

Dengan menggunakan hubungan kovariansi dan semivariogram (persamaan 2.1), dimana h adalah jarak antara dua titik lokasi, maka dari persamaan (2.7) diperoleh,

( ) ( )

(

)

_⎥⎦⎤ ⎢⎣ ⎡ ₋ 2 0 0 ˆ _{s Z s} Z E

(

s₀ s₀

)

(

s s

)

2 _i

(

s_i s₀

)

i j i j i j i − + − − − − = γ

∑

∑

λλ γ

∑

λγ (2.8)

Nilai minimum dicapai pada saat turunan pertama dariE_⎢⎣⎡

(

Zˆ

( ) ( )

s₀ −Z s₀

)

2_⎥⎦⎤=0. Perdefinisi diperoleh turunan pertama dari persamaan (2.8) terhadap λi,

( ) ( )

(

)

i d s Z s Z E d λ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ 2 0 0 ˆ

(

)

2

(

0

)

2 j si sj si s j − + − − =

∑

λ γ γ (2.9)

Dengan membuat nilai persamaan (2.9) sama dengan nol, diperoleh:

(

)

2

(

)

0 2 − + − ₀ = −

∑

_j s_i s_j s_i s j γ γ λ

(

)

2

(

0

)

2 _j s_i s_j s_i s j − = −

∑

λ γ γ

Himpunan berbobot yang meminimumkan variansi error dapat ditulis dengan

1 + n persamaan berikut:

(

si sj

)

(

si s0

)

j j − = −

∑

λ γ γ ∀i=1_Kn

Dalam bentuk matriks,

(

)

(

)

(

)

(

)

⎟⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − − n n n n s s s s s s s s γ γ γ γ L M O M K 1 1 1 1 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ n λ λ M 1 =

(

)

(

)

⎟⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − 0 0 s s s s n i γ γ M (2.10)

Bentuk matriks (2.10) di atas dapat ditulis menjadi,

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ n λ λ M 1 =

(

)

(

)

(

)

(

)

1 1 1 1 1 − ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − − n n n n s s s s s s s s γ γ γ γ L M O M K

(

)

(

)

⎟⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − 0 0 s s s s n i γ γ M (2.11)

Untuk i=1Ln; j=1Ln; γ

(

s_i −s_j

)

merupakan konstanta. Selanjutnya matriks (2.11) dapat ditulis menjadi,

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ n λ λ M 1 = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ nn n n a a a a L M O M K 1 1 11

(

)

(

)

⎟⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − 0 0 s s s s n i γ γ M

Sehingga dapat diperoleh nilai, λ_{i ij}

(

_{i j}

)

j s s a − =

∑

γ , i=1_Ln

Substitusi λ_i dalam persamaan (2.5) , sehingga diperoleh

( )

0 ˆ _s Z i

(

si s0

)

i − =

∑

βγ dengan ij

( )

j j i =

∑

a Z s β (2.12)

Dalam pengolahan data, persamaan (2.12) menyatakan bahwa dengan memasukkan nilai koordinat titik observasi, maka akan diperoleh persamaan sebanyak i. Pada akhirnya akan diperoleh data hasil prediksi Zˆ

( )

s0 untuk