Isomorfisma Barisan Eksak

(1)

Nur Erawaty

†

Abstrak

Modul yang saling isomorfik mempunyai struktur yang mirip satu sama lain. Demikian pula halnya bagi barisan modul yang saling isomorfik. Jika yang satu eksak, yang lainnya juga eksak. Begitu pula barisan eksak yang sebagian besar modulnya saling isomorfik maka dapat ditunjukkan bahwa semua modulnya isomorfik.

Kata Kunci : Isomorfik, barisan eksak.

1. Pendahuluan

Salah satu obyek aljabar yang lebih umum dari grup, gelanggang, lapangan maupun ruang vektor adalah modul. Seperti pada obyek aljabar yang lain, modul dapat dibandingkan dengan modul yang lain, apakah mereka isomorfik atau tidak, apakah cuma pemetaan satu-satu atau pada saja. Tulisan ini akan difokuskan pada barisan eksak dari modul, apakah isomorfik mempertahankan sifat eksak dari barisan modul.

2. Pembahasan

Tulisan ini diawali dengan memperkenalkan modul dan homomorfisma modul. Definisi 1.

Misalkan

R

gelanggang. Grup abel



A, 



disebut modul atas

R

atau lebih sederhana

R

-modul jika ada operasi RxA A yang ditulis

 

r,a r*a sedemikian sehingga untuk setiap

A

b

a

,



dan

r

,

s



R

memenuhi kondisi berikut: 1. r*



ab



r*a

2.



rs



*ar*as*a 3.

 

rs *ar*



s*a



Jika

R

memiliki unsur 1 sedemikian sehingga 4. 1*aa untuk setiap aA maka

A

disebut

R

-modul uniter. Contoh:

a. Jika

K

lapangan maka

K

-modul uniter merupakan ruang vektor atas

K

.

b.

Z

-modul uniter sama dengan grup abel, aksi

Z

ditulis n*a a...a jika

n



0

.

c. Setiap grup abel

A

dapat dijadikan suatu modul atas gelanggang

R

sebarang dengan aksi trivial r*a0 untuk setiap

r



R

dan setiap aA.

(2)

d. Misalkan

R

gelanggang, jika

I

ideal

R

maka

I

suatu

R

-modul dengan r*x:rx (perkalian dalam

R

) dan gelanggang kuosien R I suatu

R

-modul dengan



y I



ry I

r*  :  .

Berikut ini akan didefinisikan submodul dan homomorfisma modul. Untuk menyederhanakan notasi, selanjutnya aksi * ditulis dalam notasi justaposition.

Definisi 2.

Misalkan

A

suatu

R

-modul.

a. Dubgrup U  A disebut

R

-modul dari

A

jika ruU untuk setiap

r



R

dan setiap uU , yaitu U sendiri merupakan modul atas aksi pada

R

.

b. Jika U  A suatu

R

-submodul maka grup kuosien AU menjadi

R

-modul dengan



a U

 

r a



U

r  :   . Modul ini disebut modul kuosien dari

A

modulo U . Definisi 3.

Misalkan

A

dan

B

R

-modul. Pemetaan

f

:

A



A

disebut homomorfisma

R

-modul jika



a a'



f

   

a f a'

f    dan f



ra



rf

 

a untuk semua

a

,

a

'



A

dan

r



R

. Dengan kata lain, homomorfisma

R

-modul merupakan homomorfisma grup yang

R

-linear dalam artian komutatif dengan aksi

R

.

Homomorfisma modul yang bijektif

f

disebut isomorfisma modul. Dalam kasus ini, pemetaan inversnya f 1 juga merupakan homomorfisma modul.

Teorema-teorema yang berlaku pada grup juga berlaku di dalam modul.

Teorema isomorfisma.

1. Misalkan



:

A



B

homomorfisma

R

-modul maka

im





ker



. 2. Misalkan ABC submodul atas

R

-modul maka

C

B

A

B

A

C



.

3. Misalkan

A

,

B

submodul dari

R

-modul C maka

B A A B B A    .

Berikut ini akan dipaparkan konsep barisan eksak modul-modul.

Definisi 4.

Misalkan

R

gelanggang. Barisan

...



₁







1





₁



...

   n f n f n

A

n n

_R

_{-modul dan}

(3)

Barisan eksak dalam bentuk khusus

 

0  A B C

 

0 disebut barisan eksak pendek. Di sini



injektif,



surjektif dan im

 



ker

 



.

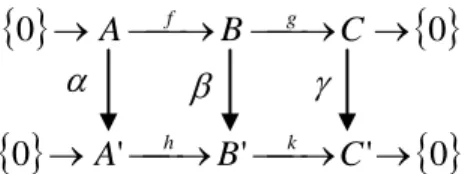
Perhatikan diagram berikut.

Diagram ini komutatif dalam artian komutatif modul dan isomorfisma dengan



,



,



isomorfisma dapat ditulis

h







f

dan

k







g

. Barisan atas eksak jika dan hanya jika barisan bawah eksak. Hal ini dapat dibuktikan sebagai berikut.

Misalkan barisan atas eksak, artinya im

 

h ker

 

k .

1. Ambil xim

 

h sebarang, maka xh

 

a' untuk suatu a'A'. Karena



isomorfisma, ada aA sehingga . xh

 

a' h





 

a

      

 h



a 



f a . Karena diagramnya komutatif,

h







f

.

Dan k

 

x k





f

 

a

    

 k



f a . Karena diagramnya komutatif,

k







g

sehingga

     

x 



g f a 





g



f

 

a



  





0 0

k (karena im

 

f ker

 

g dan



homomorfisma). Dengan demikian k

 

x 0 dan

x



ker

K

. Jadi im

 

h ker

 

k .

2. Ambil y'ker

 

k sebarang, maka k

 

y' 0. Karena

y

'



B

'

dan



pada maka y'



 

k untuk suatu

y



B

 

y' 0 k

 



y



0 k



Karena

k







g

maka





g

 

y

   

 k



y 0.



homomorfisma 1-1 sehingga g

 

y 0 akibatnya yker

 

g im

 

f . Tulis y  f

 

a untuk suatu aA.

Sekarang y'



 

y 





f

 

a

      





f a  h



a h





 

a



. Sebut



 

a a', berarti ada a'A' sedemikian sehingga y'h

 

a' . Dengan demikiany'im

 

h , dan

 

k im

 

h

ker .

Dari 1 dan 2, im

 

h ker

 

k . Dengan kata lain barisan bawah eksak.

Sebaliknya misalkan barisan bawah eksak, im

 

h ker

 

k . Akan dibuktikan bahwa barisan atas eksak atau im

 

f ker

 

g .

(i). Jika xim

 

f sebarang, maka x f

 

a untuk setiap aA sehingga

 



x



k



f

 

a



k



f

 

a



k



h

 

a



k















dan k





f

 

a

        

 k



f a 



g f a . Perhatikan bahwa k



h



 

a



0 karena im

 

h ker

 

k . Akibat

   



g f a 0. Karena



homomorfisma satu-satu maka gf

 

a 0. Dengan demikian g

 

x 0 (karena x f

 

a ). Jadi xker

 

g dan im

 

f ker

 

g .

 

a a'



 

0 Af Bg C

 

0

 

0  A'h B'k C'

 

0

(4)

(ii). Jika xker

 

g maka g

 

x 0 dan k





 

x

      

 k



x 



g x 





g

 

x

  





0 0 akibatnya



 

x ker

 

k im

 

h dan



   

x ha' untuk suatu a'A'.

Perhatikan bahwa



pada, sehingga



a



A

a'



 

a . Dengan demikian

   



 

   

  

f

a



f

 

a



a

h

a

h

a

h

x









'

Dan



pemetaan satu-satu, sehingga x f

 

a . Jadi ada aA sehingga x f

 

a atau

 

f im

x dan ker

 

g im

 

f .

Dari (i)dan (ii) im

 

f ker

 

g , artinya bahwa barisan bawah eksak.

Selanjutnya hasil ini dapat diperluas menjadi barisan eksak dari 5 modul yang dikenal hasilnya dengan Lemma Lima (five lemma).

Lemma Lima.

Diagram komutatif berikut mempunyai barisan-barisan eksak

Jika



,



,



dan



isomorfisma maka



juga isomorfisma. Bukti:

Misalkan barisan atas dan barisan bawah merupakan barisan eksak.

Sehingga pemetaan p,q,r,s,t,u,v,w merupakan pemetaan homomorfisma dan











,

juga homomorfisma. Dan

 

   

 

v

 

w

im

v

u

im

u

t

im

s

r

im

r

q

im

q

p

im

ker

,

ker

,

ker

,

ker

,

ker

,

ker



Diketahui pula

t







p

,

u







q

,

v







r

dan

w







s

.

Jika



,



,



,



isomorfisma, jelas bahwa



homomorfisma, sehingga tinggal ditunjukkan bahwa



pemetaan bijektif.

Jika xker

   



,



x 0, sehingga



       

r

 

x 



r x  v



x v





 

x

  

v0 0 dan



suatu homomorfisma satu-satu, maka r

 

x 0 sehingga xker

 

r im

 

q .

Misalkan xq

 

y untuk suatu

y



B

 

x





q

 

y

      



q y u



y u





 

y





   



0 . Dengan demikian



 

y ker

 

u im

 

t .

E

D

C

B

A

















'

B

C

D

E

A



















_







E

D

C

B

A





p





q





r





s ' ' ' ' ' B C D E A _t _u _v _w



_







(5)

Tulis



   

y t a' untuk suatu a'A'. Karena



pada, diperoleh aA, a'



 

a sehingga

 

y t





 

a

      

t



a



p a





p

 

a





    .



satu-satu mengakibatkan y p

 

a . Dengan demikian yim

 

p ker

 

q . Jadi q

 

y 0 padahal xq

 

y . Jadi x0 sehingga



pemetaan satu-satu.

Selanjutnya akan ditunjukkan



pemetaan pada.

Misalkan c'C' sebarang. Perhatikan bahwa v

 

c' 0. Karena



pada, maka v

   

c' 



d untuk suatu dD sehingga w





 

d



w



v

 

c'



0 (ker

 

w im

 

v ).

Padahal w





 

d

      

 w



d 



s d 





s

 

d



. Akibatnya





s

 

d



0. Dengan demikian karena



satu-satu, s

 

d 0 dan dker

 

s im

 

r .

Selanjutnya tulis d r

 

c dengan cC dan

   

c



d



       

r

 

c



r c v



c v





 

c





'      sehingga v

 

c' v





 

c



0.



homomorfisma,





c'



 

c



0 dengan demikian c'



 

c ker

 

v im

 

u artinya ada '

' B

b sedemikian sehingga c'



   

c u b' . Karena



pada, ada bB sehingga b'



 

b dan c'



   

c ub' u





 

b

      

 u



b 



q b 





q

 

b



Atau c'



 

c 





q

 

b









cq

 

b



. Sebut cq

 

b c1. Sehingga ada c1C sehingga

 

1

' c

c



. Jadi



pemetaan pada.

Kesimpulannya



homomorfisma satu-satu pada atau



isomorfisma.

3. Kesimpulan

Dari hasil penjabaran di atas dapat disimpulkan :

1. Barisan modul yang isomorfik, akan sama-sama eksak atau sama-sama tidak eksak. 2. Jika dipunyai barisan-barisan eksak yang beberapa modulnya saling isomorfik maka

dapat dipastikan seluruh barisan tersebut isomorfik.

Daftar Pustaka

1. Lang, S., Algebra, Addison-Wesley. 1965.

2. Passman, D. S., A Course in Ring Theory, Wadsworth. Inc., Belmont, California, 1991. 3. Spindler, K., Abstract Algebra with Applications, Volume II, Marcel Dekker Inc., 1994.