ABSTRACT. Mathematics, IPB. For censored data, survival time using Exponential method is St ˆ( ) = e λ

(1)

ANALISIS DATA SURVIVAL WAKTU TUNGGU MENDAPATKAN

PEKERJAAN PERTAMA DENGAN MENGGUNAKAN METODE

EKSPONENSIAL DAN WEIBULL

MARLINA RAHMAWATI

G54103032

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(2)

ABSTRACT

MARLINA RAHMAWATI. Analysis survival data waiting time to get a first job by using Eksponensial dan Weibull methods.Supervised by HADI SUMARNO and RETNO BUDIARTI.

In daily life human always involved with time, one example is period time some alumny from graduation until they are getting a job. This data can’t be observed entirely or censored because there are objects that didn’t get a job until the end of the observed so that it is needed a suitable method. In this paper two parametric methods, there are Exponential and Weibull methods were used to analysis the waiting time to get a first job of alumny 1998 until 2003 of Department of Mathematics, IPB . For censored data, survival time using Exponential method is S tˆ( )=e−λˆt , and using Weibull method is

ˆ ˆ ˆ( ) t S t e γ λ −

= with λˆ is scale parameter, γˆ is shape parameter and is survival time. Based on these analysis, Weibull method is more suitable than Exponential method. The result of covariate analysis using the Weibull method showed that age and GPA have significant effect on waiting time to get a first job.

(3)

ABSTRAK

MARLINA RAHMAWATI. Analisis data survival waktu tunggu mendapatkan pekerjaan pertama dengan menggunakan metode Eksponensial dan Weibull. Dibimbing oleh HADI SUMARNO dan RETNO BUDIARTI.

Dalam kehidupan sehari-hari manusia selalu berhubungan dengan waktu, salah satu contoh yaitu jangka waktu alumni dari kelulusan hingga mendapatkan pekerjaan. Data ini tidak bisa diamati secara utuh atau tersensor karena ada objek yang tidak mendapatkan pekerjaan hingga akhir pengamatan, sehingga diperlukan metode yang sesuai. Dalam karya ilmiah ini digunakan dua metode parametrik yaitu metode Eksponensial dan Weibull untuk menganalisis waktu tunggu mendapatkan pekerjaan pertama dari alumni Departemen Matematika, FMIPA IPB tahun masuk 1998 s/d 2003. Tingkat survival metode Eksponensial dapat dicari dengan persamaanS tˆ( )=e−λˆt sedangkan metode Weibull

ˆ ˆ ˆ( ) t

S t =e−λγ dengan λˆ adalah parameter scale, γˆ adalah parameter shape dan t adalah waktu survival. Berdasarkan hasil analisis data yang digunakan, metode Weibull lebih sesuai daripada metode Eksponensial. Sedangkan hasil analisis metode Weibull, covariate yang berpengaruh nyata terhadap waktu tunggu mendapatkan pekerjaan pertama adalah usia dan IPK.

(4)

ANALISIS DATA SURVIVAL TIDAK MENDAPATKAN PEKERJAAN

DENGAN MENGGUNAKAN METODE EKSPONENSIAL DAN

WEIBULL

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

MARLINA RAHMAWATI

G54103032

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(5)

Judul :

Analisis

Data

Survival

Waktu Tunggu Mendapatkan Pekerjaan

Pertama Menggunakan Metode

Eksponensial

dan

Weibull

Nama :

Marlina

Rahmawati

NRP :

G54103032

Menyetujui :

Pembimbing I,

Dr. Ir. Hadi Sumarno, MS.

NIP 131430804

Pembimbing

II,

Ir. Retno Budiarti, MS.

NIP 131842409

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP 131578806

(6)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT. Atas limpahan nikmat dan kasih sayang-Nya penulis dapat menyelesaikan karya ilmiah ini. Shalawat serta salam semoga selalu tercurah kepada Rasulullah Muhammad SAW yang menjadi panutan bagi umatnya hingga akhir jaman.

Sebagai manusia biasa, keterbatasan dan kekurangan menjadi bagian dalam penulisan karya ilmiah ini. Selama proses penulisan karya ilmiah ini, penulis banyak memerlukan bantuan, baik bantuan moril dan materil. Oleh karena itu, pada kesempatan ini penulis ingin mengucapkan banyak terima kasih kepada:

1. Bapak Hadi Sumarno selaku Pembimbing I, yang telah banyak meluangkan waktu, pikiran, masukkan, dan arahan selama proses pengerjaan karya ilmiah ini, Ibu Retno Budiarti selaku Pembimbing II atas bimbingan dan saran yang telah diberikan, juga kepada Bapak Kutha atas kesediaan beliau menjadi penguji serta saran dan masukkan yang telah diberikan.

2. Mimi dan Bapak serta Mimi Ua, terima kasih atas dukungan baik moral maupun materiil. Kakakku Dina dan Kedua adikku tercinta, Novi dan Leli, terima kasih atas segala dukungan kalian.

3. Seluruh dosen Departemen Matematika IPB, atas ilmu yang telah diberikan selama masa kuliah. Serta kepada seluruh staf Departemen Matematika, terima kasih atas bantuan yang telah diberikan.

4. Aam, Ali dan Dwi atas kesediaannya menjadi pembahas pada saat seminar.

5. Sahabat-sahabat terbaikku Elis, Nchie, Ulfa, , Sriti, Mayang dan Yuda atas persahabatan, cinta, dukungan, semangat dan doa yang telah kalian berikan selama ini.

6. Keluarga besar Matematika ’40: Elis, Sri, ulfa (atas kesetiaan kalian menungguku selama sidang), Aam, Ali, Abay,Vina, Septi, Tiwi, Ifni, Lili, Mayang, Mita, Mufti, Yuda, Icha, Azis, Prima, Ari, Mika, Ully, Abdillah, Jayoe, Yudi, Rusli, Berri, Dwi, Rama, Indah, Anton, Dimas, Walidah, Metha, Achie, Herni, Amie, Gatha, Febrian, Yusuf, Demi Nisa, dan Putra. Terima kasih atas persabahatan, kebersamaan , dan keceriaan yang telah kita lewati selama masa perkuliahan. Kalian adalah sebaik-baik teman yang selalu menjadikan masa-masa kebersamaan kita penuh warna. Semoga kebersamaan ini akan tetap terjaga.

7. Ukhuwah crew: Ulfa, Alien, Ulan, Resti, Elis, Mbak Dwi, Ika dan Mila atas dukungan, semangat, doa, dan kebersamaan yang telah kalian berikan.

8. Seluruh Mahasiswa Matematika, kakak kelas dan adik kelas yang telah membantu dan memberikan semangat serta doanya.

9. Untuk T’Euis, Ita, Eci, A’Lutfi, A’ Ade dan A’Endang, terima kasih atas dukungannya. 10. Serta kepada semua pihak yang telah banyak membantu selama proses penyelesaian tugas

akhir ini. Mohon maaf karena keterbatasan penulis tidak dapat meyebutkan satu per satu. Penulis menyadari masih ada kekurangan dalam karya ilmiah ini. Oleh karena itu, kritik dan saran dari berbagai pihak akan sangat membantu menyempurnakan tulisan ini. Akhir kata, penulis berharap semoga karya ilmiah ini dapat memberikan manfaat bagi kita semua.

Bogor, Januari 2008

(7)

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 15 Oktober 1985 sebagai anak kedua dari empat

bersaudara. Ayah bernama Nanang Saputra, BA dan Ibu bernama Lilih Puliah.

Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1997 di SD Negeri Harjasari I, Sekolah Lanjutan Tingkat Pertama Negeri 9 Bogor tahun 2000, Sekolah Menengah Umum Negeri 3 Bogor tahun 2003, dan masuk Departemen Matematika Institut Pertanian Bogor melalui jalur USMI pada tahun 2003.

Selama masa perkuliahan, penulis pernah menjadi anggota aktif dalam himpunan profesi Gugus Mahasiswa Matematika IPB sebagai staf Departemen Keputrian pada periode 2004/2005 dan sebagai staf Departemen Wira Usaha periode 2005/2006.

(8)

DAFTAR ISI

Halaman

Daftar Grafik ... ii

Daftar Lampiran ... iii

PENDAHULUAN... 1

Latar Belakang ... 1

Permasalahan ... 1

Tujuan ... 1

DEFINISI DAN NOTASI... 1

DATA DAN METODE ... 4

Data Survival... 4

Fungsi Survivor metode Eksponensial... 5

Fungsi Survivor metode Weibull... 5

Fungsi Hazard metode Eksponensial... 6

Fungsi Hazard metode Weibull ... 6

Pendugaan Parameter Metode Parametrik Tanpa Covariate... 7

Penduga dan Standar Error bagi Parameter λ metode Eksponensial... 7

Penduga dan Standar Error bagi Parameter λ dan γ metode Weibull... 9

Metode Weibull dengan Covariate... 9

Bentuk Log-linear dari metode Weibull Proportional Hazard... 10

CONTOH KASUS ... 11

SIMPULAN DAN SARAN ... 20

DAFTAR PUSTAKA ... 20

(9)

DAFTAR GRAFIK

Halaman

Grafik 1. Fungsi Survivor metode Eksponensial untuk parameter λ =1 dan λ =0.1... 5

Grafik 2. Fungsi Survivor metode Weibull untuk parameter λ=1 dan γ yaitu 3 dan 1.5 ... 6

Grafik 3. Fungsi Survivor metode Weibull untuk parameter λ=0.1 dan γ yaitu 3 dan 1.5 6

Grafik 4. Fungsi Hazard metode Eksponensial untuk parameter λ=1 dan λ=0.1... 6

Grafik 5. Fungsi Hazard metode Weibull untuk parameter λ =0.1 dan γ yaitu 3 dan 1.5.. 7

Grafik 6. Fungsi Hazard metode Weibull untuk parameter λ =1 dan γ yaitu 3 dan 1.5 ... 7

Grafik 7. Fungsi Survivor metode Eksponensial data tersensor tanpa covariate... 12

Grafik 8. Fungsi Hazard metode Eksponensial data tersensor tanpa covariate... 12

Grafik 9. Fungsi Survivor metode Weibull data tersensor tanpa covariate... 12

Grafik 10. Fungsi Hazard metode Weibull data tersensor tanpa covariate... 12

Grafik 11. Fungsi Survivor metode Weibull data tersensor 1 covariate wanita dan laki-laki . 13

Grafik 12. Fungsi Hazard metode Weibull data tersensor 1 covariate wanita dan laki-laki .... 14

Grafik 13. Fungsi Survivor metode Weibull data tersensor 1 covariate usia 20 dan 24... 15

Grafik 14. Fungsi Hazard metode Weibull data tersensor 1 covariate usia 20 dan 24... 15

Grafik 15. Fungsi Survivor metode Weibull data tersensor 1 covariate IPK 2.5 dan 3... 16

Grafik 16. Fungsi Hazard metode Weibull data tersensor 1 covariate IPK 2.5 dan 3... 16

Grafik 17. Fungsi Survivor metode Weibull data tersensor multiple covariate usia 20 dan 24 17

Grafik 18. Fungsi Hazard metode Weibull data tersensor multiple covariate usia 20 dan 24.. 18

Grafik 19. Fungsi Survivor metode Weibull data tersensor multiple covariate usia IPK 2.5 dan 3 ... 18

Grafik 20. Fungsi Hazard metode Weibull data tersensor multiple covariate usia IPK 2.5 dan 3 ... 18

Grafik 21. Fungsi Survivor metode Weibull data tersensor multiple covariate wanita dan Laki-laki ... 19

Grafik 22. Fungsi Hazard metode Weibull data tersensor multiple covariate wanita dan Laki-laki ... 19

(10)

DAFTAR LAMPIRAN

Halaman

Standar error persentil t p( ) ... 22

Transformasi fungsi Survivor T_i dengan fungsi Survivor metode Weibull Proportional Hazard... 23

Data survival waktu tunggu mendapatkan pekerjaan pertama alumni Matematika IPB ... 24

Data tersensor dengan multiple covariate antara usia 20 dengan 21,22 dan 23 tahun ... 25

Analisis Survival Software SAS Data tersensor tanpa covariate... 28

Analisis Survival Software SAS Data tersensor dengan 1 covariate... 30

(11)

PENDAHULUAN

Latar belakang

Data survival sering dijumpai dalam pengamatan yang mengandung resiko bahwa subjek tidak dapat diamati sampai muncul kejadian yang dimaksud seperti kematian setelah seseorang mengidap penyakit, waktu mendapat pekerjaan setelah seseorang lama menganggur dll.

Untuk mempelajari data survival yang umumnya tidak dapat diamati secara utuh (censored) diperlukan suatu analisis yang berbeda dibandingkan dengan analisis data tidak tersensor. Data tersensor merupakan data yang tidak lengkap sehingga diperlukan metode yang cocok menganalisisnya.

Data survival dimanfaatkan dalam bidang kedokteran, industri, ekonomi, sosial dan lain-lain. Bidang kedokteran: lamanya seseorang mengidap penyakit, bidang industri: lamanya suatu mesin bertahan sampai rusak, bidang ekonomi: lamanya barang produksi sampai terjual dan bidang sosial: berkaitan dengan perjodohan seseorang.

Permasalahan

Beberapa analisis data yang sering digunakan adalah metode Life Table dan metode Kaplan Meier. Jika ada data survival yang melibatkan peubah penjelas atau covariate maka analisis metode Life table dan Kaplan Meier menjadi tidak sesuai karena terlalu banyak populasi yang harus dibandingkan sehingga diperlukan metode lain yang lebih baik untuk mengamati permasalahan tersebut.

Tujuan

Tujuan penulisan karya ilmiah ini adalah 1. Mempelajari metode dan analisis data

survival menggunakan metode parametrik yaitu metode Eksponensial dan Weibull. 2. Memeriksa pengaruh jenis kelamin, usia

dan IPK terhadap tingkat survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni departemen matematika IPB menggunakan metode yang lebih baik antara metode Eksponensial dan Weibull.

DEFINISI DAN NOTASI Definisi 1 [ Ruang Contoh ]

Ruang contoh adalah himpunan semua hasil yang mungkin dari suatu percobaan acak dan dinotasikan Ω.

(Grimmet & Stirzaker, 1992) Definisi 2 [ Kejadian ]

Kejadian adalah suatu himpunan bagian dari ruang contoh.

(Grimmet & Stirzaker, 1992) Definisi 3 [Medan -σ ]

Medan -σ adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian dari

yang memenuhi kondisi berikut: Ω 1.∅ ∈F 2. Jika A A₁, ₂, ...∈F maka 1Ai F i ∞ ∈ = ∪ 3. Jika A∈F maka Ac∈F

(Grimmet & Stirzaker, 1992) Definisi 4 [ Peubah Acak ]

Misalkan F adalah medan-σ dari ruang

contoh. Suatu peubah acak X adalah suatu fungsi X:Ω →R dengan sifat

{ω∈ Ω:X( )ω ≤x}∈F untuk setiap x∈R. (Grimmet & Stirzaker, 1992) Definisi 5 [ Fungsi Sebaran ]

Fungsi sebaran dari suatu peubah acak X adalah suatu fungsi yang diberikan oleh

: [0, F R→ 1]

( ) ( ).

F_X x =P X ≤x

(Grimmet & Stirzaker, 1992) Definisi 6 [ Peubah Acak Kontinu ]

Peubah acak X dikatakan kontinu jika fungsi sebarannya dapat dinyatakan sebagai

( ) ( ) ,

x

F_X x = ∫ f u du x∈R −∞

dengan adalah fungsi yang terintegralkan. Fungsi dikatakan fungsi kepekatan peluang dari peubah acak.

: [0,

f R→ ∞) ( )

f x

(12)

Definisi 7 [ Nilai Tengah suatu Peubah Acak ]

Misalkan X adalah peubah acak dengan sebaran kontinu maka nilai tengah bagi X adalah

( ) ( )

E X xf x dx

µ= = ∫∞

−∞

(Hogg & Craig, 1995) Definisi 8 [ Ragam suatu Peubah Acak]

Bila X adalah peubah acak dengan sebaran kontinu maka ragam bagi X adalah

2 2 2 [( ) ] ( 2 ) 2 ( ) 2 ( ) 2 2 2 ( ) 2 2 2 ( ) E X E X X E X E X E X E X σ µ µ µ2 2 µ µ µ µ µ = − = − + = − + = − + = −

(Hogg & Craig, 1995) Definisi 9 [ Data Survival ]

Data survival adalah data yang didapat pada jangka waktu awal pengamatan sampai terjadi suatu peristiwa (resiko). Data survival dapat diamati secara lengkap (data tidak tersensor) dan tidak lengkap (data tersensor).

(Lee, 1992) Definisi 10 [ Data Tersensor ]

Data survival individu dikatakan tersensor jika individu tersebut tidak bisa diamati sampai akhir karena adanya individu yang hilang ataupun dengan alasan lain sehingga data tidak bisa diamati atau sampai akhir pengamatan individu tersebut belum mengalami peristiwa (resiko).

(Collet, 1994) Definisi 11 [Sensor Titik]

Sensor titik adalah salah satu jenis sensor terhadap objek yang diamati mulai dari waktu

sampai dan selama itu objek dapat dimonitor secara kontinu dan waktu kejadian dapat dilihat dengan baik. Sensor titik (Point censoring) terdiri dari :

0

T T₁

a. Sensor kanan :

- sensor kanan jenis I;

tersensor karena tidak mengalami kejadian sampai akhir masa pengamatan - sensor kanan jenis II;

tersensor karena tidak bisa

mengikuti pengamatan sampai akhir akibat adanya kejadian lain di luar yang menjadi perhatian

b. Sensor kiri :

Tersensor karena objek sudah mengalami kejadian sebelum awal pengamatan. Sebuah kasus tentang data tersensor kiri misalnya ketika objek amatan dalam studi AIDS sudah terkena HIV-1 seropositive saat didaftar dan variabel waktu menjadi perhatian adalah inkubasi dari AIDS c. Sensor kiri dan kanan :

Tersensor karena mengalami sensor kiri dan kanan. Misalnya pada kasus AIDS, seseorang sudah terkena HIV-1 seropositive pada saat didaftar tetapi sampai akhir pengamatan masih bebas AIDS.

d. Sensor kiri dan kanan secara lengkap : Dalam beberapa aplikasi, sering kali waktu awal dan waktu akhir dari suatu kejadian terjadi sebelum waktu pengamatan dimulai atau setelah waktu pengamatan selesai yang dikenal sebagai sensor kiri secara lengkap dan sensor kanan secara lengkap.

(Lee, 1992) Definisi 12 [ Metode Parametrik ]

Metode parametrik adalah metode analisis yang memiliki asumsi sebaran misalnya data yang diamati menyebar normal, binom dan lain-lain.

(Hogg & Craig, 1995) Definisi 13 [Fungsi Survivor ]

Fungsi Survivor (S(t)) adalah fungsi yang menyatakan peluang seseorang dapat bertahan hingga atau lebih dari waktu t. Rumus umum dari fungsi Survivor didefinisikan sebagai berikut

( ) ( ) 1 ( )

S t =P T ≥ = −t F t

Dengan metode fungsi sebaran F(t) didefinisikan sebagai berikut

0

( ) ( ) ( )

t

F t =P T ≤ =t

∫

f u du

Variabel acak T mempunyai fungsi kepekatan peluang f(t) adalah

( ) ( ) dS t f t dt − =

(13)

Teorema 1:

Jika fungsi Survivor maka dapat ditunjukkan bahwa fungsi kepekatan peluang dari T adalah

( ) ( ) S t =P T≥t ( ) ( ) dS t f t dt = − Bukti: ( ) ( ) 1 ( ) ( ) 1 t f u du S t t f u du f u du t + = ∫ −∞ ∞ + = ∫ ∫ −∞ 1 () ( ) t S t f u du − = ∫ −∞ kedua ruas diturunkan terhadap t

[ ] [1 ( )] ( ) ( ) t d fudu d S t dt dt dS t f t dt ∫ − _−∞ = − = Terbukti. (Collet, 1994). Definisi 14 [ Fungsi Hazard ]

Fungsi hazard (h(t)) adalah fungsi yang menyatakan peluang seseorang mengalami resiko atau suatu kejadian seperti meninggal, kegagalan atau mendapatkan pekerjaan pada waktu dengan syarat bahwa seseorang itu telah bertahan (survive) hingga waktu . Waktu kelangsungan pengangguran seseorang pada saat terletak antara dan t

t

t T t +δt, jika seseorang itu telah bertahan tidak mendapatkan pekerjaan waktu t dengan nilai

lebih besar dari yang ditulis

T t

( ) ( | )

h t =P t≤ ≤ +T t δt T ≥t

Limit dari fungsi Hazard dibagi dengan δt ketika δt mendekati 0 yaitu

( | ( ) lim 0 P t T t t T t h t t _t δ δ δ ≤ ≤ + ≥ = → )

dari definisi di atas didapat hubungan antar fungsi Survivor dan fungsi Hazar ( lim ( | ) lim 0 0 ( ) P t T t t P t T t t T t t t P T t ) δ δ δ δ ≤ < + ≤ ≤ + ≥ = → → ≥ ( ) ( ) 1 lim 0 ( ) ( ) ( ) F t t F t t t S f t S t δ δ δ + − = → = t karena f t( ) dS t( ) dt = − , maka ( ) 1 ( ) ( ) ( ) ( ) ( ) dS t h t dt S t dS t h t dt S t = − = −

kedua ruas diintegralkan ( ) ( ) ( ) ( ) ln( ( )) ln( ( )) ( ) ( ) exp( ( )) dS t h t dt S t H t S t S t H t S t H t = − ∫ ∫ = − = − = −

(Cox dan Oakes, 1984) Definisi 15 [ Fungsi Likelihood ]

Fungsi Likelihood dapat didefinisikan sebagai berikut

( ) ( ₁: ) ( ₂: )... ( : )

Lθ = f x θ f x θ _{f xn} θ

Fungsi ln-Likelihood didiferensiasikan terhadap θ yaitu ln ( : ) ln ( ) 0 1 i n f x L Z i θ θ θ θ ∂ ∂ = = ∑ = = ∂ ∂

dengan mencari solusi dari persamaan di atas maka akan ditemukan penduga θ yang memaksimumkan fungsi Likelihood.

(Hogg & Craig, 1995) Definisi 16 [ Ragam bagi Penduga Parameter]

Ragam bagi penduga parameter θ yang memaksimumkan fungsi Likelihood didefinisikan sebagai berikut

1 2 ln ( ) ˆ var( ) 2 d L E d θ θ θ − ≈ −

⎛

_⎜

⎧

⎪

_⎨

⎫

⎪

_⎬

⎞

_⎟

⎪

⎩

⎭

⎝

⎠

dan standar error θˆ merupakan akar dari ragam θˆ yaitu

ˆ ˆ

. .( ) var( )

s e θ = θ

(Collet, 1994) Definisi 17 [ Uji Hipotesis ]

Uji hipotesis adalah suatu pernyataan atau dugaan yang digunakan untuk menerima atau menolak suatu hipotesis dari hasil amatan. Hipotesa mengenai populasi yang akan kita terima kebenarannya sampai ada bukti menolaknya dinamakan hipotesis nol (H₀). Apabila hipotesis ini ditolak kebenarannya maka ada hipotesis lain yang kita anggap

(14)

benar yaitu hipotesis tandingan (H₁). Dalam perumusan H₁ dikenal 2 macam hipotesis yaitu:

a. Hipotesis eka arah

1. H₀:µ µ≤ ₀ 2. H₀:µ µ≥ ₀

H₁:µ µ> ₀ H₁:µ µ< ₀

b. Hipotesis dwi arah : 0 0 : 1 0 H H µ µ µ µ = ≠

(Hogg & Craig, 1995) Definisi 18 [ Persentil ]

Persentil adalah nilai-nilai yang membagi segugus pengamatan menjadi 100 bagian yang sama. Nilai-nilai itu dilambangkan dengan

bersifat bahwa 1% dari seluruh data terletak dibawah , 2% terletak dibawah

dan 99% terletak dibawah .

, ... 1 2 99 P P P 1 P 2 P P₉₉ (Walpole, 1992) Definisi 19 [ Uji Kebebasan Chi-Square ]

Uji kebebasan chi square adalah suatu pernyataan atau dugaan yang digunakan untuk menguji hipotesis kebebasan antara dua

peubah. Pernyataan hipotesis yang akan diuji adalah sebagai berikut :

: 0

H Peubah yang satu tidak mempengaruhi peubah yang lain atau dua peubah yang diamati bersifat bebas.

: 1

H Peubah yang satu mempengaruhi peubah yang lain atau dua peubah yang diamati bersifat tidak bebas. Uji kebebasan didasarkan pada besaran

2 ( ) 2 oi ei i _ei χ = ∑ − 2

χ merupakan nilai bagi peubah acak, χ2 yang sebaran penarikan contohnya sangat menghampiri sebaran chi-square. Lambang menyatakan frekuensi teramati dan lambang menyatakan frekuensi harapan. Untuk taraf nyata sebesar

oi

ei

α , nilai kritiknya

2

χα dapat diperoleh dari tabel nilai kritik sebaran chi-square. Jika χ2 >χα2 maka tolak hipoteis nol (H₀ ) dan jika selainnya maka hipotesis nol diterima.

( Walpole, 1992)

DATA DAN METODE Data Survival

Dalam karya ilmiah ini menggunakan data survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni departemen Matematika IPB. Data survival ini dapat dilihat pada lampiran 3. Data survival mengandung empat informasi yaitu:

1. Waktu kejadian (failure time ) yaitu waktu alumni mendapatkan pekerjaan.

2. Banyaknya objek yang mengalami kejadian.

3. Banyaknya objek yang tersensor c_j 4. Covariate atau variabel penjelas. Jika maka disebut data survival tidak tersensor kemudian sebaliknya jika

maka disebut data survival tersensor. Covariate yang digunakan dalam karya ilmiah ini adalah jenis kelamin, usia dan IPK. Covariate usia dan IPK merupakan data numerik sedangkan covariate jenis kelamin

merupakan data biner. Untuk jenis kelamin ditandai dengan angka 1 untuk laki-laki dan 0 untuk wanita. 0 c j = ∑ 0 c j ≠ ∑

Dalam karya ilmiah ini hanya dibahas penyelesaian masalah data survival dengan melibatkan parameter dengan menggunakan metode parametrik yaitu metode Eksponensial dan Weibull. Langkah-langkah yg digunakan dalam menganalisis data survival yaitu 1.Menganalisis data tersensor tanpa covariate

dengan menggunakan metode Eksponensial dan Weibull.

2.Metode yang lebih baik antara metode Eksponensial dan Weibull digunakan untuk menganalisis data tersensor dengan covariate.

3.Dalam menganalisis data tersensor dengan covariate digunakan langkah-langkah sebagai berikut :

- Analisis data tersensor dengan satu covariate.

- Analisis data tersensor dengan multiple covariate.

(15)

Teorema 2:

Jika fungsi kepekatan peluang metode Eksponensial _{f t}( )=λ_e−λt

maka dapat ditunjukkan bahwa fungsi Survivor adalah

( ) t S t =e−λ Akan dibuktikan: ( ) t S t =e−λ Bukti: ( ) 1 ( ) S t = −F t karena 0 ( ) ( ) t F t =

∫

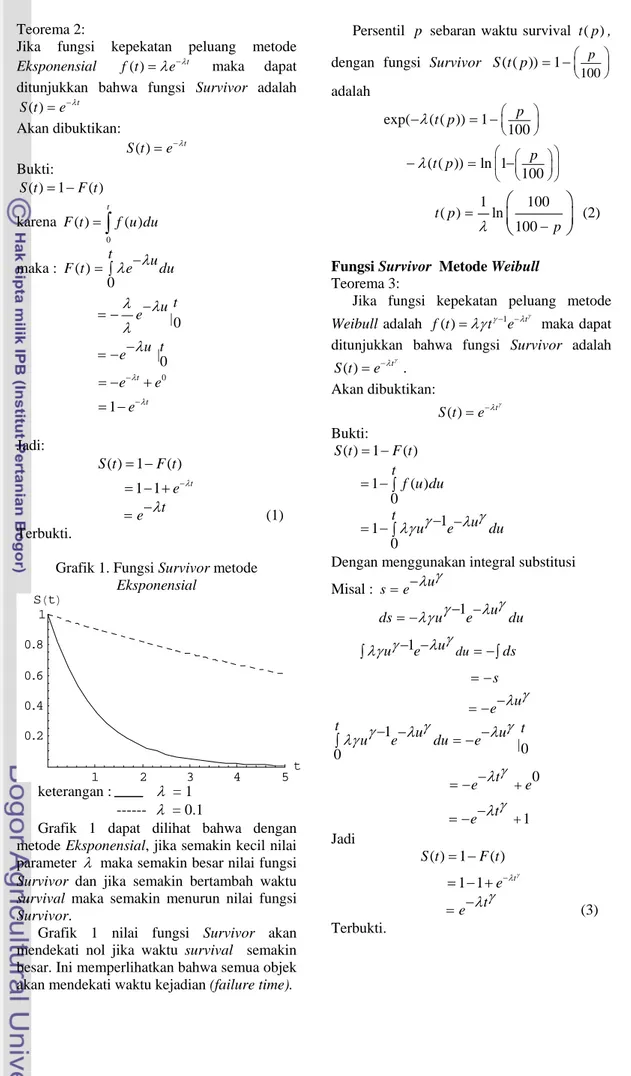
f u du maka : ( ) 0 t _u F t = ∫λe−λ du λe λu_|0t λ − = − = −e−λu t|₀ 0 1 t t e e e λ λ − − = − + = − Jadi: ( ) 1 ( ) 1 1 t S t F t e−λ = − = − + =e−λt (1) Terbukti.

Grafik 1. Fungsi Survivor metode Eksponensial 1 2 3 4 5 t 0.2 0.4 0.6 0.8 1 SHtL keterangan : λ = 1 --- λ = 0.1

Grafik 1 dapat dilihat bahwa dengan metode Eksponensial, jika semakin kecil nilai parameter λ maka semakin besar nilai fungsi Survivor dan jika semakin bertambah waktu survival maka semakin menurun nilai fungsi Survivor.

Grafik 1 nilai fungsi Survivor akan mendekati nol jika waktu survival semakin besar. Ini memperlihatkan bahwa semua objek akan mendekati waktu kejadian (failure time).

Persentil sebaran waktu survival t p , dengan fungsi Survivor

p ( ) 100 ( ( )) 1 p S t p = −⎛⎜_⎝ ⎞⎟_⎠ adalah exp( ( ( )) 1 100 ( ( )) ln 1 100 p t p p t p λ λ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ _⎛ _⎞⎞ ⎜ ⎜ ⎟⎟ ⎝ ⎠ ⎝ ⎠ − = − − = − ( ) 1ln 100 100 t p (2) p λ = −

⎛

⎞

⎜

⎟

⎝

⎠

Fungsi Survivor Metode Weibull Teorema 3:

Jika fungsi kepekatan peluang metode Weibull adalah 1

( ) t

f t =λγtγ−e−λγ maka dapat ditunjukkan bahwa fungsi Survivor adalah

( ) t S t =e−λγ . Akan dibuktikan: ( ) t S t =e−λγ Bukti: ( ) 1 ( ) 1 ( ) 0 1 1 0 S t F t t f u du t _u uγ e λ γdu λγ = − = − ∫ − − = − ∫

Dengan menggunakan integral substitusi Misal : s=e−λuγ ds u 1e u du γ γ λ λγ − − = − 1 u _du u e ds s γ γ λ λγ − − = − ∫ ∫ = − = −e−λuγ 1 |0 0 0 1 t _u _u t u e du e t e e t e γ γ γ λ λ λγ γ λ γ λ + + − − _{= −} − ∫ − = − − = − Jadi ( ) 1 ( ) 1 1 t S t F t e−λγ = − = − + =e−λtγ (3) Terbukti.

(16)

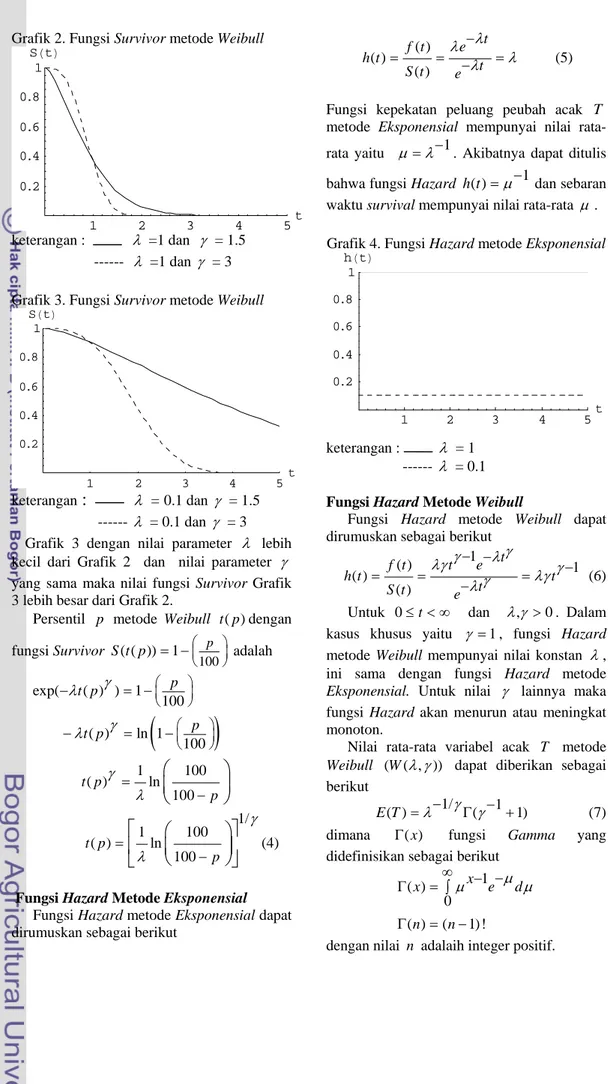
Grafik 2. Fungsi Survivor metode Weibull

1 2 3 4 5t 0.2 0.4 0.6 0.8 1 SHtL keterangan : λ =1 dan γ = 1.5 --- λ =1 dan γ = 3 Grafik 3. Fungsi Survivor metode Weibull

1 2 3 4 5 t 0.2 0.4 0.6 0.8 1 SHtL keterangan

:

λ =0.1 dan γ = 1.5 --- λ = 0.1 dan γ = 3

Grafik 3 dengan nilai parameter λ lebih kecil dari Grafik 2 dan nilai parameter γ yang sama maka nilai fungsi Survivor Grafik 3 lebih besar dari Grafik 2.

Persentil metode Weibull dengan fungsi Survivor p t p( ) 100 ( ( )) 1 p S t p = −⎛⎜_⎝ _⎠⎞⎟ adalah

(

)

exp( ( ) ) 1 100 ( ) ln 1 100 p t p p t p γ λ γ λ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ − = − − = − ( ) 1ln 100 100 t p p γ λ = −

⎛

⎞

⎜

⎟

⎝

⎠

1/ 1 100 ( ) ln 100 t p p γ λ = −

⎡

⎛

⎞

⎤

⎢

⎜

_⎝

⎟

_⎠

⎥

⎣

⎦

(4)

Fungsi Hazard Metode Eksponensial Fungsi Hazard metode Eksponensial dapat dirumuskan sebagai berikut

( ) ( ) ( ) t f t e h t t S t e λ λ λ λ − = _{= − =} (5) Fungsi kepekatan peluang peubah acak T metode Eksponensial mempunyai nilai rata-rata yaitu µ λ= −1. Akibatnya dapat ditulis bahwa fungsi Hazard h t( )=µ−1 dan sebaran waktu survival mempunyai nilai rata-rata µ. Grafik 4. Fungsi Hazard metode Eksponensial

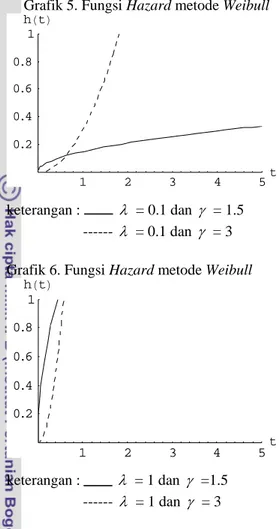
1 2 3 4 5 t 0.2 0.4 0.6 0.8 1 hHtL keterangan : λ = 1 --- λ = 0.1 Fungsi Hazard Metode Weibull

Fungsi Hazard metode Weibull dapat dirumuskan sebagai berikut

1 ( ) 1 ( ) ( ) t f t t e h t t t S t _e γ γ λ λγ _λγ γ γ λ − − − = = = − (6) Untuk 0≤ < ∞t dan λ γ, >0. Dalam kasus khusus yaitu γ =1, fungsi Hazard metode Weibull mempunyai nilai konstan λ, ini sama dengan fungsi Hazard metode Eksponensial. Untuk nilai γ lainnya maka fungsi Hazard akan menurun atau meningkat monoton.

Nilai rata-rata variabel acak T metode Weibull (W( , ))λ γ dapat diberikan sebagai berikut

1/ 1

( ) ( 1)

E T =λ− γΓ γ− + (7) dimana Γ( )x fungsi Gamma yang didefinisikan sebagai berikut

1 ( ) 0 ( ) ( 1)! x x e d n n µ µ µ ∞ ₋ ₋ Γ = ∫ Γ = −

(17)

Grafik 5. Fungsi Hazard metode Weibull

1 2 3 4 5t 0.2 0.4 0.6 0.8 1 hHtL keterangan : λ = 0.1 dan γ = 1.5 --- λ = 0.1 dan γ = 3 Grafik 6. Fungsi Hazard metode Weibull

1 2 3 4 5 t 0.2 0.4 0.6 0.8 1 hHtL keterangan : λ = 1 dan γ =1.5 --- λ = 1 dan γ = 3

Pendugaan Parameter Metode Parametrik Tanpa Covariate

Pendugaan parameter metode parametrik untuk pengamatan data survival menggunakan fungsi Likelihood dimana tidak ada pengamatan yang tersensor. Jika fungsi kepekatan peluang dari peubah acak yang berhubungan dengan waktu survival adalah maka fungsi Likelihood n pengamatan

adalah ( ) f t 1

, ...

2 n

t t

t

∏

= n i i

t

f

1

)

(

(8) Biasanya data survival mempunyai satu atau lebih waktu survival tersensor. Jika adalah banyaknya individu yang mendapatkan pekerjaan pada waktu

dan adalah banyaknya individu pada waktu t t adalah sensor kanan maka waktu mendapatkan pekerjaan r dapat dikontribusikan dalam bentuk:

r ... (1) (2) ( ) t <t < <t _r n−r * * * , ... (1) (2) t (n r− ) ( ) 1

(

)

r j j

f t

=

∏

(9)

Dalam hal ini kita tidak bisa mengindahkan informasi tentang pengamatan survival n−r individu untuk waktu survival yang tersensor yang telah dicatat yaitu waktu survival yang tersensor pada waktu

t

dan fungsi Survivor . Pengamatan terhadap data yang tersensor dapat dibentuk dalam fungsi Likelihood dengan pengamatan yaitu

*

)

(

t

*

S

n ( ) ( ) 1 1

(

)

( * )

r n r j i j i

f t

S t

− = =

∏

(10) dengan adalah data yang mendapatkan pekerjaan dan

r

n−r adalah data yang tersensor kanan I.

Lebih kompleks lagi, jika diduga bahwa data n observasi adalah

( ,

t

_i

δ

_i

)

dengan

1, 2...

i= . Notasi

δ

_i merupakan indikator variabel dengan menganggap bahwa 0 yaitu waktu survival

t

tersensor dan 1 yaitu waktu survival tidak tersensor. Fungsi Likelihood dapat didefinisikan sebagai berikut

i i

t

∏

i − i i i

S

t

f

(

)}

δ

{

(

)}

1 δ

{

(11)

Penduga dan Standar Error bagi Parameter

λ

Metode Eksponensial

Data survival memberikan keterangan bahwa yang mendapatkan pekerjaan individu dan

r n−r individu yang tersensor kanan.

Fungsi kepekatan peluang dan fungsi Survivor metode Eksponensial :

( )

t

f t

=

λ

e

−λ dan S t( )=e−λt

Persamaan di atas disubstitusikan ke persamaan (11) maka didapat fungsi Likelihood sebagai berikut

1 ( ) ( ) ( ) 1 ( ) ( ) 1 ( )( ) 1 n t_i _i t_i _i L e e i n t_i _i t_i t_{i i} e e i n _i t_{i i} t_i t_{i i} e e i λ δ λ δ λ λ λ δ λ λ δ λ λ δ λ λ δ δ λ − − − = ∏ = − − + = ∏ = − − + = ∏ = 1 n _i t_i e i δ λ λ − = ∏ = (12) dan fungsi ln-Likelihood adalah

ln ( ) ln 1 1 n n L _i t_i i i λ = ∑δ λ λ− ∑ = = Jika 1 n r i

i∑= δ = maka fungsi ln-Likelihood menjadi

(18)

ln ( ) ln 1 n L r _i i λ = λ λ− ∑ = t

Fungsi ln-Likelihood diturunkan terhadap λadalah ln ( ) 1 n d L r ti i d λ λ = λ− ∑=

Jika persamaan di atas sama dengan 0 maka didapat penduga λ yang memaksimumkan fungsi Likelihood yaitu

0 1

ˆ

n r ti i

λ

− ∑= = ˆ / (13) 1 n r _i i λ = ∑ = t

Penduga µ yang memaksimumakan fungsi Likelihood adalah ˆ ˆ 1 1 1 n ti i r µ λ= − = ∑ = (14) Ragam bagi λˆ dapat didefinisikan sebagai berikut 1 2 ln ( ) ˆ var( ) 2 d L E d λ λ λ − = −

⎡

⎢

⎧

⎪

⎨

⎫

⎪

⎬

⎤

⎥

⎪

⎢

⎩

⎭

⎥

⎣

⎦

1 2 1 ₂ 2 r E r r λ λ λ − = − − − = =

⎡

⎧

⎫

⎤

⎨

⎬

⎢

_⎩

_⎭

⎥

⎣

⎦

⎡

⎤

⎢

⎥

⎣

⎦

standar error ˆλ dapat didefinisikan sebagai berikut ˆ ˆ . .( ) s e r λ λ = (15) Metode Eksponensial penduga persentil p diberikan sebagai berikut

1 100 ˆ( ) ln ˆ ₁₀₀ t p p λ = −

⎛

⎞

⎜

⎟

⎝

⎠

Teorema 4 [ Deret Taylor ]

Jika diberikan fungsi f ∈cn+1[ , ]a b , kontinu dan terturunkan sampai turunan ke n+1. Misalkan f [ , ] 0 x ∈ a b untuk setiap [ , ]

x∈ a b terdapat yang terletak antara ( ) c=c x x dan x₀ ( ) ( ₀) ( ) ( ₀) 0 ! k f x f x x x k k ∞ = ∑ − = 2 ( ) " 0 ( ) ( )₀ '( )(₀ ₀) ( )₀ 2! ! ( ₀) _{( 1)} ( ₀) ... ( ) 1 ! 1 x x f x f x f x x x f x n n x x _n x x n f f c n n − = + − + + − ₊ − ! N + + + + + (Munir, 2003) Definisi [ Sifat Ragam ]

Bila X suatu peubah acak dan konstanta maka a 2 2 2 a aX X σ = σ ( Walpole, 1992 ) Dengan menggunakan pendekatan deret Taylor dan sifat ragam maka ragam dari suatu fungsi g( )λ dengan λ adalah

( ₀) var( ( )) var ( ₀) ! 0 var[ ( ₀) '( ₀)( ₀) "( ) 0 _...] 2! k N g k g k k g g g λ λ λ λ 0 λ λ λ λ λ λ λ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ = ∑ − = ≈ + − + − ₊ 2 2 0 [ '( ₀)] var( ₀) [ '( )] 0 var ... 2! g λ λ λ g λ λ λ ≈ + − + − +

⎛

⎞

⎜

⎟

⎝

⎠

0 2 ( ) var( ( ))g dg var( ) d λ λ λ λ ≈

⎧

_⎨

⎫

_⎬

⎩

⎭

2 1 100 _ˆ ˆ var( ( )) ln var( ) 2 ₁₀₀ t p p λ λ − ≈ −

⎡

⎛

⎞

⎤

⎢

⎜

_⎝

⎟

_⎠

⎥

⎣

⎦

Standar error dapat didefinisikan sebagai berikut ˆ( ) t p 1 100 _ˆ ˆ . .{ ( )} ₂ln . .( ) ˆ 100 s e t p s e p λ λ = −

⎛

⎞

⎜

⎟

⎝

⎠

ˆ 1 100 ln 2 ˆ 100 p r λ λ = −

⎛

⎞

⎜

⎟

⎝

⎠

1ln 100 ˆ ₁₀₀ _p _r λ = −

⎛

⎞

⎜

⎟

⎝

⎠

1 ˆ( ) r t p = (16)

Penduga dan Standar Error bagi Parameter λ dan γ Metode Weibull

Fungsi kepekatan peluang dan fungsi Survivor metode Weibull didefinisikan sebagai berikut

(19)

(

1 ( ) e t

f t =λγtγ− −λγ) dan S t( )=e−λtγ Fungsi Likelihood n waktu survival adalah

( ) ( ) 1 1 ( , ) ( ) ( ) 1 n t_i _i t_i L t_i e e i i γ γ λ δ λ δ γ λ γ = ∏ λγ − − − = − ) ( 1) ( 1 n _t i i t_i e i γ δ λ γ λγ − − = ∏ = (17) dimana δ_i yaitu 0 jika waktu survival tersensor dan 1 jika waktu survival t tidak tersensor. Fungsi ln-Likelihood dapat didefinisikan sebagai berikut

ti i ln ( , ) ln( ) ( 1) ln 1 1 1 n n n L _i _i t_i t_i i i i γ λ γ =∑δ λγ γ+ − ∑δ −λ∑ = = = dengan 1 n r i i∑= δ = , fungsi ln-Likelihood menjadi ln ( , ) ln( ) ( 1) ln 1 n L r r _ti _i i t γ λ γ = λγ + −γ − ∑λ =

Penduga λ yang mamaksimumkan fungsi Likelihood yaitu ˆ 0 ˆ ₁ n r ti i γ λ − ∑= = ˆ / ˆ 1 n r _ti i γ λ = ∑ = (18) Penduga

γ

yang memaksimumkan fungsi Likelihood yaitu ˆ ln ln 0 ˆ ˆ 1 n r r r t_i t_i t i t i i γ γ γ + −_∑ ∑= i = (19) Ragam bagi λˆ dapat didefinisikan sebagai berikut 1 2 ln ( , ) ˆ var( ) 2 1 2 1 ₂ ₂ d L E d r E r r λ γ λ λ λ λ λ − = − − = − − − = =

⎡

⎧

_⎪

⎫

_⎪

⎤

⎢

⎨

⎬

⎪

⎢

⎩

⎭

⎣

⎡

⎧

⎫

⎤

⎨

⎬

⎢

_⎩

_⎭

⎥

⎣

⎦

⎡

⎤

⎢

⎥

⎣

⎦

⎥

⎥⎦

Standar error λˆ metode Weibull didefinisikan sebagai berikut ˆ ˆ . .( ) s e r λ λ = (20) Ragam γˆ diberikan sebagai berikut

ln( 1 2 ( , )) ˆ var( ) 2 1 [ { ln ln }] 2 ₁ d L E d n r E t_i t_i i λ γ γ γ γ λ γ − = − − = − − − ∑ =

⎡

⎧

_⎪

⎫

_⎪

⎤

⎢

⎨

⎬

⎥

⎪

⎢

⎩

⎭

⎥

⎣

⎦

2 2 ln ln 1 n r _ti _i i γ tγ λγ = + ∑ = standar error ˆγ yaitu

2 ˆ ˆ . .( ) ˆ ˆ ˆ ln ln 1 s e n r t_i t_i i γ γ γ λγ = + ∑ = (21)

Metode Weibull penduga persentil p diberikan sebagai berikut

ˆ 1/ 1 100 ˆ( ) ln ˆ ₁₀₀ t p p γ λ = −

⎡

⎛

⎞

⎤

⎢

⎜

⎟

⎥

⎝

⎠

⎣

⎦

standar error dapat dilihat pada lampiran 1 adalah ˆ( ) t p ˆ( ) 2 _ˆ ˆ ˆ . . ( ) { var( ) 2 ˆ ˆ 2 2 ˆ ₍ _{ln ) var( )}ˆ _ˆ 1/ 2 ˆ_ˆ ˆ ˆ _ˆ 2 ( ln ) cov( , )} t p s e t p c p c p γ λ λγ λ λ γ λγ λ λ γ = + − + − (22) Metode Weibull dengan Covariate

Metode Weibull dengan covariate disebut juga metode Weibull Proportional Hazard. Dalam metode Proportional Hazard, Fungsi Hazard didefinisikan sebagai berikut

1 1 2 2

( ... )

( ) xi xi p i px ( )

h t_i =eβ +β + +β h_o t (23) untuk i=1, 2...n dan x x₁, ₂...,_{x p}adalah nilai

covariate p serta β adalah nilai penduga untuk covariate. Jika Penduga _{x p} dalam persamaan di atas sama dengan 0 maka fungsi Hazard untuk individu adalah . Jika individu tersebut menyebar dengan metode Weibull maka fungsi hazard didefinisikan sebagai berikut ( ) 0 h t 1 ( ) 0 h t =λγtγ− (24) Persamaan (24) disubstitusikan ke persamaan (23) adalah

1 1 2 2

( ... ) ₁

( ) xi xi p i px

(20)

1/ 1 100 ˆ( ) ln ( ' ) ˆ 100 t p x _p e γ β λ = −

⎡

⎛

⎞

⎤

⎢

⎜

_⎝

⎟

_⎠

⎥

⎣

⎦

(29) dalam notasi matriks, η_i =β'x_i dimana β

adalah koefisien vektor untuk covariate

, ... 1 2

x x _{x p}, η_i disebut komponen linier dari model atau disebut nilai resiko atau index

prognostic. Bentuk Log-linear dari metode Weibull _{Proportional Hazard} Didefinisikan S t( )=exp(−H t( )) dan

( ) ( ) 0

t

H t = ∫h u du maka

Untuk memudahkan dalam menganalisis data survival dalam menafsirkan pendugaan parameter dengan menggunakan software SAS maka dibutuhkan representasi metode Weibull Proportional Hazard dalam bentuk log-linear. Tafsiran log-linear adalah kumpulan dari peubah acak dengan waktu tunggu mendapatkan pekerjaan pertama T didefinisikan sebagai berikut

i ( ) ( ) 0 t H t = ∫h u du du ( ' ) 1 0 t _xi e β λγuγ− = ∫ 1λγu eγ ( ' )β xi |₀t γ = logT_i = +µ α_{1 1}x_i+α_{2 2}x _i+ +... α_{p p}x _i+σε_i t

dengan menggunakan definisi fungsi Survivor =λt eγ ( ' )β xi ( ) ( ) (log log ) ( ' log ) S t_i P T_i t P T_i t P µ α _xi σε_i = ≥ = ≥ = + + ≥

fungsi Survivor didefinisikan sebagai berikut

( ' ) ( ) e xi t S t e β _λγ − =

dan fungsi kepekatan peluang didefinisikan sebagai berikut log ' log ' [ ] [ ) t x P _i t x i P e e i P e e µ α ε σ µ α ε _σ ε _ξ ξ − − = ≥ − − = ≥ = ≥ − =

⎡

⎤

⎢

⎥

⎣

⎦

( ' ) ( ' ) 1 ( ) ( ) ( ) ( ) xi _e e xit f t_i S t h t e t β γ β γ λ λγ − − = =

Penduga fungsi Survivor didefinisikan sebagai berikut ˆ ˆ ( ' ) ˆ ( ) ˆ ( e ) ˆ ( e ) ˆ ( ) xi i t t S t_i e e β γ η γ λ λ − − = = (26) dan penduga fungsi Hazard didefinisikan

sebagai berikut maka fungsi Survivor dari Ti adalah

ˆ ( ' ) ( ) ˆ 1 ˆ _{( )} _{ˆ ˆ} ˆ 1 ˆ ˆ i i x h t_i e t e t β η γ λγ γ λγ − = − = (27) log ' ( ) exp[ exp{ t xi}] S t_i µ α σ − − = − (30) Dengan membandingkan fungsi Survivor dan persamaan (26) maka

Ti Fungsi yang menyatakan nilai faktor yang mempercepat objek mengalami waktu kejadian didefinisikan sebagai berikut

exp( µ) λ σ − = (31) ˆ ( ) _{ˆ 1} _ˆ ˆ ( ) ˆ ( ) ˆ 1 ˆ ( ) _ˆ 0 xi h t_i e t x_i e h t _t β _γ β λγ ψ _γ λγ − = = ₋ = (28) _{γ σ −}₌ 1₍₃₂₎ j j α β σ − = (33) Generalisasi persamaan (4), persentil

sebaran waktu survival dalam metode Weibull Proportional Hazard berubah dari λ menjadi

( ' )x e β

(21)

CONTOH KASUS

( Pengaruh jenis kelamin, usia, IPK dan TOEFL dalam penentuan tingkat survival tidak mendapatkan pekerjaan bagi alumni departemen Matematika IPB)

Dalam karya ilmiah ini diambil data alumni S1 departemen Matematika IPB tentang jangka waktu dari lulus sampai mendapatkan pekerjaan. Data ini diambil dari para alumni angkatan 35 sampai angkatan 40 yang telah lulus. Data ini dapat dilihat pada lampiran 3. Dalam contoh kasus ini akan diperiksa hubungan antara covariates dan waktu survival dari para alumni.

Dalam pengamatan peubah respon utama adalah waktu dari lulus sampai mendapatkan pekerjaan. Pada data lampiran 3 terdapat 30 alumni Matematika IPB yang berumur 20-24 tahun. Beberapa dari mereka belum mendapatkan pekerjaan, alumni ini termasuk jenis sensor kanan. Untuk alumni dengan mendapatkan pekerjaan pada saat pengamatan dengan waktu survival tertentu ditandai dengan angka 1 sedangkan 0 menjelaskan bahwa alumni mengalami sensor kanan.

Covariate yang mempengaruhi tingkat survival alumni dalam mendapatkan pekerjaan kemudian dicatat meliputi jenis kelamin, usia dan IPK. Dalam hal ini jenis kelamin ditandai dengan angka 1 untuk laki-laki dan angka 0 untuk wanita. Sebenarnya masih banyak peubah lain yang dapat berpengaruh terhadap tingkat survival tetapi dalam karya ilmiah ini hanya mengambil 3 covariate.

Diantara 30 alumni tersebut ada 30% alumni laki-laki sisanya wanita. Banyaknya alumni yang mendapatkan pekerjaan pada tiap waktu dan banyaknya alumni yang beresiko mendapatkan pekerjaan pada tiap waktu tersebut kemudian dihitung.

Untuk menentukan bentuk metode yang sesuai digunakan dua metode yaitu metode Eksponensial dan metode Weibull. Untuk data tersensor tanpa covariate diasumsikan waktu survival tidak mendapatkan pekerjaan dari alumni menyebar metode Eksponensial dengan fungsi Hazard h t( )=λ dan fungsi Survivor S t( )=e−λt dan metode Weibull dengan fungsi Hazard h t( )=λγ −tγ 1 dan fungsi Survivor yaitu S t( ) e t

γ λ −

= . Dalam analisis data tersensor tanpa covariate akan membandingkan antara metode Eksponensial dan metode Weibull mana yang lebih baik dan selanjutnya metode tersebut akan digunakan dalam menganalisis data tersensor dengan 1 covariate dan multiple covariate.

Analisis data 30 alumni Departemen Matematika IPB untuk data tersensor tanpa covariate, dengan 1 covariate dan multiple covariate menggunakan SAS (Statistic Aplication Software).

1. Data tersensor tanpa covariate Analisis Survival metode Eksponensial

Analysis of Parameter Estimates Standard 95% Confidence Chi-

Parameter DF Estimate Error Limits Square Pr > ChiSq

Intercept 1 1.6907 0.1961 1.3063 2.0750 74.32 <.0001 Scale 0 1.0000 0.0000 1.0000 1.0000 Weibull Shape 0 1.0000 0.0000 1.0000 1.0000 Intercept = µ Scale = σ ˆ 1.6907 ˆ 1 ˆ _e _e _0.1843 µ σ λ = − = − = ˆ _0.1843 26 ˆ . .( ) 0.0361 r s e λ = λ = = 1 1 ˆ 1 ˆ 1 γ σ = = = ˆ . .( ) 0 s e γ =

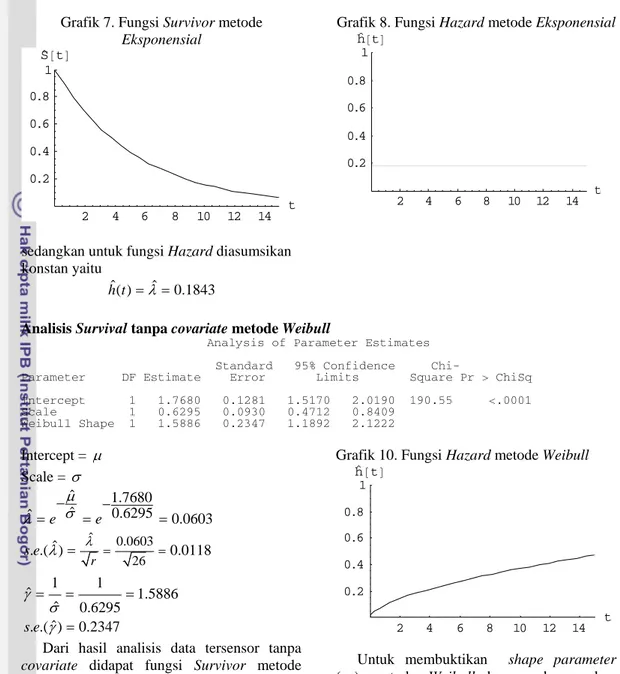
Dari hasil analisis survival data tersensor tanpa covariate maka didapat fungsi Survivor metode Eksponensial yaitu

0.1843 ˆ( ) t S t =e−

(22)

Grafik 7. Fungsi Survivor metode Eksponensial 2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 S ˆ_@_t_D

sedangkan untuk fungsi Hazard diasumsikan konstan yaitu

ˆ_{( )} ˆ _0.1843

h t = =λ

Grafik 8. Fungsi Hazard metode Eksponensial

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 h ˆ_@ tD

Analisis Survival tanpa covariate metode Weibull

Analysis of Parameter Estimates

Standard 95% Confidence Chi-

Intercept 1 1.7680 0.1281 1.5170 2.0190 190.55 <.0001 Scale 1 0.6295 0.0930 0.4712 0.8409 Weibull Shape 1 1.5886 0.2347 1.1892 2.1222 Intercept = µ Scale = σ ˆ 1.7680 ˆ 0.6295 ˆ _e _e _0.0603 µ σ λ= − = − = ˆ _0.0603 26 ˆ . .( ) 0.0118 r s e λ = λ = = 1 1 ˆ 1.5886 ˆ 0.6295 γ σ = = = ˆ . .( ) 0.2347 s e γ =

Dari hasil analisis data tersensor tanpa covariate didapat fungsi Survivor metode Weibull yaitu

1.5886 0.0603 ˆ( ) t

S t =e−

Grafik 9. Fungsi Survivor metode Weibull

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 S ˆ_@_t_D

Sedangkan untuk fungsi Hazard yaitu

0.5886 ˆ( ) (0.0603)(1.5886)

h t = t

Grafik 0. Fungsi Hazard metode Weibull 1

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 h ˆ_@ tD

Untuk membuktikan shape parameter (γ ) metode Weibull benar adanya akan dilakukan uji hipotesis. Perhatikan hipotesis nol bahwa shape parameter metode Weibull bernilai 1 lawan hipotesis alternatifnya bahwa shape parameter metode Weibull lebih besar dari 1. : 1 0 : 1 1 H H γ γ = > Nilai

z

bagi x = 1.5886 adalah

1.5886 1 2.51 0.2347 z= − = dengan demikian ( 2.51) 1 ( 2.51) value P P z P z = > = − <

(23)

1 0.9940

0.006

= − =

Nilai ini amat kecil dibandingkan dengan taraf uji nyata

P value

α, misalkan α =0.05

sehingga H₀ ditolak.

Hasil analisis survival data tersensor tanpa covariate menunjukan bahwa metode Weibull lebih baik dari metode Eksponensial. Ini dapat

dilihat dari nilai Chi-Square Pr metode Weibull lebih besar dari nilai chi-square Pr metode Eksponensial dan grafik fungsi Survivor metode Weibull bernilai lebih kecil dari metode Eksponensial.

Untuk selanjutnya hanya akan menggunakan metode Weibull untuk menganalisis data tersensor dengan 1 covariate dan multiple covariate.

2. Data Tersensor dengan 1 covariate

Analisis Survival dengan covariate Jenis Kelamin

Intercept 1 1.8514 0.2264 1.4076 2.2952 66.85 <.0001 JK 0 1 -0.1200 0.2659 -0.6412 0.4012 0.20 0.6518 JK 1 0 0.0000 . . . . . Scale 1 0.6218 0.0934 0.4632 0.8346 Weibull Shape 1 1.6083 0.2416 1.1981 2.1589 Intercept = µ Scale = σ ˆ _ˆ_/ _ˆ

β = −α σ = koefisien dari masing-masing nilai x dimana

1

x = jenis kelamin ˆ

1

β = nilai penduga untuk jenis kelamin

( 0.1200) ˆ _0.1929 1 0.6218 β = − − = 1 0.1929x i η = 1.8514 0.6218 ˆ ˆ ˆ _e _e _0.0509 µ σ λ= − = − = ˆ _0.0509 26 ˆ . .( ) 0.0099 r s e λ = λ = = 1 ˆ 1.6082 ˆ 0.6218

1

γ σ = = = ˆ . .( ) 0.2416 s e γ =

Covariate jenis kelamin

ˆ ˆ _{( )} _{exp{ exp(} ₎ˆ _} S t_i = − η λ_i tγ 1.6082 ˆ ( ) exp{ exp(0)0.0509₀ } S t = − t 1.6082 ˆ ( ) exp{ exp(0.1929)0.0509₁ } S t = − t 0 ˆ ( )

S t = peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni wanita

1

ˆ ( )

S t = peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni laki-laki

Grafik. 11. Fungsi Survivor metode Weibull untuk wanita dan laki-laki

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 S ˆ_H_t_L keterangan : = wanita --- = laki-laki ˆ 1 ˆ _{( )} i _{ˆ ˆ} h t_i =eη λγtγ− 0 0 ˆ ( )₀ (0.0509)(1.6082) h t =e t 0.1929 0. .6082 6082 ˆ ( )₁ (0.0509)(1.6082) h t =e t 0 ˆ ( )

h t =peluang mendapatkan pekerjaan pertama bagi wanita

1

ˆ ( )

h t =peluang mendapatkan pekerjaan pertama bagi laki-laki

(24)

Grafik 12. Fungsi Hazard metode Weibull untuk Wanita dan laki-laki

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 h ˆ_H tL keterangan : = wanita --- = laki-laki

Nilai faktor yang mempercepat waktu tunggu mendapatkan pekerjaan pertama akibat jenis kelamin adalah

{( ) ( )} 1 0 1 1 {(0.1929*0) (0.1929*1)} 0.8 x x e e β β ψ = − − = =

Jadi alumni wanita waktu tunggu pekerjaan pertamanya 1.25 kali lebih lama dibandingkan dengan alumni laki-laki. Hasil analisis survival menunjukkan bahwa covariate jenis

kelamin sebenarnya tidak berpengaruh nyata terhadap waktu tunggu mendapatkan pekerjaan pertama.

Nilai persentil p sebaran waktu survival t(p) jenis kelamin wanita adalah

t(25) t(50) t(75)

0 2.94 5.07 7 7.80 14 artinya bahwa 25 % sebaran waktu survival berada di bawah 2.94, 50% sebaran waktu survival berada di bawah 5.07 dan 75% berada di bawah 7.80.

Nilai persentil p sebaran waktu survival t(p) jenis kelamin laki-laki adalah

t(25) t(50) t(75)

0 2.60 4.49 6.92 14 artinya bahwa 25% sebaran waktu survival berada di bawah 2.60, 50% sebaran waktu survival berada di bawah 4.49 dan 75 % sebaran waktu survival berada di bawah 6.92.

Analisis Survival dengan covariate Usia

Intercept 1 -3.1323 1.7793 -6.6198 0.3551 3.10 0.0783 Usia 1 0.2180 0.0797 0.0618 0.3741 7.48 0.0062 Scale 1 0.5522 0.0817 0.4133 0.7379 Weibull Shape 1 1.8109 0.2678 1.3551 2.4198 Intercept = µ Scale = σ ˆ _ˆ_/ _ˆ

1 x = usia

ˆ 1

β = nilai penduga untuk usia

0.2180 ˆ _0.3947 1 0.5522 β = − = − 0.3947x i i η = − ˆ ( 3.1323) ˆ 0.5522 ˆ _e _e _290.7315 µ σ λ − − − = = = ˆ _290.7315 26 ˆ . .( ) 57.0174 r s e λ = λ = = 1 1.8109 0.5522

1

γ σ = = = ˆ . .( ) 0.2678 s e γ = Covariate Usia ˆ ˆ _{( )} _{exp{ exp(} ₎ˆ _} S t_i = − η λ_i tγ } 1.8109 ˆ _{( )} _{exp{ exp( 0.3947*20)290.7315} 20 S t = − − t } 1.8109 ˆ _{( )} _{exp{ exp( 0.3947 * 24)290.7315} 24 S t = − − t ˆ _{( )} 20

S t =peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni usia 20 tahun

=peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni usia 24 tahun

24

ˆ _{( )} S t

(25)

Grafik 13. Fungsi Survivor metode Weibull untuk usia 20 dan usia 24

5 10 15 20 25 30 35 40 t 0.2 0.4 0.6 0.8 1 S ˆ_H_t_L keterangan : = usia 20 --- = usia 24 ˆ 1 ˆ _{( )} i _{ˆ ˆ} h t_i =eη λγtγ− 0.8109 ( 0.3947)(20) ˆ _{( )} _{(290.7315)(1.8109)} 20 h t =e− t 0.8109 ( 0.3947)(24) ˆ _{( )} _{(290.7315)(1.8109)} 21 h t =e− t ˆ _{( )} 20

h t =peluang mendapatkan pekerjaan pertama bagi alumni usia 20 tahun

24 ˆ _{( )}

h t =peluang mendapatkan pekerjaan pertama bagi alumni usia 24 tahun Grafik 14. Fungsi Hazard metode Weibull

untuk usia 20 dan usia 24

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 h ˆ_H tL keterangan : = usia 20 --- = usia 24

Nilai faktor yang mempercepat waktu tunggu mendapatkan pekerjaan pertama bagi alumni usia 20 dan 24 adalah

{( _{1 20}x ) ( _{1 21}x )}

e β β

ψ = −

=e{( 0.3947*20) ( 0.3947*24)}− − − =4.85

Jadi alumni yang berusia 20 tahun waktu tunggu mendapatkan pekerjaan pertama 4.85 kali lebih cepat dibandingkan dengan alumni yang berusia 24 tahun. Hasil analisis survival menunjukkan bahwa covariate usia berpengaruh nyata terhadap waktu tunggu mendapatkan pekerjaan.

Nilai persentil p sebaran waktu survival t(p) usia 20 adalah

t(25) t(50) t(75)

0 1.71 2.78 4.08 7 14 artinya bahwa 25 % sebaran waktu survival usia 20 berada di bawah 1.71, 50% berada di bawah 2.78 dan 75% berada di bawah 4.08.

Nilai persentil p sebaran waktu survival t(p) usia 24 adalah

t(25) t(50) t(75)

0 4.09 6.667 9.77 14 artinya bahwa 25 % sebaran waktu survival usia 24 berada di bawah 4.09, 50% berada di bawah 6.66 dan 75% berada di bawah 9.07.

Analisis Survival dengan covariate IPK

Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 3.4161 0.6873 2.0690 4.7631 24.71 <.0001 Ipk 1 -0.5512 0.2236 -0.9895 -0.1130 6.08 0.0137 Scale 1 0.5509 0.0833 0.4096 0.7409 Weibull Shape 1 1.8152 0.2745 1.3496 2.4414 Intercept = µ Scale = σ ˆ _ˆ_/ _ˆ

1 x = IPK

ˆ 1

β = nilai penduga untuk IPK

( 0.5512) 0.5509 ˆ _1.0005 1 β = − − = 1.0005x i i η = 3.4161 0.5509 ˆ ˆ ˆ _e _e _0.00203 µ σ λ= − = − = ˆ _0.00203 26 ˆ . .( ) 0.00039 r s e λ = λ = =

(26)

1 ˆ 1.8152 ˆ 0.5509

1

γ σ = = = ˆ . .( ) 0.2745 s e γ = Covariate IPK ˆ ˆ _{( )} _{exp{ exp(} ₎ˆ _} S t_i = − η λ_i tγ } 1.8152 ˆ _{( )} _{exp{ exp(1.0005 * 2.5)0.00203} 2.5 S t = − t } 1.8152 ˆ ( ) exp{ exp(1.0005 *3)0.00203₃ S t = − t ˆ _{( )} 2.5

S t =peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni yang mempunyai IPK 2.5

3 ˆ ( )

S t =peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni yang mempunyai IPK 3 Grafik 15. Fungsi Survivor metode Weibull

untuk IPK 2.5 dan IPK 3

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 S ˆ_H_t_L keterangan : = IPK 2.5 --- = IPk 3 ˆ 1 ˆ _{( )} i _{ˆ ˆ} h t_i =eη λγtγ− 0.8152 (1.0005)(2.5) ˆ _{( )} _{(0.00203)(1.8152)} 2.5 h t =e t 0.8152 3 (1.0005)(3) ˆ ( ) (0.00203)(1.8152) h t =e t ˆ _{( )} 2.5

h t =peluang mendapatkan pekerjaan pertama bagi alumni yang mempunyai IPK 2.5

3 ˆ ( )

h t =peluang mendapatkan pekerjaan pertama bagi alumni yang mempunyai IPK 3

Grafik 16. Fungsi Hazard metode Weibull untuk IPK 2.5 dan IPK 3

2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 h ˆ_H tL keterangan : = IPK 2.5 --- = IPK 3

Nilai faktor yang mempercepat waktu tunggu mendapatkan pekerjaan pertama bagi alumni yang mempunyai IPK 2.5 dan IPK 3 adalah {( _{1 2.5}) ( _{1 3})} {(1.0005*2.5) (1.0005*3)} 0.61 x x e e β β ψ = − − = =

Jadi alumni yang mempunyai IPK 2.5 waktu tunggu mendapatkan pekerjaan pertama 1.6 kali lebih lama dibandingkan dengan alumni yang mempunyai IPK 3. Hasil analisis survival menunjukkan bahwa covariate IPK berpengaruh nyata terhadap waktu tunggu mendapatkan pekerjaan pertama.

Nilai persentil p sebaran waktu survival t(p) IPK 2.5 adalah

t(25) t(50) t(75)

0 3.86 6.26 9.18 14 artinya bahwa 25 % sebaran waktu survival IPK 2.5 berada di bawah 3.86, 50% berada di bawah 6.26 dan 75% berada di bawah 9.18.

Nilai persentil p sebaran waktu survival t(p) IPK 3 adalah

t(25) t(50) t(75)

0 2.91 4.76 6.97 14 artinya bahwa 25 % sebaran waktu survival IPK 3 berada di bawah 2.91, 50% berada di bawah 4.76 dan 75% berada di bawah 6.97.

(27)

3. Data tersensor multiple covariate

Analisis Survival covariate jenis kelamin, usia dan IPK

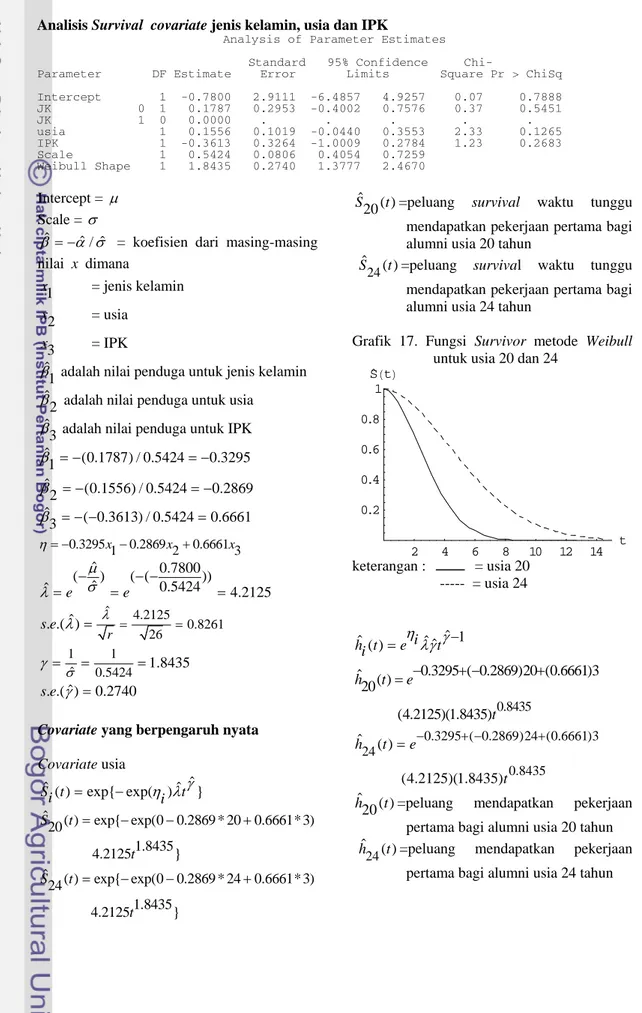
Intercept 1 -0.7800 2.9111 -6.4857 4.9257 0.07 0.7888 JK 0 1 0.1787 0.2953 -0.4002 0.7576 0.37 0.5451 JK 1 0 0.0000 . . . . . usia 1 0.1556 0.1019 -0.0440 0.3553 2.33 0.1265 IPK 1 -0.3613 0.3264 -1.0009 0.2784 1.23 0.2683 Scale 1 0.5424 0.0806 0.4054 0.7259 Weibull Shape 1 1.8435 0.2740 1.3777 2.4670 Intercept = µ Scale = σ ˆ _ˆ_/ _ˆ

β = −α σ = koefisien dari masing-masing nilai x dimana 1 x = jenis kelamin 2 x = usia 3 x = IPK ˆ 1

β adalah nilai penduga untuk jenis kelamin

ˆ 2

β adalah nilai penduga untuk usia

ˆ 3

β adalah nilai penduga untuk IPK ˆ _{(0.1787) / 0.5424} _0.3295 1 ˆ _{(0.1556) / 0.5424} _0.2869 2 β β = − = − = − = − ˆ _{( 0.3613) / 0.5424} _0.6661 3 β = − − = 0.3295x₁ 0.2869x₂ 0.6661x₃ η= − − + ˆ 0.7800 ( ) ( ( )) ˆ 0.5424 ˆ _e _e _4.2125 µ σ λ = − = − − = ˆ _4.2125 0.8261 26 ˆ . .( ) r s e λ = λ = = 1 1 ˆ 0.5424 1.8435 σ γ = = = ˆ . .( ) 0.2740 s e γ =

Covariate yang berpengaruh nyata Covariate usia ˆ ˆ _{( )} _{exp{ exp(} ₎ˆ _} S t_i = − η λ_i tγ ˆ _{( )} _{exp{ exp(0 0.2869 * 20} _{0.6661* 3)} 20 1.8435 4.2125 } S t t = − − + ˆ _{( )} _{exp{ exp(0 0.2869 * 24} _{0.6661* 3)} 24 1.8435 4.2125 } S t t = − − + ˆ _{( )} 20

S t =peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni usia 20 tahun

=peluang survival waktu tunggu mendapatkan pekerjaan pertama bagi alumni usia 24 tahun

24

ˆ _{( )} S t

Grafik 17. Fungsi Survivor metode Weibull untuk usia 20 dan 24

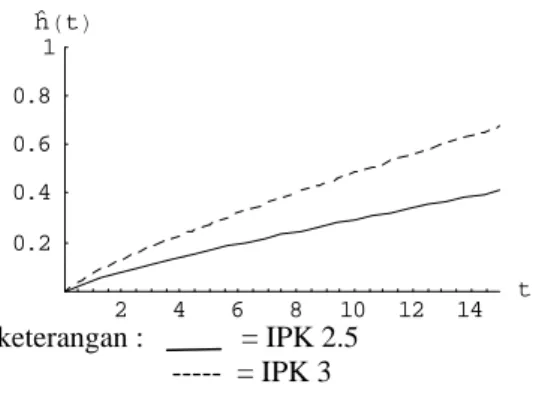
2 4 6 8 10 12 14 t 0.2 0.4 0.6 0.8 1 S ˆ_H_t_L keterangan : = usia 20 --- = usia 24 ˆ 1 ˆ_{( )} i _{ˆ ˆ} h t_i =eη λγ −tγ 0.8435 0.3295 ( 0.2869)20 (0.6661)3 ˆ _{( )} 20 (4.2125)(1.8435) h t e t − + − + = 0.3295 ( 0.2869)24 (0.6661)3 24 0.8435 ˆ _{( )} (4.2125)(1.8435) h t e t − + − + = ˆ _{( )} 20

h t =peluang mendapatkan pekerjaan pertama bagi alumni usia 20 tahun =peluang mendapatkan pekerjaan

pertama bagi alumni usia 24 tahun

24

ˆ _{( )} h t