ANALISIS REGRESI SEMIPARAMETRIK PADA KASUS HILANGNYA RESPON

124

Irma Yahya1), I Nyoman Budiantara2), dan Kartika Fitriasari2) 1)

Jurusan Matematika FMIPA, Universitas Haluoleo Kendari 2)

Jurusan Statistika FMIPA, ITS Sukolilo Surabaya

Abstract. In the specific cases of experiment, not all data (response) may be available,

which is called missing response cases. It’s appear for various reasons. For the existing problem, inference statistics cannot be applied directly. The aim of this research is to consider about certain method to impute the missing response which is related to semiparametric regression, as a goodness of fit measurement of the used method, suppose an estimator ˆθ which is compared to the mean of complete response, then consider asymptotic distribution, consistency and efficiency of parametrics component estimator. By using Kernel approximation, the resulted of nonparametrics estimator and by least square method, the resulted parametric component .The application to minimum temperature’s data in 56 cities at USA, estimator value of ˆθ for several confidence interval tend to be similar to the mean value of complete response.

Keywords: Asymptotic, Kernel Estimator, Missing Response, Semiparametric Regression.

1. PENDAHULUAN

Berbicara tentang inferensi statis-tik, dimana teori probabilitas digunakan sebagai pondasinya atau dasarnya, sama halnya berbicara masalah estimasi, baik estimasi interval maupun estimasi titik dan masalah pengujian hipotesis. Ketika mela-kukan inferensi statistik dibutuhkan data yang lengkap. Namun tak dapat dipungkiri bahwa dalam suatu penelitian dengan ber-bagai alasan sering terjadi kehilangan in-formasi untuk mendapatkan data (respon) lengkap yang dibutuhkan, yang biasanya disebut sebagai kasus hilangnya (missing) respon. Misalnya karena ketidaksediaan dari unit-unit sampel untuk memberikan informasi atau karena adanya faktor-faktor yang tidak terkontrol. Untuk mengatasi masalah kehilangan respon tersebut, hal yang biasanya dilakukan yaitu dengan cara membuang nilai variabel-variabel predik-tor yang bersesuaian dengan nilai respon yang hilang, tetapi hal ini tidak selamanya dapat dilakukan ketika kontribusi dari nilai variabel-variabel prediktor itu sangat dibu-tuhkan, atau dengan cara mengganti setiap respon yang hilang dengan suatu nilai yang wajar kemudian dilakukan analisis statistik berdasarkan data yang lengkap, namun hal

ini juga akan mengakibatkan inferensi sta-tistik dengan bias yang besar.

Dalam beberapa tahun terakhir ini telah banyak peneliti yang membahas ten-tang isu di atas dengan berbagai metode diantaranya yang berhubungan dengan re-gresi linier [11], [3], metode ratio [4], [7] mengawali metode kernel untuk missing respon, menggunakan estimasi regresi non-parametrik untuk mengestimasi respon ya-ng hilaya-ng deya-ngan asumsi MAR, [8] meya-ng- meng-gunakan densitas kernel yang dikombinasi-kan dengan nonparametrik bootstrap, Efron (1994) dengan pendekatan Bayesian

bootstrap, [2] dengan pendekatan kernel

untuk nonparametrik, pendekatan regresi multivariat [6], pendekatan Likelihood [4].

Dalam tulisan ini akan dibahas sua-tu metode unsua-tuk mengganti respon yang hilang didasarkan pada persamaan regresi semiparametrik:

( )

T

i i i i

Y =X

β

+g T +

ε

, i = 1,2,…,n (1.1), dimana Y adalah variabel respon, _i

i i

X dan T adalah variabel prediktor, g

( )

.

adalah fungsi yang tidak diketahui dan

ε

_i adalah error yang independen dengan

mean nol dan varians σ2. Diasumsikan Y i hilang secara acak (missing at random,

MAR) Untuk mengukur kebaikan metode

yang digunakan, diberikan suatu ukuran [10] yang didefinisikan:

(

)

( )

1 1 1 ( n T i i i i i i Y X g T n θ δ δ β =   =

∑

_ + − + _. (1.2) Sebagai ukuran kebaikan dari me-tode ini, yaitu bahwa nilai

θ

ˆ akan mende-kati nilai rata-rata dan nilai estimasi kurva respon lengkap.

2. ESTIMASI FUNGSI g

( )

. DAN

PARAMETER β

Jika persamaan (1.1) dihubungkan dengan kasus hilangnya respon dan β di-ketahui sebagai parameter yang benar maka untuk mengestimasi fungsi g1(t)

dan g2(t), dilakukan dengan langkah awal

yaitu persamaan (1.1) dikalikan dengan suatu indikator

δ

i, dimana

δ

i=0 jika Yi hi-lang (missing) dan

δ

i=1 jika Yi tidak hi-lang, sehingga persamaan (1.1) menjadi:

( )

T

i iY iXi ig Ti i

δ

=

δ

β δ

+ +

δ

εi (2.1) Selanjutnya persamaan (2.1) diekspektasi-kan dengan syarat (T=t) maka diperoleh

(

)

(

T

)

(

)

( )

i i i i i E δY T t= =E δX T t= β+Eδ T t g t= sehingga:

(

)

(

)

(

(

)

)

( ) T i i i i i i i i i i E X T t E Y T t g t E T t E T t

δ

δ

β

δ

δ

= = = − = = . (2.2) Persamaan (2.2) dapat ditulis sebagai berikut:

tor dari g t₁( ) , g t₂( ) ,dan g t( ) masing-masing sebagai berikut

(

)

(

)

1 1 1 1 1 1 1 1 ˆ ( ) ( ) i n i h i i n i i h i i n i i h i i n K t T X g t W t X n K t T δ δ δ − = − = = − = = −

∑

∑

∑

(2.4)

(

)

(

)

1 1 1 1 2 1 1 1 ˆ ( ) ( ) i n i h i i n i i h i n i i h i i n K t T Y g t W t Y n K t T δ δ δ − = − = = − = = −

∑

∑

∑

(2.5) dimana 1 ( ) ( ) i ni _n i i i t t K h W t t t K h δ = − =  ₋     

∑

.

Setelah estimator-estimator dari bagian nonparametrik diperoleh, selanjut-kan ditentuselanjut-kan estimator parametrik yaitu

ˆ

β, Untuk mengetimasi estimator ini digu-nakan metode kuadrat terkecil dan dengan meminimumkan

( )

(

)

(

( )

)

2 2 2 1 1 1 ˆ ˆ n n _T i i n i i n i i i Q ε Y g t X g t β = =   =

∑ ∑

= _ − − − _ , (2.6) maka diperoleh

(

)(

)

×         − − = − =

∑

1 1 1 1 ( ) ˆ ( ) ˆ ˆ n i T i n i i n i i n δ X g t X g t β

∑

[

(

)(

)

]

= − − n i i n i i n i i X g t Y g t 1 2 1 ( ) ˆ ( ) ˆ

δ

. (2.7) Estimator-estimator yang telah di-peroleh, kemudian disubtitusikan kedalam

3. APLIKASI DATA

Untuk aplikasi digunakan rata-rata suhu minimum bulan Januari di 56 kota Amerika Serikat. Ingin diketahui bagaima-na pengaruh letak suatu kota berdasarkan derajat bujur (longitude) dan derajat lin-tang (latitude) terhadap suhu rata-rata mi-nimum.

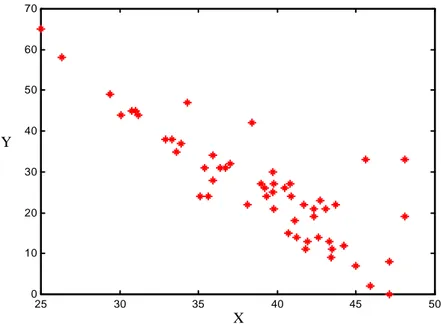
Sebagai langkah awal yaitu menen-tukan variabel-variabel prediktor yang ma-na sebagai variabel parametrik dan varia-bel nonparametrik. Salah satu cara untuk melihat hal tersebut yaitu dengan melihat plot antara masing-masing variabel predik-tor dengan varibel respon, jika plot antara variabel prediktor dengan variabel respon mengarah ke suatu bentuk kurva tertentu maka variabel prediktor tersebut merupa-kan varibel parametrik sedangmerupa-kan jika plot tersebut tidak jelas bentuk kurvanya maka

variabel prediktor tersebut adalah variabel nonparametrik.

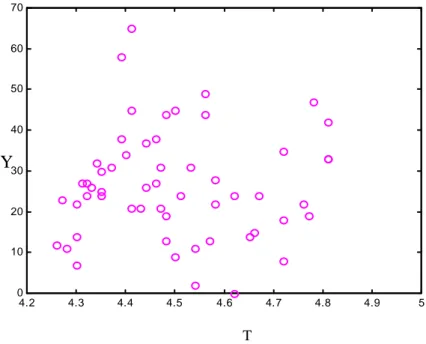
Berdasarkan Gambar (3.1) terlihat bahwa antara variabel X (lintang) dan variabel Y (suhu minimum), jelas plotnya mengarah ke suatu bentuk kurva tertentu sehingga variabel X ditetapkan sebagai varibel parametrik sedangkan dari Gambar (3.2) plot antara variabel T (bujur) dan variabel Y (suhu minimum) tidak menga-rah ke suatu bentuk kurva tertentu sehing-ga variabel T ditetapkan sebasehing-gai variabel nonparametrik.

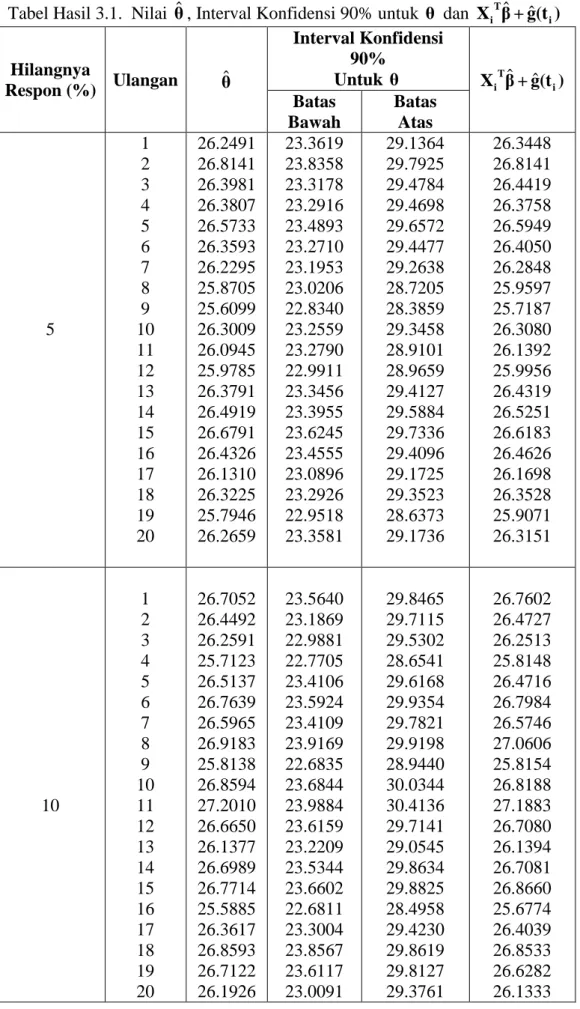
Pada proses hilangnya respon 5% dan 10 % dengan interval konvidensi 90% diperoleh nilai θˆ dan nilai estimasi kurva.

Pada Tabel 3.1 di halaman lampiran, terlihat dengan jelas nilai-nilai θˆ hampir sama dengan rata-rata respon lengkap yaitu

26,5179 . 25 30 35 40 45 50 0 10 20 30 40 50 60 70

Gambar 3.1. Plot antara Suhu Minimum (Y) dan Garis Lintang(X)

Y

4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5 0 10 20 30 40 50 60 70

Gambar 3.2. Plot antara Suhu Minimum (Y) dan Garis Bujur (T)

0 2 4 6 8 10 12 14 16 18 20 22 23 24 25 26 27 28 29 30 Batas atas θ Batas bawah θ ˆ θ : -*-*-* ˆ ˆT _{ˆ ( )} i i X β+g t : oooo Y Y T

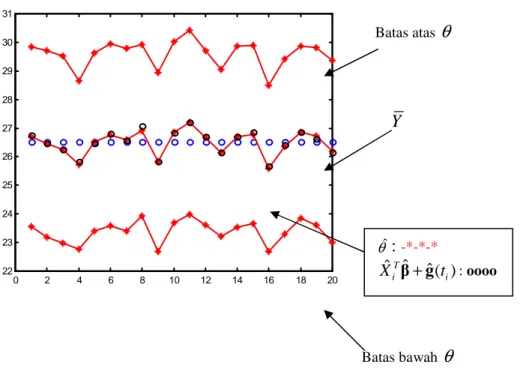
Gambar 3.4. Plot Nilai θˆ, Interval Konfidensi 90 % untuk θ dan Estimasi Kurva Regresi Hilangnya Respon 10%.

Gambar 3.3. Plot Nilai θˆ, Interval Konfidensi 90 % untuk θ dan Estimasi Kurva Regresi Hilangnya Respon 15%. 0 2 4 6 8 10 12 14 16 18 20 22 23 24 25 26 27 28 29 30 31 Batas bawah θ ˆ θ : -*-*-* ˆ ˆT _{ˆ ( )} i i X β+g t : oooo Y Batas atas θ 0 2 4 6 8 10 12 14 16 18 20 22 23 24 25 26 27 28 29 30 31 ˆ θ : -*-*-* ˆ ˆT _{ˆ ( )} i i X β+g t : oooo Batas bawah θ Batas atas θ Y

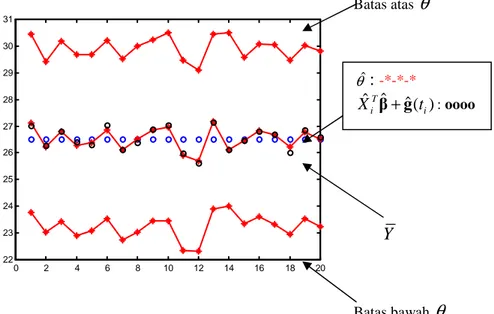
Gambar 3.4. Plot Nilai θˆ, Interval Konfidensi 90 % untuk θ dan Estimasi Kurva Regresi Hilangnya Respon 20%. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1 2 3 4 5 R ^ 2

Gambar 3.5. Diagram Batang R2 Respon Lengkap Dan Respon Hilang dengan Interval Konfidensi 90%. 30 40 50 60 M S E 1. Respon Lengkap. 2. Hilang Respon 5% 3. Hilang Respon 10% 4. Hilang Respon 15% 5. Hilang Respon 20% 0 2 4 6 8 10 12 14 16 18 20 22 23 24 25 26 27 28 29 30 31 Batas atas θ Y Batas bawah θ ˆ θ : -*-*-* ˆ ˆT _{ˆ ( )} i i X β+g t : oooo

Dari Gambar 3.3 dapat dilihat bahwa batas bawah θ terkecil 22,8340 dan terbesar adalah 23,8358 sedangkan batas atas terkecil 28,3859 dan terbesar 29,7925. Pada Gambar 3.4 diperoleh batas bawah terkecil 22,6811 dan terbesar 23,9884 serta batas atas terkecil 28,4958 dan yang terbe-sar 30,4136. Terlihat juga bahwa nilai-nilai estimasi kurva regresi dan nilai rata-rata respon lengkap berada diantara batas atas dan batas bawah tersebut.

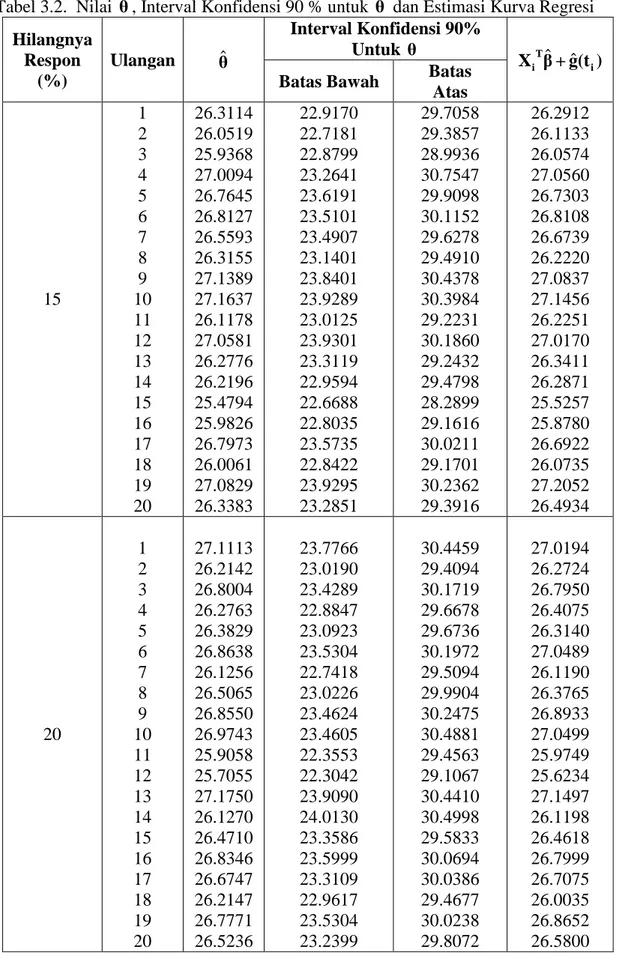
Pada proses hilangnya respon 15% dan 20 % dengan interval konvidensi 90% diperoleh nilai θˆdan nilai estimasi kurva. Pada Tabel 3.2 di halaman lampiran, terlihat bahwa nilai-nilai θˆ hampir sama dengan nilai rata-rata respon lengkapyaitu

26.5179.

Dari Gambar 3.3 di atas dapat di-simpulkan bahwa batas bawah θ terkecil 22,6688 dan terbesar adalah 23,9301 se-dangkan batas atas terkecil 28,2899 dan terbesar 30,7545. Pada Gambar 3.4 diper-oleh batas bawah terkecil 22,3042 dan terbesar 24,0130 serta batas atas terkecil 29,1067 dan yang terbesar 30,4998. Nilai estimasi kurva regresi dan nilai rata-rata respon lengkap berada diantara batas atas dan batas bawah.

Untuk nilai R2 dan MSE dari hilangnya respon 5%, 10%, 15 dan 20% (Gambar 3.5 dan Gambar 3.6) di atas, nilai-nilai tersebut cenderung sama dengan nilai R2 dan MSE dari respon lengkap, sehingga dapat disimpulkan bahwa proses penggantian respon yang hilang dengan mempergunakan metode ini adalah tidak merubah sifat dari respon lengkap atau metode ini cukup baik.

4. DAFTAR PUSTAKA

[1] Bartle,R. G. dan Sh erbh et, D.R, (1982), Introduction to Real Analysis, John Wiley & Sons, Inc, New York.

[2] Cheng,P.E., (1994), Nonparametric

Estimation of Mean Functional with Data Missing at Random, J. Amer.

Statist. Assoc., 89: 81-87.

[3] Healy,M.J.R. dan Westmacoot,M. (1996), Missing Values in

Experi-ments Analyzed on Automatic Compu-ters, J.App. Statist.

[4] Rao,J.N.K.,(1996), On Variance

Esti-mation with Impute Survey Data, J.

Amer. Statist Asso., 91: 499-520. [5] Rohatgi,V.K., (1976), An Introduction

to Probability Theory and Mathema-tical Statistics, John Wiley & Sons,

New York.

[6] Robins,J.dan Rotnizky,A., (1995),

Semiparametric Efficiency in

Multi-variate Regression Models with

Missing Data, Journal of the

American Statistical Association, . 90: 122-129.

[7] Titterington,D.M. dan Mill,G.M, (1983), Kernel Based Density

Esti-mates from Incomplete Data, Journal

of the Royal Statistical Society B,

45:258-266.

[8] Titterington,D.M. dan Sedransk, J, (1989), Imputation of Missing Values

Using Density Estimation Statistics & Probability Letters, 8: 411-418.

[9] Wang,Q.H. dan Rao,J.N.K. (2002),

Empirical Likelihood for Linier Re-gression Model Under Imputation for Missing Respon, The Canadian

Jour-nal of Statistics, 29: 597-608.

[10] Wang, Q.H. dan Linton, O (2004),

Semiparametric Regression Analysis with Missing Response at Random,

Journal of the American Statistical Association, 99: 334-345.

[11] Yates,F (1993), The Analysis of

Replicated Experiments Where Field Result are Incomplete, J. Exp. Agric.,

LAMPIRAN

Tabel Hasil 3.1. Nilai θˆ, Interval Konfidensi 90% untuk θ dan X_iTβˆ+ g(t ) ˆ _i

Hilangnya Respon (%) Ulangan θˆ Interval Konfidensi 90% Untuk θ X_iTβˆ+ g(t ) ˆ _i Batas Bawah Batas Atas 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 26.2491 26.8141 26.3981 26.3807 26.5733 26.3593 26.2295 25.8705 25.6099 26.3009 26.0945 25.9785 26.3791 26.4919 26.6791 26.4326 26.1310 26.3225 25.7946 26.2659 23.3619 23.8358 23.3178 23.2916 23.4893 23.2710 23.1953 23.0206 22.8340 23.2559 23.2790 22.9911 23.3456 23.3955 23.6245 23.4555 23.0896 23.2926 22.9518 23.3581 29.1364 29.7925 29.4784 29.4698 29.6572 29.4477 29.2638 28.7205 28.3859 29.3458 28.9101 28.9659 29.4127 29.5884 29.7336 29.4096 29.1725 29.3523 28.6373 29.1736 26.3448 26.8141 26.4419 26.3758 26.5949 26.4050 26.2848 25.9597 25.7187 26.3080 26.1392 25.9956 26.4319 26.5251 26.6183 26.4626 26.1698 26.3528 25.9071 26.3151 10 1 2 3 4 5 6 7 8 9 10 11 26.7052 26.4492 26.2591 25.7123 26.5137 26.7639 26.5965 26.9183 25.8138 26.8594 27.2010 23.5640 23.1869 22.9881 22.7705 23.4106 23.5924 23.4109 23.9169 22.6835 23.6844 23.9884 29.8465 29.7115 29.5302 28.6541 29.6168 29.9354 29.7821 29.9198 28.9440 30.0344 30.4136 26.7602 26.4727 26.2513 25.8148 26.4716 26.7984 26.5746 27.0606 25.8154 26.8188 27.1883

Tabel 3.2. Nilai θˆ, Interval Konfidensi 90 % untuk θ dan Estimasi Kurva Regresi Hilangnya Respon (%) Ulangan θˆ Interval Konfidensi 90% Untuk θ _ˆ ˆ T i i X β+ g(t )

Batas Bawah Batas

Atas 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 26.3114 26.0519 25.9368 27.0094 26.7645 26.8127 26.5593 26.3155 27.1389 27.1637 26.1178 27.0581 26.2776 26.2196 25.4794 25.9826 26.7973 26.0061 27.0829 26.3383 22.9170 22.7181 22.8799 23.2641 23.6191 23.5101 23.4907 23.1401 23.8401 23.9289 23.0125 23.9301 23.3119 22.9594 22.6688 22.8035 23.5735 22.8422 23.9295 23.2851 29.7058 29.3857 28.9936 30.7547 29.9098 30.1152 29.6278 29.4910 30.4378 30.3984 29.2231 30.1860 29.2432 29.4798 28.2899 29.1616 30.0211 29.1701 30.2362 29.3916 26.2912 26.1133 26.0574 27.0560 26.7303 26.8108 26.6739 26.2220 27.0837 27.1456 26.2251 27.0170 26.3411 26.2871 25.5257 25.8780 26.6922 26.0735 27.2052 26.4934 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 27.1113 26.2142 26.8004 26.2763 26.3829 26.8638 26.1256 26.5065 26.8550 26.9743 25.9058 25.7055 27.1750 26.1270 26.4710 26.8346 26.6747 26.2147 26.7771 26.5236 23.7766 23.0190 23.4289 22.8847 23.0923 23.5304 22.7418 23.0226 23.4624 23.4605 22.3553 22.3042 23.9090 24.0130 23.3586 23.5999 23.3109 22.9617 23.5304 23.2399 30.4459 29.4094 30.1719 29.6678 29.6736 30.1972 29.5094 29.9904 30.2475 30.4881 29.4563 29.1067 30.4410 30.4998 29.5833 30.0694 30.0386 29.4677 30.0238 29.8072 27.0194 26.2724 26.7950 26.4075 26.3140 27.0489 26.1190 26.3765 26.8933 27.0499 25.9749 25.6234 27.1497 26.1198 26.4618 26.7999 26.7075 26.0035 26.8652 26.5800