ABSTRAK
Filter Kalman adalah proses pendugaan keadaan optimal yang diterapkan
pada suatu sistem dinamis dan melibatkan derau acak. Pendugaan ini bersifat
rekursif, sehingga memudahkan peneliti ataupun teknisi dalam menangani data
yang terus bertambah dalam periode waktu tertentu.
Tujuan dari tulisan ini yaitu menurunkan algoritma filter Kalman, yaitu
algoritma untuk menduga keadaan optimal dari suatu sistem dinamis, baik diskret
maupun kontinu. Simulasi algoritma filter Kalman dilakukan dengan menggunakan software MATLAB R2010a. Hasilnya menunjukkan bahwa filter Kalman dapat menghasilkan penduga yang memiliki sifat kovariansi eror minimum.
Kata kunci: filter Kalman, derau, error, kovariansi, sistem dinamis, penduga
ABSTRACT
Kalman filter is an estimation process of optimal state, which applied to a
dynamic system that involves noise. This estimation is recursive so that it is easily
applied by scientist or engineer in handling data which grows continuously within
a certain period of time.
The purpose of this thesis is to derive the Kalman filter algorithm, which is
used to estimate the optimal state of a dynamic system, including discrete and
continuous models. The simulation is done using MATLAB R2010a. The result shows that Kalman filter gives a good estimator, which has minimum error covariance.
i
FILTER KALMAN
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun oleh: Auxilia Maria Aroran
NIM: 123114004
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
A KALMAN FILTER
THESIS
Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains
Mathematics Study Program
Written by: Auxilia Maria Aroran Student ID: 123114004
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
iii
SKRIPSI
FILTER KALMAN
Disusun oleh:
Auxilia Maria Aroran
NIM: 123114004
Telah disetujui oleh:
Dosen Pembimbing Skripsi
iv
SKRIPSI
FILTER KALMAN
Dipersiapkan dan ditulis oleh:
Auxilia Maria Aroran
NIM: 123114004
Telah dipertahankan di hadapan Panitia Penguji
Pada tanggal 31 Januari 2017
Dan dinyatakan telah memenuhi syarat
SUSUNAN PANITIA
Nama Lengkap Tanda Tangan
Ketua : Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. ...
Sekretaris : Ir. Ig. Aris Dwiatmoko, M.Sc. ...
Anggota : Hartono, Ph.D. ...
Yogyakarta, 31 Januari 2017
Fakultas Sains dan Teknologi
Universitas Sanata Dharma
Dekan,
v
HALAMAN PERSEMBAHAN
Skripsi ini saya persembahkan untuk
Tuhan Yesus dan Bunda Maria
Kedua Orang Tua, Nixon Aroran dan Maryke Pontoan
Adik Lafio Aroran & Adik ipar Cyprianus Warouw
Keponakan Karlen Junno Aquinas Warouw
Kakek, Nenek, Keluarga Besar dan Sanak Saudara
Pastor Yong Ohoitimur dan keluarga besar Yayasan Pendidikan Lokon
vi
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak
memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam
kutipan dan daftar pustaka sebagaimana layaknya karya ilmiah.
Yogyakarta, 31 Januari 2017
vii
ABSTRAK
Filter Kalman adalah proses pendugaan keadaan optimal yang diterapkan
pada suatu sistem dinamis dan melibatkan derau acak. Pendugaan ini bersifat
rekursif, sehingga memudahkan peneliti ataupun teknisi dalam menangani data
yang terus bertambah dalam periode waktu tertentu.
Tujuan dari tulisan ini yaitu menurunkan algoritma filter Kalman, yaitu
algoritma untuk menduga keadaan optimal dari suatu sistem dinamis, baik diskret
maupun kontinu. Simulasi algoritma filter Kalman dilakukan dengan menggunakan software MATLAB R2010a. Hasilnya menunjukkan bahwa filter Kalman dapat menghasilkan penduga yang memiliki sifat kovariansi eror minimum.
Kata kunci: filter Kalman, derau, error, kovariansi, sistem dinamis, penduga
viii
ABSTRACT
Kalman filter is an estimation process of optimal state, which applied to a
dynamic system that involves noise. This estimation is recursive so that it is easily
applied by scientist or engineer in handling data which grows continuously within
a certain period of time.
The purpose of this thesis is to derive the Kalman filter algorithm, which is
used to estimate the optimal state of a dynamic system, including discrete and
continuous models. The simulation is done using MATLAB R2010a. The result shows that Kalman filter gives a good estimator, which has minimum error covariance.
ix
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Auxilia Maria Aroran
NIM : 123114004
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan
Universitas Sanata Dharma karya ilmiah saya yang berjudul:
“Filter Kalman”
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan
kepada Perpustakaan Universitas Sanata Dharma untuk menyimpan, mengalihkan
ke dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data,
mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media
lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun
memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai
penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada tanggal 31 Januari 2017
Yang menyatakan
x
KATA PENGANTAR
Puji dan syukur kepada Tuhan atas berkat dan penyertaannya sampai pada
saat penulis dapat menyelesaikan tugas akhir ini. Skripsi yang berjudul “Filter Kalman” ini disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika Universitas Sanata Dharma. Selama proses
penyusunan, tentu saja penulis menemui berbagai macam hambatan sampai
akhirnya bisa selesai berkat penyertaan Tuhan dan dukungan dari berbagai pihak.
Ucapan terima kasih atas berbagai dukungan yang diterima ingin disampaikan
oleh penulis kepada:
1. Bapak Hartono, Ph.D., selaku dosen pembimbing skripsi, sekaligus Ketua
Program Studi Matematika dan Dosen Pembimbing Akademis atas semua
bentuk bimbingan dan saran yang diberikan baik selama proses penyusunan
skripsi, maupun sejak penulis berada di Program Studi Matematika ini.
2. Bapak/Ibu/Romo dosen yang telah membagikan ilmu pengetahuannya selama
penulis menjalani perkuliahan di Universitas Sanata Dharma.
3. Keluarga dan sanak saudara di Manado atas segala bentuk doa, dukungan,
dan dorongan sehingga penulis bisa menyelesaikan skripsi ini.
4. Yayasan Pendidikan Lokon yang telah memberikan kesempatan kepada
penulis untuk menempuh pendidikan di USD, serta dorongan dan semangat
yang telah diberikan sampai penulis bisa menyelesaikan skripsi.
5. Teman-teman Matematika USD angkatan 2012 (Ajeng, Anggun, Arum, Boby,
xi
Ryan, Sila, Tika) atas semangat dan dorongan selama penulisan, juga selama
berdinamika bersama sebagai bagian dari keluarga Prodi Matematika USD.
6. Keluarga Besar Program Studi Matematika Universitas Sanata Dharma,
kakak-kakak dan adik-adik angkatan, juga keluarga besar FST USD,
karyawan dan staff yang baik secara langsung maupun secara tidak langsung
memberikan bantuan kepada penulis.
7. Zilvi, Tri, dan juga teman-teman befi yang memberikan semangat dan
menjadi teman diskusi selama penulis mengerjakan skripsi, serta BF dan
semua pihak yang tidak sempat disebutkan, yang secara tidak langsung telah
menyemangati penulis sehingga bisa menyelesaikan skripsi ini.
Penulis menyadari, bahkan dengan bantuan dan keterlibatan dari berbagai
pihak, tulisan ini adalah karya dari penulis, manusia biasa yang tak luput dari
kesalahan. Oleh karena itu, penulis dengan tangan terbuka menerima segala
bentuk kritik dan saran dari pembaca sekalian. Semoga kiranya tulisan ini dapat
bermanfaat bagi para pembaca.
Yogyakarta, 31 Januari 2017
xii
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
ABSTRAK ... vii
ABSTRACT ... viii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR GAMBAR ... xiv
DAFTAR TABEL ... xv
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah... 1
B. Rumusan Masalah ... 5
C. Pembatasan Masalah ... 5
D. Tujuan Penulisan ... 5
E. Manfaat Penulisan ... 6
F. Metoda Penelitian ... 6
xiii
BAB II PENDUGA KUADRAT TERKECIL ... 9
A. Matriks ... 9
B. Variabel Acak dan Proses Stokastik ... 21
C. Penduga Kuadrat Terkecil ... 27
BAB III FILTER KALMAN ... 45
A. Filter Kalman dengan Waktu Diskret ... 45
B. Persamaan Filter Kalman Satu Langkah ... 52
C. Derau Proses Pendugaan ... 58
D. Derau Pengukuran ... 60
E. Filter Kalman dengan Waktu Kontinu ... 61
F. Linearisasi Filter Kalman ... 67
G. Perluasan Filter Kalman dengan Waktu Kontinu ... 70
H. Perluasan Filter Kalman dengan Waktu Diskret ... 72
BAB IV SIMULASI FILTER KALMAN ... 76
A. Simulasi Filter Kalman untuk Menduga Suatu Konstan ... 76
B. Simulasi Filter Kalman untuk Menduga Posisi dan Kecepatan ... 80
C. Penerapan Filter Kalman dalam Berbagai Bidang ... 86
BAB V PENUTUP ... 89
A. Kesimpulan ... 89
B. Saran ... 91
DAFTAR PUSTAKA ... 93
xiv
DAFTAR GAMBAR
Gambar 1.1 Bagan Penerapan Filter Kalman ... 3
Gambar 1.2 Algoritma Filter Kalman... 4
Gambar 2.1 Pendugaan kuadrat terkecil & nya ... 31
Gambar 2.2 Pendugaan kuadrat terkecil berbobot & nya ... 32
Gambar 2.3 Pendugaan kuadrat terkecil rekursif & nya ... 38
Gambar 3.1 Hubungan antara penduga keadaan priori dan posteriori, dan kovariansi pendugaannya ... 47
Gambar 3.2 Variansi penduga posisi 5 langkah pertama filter Kalman ... 56
Gambar 3.3 Variansi penduga posisi 60 langkah pertama filter Kalman ... 57
Gambar 3.4 pengukuran dan pendugaan untuk contoh 3.2 ... 57
Gambar 4.1 Pendugaan konstan ... 76
Gambar 4.2 pendugaan konstan... 77
Gambar 4.3 Variansi pendugaan konstan ... 77
Gambar 4.4 Posisi kendaraan & nya ... 80
xv
DAFTAR TABEL
Tabel 3.1 Hubungan antara penduga dan kovariansi pada pendugaan kuadrat
terkecil dan filter Kalman ... 51
Tabel 4.1 Data hasil simulasi filter Kalman untuk menduga suatu konstan ... 78
Tabel 4.2 Data hasil simulasi filter Kalman untuk menduga posisi dan kecepatan... 81
Tabel 4.3 Tujuan dan metode filter Kalman yang berkaitan ... 87
Tabel 5.1 Filter Kalman dengan waktu diskret ... 89
Tabel 5.2 Filter Kalman dengan waktu kontinu ... 90
Tabel 5.3 Perluasan Filter Kalman dengan waktu kontinu ... 90
1 BAB I PENDAHULUAN
A. Latar Belakang Masalah
Pada tahun 1960, R.E. Kalman menerbitkan paper yang mendeskripsikan
suatu solusi rekursif terhadap masalah filter data diskret linear, yang
kemudian dikenal dengan nama Filter Kalman. Filter yang dimaksud adalah
sebuah algoritma pemrosesan data. Pada umumnya, filter bertujuan untuk
memperoleh pendugaan optimal atas suatu susunan data. Sama seperti
filter-filter lainnya, filter-filter Kalman juga bertujuan untuk memperoleh pendugaan
optimal atas data yang diberikan oleh sumber berderau.
Filter Kalman adalah proses pendugaan keadaan optimal yang diterapkan
pada suatu sistem dinamis dan melibatkan derau acak. Optimal di sini berarti
meminimalkan error. Filter Kalman disebut juga sebagai penduga kuadrat
terkecil linear karena meminimalkan rata-rata kuadrat pendugaan suatu sistem
linear stokastik. Terdapat tiga alasan dasar mengapa sistem deterministik dan
teori kontrol tidak cukup akurat dalam analisis, antara lain:
Tidak ada model sistem matematis yang sempurna.
Sistem dinamis dipengaruhi bukan hanya oleh kontrol input awal, tetapi
juga oleh gangguan-gangguan yang tak terkontrol atau tak bisa
dimodel-kan secara deterministik.
Sensor tidak memberikan data yang sempurna dan lengkap dari sebuah
Filter Kalman menggabungkan semua pengukuran yang tersedia, tanpa
memperhatikan ketepatannya, untuk menduga nilai terbaru dari variabel yang
diteliti dengan menggunakan (1) pengetahuan tentang sistem dan alat
pengukuran, (2) deskripsi statistis dari derau sistem, pengukuran, dan
ketidakpastian dalam model dinamis, dan (3) informasi yang tersedia tentang
keadaan awal dari variabel yang diteliti.
Salah satu yang membedakan filter Kalman dengan konsep pemrosesan
data tertentu adalah konsep rekursif. Dengan sifat rekursif ini, filter Kalman
tidak perlu menyimpan semua data yang sebelumnya telah diperoleh
kemudian memroses kembali semua data tersebut setiap diperoleh data
pengukuran yang baru.
Tujuan utama dari filter kalman yaitu untuk menduga keadaan dari
sistem dinamis. Keadaan yang akan diduga yaitu pada sistem dinamis
dari pengetahuan tentang hasil pengukuran
dengan , , dan adalah matriks transisi keadaan, matriks input, dan
matriks output. Vektor- vektor , , dan masing-masing menyatakan
vektor keadaan, vektor kontrol, dan vektor output, sedangkan dan
merupakan proses derau yang terlibat. Untuk lebih jelasnya lihat gambar 1.1.
Filter Kalman telah digunakan secara luas dalam berbagai bidang industri
dan pemerintahan, seperti sistem tracking pada video dan laser, navigasi
Dengan berkembangnya komputer berkecepatan tinggi, filter Kalman menjadi
lebih berguna dalam aplikasi masa kini.
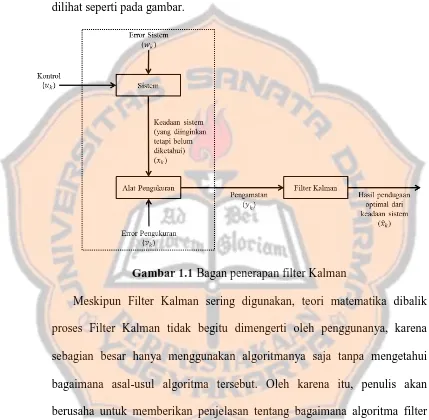
Secara sederhana, penerapan filter Kalman pada suatu sistem dapat
dilihat seperti pada gambar.
Gambar 1.1 Bagan penerapan filter Kalman
Meskipun Filter Kalman sering digunakan, teori matematika dibalik
proses Filter Kalman tidak begitu dimengerti oleh penggunanya, karena
sebagian besar hanya menggunakan algoritmanya saja tanpa mengetahui
bagaimana asal-usul algoritma tersebut. Oleh karena itu, penulis akan
berusaha untuk memberikan penjelasan tentang bagaimana algoritma filter
Kalman ini diperoleh. Algoritma filter Kalman bermula dari pedugaan
kuadrat terkecil dengan mengikuti langkah-langkah penurunan sebagai
berikut:
1. Mulai dengan deskripsi matematis dari suatu sistem dinamis yang akan
2. Menerapkan persamaan yang mendeskripsikan bagaimana rata-rata dari
keadaan yang diteliti dan kovariansinya merambat bersesuaian dengan
waktu.
3. Pilih sistem dinamis yang menggambarkan perambatan rata-rata dan
kovariansi keadaan tersebut kemudian menerapkan persamaan yang
diperoleh. Persamaan ini merupakan dasar dari penurunan Filter Kalman
sebab rata-rata dari keadaan tersebut merupakan pendugaan Filter
Kalman atas keadaan tersebut.
4. Setiap kali hasil pengukuran diperoleh, maka rata-rata dan kovariansinya
akan diperbaharui secara rekursif.
Algoritma filter Kalman dapat dicantumkan dalam bagan sebagai berikut.
Gambar 1.2 Algoritma filter Kalman
Penjelasan mengenai bagaimana memperoleh persamaan-persamaan
Sebelumnya, pada bab kedua akan dibahas terlebih dahulu tentang teori-teori
dasar yang dibutuhkan, khususnya pendugaan kuadrat terkecil.
B. Rumusan Masalah
Berdasarkan latar belakang yang telah dipaparkan, masalah-masalah
yang akan dibahas dalam tulisan ini antara lain:
1. Bagaimana proses untuk memperoleh algoritma filter Kalman?
2. Bagaimana contoh simulasi filter Kalman dalam kehidupan sehari-hari?
C. Pembatasan Masalah
Masalah yang akan dibahas dalam tulisan ini dibatasi sebagai berikut:
1. Filter Kalman yang dibahas dalam tulisan ini adalah filter Kalman
dengan waktu diskret dan waktu kontinu, sampai pada perluasannya.
2. Jenis-jenis filter Kalman seperti Ensemble Kalman Filter (EnKF),
Adaptive Kalman Filter (AKF) dan lainnya tidak akan dibahas dalam
tugas akhir dalam program studi Matematika Universitas Sanata Dharma,
1. Menjelaskan bagaimana proses memperoleh algoritma filter Kalman.
2. Memberi contoh simulasi filter Kalman dan penerapan filter Kalman
dalam berbagai bidang.
3. Memperluas wawasan pembaca tentang aplikasi ilmu matematika
khususnya mengenai filter Kalman.
E. Manfaat Penulisan
Manfaat dari penulisan tugas akhir ini adalah sebagai berikut:
1. Penulis memperoleh pengetahuan baru selama mengerjakan tulisan ini.
2. Pembaca mendapat gambaran tentang aplikasi ilmu matematika dalam
kehidupan sehari-hari, yaitu penerapan filter Kalman.
F. Metode Penelitian
Metode yang digunakan penulis dalam penyusunan tugas akhir yaitu
studi pustaka, yaitu dengan mempelajari buku dan/atau jurnal yang
membahas tentang Filter Kalman maupun aplikasinya.
G. Sistematika Penulisan
BAB I. PENDAHULUAN
A. Latar Belakang Masalah
B. Perumusan Masalah
C. Pembatasan Masalah
E. Manfaat Penulisan
F. Metode Pemulisan
G. Sistematika Penulisan
BAB II. LANDASAN TEORI
A. Matriks
B. Derau Putih
C. Penduga Kuadrat Terkecil
BAB III. FILTER KALMAN
A. Filter Kalman dengan Waktu Diskret
B. Persamaan Filter Kalman Satu Langkah
C. Derau Proses Pendugaan
D. Derau Pengukuran
E. Filter Kalman dengan Waktu Kontinu
F. Linearisasi Filter Kalman
G. Perluasan Filter Kalman dengan Waktu Kontinu
H. Perluasan Filter Kalman dengan Waktu Diskret
BAB IV. SIMULASI FILTER KALMAN
A. Simulasi Filter Kalman untuk Menduga Suatu Konstan
B. Simulasi Filter Kalman untuk Menduga Posisi dan Kecepatan
C. Penerapan Filter Kalman dalam Berbagai Bidang
BAB V. PENUTUP
A. Kesimpulan
DAFTAR PUSTAKA
9 BAB II
PENDUGA KUADRAT TERKECIL
Dalam bab ini, terdapat subbab-subbab yang merupakan landasan teori untuk
mempelajari filter Kalman pada bab selanjutnya. Sebelumnya telah disebutkan
bahwa filter Kalman juga merupakan penduga kuadrat terkecil. Oleh karena itu,
pokok dari bab ini adalah membahas mengenai penduga kuadrat terkecil. Selain
itu, terdapat beberapa materi berkaitan yang juga perlu untuk dibahas terlebih
dahulu, yaitu matriks dan proses stokastik. Materi-materi tersebut dirangkum
dalam subbab-subbab berikut.
A. Matriks
Materi tentang matriks yang akan dibahas dalam subbab ini adalah
lemma invers matriks, maktriks pseudo invers, kalkulus matriks, dan matriks
definit positif. Pembahasan materi-materi berikut didasari dengan asumsi
bahwa pembaca telah menguasai konsep-konsep dasar aljabar linear seperti
sistem linear, operasi aljabar matriks, invers matriks, ruang baris dan ruang
kolom, serta ruang hasilkali dalam.
1. Lemma Invers Matriks
Pada bagian ini akan dibahas tentang lemma invers matriks yang
nantinya akan digunakan pada bagian selanjutnya. Lemma invers matriks
Misalkan terdapat matriks gabungan dengan matriks ,
matriks , keduanya tak singular, sedangkan matriks dan
matriks . Definisikan matriks dan dengan
maka:
a. Andaikan mempunyai invers, dapat ditunjukkan bahwa
merupakan invers dari
b. Andaikan mempunyai invers, dapat ditunjukkan bahwa
juga merupakan invers dari
c.
Bukti
a.
c. Dari a dan b, matriks dan matriks
keduanya merupakan invers dari matriks
sehingga berdasarkan teorema ketunggalan invers, kedua matriks
tersebut sama. Dan dengan kesamaan dua matriks, diperoleh
. ■
Selanjutnya, karena dan , maka
Bentuk ini disebut lemma invers matriks. Bentuk lainnya yang ekuivalen
yaitu
Untuk memahami lebih jelas, berikut ini diberikan contoh penggunaan
lemma invers di atas.
Contoh 2.1
Misalkan terdapat matriks
Akan dicari invers dari matriks .
Tanpa menghitung invers matriks dari awal, dapat diperoleh
dengan menggunakan hasil invers dari matriks . Perhatikan bahwa
, dengan , , dan
Dengan menggunakan lemma invers matriks, diperoleh
2. Matriks Pseudo Invers
Selain lemma invers matriks, matriks pseudo invers juga akan disebutkan
pada bagian selanjutnya, sehingga penting untuk dibahas sebelumnya. Bentuk
pseudo invers dari matriks merupakan perumuman dari matriks invers
yang biasanya, dimana matriks tidak harus memenuhi semua sifat-sifat
matriks yang bisa dibalik.
Misalkan matriks . Hal ini sama saja dengan mengatakan bahwa
ruang baris dari paling banyak berdimensi dan ruang kolomnya paling
banyak berdimensi . Karena ruang baris dan ruang kolom memiliki dimensi
yang sama (rank dari ), jika , maka rank dari paling besar adalah
Singularitas matriks dibutuhkan untuk menentukan matriks pseudo
invers dari . Berikut diberikan teorema tentang singularitas matriks .
Teorema 2.1
Jika merupakan matriks dengan rank penuh, maka tak singular.
Bukti
Teorema akan terbukti dengan memperlihatkan jika untuk
sebarang , maka . Jika maka dengan mengalikan kedua ruas
dengan , diperoleh ,
sehingga . Karena mempunyai rank penuh, diperoleh .
Dengan demikian, terbukti tak singular. ■
Jika merupakan matriks dengan rank kolom penuh, yaitu
, maka tidak singular, jadi punya invers. Bentuk
disebut pseudo invers kiri dari , dimana . Rank dari
dan adalah .
Jika merupakan matriks dengan rank baris penuh, yaitu
, maka tidak singular, jadi punya invers. Selanjutnya, bentuk
disebut pseudo invers kanan dari . Rank dari dan
adalah . Berikut diberikan contoh untuk mencari pseudo invers dari matriks
Contoh 2.2
Misalkan terdapat matriks . adalah matriks
dengan dan . Diperoleh , dan . Matriks
adalah matriks singular, sedangkan
mempunyai invers, yaitu . Pseudo invers
kirinya tidak terdefinisi karena bukan matriks dengan rank kolom penuh,
sedangkan pseudo invers kanannya adalah
dengan .
3. Kalkulus Matriks
Bagian selanjutnya adalah kalkulus matriks. Bagian ini akan membahas
definisi-definisi tentang turunan matriks, serta persamaan-persamaan yang
dihasilkannya. Bagian ini penting dikuasai untuk digunakan dalam mencari
Definisi 2.1
Misalkan matriks , dimana elemen-elemennya berupa fungsi
terhadap waktu. Didefinisikan turunan matriks sebagai berikut
menyebabkan merupakan matriks konstan sehingga
turunannya sama dengan nol. Penurunan dapat juga dihitung dengan
Karena turunannya sama dengan nol, maka dapat diperoleh turunan dari
yaitu
Definisi 2.2 (Turunan parsial fungsi terhadap vektor)
Misalkan vektor dan fungsi skalar dari elemen-elemen ,
maka turunan parsial fungsi terhadap vektor adalah
Definisi 2.3 (Turunan parsial fungsi terhadap matriks)
Misalkan matriks dan fungsi skalar. Turunan parsial
Dengan definisi-definisi tersebut, dapat dihitung turunan parsial dari hasil
perkalian antara dua vektor. Misalkan dan vektor kolom dengan elemen.
Dengan cara yang sama, diperoleh
Untuk bentuk kuadratik
Jika matriks simetri, maka sehingga diperoleh
Definisi 2.4 (Turunan parsial vektor terhadap vektor lain)
Misalkan dan . Maka
Jika salah satu dari maupun ditranspos, maka turunan parsialnya
juga ditranspos, yaitu
Dari definisi-definisi di atas, dapat diperoleh persamaan-persamaan
berikut.
Definisi 2.5 (Turunan parsial trace matriks terhadap matriks ) Misalkan matriks dan matriks .
Turunan parsial terhadap adalah
4. Matriks Definit Positif
Bagian selanjutnya akan membahas tentang matriks definit positif.
Matriks definit positif berperan penting dalam menentukan nilai minimum
suatu fungsi objektif. Berikut merupakan beberapa hal yang perlu diingat
tentang matriks definit positif.
Definisi 2.6
Matriks simetri disebut definit positif jika untuk semua
vektor yang tak nol.
Teorema 2.2
Jka mempunyai rank penuh, maka merupakan matriks definit
positif
Bukti
Karena , maka matriks simetri.
Selanjutnya, mempunyai rank penuh, tidak nol untuk sebarang taknol.
Jadi perkalian titik . Dan untuk sebarang vektor ,
diperoleh , jadi berdasarkan definisi, adalah
matriks definit positif. ■
Definisi 2.7
Matriks Hessian adalah matriks simetri yang elemen-elemennya
vektor. Misalkan terdapat suatu fungsi dan vektor , matriks Hessian
dari fungsi adalah matriks , dimana , yaitu
Teorema 2.3
Titik stasioner meminimumkan jika matriks Hessian dari yang
dievaluasi pada adalah definit positif.
Bukti
Ekspansi Taylor sampai orde kedua di sekitar adalah
Karena titik stasioner, maka
jadi
bernilai positif. Padahal jika ruas kanan tersebut ditulis dalam bentuk matriks
diperoleh
Sedangkan
merupakan matriks Hessian dari . Jadi adalah matriks definit positif,
sehingga meminimumkan ketika matriks Hessian dari yang dievaluasi
pada definit positif. ■
B. Variabel Acak dan Proses Stokastik
Sub-bab ini akan membahas mengenai variabel acak dan proses stokastik.
Namun sebelumnya akan dibahas terlebih dahulu beberapa teori dasar
peluang.
Peluang kejadian didefinisikan dengan
dengan merupakan banyaknya anggota ruang sampel pada kejadian ,
dan merupakan banyaknya semua anggota ruang sampel, dengan .
Misalnya dalam pelemparan dadu, , maka .
Peluang kejadian munculnya mata dadu 4 pada permukaan dadu adalah
terdapat 36 anggota ruang sampel , yaitu , dan peluang kejadian
munculnya mata dadu 2 dan 3 dalam sekali pelemparan adalah , sebab
, dan .
Peluang suatu kejadian juga bisa berkaitan dengan peluang kejadian yang
lainnya. Peluang terjadinya kejadian setelah terjadi disebut peluang
bersyarat. Secara matematis, peluang bersyarat didefinisikan sebagai berikut.
Definisi 2.8
Peluang terjadinya kejadian terjadi setelah kejadian adalah
dengan adalah peluang kejadian dan keduanya terjadi.
Dua kejadian dikatakan saling bebas jika terjadinya suatu kejadian tidak
mempengaruhi kejadian lainnya. Secara matematis, terdapat beberapa cara
untuk menyatakan kejadian dan saling bebas, yaitu
Variabel acak didefinisikan sebagai suatu pemetaan fungsional dari
himpunan hasil percobaan ke himpunan bilangan real. Sebagai contoh, hasil
pelemparan dadu dapat dilihat sebagai variabel acak jika munculnya mata
dadu 1 pada permukaan dadu dipetakan ke bilangan satu, mata dadu 2
Sebuah variabel acak bisa kontinu atau diskret. pelemparan dadu
merupakan variabel acak diskret, sebab hasil realisasinya merupakan
himpunan nilai-nilai yang diskret. Pengukuran temperatur merupakan
variabel acak kontinu karena hasil realisasinya merupakan himpunan
nilai-nilai yang kontinu. Baik variabel acak diskret maupun kontinu, keduanya
memiliki fungsi densitas peluang dan fungsi distribusi kumulatif.
Fungsi-fungsi tersebut didefinisikan sebagai berikut.
Definisi 2.9
merupakan fungsi densitas peluang dari variabel acak diskret
jika untuk setiap berlaku
Definisi 2.10
merupakan fungsi densitas peluang dari variabel acak kontinu
jika berlaku
Definisi 2.11
Fungsi distribusi kumulatif dari variabel acak diskret dengan fungsi
densitas peluang adalah , dimana
Definisi 2.12
Fungsi distribusi kumulatif dari variabel acak kontinu dengan fungsi
densitas peluang adalah , dimana
Masing-masing variabel acak mempunyai karakteristik, seperti rata-rata
atau nilai harapan dan variansi. Definisi rata-rata atau nilai harapan dari
variabel acak didefinisikan sebagai berikut.
Definisi 2.13
Misalkan variabel acak dengan fungsi densitas peluang .
Variansi dari variabel acak menunjukkan seberapa besar variabel acak
akan bervariasi dari rata-ratanya. Dalam kasus-kasus tertentu, misalnya jika
variabel acak hanya memiliki satu nilai (misalnya jika pada saat melempar
dadu selalu muncul mata dadu 4), maka disebut bahwa variansi dari sama
dengan 0. Kasus lainnya adalah jika nilai dari berada di antara dengan
peluang yang sama, maka disebut bahwa variansi dari sama dengan .
Variansi dari variabel acak didefinisikan secara formal sebagai berikut.
Definisi 2.14
Misalkan variabel acak dengan fungsi densitas peluang dan
rata-rata . Variansi dari adalah
Standar deviasi dari variabel acak dinotasikan dengan , merupakan akar
kuadrat dari variansi. Perhatikan bahwa variansi bisa ditulis
Notasi digunakan untuk menyatakan bahwa merupakan
Sebuah variabel acak kontinu disebut Gaussian atau normal jika fungsi
densitas peluangnya yaitu
Selanjutnya misalkan terdapat dua variabel acak yaitu dan . Sama
halnya dengan kejadian saling bebas, Variabel acak dan dikatakan saling
bebas jika memenuhi
Akibatnya,
Kovariansi dari variabel acak skalar dan adalah
Proses stokastik merupakan variabel random yang berubah-ubah
menurut waktu, sehingga fungsi distribusi dan fungsi densitasnya merupakan
fungsi terhadap waktu. Fungsi distribusi kumulatif dari adalah
Rata-rata dan kovariansi dari juga merupakan fungsi dari waktu,
Perhatikan bahwa pada waktu dan merupakan dua variabel
acak yang berbeda, yaitu dan . Jika kedua variabel acak
dan saling bebas, untuk semua , maka disebut derau putih
(white noise). Jika tidak, maka disebut derau berwarna.
C. Penduga Kuadrat Terkecil
Penduga kuadrat terkecil adalah dasar dari penurunan algoritma filter
Kalman. Sub-bab ini akan membahas mengenai penduga kuadrat terkecil
berbobot dan penduga kuadrat terkecil rekursif.
1. Penduga Kuadrat Terkecil Berbobot
Misalkan adalah vektor konstan dengan -elemen yang tidak diketahui,
dan adalah vektor hasil pengukuran yang mengandung komponen derau
dengan elemen. Untuk mencari penduga terbaik dari , dimisalkan setiap
elemen pengukuran pada vektor sebagai kombinasi linear dari
elemen-elemen dalam vektor dengan ditambah derau pengukuran, yaitu
dengan adalah vektor dengan elemen, vektor pengukuran dengan
elemen, , matriks observasi berukuran , dan vektor derau
yang memiliki elemen. Selisih antara dan didefinisikan dengan ,
yaitu
dan disebut sebagai sisa pengukuran. Menurut Karl Gauss, nilai yang paling
mungkin untuk vektor adalah vektor yang meminimumkan jumlah
kuadrat dari selisih antara nilai yang diamati dengan vektor . Jadi akan
dicari yang meminimumkan fungsi objektif , dimana
Substitusi , diperoleh
mencapai minimum saat turunan parsial pertamanya terhadap sama
dengan nol, yaitu
Vektor kemudian diperoleh dengan menyelesaikan persamaan tersebut,
Dengan , pseudo invers kiri dari matriks ada jika
dan matriks dengan rank penuh.
Dalam setiap pengukuran, terdapat derau yang variansinya bisa berbeda.
Dengan variansi yang berbeda-beda, dimisalkan
Penduga kuadrat terkecil berbobot bisa diperoleh dengan menurunkan
fungsi objektif yang sisa pengukurannya berdistribusi normal. Dengan asumsi
bahwa derau dari setiap pengukuran mempunyai rata-rata 0 dan saling bebas,
matriks kovariansinya adalah
Pendugaan yang melibatkan variansi derau pengukuran inilah disebut
pendugaan kuadrat terkecil berbobot. Dalam pendugaan ini, fungsi objektif
yang akan diminimumkan adalah
mencapai minimum ketika
sehingga diperoleh
Perhatikan bahwa adalah matriks Hessian yang definit positif
ketika mempunyai rank , sehingga bisa dipastikan bahwa
meminimumkan fungsi objektif .
Berikut diberikan contoh pendugaan kuadrat terkecil sebelum dan
sesudah diboboti.
Contoh 2.3
Misalkan diperoleh data hasil pengukuran ( ) berturut-turut 0.98, 0.37,
0.88, 0.91, 0.79, 0.67, 0.72, 0.65, 0.49, dan 0.77. Akan dicari garis yang
Dengan metode kuadrat terkecil, diduga dengan ,
diperoleh persamaan hasil pendugaan yaitu , dengan
jumlah kuadrat nya Plot hasil perhitungan dan perhitungannya
adalah sebagai berikut.
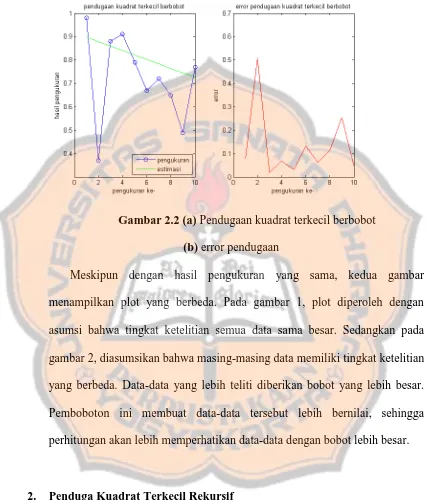
Gambar 2.1 (a) Pendugaan kuadrat terkecil (b) error pendugaan
Gambar 2.2 (a) Pendugaan kuadrat terkecil berbobot (b) error pendugaan
Meskipun dengan hasil pengukuran yang sama, kedua gambar
menampilkan plot yang berbeda. Pada gambar 1, plot diperoleh dengan
asumsi bahwa tingkat ketelitian semua data sama besar. Sedangkan pada
gambar 2, diasumsikan bahwa masing-masing data memiliki tingkat ketelitian
yang berbeda. Data-data yang lebih teliti diberikan bobot yang lebih besar.
Pemboboton ini membuat data-data tersebut lebih bernilai, sehingga
perhitungan akan lebih memperhatikan data-data dengan bobot lebih besar.
2. Penduga Kuadrat Terkecil Rekursif
Setiap diperoleh pengukuran yang baru, diperoleh juga matriks baru
yang ukurannya bersesuaian dengan banyaknya pengukuran. Jika pengukuran
hasil pengukuran yang baru. Dengan demikian, pada setiap pengukuran akan
diperoleh juga matriks baru. Selanjutnya ketika pendugaan dilakukan
kembali dengan matriks yang baru, pendugaan berikutnya akan
menmberikan hasil yang berbeda. Ketika banyaknya hasil pengukuran
meningkat, proses penghitungan akan menjadi lebih sulit. Contohnya
pengukuran terhadap ketinggian satelit setiap 1 detik. Setelah satu jam, akan
terdapat 3600 data hasil pengukuran, dan bahkan pengukurannya masih
berlanjut. Dengan menggunakan penduga kuadrat terkecil, setiap detik
pendugaan dilakukan dengan matriks baru yang ukurannya semakin
membesar. Di sini, masalah pertama yang muncul adalah pengukuran masih
terus berlanjut, sedangkan yang diinginkan adalah menduga ketinggian satelit
setiap detik. Masalah berikutnya adalah apakah penghitungan bisa tetap
dilanjutkan setiap detik. Untuk meminimumkan masalah-masalah tersebut,
muncul penduga kuadrat terkecil rekursif yang menghitung hasil pendugaan
setiap kali pengukuran dilakukan tanpa mengabaikan hasil pendugaan
sebelumnya. Penjelasan mengenai proses pendugaan kuadrat terkecil rekursif
adalah sebagai berikut.
Misalkan setelah pengukuran ke , diperoleh , kemudian
pengukuran selanjutnya menghasilkan suatu nilai hasil pengukuran baru .
Hal ini menunjukkan bahwa diperoleh berdasarkan dan hasil
pengukuran baru . merupakan matriks perolehan (matriks gain) yang
nantinya akan ditentukan. Suku disebut suku koreksi. Jika
suku ini bernilai nol, atau adalah matriks nol, maka pendugaan tidak
mengalami perubahan dari langkah ke langkah .
Rata-rata dari pendugaan dapat dihitung sebagai berikut
Selanjutnya kriteria optimal untuk menentukan adalah meminimalkan
jumlah variansi dari error pendugaan pada saat , yaitu
Dengan . Untuk memperoleh perhitungan rekursif ,
tidak bergantung pada , maka bisa ditulis
karena nilai harapan keduanya sama dengan nol, sehingga diperoleh
dengan adalah kovariansi . Rumus ini merupakan bentuk rekursif untuk
kovariansi dari error pendugaan kuadrat terkecil. Hal ini sesuai dengan intuisi
bahwa pada saat derau pengukuran meningkat, ketidak-pastian dalam
pendugaan juga meningkat. Perhatikan bahwa harus berupa matriks definit
positif, dan rumus di atas menjamin bahwa definit positif dengan asumsi
bahwa dan adalah matriks definit positif.
Selanjutnya akan dicari nilai sehingga fungsi objektif menjadi
seminimal mungkin. Rata-rata error pendugaan adalah 0 untuk setiap nilai
dari . Sehingga jika kita memilih untuk membuat fungsi objektifnya
lebih kecil, maka error pendugaan tidak akan hanya mempunyai rata-rata 0,
tetapi juga akan semakin mendekati nol. Untuk mencari nilai terbaik untuk ,
jika simetri. Selanjutnya dengan menerapkan aturan rantai pada dan ,
diperoleh
Agar diperoleh nilai yang meminimumkan , maka haruslah
sehingga
, , dan membentuk penduga kuadrat terkecil rekursif. Secara
ringkas, langkah-langkah pendugaan kuadrat terkecil rekursif dapat dituliskan
sebagai berikut
1. Tetapkan penduga yaitu
Jika tidak diketahui sebelum dilakukan pengukuran, maka
ditentukan dengan sebuah matriks identitas dimana komponennya berupa
sebarang bilangan yang nilainya besar pada diagonalnya. Jika keadaan
2. Untuk , langkah-langkah yang dilakukan adalah
a. Catat hasil pengukuran , dengan asumsi bahwa ditentukan
dengan , dimana adalah vektor random yang
mempunyai rata-rata 0 dengan kovariansi . Selanjutnya,
asumsikan bahwa derau pengukuran setiap langkah ke- saling
bebas, yaitu ketika dan ketika .
akibatnya, derau pengukuran merupakan derau putih (white noise).
b. Perbaharui nilai pendugaan dan kovariansi error pendugaan
sebagai berikut:
Contoh 2.4
Dari data pengukuran pada Contoh 2.3, bisa juga diperoleh melalui
pendugaan kuadrat terkecil rekursif, yakni dengan
sesuai dengan langkah-langkah yang baru saja diperoleh. Pendugaan ini
menghasilkan plot seperti pada gambar 2.3.
Dibandingkan dengan pendugaan sebelumnya, pendugaan secara rekursif
ini memperhitungkan hasil dugaan sebelumnya, sehingga diperoleh yang
bergantung pada sebelumnya. Hasilnya, untuk setiap hasil pengukuran
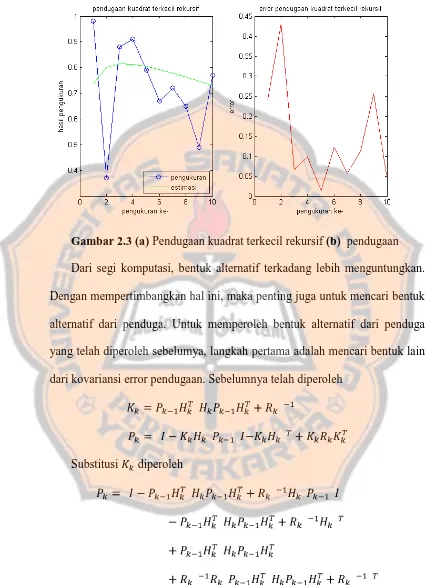
Gambar 2.3 (a) Pendugaan kuadrat terkecil rekursif (b) pendugaan
Dari segi komputasi, bentuk alternatif terkadang lebih menguntungkan.
Dengan mempertimbangkan hal ini, maka penting juga untuk mencari bentuk
alternatif dari penduga. Untuk memperoleh bentuk alternatif dari penduga
yang telah diperoleh sebelumya, langkah pertama adalah mencari bentuk lain
dari kovariansi error pendugaan. Sebelumnya telah diperoleh
Substitusi diperoleh
Dimisalkan suatu variabel bantu . Persamaan di
Dalam persamaan tersebut, muncul secara implisit, sehingga dengan
menuliskan kembali, diperoleh
Persamaan ini lebih sederhana dari bentuk sebelumnya, namun masalah
komputasi numeris dapat menyebabkan tidak definit positif meskipun
Dengan menerapkan lemma invers matriks, bisa dicari bentuk yang lain
dari yaitu
Dari persamaan ini, gunakan lemma invers matriks dengan
Menurut lemma invers matriks, maka
diperoleh
Sehingga diperoleh
Persamaan ini dapat digunakan untuk mencari bentuk ekuivalen dari
persamaan sebagai berikut
Mengalikan ruas kanan dengan (matriks identitas) di sebelah kiri,
Substitusi , diperoleh
Secara umum, algoritma kuadrat terkecil rekursif dapat dirangkum
dengan persamaan-persamaan di bawah ini.
Hasil pengukuran dituliskan:
dengan
Dugaan awal dari vektor konstan yaitu
Untuk
Pada contoh-contoh berikut, akan ditunjukkan bagaimana menerapkan
algoritma pendugaan kuadrat terkecil. Contoh 2.5 akan menunjukkan bahwa
yang diperoleh tidak akan pernah negatif.
Contoh 2.5
Misalkan terdapat parameter observasi skalar dengan pengukuran yang
sempurna, yaitu dan . Pemisalan selanjutnya yaitu kovariansi
pendugaan awal , dan komputer yang digunakan memberikan skala
ketepatan 3 digit desimal untuk setiap perhitungan yang dilakukan.
Selanjutnya untuk mencari , digunakan persamaan yang telah
diperbaharui, yaitu
Perhatikan bahwa dihitung
sebagai 0 karena komputer yang digunakan memiliki ketelitian tiga angka
desimal. Bentuk yang diperoleh dari ini menjamin bahwa tidak pernah
negatif, meskipun terdapat perhitungan numeris pada , , dan .
Contoh 2.6
Penduga kuadrat terkecil rekursif juga bisa diterapkan pada masalah
curve fitting. Misalkan akan dicari suatu garis lurus yang cocok dengan
dimana adalah variabel bebas (contohnya variabel waktu), data dengan
derau, dan akan dicari relasi linear antara dan . Dengan kata lain, akan
dicari nilai dan yang konstan. Matriks pengukurannya yaitu
Penduga rekursifnya diawali dengan
Dugaan rekursif dari vektor dengan dua anggota kemudian diperoleh
sebagai berikut
45 BAB III FILTER KALMAN
A. Filter Kalman dengan Waktu Diskret
Pada sub-bab ini, akan dicari persamaan-persamaan untuk filter Kalman
dengan waktu diskret.
Misalkan terdapat sistem linear dengan waktu diskret sebagai berikut
Proses derau dan merupakan derau putih, dengan rata-rata nol,
tidak berkorelasi, dan matriks kovariansinya berturut turut dan , yaitu
Karena dan tidak berkorelasi, maka untuk semua .
Tujuan menurunkan model filter Kalman yaitu untuk menduga keadaan ,
berdasarkan pengetahuan mengenai system dinamis dan ketersediaan
pengukuran dengan derau . Ketika data pengukuran yang akan digunakan
untuk menduga tersedia sampai pada saat , dapat dibentuk suatu
pendugaan posteriori, yang dilambangkan dengan . Salah satu cara
harapan dengan syarat berupa semua hasil pengukuran sampai ke- dan
pengukuran pada saat , yaitu
Jika data pengukuran yang akan digunakan untuk menduga tersedia
sebelum waktu (data pada saat tidak tersedia), maka bisa dibentuk
pendugaan priori. Salah satu cara membentuknya adalah dengan menghitung
nilai harapan dengan syarat berupa semua hasil pengukuran sebelum
waktu , tidak termasuk pengukuran pada saat , yaitu
Perhatikan bahwa baik maupun keduanya digunakan untuk
menduga hal yang sama, yaitu . Meskipun demikian, merupakan
pendugaan untuk sebelum diperhitungkan, sedangkan menduga
setelah diperhitungkan. Secara intuisi, bisa dikatakan adalah
pendugaan yang lebih baik dari karena informasi yang digunakan pada
saat mencari lebih banyak.
melambangkan pendugaan awal , sebelum hasil pengukuran
tersedia. Pengukuran pertama dilakukan pada waktu . Karena tidak ada
hasil pengukuran untuk menduga , maka dibentuk sebagai nilai harapan
dari keadaan awal , yaitu
melambangkan kovariansi dari pendugaan , dan
Untuk memahami lebih jelas hubungan antara penduga keadaan priori,
posteriori, dan kovariansi pendugaannya, perhatikan gambar 3.1.
Gambar 3.1 Hubungan antara penduga keadaan priori dan posteriori,
dan kovariansi pendugaan
Dari gambar terlihat hasil pendugaan priori pada waktu yaitu
dan kovariansi error penduganya diperoleh sebelum dilakukan
pengukuran pada waktu . Setelah pengukuran dilakukan, diperoleh hasil
pengukuran posteriori dan . Keduanya kemudian digunakan untuk
mencari penduga priori pada waktu yaitu dan . Setelah pengukuran
pada waktu tersedia, diperoleh hasil pendugaan posteriori pada waktu ,
yaitu dengan kovariansi error pendugaannya .
Proses pendugaan dimulai dari , yaitu dugaan paling baik untuk
kondisi awal . Setelah diketahui, langkah selanjutnya adalah
meng-hitung . Tetapkan . Lihat kembali bahwa dan
Persamaan tersebut menunjukkan bagaimana memperoleh dari . Secara umum dapat dituliskan
Persamaan ini disebut persamaan pembaharuan waktu untuk .
Selanjutnya akan dihitung persamaan pembaharuan waktu untuk . Jelas
bahwa . Jika nilai tidak diketahui, maka dimisalkan dengan
sebuah matriks identitas dengan komponennya berupa sebarang bilangan
besar pada diagonal utamannya. Umumnya mewakili ketidakpastian dari
dugaan awal , dimana
Sama halnya dengan , juga dapat diperoleh dari . Kovariansi
merambat terhadap waktu dengan , sehingga
diperoleh
Secara umum dapat ditulis
yang disebut persamaan update waktu untuk .
Selanjutnya yang akan dicari adalah persamaan update pengukuran untuk
dan , yakni diketahui kemudiah dihitung . Diingat kembali bahwa
dimana dan adalah penduga dan kovariansi pendugaan sebelum
hasil pengukuran diperoleh, dan dan adalah penduga dan kovariansi
pendugaan setelah diperoleh. Jadi, untuk memperoleh persamaan dalam
bentuk penduga priori, diganti dan diganti . Sedangkan
untuk memperoleh persamaan dalam bentuk penduga posteriori, diganti
dan diganti , sehingga diperoleh
yang merupakan persamaan pembaharuan pengukuran untuk dan .
Matriks di atas disebut Kalman filter gain.
Setelah diturunkan, persamaan-persamaan yang telah dibahas dapat
dirangkum dalam suatu algoritma yaitu sebagai berikut.
2. Filter Kalman diawali dengan
3. Filter Kalman dihitung untuk setiap waktu
ke-Bentuk pertama dari akan menjamin bahwa akan selalu berupa
matriks simetri yang definit positif, selama juga merupakan matriks
simetri yang definit positif. Bentuk ketiga dari lebih sederhana
penghitungannya dibandingan dengan bentuk pertama, tetapi tidak menjamin
apakah matriks yang diperoleh merupakan matriks simetri atau definit positif.
Jika dalam perhitungan digunakan bentuk kedua dari , maka perhitungan
untuk menghitung digunakan bentuk kedua yang tidak bergantung pada
. Adapun bentuk-bentuk ini mirip dengan yang telah dibahas pada
pendugaan kuadrat terkecil. Tabel 3.1 berisi hubungan antara pendugaan dan
kovariansi errornya pada pendugaan kuadrat terkecil dan filter Kalman.
Tabel 3.1 Hubungan antara penduga dan kovariansi pada pendugaan kuadrat
terkecil dan filter Kalman
Pendugaan kuadrat terkecil Filter Kalman = pendugaan sebelum diketahui = penduga priori = kovariansi sebelum diketahui = kovariansi priori = pendugaan setelah diketahui = penduga posteriori = kovariansi setelah diketahui = kovariansi posteriori
Contoh 3.1
Contoh ini akan menunjukkan penerapan persamaan filter Kalman
dengan waktu diskret. Misalkan terdapat sebuah sistem pengukuran dimana
diketahui , , , , dan ,
dengan , , dan , perhitungan filter Kalman pada saat
Langkah-langkah tersebut kemudian diulangi sampai waktu ke- untuk
memperoleh penduga .
B. Persamaan Filter Kalman Satu Langkah
Persamaan filter Kalman priori dan posteriori dapat digabungkan dalam
satu persamaan. Persamaan penduga keadaan priori dengan indeks dinaikkan
menjadi
Sedangkan persamaan posteriori untuk adalah
Langkah yang sama diterapkan untuk memperoleh kovariansi
pendugaannya. Persamaan priori kovariansi dengan indeks dinaikkan menjadi
Substitusi diperoleh
Substitusi diperoleh
Dengan cara demikian pula, dapat diperoleh persamaan posteriori satu
langkah untuk penduga keadaan dan kovariansi penduga. Bentuk awal
persamaan penduga keadaan posteriori adalah
Substitusi persamaan priori , diperoleh
Dengan substitusi , diperoleh
Contoh 3.2
Misalkan terdapat sistem Newton yang bebas derau dengan vektor posisi
, kecepatan , dan percepatan . Dengan kecepatan merupakan turunan dari
posisi dan percepatan merupakan turunan dari kecepatan, yaitu dan
.
Sistem tersebut dapat dituliskan
Dengan memisalkan
sistem tersebut menjadi
Diskretisasi dari sistem ini dengan sampel waktu dapat ditulis
dimana
Filter Kalman untuk sistem tersebut adalah
karena . Diperoleh Kalman gain yaitu
Terlihat bahwa trace dari kurang dari . Dari sini bisa disimpulkan
bahwa kovariansi penduga semakin mengecil, dan pendugaan menjadi lebih
terpercaya.
Simulasi pertama sistem ini dilakukan dengan 5 unit sampel waktu
atau , dan standar deviasi 30 unit. Gambar 3.2 menunjukkan variansi
dari penduga posisi ( dan ) untuk 5 langkah pertama filter Kalman.
Bisa dilihat bahwa variansinya membesar di setiap langkah, tetapi
berkurang setiap diperoleh hasil pengukuran yang baru. Hal yang sama juga
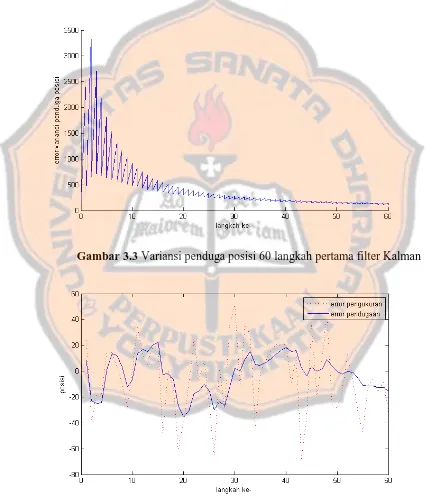
terlihat pada Gambar 3.3 yang menunjukkan variansi dari penduga posisi
( dan ) untuk 60 langkah pertama.
Gambar 3.3 Variansi penduga posisi 60 langkah pertama filter Kalman
Selanjutnya Gambar 3.4 menunjukkan eror pengukuran posisi (dengan
standar deviasi dan hasil pendugaannya. Simulasi ini menunjukkan bahwa
filter Kalman efektif untuk menduga keadaan.
C. Derau Proses Pendugaan
Perhatikan sistem waktu diskret di bawah ini dengan matriks identitas
keadaan transisi dan sampel waktu :
dengan adalah proses derau putih dengan waktu diskret.
meyatakan bahwa merupakan variabel acak Gaussian dengan rata-rata 0
dan variansi . Akan dilihat bagaimana pengaruh derau putih terhadap
kovariansi dari keadaan tersebut. Sistem waktu diskret dapat diselesaikan
sebagai berikut:
Kovariansi dari keadaan tersebut menjadi:
Nilai dari parameter waktu kontinu sama dengan banyaknya langkah
Kovariansi dari keadaan meningkat secara linear sebanding dengan
waktu untuk sampel waktu yang diberikan. Selanjutnya perhatikan sistem
waktu kontinu dengan matriks identitas keadaan transisi:
dimana adalah derau putih dengan waktu kontinu. Definisi untuk
derau putih dengan waktu kontinu yaitu
dimana dan memiliki arti yang sama dengan dan pada sistem waktu
diskret. merupakan fungsi impuls-respon waktu diskret, yaitu fungsi
dengan nilai saat , dan 0 selainnya, dengan luas 1. Kovariansi dari
adalah
Substitusi ke persamaan di atas diperoleh
Dibandingkan dengan kovariansi keadaan untuk waktu diskret,
kovariansi keadaan untuk waktu kontinu juga meningkat secara linear dengan
perbandingan yang sama. Dengan kata lain, derau putih waktu diskret dengan
kovariansi pada sistem dengan sampel waktu ekuivalen dengan derau
putih waktu kontinu dengan kovariansi , dengan . Derau
putih waktu kontinu dengan rata-rata nol ditulis
yang sama artinya dengan
D. Derau Pengukuran
Misalkan terdapat pengukuran dengan waktu diskret untuk konstan
setiap detik. Waktu pengukuran adalah ,
Dari persamaan filter Kalman, diperoleh kovariansi error pendugaan
Kovariansi pada waktu independen terhadap sampel waktu jika
dengan suatu konstan. Hal ini mengimplikasikan
dimana adalah fungsi impuls waktu kontinu. Hal ini memperlihatkan
ekuivalensi antara derau putih pengukuran pada sistem waktu diskret dan
waktu kontinu. Pengaruh derau putih pengukuran pada sistem waktu diskret
akan sama dengan pengaruhnya pada sistem waktu kontinu jika
Menulis sama artinya dengan mengatakan bahwa
E. Filter Kalman dengan Waktu Kontinu
Selanjutnya misalkan terdapat sistem hasil diskretisasi dengan sampel
waktu . Diperoleh
Matriks-matriks pada sistem waktu diskret dihitung sebagai berikut:
Maktriks gain filter Kalman untuk sistem ini adalah
Kovariansi error pendugaan menjadi
Substitusi diperoleh
Kemudian dengan mengurangkan dan kedua ruas dibagi , diperoleh
Dengan mengambil limit ketika dan mengingat kembali bahwa
diperoleh
Persamaan ini disebut Persamaan diferensial Riccati dan dapat digunakan
untuk menghitung kovariansi pendugaan untuk filter Kalman waktu kontinu.
Pada bagian sebelumnya, telah diperoleh persamaan filter Kalman untuk
Dengan asumsi bahwa kecil, persamaan pembaruan pengukuran dapat
ditulis
Selanjutnya substitusi dari diperoleh
Dengan mengurangkan di kedua ruas dan dibagi , lalu diambil
limit ketika , diperoleh
Atau dapat juga ditulis
Filter Kalman waktu kontinu dapat diringkas sebagai berikut
1. Sistem dinamis dengan waktu kontinu dan persamaan pengukuran adalah
dimana dan adalah proses derau putih waktu kontinu.
Contoh 3.3
Misalkan akan dicari suatu konstan dengan derau pengukuran waktu
kontinu sebagai berikut:
Jelas bahwa , , dan . Persamaan diferensial untuk
kovariansi error penduganya adalah
Selanjutnya diperoleh Kalman gain yaitu
Persamaan pembaruan keadaan yaitu
Hal ini menunjukkan bahwa setelah diperoleh pengukuran yang tak
hingga banyaknya atas suatu konstan, pendugaan terhadap nilai konstan
tersebut menjadi sempurna, dan pengukuran tambahan tidak bisa lagi
membuat pendugaan menjadi lebih baik. Kalman gain juga menuju nol ketika
waktunya semakin membesar, yang artinya pengukuran tambahan diabaikan
karena pendugaan telah sempurna. Selanjutnya kovariansi juga menuju nol,
menunjukkan tingkat ketidakpercayaan atas pendugaan sama dengan nol,
sama saja dengan mengatakan bahwa hasil pendugaan sempurna pada waktu
F. Linearisasi Filter Kalman
Filter Kalman pada bagian sebelumnya diterapkan langsung hanya untuk
sistem linear. Agar metode tersebut bisa digunakan dalam sistem nonlinear,
maka terlebih dahulu dilakukan linearisasi terhadap sistem tersebut.
Misalnya terdapat sistem nonlinear:
dengan dan fungsi nonlinear. Dengan menggunakan deret Taylor,
fungsi-fungsi tersebut akan dilinearisasi untuk memperoleh dan yang
linear sebagai berikut
Asumsikan bahwa derau dan keduanya selalu nol, maka
diperoleh dan . Lebih jauh lagi, diasumsikan
pula bahwa diketahui sebab ditentukan oleh kontrol sistem
sehingga tidak terdapat ketidak-pastian pada nilainya. Artinya
dan . Tetapi nyatanya bisa juga terdapat ketidakpastian pada
terjadi kasus seperti ini, maka kontrol untuk bisa ditulis sebagai
, dengan diketahui merupakan variabel random
dengan rata-rata nol, sehingga sistem bisa ditulis kembali dengan kontrol
signal yang diketahui, dan termasuk bagian dari derau proses.
Selanjutnya didefinisikan nominal sistem trajektori yaitu
Definisikan
Dengan definisi tersebut, diperoleh
Persamaan tersebut merupakan sistem linear dengan keadaan dan
pengukuran , sehingga dapat digunakan filter Kalman untuk menduga .
Dari sini diperoleh persamaan filter Kalman untuk linearisasi filter Kalman
Linearisasi filter Kalman waktu kontinu dapat dirangkum sebagai berikut:
1. Sistem persamaannya yaitu
dengan nominal trajektori
3. Hitung matriks-matriks
4. Definisikan sebagai selisih antara pengukuran yang sebenarnya
dengan pengukuran nominal :
5. Kerjakan persamaan filter Kalman berikut:
6. Keadaan diduga dengan:
G. Perluasan Filter Kalman dengan Waktu Kontinu
Dengan menggabungkan dan
, diperoleh
Selanjutnya dipilih sehingga dan .
Persamaan ini menjadi ekuivalen dengan linearisasi filter Kalman kecuali
bahwa , dan bahwa bisa diperoleh secara langsung dari persamaan.
Kalman gain tetap sama dengan yang diperoleh pada linearisasi filter
Kalman.
Perluasan Filter Kalman waktu kontinu bisa diringkas sebagai berikut:
1. Sistem persamaannya yaitu:
2. Hitung turunan parsial:
3. Hitung matriks-matriks:
dengan nilai nominal derau dan .
H. Perluasan Filter Kalman dengan Waktu Diskret
Misalkan terdapat model sistem
Dengan menerapkan ekspansi deret Taylor pada persamaan keadaan di
sekitar dan , diperoleh:
Persamaan pengukuran dilinearkan di sekitar dan ,
diperoleh
dan didefinisikan:
Dengan menggunakan persamaan filter Kalman biasa yang telah
diperoleh di bagian sebelumnya, berikut adalah persamaan-persamaan
perluasan filter Kalman waktu diskret:
Perluasan filter Kalman dengan waktu diskret dapat dirangkum sebagai
berikut:
2. Awali filter dengan
3. Untuk , lakukan:
a. Hitung turunan diferensial
b. Perbarui waktu dari penduga keadaan dan kovariansi error
pendugaan:
c. Hitung turunan diferensial
d. Perbarui pengukuran dari penduga keadaan dan kovariasi error
76 BAB IV
SIMULASI FILTER KALMAN
Materi pada bab sebelumnya telah menjabarkan bagaimana memperoleh
algoritma dari beberapa jenis filter Kalman. Bab ini berisi simulasi filter Kalman
dalam beberapa masalah, serta beberapa penerapan filter Kalman dalam
kehidupan sehari-hari.
A. Simulasi Filter Kalman untuk Menduga Suatu Konstan
Simulasi dimulai dengan memilih suatu skalar konstan secara acak.
Misalkan . Setelah itu tetapkan 50 sampel pengukuran yang
errornya berdistribusi normal dengan rata-rata nol dan standar deviasi 0,1.
Dengan kovariansi awal , dan dugaan awal , hasil simulasi
filter Kalman untuk menduga nilai dari sampel yang tersedia bisa dilihat
seperti pada gambar-gambar berikut.
Gambar 4.1 memperlihatkan bagaimana hasil dugaan yang diperoleh
semakin mendekati nilai sebenarnya. Bisa dilihat pula bagaimana eror
pendugaan semakin mendekati nol, yang artinya pendugaan semakin baik.
Begitu juga dengan variansi yang semakin mendekati nol, menandakan
tingkat kepercayaan akan pendugaan semakin tinggi.
Gambar 4.2 Pendugaan konstan
Data-data sampel pengukuran, hasil pengukuran, pendugaan dan variansi
nya pada setiap langkah pengukuran dalam simulasi pertama ini dapat dilihat
pada tabel berikut.
Tabel 4.1 Data Hasil Simulasi Filter Kalman untuk Menduga Suatu Konstan
Langkah
ke- Pengukuran Pendugaan
Error
B. Simulasi Filter Kalman untuk Menduga Posisi dan Kecepatan
Masalah untuk simulasi selanjutnya adalah untuk menduga posisi dan
kecepatan dari sebuah kendaraan. Simulasi dilakukan 1 menit dengan
pengukuran sebanyak satu kali per detik ( pada sistem dinamis
berikut
Diperoleh matriks transisi , matriks input , dan
matriks pengukuran .
Hasil simulasi bisa dilihat pada gambar-gambar berikut.
Gambar 4.4 (a) Posisi kendaraan (b) error Posisi
Gambar 4.4 (a) menunjukkan posisi sebenarnya, posisi hasil pengukuran
dan posisi hasil pendugaan. Meskipun ketiganya terlihat berhimpitan, gambar
4.4 (b) menunjukkan hasil pengukuran dan hasil pendugaan terhadap posisi
Gambar 4.5 (a) Kecepatan kendaraan (b) error kecepatan
Hasil yang mirip terlihat pada gambar 4.5. Kecepatan hasil dugaan
hampir berhimpitan dengan kecepatan sebenarnya, dengan berada di sekitar
nol. Data untuk simulasi kedua ini dapat dilihat pada tabel-tabel berikut.
Tabel 4.2 (a) Data Hasil Simulasi Filter Kalman untuk Menduga Posisi
Langkah
38 151.009 158.961 150.967 -7.9527 0.0414
Tabel 4.2 (b) Data Hasil Simulasi Filter Kalman untuk Menduga Kecepatan
C. Penerapan Filter Kalman dalam Berbagai Bidang
Filter Kalman sering digunakan dalam sistem robotik. Dari berbagai
faktor yang mempengaruhi performa sistem robotik, filter Kalman memiliki
kontribusi yang besar terhadap persepsi visi robot. Dalam hal ini, filter
Kalman menyelesaikan masalah ketidakpastian dalam lokalisasi robot,
navigasi, tracking, kontrol gerak, dan lain-lain. Lokalisasi oleh visi artifisial
merupakan kunci bagi robot bergerak, khususnya pada lingkungan dimana
GPS tidak akurat dan sensor inertial tidak tersedia.
Peranan filter Kalman dalam berbagai persepsi visi robot yang paling
signifikan antara lain:
1. Kontrol robot
2. Tracking objek
3. Mengikuti jalur
4. Pendugaan dan prediksi data
5. Lokalisasi robot
6. Manipulasi robotik
7. Navigasi visual
Sedangkan metode-metode untuk menyelesaikan masalah visi robot
antara lain:
1. Filter Kalman
2. Filter Kalman keadaan seimbang
3. Ensemble Kalman Filter (EnKF)