APROKSIMASI NON-UNIFORM SPASIAL PERSAMAAN PANAS 1D DENGAN FINITE POINTSET METHOD

APROKSIMASI NON-UNIFORM SPASIAL PERSAMAAN PANAS 1D DENGAN

FINITE POINTSET METHOD

Putu Harry Gunawan1_{, Friska Fristella}2

1_{Industrial and Financial Mathematics Research Group. Faculty of Mathematics and Natural sciences, Institut} Teknologi Bandung, Jalan Ganesha 10, Bandung 40132, Indonesia.

1_{Computational Science. Faculty of Mathematics and Natural sciences, Institut Teknologi Bandung, Jalan} Ganesha 10, Bandung 40132, Indonesia

1_{harry.gunawan.putu@gmail.com,} 2_{friskafristella@ymail.com}

Abstrak

Hampiran numerik satu dimensi (1D) dari persamaan panas dengan metoda partikel dijabarkan. Metoda Finite Pointset Method (FPM) digunakan untuk mencari solusi numerik dari persamaan panas. Komparasi hasil numerik FPM dengan hasil numerik metoda beda hingga dan solusi analitik juga diperlihatkan. Hasil solusi numerik metoda FPM diperlihatkan sesuai dengan solusi analitik. Tabel diskrit

L

1-norm eror juga diberikan untuk melihat kekonvergenan solusi numerik terhadap solusi analitik.

Kata kunci : Persamaan panas, metoda numerik, metoda partikel, FPM.

1. Pendahuluan

Persamaan panas merupakan persamaan diferensial parsial tipe hiperbolik yang menggambarkan suatu perpindahan panas seperti temperatur pada suatu daerah dan waktu tertentu. Dalam satu dimensi (1D), persamaan panas pada daerah perhitungan atau domain





( L

0

,

)

dapat ditulis dalam bentuk

₂ 2

x

u

t

u











_

,

t



0

,

x





(1)

u

(

t

,

x

)



0

,

t



0

,

x







(2)

dengan



adalah konstanta positif, dan

u

adalah suatu fungsi yang menggambarkan temperatur panas pada lokasi spasial

x

dan akan berubah nilai bergantung terhadap waktu

t

. Batas daerah perhitungan atau domain ditetapkan dengan batas dirichlet yaitu dengan batas nilai tetap konstan (dalam hal ini 0) untuk setiap waktu.

Berbagai macam metoda numerik untuk menghampiri solusi persamaan (1-2) diatas sudah dipaparkan di dalam berbagai referensi (sebagai contohnya dapat dilihat di [1,3,6]). Salah satu metoda numerik yang sangat sederhana yang biasanya digunakan untuk menghampiri solusi persamaan (1-2) adalah metoda beda hingga (Finite

Difference Method - FDM). Metoda tersebut menggunakan expansi Taylor untuk menghampiri suatu turunan fungsi,

dalam tulisan ini yakni fungsi

u

. Selain itu, metoda beda hingga merupakan mesh method yaitu suatu metoda dimana diskritisasi spasial dilakukan dengan membagi domain perhitungan menjadi beberapa grid atau titik.

Dalam penelitian ini, kami tertarik untuk menggunakan metoda lain selain metoda beda hingga, dimana dalam diskritisasi spasial tidak menggunakan grid atau meshfree yaitu dengan Finite Pointset Method (FPM) yang diperkenalkan oleh Tiwari, dkk [2,7,8,9,10]. Metoda FPM dikenal sebagai particle method karena domain perhitungan tidak lagi berupa grid akan tetapi berupa partikel-partikel bebas yang posisinya bisa berubah di setiap waktu (lihat [7,10]). Pada tulisan ini akan dijelaskan bagaimana metoda FPM dapat digunakan untuk menghampiri turunan spasial suatu partikel dari beberapa partikel tetangganya. Meskipun menghampiri turunan spasial suatu partikel dengan jumlah partikel tetangga yang banyak, metoda ini tidak banyak membutuhkan perubahan dalam skema numerik yang dapat terjadi pada metoda FDM. Hal inilah yang menjadi kelebihan dari metoda FPM dalam menghampiri turunan spasial terhadap metoda grid lainnya. Sebagai tambahan, dengan adanya nilai turunan setiap partikel maka diharapakan dapat diaplikasikan untuk menghampiri persamaan panas.

Dalam penyusunan diskritisasi inisial partikel pada penelitian ini, diharapkan dapat disebarkan secara

non-uniform (tidak seragam). Tentu saja, dengan menggunakan metoda FPM, diskritisasi partikel secara tidak seragam

sangat mudah ditangani. Sebagai tambahan, simulasi numerik dari FPM akan diberikan dengan perbandingan terhadap solusi analitik dan juga dari FDM. Untuk melihat kekonvergenan solusi numerik dari FPM, maka dalam

80 Makalah ini disusun sebagai berikut, pada Bab 2 Metoda FPM akan dijabarkan untuk menghampiri turunan-turunan spasial. Bab 3 akan membahas hasil simulasi numerik dari persamaan panas. Terakhir, kesimpulan dari makalah akan diberikan pada Bab 4.

2. Finite Pointset Method

FPM merupakan metoda partikel yakni tanpa menggunakan diskritisasi grid. Metoda ini sudah banyak diaplikasikan dalam berbagai simulasi aliran fluida yang compressible maupun incompressible (lihat [7,8,10]). Pada umumnya, metoda ini digunakan untuk masalah yang memiliki daerah komputasi dua dimensi (







2). Akan tetapi, dalam penelitian ini penulis akan menggunakan FPM pada persamaan panas untuk satu dimensi







.

Gambar 1. Hampiran partikel

i

dalam fungsi kernel

W

dengan radius

h

.

Diberikan sebaran posisi

N

partikel

x



_j





,

j



1 

,

2

,

,

N

yang sebarannya dapat berupa sebaran acak (lihat Gambar 1). Partikel-partikel tersebut merupakan titik-titik grid dari daerah komputasi yang akan kami gunakan. Selanjutnya, misalkan sembarang partikel

x



_i





dan tentukan juga partikel tetangganya yang berjarak tidak lebih dari radius

h

. Selain itu, pada penelitian ini kami perkenalkan weight function atau fungsi kernel

)

,

(

x

x

h

W

W

i j





_



dengan nilai compact support

h

yang biasanya bernilai cukup kecil. Berbagai macam fungsi kernel untuk metoda partikel dapat dilihat di berbagai macam referensi [4-5]. Dalam tulisan ini kami akan menggunakan Gaussian weight function yang juga dapat ditemukan di [7,10] dengan bentuk:





























otherwise

h

r

if

h

r

h

x

x

W

_{i j}

0

1

exp

)

,

(

2 2







(3)

dengan

r



x



_i



x



_j dan sebuah konstanta positif



.

Untuk menghampiri persamaan panas satu dimensi, FPM mengaproksimasi fungsi

u

(x



)

, dalam hal ini

x





x

pada setiap partikel dengan menggunakan ekspansi Taylor.

i i i i

x

x

e

x

u

x

x

x

u

x

u

x

u





















2 2 2

)

(

2

1

)

(

)

(

)

(

(4)

dengan

x

_imenyatakan posisi partikel ke-

i

(

i



1

,

2

,



,

N

),

N

adalah jumlah partikel dalam simulasi dan

e

_i

merupakan residu eror.

Selanjutnya, tulis persamaan (4) dalam bentuk persamaan matriks yakni,

b

a

M

e











(5) dengan























2 2 1 2 1 2 1 1 N N

dx

dx

dx

dx

M





, (6)



























)

(

)

(

)

(

)

(

1

x

u

x

u

x

u

x

u

b

N





, (7) dan



































2 2

x

u

x

u

a



. (8)

Menurut Tiwari [7], vektor

a



dapat dihitung dengan meminimumkan weighted error pada titik-titik tetangganya. Sehingga, harus meminimumkan persamaan bentuk kuadratik berikut



M

a

b

 

M

a

b



e

W

J

T N i i i









_

_

_







1 2 , (9) dengan

























N

W

W











0

0

0

0

0

1 . (10)

Dengan meminimumkan

J

dari persamaan (9), vektor

a



dapat diperoleh sebagai berikut



M

M

 

M



b

a

T T











1 , (11)

dimana kondisi matriks

M

T



M

harus berupa matriks non singular. Nilai dari vektor

a



pada persamaan (8) terdiri dari nilai hampiran turunan spasial pertama dan kedua yang selanjutnya akan digunakan untuk menghampiri persamaan (1). Berikut bentuk diskrit untuk persamaan (1)

FPM n i n i x u t u u _             2 2 1 _{ (12)} dengan 1

(

,

i

)

n i

u

t

t

x

u









dan FPM

x

u

















2 2

adalah nilai dari vektor

a



baris kedua.

3. Simulasi Numerik

Dalam bab berikut ini, algoritma dari persamaan-persamaan FPM pada Bab 2 akan diberikan untuk menghampiri persamaan panas satu dimensi. Selanjutnya beberapa simulasi numerik akan ditampilkan untuk melihat kemampuan FPM untuk menghampiri persamaan panas satu dimensi dengan jarak antar partikel tidak seragam. Sebagai tambahan, tabel diskrit

L

1-norm eror akan disuguhkan untuk melihat kekonvergenan solusi numerik yang didapatkan.

3.1. Algoritma

Berikut akan diberikan algoritma FPM diatas untuk menghampiri solusi persamaan panas satu dimensi.

Tabel 1 Algoritma FPM

Langkah Instruksi 0 Mulai

82

2 Bentuk matriks

M

dari persamaan (6), matriks



dari persamaan (10) dan vektor

b



dari persamaan (7).

3 Selesaikan persamaan (11) untuk mendapatkan nilai hampiran turunan spasial kedua.

4 Hitung persamaan (12) untuk mendapatkan nilai hampiran di setiap langkah waktu.

5 Lakukan langkah 2-4 sampai waktu yang diinginkan.

6 Selesai

Pada Tabel 1, tersusun algoritma untuk menghampiri solusi persamaan panas satu dimensi dengan menggunakan persamaan-persamaan FPM yang telah dijabarkan di Bab 2. Algoritma ini selanjutnya akan digunakan sebagai acuan untuk menyelesaikan beberapa simulasi numerik di subbab berikutnya.

3.2. Simulasi Persamaan Panas

Simulasi numerik yang kami lakukan pada penelitian ini menggunakan persamaan panas satu dimensi (1), dengan domain





(

0

,

1

)

, kondisi awal :

u

(

0

,

x

)



4

x

(

1



x

)

dan kondisi batas dirichlet :

u

(

t

,

0

)



0

,

u

(

t

,

1

)



0

. Pada simulasi ini sebaran posisi awal partikel diskritisasi secara tidak seragam, domain dibagi menjadi 2 bagian, kiri (0,0.5) dan kanan (0.5,1), dengan jarak antar partikel pada domain kiri



x

₁ dan pada domain kanan



x

₂. Dipilih

)

(



x

₁





x

₂ , parameter lain yang digunakan :



=1,



t



0

.

5

(



x

₂

)

2,

2

3

x

1

x

2

h









.

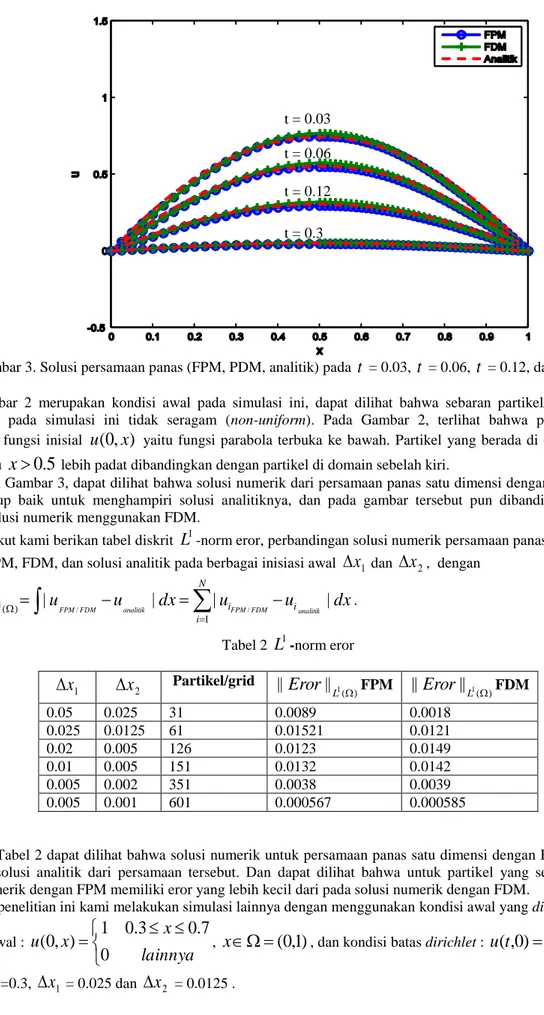
Gambar 3. Solusi persamaan panas (FPM, PDM, analitik) pada

t

= 0.03,

t

= 0.06,

t

= 0.12, dan

t

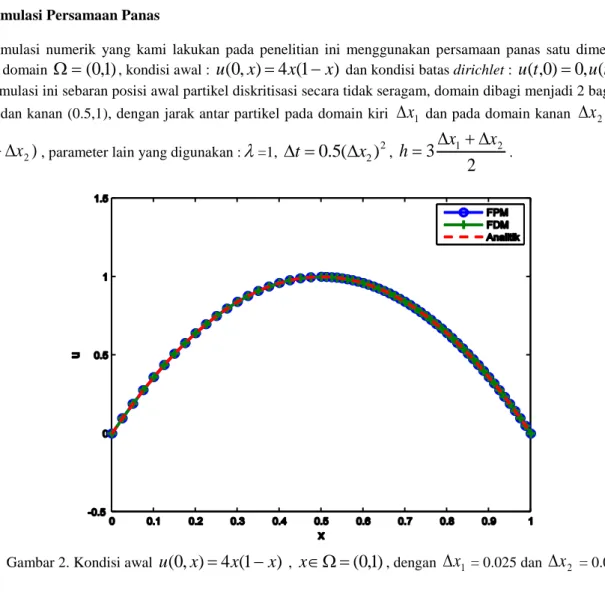
= 0.3 Gambar 2 merupakan kondisi awal pada simulasi ini, dapat dilihat bahwa sebaran partikel/titik grid yang digunakan pada simulasi ini tidak seragam (non-uniform). Pada Gambar 2, terlihat bahwa partikel tersebar mengikuti fungsi inisial

u

( x

0

,

)

yaitu fungsi parabola terbuka ke bawah. Partikel yang berada di domain sebelah kanan atau

x



0

.

5

lebih padat dibandingkan dengan partikel di domain sebelah kiri.

Pada Gambar 3, dapat dilihat bahwa solusi numerik dari persamaan panas satu dimensi dengan menggunakan FPM cukup baik untuk menghampiri solusi analitiknya, dan pada gambar tersebut pun dibandingkan hasilnya dengan solusi numerik menggunakan FDM.

Berikut kami berikan tabel diskrit

L

1-norm eror, perbandingan solusi numerik persamaan panas satu dimensi dengan FPM, FDM, dan solusi analitik pada berbagai inisiasi awal



x

₁ dan



x

₂, dengan





 









N i i i L

u

u

dx

u

u

dx

Eror

analitik FDM FPM analitik FDM FPM 1 ) (

|

|

|

|

||

||

/ / 1 .

Tabel 2

L

1-norm eror

1

x





x

₂ Partikel/grid ) ( 1

||

||

_ L

Eror

FPM ) ( 1

||

||

_ L

Eror

FDM 0.05 0.025 31 0.0089 0.0018 0.025 0.0125 61 0.01521 0.0121 0.02 0.005 126 0.0123 0.0149 0.01 0.005 151 0.0132 0.0142 0.005 0.002 351 0.0038 0.0039 0.005 0.001 601 0.000567 0.000585

Dari Tabel 2 dapat dilihat bahwa solusi numerik untuk persamaan panas satu dimensi dengan FPM konvergen terhadap solusi analitik dari persamaan tersebut. Dan dapat dilihat bahwa untuk partikel yang semakin banyak, solusi numerik dengan FPM memiliki eror yang lebih kecil dari pada solusi numerik dengan FDM.

Pada penelitian ini kami melakukan simulasi lainnya dengan menggunakan kondisi awal yang diskontinu. Kondisi awal :













lainnya

x

x

u

0

7

.

0

3

.

0

1

)

,

0

(

,

x







(

0

,

1

)

, dan kondisi batas dirichlet :

u

(

t

,

0

)



0

,

u

(

t

,

1

)



0

, t = 0.03

t = 0.06 t = 0.12 t = 0.3

84 (a) (b)

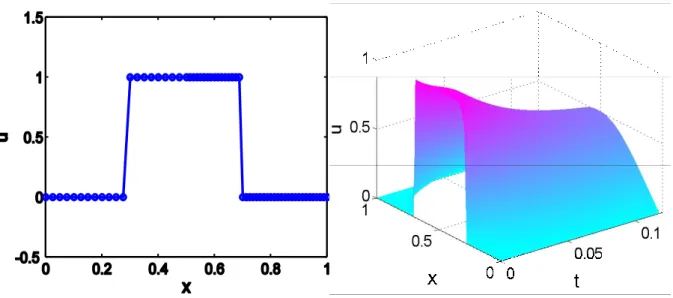
Gambar 4. (a). Kondisi awal (b). Solusi numerik dengan FPM

Pada Gambar 4(a) dapat dilihat bahwa sebaran partikel mengikuti fungsi inisial

u

( x

0

,

)

yang diskontinu berupa fungsi tangga dan untuk hasil solusi numerik dengan FPM di setiap waktu dapat dilihat pada Gambar 4(b). Sesuai dengan sifat dari solusi persamaan panas [3], maka dengan fungsi inisial yang diskontinu, solusi pada

t



0

akan selalu smooth atau kontinu. Hal ini sesuai dengan hasil solusi numerik yang ditampilkan pada Gambar 4(b).

4. Kesimpulan

Finite Pointset Method (FPM) yang merupakan metoda meshfree, metoda ini dapat digunakan untuk

menghampiri solusi persamaan panas. Diskritisasi partikel-partikel pada FPM diberikan secara tidak seragam atau

non-uniform. Perbandingan antara solusi numerik FPM dengan solusi numerik dari metoda beda hingga (FDM) dan

solusi analitik menunjukkan hasil yang sangat baik. Beberapa simulasi numerik dihadirkan untuk melihat kemampuan FPM untuk menangani persamaan panas satu dimensi dengan fungsi inisial yang beragam. Sebagai tambahan, tabel diskrit

L

1-norm eror dibuat untuk melihat kekonvergenan solusi numerik terhadap solusi analitik dengan meningkatkan jumlah diskritisasi partikel/grid pada FPM dan FDM. Hasil kekonvergenan FPM yang ditunjukkan pada Tabel 1 sedikit lebih baik dibandingkan dengan FDM seiring dengan bertambahnya jumlah partikel untuk FPM atau titik grid untuk FDM.

Daftar Pustaka: [1] [2] [3] [4] [5] [6] [7] [8] [9]

Burden, R. L., & Faires, J. D. 2001. Numerical analysis. Brooks/Cole, 7.

Drumm, C., Tiwari, S., Kuhnert, J., & Bart, H. J. 2008. Finite pointset method for simulation of the liquid–liquid flow field in an extractor. Computers & Chemical Engineering, 32(12), 2946-2957. Mattheij, R. M., Rienstra, S. W., & ten Thije Boonkkamp, J. H. 2005. Partial differential equations:

modeling, analysis, computation. Siam.

Monaghan, J. J. 2005. Smoothed particle hydrodynamics. Reports on progress in physics, 68(8), 1703. Liu, G. R., & Liu, M. B. 2003. Smoothed particle hydrodynamics: a meshfree particle method. World Scientific.

Thomas, J. W. 2013. Numerical partial differential equations: finite difference methods (Vol. 22). Springer Science & Business Media.

Tiwari, S., Klar, A., & Hardt, S. 2014. Numerical simulation of wetting phenomena by a meshfree particle method. arXiv preprint arXiv:1406.4734.

Tiwari, S., & Kuhnert, J. 2003. Finite pointset method based on the projection method for simulations of

the incompressible Navier-Stokes equations (pp. 373-387). Springer Berlin Heidelberg.

Tiwari, S., & Kuhnert, J. 2005. A Numerical Scheme for Solving Incompressible and Low Mach Number Flows by the Finite Pointset Method. In Meshfree Methods for Partial Differential Equations II (pp.

191-[10]

206). Springer Berlin Heidelberg.

Tiwari, S., & Kuhnert, J. 2007. Modeling of two-phase flows with surface tension by finite pointset method (FPM). Journal of computational and applied mathematics, 203(2), 376-386.