PELUANG KEBANGKRUTAN PERUSAHAAN ASURANSI SAAT INTERVAL ANTAR PEMBAYARAN MEMILIKI SEBARAN EKSPONENSIAL YANG TIDAK SAMA LUSSI KURNIAWATI

PELUANG KEBANGKRUTAN PERUSAHAAN ASURANSI

SAAT INTERVAL ANTAR PEMBAYARAN MEMILIKI

SEBARAN EKSPONENSIAL YANG TIDAK SAMA

LUSSI KURNIAWATI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2014

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa skripsi berjudul Peluang Kebangkrutan Perusahaan Asuransi Saat Interval Antar Pembayaran Memiliki Sebaran Eksponensial yang Tidak Sama adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Agustus 2014

Lussi Kurniawati

ABSTRAK

LUSSI KURNIAWATI. Peluang Kebangkrutan Perusahaan Asuransi Saat Interval Antar Pembayaran Memiliki Sebaran Eksponensial yang Tidak Sama. Dibimbing oleh RUHIYAT dan HADI SUMARNO.

Pada model risiko klasik, keuntungan perusahaan asuransi dipengaruhi oleh tiga hal, yaitu besarnya keuntungan awal perusahaan, besarnya pendapatan (premi) yang dibayarkan para pemegang polis, dan besarnya klaim yang dikeluarkan perusahaan untuk pemegang polis. Perusahaan asuransi dikatakan bangkrut jika keuntungan perusahaan asuransi bernilai negatif, yaitu ketika besarnya klaim yang dibayarkan melebihi besarnya keuntungan awal ditambah dengan besarnya pendapatan (premi) yang diterima dari para pemegang polis. Pada penelitian ini ditentukan peluang kebangkrutan perusahaan asuransi saat interval antar pembayaran memiliki sebaran eksponensial yang tidak sama dan besarnya pembayaran memiliki sebaran eksponensial yang identik. Selain itu, diberikan pula ilustrasi proses keuntungannya.

Kata kunci: asuransi, interval antar pembayaran, peluang kebangkrutan, sebaran eksponensial yang tidak sama

ABSTRACT

LUSSI KURNIAWATI. Ruin Probability of an Insurance Company in a Case of Intervals between Payments are Distributed Exponentially Unequally. Supervised by RUHIYAT and HADI SUMARNO.

In the classical risk model, insurance company profit is affected by three factors i.e., the amount of the initial profit, the amount of revenue (premium) obtained, and the amount of the claims insurance company paid for the customers. The insurance company is called to get ruined if the profit is negative, when the amount of claims paid exceeds the initial profit plus the amount of income (premium) received. In this study such ruin probability was determined for the insurance company in the case where intervals between payments are distributed exponentially unequally and the amount of payments have identical exponential distributions. In this work, we also provide an illustrative surplus process.

Key words: insurance, interval between payments, probability of ruin, unequal exponential distributions

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PELUANG KEBANGKRUTAN PERUSAHAAN ASURANSI

SAAT INTERVAL ANTAR PEMBAYARAN MEMILIKI

SEBARAN EKSPONENSIAL YANG TIDAK SAMA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2014

Judul Skripsi : Peluang Kebangkrutan Perusahaan Asuransi Saat Inteval Antar Pembayaran Memiliki Sebaran Eksponensial yang Tidak Sama Nama : Lussi Kurniawati

NIM : G54100045 Disetujui oleh Ruhiyat, MSi Pembimbing I Dr Hadi Sumarno, MS Pembimbing II Diketahui oleh Dr Toni Bakhtiar, MSc Ketua Departemen Tanggal Lulus:

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah Subhanahu Wa Ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2013 ini ialah asuransi, dengan judul Peluang Kebangkrutan Perusahaan Asuransi saat Interval antar Pembayaran Memiliki Sebaran Eksponensial yang Tidak Sama.

Terima kasih penulis ucapkan kepada Ruhiyat, MSi dan Dr Hadi Sumarno, MS selaku pembimbing, serta Ir Retno Budiarti, MS yang telah banyak memberi saran. Di samping itu, penghargaan penulis sampaikan kepada seluruh dosen dan staf di Departemen Matematika atas segala ilmu dan bantuan yang diberikan semasa perkuliahan. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, adik, serta seluruh keluarga besar, atas segala doa dan kasih sayangnya. Tak lupa juga, penulis ucapkan terimakasih kepada seluruh keluarga di Departemen Matematika, khususnya angkatan 47, kakak dan adik kelas, teman kos wisma Do’i serta seluruh pihak yang telah mendukung dan mendoakan penulis hingga terselesaikannya karya ilmiah ini.

Semoga karya ilmiah ini bermanfaat.

Bogor, Agustus 2014

DAFTAR ISI

DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Perumusan Masalah 2 Tujuan Penelitian 2 TINJAUAN PUSTAKA 2 Peluang 2 Proses Stokastik 4 Asuransi 5

Peluang Kebangkrutan pada Proses Risiko Klasik 5

HASIL DAN PEMBAHASAN 7

Perumusan Peluang Kebangkrutan 7

Perhitungan Peluang Kebangkrutan dan Simulasi Keuntungan Perusahaan 12

SIMPULAN 15

DAFTAR PUSTAKA 16

LAMPIRAN 17

DAFTAR GAMBAR

1 Contoh proses keuntungan perusahaan 5

2 Ilustrasi proses kedatangan klaim 7

3 Ilustrasi proses keuntungan perusahaan 8

4 Proses keuntungan saat modal awal 10 dan banyaknya klaim 10 13 5 Proses keuntungan saat modal awal 10 dan banyaknya klaim 20 14 6 Proses keuntungan saat modal awal 10 dan banyaknya klaim 30 14 7 Proses keuntungan saat modal awal 5 dan banyaknya klaim 10 15

DAFTAR LAMPIRAN

1 Pembuktian persamaan (6) 17

2 Pembuktian 𝛼_𝑖(𝑥) adalah polinomial berderajat 𝑖 − 1 18

3 Pembuktian persamaan (8), (9), dan (10) 20

4 Pembuktian persamaan (11) 22

5 Pembuktian persamaan (13) 23

6 Pembuktian persamaan (15), (16), dan (17) 24 7 Pembuktian persamaan (18), (19), dan (20) 26

8 Pembuktian persamaan (21) 28

9 Contoh program perhitungan peluang kebangkrutan 30

10 Contoh program pembangkitan data 31

PENDAHULUAN

Latar Belakang

Setiap orang mungkin memiliki peluang tertimpa kejadian-kejadian yang tidak diharapkan sehingga akan timbul kerugian keuangan semenjak lahir sampai proses kematiannya, karena hidup seseorang dikelilingi dengan risiko. Oleh karena itu, perlu usaha untuk mengantisipasi atau mengurangi kerugian keuangan yang timbul dari kejadian tersebut. Salah satu cara mengantipasi kerugian keuangan yang akan terjadi akibat kejadian yang tidak diharapkan adalah dengan mengikuti program asuransi.

Perusahaan asuransi memperoleh pendapatan dari pembayaran premi yang diterima dari peserta asuransi. Di lain pihak perusahaan asuransi juga mengeluarkan klaim. Perusahaan asuransi memiliki modal awal yang diasumsikan sebagai keuntungan awal. Maka dari itu keuntungan perusahaan asuransi dapat dilihat dari modal awal ditambah dengan total premi dikurangi total klaim yang dikeluarkan. Besarnya premi dan klaim yang dikeluarkan biasanya telah diatur dalam suatu kontrak antara perusahaan asuransi dengan peserta asuransi. Perusahaan asuransi dikatakan bangkrut jika modal awal ditambah dengan total pendapatan (premi) yang masuk dari peserta asuransi lebih kecil dibandingkan dengan klaim yang diberikan kepada peserta asuransi.

Sejalan dengan perkembangan ilmu pengetahuan dan teknologi pada dasarnya perusahaan asuransi ingin mengetahui perkembangan operasional dan keuangan yang dimiliki, sehingga dapat membantu mengubah strategi perusahaan. Jika strategi yang dijalankan berdampak baik maka strategi tersebut dapat terus digunakan. Sebaliknya jika tidak maka perusahaan harus mengganti strategi agar kondisinya tidak semakin buruk. Oleh karena itu, dibutuhkan suatu model untuk menduga bagaimana kondisi perusahaan asuransi tersebut. Salah satunya adalah dengan melihat peluang kebangkrutan.

Teori kebangkrutan dapat dimanfaatkan oleh berbagai pihak. Salah satunya dalam bidang asuransi yaitu dari para pemegang kepentingan dalam perusahaan asuransi. Hal tersebut dikarenakan dengan melihat peluang kebangkrutan dari perusahaan asuransi akan mempengaruhi para investor untuk menanamkan modalnya. Semakin kecil peluang kebangkrutan yang dimiliki perusahaan asuransi akan semakin menarik para investor untuk menanamkan modalnya dan begitu juga sebaliknya.

Selain itu pengembangan teori kebangkrutan juga dapat dijadikan sebagai suatu rujukan bagi pemerintah. Rujukan tersebut dapat digunakan untuk membuat kebijakan pada bidang asuransi dalam menentukan jumlah dana minimal yang harus dimiliki oleh suatu perusahaan asuransi, sehingga perusahaan asuransi itu dapat diizinkan beroperasi pada periode waktu tertentu. Hal tersebut sangat membantu pemerintah agar perusahaan asuransi yang beroperasi dapat berjalan dengan baik dan dapat membantu perekonomian negara. Usaha pemerintah ini juga akan membuat masyarakat merasa nyaman untuk berasuransi. Karya ilmiah ini berlandaskan pada artikel yang ditulis oleh Vinogradov (1997) yang berjudul Ruin

Probability of an Insurance Company in the Case where Intervals between Payment Have Unequal Exponential Distributions.

2

Perumusan Masalah

Perusahaan asuransi dapat terus beroperasi jika keuntungan bersihnya positif atau baik. Pada umumnya keuntungan dalam perusahaan asuransi tidak selamanya positif atau baik, karena dipengaruhi oleh beberapa faktor. Faktor tersebut di antaranya dari klaim asuransi yang datang. Ketidakmampuan perusahaan asuransi dalam membayar klaim bisa saja terjadi, bila jumlah kejadian klaim yang datang cenderung lebih besar sehingga melebihi modal awal ditambah premi yang diterima perusahaan asuransi tersebut.

Pada intinya, hal ini terjadi karena klaim-klaim yang datang tidak seperti perkiraan yang diharapkan. Akibatnya perusahaan asuransi akan mengalami kebangkrutan.

Tujuan Penelitian Tujuan penelitian ini adalah sebagai berikut:

1. Merumuskan peluang kebangkrutan asuransi saat interval antar pembayaran memiliki sebaran eksponensial yang tidak sama.

2. Menghitung peluang kebangkrutan dan melakukan ilustrasi proses keuntungannya.

TINJAUAN PUSTAKA

Agar lebih memperjelas uraian berikutnya, diberikan beberapa definisi sebagai berikut.

Peluang Definisi 1 (Percobaan Acak)

Percobaan acak adalah percobaan yang dapat dilakukan berulang-ulang dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul dapat diketahui, tetapi hasil pada percobaan berikutnya tidak dapat ditebak dengan tepat (Grimmett & Stirzaker 1992).

Definisi 2 (Ruang Contoh dan Kejadian)

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω. Suatu kejadian A adalah himpunan bagian dari Ω (Grimmett & Stirzaker 1992).

Definisi 3 (Medan-𝝈)

Medan-𝜎 adalah himpunan ℱ yang anggotanya adalah himpunan bagian dari ruang contoh Ω, yang memenuhi kondisi berikut:

1. ∅ ∈ ℱ;

2. Jika 𝐴₁, 𝐴₂, … . ∈ ℱ, maka ⋃_𝑖=1∞ 𝐴_𝑖 ∈ ℱ; 3. Jika 𝐴 ∈ ℱ, maka 𝐴𝐶 ∈ ℱ

(Grimmet & Stirzaker 1992).

3 Definisi 4 (Ukuran Peluang)

Misalkan ℱ adalah medan-𝜎 dari ruang contoh Ω. Ukuran peluang adalah suatu fungsi 𝑃: ℱ → [0,1] pada (ℱ, Ω) yang memenuhi:

1. 𝑃(∅) = 0, 𝑃(Ω) = 1;

2. Jika 𝐴1, 𝐴2, … . ∈ ℱ adalah himpunan yang saling lepas, yaitu 𝐴𝑖 ∩ 𝐴𝑗 = ∅

untuk setiap pasangan 𝑖 ≠ 𝑗, maka

𝑃(⋃_𝑖=1∞ ) = Σ_𝑖=1∞ _𝑃(𝐴 𝑖).

(Grimmet & Stirzaker 1992). Definisi 5 (Peubah Acak)

Misalkan Ω adalah ruang contoh dari suatu percobaan acak. Fungsi 𝑋 yang terdefinisi pada Ω yang memetakan setiap unsur 𝜔 ∈ Ω ke satu dan hanya satu bilangan real 𝑋(𝜔) = 𝑥 disebut peubah acak. Ruang dari 𝑋 adalah himpunan bagian bilangan real.

𝒜 = {𝑥: 𝑥 = 𝑋(𝜔), 𝜔 ∈ Ω}. (Grimmett & Stirzaker 1992).

Definisi 6 (Fungsi Sebaran)

Misalkan 𝑋 adalah peubah acak dengan ruang 𝒜. Misalkan kejadian 𝐴 = (−∞, 𝑥] ⊂ 𝒜, maka peluang dari kejadian 𝐴 adalah

𝑃(𝑋 ≤ 𝑥) = 𝐹_𝑋(𝑥).

Fungsi 𝐹_𝑋 disebut fungsi sebaran dari peubah acak 𝑋 (Grimmet & Stirzaker 1992). Definisi 7 (Fungsi Massa Peluang)

Fungsi massa peluang dari peubah acak diskret 𝑋 adalah fungsi 𝑝_𝑋: ℝ → [0,1] yang diberikan oleh 𝑝𝑋(𝑥) = 𝑃(𝑋 = 𝑥) (Grimmet & Stirzaker 1992).

Definisi 8 (Peubah Acak Kontinu)

Peubah acak 𝑋 dikatakan peubah acak kontinu jika fungsi sebarannya adalah 𝐹𝑋(𝑥) = ∫ 𝑓(𝑢)𝑑𝑢

𝑥 −∞

untuk fungsi 𝑓: ℝ → [0, ∞) yang dapat diintegralkan. Fungsi 𝑓 = 𝑓𝑋 disebut fungsi

kepekatan peluang bagi 𝑋 (Grimmett & Stirzaker 1992). Definisi 9 (Peubah Acak Eksponensial)

Peubah acak kontinu 𝑋 disebut menyebar eksponensial dengan parameter 𝜆 > 0, jika fungsi kepekatan peluanganya adalah

𝑓_𝑋(𝑥; 𝜆) = {𝜆𝑒−𝜆𝑥 , 𝑥 ≥ 0 0 , 𝑥 < 0 (Ross 1996).

Definisi 10 (Peubah Acak Gamma)

Peubah acak 𝑋 disebut menyebar gamma dengan parameter (𝑛, 𝜆) , 𝜆 > 0 jika fungsi kepekatan peluangnya adalah

𝑓_𝑋(𝑥; 𝑛, 𝜆) =𝜆𝑒

−𝜆𝑥_(𝜆𝑥)𝑛−1

(𝑛 − 1)! , 𝑥 ≥ 0 (Ross 1996).

4

Proses Stokastik Definisi 11 (Proses Stokastik)

Proses Stokastik 𝑿 = {𝑋(𝑡), 𝑡 ∈ 𝑇} adalah suatu himpunan dari peubah acak yang memetakan suatu ruang contoh ke suatu ruang state (Ross 1996).

Definisi 12 (Proses Pencacahan)

Proses stokastik {𝑁(𝑡), 𝑡 ≥ 0} disebut proses pencacahan (counting process) jika 𝑁(𝑡) menyatakan banyaknya kejadian yang telah terjadi sampai waktu 𝑡 . Proses pencacahan 𝑁(𝑡) harus memenuhi:

1. 𝑁(𝑡) ≥ 0;

2. Nilai 𝑁(𝑡) adalah integer; 3. Jika 𝑠 < 𝑡, maka 𝑁(𝑠) ≤ 𝑁(𝑡);

4. Untuk 𝑠 < 𝑡, maka 𝑁(𝑡) − 𝑁(𝑠) sama dengan banyaknya kejadian yang terjadi pada selang (𝑠, 𝑡]

(Ross 1996).

Definisi 13 (Proses Poisson)

Suatu proses pencacahan {𝑁(𝑡), 𝑡 ≥ 0} disebut proses Poisson dengan intensitas 𝜆, 𝜆 > 0 jika:

1. 𝑁(0) = 0;

2. Proses tersebut memiliki inkremen bebas;

3. Banyaknya kejadian pada sembarang 𝑡, memiliki sebaran Poisson dengan rataan 𝜆𝑡. Jadi untuk semua 𝑡 > 0, 𝑠 > 0, maka:

𝑃{𝑁(𝑡 + 𝑠) − 𝑁(𝑠) = 𝑛} = 𝑒−𝜆𝑡(𝜆𝑡)

𝑛

𝑛! , 𝑛 = 0,1 … (Ross 1996).

Definisi 14 (Proses Poisson Majemuk)

Suatu proses {𝑌(𝑡), 𝑡 ≥ 0} disebut proses Poisson majemuk jika proses tersebut dinyatakan sebagai:

𝑌(𝑡) = ∑ 𝑍_𝑖

𝑁(𝑡)

𝑖=1

, 𝑡 ≥ 0

dengan {𝑁(𝑡), 𝑡 ≥ 0} adalah suatu proses Poisson dengan intensitas 𝜆 dan 𝑍₁, 𝑍₂, … adalah suatu barisan peubah acak independent and identically distributed (i.i.d.) yang juga bebas terhadap {𝑁(𝑡), 𝑡 ≥ 0} (Ross 1996).

Definisi 15 (Waktu antar Kedatangan)

Barisan {Δ_𝑛, 𝑛 = 1,2, … } disebut barisan waktu antar kedatangan dari suatu proses Poisson dengan Δ_𝑛 menyatakan jarak antarwaktu kejadian proses Poisson ke-(𝑛 − 1) dengan kejadian proses Poisson ke-𝑛 (Ross 1996).

5 Asuransi

Definisi 16 (Perusahaan Asuransi)

Berdasarkan Undang-Undang Republik Indonesia Nomor 2 Tahun 1992 tentang Usaha Perasuransian, asuransi atau pertanggungan adalah perjanjian antara dua pihak atau lebih, dengan mana pihak penanggung mengikatkan diri kepada tertanggung, dengan menerima premi asuransi, untuk memberikan penggantian kepada tertanggung karena kerugian, kerusakan atau kehilangan keuntungan yang diharapkan, atau tanggung jawab hukum pihak ketiga yang mungkin akan diderita tertanggung, yang timbul dari suatu peristiwa yang tidak pasti, atau memberikan suatu pembayaran yang didasarkan atas meninggal atau hidupnya seseorang yang dipertanggungkan.

Definisi 17 (Polis, Premi, dan Klaim Asuransi)

Polis adalah suatu kontrak yang dibuat oleh perusahaan asuransi dengan peserta asuransi yang berisi perjanjian membayar cicilan dengan jumlah tertentu selama periode tertentu. Premi adalah biaya yang harus dibayarkan oleh peserta asuransi kepada perusahaan asuransi sesuai dengan polis yang disepakati. Klaim adalah jaminan terhadap risiko atau kerusakan yang terjadi oleh perusahaan asuransi kepada peserta asuransi sesuai kesepakatan polis (Bowers et al. 1997).

Peluang Kebangkrutan pada Proses Risiko Klasik

Keuntungan perusahaan asuransi pada saat 𝑡 > 0 dalam model risiko klasik ditentukan oleh tiga hal, yaitu besarnya keuntungan awal, besarnya pendapatan (premi) yang diperoleh dari pemegang polis sampai waktu 𝑡, dan besarnya klaim yang dibayarkan kepada pemegang polis sampai waktu 𝑡.

Gambar 1 Contoh proses keuntungan perusahaan

Gambar 1 menunjukkan bahwa nilai keuntungan perusahaan asuransi berubah dari waktu ke waktu dikarenakan oleh pembayaran klaim. Suatu saat, pembayaran klaim menyebabkan nilai keuntungan perusahaan asuransi negatif, dengan kata lain 𝑋(𝑡) < 0. Dari Gambar 1 terlihat bahwa kebangkrutan terjadi pada saat 𝜏, di mana 𝑋(𝜏) < 0.

6

Misalkan {𝑁(𝑡), 𝑡 ≥ 0} adalah proses kedatangan klaim, maka untuk 𝑡 > 0, peubah acak 𝑁(𝑡) menyatakan banyaknya klaim yang datang pada interval waktu [0, 𝑡]. Dalam proses risiko klasik diasumsikan bahwa {𝑁(𝑡), 𝑡 ≥ 0} adalah proses Poisson. Besarnya klaim yang datang dimodelkan sebagai barisan peubah acak

independent and identically distributed (i.i.d.) {𝑍_𝑖, 𝑖 ≥ 1} , maka 𝑍_𝑖 merupakan besarnya klaim pada saat ke-𝑖. Besarnya klaim agregrat sampai waktu 𝑡 adalah

𝑌(𝑡) = ∑ 𝑍𝑖 𝑁(𝑡)

𝑖=1

dengan 𝑌(𝑡) = 0 saat 𝑁(𝑡) = 0. Proses klaim agregrat {𝑌(𝑡), 𝑡 ≥ 0} merupakan proses Poisson majemuk.

Misalkan {𝑋(𝑡), 𝑡 ≥ 0} adalah proses keuntungan perusahaan asuransi dengan {𝑌(𝑡), 𝑡 ≥ 0}.

𝑋(𝑡) = 𝑥 + 𝑐𝑡 − 𝑌(𝑡)

dengan 𝑥 adalah modal awal perusahaan asuransi dan 𝑐 adalah laju peningkatan premi per satuan waktu yang diterima secara kontinu.

Peluang kebangkrutan perusahaan asuransi didefinisikan sebagai 𝜓(𝑥) = 𝑃(𝑋(𝑡) < 0 untuk suatu 𝑡 > 0).

Dengan kata lain, 𝜓(𝑥) adalah peluang bahwa keuntungan perusahaan asuransi berada di bawah nol pada suatu waktu di masa depan dikarenakan klaim yang datang melebihi modal awal ditambah dengan premi yang masuk pada perusahaan asuransi.

Definisikan 𝑅(𝑥) = 1 − 𝜓(𝑥) sebagai peluang ketidakbangkrutan dengan keuntungan perusahaan awal sebesar 𝑥. Dengan mempertimbangkan waktu dan besarnya klaim pertama, didapatkan

𝑅(𝑥) = ∫ 𝜆𝑒−𝜆𝑡 ∞ 0 ∫ 𝑓(𝑧)𝑅(𝑥 + 𝑐𝑡 − 𝑧)𝑑𝑧 𝑑𝑡 𝑢+𝑐𝑡 0

dengan catatan jika klaim pertama terjadi pada waktu 𝑡, besarnya tidak melebihi 𝑥 + 𝑐𝑡, agar tidak terjadi kebangkrutan. Dengan melakukan substitusi 𝑠 = 𝑥 + 𝑐𝑡 diperoleh 𝑅(𝑥) =1 𝑐∫ 𝜆𝑒 −𝜆(𝑠−𝑢)_𝑐 ∞ 𝑢 ∫ 𝑓(𝑧)𝑅(𝑠 − 𝑧)𝑑𝑧 𝑑𝑠 𝑠 0 =𝜆 𝑐𝑒 𝜆𝑢 𝑐∫ 𝑒−𝜆 𝑠 𝑐 ∞ 𝑢 ∫ 𝑓(𝑧)𝑅(𝑠 − 𝑧)𝑑𝑧 𝑑𝑠 𝑠 0 .

Penyelesaian eksplisit bagi 𝑅(𝑥) dapat diperoleh dengan melakukan penurunan sebagai berikut.

𝑑 𝑑𝑢𝑅(𝑥) = 𝜆2 𝑐2𝑒 −𝜆 𝑢/𝑐_{∫ 𝑒}−𝜆𝑠 𝑐 ∞ 𝑢 ∫ 𝑓(𝑧)𝑅(𝑠 − 𝑧)𝑑𝑧 𝑑𝑠 𝑠 0 −𝜆 𝑐∫ 𝑓(𝑧)𝑅(𝑢 − 𝑧)𝑑𝑧 𝑢 0 =𝜆 𝑐𝑅(𝑥) − 𝜆 𝑐∫ 𝑓(𝑧)𝑅(𝑢 − 𝑧)𝑑𝑧. 𝑢 0 (Dickson 2005).

7

HASIL DAN PEMBAHASAN

Perumusan Peluang Kebangkrutan

Keuntungan perusahaan asuransi diperoleh dari modal awal perusahaan asuransi ditambah dengan total pendapatan (premi) dari peserta asuransi dikurang dengan total pembayaran klaim-klaim yang datang pada perusahaan asuransi. Modal awal perusahaan asuransi dinotasikan dengan 𝑥 yang diasumsikan sebagai keuntungan awal 𝑋(0) = 𝑥. Keuntungan perusahaan asuransi pada waktu 𝑡 , di mana 𝑡 ≥ 0 dinotasikan dengan 𝑋(𝑡). Nilai 𝑋(𝑡) selalu berubah dari waktu ke waktu, bergantung dari total premi yang diterima dan pembayaran klaim yang datang dari peserta asuransi. Oleh karena itu nilai keuntungan perusahaan asuransi pada waktu 𝑡 didefinisikan sebagai:

𝑋(𝑡) = 𝑥 + 𝑆(𝑡) − ∑ 𝑍_𝑖

𝑁(𝑡)

𝑖=1

, 𝑡 > 0 dengan

a. 𝑥 = 𝑋(0) adalah modal awal perusahaan asuransi, dengan 𝑥 > 0.

b. 𝑆(𝑡) adalah total pendapatan (premi) yang diterima dari peserta asuransi pada interval waktu [0, 𝑡].

c. 𝑍_𝑖 adalah besarnya klaim ke-𝑖 yang dibayarkan perusahaan asuransi, 𝑖 ≥ 1. d. 𝑁(𝑡)= max(𝑖: 𝑇_𝑖 ≤ 𝑡) adalah banyaknya klaim yang datang pada interval waktu

[0, 𝑡], dengan 𝑇𝑖 adalah waktu pembayaran klaim ke-𝑖, 𝑖 ≥ 1 dengan 0 ≤ 𝑇1 ≤

𝑇2 ≤ ⋯ ≤ 𝑇𝑛 dan Δ1 = 𝑇1, Δ𝑖 = 𝑇𝑖 − 𝑇𝑖−1, untuk 𝑖 ≥ 2.

Asumsi-asumsi untuk model pada analisis sebagai berikut:

a. Besarnya klaim (𝑍1, 𝑍2, … ) saling bebas dan menyebar eksponensial dengan

fungsi sebaran 𝐹(𝑧) = 1 − 𝑒−𝑧.

b. Premi dari peserta asuransi meningkat secara linear pada setiap interval Δ_𝑖 dengan kenaikan sebesar 𝑐_𝑖 ≥ 0.

c. {𝑍_𝑖}, {Δ_𝑖} saling bebas dan setiap interval Δ_𝑖 memiliki sebaran eksponensial dengan parameter 𝛿_𝑖 .

𝑍1 𝑍2 𝑍3 𝑍4

0 𝑇1 𝑇2 𝑇3 t 𝑇4

Δ₁ Δ₂ Δ₃ Δ₄ 𝑐₁ 𝑐₂ 𝑐₃ 𝑐₄

Gambar 2 Ilustrasi proses kedatangan klaim

Gambar 2 menunjukkan proses kedatangan klaim pada interval waktu [0, 𝑡]. Ada tiga kejadian klaim {𝑍₁, 𝑍₂, 𝑍₃} yang terjadi pada interval tersebut dengan kenaikan premi berturut-turut {𝑐₁, 𝑐₂, 𝑐₃}. Total premi yang diperoleh perusahaan

8

asuransi pada interval waktu tersebut adalah 𝑆(𝑡) = Δ₁𝑐₁+ Δ₂𝑐₂+ Δ₃𝑐₃ + (𝑡 − 𝑇3)𝑐4.

Gambar 3 Ilustrasi proses keuntungan perusahaan

Gambar 3 menunjukkan proses kedatangan klaim berdasarkan ilustrasi Gambar 2 ada tiga klaim yang terjadi saat interval waktu [0, 𝑡] kondisi keuntungan perusahaan positif. Namun saat interval waktunya ditambah dengan premi menjadi 𝑆(𝑡) = Δ₁𝑐₁+ Δ₂𝑐₂+ Δ₃𝑐₃+Δ₄𝑐₄terjadi klaim ke-4 yang besarnya melebihi modal awal dan total premi yang diterima perusahaan, sehingga keuntungan perusahaan negatif.

Peluang kebangkrutan didefinisikan sebagai

𝜓(𝑥) = 𝑃(𝑋(𝑡) < 0 untuk suatu 𝑡 > 0).

Untuk mencari peluang kebangkrutan perusahaan asuransi, dicari terlebih dahulu peluang ketidakbangkrutan. Peluang ketidakbangkrutan adalah peluang keadaaan keuntungan perusahaan asuransi tidak pernah negatif. Peluang ketidakbangkrutan dilambangkan dengan 𝑅(𝑥). Karena penjumlahan dalam ukuran peluang adalah satu, maka

𝑅(𝑥) = 1 − 𝜓(𝑥). (1)

Persamaan (1) menggambarkan peluang ketidakbangkrutan dan peluang kebangkrutan. Waktu kebangkrutan dinotasikan dengan 𝜏 adalah waktu di mana nilai keuntungan perusahaan pada saat itu negatif, sehingga dapat dimodelkan dalam bentuk

𝜏 = inf(𝑡: 𝑋(𝑡) < 0).

Untuk menghitung 𝑅(𝑥) dan 𝜓(𝑥), pertama diasumsikan bahwa banyaknya pembayaran klaim berhingga dan sama dengan 𝑛. Misalkan 𝜓_𝑛(𝑥) dan 𝑅_𝑛(𝑥) berturut-turut melambangkan peluang kebangkrutan dan peluang ketidakbangkrutan dengan 𝑛 pembayaran klaim. Jadi,

𝜓(𝑥) = lim

𝑛→∞𝜓𝑛(𝑥),

𝑅(𝑥) = lim

𝑛→∞𝑅𝑛(𝑥).

9 𝜓𝑛(𝑥) = 𝜓𝑛(𝑥, 𝛿1, 𝑐1, 𝛿2, 𝑐2, 𝛿3, 𝑐3, … , 𝛿𝑛, 𝑐𝑛).

Untuk mempermudah dalam proses perhitungan akan digunakan permutasi terhadap barisan {𝛿_𝑖} dan {𝑐_𝑖}. Permutasi yang digunakan adalah 𝛿_𝑖 → 𝛿_{𝑛−𝑖+1} dan 𝑐_𝑖 → 𝑐_{𝑛−𝑖+1}, 𝑖 = 1, … , 𝑛 . Setelah dilakukan permutasi, interval waktu sebelum pembayaran pertama memiliki sebaran eksponensial dengan parameter 𝛿_𝑛 dan laju pertambahan premi pada interval ini menjadi 𝑐_𝑛. Interval waktu antara pembayaran pertama dan pembayaran kedua memiliki sebaran eksponensial dengan parameter 𝛿_𝑛−1 dan laju pertambahan premi menjadi 𝑐_𝑛−1 dan seterusnya.

Lambangkan 𝜓̃_𝑛(𝑥)dan 𝑅̃_𝑛(𝑥) berturut-turut sebagai peluang kebangkrutan dan peluang ketidakbangkrutan yang telah dipermutasi, sehingga

𝜓̃𝑛(𝑥) = 𝜓𝑛(𝑥, 𝛿𝑛, 𝑐𝑛, 𝛿𝑛−1, 𝑐𝑛−1, 𝛿𝑛−2, 𝑐𝑛−2, … , 𝛿1, 𝑐1).

Misalkan klaim pertama terjadi pada waktu 𝑦 > 0 dan besarnya klaim tersebut adalah 𝑧. Ada dua kemungkinan kejadian, yaitu:

a. Kebangkrutan terjadi pada saat klaim pertama, sehingga 𝑧 > 𝑥 + 𝑆(𝑦) atau b. Kebangkrutan tidak terjadi pada saat klaim pertama, sehingga keuntungan

perusahaan setelah pembayaran pertama, 𝑥 + 𝑆(𝑡) − 𝑧 tidak negatif atau 𝑧 < 𝑥 + 𝑆(𝑦), sehingga diperoleh persamaan berikut:

𝑅̃𝑖(𝑥) = ∫ 𝛿𝑖𝑒−𝛿𝑖𝑦 ∞ 0 ∫ 𝑅̃𝑖−1( 𝑥+𝑐𝑖𝑦 0 𝑥 + 𝑐𝑖𝑦 − 𝑧)𝑑𝐹(𝑧)𝑑𝑦 = 𝛿_𝑖∫ 𝑒−𝛿𝑖𝑦 ∞ 0 [ ∫ 𝑅̃_𝑖−1( 𝑥+𝑐𝑖𝑦 0 𝑥 + 𝑐_𝑖𝑦 − 𝑧)𝑒−𝑧𝑑𝑧] 𝑑𝑦, ₍₂₎ dengan 𝑅̃0(𝑥) = 1.

Misalkan 𝑥 + 𝑐𝑖𝑦 = 𝑢, maka 𝑑𝑢 = 𝑐𝑖𝑑𝑦 sehingga 1

𝑐𝑖𝑑𝑢 = 𝑑𝑦. Ketika 𝑦 =

0 diperoleh 𝑢 = 𝑥 dan 𝑦 → ∞ diperoleh 𝑢 → ∞. Persamaan (2) akan menjadi 𝑅̃_𝑖(𝑥) =𝛿𝑖 𝑐_𝑖∫ 𝑒 − 𝛿𝑖 𝑐𝑖 (𝑢−𝑥) ∞ 𝑥 [∫ 𝑅̃_𝑖−1( 𝑢 0 𝑢 − 𝑧)𝑒−𝑧𝑑𝑧] 𝑑𝑢. (3) Misalkan 𝛽_𝑖 =𝛿𝑖

𝑐𝑖, maka persamaan (3) menjadi

𝑅̃_𝑖(𝑥) = 𝛽𝑖∫ 𝑒− 𝛽𝑖 (𝑢−𝑥) ∞ 𝑥 [∫ 𝑅̃_𝑖−1( 𝑢 0 𝑢 − 𝑧)𝑒−𝑧_{𝑑𝑧] 𝑑𝑢.} = 𝛽𝑖𝑒𝛽𝑖𝑥∫ 𝑒−𝛽𝑖𝑢 ∞ 𝑥 [∫ 𝑅̃𝑖−1( 𝑢 0 𝑢 − 𝑧)𝑒−𝑧𝑑𝑧] 𝑑𝑢. (4) Untuk mencari peluang ketidakbangkrutan pertama misalkan 𝜓̃_𝑖(𝑥) = 𝜆_𝑖𝑒−𝑥_𝛼

𝑖(𝑥) dengan 𝜆𝑖 = 𝛽𝑖⁄(1 + 𝛽𝑖) dan fungsi 𝛼𝑖(𝑥)

𝛼_𝑖(𝑥) = 1 + 𝜆𝑖−1∫ 𝛼𝑖−1(𝑧) 𝑥 0 𝑑𝑧 + 𝜆_𝑖−1𝑒 𝑥 𝑎𝑖_{∫ 𝑒}− 𝑧 𝑎𝑖 ∞ 𝑥 𝛼_𝑖−1(𝑧)𝑑𝑧, (5)

10

dengan 𝛽₀ = 𝜆₀ = 0, 𝑎_𝑖 = (1 + 𝛽_𝑖)−1 _{dan 𝛼}

0(𝑥) = 0 untuk 𝑖 = 1,2, … , 𝑛.

Untuk sembarang bilangan positif b dan bilangan bulat taknegatif k, berlaku persamaan 𝑒𝑥/𝑏∫ 𝑒−𝑠/𝑏 ∞ 𝑥 𝑠𝑘𝑑𝑠 = 𝑘! ∑𝑥 𝑗_𝑏𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 . (6)

Bukti dapat dilihat pada Lampiran 1.

Berdasarkan persamaan (5) dan (6) 𝛼_𝑖(𝑥) adalah polinom berderajat 𝑖 − 1, sehingga 𝛼_𝑖(𝑥) dapat dituliskan dalam bentuk

𝛼_𝑖(𝑥) = ∑ 𝐴̃_𝑖(𝑘)𝑥𝑘

𝑖−1

𝑘=0

(7) dan 𝐴̃𝑖(𝑘) = 0 , untuk 𝑘 ≥ 𝑖 . Bukti dapat dilihat pada Lampiran 2. Substitusi

persamaan (7) ke persamaan (5), lalu gunakan persamaan (6), maka untuk 𝑖 = 1, … , 𝑛 𝐴̃_𝑖(0) = 1 + 𝜆𝑖−1∑ 𝑙! 𝑎𝑖𝑙+1 𝑖−2 𝑙=0 𝐴̃_𝑖−1(𝑙), (8) 𝐴̃𝑖(𝑘) = 𝜆_𝑖−1 𝑎_𝑖𝑘𝑘! ∑ 𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=𝑘−1 𝐴̃𝑖−1(𝑙), (9) untuk 𝑘 = 1, … , 𝑖 − 2, dan 𝐴̃𝑖(𝑖 − 1) = 𝜆𝑖−1 𝐴̃_𝑖−1 (𝑖 − 2) 𝑖 − 1 . (10)

Bukti dapat dilihat pada Lampiran 3. Agar mendapatkan bentuk eksplisit untuk rumus barisan {𝐴̃_𝑖(𝑘)}, di mana 𝑖 = 1, … , 𝑛, 𝑘 = 0, … , 𝑖 − 1, persamaan (8), (9), dan (10) diubah menjadi bentuk yang sederhana. Masukkan nilai 𝑘 = 1 pada persamaan (9), maka diperoleh

𝐴̃𝑖(1) = 𝜆_𝑖−1 𝑎𝑖 ∑ 𝑙! 𝑎_𝑖𝑙+1 𝑖−2 𝑙=0 𝐴̃𝑖−1(𝑙),

sehingga berdasarkan persamaan (8) menjadi:

𝐴̃𝑖(0) = 1 + 𝑎𝑖𝐴̃𝑖(1). (11)

Bukti dapat dilihat pada Lampiran 4. Jika 𝑘 < 𝑖 − 2, maka berdasarkan persamaan (9):

11 𝐴̃_𝑖(𝑘 + 1) = 𝜆𝑖−1 (𝑘 + 1)! 𝑎_𝑖𝑘+1[ ∑ 𝑙! 𝑎𝑖𝑙+1 𝑖−2 𝑙=𝑘−1 𝐴̃_𝑖−1(𝑙) − (k − 1)! 𝑎_𝑖𝑘𝐴̃_𝑖−1(𝑘 − 1)]. (12)

Dari persamaan persamaan (9) dan (12) didapatkan untuk 0 < 𝑘 < 𝑖 − 1 𝐴̃_𝑖(𝑘) = (𝑘 + 1)𝑎_𝑖𝐴̃_𝑖(𝑘 + 1) +𝜆𝑖−1

𝑘 𝐴̃𝑖−1(𝑘 − 1). (13)

Bukti dapat dilihat pada Lampiran 5. Jadi terbukti bahwa barisan {𝐴̃_𝑖(𝑘)} memenuhi persamaan (10)-(13). Untuk 𝑘 > 0 diatur sebagai berikut:

𝐴̃𝑖(𝑘) =

𝜆𝑖−𝑘𝜆𝑖−𝑘+1…𝜆𝑖−1

𝑘! 𝐵̃𝑖(𝑘), 𝐴̃𝑖(0) = 𝐵̃𝑖(0). (14)

Dari definisi persamaan (10)-(13) diperoleh

𝐵̃_𝑖(0) = 1 + 𝑎𝑖𝜆𝑖−1𝐵̃𝑖(1), (15)

𝐵̃𝑖(𝑘) = 𝑎𝑖𝜆𝑖−𝑘−1𝐵̃𝑖(𝑘 + 1) + 𝐵̃𝑖(𝑘 − 1), (16)

untuk 0 < 𝑘 < 𝑖 − 1 dan

𝐵̃_𝑖(𝑖 − 1) = 𝐵̃_𝑖−1(𝑖 − 2). (17) Bukti dapat dilihat pada Lampiran 6. Karena 𝛼₀(𝑥) = 0, maka dari persamaan (5) didapatkan bahwa 𝛼₁(𝑥) = 1, sehingga

𝐵̃_𝑖(0) = 1. (18)

Ditunjukkan bahwa persamaan (15)-(18) mendefinisikan secara unik barisan 𝐵̃𝑖(𝑘)

dan begitu pula barisan 𝐴̃𝑖(𝑘). Persamaan (17) dan (18) akan berimplikasi bahwa

untuk 𝑖 = 1, … 𝑛 dipenuhi persamaan

𝐵̃_𝑖(𝑖 − 1) = 1. (19)

Substitusikan 𝑘 = 𝑖 − 2 pada persamaan (16) dan menggunakan persamaan (19), maka didapatkan untuk 1 < 𝑖 ≤ 𝑛 adalah

𝐵̃𝑖(𝑖 − 2) = 1 + 𝜆𝑖∑ 𝑎𝑙 𝑖

𝑙=2

. (20)

Bukti dapat dilihat pada Lampiran 7.

Menggunakan persamaan (16) dan (20) dan argumen yang serupa, didapatkan bentuk eksplisit dari 𝐵̃_𝑖(𝑖 − 3) , jika 2 < 𝑖 < 𝑛 + 1 . Secara analogi didapatkan bentuk eksplisit untuk 𝐵̃_𝑖(𝑘) untuk 𝑖 = 1, … , 𝑛 + 1, 𝑘 = 0, … , 𝑖 − 1 . Jadi telah terbukti bahwa persamaan (15)-(18) mendefiniskan secara unik barisan 𝐵̃_𝑖(𝑘) . Menggunakan teknik dasar komputasi didapatkan barisan

12 𝐵̃_𝑖(𝑘) = 1 + 𝜆_{𝑖−𝑘−1} ∑ 𝑎_𝑙 𝑖 𝑙=𝑖−𝑘 + 𝜆_{𝑖−𝑘−2}𝜆_{𝑖−𝑘−1} ∑ ∑ 𝑎_𝑙1𝑎_𝑙2 𝑙1 𝑙2=𝑖−𝑘−1 𝑖 𝑙1=𝑖−𝑘 + ⋯ + 𝜆1𝜆2… 𝜆𝑖−𝑘−1 ∑ ∑ … 𝑙1 𝑙2=𝑖−𝑘−1 𝑖 𝑙1=𝑖−𝑘 ∑ 𝑎𝑙1𝑎𝑙2 𝑙1−𝑘−2 𝑙𝑖−𝑘−1=2 … 𝑎𝑙𝑖−𝑘−1 ₍₂₁₎

dengan 𝜆𝑝= 0 untuk 𝑝 ≤ 0 memenuhi persamaan (15)-(18) dengan 1 ≤ 𝑖 ≤ 𝑛,

0 ≤ 𝑘 ≤ 𝑖 − 1. Bukti dapat dilihat pada Lampiran 8. Teorema 1 𝜓̃𝑛(𝑥) = 𝑒−𝑥[∑ 𝜆_𝑛−𝑘𝜆_{𝑛−𝑘+1}… 𝜆_𝑛 𝑘! 𝐵̃𝑛 𝑛−1 𝑘=0 (𝑘)𝑥𝑘],

dengan 𝐵̃𝑛(𝑘) berlaku yang diberikan pada persamaan (21) dengan 𝑖 = 𝑛.

Menggunakan permutasi dengan membuat perubahan kembali pada indeks 𝑖 → 𝑛 − 𝑖 + 1, diperoleh: Teorema 2 𝜓_𝑛(𝑥) = 𝑒−𝑥_[∑𝜆1… 𝜆𝑘+1 𝑘! 𝐵𝑛(𝑘) 𝑛−1 𝑘=0 𝑥𝑘_],

dengan 𝜆𝑝= 0, jika 𝑝 > 𝑛 dan

𝐵𝑛(𝑘) = 1 + 𝜆𝑘+2∑ 𝑎𝑙 𝑘+1 𝑙=1 + 𝜆𝑘+2𝜆𝑘+3 ∑ ∑ 𝑎𝑙1𝑎𝑙2 𝑘+2 𝑙2=𝑙1 𝑘+1 𝑙1=1 + ⋯ + 𝜆_𝑘+2… 𝜆_𝑛 ∑ ∑ … 𝑘+2 𝑙2=𝑙1 𝑘+1 𝑙1=1 ∑ 𝑎_𝑙1𝑎_𝑙2 𝑛−1 𝑙𝑛−𝑘−1=𝑙𝑛−𝑘−2 … 𝑎_{𝑙𝑛−𝑘−1}.

Perhitungan Peluang Kebangkrutan dan Simulasi Keuntungan Perusahaan Perhitungan peluang kebangkrutan dan keuntungan perusahaan asuransi dilakukan menggunakan bantuan perangkat lunak Mathematica 9.0 dan Microsoft

Excel. Satuan mata uang yang digunakan adalah Rp10 000 000, sedangkan satuan

waktu yang digunakan adalah bulan. Perhitungan peluang kebangkrutan dapat dilihat pada Lampiran 9. Pembangkitan data dapat dilihat pada Lampiran 10. Simulasi keuntungan perusahaan dapat dilihat pada Lampiran 11.

Contoh proses perhitungan di mana modal awal 10 dan terjadi satu kali klaim (𝑛 = 1) dengan 𝛿1 = 2 (𝛿𝑖 = parameter interval klaim) dan 𝑐1 = 1 (𝑐𝑖 = laju

premi perbulan) agar bisa menggunakan rumus peluang kebangkrutan yang telah diperoleh. Terlebih dahulu dicari nilai 𝛽, 𝜆, dan 𝑎. Nilai 𝛽 diperoleh dari 𝛽₁ =𝛿1

𝑐1,

13 𝐵₁(0) dan akhirnya akan diperoleh peluang kebangkrutan saat modal awal 10 dengan satu kejadian klaim (𝜓₁(10)).

Ilustrasi 1

Parameter yang digunakan adalah 𝑥 = 10, 𝑛 = 10, {𝛿_𝑖, 1 ≤ 𝑖 ≤ 10} = {2, 2, 3, 3, 2, 3, 3, 1, 2, 2}, dan {𝑐𝑖, 1 ≤ 𝑖 ≤ 10} = {1, 1.2, 1.5, 2, 1, 1.5, 2, 1, 1, 2}.

Hasil yang diperoleh dengan melakukan proses perhitungan seperti contoh proses perhitungan menghasilkan peluang kebangkrutan sebesar 0.0627361. Grafik keuntungan perusahaan asuransinya ditunjukkan oleh Gambar 4.

Gambar 4 Proses keuntungan saat modal awal 10 dan banyaknya klaim 10 Gambar 4 menunjukkan keuntungan perusahaan asuransi dengan modal awal Rp100 000 000 ada 10 kejadian klaim mengalami naik turun. Klaim ke-10 terjadi setelah 13.8 bulan sebesar Rp19 525 600, sehingga keuntungan perusahaan asuransi di akhir klaim ke-10 menjadi Rp115 276 943.

Ilustrasi 2

Parameter yang digunakan adalah 𝑥 = 10, 𝑛 = 20, {𝛿_𝑖, 1 ≤ 𝑖 ≤ 20} = {2, 2, 3, 3, 2, 3, 3, 1, 2, 2, 3, 1, 3, 2, 1, 2, 1, 1, 4, 1}, {𝑐_𝑖, 1 ≤ 𝑖 ≤ 20} = {1, 1.2, 1.5, 2, 1, 1.5, 2, 1, 1, 2, 1.5,1.2, 1.5, 1.2, 1,1.6, 1.1, 2, 1.2, 1}.

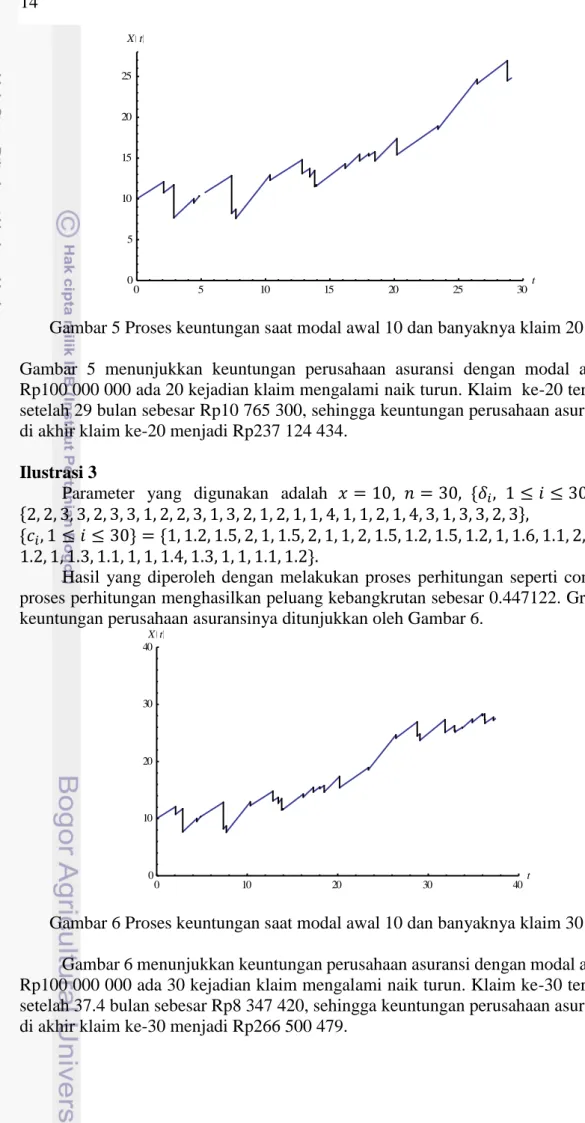
Hasil yang diperoleh dengan melakukan proses perhitungan seperti contoh proses perhitungan menghasilkan peluang kebangkrutan sebesar 0.255399. Grafik keuntungan perusahaan asuransinya ditunjukkan oleh Gambar 5.

0 2 4 6 8 10 12 14 t 0 5 10 15 20 X t

14

Gambar 5 Proses keuntungan saat modal awal 10 dan banyaknya klaim 20 Gambar 5 menunjukkan keuntungan perusahaan asuransi dengan modal awal Rp100 000 000 ada 20 kejadian klaim mengalami naik turun. Klaim ke-20 terjadi setelah 29 bulan sebesar Rp10 765 300, sehingga keuntungan perusahaan asuransi di akhir klaim ke-20 menjadi Rp237 124 434.

Ilustrasi 3

Parameter yang digunakan adalah 𝑥 = 10, 𝑛 = 30, {𝛿_𝑖, 1 ≤ 𝑖 ≤ 30} = {2, 2, 3, 3, 2, 3, 3, 1, 2, 2, 3, 1, 3, 2, 1, 2, 1, 1, 4, 1, 1, 2, 1, 4, 3, 1, 3, 3, 2, 3}, dan {𝑐_𝑖, 1 ≤ 𝑖 ≤ 30} = {1, 1.2, 1.5, 2, 1, 1.5, 2, 1, 1, 2, 1.5, 1.2, 1.5, 1.2, 1, 1.6, 1.1, 2, 1.2, 1, 1.3, 1.1, 1, 1, 1.4, 1.3, 1, 1, 1.1, 1.2}.

Hasil yang diperoleh dengan melakukan proses perhitungan seperti contoh proses perhitungan menghasilkan peluang kebangkrutan sebesar 0.447122. Grafik keuntungan perusahaan asuransinya ditunjukkan oleh Gambar 6.

Gambar 6 Proses keuntungan saat modal awal 10 dan banyaknya klaim 30 Gambar 6 menunjukkan keuntungan perusahaan asuransi dengan modal awal Rp100 000 000 ada 30 kejadian klaim mengalami naik turun. Klaim ke-30 terjadi setelah 37.4 bulan sebesar Rp8 347 420, sehingga keuntungan perusahaan asuransi di akhir klaim ke-30 menjadi Rp266 500 479.

0 5 10 15 20 25 30t 0 5 10 15 20 25 X t 0 10 20 30 40t 0 10 20 30 40 X t

15

Ilustrasi 4

Parameter yang digunakan adalah 𝑥 = 5, 𝑛 = 10, {𝛿𝑖, 1 ≤ 𝑖 ≤ 10} =

{5, 2, 2, 4, 2, 2, 3, 2, 1, 2}, dan {𝑐𝑖, 1 ≤ 𝑖 ≤ 10} = {0.8, 0.5, 0.4, 0.3, 0.5, 0.7, 0.1,

0.2, 0.5, 0.2}.

Hasil yang diperoleh dengan melakukan proses perhitungan seperti contoh proses perhitungan menghasilkan peluang kebangkrutan sebesar 0.832354. Grafik keuntungan perusahaan asuransinya ditunjukkan oleh Gambar 7.

Gambar 7 Proses keuntungan saat modal awal 5 dan banyaknya klaim 10 Gambar 7 menunjukkan keuntungan perusahaan asuransi dengan modal awal Rp50 000 000 ada 10 kejadian klaim mengalami naik turun. Pada saat klaim ke-7 yang terjadi setelah 11.4 bulan sebesar Rp76 651 500 mengakibatkan keuntungan perusahaan sudah negatif (bangkrut) dikarenakan klaim yang datang melebihi modal awal ditambah dengan premi.

Dari empat ilustrasi di atas jika dibandingkan satu dengan yang lainnya, semakin banyak klaim yang datang mengakibatkan semakin besar peluang kebangkrutannya. Semakin kecil modal awal yang dimiliki perusahaan asuransi juga mengakibatkan semakin besar hasil peluang kebangkrutannya.

SIMPULAN

Perusahaan asuransi akan memiliki peluang untuk bangkrut, meskipun perusahaan asuransi tersebut telah memperhitungkan terjadinya klaim asuransi pada kurun waktu tertentu dengan berbagai cara, seperti menetapkan premi yang masuk. Perusahaan asuransi dikatakan bangkrut jika keuntungan perusahaan bernilai negatif.

Dengan mengasumsikan banyaknya pembayaran terbatas dan sama dengan 𝑛 maka peluang kebangkrutan setelah 𝑛 kali pembayaran klaim dapat dihitung dengan rumus 𝜓_𝑛(𝑥) = 𝑒−𝑥_[∑𝜆1… 𝜆𝑘+1 𝑘! 𝐵𝑛(𝑘) 𝑛−1 𝑘=0 𝑥𝑘_]. 5 10 15 20t 2 0 2 4 6 8 X t

16

Keuntungan perusahaan asuransi tidak akan terus menaik akan ada kalanya turun dikarenakan klaim yang datang. Oleh kerena itu peluang kebangkrutannya juga akan berubah-ubah. Jika peluang kebangkrutan yang diperoleh kecil, maka perusahaan asuransi dapat terus beroperasi sampai batas waktu tertentu di waktu mendatang. Jika peluang kebangkrutan yang diperoleh besar maka perusahaan asuransi akan bangkrut atau keuntungan perusahaannya di bawah nol.

DAFTAR PUSTAKA

Bowers NL, Gerber HU, Hickman JC, Jones DA, Nesbitt CJ. 1997. Actuarial

Mathematics. Ed ke-2. Schaumburg (US): The Society of Actuaries.

Dickson DCM. 2005. Insurance Risk and Ruin. Cambridge (GB): Cambridge University Press.

Grimmet GR, Stirzaker DR. 1992. Probability and Random Processes. Ed ke-2. New York (US): Clarendon Press Oxford.

Pemerintah Republik Indonesia. 1992. Undang-Undang Republik Indonesia Nomor 2 Tahun 1992 tentang Usaha Perasuransian. Jakarta (ID): Sekretariat Negara. Ross SM. 1996. Stochastic Processes. Ed ke-2. New York (US): John Wiley &

Sons.

Vinogradov OP. 1997. Ruin probability of an insurance company in the case where intervals between payment have unequal exponential distributions. Theory

17 Lamipran 1 Pembuktian persamaan (6)

Akan dibuktikan bahwa

𝑒𝑥/𝑏∫ 𝑒−𝑠/𝑏 ∞ 𝑥 𝑠𝑘𝑑𝑠 = 𝑘! ∑𝑥 𝑗_𝑏𝑘−𝑗+1 𝑗! 𝑘 𝑗=0

Bukti: Misalkan 𝑋 mengikuti sebaran Gamma (𝛼 > 0, 𝜆 > 0). Fungsi kepekatan peluangnya adalah

𝑓(𝑥) =𝜆

𝛼_𝑥𝛼−1_𝑒−𝜆𝑥

Γ(α) dan fungsi sebarannya adalah

𝐹(𝑥) = 1 − ∑ 𝑒−𝜆𝑥(𝜆𝑥) 𝑗 𝑗! 𝛼−1 𝑗=0 . Diperoleh 𝑃(𝑋 > 𝑥) = 1 − 𝑃(𝑋 ≤ 𝑥) = 1 − 𝐹(𝑥) 𝜆𝛼 Γ(𝑥)∫ 𝑠 𝛼−1 ∞ 𝑥 𝑒−𝜆𝑠_{𝑑𝑠 = ∑ 𝑒}−𝜆𝑥(𝜆𝑥) 𝑗 𝑗! 𝛼−1 𝑗=0 ∫ 𝑠𝛼−1 ∞ 𝑥 𝑒−𝜆𝑠𝑑𝑠 =Γ(𝛼) 𝜆𝛼 ∑ 𝑒 −𝜆𝑥(𝜆𝑥)𝑗 𝑗! 𝛼−1 𝑗=0 𝑒𝜆𝑥_{∫ 𝑠}𝛼−1 ∞ 𝑥 𝑒−𝜆𝑠_{𝑑𝑠 =}Γ(𝛼) 𝜆𝛼 ∑ (𝜆𝑥)𝑗 𝑗! 𝛼−1 𝑗=0 .

Dengan melakukan substitusi 𝜆 =1

𝑏, 𝛼 − 1 = 𝑘, 𝛼 = 𝑘 + 1, diperoleh 𝑒𝑥𝑏∫ 𝑠𝑘 ∞ 𝑥 𝑒−𝑠𝑏𝑑𝑠 =Γ(𝑘 + 1) 𝑏−𝑘−1 ∑ 𝑥𝑗 𝑏𝑗 𝑗! 𝑘 𝑗=0 = 𝑘! ∑𝑥 𝑗_𝑏𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 .

18

Lampiran 2 Pembuktian 𝛼_𝑖(𝑥) adalah polinom berderajat 𝑖 − 1 Akan dibuktikan dengan induksi matematika bahwa 𝛼_𝑖(𝑥) = 1 + 𝜆𝑖−1∫ 𝛼𝑖−1(𝑧)

𝑥

0 𝑑𝑧 + 𝜆𝑖−1𝑒

𝑥/𝑎𝑖_{∫ 𝑒}∞ −𝑧/𝑎𝑖

𝑥 𝛼𝑖−1(𝑧)𝑑𝑧 adalah polinom berderajat

𝑖 − 1. Bukti:

I. Basis induksi: akan dibuktikan 𝛼_𝑖(𝑥) adalah polinom berderajat 0 (𝑖 = 1). Karena 𝛽0 = 𝜆0 = 0 dan 𝛼0(𝑥) = 0, maka 𝛼1(𝑥) = 1 + 0 = 1 yang

merupakan polinom berderajat 0.

II. Hipotesis induksi: dianggap benar untuk 𝑖 = 𝑚, yaitu 𝛼𝑚(𝑥) adalah

polinom berderajat 𝑚 − 1, maka

𝛼_𝑚(𝑥) = ∑ 𝑐_𝑛𝑥𝑛

𝑚−1

𝑛=0

.

III. Langkah induksi: akan dibuktikan (berdasarkan hipotesis induksi) benar untuk 𝑖 = 𝑚 + 1, yaitu 𝛼𝑚+1 adalah polinom berderajat 𝑚.

Berdasarkan hipotesis induksi,

∫ 𝛼_𝑚(𝑧) 𝑥 0 𝑑𝑧 = ∫ ∑ 𝑐_𝑛𝑧𝑛 𝑚−1 𝑛=0 𝑥 0 𝑑𝑧 = ∑ 𝑐𝑛 𝑚−1 𝑛=0 ∫ 𝑧𝑛 𝑥 0 𝑑𝑧 = ∑ 𝑐𝑛 𝑚−1 𝑛=0 𝑥𝑛+1 𝑛 + 1 dan 𝑒 𝑥 𝑎𝑚+1_{∫ 𝑒}− 𝑧 𝑎𝑚+1 ∞ 𝑥 𝛼𝑚(𝑧)𝑑𝑧 = 𝑒 𝑥 𝑎𝑚+1_{∫ ∑ 𝑐𝑛𝑧}𝑛 𝑚−1 𝑛=0 𝑥 0 𝑒− 𝑧 𝑎𝑚+1_𝑑𝑧 = ∑ 𝑐𝑛𝑒 𝑥 𝑎𝑚+1 𝑚−1 𝑛=0 ∫ 𝑧𝑛 𝑥 0 𝑒− 𝑧 𝑎𝑚+1_𝑑𝑧 = ∑ 𝑐_𝑛𝑛! 𝑚−1 𝑛=0 (∑𝑥 𝑗_𝑎 𝑚+1 𝑛−𝑗+1 𝑗! 𝑛 𝑗=0 ),

19 sehingga 𝛼_𝑚+1(𝑥) = 1 + 𝜆𝑚[ ∑ 𝑐𝑛 𝑚−1 𝑛=0 𝑥𝑛+1 𝑛 + 1+ ∑ 𝑐𝑛𝑛! 𝑚−1 𝑛=0 (∑𝑥 𝑗_𝑎 𝑚+1 𝑛−𝑗+1 𝑗! 𝑛 𝑗=0 )].

20

Lampiran 3 Pembuktian persamaan (8), (9) dan (10) Pembuktian persamaan (8): Akan dibuktikan bahwa 𝐴̃𝑖(0) = 1 + 𝜆𝑖−1∑ 𝑙! 𝑎𝑖𝑙+1

𝑖−2

𝑙=0

𝐴̃𝑖−1(𝑙)

untuk 𝑖 = 1,2, … , 𝑛.

Bukti: Diketahui bahwa 𝛼𝑖(𝑥) = ∑𝑖−1𝑘=0𝐴̃𝑖(𝑘)𝑥𝑘,dengan mengganti indeks 𝑖 → 𝑖 −

1 akan didapat 𝛼_𝑖−1(𝑥) = ∑𝑖−2_𝑘=0𝐴̃_𝑖−1(𝑘)𝑥𝑘_. 𝛼𝑖(𝑥) = 1 + 𝜆𝑖−1∫ 𝛼𝑖−1(𝑧)𝑑𝑧 𝑥 0 + 𝜆𝑖−1𝑒 𝑥/𝑎𝑖_{∫ 𝑒}∞ −𝑧/𝑎𝑖 𝑥 𝛼𝑖−1(𝑧)𝑑𝑧 = 1 + 𝜆𝑖−1∫ [∑ 𝐴̃𝑖−1 𝑖−2 𝑘=0 (𝑘)𝑧𝑘] 𝑥 0 𝑑𝑧 + 𝜆𝑖−1𝑒 𝑥 𝑎𝑖_{∫ [𝑒}− 𝑧 𝑎𝑖_{∑ 𝐴̃𝑖−1} 𝑖−2 𝑘=0 (𝑘)𝑧𝑘] ∞ 𝑥 𝑑𝑧 = 1 + 𝜆𝑖−1∑𝑖−2𝑘=0𝐴̃𝑖−1(𝑘) ∫ 𝑧𝑘𝑑𝑧 𝑥 0 + 𝜆𝑖−1∑ 𝐴̃𝑖−1 𝑖−2 𝑘=0 (𝑘)𝑒𝑥/𝑎𝑖∫ 𝑒−𝑧/𝑎𝑖 ∞ 𝑥 𝑧 𝑘_{𝑑𝑧 ,} = 1 + 𝜆_𝑖−1∑𝑖−2_𝑘=0𝐴̃_𝑖−1(𝑘) (_𝑘+11 ) 𝑥𝑘+1_{+ 𝜆} 𝑖−1∑𝑖−2𝑘=0𝐴̃𝑖−1(𝑘)𝑘! ∑ 𝑥𝑗𝑏𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 dari persamaan (6) = 1 + 𝜆𝑖−1∑ 𝐴̃𝑖−1 𝑖−2 𝑘=0 (𝑘) [( 1 𝑘 + 1) 𝑥 𝑘+1_{+ 𝑘! ∑}𝑥 𝑗_𝑏𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 ] dimana 𝑖 = 1, … , 𝑛

maka persamaan 𝛼_𝑖(𝑥) = ∑𝑖−1_𝑘=0𝐴̃_𝑖(𝑘)𝑥𝑘, jika diuraikan menjadi 𝛼_𝑖(𝑥) = 𝐴̃_𝑖(0)𝑥0_{+ 𝐴̃} 𝑖(1)𝑥1+ 𝐴̃𝑖(2)𝑥2+ ⋯ + 𝐴̃𝑖(𝑖 − 1)𝑥𝑖−1 Perhatikan 𝜆_𝑖−1∑𝑖−2_𝑘=0𝐴̃_𝑖−1(𝑘)[( 1 𝑘+1) 𝑥 𝑘+1_{+ 𝑘! ∑} 𝑥𝑗𝑎𝑖 𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 ], Jika 𝑘 = 0 → 𝜆𝑖−1𝐴̃𝑖−1(0)𝑥 + 𝜆𝑖−1𝐴̃𝑖−1(0)𝑎𝑖 𝑘 = 1 → 𝜆_𝑖−1𝐴̃_𝑖−1(1)1₂𝑥2_{+ 𝜆} 𝑖−1𝐴̃𝑖−1(1)1! [𝑎𝑖2+ 𝑥𝑎𝑖] 𝑘 = 2 → 𝜆_𝑖−1𝐴̃_𝑖−1(2)1₂𝑥3_{+ 𝜆} 𝑖−1𝐴̃𝑖−1(2)2! [𝑎𝑖3+ 𝑥𝑎𝑖2+ 𝑥2𝑎𝑖 2! ],

dan seterusnya maka didapat, ambil variabel yang 𝑥0 untuk 𝐴̃_𝑖(0) 𝐴̃𝑖(0) = 1 + 𝜆𝑖−1(𝐴̃𝑖−1(0)0! 𝑎𝑖 + 𝐴̃𝑖−1(1)1! 𝑎𝑖2+ 𝐴̃𝑖−1(2)2! 𝑎𝑖3+ ⋯

+ 𝐴̃_𝑖−1(𝑖 − 2)(𝑖 − 2)! 𝑎_𝑖𝑖−1₎

= 1 + 𝜆_𝑖−1∑𝑖−2_𝑙=0𝑙! 𝑎_𝑖𝑙+1𝐴̃_𝑖−1(𝑙).

Pembuktian persamaan (9): Akan dibuktikan bahwa 𝐴̃_𝑖(𝑘) = 𝜆𝑖−1 𝑎_𝑖𝑘𝑘! ∑ 𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=𝑘−1 𝐴̃_𝑖−1(𝑙) untuk 𝑘 = 1,2, … , 𝑖 − 2 dan 𝑖 = 1,2, … , 𝑛. Bukti: Sebelumnya telah didapatkan 𝛼𝑖(𝑥) = 1 + 𝜆𝑖−1∑𝑖−2𝑘=1𝐴̃𝑖−1(𝑘)[( 1 𝑘+1) 𝑥 𝑘+1_{+ 𝑘! ∑} 𝑥𝑗𝑎𝑖 𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 ],

sedangkan dari persamaan (7) diketahui bahwa 𝛼_𝑖(𝑥) = 𝐴̃𝑖(0)𝑥0+ 𝐴̃𝑖(1)𝑥1 +

𝐴̃_𝑖(2)𝑥2_{+ ⋯ + 𝐴̃}

21 Perhatikan 𝜆_𝑖−1∑𝑖−2_𝑘=0𝐴̃_𝑖−1(𝑘)[( 1 𝑘+1) 𝑥 𝑘+1_{+ 𝑘! ∑} 𝑥𝑗𝑎𝑖 𝑘−𝑗+1 𝑗! 𝑘 𝑗=0 ], Jika 𝑘 = 0 → 𝜆_𝑖−1𝐴̃_𝑖−1(0)𝑥 + 𝜆_𝑖−1𝐴̃_𝑖−1(0)𝑎₁ 𝑘 = 1 → 𝜆_𝑖−1𝐴̃_𝑖−1(1)1₂𝑥2_{+ 𝜆} 𝑖−1𝐴̃𝑖−1(1)[𝑎𝑖2+ 𝑥𝑎𝑖], 𝑘 = 2 → 𝜆𝑖−1𝐴̃𝑖−1(2) 1 2𝑥 3_{+ 𝜆} 𝑖−1𝐴̃𝑖−1(2)2! [𝑎𝑖3+ 𝑥𝑎𝑖2+ 𝑥2𝑎𝑖 2! ]

dan seterusnya sehingga didapat 𝐴̃𝑖(1) = 𝜆𝑖−1[ 𝐴̃_𝑖−1(0)0! 𝑎_𝑖0_{+ 𝐴̃} 𝑖−1(1)1! 𝑎𝑖1+ 𝐴̃𝑖−1(2)2! 𝑎𝑖2+ ⋯ + 𝐴̃𝑖−1(𝑖 − 2) (𝑖 − 2)! 𝑎_𝑖𝑖−2 ] = 𝜆𝑖−1 ∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖𝑙 𝑖−2 𝑙=0 = 𝜆𝑖−1 𝑎_𝑖11!∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=0 𝐴̃𝑖(2) = 𝜆𝑖−1[𝐴̃𝑖−1(2)2! 𝑎_𝑖1 2! + 𝐴̃𝑖−1(3)3! 𝑎_𝑖2 2! + ⋯ + 𝐴̃𝑖−1(𝑖 − 2)(𝑖 − 2)! 𝑎_𝑖𝑖−3 2! ] = 𝜆𝑖−1 2! ∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖 𝑙−1 𝑖−2 𝑙=1 =𝜆𝑖−1 𝑎_𝑖22!∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=1 dan seterusnya 𝐴̃_𝑖(𝑘) = 𝜆𝑖−1 𝑎_𝑖𝑘𝑘!∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=𝑘−1 .

Pembuktian persamaan (10): Akan dibuktikan bahwa 𝐴̃𝑖(𝑖 − 1) = 𝜆𝑖−1

𝐴̃_𝑖−1 (𝑖 − 2) 𝑖 − 1 untuk 𝑖 = 1,2, … , 𝑛.

Bukti: Diketahui dari persamaan (9) bahwa untuk 𝑘 = 1,2, … , 𝑖 − 2 maka 𝐴̃_𝑖(𝑘) =

𝜆_𝑖−1

𝑎_𝑖𝑘𝑘!∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖 𝑙+1 𝑖−2

𝑙=𝑘−1 dengan memasukan nilai 𝑘 = 𝑖 − 1 pada persamaan

tersebut, maka 𝐴̃_𝑖(𝑖 − 1) =

𝜆

𝑖−1 𝑎_𝑖𝑖−1(𝑖 − 1)! ∑ 𝐴̃𝑖−1(𝑙)𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=𝑖−2 =

𝜆

𝑖−1 𝑎_𝑖𝑖−1(𝑖 − 1)!(𝑖 − 2)! 𝐴̃𝑖−1(𝑖 − 2)𝑎𝑖 𝑖−1 =

𝜆

𝑖−1 𝐴̃𝑖−1(𝑖 − 2)

𝑖 − 1

.

22

Lampiran 4 Pembuktian persamaan (11) Akan dibuktikan bahwa

𝐴̃_𝑖(0) = 1 + 𝐴̃_𝑖(1)𝑎_𝑖. Bukti: Dari persamaan (8) diketahui

𝐴̃𝑖(0) = 1 + 𝜆𝑖−1∑ 𝑙! 𝑎𝑖𝑙+1 𝑖−2

𝑙=0

𝐴̃𝑖−1(𝑙),

sedangkan dari persamaan umum 𝐴̃𝑖(𝑘) dengan mensubstitusi 𝑘 = 1,

𝐴̃_𝑖(1) =𝜆𝑖−1 𝑎_𝑖 ∑ 𝑙! 𝑎𝑖 𝑙+1 𝑖−2 𝑙=0 𝐴̃_𝑖−1(𝑙), sehingga 𝐴̃_𝑖(0) dapat disederhanakan menjadi

𝐴̃𝑖(0) = 1 + 𝜆𝑖−1∑ 𝑙! 𝑎𝑖𝑙+1 𝑖−2 𝑙=0 𝐴̃𝑖−1(𝑙) 𝐴̃_𝑖(0) = 1 + [𝜆𝑖−1 𝑎𝑖 ∑ 𝑙! 𝑎_𝑖𝑙+1 𝑖−2 𝑙=0 𝐴̃_𝑖−1(𝑙)] 𝑎_𝑖 𝐴̃𝑖(0) = 1 + 𝐴̃𝑖(1)𝑎𝑖. .

23 Lampiran 5 Pembuktian persamaan (13)

Akan dibuktikan bahwa

𝐴̃𝑖(𝑘) = (𝑘 + 1)𝑎𝑖𝐴̃𝑖(𝑘 + 1) +

𝜆_𝑖−1

𝑘 𝐴̃𝑖−1(𝑘 − 1).

Bukti: Diketahui dari persamaan (12) kita dapatkan persamaan 𝐴̃𝑖(𝑘 + 1)

𝐴̃𝑖(𝑘 + 1) = 𝜆_𝑖−1 (𝑘 + 1)! 𝑎_𝑖𝑘+1[ ∑ 𝑙! 𝑎𝑖𝑙+1 𝑖−2 𝑙=𝑘−1 𝐴̃𝑖−1(𝑙) − (k − 1)! 𝑎𝑖𝑘𝐴̃𝑖−1(𝑘 − 1)] 𝐴̃𝑖(𝑘 + 1) = 𝜆_𝑖−1 (𝑘 + 1)! 𝑎_𝑖𝑘+1 ∑ 𝑙! 𝑎𝑖𝑙+1 𝑖−2 𝑙=𝑘−1 𝐴̃𝑖−1(𝑙) − 𝜆𝑖−1 (𝑘 + 1)! 𝑎_𝑖𝑘+1(k − 1)! 𝑎𝑖𝑘𝐴̃𝑖−1(𝑘 − 1) 𝐴̃_𝑖(𝑘 + 1) = 𝜆𝑖−1 (𝑘 + 1)𝑘! 𝑎_𝑖𝑘_𝑎 𝑖 ∑ 𝑙! 𝑎_𝑖𝑙+1 𝑖−2 𝑙=𝑘−1 𝐴̃_𝑖−1(𝑙) − 𝜆𝑖−1 (𝑘 + 1)𝑘(𝑘 − 1)! 𝑎_𝑖𝑘_𝑎 𝑖 (𝑘 − 1)! 𝑎_𝑖𝑘_𝐴̃ 𝑖−1(𝑘 − 1) 𝐴̃𝑖(𝑘 + 1) = 𝜆_𝑖−1 (𝑘 + 1)𝑘! 𝑎_𝑖𝑘_𝑎 𝑖 𝐴̃_𝑖(𝑘) 𝜆𝑖−1 𝑎_𝑖𝑘𝑘! − 𝜆𝑖−1 (𝑘 + 1)𝑘(𝑘 − 1)! 𝑎_𝑖𝑘_𝑎 𝑖 (𝑘 − 1)! 𝑎_𝑖𝑘𝐴̃_𝑖−1(𝑘 − 1) 𝐴̃𝑖(𝑘 + 1) = 𝐴̃_𝑖(𝑘)𝑎_𝑖𝑘_𝑘! (𝑘 + 1)𝑘! 𝑎_𝑖𝑘_𝑎 𝑖 − 𝜆𝑖−1 (𝑘 + 1)𝑘(𝑘 − 1)! 𝑎_𝑖𝑘_𝑎 𝑖 (𝑘 − 1)! 𝑎_𝑖𝑘𝐴̃𝑖−1(𝑘 − 1) 𝐴̃_𝑖(𝑘 + 1) = 𝐴̃𝑖(𝑘) (𝑘 + 1)𝑎𝑖 − 𝜆𝑖−1 (𝑘 + 1)𝑘𝑎𝑖 𝐴̃_𝑖−1(𝑘 − 1).

Kemudian untuk mendapatkan 𝐴̃_𝑖(𝑘) kalikan kedua ruas dengan (𝑘 + 1)𝑎_𝑖 (𝑘 + 1)𝑎_𝑖𝐴̃_𝑖(𝑘 + 1) = 𝐴̃_𝑖(𝑘) −𝜆𝑖−1

𝑘 𝐴̃𝑖−1(𝑘 − 1) 𝐴̃_𝑖(𝑘) = (𝑘 + 1)𝑎_𝑖𝐴̃_𝑖(𝑘 + 1) +𝜆𝑖−1

24

Lampiran 6 Pembuktian persamaan (15), (16) dan (17) Pembuktian persamaan (15)

Akan dibuktikan bahwa

𝐵̃_𝑖(0) = 1 + 𝑎𝑖𝜆𝑖−1𝐵̃𝑖(1)

untuk 𝑖 = 1,2, … , 𝑛.

Bukti: Dari persamaan (11) diketahui 𝐴̃_𝑖(0) = 1 + 𝑎_𝑖𝐴̃_𝑖(1) , sedangkan dari definisi diketahui pula 𝐴̃𝑖(𝑘) =

𝜆𝑖−𝑘𝜆𝑖−𝑘+1…𝜆𝑖−1

𝑘! 𝐵̃𝑖(𝑘), 𝐴̃𝑖(0) = 𝐵̃𝑖(0) untuk 𝑘 > 0.

Substitusikan nilai 𝑘 = 1 pada persamaan tersebut menjadi 𝐴̃_𝑖(1) =𝜆𝑖−1 1! 𝐵̃𝑖(1) maka 𝐵̃𝑖(0) = 𝐴̃𝑖(0) = 1 + 𝑎𝑖𝐴̃𝑖(1) = 1 + 𝑎𝑖[ 𝜆𝑖−1 1! 𝐵̃𝑖(1)] = 1 + 𝑎_𝑖𝜆_𝑖−1𝐵̃_𝑖(1). Pembuktian persamaan (16)

Akan dibuktikan bahwa

𝐵̃𝑖(𝑘) = 𝑎𝑖𝜆𝑖−𝑘−1𝐵̃𝑖(𝑘 + 1) + 𝐵̃𝑖(𝑘 − 1)

untuk 0 < 𝑘 < 𝑖 − 1 dan 𝑖 = 1,2, … , 𝑛.

Bukti: Dari persamaan (13) diketahui 𝐴̃_𝑖(𝑘) = (𝑘 + 1)𝑎_𝑖𝐴̃_𝑖(𝑘 + 1) +

𝜆𝑖−1

𝑘 𝐴̃𝑖−1(𝑘 − 1), sedangkan dari pendefinisian diketahui juga bahwa 𝐴̃𝑖(𝑘) = 𝜆𝑖−𝑘𝜆𝑖−𝑘+1…𝜆𝑖−1 𝑘! 𝐵̃ (𝑘) untuk 𝑘 > 0, sehinggga 𝑖 𝐵̃_𝑖(𝑘) = 𝑘! 𝜆_𝑖−𝑘𝜆_{𝑖−𝑘+1}… 𝜆_𝑖−1 𝐴̃𝑖(𝑘) 𝐵̃_𝑖(𝑘) = 𝑘! 𝜆_𝑖−𝑘𝜆_{𝑖−𝑘+1}… 𝜆_𝑖−1 ((𝑘 + 1)𝑎𝑖𝐴̃𝑖(𝑘 + 1) + 𝜆𝑖−1 𝑘 𝐴̃𝑖−1(𝑘 − 1)) 𝐵̃_𝑖(𝑘) = 𝑘! 𝜆_𝑖−𝑘𝜆_{𝑖−𝑘+1}… 𝜆_𝑖−1 ((𝑘 + 1)𝑎𝑖( 𝜆_{𝑖−𝑘−1}𝜆_{𝑖−𝑘+1}… 𝜆_𝑖−1 (𝑘 + 1)! 𝐵̃𝑖(𝑘 + 1)) +𝜆𝑖−1 𝑘 ( 𝜆_{𝑖−1−𝑘+1}𝜆_{𝑖−𝑘+1}… 𝜆_𝑖−2 (𝑘 − 1)! 𝐵̃𝑖−1(𝑘 − 1))) 𝐵̃𝑖(𝑘) = 𝑘! (𝑘 + 1)𝑎_𝑖𝜆_{𝑖−𝑘−1} (𝑘 + 1)! 𝐵̃𝑖(𝑘 + 1) + 𝑘! 𝑘(𝑘 − 1)!𝐵̃𝑖−1(𝑘 − 1) 𝐵̃𝑖(𝑘) = 𝑘! (𝑘 + 1)𝑎𝑖𝜆𝑖−𝑘−1 (𝑘 + 1)𝑘! 𝐵̃𝑖(𝑘 + 1) + 𝑘(𝑘 − 1)! 𝑘(𝑘 − 1)!𝐵̃𝑖−1(𝑘 − 1) 𝐵̃𝑖(𝑘) = 𝑎𝑖𝜆𝑖−𝑘−1𝐵̃ (𝑘 + 1) + 𝐵̃𝑖 𝑖−1(𝑘 − 1). Pembuktian persamaan (17) Akan dibuktikan bahwa

𝐵̃𝑖(𝑖 − 1) = 𝐵̃𝑖−1(𝑖 − 2)

untuk 𝑖 = 1,2, … . , 𝑛.

25 Masukkan nilai 𝑘 = 𝑖 − 1 menjadi

𝐵̃𝑖(𝑖 − 1) = 𝑎𝑖𝜆𝑖−𝑖+1−1𝐵̃𝑖(𝑖 − 1 + 1) + 𝐵̃𝑖−1(𝑖 − 1 − 1)

𝐵̃𝑖(𝑖 − 1) = 𝑎𝑖𝜆0𝐵̃𝑖(𝑖) + 𝐵̃𝑖−1(𝑖 − 2)

𝐵̃𝑖(𝑖 − 1) = 𝐵̃𝑖−1(𝑖 − 2).

26

Lampiran 7 Pembuktian persamaan (18), (19), dan (20) Pembuktian persamaan (18)

Akan dibuktikan bahwa

𝐵̃_𝑖(0) = 1.

Bukti: Karena 𝛼0(𝑥) = 0 maka dari persamaan (7) 𝛼𝑖(𝑥) = ∑𝑖−1𝑘=0𝐴̃𝑖(𝑘)𝑥𝑘

didapatkan 𝛼₁(𝑥) = 1 sehingga 𝛼₁(𝑥) = ∑1−1𝐴̃_𝑖(𝑘)𝑥𝑘 𝑘=0 𝛼₁(𝑥) = ∑ 𝐴̃_𝑖(𝑘)𝑥𝑘 0 𝑘=0 𝛼₁(𝑥) = 𝐴̃_𝑖(0)𝑥0 𝛼₁(𝑥) = 𝐴̃_𝑖(0) 𝐴̃_𝑖(0) = 1

Diketahui sebelumnya 𝐴̃_𝑖(0) = 𝐵̃_𝑖(0), karena 𝐴̃_𝑖(0) = 1 maka 𝐵̃_𝑖(0) = 1. Pembuktian persamaan (19)

Akan dibuktikan bahwa

𝐵̃_𝑖(𝑖 − 1) = 1 untuk 𝑖 = 1,2, … , 𝑛.

Bukti :

i. Basis induksi untuk 𝑖 = 1 akan dibuktikaan persamaan tersebut benar. 𝑖 = 1 → 𝐵̃_𝑖(1 − 1) = 𝐵̃_𝑖(0) = 1. Benar berdasarkan persamaan (18). ii. Hipotesis induksi anggap benar untuk 𝑖 = 𝑚

𝐵̃𝑚(𝑚 − 1) = 1

iii. Langkah induksi akan dibuktikan untuk 𝑖 = 𝑚 + 1 → 𝐵̃_𝑚+1(𝑚) = 1 benar

𝐵̃𝑚+1(𝑚) = 𝐵̃𝑚+1−1(𝑚 − 1) berdasarkan persamaan (6)

= 𝐵̃_𝑚(𝑚 − 1) = 1

Pembuktian persamaan (20) Akan dibuktikan bahwa

𝐵̃_𝑖(𝑖 − 2) = 1 + 𝜆1∑ 𝑎𝑙 𝑖

𝑙=2

dengan 1 ≤ 𝑖 ≤ 𝑛.

Bukti: Diketahui dari persamaan (16) bahwa 𝐵̃_𝑖(𝑘) = 𝑎_𝑖𝜆_{𝑖−𝑘−1}𝐵̃_𝑖(𝑘 + 1) + 𝐵̃_𝑖−1(𝑘 − 1). Substitusi 𝑘 = 𝑖 − 2 pada persamaan diperoleh

𝐵̃_𝑖(𝑖 − 2) = 𝑎𝑖𝜆𝑖−(𝑖−2)−1𝐵̃𝑖(𝑖 − 1) + 𝐵̃𝑖−1(𝑖 − 3) = 𝑎_𝑖𝜆₁+ 𝐵̃_𝑖−1(𝑖 − 3) = 𝑎₁𝜆₁+ 𝑎_𝑖−1𝜆₁𝐵̃_𝑖−1(𝑖 − 2) + 𝐵̃𝑖−2(𝑖 − 4) = 𝜆₁(𝑎₁+ 𝑎_𝑖−1) + (𝑎_𝑖−2𝜆₁+ 𝐵̃_𝑖−3(𝑖 − 5)) = 𝜆1(𝑎1+ 𝑎𝑖−1+ 𝑎𝑖−2) + 𝐵̃𝑖−3(𝑖 − 5) .

27 .

.

= 𝜆₁(𝑎1+ 𝑎𝑖−1+ 𝑎𝑖−2+ ⋯ + 𝑎3) + 𝐵̃2(0) buat seperti definisi

Dari defisini diketahui bahwa 𝐴̃_𝑖(0) = 𝐵̃𝑖(0), maka

𝐵̃₂(0) = 𝐴̃₂(0) = 1 + 𝑎2𝐴̃2(1) = 1 + 𝑎2[ 𝜆₁ 𝑎2 (0! 𝑎2𝐴̃1(0))] = 1 + 𝑎2𝜆1 sehingga diperoleh 𝐵̃_𝑖(𝑖 − 2) = 𝜆1(𝑎𝑖 + 𝑎𝑖−1+ 𝑎𝑖−2+ ⋯ + 𝑎3+ 𝑎2) + 1 = 1 + 𝜆₁∑ 𝑎_𝑙 𝑖 𝑙=2 .

28

Lampiran 8 pembuktian persamaan (21) Akan dibuktikan bahwa

𝐵̃_𝑖(𝑘) = 1 + 𝜆𝑖−𝑘−1 ∑ 𝑎𝑙 𝑖 𝑙=𝑖−𝑘 + 𝜆_{𝑖−𝑘−2}𝜆_{𝑖−𝑘−1} ∑ ∑ 𝑎_𝑙1𝑎_𝑙2 𝑙1 𝑙2=𝑖−𝑘−1 𝑖 𝑙1=𝑖−𝑘 + ⋯ + 𝜆₁𝜆₂… 𝜆_{𝑖−𝑘−1} ∑ ∑ … 𝑙1 𝑙2=𝑖−𝑘−1 𝑖 𝑙1=𝑖−𝑘 ∑ 𝑎_𝑙1𝑎_𝑙2 𝑙1−𝑘−2 𝑙𝑖−𝑘−1=2 … 𝑎_{𝑙𝑖−𝑘−1}, dengan 𝜆_𝑝= 0 untuk 𝑝 ≤ 0 dan 1 ≤ 𝑖 ≤ 𝑛, 0 ≤ 𝑘 ≤ 𝑖 − 1.

Bukti: Dari persamaan (16) bahwa 𝐵̃_𝑖(𝑘) = 𝑎_𝑖𝜆_{𝑖−𝑘−1}𝐵̃_𝑖(𝑘 + 1) + 𝐵̃_𝑖(𝑘 − 1) sedangkan diketahui pula bahwa 𝐵̃_𝑖(𝑖 − 2) = 1 + 𝜆_𝑖∑𝑖_𝑙=2𝑎_𝑙 , sehingga

𝐵̃_𝑖(𝑖 − 3) = 𝑎𝑖𝜆𝑖−(𝑖−3)−1𝐵̃𝑖(𝑖 − 2) + 𝐵̃𝑖−1(𝑖 − 4) = 𝑎_𝑖𝜆₂(1 + 𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 ) + 𝑎_𝑖−1𝜆₂𝐵̃_𝑖−1(𝑖 − 3) + 𝐵̃𝑖−2(𝑖 − 5) = 𝑎_𝑖𝜆₂+ 𝑎_𝑖𝜆₂𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 + 𝑎_𝑖−1𝜆₂(1 + 𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 ) + 𝑎_𝑖−2𝜆₂(1 + 𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 ) + 𝐵̃_𝑖−3(𝑖 − 6) = 𝑎_𝑖𝜆₂+ 𝑎_𝑖𝜆₂𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 + 𝑎_𝑖−1𝜆₂+ 𝑎_𝑖−1𝜆₂𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 + 𝑎_𝑖−2𝜆₂+ 𝑎_𝑖−2𝜆₂𝜆_𝑖∑ 𝑎_𝑙 𝑖 𝑙=2 + 𝐵̃𝑖−3(𝑖 − 6) = 𝜆₂(𝑎_𝑖 + 𝑎_𝑖−1+ 𝑎_𝑖−2+ ⋯ + 𝑎₄) + 𝜆₁𝜆₂(𝑎_𝑖 + 𝑎_𝑖−1+ 𝑎_𝑖−2+ ⋯ + 𝑎₄) ∑ 𝑎_𝑙 𝑖 𝑙=2 + 𝐵̃₃(0) (a)

Dari definisi diketahui bahwa 𝐴̃𝑖(0) = 𝐵̃𝑖(0), maka

𝐵̃₃(0) = 𝐴̃₃(0) = 1 + 𝑎3𝐴̃3(1) = 1 + 𝑎3[ 𝜆₂ 𝑎₃(0! 𝑎3𝐴̃2(0) + 1! 𝑎3 2_𝐴̃ 2(1))] = 1 + 𝜆₂[𝑎₃(1 + 𝑎₂𝜆₁+ 𝑎₃2𝜆₁] = 1 + 𝑎₃𝜆₂+ 𝑎₂𝑎₃𝜆₁𝜆₂+ 𝑎₃2_𝜆 1𝜆2 (b)

Dari (a) dan (b) didapat

𝐵̃_𝑖(𝑖 − 3) = 1 + 𝜆₂(𝑎_𝑖 + 𝑎_𝑖−1+ ⋯ + 𝑎₃) + 𝜆₁𝜆₂(𝑎₂𝑎₃)(𝑎₃) + 𝜆₁𝜆₂(𝑎_𝑖+ 𝑎_𝑖−1 + ⋯ + 𝑎₄) ∑ 𝑎_𝑙 𝑖 𝑙=2 = 1 + 𝜆2∑ 𝑎𝑙 𝑖 𝑙=3 + 𝜆1𝜆2 ∑ ∑ 𝑎𝑙1 𝑙1 𝑙2=2 𝑎𝑙2 𝑖 𝑙1=3

29 𝐵̃_𝑖(𝑖 − 4) = 1 + 𝜆₃∑ 𝑎_𝑙 𝑖 𝑙=4 + 𝜆₂𝜆₃ ∑ ∑ 𝑎_𝑙1 𝑙1 𝑙2=3 𝑎_𝑙2 𝑖 𝑙1=4 + 𝜆1𝜆2𝜆3 ∑ ∑ ∑ 𝑎𝑙1 𝑖 𝑙3=2 𝑎𝑙2 𝑙1 𝑙2=3 𝑎𝑙3 𝑖 𝑙1=4 . . . 𝐵̃𝑖(𝑖 − 𝑛) = 1 + 𝜆𝑛−1∑ 𝑎𝑙 𝑖 𝑙=𝑛 + 𝜆_𝑛−2𝜆₋₁ ∑ ∑ 𝑎_𝑙1 𝑙1 𝑙2=𝑛−1 𝑎_𝑙2+ ⋯ 𝑖 𝑙1=𝑛 + 𝜆₁… 𝜆_𝑛−1 ∑ ∑ … 𝑙1 𝑙2=𝑛−1 𝑖 𝑙1=𝑛 ∑ 𝑎_𝑙1… 𝑎_𝑙𝑛−1 𝑙𝑛−2 𝑙𝑛−1=2

Ganti indeks 𝑘 = 𝑖 − 𝑛 → 𝑛 = 𝑖 − 𝑘 pada persamaan (*) menjadi : 𝐵̃𝑖(𝑘) = 1 + 𝜆𝑖−𝑘−1 ∑ 𝑎𝑙 𝑖 𝑙=𝑖−𝑘 + 𝜆𝑖−𝑘−2𝜆𝑖−𝑘−1 ∑ ∑ 𝑎𝑙1𝑎𝑙2 𝑙1 𝑙2=𝑖−𝑘−1 𝑖 𝑙1=𝑖−𝑘 + ⋯ + 𝜆1𝜆2… 𝜆𝑖−𝑘−1 ∑ ∑ … 𝑙1 𝑙2=𝑖−𝑘−1 𝑖 𝑙1=𝑖−𝑘 ∑ 𝑎𝑙1𝑎𝑙2 𝑙1−𝑘−2 𝑙𝑖−𝑘−1=2 … 𝑎𝑙𝑖−𝑘−1. (*)

30

Lampiran 9 Contoh program perhitungan peluang kebangkrutan

31 Lampiran 10 Contoh program pembangkitan data

33 Lampiran 11 Hasil ilustrasi proses keuntungan

Modal Awal (x) Delta {Δ𝑖} 𝑐𝑖 Klaim {𝑍𝑖} Keuntungan {𝑋(𝑡)} 10 2.0858700 1.0 1.3255500 10.7603200 0.7935190 1.2 4.0311600 7.6813828 1.5516700 1.5 0.4966790 9.5122088 0.4169070 2.0 0.0238875 10.3221353 2.5182600 1.0 4.6155300 8.2248653 0.3276160 1.5 1.0950200 7.6212693 2.6542000 2.0 0.6394340 12.2902353 2.4944100 1.0 1.6746400 13.1100053 0.5906240 1.0 0.9832850 12.7173443 0.3814550 2.0 1.9525600 11.5276943 0.1196910 1.5 0.1279180 11.5793128 2.2540700 1.2 0.5120430 13.7721538 1.1176900 1.5 0.7817000 14.6669888 0.7108830 1.2 0.2358690 15.2841794 0.4825790 1.0 1.1175000 14.6492584 1.7040000 1.6 1.9660100 15.4096484 3.1860700 1.1 0.3517730 18.5625524 3.0431200 2.0 0.5440140 24.1047784 2.3485900 1.2 2.4377400 24.4853464 0.3036270 1.0 1.0765300 23.7124434 2.7733000 1.3 2.2287900 25.0889434 1.0447400 1.1 0.8535380 25.3846194 0.0581612 1.0 0.2795260 25.1632546 0.8096410 1.0 0.1089480 25.8639476 1.0976600 1.4 0.5422330 26.8584386 1.1039800 1.3 0.2460170 28.0475956 0.2573420 1.0 0.9939820 27.3109556 0.0287411 1.0 0.6455440 26.6941527 0.9430240 1.1 0.4999180 27.2315611 0.2110240 1.2 0.8347420 26.6500479 Modal Awal (x) Delta {Δ𝑖} 𝑐𝑖 Klaim {𝑍𝑖} Keuntungan {𝑋(𝑡)} 5 0.639588 0.8 0.303637 5.208033 1.024090 0.5 2.773300 2.946778 1.536400 0.4 0.058162 3.503176 0.943477 0.3 0.214710 3.571510

34 2.234990 0.5 0.365886 4.323119 3.932030 0.7 1.103980 5.971560 1.055320 0.1 7.665150 -1.588059 1.088030 0.2 0.009580 -1.380033 2.437740 0.5 0.471512 -0.632675 2.153070 0.2 0.070341 -0.272402

35

RIWAYAT HIDUP

Penulis dilahirkan di Kuningan pada tanggal 13 Oktober 1991. Penulis merupakan puteri pertama dari dua bersaudara dari Bapak Wawan dan Ibu Eti Kurniati. Tahun 2010 penulis lulus dari SMA Negeri 1 Kuningan dan pada tahun yang sama penulis diterima sebagai mahasiswi Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis tercatat sebagai mahasiswi Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA). Selain itu penulis juga tercatat merupakan mahasiswi yang beruntung mendapatkan Beasiswa Bidik Misi dari Pemerintah.

Selama mengikuti perkuliahan, penulis aktif di berbagai kegiatan organisasi dan kepanitiaan. Penulis aktif tergabung dalam kepungurusan Gugus Mahasiswa Matematika (Gumatika) selama dua periode yaitu 2012 dan 2013. Selama dua tahun tersebut, penulis diamanahi sebagai bendahara divisi Informasi dan Komunikasi dan Staf Divisi Sosial Lingkungan. Selain itu, penulis juga aktif dalam kegiatan kepanitiaan, di antaranya menjadi anggota divisi Lead Oficcer (LO) dari kegiatan Pesta Sains Nasional, bendahara divisi konsumsi dari Mathematics Camp tahun 2011, anggota divisi Master of Discipline (MOD) dalam kegiatan Masa Perkenalan Fakultas tahun 2012, anggota MOD dalam Masa Perkenalan Departemen dua periode tahun 2012 dan 2013, bendahara Divisi Kesekretariatan dalam acara IPB

Mathematics Challenge (IMC) pada tahun 2013.

Penulis juga berkesempatan magang di Bank Indonesia pada bulan Juli-Agustus 2013. Prestasi yang pernah diraih penulis dalam bidang olahraga dan seni adalah menjadi juara 2 bola basket tingkat fakultas dalam acara Gebyar Semarak Bidik Misi pada tahun 2012 dan menjadi juara 3 dalam lomba bola basket pada acara SPIRIT FMIPA pada tahun 2013.