3
BAB 2
LANDASAN TEORI
2.1.Konsep Dasar Graf
Definisi 2.1.1 Graf G didefinisikan sebagai pasangan himpunan (V, E), yang dalam
hal ini:
V = himpunan tidak kosong dari simpul-simpul (vertices atau node)
={v1, v2, …, vn
E= himpunan sisi (edges atau arcs) yang menghubungkan sepasang simpul
} dan
={e1, e2, … ,en
Atau dapat ditulis singkat notasi G = (V, E). }
Definisi 2.1.1 menyatakan bahwa V tidak boleh kosong, sedangkan E boleh kosong.
Jadi sebuah graf dimungkinkan tidak mempunyai jalur satu buah pun, tetapi
simpulnya hanya ada minimal satu. Graf yang hanya mempunyai satu buah simpul
tanpa sebuah jalur dinamakan graf trivial. (Munir, 2003)
Contoh dari graf G
1
4
Gambar 2.1. Graf G
Gambar 2.1. memperlihatkan graf dengan himpunan simpul V dan himpunan jalur E
dimana: V = {1, 2, 3, 4 }
E = {(1, 2), (1, 3), (2, 3), (2, 4), (3, 4)}
2.2. Jenis-jenis Graf
Graf dapat dikelompokkan menjadi beberapa kategori (jenis) bergantung pada
sudut pandang pengelompokkanya.
Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graf, maka secara
umum graf dapat digolongkan menjadi dua jenis:
1. Graf sederhana (Simple Graf)
Graf yang tidak mengandung gelang maupun sisi ganda dinamakan graf
sederhana.
2. Graf tak-sederhana (Unsimple-Graf)
Graf yang mengandung sisi ganda atau gelang dinamakan graf tak-sederhana.
Berdasarkan jumlah simpul pada suatu graf, maka secara umum graf dapat
digolongkan menjadi dua jenis :
1. Graf berhingga
Graf berhingga adalah graf yang jumlah simpulnya, n, berhingga.
2. Graf tak-berhingga
Graf yang jumlah simpulnya, n, tidak berhingga banyaknya disebut graf tak
berhingga.
Berdasarkan orientasi arah pada sisi maka secara umum graf dibedakan atas dua
jenis :
1. Graf tak berarah
Graf yang sisinya tidak mempunyai orientasi arah disebut graf tak-berarah. Pada
graf tak-berarah, urutan pasangan simpul yang dihubungkan oleh sisi tidak
2. Graf berarah
Graf yang setiap sisinya diberikan orientasi arah disebut sebagai graf berarah.
Pada graf berarah, (vj , vk) (vk , vj). untuk busur (vj , vk), simpul vj dinamakan
simpul asal (initial vertex) dan simpul vk dinamakan simpul terminal (terminal
vertex).
2.3. Terminologi Dasar
Definisi 2.3.1 Walk
Walk dengan panjang n dari v ke w adalah barisan v0, e1, v1, e2, v2, …, vn-1, en,
vn dengan v0 = v ; vn = w ; vi-1 ; dan vi adalah simpul-simpul ujung jalur ei. (Siang,
2006)
Definisi 2.3.2 Path
Path dengan panjang n dari v ke w adalah walk dari v ke w yang semua
jalurnya berbeda. Path dari v ke w dituliskan sebagai (v = v0, e1, v1, e2, v2, …, vn-1, en,
vn = w) dengan ei ≠ ej untuk i ≠ j. (Siang, 2006)
Path dengan panjang n dari v ke w adalah path dari v ke w yang semua
simpulnya berbeda. Path dari v ke w berbentuk (v = v0, e1, v1, e2, v2, …, vn-1, en, vn =
w) dengan ei≠ ej untuk i ≠ j dan vk ≠ vm untuk k ≠ m.
Definisi 2.3.3 Sirkuit (Cycle)
Sirkuit dengan panjang n adalah path yang dimulai dan diakhiri pada simpul
yang sama. Sirkuit adalah path yang berbentuk (v0, e1, v1, e2, v2, …, vn-1, en, vn)
dengan v0 = vn. (Siang, 2006)
Sirkuit (sikel) dengan panjang n adalah path yang dimulai dan diakhiri pada
simpul yang sama. Sirkuit adalah path yang berbentuk (v0, e1, v1, e2, v2, …, vn-1, en,
10
Definisi 2.3.4 Connected Graf dan Disconnected Graf
Suatu graf G dikatakan connected graf jika untuk setiap pasangan vertex di
dalam G terdapat paling sedikit satu path. Sebaliknya jika dalam suatu graf G ada
pasangan vertex yang tidak mempunyai path penghubung maka graf yang demikian
dinamakan disconnected graf.
Definisi 2.3.5 Graf Berbobot dan Graf Berlabel
Graf berbobot adalah graf yang setiap sisinya diberi sebuah bobot sedangkan
graf berlabel adalah graf yang tidak memiliki bobot.
Contoh dari graf berbobot:
Gambar 2.2 Graf berbobot pada Graf tak berarah
Gambar 2.3 Graf berbobot pada graf berarah
2.4. Optimasi
2.4.1. Pengertian Optimasi
Optimasi ialah suatu proses untuk mencapai hasil yang ideal atau optimal
(nilai efektif yang dapat dicapai). Dalam disiplin matematika optimasi merujuk pada
tidak melanggar batasan-batasan yang ada yang paling mempunyai nilai tujuan
terbesar atau terkecil, tergantung dari fungsi tujuannya yaitu maksimal atau minimal.
(Hillier and Lieberman, 2005 :35).
Solusi Optimal adalah solusi fisibel yang memberikan nilai “terbaik” bagi
fungsi tujuannya. “Terbaik” di sini berarti nilai terbesar atau terkecil, bergantung pada
apakah tujuanya maksimasi atau minimasi. (Dimyati, 1987: 28).
2.4.2. Nilai Optimal
Nilai optimal adalah nilai yang paling menguntungkan, terbaik & tertinggi.
(Departemen Pendidikan dan Kebudayaan. 1995: 705).
Sebuah sumber dan tujuan diwakili dengan sebuah simpul. Busur yang
menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman barang
tersebut. Jumlah penawaran di sumber i adalah ai dan permintaan di tujuan j adalah bj
. Biaya unit transportasi antara sumber i dan j adalah cij. Anggap xij
Minimumkan : z = ∑��=1∑��=1������
mewakili jumlah
barang yang dikirimkan dari sumber i ke tujuan j, maka model program linier yang
mewakili masalah transportasi ini diketahui secara umum sebagai berikut :
Dengan batasan : ∑��=1��� ≤ aij; �= 1,2, … ,�
∑��=1��� ≥ bj; j = 1,2, … , n
Kelompok batasan pertama menetapkan bahwa jumlah pengiriman dari
sebuah sumber tidak dapat melebihi penawarannya. Demikian pula kelompok batasan
kedua mengharuskan bahwa jumlah pengiriman ke sebuah tujuan harus memenuhi
permintaanya. Model yang baru digambarkan diatas menyiratkan bahwa penawaran
total ∑��=1�� harus setidaknya sama dengan permintaan total ∑��=1��. Ketika
penawaran total sama dengan permintaan total ∑��=1�� = ∑��=1��, formulasi yang
dihasilkan disebut Model Transportasi Berimbang (balanced transportation model).
Model ini berbeda dengan model di atas hanya dalam fakta bahwa semua batasan
� ��� �
�=1
= ��; � = 1,2, … ,�
� ��� �
�=1
= ��; � = 1,2, … ,�
2.5.Travelling Salesman Problem (TSP)
2.5.1. Sejarah Permasalahan Travelling Salesman Problem (TSP)
Permasalahan matematika tentang Travelling Salesman Problem
dikemukakan pada tahun 1800 oleh matematikawan Irlandia William Rowan
Hamilton dan matematikawan Inggris Thomas Penyngton. Bentuk umum dari
persoalan TSP pertama kali dipelajari oleh para matematikawan mulai tahun1930 –an
oleh Karl Menger di Vienna dan Harvard. Persoalan tersebut kemudian dikembangkan
oleh Hassler Whitney dan Merril Flood di Princeton. (Filman Ferdinan. 2006).
Dekripsi persoalannya adalah sebagai berikut: diberikan sejumlah kota dan
jarak antar kota, tentukan sirkuit terpendek yang harus dilalui oleh seorang pedagang
bila pedagang itu berangkat dari sebuah kota asal dan menyinggahi setiap kota tepat
satu kali dan kembali lagi ke kota asal keberangkatan. Kota dapat dinyatakan sebagai
sebuah simpul graf, sedangkan sisi menyatakan jalan yang menghubungkan antara dua
kota. Bobot pada sisi menyatakan jumlah antara dua buah kota. Persoalan ini adalah
persoalan yang menentukan sirkuit Hamilton dengan sisi memiliki bobot minimum
2.5.2. Pengertian Travelling Salesman Problem
Travelling Salesman Problem adalah permasalahan dimana seorang salesman
harus mengunjungi semua kota dimana tiap kota hanya dikunjungi sekali dan dia
harus mulai dari dan kembali ke kota asal. Tujuannya adalah menentukan rute dengan
jarak total atau biaya yang paling minimum. (Aulia Rahma Amin. 2006).
Travelling Salesman Problem berhubungan dengan pencarian rute terpendek
atau rute terdekat pada n-kota, dimana setiap kota hanya dikunjungi sekali. Beberapa
metode yang digunakan dalam menyelesaikan masalah Travelling Salesman Problem
yaitu algoritma Branch and Bound dan algoritma Nearest Neighbor . (Hamdy A.
Taha. 2007: 381). Secara khusus didefinisikan :
2.6. Algoritma dalam Travelling Salesman Problem
2.6.1. Kompleksitas Algoritma
Algoritma adalah urutan langkah-langkah penyelesaian masalah secara
sistematis. Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus
(efisien). Kemangkusan algoritma diukur dari berapa jumlah waktu dan ruang memori
yang dibutuhkan untuk menjalankan. Algoritma yang mangkus adalah algoritma yang
meminimumkan kebutuhan waktu dan ruang. Ada dua macam kompleksitas
algoritma, yaitu kompleksitas waktu dan kompleksitas ruang. Kompleksitas waktu
diukur dari jumlah tahapan komputasi yang dibutuhkan untuk menjalankan algoritma
sebagai fungsi dari ukuran masukan n.
Untuk membuktikan kompleksitas kedua algoritma di atas maka kita harus
mengetahui teori yang mendukung yaitu:
Definisi 2.6.1. T(n) = O (f(n)) yang artinya T (n) berorde paling besar f(n). bila
terdapat tetapan c dan n0 sedemikian sehingga T(n) ≤ c (f(n)) untuk n ≥ n0.
Arti dari definisi di atas adalah jika sebuah algoritma mempunyai waktu
asimptotik O(f(n)), maka jika n dibuat semakin besar waktu yang dibutuhkannya tidak
2.6.2. Algoritma Branch and Bound
Algoritma Branch and Bound diusulkan pertama kali oleh A. Land dan G.
Doig pada tahun 1960. Sebenarnya metode ini dibuat untuk pemograman linier (linier
programming). Namun kenyataanya metode ini mampu menyelesaikan permasalahan
seperti Travelling Salesman Problem (TSP) dan beberapa masalah lain. Metode ini
menggunakan pohon pencarian (search tree), setiap simpul di pohon merupakan
representasi dari sejumlah kemungkinan solusi dari Travelling Salesman Problem
(TSP). Metode ini hanya dapat digunakan untuk masalah optimasi saja (optimazion
problem). Algoritma ini memiliki kompleksitas algoritma (n-1)!, dimana n adalah
jumlah kota. Berikut ini merupakan langkah-langkah penyelesaian dengan Branch and
Bound :
1. Gambarkan problem dengan diagraph G = (V,E).
2. Cij
dimana C
= nilai (cost) pada edge (i,j)
ij
3. Dengan definisi nilai (cost) di atas, bangun Cost Matrix dari TSP.
= ∞, jika tidak ada edge antara i dan j.
4. Lakukan reduksi terhadap Cost Matrix , di dapat Reduced Cost Matrix.
5.Gunakan fungsi pembatas (bound) untuk membangun Search Tree dari Reduced
Cost Matrix.
6. Dan seterusnya hingga didapat solusi yang diinginkan.
Pada n > 10, Algoritma di atas tidak dapat dikerjakan secara manual sehingga
pengerjaanya dilakukan dengan bantuan software Quantitative System (QS).
2.6.3 Algoritma Nearest Neighbor
Pada algoritma Nearest Neighbor, solusi dari masalah Travelling Salesman
dengan yang terdekat. Node hanya ditambahkan kemudian dikaitkan dengan node
terdekat dan proses berlanjut sampai tur terbentuk. Komplksitas algoritma ini memang
sangat mengangumkan yaitu O(n), tetapi hasil yang didapat bisa sangat jauh dari hasil
yang optimal. Berikut ini merupakan langkah-langkah penyelesaian Nearest Neighbor
:
a. Buat peta aliran yang menggambarkan letak-letak outlet penjualan beserta jarak
antar oulet.
b. Proses pengerjaan dengan melihat outlet dengan jarak terpendek. Setiap mencapai
satu outlet, algoritma ini akan memilih outlet selanjutnya yang belum dikunjungi
dan memiliki jarak yang paling minimum.
c. Perhitungan nilai optimal dengan menjumlah jarak dari awal sampai akhir
perjalanan.
Algoritma Nearest Neighbor dikerjakan dengan menggunakan Microsoft
Excel dengan mencari function MIN.
2.7. Contoh :
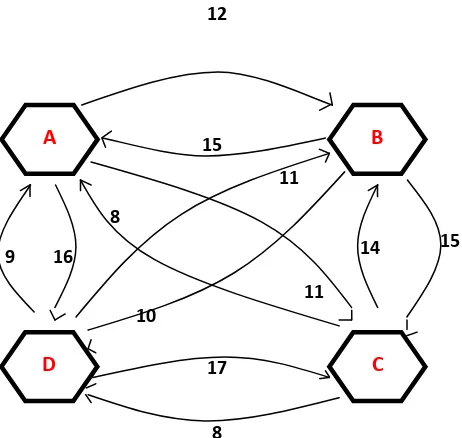
Diberikan graf berbobot G = (V, E) dan sebuah simpul awal A. Misalkan simpul
pada graf dapat merupakan kota, sedangkan sisi menyatakan jalan yang
menghubungkan dua buah kota. Bobot sisi graf dapat menyatakan jarak antara dua
buah kota. Tentukan rute optimal dari simpul A ke simpul D pada graf berbobot di
15
Gambar 2.4 Contoh Soal Masalah TSP
a. Penyelesaian dengan Algoritma Branch and Bound:
Bentuk Matriks: �
1. Reduced Cost Matrix (RCM)
a. Untuk setiap baris, cari nilai terkecil, nyatakan dengan c(i). Kurangi semua
nilai di baris itu dengan c(i).
b. Untuk setiap kolom, cari nilai terkecil, nyatakan dengan c(j). Kurangi semua
nilai di kolom itu dengan c(j).
c. Jumlahkan total semua nilai c(i) dan c(j) menjadi nilai R (total reduction).
Nilai ini adalah total nilai yang berhasil direduksi/dikurangi
2. Perhitungan RCM
A B
3. Langkah Membangun Search Tree
a.Pada saat Space Tree dimulai, nilai b untuk root node adalah nilai R untuk
RCM root node. Nilai u adalah ∞.
b.Setiap kali E-node yang baru dibuka, akan dihitung RCM untuk node tersebut.
c. Cara membuat RCM baru untuk node (i,j):
• RCM baru dibuat berdasarkan RCM dari parent node • Beri warna merah pada elemen di posisi (i,j)
• Ubah seluruh nilai di baris i menjadi ∞, beri warna biru
• Ubah seluruh nilai di kolom j menjadi ∞, beri warna biru
• Ubah elemen di posisi (j,1) menjadi ∞, beri warna ungu
• Lakukan reduksi matriks, jumlahkan seluruh nilai yang berhasil direduksi menjadi nilai R
d.Dengan dihitungnya RCM, maka bisa dihitung nilai b untuk root tersebut
dengan rumus :
• b(i,j) = b(parent) + c(i,j) of parent RCM + R (new RCM)
• c(i,j) adalah nilai elemen (i,j) dari parent RCM (lokasinya ditandai
dengan warna hijau di new RCM)
e.Dari semua E-node yang telah dihitung RCM-nya, dipilih yang memiliki cost b
paling kecil (Least Cost B&B). Node yang dipilih akan dibuka dan
menghasilkan E-node baru. Proses ini merupakan proses Branch.
f. Ketika E-node terbawah dibuka (diitemukan kandidat solusi), maka nilai u
diset menjadi nilai b dari node terbawah. Kemudian diperiksa apakah nilai b
terkecil berikutnya dari seluruh tree ada yang bernilai lebih kecil dari u. Semua
E-node yang memiliki nilai b > u dinyatakan sebagai D-node. Proses
pembuatan Space Tree dilanjutkan dari E-node yang tersisa. Inilah yang
dinamakan proses Bound.
g.Jika tidak ada, maka jalur dari root menuju E-node terakhir merupakan solusi
Gambar 2.5 Proses Branch and Bound
Gambar 2.6 Proses Branch and Bound
15
11
8 11
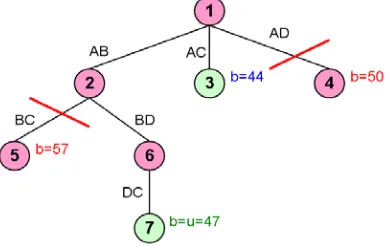
Gambar 2.8 Solusi dengan Branch and Bound
Dari hasil di atas dapat dilihat bahwa sirkuit yang dipilih adalah : A-C-B-D-A
Dengan total jarak tempuh adalah 11+14+10+9 = 44
b. Penyelesaian dengan Nearest Neighbor
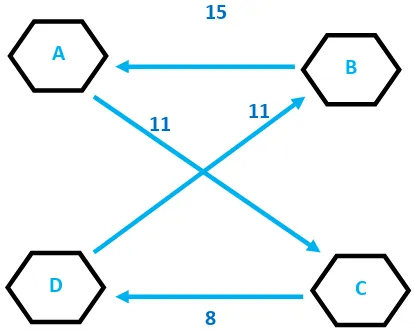
Gambar 2.9 Solusi dengan Nearest Neighbor
Dari hasil di atas dapat dilihat bahwa rute yang dipilih adalah : A-C-D-B-A
Dengan total jarak tempuh adalah 11+8+11+15 = 45
A
B