PENDUGAAN HAZARD RATE GEMPA DI PROVINSI ACEH DENGAN METODE SINGLE DECREMENT IKHSAN MAULIDI

PENDUGAAN HAZARD RATE GEMPA DI PROVINSI ACEH

DENGAN METODE SINGLE DECREMENT

IKHSAN MAULIDI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2014

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Pendugaan Hazard

Rate Gempa di Provinsi Aceh dengan Metode Single Decrement adalah benar

karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Januari 2014

Ikhsan Maulidi

ABSTRAK

IKHSAN MAULIDI. Pendugaan Hazard Rate Gempa di Provinsi Aceh dengan Metode Single Decrement. Dibimbing oleh I WAYAN MANGKU dan HADI SUMARNO.

Hazard rate memegang peranan penting dalam prakiraan kemunculan

gempa. Jika hazard rate diketahui maka sebaran kepekatan bersama kemunculan gempa dapat diketahui. Oleh karena itu diperlukan suatu model penduga hazard

rate yang akurat untuk menduga nilai hazard rate. Dalam karya ilmiah ini dibahas

suatu metode untuk menduga hazard rate di titik 𝑡0. Metode yang digunakan adalah metode single decrement. Ada dua pendekatan yang dapat digunakan untuk menduga hazard rate dengan menggunakan metode single decrement, yaitu pendekatan likelihood dan pendekatan momen. Pada pendekatan likelihood dibutuhkan asumsi sebaran waktu tunggu kemunculan gempa. Dalam karya ilmiah ini sebaran waktu tunggu kemunculan gempa diasumsikan menyebar linear, eksponensial, dan hiperbolik. Pendugaan hazard rate menggunakan data gempa bumi di Aceh dengan kekuatan lebih dari atau sama dengan 5 SR. Pendekatan yang digunakan adalah pendekatan likelihood. Model parametrik yang diperoleh dari metode ini diharapkan mampu menduga nilai hazard rate secara akurat. Kata kunci: gempa bumi, hazard rate, sebaran kepekatan bersama, waktu tunggu.

ABSTRACT

IKHSAN MAULIDI. Estimation of Hazard Rate of Earthquake in Aceh Province with Single Decrement Method. Supervised by I WAYAN MANGKU and HADI SUMARNO.

Hazard rate has a significant effect on the earthquake forecasting. If the hazard rate is given then the joint density distribution of earthquake occurrences can be identified. Therefore we need a parametric model that accurately estimates the hazard rate. In this paper a method to estimate the hazard rate at a point 𝑡0 is discussed. The method used is single decrement method. There are two approaches that can be used to estimate the hazard rate using the method of single decrement, those are likelihood approach and the moment approach. The likelihood approach requires an assumption on the distribution of the waiting time of earthquake occurrences. In this paper the distribution of waiting time of earthquake occurrences is assumed to be linear, exponential, and hyperbolic. Estimation of the hazard rate uses earthquake data in Aceh with power greater than or equal to 5 SR. The approach used is likelihood approach. Parametric model obtained from this method is expected to estimate the hazard rate accurately.

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PENDUGAAN HAZARD RATE GEMPA DI PROVINSI ACEH

DENGAN METODE SINGLE DECREMENT

IKHSAN MAULIDI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2014

Judul Skripsi : Pendugaan Hazard Rate Gempa di Provinsi Aceh dengan Metode

Single Decrement

Nama : Ikhsan Maulidi

NIM : G54100103

Disetujui oleh

Prof Dr Ir I Wayan Mangku, MSc Pembimbing I Dr Ir Hadi Sumarno, MS Pembimbing II Diketahui oleh Dr Toni Bakhtiar, MSc Ketua Departemen Tanggal Lulus:

PRAKATA

Puji dan syukur penulis panjatkan kepada Tuhan yang maha esa atas segala karunia-Nya sehingga karya ilmiah ini yang berjudul Pendugaan Hazard Rate di Provinsi Aceh dengan Metode Single Decrement berhasil diselesaikan.

Terima kasih penulis ucapkan kepada Bapak Prof Dr Ir I Wayan Mangku dan Bapak Dr Hadi Sumarno selaku pembimbing serta Bapak Dr Paian Sianturi selaku dosen penguji yang telah banyak memberi saran dan bantuannya selama penulisan karya ilmiah. Di samping itu, penghargaan penulis sampaikan kepada Badan Meteorologi dan Geofisika yang telah membantu selama pengumpulan data. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, seluruh keluarga, serta teman-teman semua atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Mei 2014

DAFTAR ISI

DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Perumusan Masalah 2 Tujuan Penelitian 2

METODE PENDUGAAN HAZARD RATE SINGLE DECREMENT (HRSD) 2

Pendugaan Likelihood dalam Single Decrement 3

Asumsi Linear 4

Asumsi Eksponensial 5

Asumsi Hiperbolik 6

Pendugaan Momen dalam Single Decrement 7

Contoh Aplikasi Pendugaan Nilai dan Persamaan Hazard Rate 8

SIMPULAN 15

DAFTAR PUSTAKA 16

LAMPIRAN 17

DAFTAR TABEL

1. Hasil Pendugaan HRSD untuk Asumsi Waktu Tunggu Bersebaran Linear Melalui Prosedur Maksimum Likelihood jika Diketahui Belum

Terjadi Gempa Hingga Saat t₀. 10

2. Hasil Pendugaan HRSD untuk Asumsi Waktu Tunggu Bersebaran Eksponensial Melalui Prosedur Maksimum Likelihood jika Diketahui

Belum Terjadi Gempa Hingga Saat t₀. 11

3. Dugaan Persamaan Hazard Rate pada Tabel 1. 13

4. Dugaan Persamaan Hazard Rate pada Tabel 2. 15

DAFTAR GAMBAR

1. Plot magnitudo terhadap waktu untuk area studi. 9

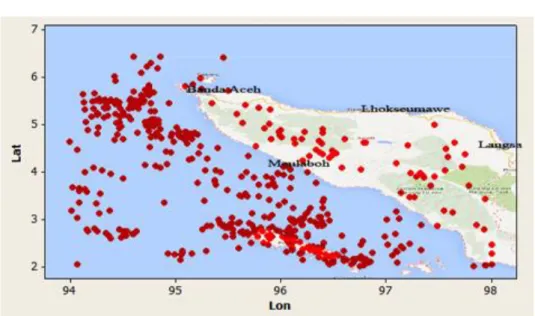
2. Plot lokasi kejadian gempa untuk area studi. 9

3. Plot hazard rate proses titik terhadap tahun dengan asumsi waktu

tunggu menyebar linear. 12

4. Plot hazard rate proses titik terhadap tahun dengan asumsi waktu

tunggu menyebar eksponensial. 12

5. Kurva perbandingan pendugaaan model hazard rate Tabel 1 yang telah ditransformasi dengan asumsi linear, kuadratik, dan kubik. 14 6. Kurva perbandingan pendugaaan model hazard rate Tabel 2 yang

telah ditransformasi dengan asumsi linear, kuadratik, dan kubik. 15

DAFTAR LAMPIRAN

1. Data gempa bumi di wilayah Aceh tahun 1980-2013 dengan

magnitudo lebih dari atau sama dengan 5 SR. 17

2. QQ-Plot hazard rate pada Tabel 1 dan 2 (Sebelum data

ditransformasi). 29

3. Box-plot nilai hazard rate pada Tabel 1 dan 2 untuk melihat nilai

pencilan (outlier). 30

4. Hasil transformasi Box-Cox nilai hazard rate pada Tabel 1 dan 2. 31

PENDAHULUAN

Latar Belakang

Gempa bumi merupakan pelepasan energi dari dalam bumi secara tiba-tiba, cepat dan merambat ke segala arah sebagai gelombang seismik. Secara umum sumber terjadinya gempa bumi dikategorikan menjadi 3 bagian, yaitu gempa bumi runtuhan, gempa bumi vulkanik, dan gempa bumi tektonik. Gempa bumi tektonik merupakan gempa bumi yang paling sering terjadi.

Secara geografis kepulauan Indonesia berada di antara 60 LU dan 110 LS serta di antara 950 _{BT dan 141}0 _{BT dan terletak pada pertemuan tiga} lempeng kerak bumi yaitu Eurasia, Pasifik, dan Indo-Australia. Ditinjau secara geologis, kepulauan Indonesia berada pada pertemuan 2 jalur gempa utama, yaitu Sirkum Pasifik dan Alpide Transasiatic. Karena itu, kepulauan Indonesia berada pada daerah yang mempunyai aktivitas gempa bumi cukup tinggi. Beberapa tahun terakhir bencana alam akibat gempa bumi di Laut Flores yang terjadi pada 12 Desember 1992 dengan magnitudo surface (Ms) sebesar 7.5, Lampung pada 16 Februari 1994 dengan 𝑀𝑠 = 7.2, , Banyuwangi pada 3 Juni 1994, Bengkulu pada 4 Juni 2000, Nabire pada 6 Februari 2004 dengan 𝑀𝑠 = 6.9 dan 26 Nopember 2004 dengan 𝑀𝑠 = 6.1 yang menimbulkan korban jiwa dan kerugian harta penduduk yang besar. Gempa terbesar terakhir yang terjadi pada 26 Desember 2004 dengan pusat gempa di lepas pantai barat Provinsi Nangroe Aceh Darussalam dengan 𝑀𝑠 = 8.9. Gempa tersebut telah memicu gelombang tsunami yang dampaknya terasa di 11 negara Asia dengan jumlah korban diperkirakan tidak kurang dari 80.000 jiwa (Firmansyah dan Irsyam 1999).

Hazard rate memegang peranan penting dalam teori likelihood proses

kemunculan gempa. Jika hazard rate diketahui, maka sebaran kepekatan bersama untuk realisasi data kemunculan dalam (0, 𝑇) dapat diketahui. Oleh karena itu, penting memperoleh model parametrik yang akurat untuk menduga hazard rate. Umumnya, hazard rate gempa diduga berdasarkan persamaan likelihood proses titik yang diperkenalkan oleh Vere-Jones pada tahun 1995 (Daley dan Vere-Jones 2003). Persamaan ini merupakan persamaan non linear yang tidak mudah diselesaikan secara analitik sehingga sering kali diselesaikan secara numerik.

Pada skripsi ini dibahas metode lain dalam menduga hazard rate gempa yaitu metode single decrement (Darwis et al. 2009). Metode ini diadaptasi dari metode pendugaan dalam studi aktuaria yang biasa digunakan dalam pembuatan tabel mortalitas. Hasil studi kasus yang telah dilakukan Sunusi (2010) menunjukkan bahwa pendugaan melalui metode

hazard rate single decrement lebih informatif daripada hazard rate likelihood proses titik.

Perumusan Masalah

Pendugaan hazard rate dengan metode single decrement terdiri dari dua sub metode yaitu dengan pendekatan likelihood dan pendekatan momen. Dengan pendekatan likelihood dibutuhkan informasi exit time yaitu informasi banyaknya kejadian gempa bumi setelah t0. Setelah diperoleh nilai dugaan hazard rate, selanjutnya akan dirumuskan persamaan terbaik untuk menduga nilai hazard rate. Persamaan terbaik tersebut merupakan persamaan yang memberikan nilai Mean Square Error (MSE) terkecil.

Data yang digunakan dalam penelitian ini merupakan data yang diperoleh langsung dari BMKG pusat di Jakarta. Data yang digunakan adalah data gempa bumi di Aceh selama periode waktu 1980-2013. Analisis data dilakukan dengan menggunakan Microsoft Excel 2013 dan beberapa

software statistika lainnya.

Tujuan Penelitian Tujuan dari penelitian ini adalah :

1. Menduga nilai hazard rate gempa dari data gempa bumi Aceh tahun 1980-2012 dengan asumsi waktu tunggu menyebar linear dan eksponensial.

2. Menentukan persamaan yang lebih baik untuk menduga hazard rate dengan menggunakan asumsi persamaan linear, kuadratik,

dan kubik.

METODE PENDUGAAN HAZARD RATE SINGLE

DECREMENT (HRSD)

Hazard rate memegang peranan penting dalam hal prakiraan peluang

kemunculan kejadian dalam suatu interval waktu tertentu. Hal ini berkaitan dengan pendugaan parameter yang terlibat di dalamnya. Metode Pendugaan

hazard rate single decrement didasari oleh pembuatan Tabel mortalitas di

bidang aktuaria. Metode ini terdiri dari dua sub metode yaitu metode maksimum likelihood dan metode momen. Sebagaimana biasanya dalam teori aktuaria, di dalam karya ilmiah ini hazard rate di titik 𝑡0 disimbolkan dengan 𝜇to.

Misalkan 𝑋(𝑡₀) = 𝑇 – 𝑡₀ menyatakan waktu tunggu hingga kemunculan gempa berikutnya, jika diketahui 𝑡0 waktu kemunculan gempa yang pertama dan 𝑇 adalah waktu kemunculan kembali gempa berikutnya. Sebagai ilustrasi, jika gempa yang pertama terjadi pada tahun 2010 dan gempa berikutnya terjadi pada tahun 2013 maka 𝑋(𝑡) = 2013 − 2010 = 3 tahun.

Misalkan 𝜇, S, dan f berturut-turut menyatakan hazard rate, fungsi ketahanan (survival function), dan fungsi kepekatan peluang. Hazard rate 𝜇𝑡0 dapat dinyatakan sebagai

3 𝜇_𝑡0

= lim

∆𝑡0→0 𝑃(𝑡₀≤𝑇≤𝑡₀+∆𝑡₀ | 𝑇>𝑡₀₎ ∆𝑡0

≈

𝑓(𝑡₀₎ 𝑆(𝑡0). (1) Misalkan 𝑦 = 𝑡0, maka persamaan (1) menjadi

𝜇_𝑦 = 𝑓(𝑦) 𝑆(𝑦) = − 𝑆′(𝑦) 𝑆(𝑦) = − 𝑑 ln(𝑆(𝑦)) 𝑑𝑦 . 𝜇𝑦 𝑑𝑦= −𝑑 ln(𝑆(𝑦)). (2) Dengan mengintegralkan kedua ruas pada persamaan (2) diperoleh

ln(𝑆(𝑦)) = − ∫ 𝜇𝑦𝑑𝑦 𝑡0+∆𝑡0

𝑡0

𝑆(𝑦) = 𝑒𝑥𝑝 [− ∫_𝑡𝑡0+∆𝑡0𝜇_𝑦𝑑𝑦

0 ].

Misalkan 𝑡₀ = 0 , yaitu sesaat setelah terjadi gempa , maka 𝑝_𝑡𝑜

∆𝑡0 = 𝑆(𝑡0) = 𝑃(𝑇 > 𝑡0+ ∆𝑡0 | 𝑇 > 𝑡0) = 𝑒𝑥𝑝 [− ∫ 𝜇(𝑡0+ 𝑠) 𝑑𝑠 ∆𝑡0

0

] merupakan fungsi ketahanan. Prakiraan gempa diformulasikan sebagai peluang bersyarat kemunculan gempa hingga 𝑡₀+ ∆𝑡₀ jika diberikan informasi bahwa belum terjadi gempa hingga saat 𝑡₀. Sebaran waktu kemunculan kembali 𝑇 dan waktu tunggu hingga kemunculan gempa berikutnya 𝑋(𝑡0) masing-masing dinyatakan sebagai berikut (Bowers et al. 1986)

𝑇~

_∆𝑡0

𝑝

_𝑡0

𝜇

_𝑡0

dan

𝑋~

_∆𝑡

𝑝

_𝑡𝑜

0

𝜇

𝑡0+∆𝑡0

.

Dalam ekspresi ini, _∆𝑡0𝑝_𝑡0𝜇_{𝑡0+∆𝑡0} menyatakan peluang bahwa suatu gempa muncul antara 𝑡₀ dan 𝑡₀+ ∆𝑡₀ jika diketahui belum terjadi gempa hingga saat 𝑡₀, dan

∫₀∞_∆𝑡0𝑝_𝑡0𝜇_{𝑡0+∆𝑡0} = 1 ; 𝑑

𝑑𝑡∆𝑡0𝑝𝑡0 = −∆𝑡0𝑝𝑡0𝜇𝑡0+∆𝑡0.

Pendugaan Likelihood dalam Single Decrement

Pendugaan hazard rate dengan pendekatan single decrement dengan metode Maximum Likelihood Estimation (MLE) membutuhkan informasi

exit time, yaitu waktu pada saat terjadi gempa. Misalkan 𝑑_𝑡0 menyatakan banyaknya gempa yang terjadi pada interval (𝑡0 , 𝑡0+ 1] dan 𝑛𝑡0− 𝑑𝑡0 menyatakan banyaknya gempa yang terjadi setelah 𝑡0+ 1. Likehood 𝐿 untuk gempa ke-i pada interval (𝑡𝑖 , 𝑡𝑖 + 1 ] diberikan oleh berikut jika diketahui tidak terjadi gempa hingga saat 𝑡0.

𝐿_𝑖 = 𝑓(𝑡₀(𝑖) | 𝑇 > 𝑡₀(𝑖)) =𝑓(𝑡0(𝑖)) 𝑆(𝑡0) =

𝑆(𝑡0(𝑖)) 𝜇(𝑡0(𝑖))

𝑆(𝑡0(𝑖)) , (3) yaitu kontribusi kempa ke-i pada L. Jika 𝑦𝑖 = 𝑡0(𝑖) + 𝑡0adalah waktu kemunculan gempa ke-i dalam interval (𝑡0 , 𝑡0+ 1] dengan 0 < 𝑦𝑖 ≤ 1, maka

𝐿

_𝑖

=

𝑆(𝑡0+𝑦𝑖) 𝜇(𝑡0+𝑦𝑖)

Kontribusi banyaknya gempa 𝑑𝑡0 pada 𝐿 adalah ∏ 𝑦𝑖𝑝𝑡0𝜇𝑡0+𝑦𝑖 𝑑

𝑖=1 . Kontribusi 𝑛_𝑡0− 𝑑_𝑡0 yaitu banyaknya gempa yang muncul setelah 𝑡₀+ 1 adalah (𝑝𝑡0)

𝑛_𝑡0−𝑑_𝑡0

. Dalam hal ini 𝑛𝑡0 merupakan banyaknya gempa yang muncul saat atau setelah 𝑡₀. Dengan demikian likelihood total adalah

𝐿 = (1 − 𝑞

_𝑡0

)

𝑛𝑡0−𝑑𝑡0

_∏

_𝑝

_𝑡 0

𝑦𝑖

𝜇

𝑡0+𝑦𝑖

𝑑_𝑡0

𝑖=1

.

(5)

Untuk menyelesaikan persamaan (5) dibutuhkan asumsi bahwa sebaran 𝑦𝑖𝑝𝑡0𝜇𝑡0+𝑦𝑖dapat dinyatakan dalam bentuk 𝑞𝑡0. Berikut ini ditinjau tiga kasus, yakni jika 𝑙_𝑡0+𝑦 yang merupakan banyak gempa setelah 𝑡₀+ 𝑦 diasumsikan bersebaran linear, eksponensial, dan hiperbolik yang diperlukan untuk menyatakan 𝑦𝑖𝑝𝑡0𝜇𝑡0+𝑦𝑖. Jika sebaran 𝑝𝑦𝑖 𝑡0𝜇𝑡0+𝑦𝑖 diketahui maka sebaran waktu tunggu 𝑋 juga akan diketahui.

Asumsi Linear Misalkan

𝑙𝑡0+𝑦 = 𝑎 + 𝑏𝑦

maka untuk 𝑦 = 0 diperoleh 𝑎 = 𝑙_𝑡0 dan untuk 𝑦 = 1 diperoleh 𝑎 + 𝑏 = 𝑙𝑡0+1 , 𝑏 = 𝑙𝑡0+1− 𝑎 = 𝑙𝑡0+1− 𝑙𝑡0 = −𝑑𝑡0. Sehingga diperoleh persamaan: 𝑙_𝑡0+𝑦 = 𝑙_𝑡0 − 𝑑_𝑡0y, (6) dengan 𝑙_𝑡0 = ∑𝜔−1_𝑡0 𝑑₀+ 𝑑₁+. . . +𝑑_𝜔−1. Dari persamaan (6) kita peroleh 𝑙𝑡0−𝑑𝑡0y 𝑙_𝑡0 = 𝑙_𝑡0+𝑦 𝑙_𝑡0 = 𝑝𝑦 𝑡0 = 1 − 𝑞𝑦 𝑡0 = 1 − 𝑦 𝑞𝑡0. (7) Karena 𝑞_𝑡0 =𝑑𝑡0

𝑙_𝑡0 maka persamaan (7) menjadi 𝑦𝑝𝑡0 = 1 − 𝑦 𝑑_𝑡0

𝑙_𝑡0. (8) Sehingga dengan menggunakan asumsi linear diketahui bahwa:

𝜇_𝑡0+𝑦 = − 𝑑 𝑑𝑠(𝑙𝑡0+𝑦) 𝑙_𝑡0+𝑦 = −𝑑 𝑑𝑦(𝑙𝑡0−𝑑𝑡0𝑦) 𝑙_𝑡0+𝑦 = 𝑑𝑡0 𝑙_𝑡0+𝑦 = 𝑑_𝑡0 𝑝_𝑡0 .𝑙_𝑡0 𝑦 = 𝑞𝑡0 𝑝_𝑡0 𝑦 = 𝑞𝑡0 1−𝑦 𝑞_𝑡0. Jadi 𝜇𝑡0+𝑦𝑖 = 𝑞_𝑡0 1−𝑦𝑖 𝑞_𝑡0. (9) Substitusikan (7) dan (9) ke persamaan (5) diperoleh

𝐿 = (1 − 𝑞𝑡0) 𝑛_𝑡0−𝑑_𝑡0 ∏ 𝑦𝔇 𝑖𝑝𝑡0 𝜇𝑡0+𝑦 = (1 − 𝑞_𝑡0)𝑛𝑡0−𝑑𝑡0∏ 𝑞𝑡0 1−𝑦𝑖𝑞_𝑡0(1 − 𝑦𝑖𝑞𝑡0) 𝔇 = (1 − 𝑞_𝑡0)𝑛𝑡0−𝑑𝑡0∏ 𝑞𝔇 𝑡0

5

= (1 − 𝑞_𝑡0)𝑛𝑡0−𝑑𝑡0(𝑞_𝑡0)𝑑𝑡0. (10)

Misalkan l = ln 𝐿 = (𝑛𝑡0 − 𝑑𝑡0) ln(1 − 𝑞𝑡0) + 𝑑𝑡0ln 𝑞𝑡0, maka dengan menggunakan syarat perlu optimalitas turunan orde pertama

𝛿 𝛿𝑞(ln 𝐿) = 𝑑_𝑡0 𝑞_𝑡0− (𝑛_𝑡0−𝑑_𝑡0) 1− 𝑞_𝑡0 = 0 − 𝑞_𝑡0𝑛_𝑡0+𝑞_𝑡0𝑑_𝑡0+ 𝑑_𝑡0−𝑞_𝑡0𝑑_𝑡0 (1− 𝑞_𝑡0)𝑞_𝑡0 = 0 diperoleh 𝑞̂ =𝑡0 𝑑_𝑡0 𝑛_𝑡0. (11) Selanjutnya dengan turunan orde dua diperoleh

𝜕2 𝜕𝑞2(ln 𝐿) = − 𝑑_𝑡0 (𝑞_𝑡0)2− (𝑛_𝑡0−𝑑_𝑡0) (1− 𝑞_𝑡0)2 = −𝑑𝑡0(1− 𝑞𝑡0) 2 −(𝑛_𝑡0−𝑑_𝑡0)(𝑞_𝑡0)2 (𝑞_𝑡0)2_{(1− 𝑞} 𝑡0) 2 . (12)

Persamaan (12) akan bernilai negatif karena 𝑑𝑡0 > 0, (1 − 𝑞𝑡0) > 0, dan (𝑛_𝑡0− 𝑑_𝑡0) > 0 . Akibatnya 𝑞̂ =_𝑡0 𝑑𝑡0

𝑛_𝑡0 merupakan maximum likelihood estimation bagi 𝑞_𝑡0. Selanjutnya nilai hazard rate dapat diperoleh dengan menggunakan persamaaan 𝜇̂ =𝑡0

𝑞̂_𝑡0

1−𝑞̂_𝑡0. Setelah nilai hazard rate untuk setiap titik diperoleh maka diduga persamaan untuk menduga nilai hazard

rate dengan menggunakan metode regresi.

Asumsi Eksponensial

Misalkan 𝑙_𝑡0+𝑦 bersebaran eksponensial maka 𝑙_𝑦 = 𝑎𝑏𝑦. Untuk 𝑦 = 0 maka 𝑙_𝑡0 = 𝑎, dan untuk 𝑦 = 1 maka 𝑙_𝑡0+1 = 𝑎𝑏, 𝑏 =𝑙𝑡0+1

𝑙_𝑡0 . Jadi 𝑙𝑡0+𝑦 = 𝑙𝑡0( 𝑙_𝑡0+1 𝑙_𝑡0 ) 𝑦 = (𝑙𝑡0+1)(𝑙𝑡0) 1−𝑦_{. (13)} Telah kita ketahui bahwa 𝑝_𝑡0 = 𝑙𝑡0+1

𝑙_𝑡0 dan 𝑙𝑡0+1 = 𝑝𝑡0𝑙𝑡0. Sehingga dengan menyubstitusikan persamaan ini ke persamaan (13) diperoleh

𝑙𝑡0+𝑦 = (𝑝𝑡0𝑙𝑡0) 𝑦 (𝑙𝑡0) 1−𝑦 = (𝑝_𝑡0)𝑦(𝑙_𝑡0) (𝑝_𝑡0)𝑦 = 𝑙𝑡0+𝑦 𝑙_𝑡0 = 𝑝𝑦 𝑡0 (14) 𝑞_𝑡0 = 1 − 𝑝_{𝑦 𝑡0} = 1 − (𝑝_𝑡0)𝑦 = 1 − (1 − 𝑞_𝑡0)𝑦. (15)

Nilai hazard rate 𝜇 diperoleh dari persamaan berikut 𝜇_𝑡0+𝑦 =− 𝑑 𝑑𝑠(𝑙𝑡0+𝑦) 𝑙_𝑡0+𝑦 = −𝑙_𝑡0(𝑝_𝑡0)𝑦ln (𝑝_𝑡0) 𝑙_𝑡0(𝑝_𝑡0)𝑦 −ln 𝑝𝑡0 = 𝜇𝑡0+𝑦. (16) Substitusikan persamaan (14) dan (16) ke persamaan (5) diperoleh

𝐿 = (1 − 𝑞

_𝑡0

)

𝑛𝑡0−𝑑𝑡0

_{∏ 𝑝}

_𝑡 0 𝑦_𝑖

𝜇

𝑡₀+𝑦_𝑖 𝑑_𝑡0 𝑖=1 = (1 − 𝑞𝑡0) 𝑛_𝑡0−𝑑_{𝑡0∏ 𝜇} 𝑡0+𝑦 𝑑_𝑡0 𝑖=1 (𝑝𝑡0) 𝑦𝑖 = (𝑝_𝑡0)𝑛𝑡0−𝑑𝑡0_{∏ 𝜇𝑡} 0+𝑦 𝑑_𝑡0 𝑖=1 (𝑝_𝑡0)𝑦𝑖 = (exp(−𝜇))𝑛𝑡0−𝑑𝑡0_𝜇𝑑𝑡0_{exp( −𝜇 ∑ 𝑦𝑖)} = 𝜇𝑑𝑡0_{exp [−μ(𝑛𝑡} 0 − 𝑑𝑡0) + ∑ yi 𝑑_𝑡0 i=0 ]. (17) Dengan mengambil logaritma natural dari persamaan (17) diperoleh

𝑙 = ln 𝐿= 𝑑_𝑡0ln 𝜇 − 𝜇 [(𝑛_𝑡0 − 𝑑_𝑡0) + ∑ 𝑦_𝑖]. (18). Syarat perlu orde pertama memberikan 𝑑𝑙

𝑑𝜇 = 𝑑_𝑡0

𝜇 − [(𝑛𝑡0− 𝑑𝑡0) ∑ 𝑦𝑖] =0. Sehingga diperoleh nilai dugaan hazard rate 𝜇̂ = 𝑑𝑡0

(𝑛_𝑡0−𝑑_𝑡0)+∑𝑑𝑡0_i=0yi

. (19)

Selanjutnya karena turunan kedua l, 𝑑 𝑙 2 𝑑𝜇2 = −

𝑑_𝑡0

𝜇2 < 0 maka nilai 𝜇̂ yang diperoleh merupakan maximum likelihood estimation bagi 𝜇. Karena q berkorespondensi 1-1 dengan 𝜇 maka 𝑞̂ = 1 − 𝑝_𝑡0 ̂ = (1 − 𝑒_𝑡0 −𝜇).

Asumsi Hiperbolik

Misalkan 𝑙𝑡0+𝑦 merupakan persamaan yang hiperbolik maka 𝑙_𝑡0+𝑦 = 1

𝑎+𝑏𝑦 . Dengan mengambil nilai y = 0 diperoleh 𝑙𝑡0 = 1 𝑎 ↔ 𝑎 = 1 𝑙_𝑡0 . Untuk y = 1, 𝑙𝑡0+1 = 1 𝑎+𝑏 ↔ 𝑎 + 𝑏 = 1

𝑙_𝑡0+1. Sehingga diperoleh nilai 𝑏 = 1

𝑙_𝑡0+1− 1

𝑙_𝑡0. Dengan demikian diperoleh 𝑙𝑡0+𝑠= 1 1 𝑙𝑡0+( 1 𝑙𝑡0+1− 1 𝑙𝑡0) 𝑠 . (20)

7

Persamaan (19) dapat juga dinyatakan sebagai berikut 1 𝑙_𝑡0+𝑦 = 1 𝑙_𝑡0+ 𝑦 1 𝑙_𝑡0+1− 1 𝑙_𝑡0 = 𝑦 𝑙_𝑡0+1+ (1−𝑦) 𝑙_𝑡0 (21) Selanjutnya 1 𝑝_𝑡0 𝑦 = 𝑙_𝑡0 𝑙_𝑡0+𝑦= 𝑙𝑡0( 𝑦 𝑙_𝑡0+1+ (1−𝑦) 𝑙_𝑡0 ) = (1 − 𝑦) + 𝑦 𝑝_𝑡0 =𝑦+(1−𝑦)𝑝𝑡0 𝑝_𝑡0 =𝑝𝑡0+(1−𝑝𝑡0)𝑦 𝑝_𝑡0 = 𝑝𝑡0+𝑞𝑡0𝑦 𝑝_𝑡0 . (22) Dengan demikian 𝑦𝑝𝑡0 = 𝑝_𝑡0 𝑝_𝑡0+𝑞_𝑡0𝑦. (23)

Fungsi hazard rate diperoleh dari persamaan berikut: 𝜇_𝑡0+𝑦 = −𝑑( 𝑝𝑡0𝑦 ) 𝑑𝑦 𝑝_𝑡0 𝑦 = 𝑝𝑡0+𝑞𝑡0 (𝑝𝑡0+𝑞𝑡0𝑦)2 𝑝𝑡0 𝑝𝑡0+𝑞𝑡0𝑦 = 𝑞𝑡0 𝑝_𝑡0+𝑞_𝑡0𝑦. = 𝑞𝑡0 (1−𝑞_𝑡0)+𝑞_𝑡0𝑦= 𝑞_𝑡0 1−(1−𝑦)𝑞_𝑡0. (24) Dari persamaan (23) dan (24) diperoleh

𝑝_𝑡0 𝑠 𝜇𝑡0+𝑦 = 𝑝_𝑡0 𝑝_𝑡0+𝑞_𝑡0𝑦= 𝑞_𝑡0 1−(1−𝑦)𝑞_𝑡0 = 𝑞_𝑡0(1−𝑝_𝑡0) (1−(1−𝑦)𝑞_𝑡0)2 . (25) Misalkan 𝑥 = (1 − 𝑦)𝑞_𝑡0, maka persamaan (24) akan menjadi

𝜇𝑡0+𝑦 = 𝑞_𝑡0

1−𝑥. (26) Karena 1

1−𝑥 = 1 + 𝑥 + 𝑥

2_{+ ⋯ ,maka dari persamaan (26) diperoleh} 𝜇_𝑡0+𝑦 = 𝑞_𝑡0(1 + 𝑥 + 𝑥2_{+ ⋯ ).}

= (𝑞_𝑡0+ 𝑞_𝑡0𝑥 + 𝑞_𝑡0𝑥2_{+ ⋯ )}

= 𝑞_𝑡0 + (1 − 𝑦)𝑞_𝑡02+ (1 − 𝑦)2𝑞_𝑡03+ ⋯. Jika suku-suku kuadrat dan setelahnya diabaikan, maka

𝜇_𝑡0+𝑦 ≈ 𝑞_𝑡0. (27) Persamaan (27) menunjukkan bahwa 𝜇_𝑡0+𝑦 dapat dihampiri 𝑞_𝑡0 yang merupakan peluang munculnya kejadian pada interval (𝑡₀, 𝑡₀+ 1] dimana diketahui belum ada kejadian hingga saat 𝑡₀.

Pendugaan Momen dalam Single Decrement

Pendugaan nilai hazard rate dengan menggunakan metode momen

membutuhkan dua tahapan. Tahap pertama adalah menentukaan suatu ekspresi tentang banyaknya kejadian dalam interval (𝑡₀, 𝑡₀ + 1]. Kemudian tahap kedua adalah menyelesaikan persamaan momen. Prinsip yang digunakan dalam menyelesaikan persamaan momen adalah prinsip statistik,

yaitu banyaknya kejadian yang diharapkan sama dengan banyaknya kejadian yang diobservasi.

Misalkan kemunculan gempa ke-i yang masuk dalam interval pendugaan (𝑡₀, 𝑡₀+ 1] terjadi pada 𝑡₀+ 𝑟_𝑖 dengan 0 < 𝑟_𝑖 < 1 , dan gempa berikutnya terjadi pada 𝑡₀+ 𝑠_𝑖. Maka (𝑡₀, 𝑠_𝑖) merupakan interval waktu kemunculan dua gempa pada periode (𝑡0, 𝑡0+ 1]. Untuk kemunculan gempa ke-i, jika peluang terjadinya satu kejadian gempa adalah _{𝑠𝑖−𝑟𝑖}𝑞_{𝑡0+𝑟𝑖}dan peluang tidak terjadi gempa adalah 𝑠𝑖−𝑟𝑖𝑝𝑡0+𝑟𝑖, maka peluang bersyarat terjadi gempa sebelum 𝑡₀+ 𝑠_𝑖 jika diketahui belum terjadi gempa hingga 𝑡₀ + 𝑟_𝑖 adalah

1.𝑠𝑖−𝑟𝑖𝑞𝑡0+𝑟𝑖+0. 𝑠𝑖−𝑟𝑖𝑝𝑡0+𝑟𝑖 = 𝑠𝑖−𝑟𝑖𝑞𝑡0+𝑟𝑖. (28) Berdasarkan persamaan (28) diperoleh total banyaknya kejadian gempa adalah ∑𝑛_{𝑖=𝑠𝑖−𝑟𝑖}𝑞_{𝑡0+𝑟𝑖}. Selanjutnya diperoleh persamaan momen sebagai berikut:

𝐸[𝐷_𝑡0] = ∑𝑛_{𝑖=1𝑠𝑖−𝑟𝑖}𝑞_{𝑡0+𝑟𝑖} = 𝑑_𝑡0 (29) di mana 𝐷_𝑡0 merupakan peubah acak untuk kemunculan gempa dalam (𝑡₀, 𝑡₀+ 1] dan 𝑑_𝑡0 merupakan banyaknya amatan pada (𝑡₀, 𝑡₀+ 1].

Untuk estimasi 𝑞_𝑡0, digunakan aproksimasi 𝑞_{𝑡0+𝑟𝑖} ≈ (𝑠_𝑖− 𝑟_𝑖)𝑞_𝑡0 𝑠𝑖−𝑟𝑖 .

Sehingga persamaan (29) menjadi 𝐸[𝐷_𝑡0] = 𝑞_𝑡0∑𝑛 (𝑠_𝑖 − 𝑟_𝑖) = 𝑖=1 𝑑𝑡0. Dengan demikian diperoleh

𝑞̂ =𝑡0

𝑑_𝑡0 ∑𝑛𝑖=1(𝑠𝑖− 𝑟𝑖)

.

Untuk waktu tunggu yang menyebar eksponensial, maka fungsi hazard rate bernilai konstan dengan 𝜇(𝑡) = 𝜇 untuk setiap 𝑡. Diketahui bahwa

𝑝_𝑡0 = 𝑆(𝑡0+ 1) 𝑆(𝑡₀) =

𝑒−𝜇(𝑡0+1) 𝑒−𝜇(𝑡0) = 𝑒

−𝜇_, maka 𝜇 = −ln (𝑝_𝑡0) atau 𝑝_𝑡0 = 𝑒−𝜇_{. Karena itu, diperoleh 𝑞}

𝑡0

̂ = 1 − 𝑒−𝜇̂_. Dengan demikian, 𝜇̂ = −ln (1 − 𝑞_{𝑡0 𝑡0}).

Contoh Aplikasi Pendugaan Nilai dan Persamaan Hazard Rate Dalam karya ilmiah ini contoh aplikasi dari pendugaan nilai dan persamaan hazard rate ditentukan dari data yang diperoleh langsung dari BMKG pusat di Jakarta. Adapun data yang digunakan untuk perhitungan merupakan data gempa di wilayah Aceh dalam interval waktu 1980-2013 yang memiliki kekuatan gempa lebih dari atau sama dengan 5 SR (Data terlampir).

9

Berikut ditampilkan plot magnitudo terhadap waktu dan plot lokasi terjadinya gempa untuk area studi.

Gambar 1. Plot magnitudo terhadap waktu untuk area studi.

Gambar 2. Plot lokasi kejadian gempa untuk area studi.

Selanjutnya ditentukan nilai hazard rate dengan menggunakan metode

single decrement pendekatan likelihood. Kita ketahui dalam pendekatan likelihood dibutuhkan asumsi sebaran waktu tunggu terjadinya gempa.

Dalam aplikasi ini asumsi sebaran waktu tunggu yang dibahas adalah asumsi waktu tunggu menyebar linear dan menyebar eksponensial. Maka dengan menggunakan persamaan hazard rate yang telah dirumuskan sebelumnya diperoleh nilai hazard rate sebagai berikut:

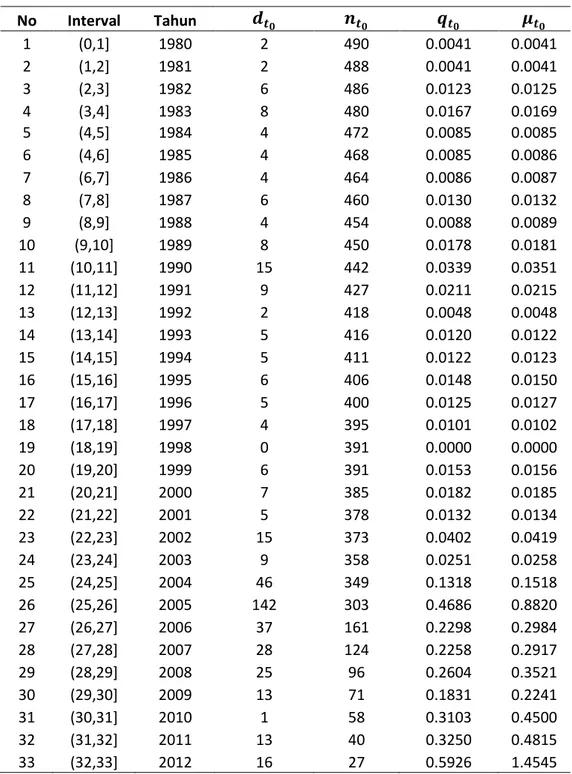
Tabel 1. Hasil Pendugaan HRSD untuk Asumsi Waktu Tunggu Bersebaran Linear Melalui Prosedur Maksimum Likelihood jika Diketahui Belum Terjadi Gempa Hingga Saat 𝑡0.

No Interval Tahun 𝒅𝒕𝟎 𝒏𝒕𝟎 𝒒𝒕𝟎 𝝁𝒕𝟎 1 (0,1] 1980 2 490 0.0041 0.0041 2 (1,2] 1981 2 488 0.0041 0.0041 3 (2,3] 1982 6 486 0.0123 0.0125 4 (3,4] 1983 8 480 0.0167 0.0169 5 (4,5] 1984 4 472 0.0085 0.0085 6 (4,6] 1985 4 468 0.0085 0.0086 7 (6,7] 1986 4 464 0.0086 0.0087 8 (7,8] 1987 6 460 0.0130 0.0132 9 (8,9] 1988 4 454 0.0088 0.0089 10 (9,10] 1989 8 450 0.0178 0.0181 11 (10,11] 1990 15 442 0.0339 0.0351 12 (11,12] 1991 9 427 0.0211 0.0215 13 (12,13] 1992 2 418 0.0048 0.0048 14 (13,14] 1993 5 416 0.0120 0.0122 15 (14,15] 1994 5 411 0.0122 0.0123 16 (15,16] 1995 6 406 0.0148 0.0150 17 (16,17] 1996 5 400 0.0125 0.0127 18 (17,18] 1997 4 395 0.0101 0.0102 19 (18,19] 1998 0 391 0.0000 0.0000 20 (19,20] 1999 6 391 0.0153 0.0156 21 (20,21] 2000 7 385 0.0182 0.0185 22 (21,22] 2001 5 378 0.0132 0.0134 23 (22,23] 2002 15 373 0.0402 0.0419 24 (23,24] 2003 9 358 0.0251 0.0258 25 (24,25] 2004 46 349 0.1318 0.1518 26 (25,26] 2005 142 303 0.4686 0.8820 27 (26,27] 2006 37 161 0.2298 0.2984 28 (27,28] 2007 28 124 0.2258 0.2917 29 (28,29] 2008 25 96 0.2604 0.3521 30 (29,30] 2009 13 71 0.1831 0.2241 31 (30,31] 2010 1 58 0.3103 0.4500 32 (31,32] 2011 13 40 0.3250 0.4815 33 (32,33] 2012 16 27 0.5926 1.4545 Keterangan:

𝑛_𝑡0: banyaknya gempa yang terjadi pada saat atau setelah 𝑡₀. 𝑑_𝑡0: banyaknya gempa yang terjadi pada interval (𝑡₀, 𝑡₀ + 1].

𝑞_𝑡0: peluang munculnya kejadian gempa pada interval (𝑡₀, 𝑡₀+ 1] jika diketahui belum ada gempa hingga saat 𝑡0.

11

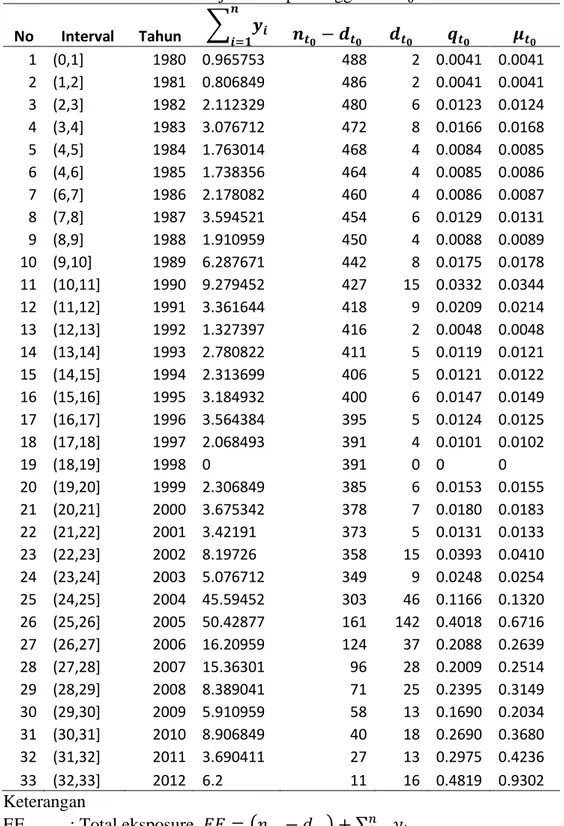
Tabel 2. Hasil Pendugaan HRSD untuk Asumsi Waktu Tunggu Bersebaran Eksponensial Melalui Prosedur Maksimum Likelihood jika Diketahui Belum Terjadi Gempa Hingga Saat 𝑡0.

No Interval Tahun ∑ 𝒚𝒊 𝒏 𝒊=𝟏 𝒏𝒕𝟎− 𝒅𝒕𝟎 𝒅𝒕𝟎 𝒒𝒕𝟎 𝝁𝒕𝟎 1 (0,1] 1980 0.965753 488 2 0.0041 0.0041 2 (1,2] 1981 0.806849 486 2 0.0041 0.0041 3 (2,3] 1982 2.112329 480 6 0.0123 0.0124 4 (3,4] 1983 3.076712 472 8 0.0166 0.0168 5 (4,5] 1984 1.763014 468 4 0.0084 0.0085 6 (4,6] 1985 1.738356 464 4 0.0085 0.0086 7 (6,7] 1986 2.178082 460 4 0.0086 0.0087 8 (7,8] 1987 3.594521 454 6 0.0129 0.0131 9 (8,9] 1988 1.910959 450 4 0.0088 0.0089 10 (9,10] 1989 6.287671 442 8 0.0175 0.0178 11 (10,11] 1990 9.279452 427 15 0.0332 0.0344 12 (11,12] 1991 3.361644 418 9 0.0209 0.0214 13 (12,13] 1992 1.327397 416 2 0.0048 0.0048 14 (13,14] 1993 2.780822 411 5 0.0119 0.0121 15 (14,15] 1994 2.313699 406 5 0.0121 0.0122 16 (15,16] 1995 3.184932 400 6 0.0147 0.0149 17 (16,17] 1996 3.564384 395 5 0.0124 0.0125 18 (17,18] 1997 2.068493 391 4 0.0101 0.0102 19 (18,19] 1998 0 391 0 0 0 20 (19,20] 1999 2.306849 385 6 0.0153 0.0155 21 (20,21] 2000 3.675342 378 7 0.0180 0.0183 22 (21,22] 2001 3.42191 373 5 0.0131 0.0133 23 (22,23] 2002 8.19726 358 15 0.0393 0.0410 24 (23,24] 2003 5.076712 349 9 0.0248 0.0254 25 (24,25] 2004 45.59452 303 46 0.1166 0.1320 26 (25,26] 2005 50.42877 161 142 0.4018 0.6716 27 (26,27] 2006 16.20959 124 37 0.2088 0.2639 28 (27,28] 2007 15.36301 96 28 0.2009 0.2514 29 (28,29] 2008 8.389041 71 25 0.2395 0.3149 30 (29,30] 2009 5.910959 58 13 0.1690 0.2034 31 (30,31] 2010 8.906849 40 18 0.2690 0.3680 32 (31,32] 2011 3.690411 27 13 0.2975 0.4236 33 (32,33] 2012 6.2 11 16 0.4819 0.9302 Keterangan EE : Total eksposure, 𝐸𝐸 = (𝑛_𝑡0− 𝑑_𝑡0) + ∑𝑛_𝑖=1𝑦_𝑖.

𝑑_𝑡0 : Banyaknya gempa yang terjadi pada interval (𝑡₀, 𝑡₀+ 1]. 𝑛_𝑡0 − 𝑑_𝑡0: Banyaknya gempa yang terjadi setelah 𝑡0+ 1.

𝑞_𝑡0 : Peluang munculnya kejadian gempa pada interval(𝑡₀, 𝑡₀ + 1] jika diketahui belum ada gempa hingga saat 𝑡₀.

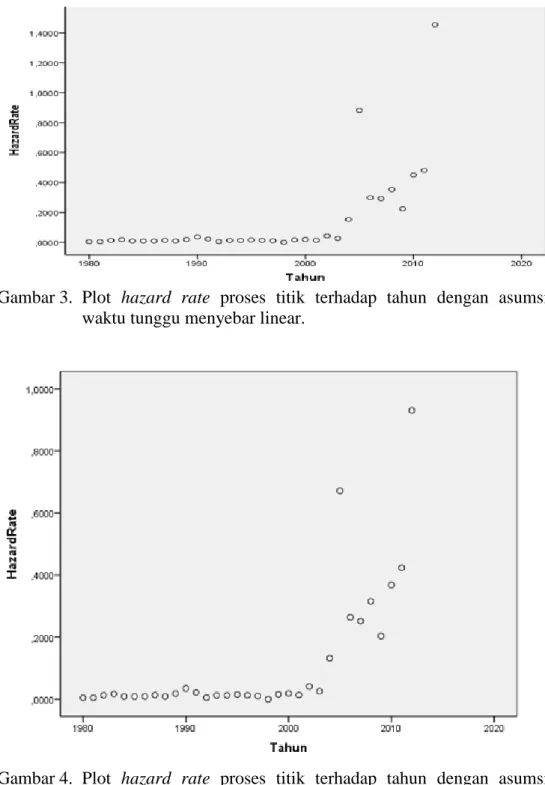
Gambar 3. Plot hazard rate proses titik terhadap tahun dengan asumsi waktu tunggu menyebar linear.

Gambar 4. Plot hazard rate proses titik terhadap tahun dengan asumsi waktu tunggu menyebar eksponensial.

Hasil pada Tabel 1 dan Tabel 2 berturut-turut merupakan nilai hazard

rate dengan asumsi waktu tunggu tunggu menyebar linear dan menyebar

eksponensial pada waktu t0 yang dinotasikan dengan simbol µt0. Untuk menduga persamaan regresi dari hazard rate dibutuhkan sifat bahwa

hazard rate harus menyebar normal. Akan tetapi menurut hasil QQ-plot dari

hazard rate pada Tabel 1 dan Tabel 2 menunjukkan bahwa hazard rate tidak menyebar normal, sehingga perlu dilakukan normalisasi untuk nilai

13

hazard rate ini dengan terlebih dahulu menghilangkan nilai hazard rate

yang bersifat pencilan.

Dengan melakukan transformasi Box-Cox pada nilai hazard rate dari Tabel 1 dan Tabel 2 diperoleh nilai λ berturut-turut -0.5 dan -0.5. Artinya transformasi yang dilakukan adalah μ_𝑡∗₀ = (μ𝑡0)

−0.5 _{untuk hazard rate} dengan waktu tunggu menyebar linear dan μ𝑡0

∗ _{= (μ} 𝑡0)

−0.5 _{untuk hazard} rate dengan waktu tunggu menyebar eksponensial. Sehingga diperlukan

transformasi balik agar diperoleh nilai dugaan hazard rate yang diinginkan. Transformasi balik yang dilakukan adalah μ_𝑡0 = (μ_𝑡∗₀)−2= 1

µ_𝑡0∗ 2.

Proses penentuan model parametrik untuk HRSD dilakukan dengan metode regresi untuk nilai hazard rate tersebut dengan menggunakan model linear μ_𝑡∗₀ = 𝛽₀+ 𝛽₁𝑡₀+ 𝜀 , model kuadratik μ∗_𝑡0 = 𝛽₀+ 𝛽₁𝑡₀+ 𝛽₂𝑡₀2+ 𝜀 , dan model kubik μ_𝑡∗₀ = 𝛽₀+ 𝛽₁𝑡₀+ 𝛽₂𝑡₀2+ 𝛽₃𝑡₀3+ 𝜀.

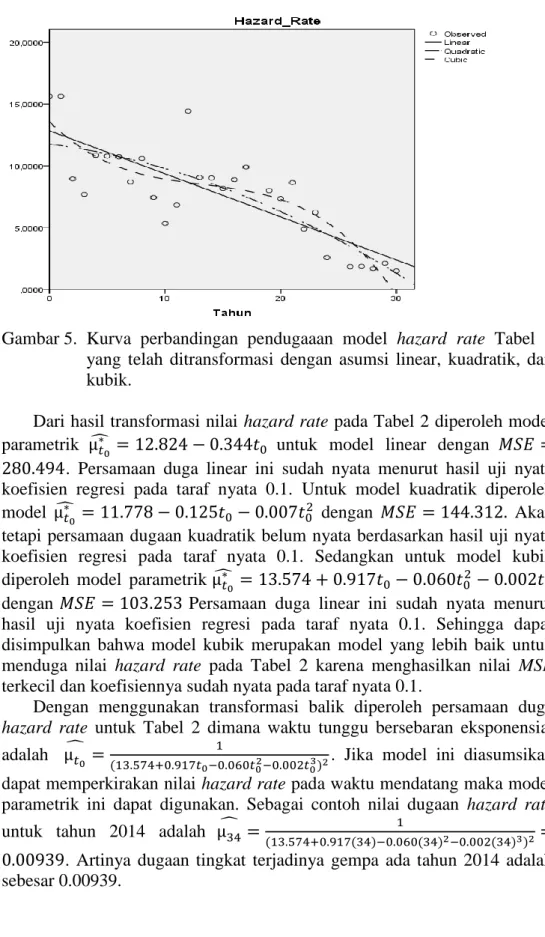
Dari hasil transformasi nilai hazard rate pada Tabel 1 diperoleh model parametrik μ̂ = 12.838 − 0.349𝑡_𝑡∗_{0 0} untuk model linear dengan 𝑀𝑆𝐸 = 287.346. Persamaan duga linear ini sudah nyata menurut hasil uji nyata koefisien regresi pada taraf nyata 0.1. Untuk model kuadratik diperoleh model μ̂ = 11.762 − 0.123𝑡_𝑡∗_{0 0}− 0.008𝑡₀2 dengan 𝑀𝑆𝐸 = 147.970. Akan tetapi persamaan dugaan kuadratik belum nyata berdasarkan hasil uji nyata koefisien regresi pada taraf nyata 0.1. Sedangkan untuk model kubik diperoleh model parametrik μ_{̂ = 13.567 − 0.919𝑡𝑡}∗₀

0+ 0.061𝑡02 − 0.002𝑡03 dengan 𝑀𝑆𝐸 = 105.768. Persamaan duga linear ini sudah nyata menurut hasil uji nyata koefisien regresi pada taraf nyata 0.1. Sehingga dapat disimpulkan bahwa model kubik merupakan model yang lebih baik untuk menduga nilai hazard rate pada Tabel 1 karena menghasilkan nilai MSE terkecil dan koefisiennya sudah nyata pada taraf nyata 0.1.

Dengan menggunakan transformasi balik diperoleh persamaan duga

hazard rate untuk Tabel 1 dimana waktu tunggu bersebaran linear adalah

μ̂ =𝑡0

1

(13.567−0.919𝑡0+0.061𝑡02−0.002𝑡03)2. Jika model ini diasumsikan dapat memperkirakan nilai hazard rate pada waktu mendatang maka model parametrik ini dapat digunakan. Sebagai contoh nilai dugaan hazard rate untuk tahun 2014 adalah μ̂ =₃₄ 1

(13.567−0.919(34)+0.061(34)2_−0.002(34)3₎2 = 0.00151. Artinya dugaan tingkat terjadinya gempa ada tahun 2014 adalah sebesar 0.00151.

Tabel 3. Dugaan Persamaan Hazard Rate pada Tabel 1.

Persamaan MSE Uji Nyata Regresi

(𝛂 = 𝟎. 𝟏) μ̂𝑡∗₀= 12.838 − 0.349𝑡0 287.346 Nyata μ̂𝑡∗₀ = 11.762 − 0.123𝑡0− 0.008𝑡02 147.970 Tidak nyata μ_̂𝑡∗_{0 = 13.567 − 0.919𝑡} 0+ 0.061𝑡02 − 0.002𝑡₀3 105.768 Nyata

Gambar 5. Kurva perbandingan pendugaaan model hazard rate Tabel 1 yang telah ditransformasi dengan asumsi linear, kuadratik, dan kubik.

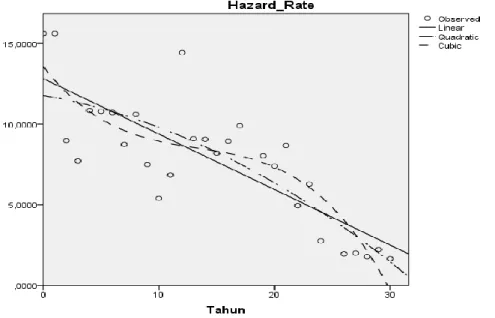
Dari hasil transformasi nilai hazard rate pada Tabel 2 diperoleh model parametrik μ̂ = 12.824 − 0.344𝑡_𝑡∗_{0 0} untuk model linear dengan 𝑀𝑆𝐸 = 280.494. Persamaan duga linear ini sudah nyata menurut hasil uji nyata koefisien regresi pada taraf nyata 0.1. Untuk model kuadratik diperoleh model μ̂ = 11.778 − 0.125𝑡_𝑡∗_{0 0} − 0.007𝑡₀2 dengan 𝑀𝑆𝐸 = 144.312. Akan tetapi persamaan dugaan kuadratik belum nyata berdasarkan hasil uji nyata koefisien regresi pada taraf nyata 0.1. Sedangkan untuk model kubik diperoleh model parametrik μ_{̂ = 13.574 + 0.917𝑡𝑡}∗₀

0− 0.060𝑡02− 0.002𝑡03 dengan 𝑀𝑆𝐸 = 103.253 Persamaan duga linear ini sudah nyata menurut hasil uji nyata koefisien regresi pada taraf nyata 0.1. Sehingga dapat disimpulkan bahwa model kubik merupakan model yang lebih baik untuk menduga nilai hazard rate pada Tabel 2 karena menghasilkan nilai MSE terkecil dan koefisiennya sudah nyata pada taraf nyata 0.1.

Dengan menggunakan transformasi balik diperoleh persamaan duga

hazard rate untuk Tabel 2 dimana waktu tunggu bersebaran eksponensial

adalah μ̂ =_𝑡0 1

(13.574+0.917𝑡0−0.060𝑡02−0.002𝑡03)2

. Jika model ini diasumsikan dapat memperkirakan nilai hazard rate pada waktu mendatang maka model parametrik ini dapat digunakan. Sebagai contoh nilai dugaan hazard rate untuk tahun 2014 adalah μ̂ =₃₄ 1

(13.574+0.917(34)−0.060(34)2_−0.002(34)3₎2 = 0.00939. Artinya dugaan tingkat terjadinya gempa ada tahun 2014 adalah sebesar 0.00939.

15

Tabel 4. Dugaan Persamaan Hazard Rate pada Tabel 2.

Persamaan MSE Uji Nyata Regresi

(𝛂 = 𝟎. 𝟏) μ̂ = 12.824 − 0.344𝑡𝑡0∗ 0 280.494 Nyata μ_{̂ = 11.778 − 0.125𝑡𝑡0}∗ 0− 0.007𝑡02 144.312 Tidak nyata μ_{̂ = 13.574 + 0.917𝑡𝑡0}∗ 0 − 0.060𝑡02 − 0.002𝑡₀3 103.253 Nyata

Gambar 6. Kurva perbandingan pendugaan model hazard rate Tabel 2 yang telah ditransformasi dengan asumsi linear, kuadratik, dan kubik.

SIMPULAN

Dalam karya ilmiah ini dibahas salah satu metode untuk menentukan nilai hazard rate proses titik temporal. Metode yang digunakan adalah metode single decrement. Metode single decrement ini merupakan metode yang didasarkan pada teori aktuaria. Pendugaan hazard rate dengan metode

single decrement dilakukan dengan dua pendekatan, yaitu pendekatan likelihood dan pendekatan momen.

Dengan menggunakan pendekatan likelihood, dibutuhkan asumsi sebaran waktu tunggu terjadinya gempa. Sebaran waktu tunggu terjadinya gempa yang digunakan adalah sebaran linear, eksponensial, dan hiperbolik.

Jika sebaran waktu tunggu adalah linear maka dugaan hazard rate (𝜇̂ ) dapat dirumuskan menjadi 𝜇_𝑡0 ̂ =_𝑡0 𝑞̂𝑡0

1−𝑞̂_𝑡0, dan 𝑞̂ =𝑡0 𝑑_𝑡0

𝑛_𝑡0 dengan 𝑞̂ menyatakan dugaan peluang terjadinya gempa pada interval (𝑡𝑡0 0, 𝑡0 + 1] jika diasumsikan belum terjadi gempa hingga 𝑡₀, 𝑑_𝑡0 menyatakan

banyaknya kejadian gempa pada interval (𝑡0, 𝑡0+ 1], serta 𝑛𝑡0menyatakan banyaknya kejadian gempa tepat atau setelah 𝑡0.

Jika sebaran waktu tunggu adalah eksponensial maka dugaan hazard

rate (𝜇̂ ) dapat dirumuskan menjadi 𝜇̂ =_𝑡0 𝑑𝑡0 (𝑛_𝑡0−𝑑_𝑡0)+∑𝑑𝑡0i=0yi

, dengan 𝑑𝑡0 menyatakan banyaknya kejadian gempa pada interval (𝑡0, 𝑡0+ 1], (𝑛𝑡0− 𝑑𝑡0) menyatakan banyaknya kejadian gempa setelah 𝑡0+ 1, dan yi adalah bilangan yang menyatakan waktu kemunculan gempa ke-i setelah 𝑡0, dalam hal ini 0 < 𝑦_𝑖 < 1. Sedangkan jika sebaran waktu tunggu adalah hiperbolik maka dugaan hazard rate 𝜇_𝑡0+𝑠 ≈ 𝑞_𝑡0, akan tetapi belum diperoleh solusi analitik untuk menentukan 𝑞𝑡0.

Perhitungan hazard rate menggunakan data gempa di Aceh periode waktu 1980-2013 dengan kekuatan gempa lebih dari atau sama dengan 5 SR. Pendugaan nilai hazard rate dilakukan dengan menggunakan pendekatan

likelihood dimana menggunakan asumsi waktu tunggu yang menyebar

linear dan eksponensial. Dari hasil perhitungan yang dilakukan diperoleh model yang lebih baik dalam menduga persamaan adalah model kubik. Model yang diperoleh ini diharapkan mampu menduga nilai hazard rate secara akurat.

DAFTAR PUSTAKA

Bowers, N.L, Gerber, H.U, Hickman, J.C, Jones, D.A, and Nesbitt, C.J. 1986. Actuarial Mathematics : The Society of Actuaries.

Daley, D.J. dan Vere-Jones, D. 2003: An Introduction to the Teory of Point

Processes. Berlin: Springer.

Darwis, S, Sunusi, N., Triyoso, W., dan Mangku, I.W. 2009. Single Decrement Approach for Estimating Eartquake Hazard Rate, Advance

and Applications in Statistics, 11(2), 229-27.

Firmansyah, J. and Irsyam, M. 1999. Development of Seismic Hazard Map for Indonesia: Konferensi Nasional Rekayasa Kegempaan.

Sunusi, N. 2010. Pengembangan Estimasi Hazard Rate Proses Titik Temporal dan Aplikasinya pada Prakiraan Kemunculan Gempa [Disertasi]. Bandung : Institut Teknologi Bandung.

17

LAMPIRAN

Lampiran 1. Data gempa bumi di wilayah Aceh tahun 1980-2013 dengan magnitudo lebih dari atau sama dengan 5 SR.

Date OT (UTC) Lat Lon Depth

(Km) Mag (SR) 1/04/1980 16:21:48 4.03 97.56 41 6.2 16/09/1980 15:23:45 3.90 95.63 40 5.2 10/02/1981 18:42:41 3.98 97.23 121 5.1 10/09/1981 14:17:43 5.45 95.35 102 5.0 13/02/1982 19:56:12 5.68 94.79 71 5.3 24/02/1982 04:22:40 4.37 97.75 52 5.4 7/03/1982 14:08:15 3.72 97.42 124 5.0 22/03/1982 08:38:33 2.47 97.02 39 5.3 3/08/1982 08:44:44 2.86 97.49 58 5.0 31/10/1982 02:48:13 2.97 96.10 62 5.5 30/01/1983 01:26:05 5.45 94.94 82 5.2 16/03/1983 09:13:11 3.48 95.79 43 5.2 4/04/1983 06:59:00 5.63 94.68 79 5.0 4/04/1983 03:03:34 5.79 94.75 69 5.9 4/04/1983 02:51:34 5.72 94.72 78 6.8 2/07/1983 09:34:04 5.75 94.71 92 5.7 17/09/1983 05:56:56 4.75 95.04 66 5.8 9/10/1983 04:51:19 5.70 94.60 33 5.0 11/04/1984 13:51:10 5.74 94.75 83 5.2 29/05/1984 04:36:09 3.57 97.14 70 5.8 13/06/1984 13:28:12 4.44 94.91 42 5.1 11/08/1984 11:56:49 5.99 95.24 131 5.4 21/03/1985 07:48:40 6.24 94.73 33 5.0 21/03/1985 08:18:38 6.45 94.86 33 5.2 5/07/1985 23:10:14 5.72 95.50 10 5.8 8/10/1985 07:14:06 3.95 96.03 64 5.1 29/04/1986 13:59:21 4.41 94.96 38 5.2 14/06/1986 14:51:03 2.04 98.00 66 5.4 8/09/1986 02:39:52 4.42 96.37 39 5.2 12/09/1986 00:11:48 2.91 96.13 36 5.0 24/02/1987 14:52:49 4.29 95.16 49 5.1 17/05/1987 12:11:09 3.02 97.12 73 5.1 10/06/1987 16:03:55 4.14 94.81 52 5.4 14/10/1987 23:30:25 4.03 95.38 58 5.1 17/11/1987 08:38:30 5.20 94.36 56 5.1

Lanjutan Lampiran 1 10/12/1987 07:22:44 3.37 96.40 52 5.2 5/01/1988 08:48:06 2.59 96.13 56 5.1 3/04/1988 14:27:09 4.69 94.42 30 5.9 22/08/1988 18:25:00 4.70 96.20 43 5.0 27/12/1988 13:50:41 4.80 95.21 56 5.3 24/02/1989 13:38:48 3.15 96.25 58 5.0 20/07/1989 06:27:25 5.05 95.64 82 5.9 30/07/1989 19:14:37 4.70 95.91 22 5.2 2/08/1989 10:24:21 2.77 96.14 28 5.1 2/08/1989 10:48:06 2.71 96.10 22 5.9 13/11/1989 15:54:40 4.70 94.50 56 5.2 21/12/1989 16:40:09 3.10 96.24 21 5.3 21/12/1989 08:08:04 3.25 96.40 21 5.6 22/01/1990 17:26:11 3.88 96.10 45 6.0 29/01/1990 20:34:20 6.10 94.68 98 5.0 22/02/1990 12:51:43 5.66 94.23 56 5.0 23/05/1990 16:07:44 4.92 94.47 51 5.0 26/06/1990 07:14:20 4.55 95.24 59 5.0 31/07/1990 18:25:50 3.81 95.37 29 5.3 12/09/1990 09:42:27 4.31 96.46 33 5.0 2/10/1990 13:27:06 3.73 95.79 59 5.0 13/10/1990 20:15:13 4.28 95.30 76 5.0 15/11/1990 05:47:22 3.92 97.35 48 5.4 15/11/1990 05:18:45 3.91 97.29 53 5.6 15/11/1990 04:48:12 3.98 97.32 30 5.8 15/11/1990 02:34:32 3.91 97.46 48 6.8 18/11/1990 16:06:54 3.88 97.36 61 5.2 18/11/1990 16:23:06 3.94 97.34 67 5.7 5/01/1991 15:45:00 5.33 94.14 36 5.1 8/01/1991 21:06:35 2.24 97.06 33 5.2 13/01/1991 10:13:14 5.83 94.75 66 5.0 17/02/1991 03:19:17 2.64 96.12 23 5.4 23/07/1991 13:25:47 3.78 95.93 46 5.8 6/08/1991 02:17:31 3.83 95.37 18 6.0 24/08/1991 00:05:57 3.78 95.21 33 5.1 25/08/1991 05:00:59 5.65 94.12 44 5.2 8/09/1991 18:20:10 6.19 94.83 29 5.0 14/06/1992 10:41:52 4.82 94.26 34 5.0 13/11/1992 16:01:03 2.40 96.27 33 5.8 20/01/1993 02:30:54 3.14 97.63 67 6.2 15/08/1993 03:06:07 5.40 94.64 38 5.1 1/09/1993 14:36:27 2.89 96.20 46 5.3 1/09/1993 14:03:19 2.99 96.12 34 6.5

19 Lanjutan Lampiran 1 2/10/1993 10:30:17 4.76 94.96 69 5.3 7/01/1994 11:05:22 4.84 96.40 173 5.4 11/02/1994 07:56:55 4.83 95.18 97 5.0 13/06/1994 14:16:49 4.10 94.86 33 5.0 31/10/1994 11:48:13 3.02 96.19 29 6.4 20/11/1994 18:34:34 4.33 97.59 153 6.3 14/03/1995 10:27:30 3.05 95.85 30 6.0 2/06/1995 23:29:07 3.43 96.41 40 5.0 3/06/1995 11:57:31 2.97 96.17 30 5.3 30/06/1995 16:29:21 3.73 95.38 54 5.2 24/09/1995 20:19:59 3.46 97.27 35 5.1 22/11/1995 13:27:52 3.09 95.92 21 6.2 22/07/1996 15:49:07 5.76 95.25 33 5.0 13/09/1996 05:04:35 2.78 96.07 33 5.8 21/09/1996 17:04:20 5.85 95.17 33 5.8 10/10/1996 15:21:04 3.44 97.94 33 6.5 15/10/1996 08:02:57 3.01 96.22 33 5.2 27/04/1997 17:37:19 4.61 96.14 33 5.0 11/06/1997 19:12:28 2.88 97.33 57 6.0 20/08/1997 07:15:15 4.36 96.49 33 6.3 26/08/1997 13:17:26 6.45 94.60 114 5.7 4/02/1999 19:28:00 4.03 95.28 55 6.3 15/02/1999 05:46:12 4.93 95.85 33 6.0 24/02/1999 07:20:48 3.37 96.04 33 5.9 22/06/1999 07:11:35 4.80 94.45 33 5.0 21/07/1999 13:46:29 4.57 97.21 175 5.9 24/11/1999 19:51:38 5.94 94.43 62 5.0 10/03/2000 21:32:12 4.74 96.01 33 6.0 3/04/2000 19:02:29 2.49 97.22 33 5.0 19/07/2000 07:11:09 4.25 96.21 33 5.8 17/08/2000 18:40:09 5.77 94.75 68 6.1 29/08/2000 07:14:48 3.11 96.44 33 5.0 4/09/2000 17:25:59 4.17 94.92 33 5.7 9/09/2000 06:01:53 6.42 95.46 229 6.1 31/03/2001 02:26:33 4.05 96.09 50 5.1 12/08/2001 12:06:09 6.32 94.77 33 6.0 12/10/2001 09:34:55 3.25 96.12 35 5.0 31/10/2001 22:04:32 5.36 94.36 33 6.1 4/12/2001 07:19:25 3.72 97.79 139 5.1 22/01/2002 20:15:06 3.49 95.63 33 5.3 24/01/2002 17:56:21 3.52 95.66 33 5.2 24/01/2002 15:24:05 3.51 95.61 33 5.3 24/01/2002 17:52:25 3.54 95.66 33 5.6

Lanjutan Lampiran 1 24/01/2002 18:12:05 3.53 95.66 33 6.1 25/01/2002 14:05:58 3.48 95.68 33 5.0 24/10/2002 21:53:43 6.03 94.42 64 6.2 2/11/2002 01:56:53 2.59 95.89 33 5.0 2/11/2002 01:45:35 2.64 96.25 33 5.2 2/11/2002 01:38:20 2.67 95.90 23 5.2 2/11/2002 09:46:46 2.95 96.39 27 6.5 2/11/2002 01:26:10 2.82 96.08 30 7.3 13/11/2002 15:53:09 3.01 96.09 39 6.0 30/11/2002 04:07:09 2.89 96.21 33 5.2 27/12/2002 13:28:36 4.11 97.72 138 5.7 22/01/2003 02:58:51 4.49 97.57 33 5.7 2/02/2003 06:17:44 4.00 95.43 80 5.2 28/06/2003 07:36:42 2.77 95.76 33 5.2 21/08/2003 16:13:41 2.26 96.53 33 5.1 5/09/2003 01:23:02 5.32 95.90 124 5.9 10/09/2003 08:26:59 2.08 96.82 33 5.8 13/09/2003 20:42:22 4.62 97.65 33 5.3 15/09/2003 12:14:33 2.59 96.07 33 5.1 29/12/2003 15:05:19 4.15 94.71 33 5.1 26/12/2004 21:25:33 4.75 94.85 30 5.0 26/12/2004 08:02:35 5.34 94.48 34 5.1 26/12/2004 13:44:08 3.97 94.39 31 5.1 26/12/2004 05:42:49 5.49 94.29 30 5.1 26/12/2004 07:11:40 4.81 94.97 35 5.2 26/12/2004 10:55:07 4.26 95.13 30 5.2 26/12/2004 14:11:28 3.67 94.02 30 5.2 26/12/2004 03:30:01 4.64 94.00 25 5.2 26/12/2004 05:23:51 3.35 94.09 18 5.2 26/12/2004 08:47:47 4.86 95.10 50 5.3 26/12/2004 03:50:22 5.51 94.25 48 5.3 26/12/2004 03:26:46 4.91 96.40 30 5.3 26/12/2004 16:21:27 5.15 94.32 41 5.4 26/12/2004 04:02:12 3.04 95.89 30 5.4 26/12/2004 06:28:48 4.96 94.79 30 5.4 26/12/2004 03:22:57 5.82 95.09 20 5.4 26/12/2004 01:17:10 4.94 94.27 30 5.5 26/12/2004 03:19:13 3.55 94.29 30 5.5 26/12/2004 16:55:17 3.86 94.50 30 5.5 26/12/2004 21:06:49 4.47 96.34 30 5.5 26/12/2004 03:40:16 5.53 94.33 30 5.6 26/12/2004 19:03:49 4.09 94.22 30 5.6 26/12/2004 01:48:52 5.43 94.46 51 5.7

21 Lanjutan Lampiran 1 26/12/2004 02:34:52 3.99 94.14 30 5.7 26/12/2004 02:59:14 3.18 94.38 30 5.7 26/12/2004 03:51:12 5.05 94.77 30 5.7 26/12/2004 04:02:56 4.98 94.72 47 5.8 26/12/2004 03:24:55 4.47 94.07 26 5.8 26/12/2004 13:56:40 2.78 94.47 30 5.9 26/12/2004 01:25:49 5.50 94.21 30 6.1 26/12/2004 15:06:33 3.65 94.09 17 6.1 26/12/2004 19:19:55 2.79 94.16 30 6.2 26/12/2004 00:58:53 3.30 95.98 30 9.0 27/12/2004 02:53:03 5.36 94.32 46 5.0 27/12/2004 16:18:12 4.82 94.26 38 5.0 27/12/2004 11:58:36 4.83 94.82 30 5.0 27/12/2004 08:11:02 5.48 94.13 19 5.0 27/12/2004 01:22:24 3.35 94.89 47 5.1 27/12/2004 08:21:40 5.52 94.61 51 5.3 27/12/2004 18:09:34 2.75 94.63 42 5.3 27/12/2004 06:59:15 3.03 95.54 27 5.6 27/12/2004 07:47:35 2.71 94.51 23 5.6 27/12/2004 10:05:05 4.72 95.11 49 5.8 27/12/2004 20:10:51 2.93 95.61 28 5.8 27/12/2004 00:32:16 5.48 94.47 33 6.1 27/12/2004 09:39:07 5.35 94.65 35 6.2 17/01/2005 02:53:40 3.87 95.92 42 5.0 19/01/2005 17:32:31 4.70 95.16 30 5.0 22/01/2005 09:24:33 3.60 94.09 30 5.0 22/01/2005 11:07:29 3.58 94.16 30 5.0 22/01/2005 12:58:32 4.91 94.86 30 5.0 22/01/2005 09:18:06 3.63 94.14 30 5.1 23/01/2005 06:16:04 2.60 94.39 27 5.0 23/01/2005 20:36:08 2.71 94.34 26 5.2 24/01/2005 17:59:23 4.75 94.81 48 5.1 24/01/2005 00:39:20 4.70 96.13 19 5.3 25/01/2005 09:54:22 5.45 94.67 30 5.1 26/01/2005 23:43:29 5.34 94.33 47 5.1 26/01/2005 16:50:09 3.24 96.28 35 5.1 26/01/2005 22:00:42 2.70 94.60 22 6.2 27/01/2005 20:09:52 5.51 94.31 30 5.6 29/01/2005 02:55:20 5.07 94.71 46 5.2 29/01/2005 18:20:59 5.51 94.32 30 5.4 31/01/2005 06:45:44 4.05 96.76 30 5.1 1/02/2005 17:14:05 2.80 94.23 26 5.2 1/02/2005 14:15:49 5.18 94.56 24 5.6

Lanjutan Lampiran 1 2/02/2005 09:04:28 5.27 94.50 45 5.2 4/02/2005 06:57:09 2.72 95.75 24 5.0 5/02/2005 04:09:54 2.33 95.07 30 5.1 5/02/2005 04:03:14 2.26 94.99 30 6.0 9/02/2005 01:02:26 2.28 95.16 28 5.0 9/02/2005 13:27:25 4.80 95.12 44 6.0 13/02/2005 02:02:08 5.07 94.80 51 5.5 13/02/2005 01:22:09 5.08 94.79 48 5.7 17/02/2005 05:31:28 4.70 95.16 47 5.9 18/02/2005 19:33:46 5.45 94.42 48 5.8 19/02/2005 03:23:39 5.04 94.44 40 5.0 19/02/2005 14:23:52 2.33 95.29 27 5.0 23/02/2005 02:42:11 2.88 95.46 25 5.1 24/02/2005 07:35:50 2.89 95.73 30 5.6 25/02/2005 20:40:31 2.74 94.26 28 5.1 26/02/2005 12:56:53 2.91 95.59 36 6.8 3/03/2005 17:10:22 3.12 95.73 26 5.0 11/03/2005 08:00:50 2.29 95.07 29 5.1 12/03/2005 22:33:14 5.48 94.69 59 5.2 13/03/2005 22:12:46 5.49 94.60 52 5.5 16/03/2005 06:39:48 5.44 94.43 30 5.3 17/03/2005 23:20:49 4.86 95.09 60 5.7 19/03/2005 03:01:17 4.00 95.67 48 5.2 25/03/2005 01:04:53 5.49 94.37 39 5.9 28/03/2005 17:03:34 2.04 96.46 30 5.0 28/03/2005 23:44:45 2.86 96.35 27 5.0 28/03/2005 16:58:36 2.28 96.18 30 5.1 28/03/2005 19:54:01 2.47 96.76 26 5.1 28/03/2005 18:50:14 2.39 97.16 30 5.2 28/03/2005 18:48:53 2.75 96.05 30 5.4 28/03/2005 16:34:40 2.34 96.60 28 5.4 28/03/2005 23:39:48 2.91 96.39 28 5.4 28/03/2005 16:44:30 2.09 96.50 30 5.5 28/03/2005 23:37:31 2.89 96.41 29 5.6 28/03/2005 16:09:37 2.09 97.11 30 8.6 29/03/2005 20:41:38 2.35 97.33 30 5.1 29/03/2005 14:16:06 2.55 96.07 24 5.1 29/03/2005 10:56:54 2.23 96.49 26 5.2 29/03/2005 05:25:25 2.14 96.63 26 5.3 29/03/2005 05:16:30 2.65 96.58 30 5.9 30/03/2005 17:29:22 2.93 95.42 25 5.7 30/03/2005 16:19:41 2.99 95.41 22 6.3 31/03/2005 14:27:27 5.11 94.58 30 5.0

23 Lanjutan Lampiran 1 31/03/2005 08:30:27 2.52 96.18 25 5.0 1/04/2005 05:55:56 2.26 96.43 30 5.0 1/04/2005 07:40:27 2.29 96.37 30 5.1 1/04/2005 14:50:41 2.70 97.09 30 5.1 1/04/2005 14:18:08 2.17 96.69 28 5.1 1/04/2005 10:37:46 2.87 96.39 26 5.4 2/04/2005 16:24:14 2.89 96.40 28 5.1 3/04/2005 11:16:46 2.80 95.89 30 5.0 3/04/2005 12:21:20 2.97 96.28 30 5.1 3/04/2005 03:10:56 2.02 97.94 36 6.3 4/04/2005 19:37:10 4.77 94.82 49 5.2 5/04/2005 13:01:55 2.41 96.30 30 5.0 10/04/2005 10:27:57 2.86 95.34 24 5.4 11/04/2005 09:53:37 2.10 96.85 28 5.0 11/04/2005 09:04:31 2.08 96.83 26 5.5 11/04/2005 06:11:12 2.17 96.76 24 6.1 15/04/2005 13:08:54 2.93 96.33 26 5.4 19/04/2005 15:10:15 2.36 96.30 26 5.0 23/04/2005 10:31:45 2.75 95.99 32 5.2 25/04/2005 03:18:31 3.03 94.07 25 5.0 28/04/2005 14:07:34 2.13 96.80 22 6.2 3/05/2005 07:29:10 2.46 95.88 21 5.0 4/05/2005 00:44:51 3.05 96.38 40 5.2 4/05/2005 05:58:54 4.71 94.87 46 5.3 5/05/2005 01:14:47 5.23 94.27 30 5.1 9/05/2005 01:30:52 5.10 94.84 30 5.5 12/05/2005 23:47:30 2.42 96.27 22 5.0 12/05/2005 16:04:24 5.06 94.47 30 5.2 21/05/2005 23:01:16 5.28 94.80 55 5.9 24/05/2005 09:37:57 2.65 94.53 30 5.2 25/05/2005 14:42:15 2.91 95.60 24 5.1 28/05/2005 06:23:31 2.04 96.67 24 5.0 31/05/2005 07:28:05 5.46 94.65 53 5.0 31/05/2005 02:29:31 5.24 94.43 30 5.5 8/06/2005 06:28:11 2.17 96.72 23 6.1 11/06/2005 17:36:56 2.12 96.60 24 5.1 13/06/2005 02:26:51 2.74 95.64 22 5.0 13/06/2005 19:59:53 2.74 94.17 18 5.9 17/06/2005 21:26:03 2.14 96.80 27 5.3 17/06/2005 02:37:39 5.62 94.75 57 5.4 20/06/2005 07:38:35 2.30 96.35 30 5.0 20/06/2005 18:50:40 4.95 94.75 30 5.0 24/06/2005 21:45:12 4.81 95.15 52 5.3

Lanjutan Lampiran 1 5/07/2005 07:57:29 2.26 95.06 28 5.1 21/07/2005 01:42:44 4.34 96.27 14 5.1 22/07/2005 09:50:08 2.43 97.14 43 5.1 23/07/2005 00:44:57 5.46 94.42 30 5.1 23/07/2005 22:53:35 5.11 94.80 48 5.6 27/07/2005 13:57:13 2.64 96.02 24 5.0 28/07/2005 02:43:59 2.73 95.62 22 5.0 30/07/2005 15:13:20 5.18 94.48 38 5.8 2/08/2005 20:56:36 5.25 94.26 36 5.0 5/08/2005 13:21:31 2.16 96.42 26 5.0 17/08/2005 07:43:48 2.01 97.83 30 5.0 28/08/2005 14:09:18 4.39 95.22 26 5.0 28/08/2005 04:43:41 5.55 94.58 51 5.4 31/08/2005 07:20:20 5.36 95.79 48 5.0 1/09/2005 16:42:39 5.07 94.79 30 5.3 3/09/2005 21:00:04 4.75 95.14 54 5.0 10/09/2005 16:57:47 4.86 95.04 41 5.8 16/09/2005 17:19:27 2.43 96.31 24 5.1 20/09/2005 15:00:00 4.51 95.40 51 5.2 22/09/2005 12:30:08 3.98 95.97 49 5.2 29/09/2005 18:12:26 5.22 94.51 48 5.2 3/10/2005 22:09:26 5.54 94.39 47 5.5 4/10/2005 12:23:25 5.56 94.28 44 5.3 5/10/2005 08:46:42 5.23 95.58 18 5.7 11/10/2005 15:05:40 4.82 95.10 30 6.0 16/10/2005 19:03:23 2.03 97.95 28 5.7 26/10/2005 00:39:33 4.03 94.30 31 5.1 27/10/2005 04:16:29 2.74 95.83 30 5.3 28/10/2005 03:07:35 2.31 96.36 27 5.0 28/10/2005 17:23:29 2.36 96.21 30 5.1 19/11/2005 06:38:55 2.82 95.47 30 5.1 19/11/2005 14:09:21 2.03 96.79 31 5.2 19/11/2005 14:10:13 2.16 96.79 21 6.5 5/12/2005 04:46:49 3.40 95.27 32 5.2 6/12/2005 05:40:11 2.39 96.28 30 5.0 18/12/2005 04:23:10 2.84 95.92 18 5.7 1/01/2006 08:47:13 4.74 95.14 51 5.7 13/01/2006 14:47:30 4.87 94.75 42 5.0 31/01/2006 19:15:51 2.70 96.07 20 5.9 6/02/2006 07:05:02 2.22 96.45 27 5.2 13/02/2006 12:05:43 2.41 96.25 26 5.0 13/02/2006 09:32:09 2.86 95.45 25 5.2 26/02/2006 21:32:49 5.61 94.69 30 5.2

25 Lanjutan Lampiran 1 1/03/2006 14:36:02 2.67 95.90 20 5.1 2/03/2006 17:15:46 4.96 94.49 30 5.2 8/03/2006 06:33:38 4.00 96.25 30 5.4 16/03/2006 15:12:16 5.07 94.78 50 5.3 19/03/2006 04:24:32 4.13 96.05 48 5.3 22/03/2006 10:08:49 2.72 95.68 25 5.0 28/03/2006 08:35:43 3.46 97.22 30 5.0 1/04/2006 10:34:48 2.27 94.93 28 5.0 2/04/2006 08:30:27 2.41 96.39 26 5.2 22/04/2006 23:22:38 2.06 96.45 27 5.1 22/04/2006 23:42:23 2.15 96.50 26 5.1 22/04/2006 23:23:06 2.09 96.49 25 5.4 8/05/2006 01:43:41 3.16 97.10 11 5.2 13/05/2006 03:11:43 5.51 94.44 45 6.0 14/06/2006 07:24:06 2.65 94.37 29 5.1 14/06/2006 00:14:33 5.51 94.57 52 5.2 2/08/2006 18:13:59 3.97 95.97 45 5.0 11/08/2006 20:54:14 2.40 96.35 22 6.2 12/08/2006 06:15:28 2.19 96.36 28 5.0 13/08/2006 08:41:46 5.52 94.66 30 5.3 23/08/2006 18:31:51 4.72 95.10 30 5.1 16/09/2006 06:17:47 5.12 94.78 49 5.6 12/10/2006 05:30:35 4.94 95.01 30 5.5 18/11/2006 13:55:21 4.75 94.78 32 5.9 18/11/2006 13:57:54 4.74 94.77 29 5.9 25/11/2006 18:50:25 2.99 97.01 53 5.0 6/12/2006 12:06:39 4.86 96.23 30 5.2 9/12/2006 09:24:47 5.08 94.75 30 5.5 17/12/2006 21:10:22 4.82 95.02 36 5.8 19/12/2006 12:48:17 2.46 98.00 66 5.2 3/01/2007 12:47:30 5.45 94.35 30 5.4 22/01/2007 16:44:34 2.82 95.81 24 5.3 8/02/2007 01:54:55 2.70 95.65 30 5.1 14/02/2007 20:11:58 5.21 94.26 30 5.3 1/03/2007 02:01:01 3.78 96.34 74 5.6 7/04/2007 09:51:52 2.92 95.70 30 6.1 27/04/2007 08:02:50 5.36 94.64 38 6.3 1/05/2007 19:44:20 5.51 94.62 52 5.0 18/05/2007 15:57:25 4.11 96.03 30 5.2 22/05/2007 03:41:12 2.01 96.75 30 5.0 23/05/2007 20:19:14 2.63 95.55 39 5.2 9/06/2007 14:59:50 2.61 96.04 24 5.2 24/06/2007 13:47:37 5.42 94.58 30 5.1

Lanjutan Lampiran 1 10/07/2007 18:28:30 3.33 94.25 24 5.0 21/07/2007 12:53:03 5.00 97.46 30 5.2 24/07/2007 14:51:32 2.27 98.00 62 5.3 18/08/2007 04:38:23 2.08 96.69 30 5.0 29/09/2007 05:32:44 2.92 95.54 35 5.7 29/09/2007 05:37:07 2.90 95.52 35 5.8 1/10/2007 14:03:34 4.09 96.58 35 5.0 17/10/2007 02:55:30 2.97 96.46 40 5.0 16/11/2007 21:23:26 2.62 94.49 27 5.1 21/11/2007 03:30:13 3.06 96.36 41 5.1 22/11/2007 23:02:13 4.74 95.06 49 5.9 7/12/2007 08:09:25 5.46 94.67 72 5.0 9/12/2007 11:32:13 2.22 96.76 35 5.0 22/12/2007 12:26:19 2.09 96.80 31 5.9 28/12/2007 05:24:15 5.42 95.66 20 5.1 5/01/2008 20:01:55 5.48 94.68 57 5.4 20/02/2008 09:32:06 2.64 95.78 22 5.0 20/02/2008 09:05:09 2.70 96.25 35 5.1 20/02/2008 08:36:39 2.54 96.06 35 5.2 20/02/2008 09:11:26 2.50 95.84 24 5.3 20/02/2008 08:28:20 2.61 96.14 35 5.4 20/02/2008 08:08:30 2.77 95.96 26 7.5 21/02/2008 03:47:44 2.48 96.08 35 5.0 25/02/2008 09:53:40 2.64 96.07 35 5.0 26/02/2008 11:38:41 2.64 95.92 35 5.1 5/03/2008 17:04:08 5.08 94.82 56 5.3 10/03/2008 05:22:46 2.38 95.60 35 5.0 15/03/2008 14:43:26 2.70 94.59 20 6.0 29/03/2008 17:30:50 2.86 95.30 20 6.5 4/04/2008 05:43:19 2.63 96.12 25 5.0 4/04/2008 00:27:38 2.90 95.43 36 5.2 8/05/2008 11:31:24 5.51 94.70 35 5.0 13/05/2008 10:29:19 4.68 95.09 35 5.6 14/07/2008 04:44:54 2.23 96.54 42 5.5 14/07/2008 04:44:47 2.15 95.05 30 5.5 10/09/2008 04:02:17 2.63 95.47 19 5.0 10/09/2008 00:18:51 2.40 96.11 15 5.1 10/09/2008 03:00:26 2.50 96.09 10 5.8 14/11/2008 22:56:34 2.29 96.20 35 5.1 21/12/2008 13:47:53 4.77 95.16 30 5.7 12/01/2009 22:14:03 2.83 95.50 10 5.0 11/02/2009 03:11:29 4.85 95.98 10 5.0 4/03/2009 10:56:41 2.78 95.26 10 5.3

27 Lanjutan Lampiran 1 12/03/2009 10:05:06 4.53 94.76 10 5.1 24/03/2009 04:35:41 5.17 94.20 10 5.2 8/05/2009 13:19:03 3.18 97.55 17 5.3 21/07/2009 06:51:53 4.38 96.40 19 5.1 15/08/2009 04:04:29 4.39 96.53 16 5.2 25/08/2009 20:26:51 5.28 94.77 24 5.0 28/08/2009 16:45:21 5.45 94.77 22 5.2 26/11/2009 05:27:37 4.89 96.00 10 5.0 9/12/2009 21:29:05 2.75 96.09 10 5.7 19/12/2009 13:43:54 2.59 95.90 10 5.4 22/01/2010 06:46:22 3.12 94.28 10 5.2 17/03/2010 09:44:55 4.34 95.69 14 5.1 6/04/2010 22:28:27 2.54 96.78 10 5.0 6/04/2010 22:54:07 2.33 97.10 29 5.4 6/04/2010 22:26:09 2.30 96.87 25 5.6 6/04/2010 22:15:04 2.31 97.11 43 7.6 7/04/2010 04:22:17 2.64 96.99 25 5.0 12/04/2010 10:28:27 4.60 96.39 10 5.8 9/05/2010 05:59:45 3.65 96.09 53 7.1 11/05/2010 12:17:49 3.41 95.89 47 5.5 3/06/2010 09:24:17 4.54 95.76 69 5.4 21/08/2010 05:42:53 2.18 96.60 24 5.8 29/09/2010 11:33:34 5.02 94.84 53 5.0 30/09/2010 09:54:10 5.02 94.82 19 5.2 15/10/2010 12:43:56 3.62 95.49 35 5.0 18/12/2010 22:56:44 5.34 94.56 49 5.0 21/12/2010 14:07:49 2.66 95.87 10 5.6 23/12/2010 00:01:35 3.72 95.88 10 5.3 15/01/2011 11:36:07 2.31 96.33 19 5.0 15/01/2011 11:45:21 2.31 96.35 27 5.1 15/01/2011 16:26:08 2.35 96.28 15 5.4 15/01/2011 11:23:53 2.40 96.30 10 5.7 18/01/2011 11:33:44 2.50 96.41 10 5.7 22/01/2011 07:34:16 2.79 95.55 10 5.3 22/01/2011 07:38:59 2.80 95.75 10 5.4 26/01/2011 15:42:30 2.16 96.81 10 5.6 29/04/2011 08:56:49 3.88 95.75 56 5.5 21/08/2011 08:18:19 4.65 94.98 53 5.1 5/09/2011 17:55:12 2.78 97.93 89 6.6 16/10/2011 17:16:20 2.32 96.05 35 5.7 30/10/2011 02:02:12 4.88 95.99 10 5.0 1/01/2012 18:09:06.3 4.46 96.49 10 5.2 13/01/2012 20:03:42.5 2.35 96.11 11 5.3

Lanjutan Lampiran 1 22/02/2012 12:02:44 4.89 94.17 37 5.4 5/03/2012 06:55:29 4.19 97.10 15 5.0 11/04/2012 12:22:17 3.19 94.01 64 5.3 11/04/2012 09:00:54 2.67 95.69 10 6.0 26/04/2012 19:21:44 2.74 94.51 10 5.4 29/04/2012 08:09:05 2.74 94.54 10 5.6 12/05/2012 00:08:00 2.04 94.07 96 5.0 5/06/2012 11:01:19 5.37 94.59 54 5.3 23/06/2012 04:34:53 2.88 97.86 90 6.3 22/07/2012 09:39:11 2.51 95.72 18 5.1 25/07/2012 00:27:45 2.52 96.12 10 6.1 4/08/2012 11:24:14 4.67 96.36 10 5.1 19/08/2012 01:57:02 4.84 94.64 10 5.0 22/12/2012 03:50:07 5.06 94.15 37 5.3 10/01/2013 13:47:06 4.61 95.11 58 6.0 21/01/2013 22:22:54 4.77 95.99 10 5.9 3/03/2013 22:24:12 2.71 95.55 10 5.1 29/04/2013 13:43:00 3.70 95.95 58 5.2 2/07/2013 15:36:47 4.62 96.81 10 5.2 2/07/2013 13:55:41 4.62 96.79 10 5.4 2/07/2013 07:37:03 4.70 96.61 10 6.2 9/07/2013 01:05:38 2.15 96.21 15 5.2 17/08/2013 04:24:06 5.35 94.22 38 5.1 13/10/2013 17:32:45 3.90 95.86 56 5.4 22/10/2013 05:40:40 5.02 95.89 10 5.4

29

Lampiran 2. QQ-Plot hazard rate pada Tabel 1 dan 2 (Sebelum data ditransformasi).

Lampiran 3. Box-plot nilai hazard rate pada Tabel 1 dan 2 untuk melihat nilai pencilan (outlier).

1,6 1,4 1,2 1,0 0,8 0,6 0,4 0,2 0,0 Ha za rd ra te 1

Boxplot of Hazard rate 1

0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0,0 H a za rd r a te 2

31

Lampiran 4. Hasil transformasi Box-Cox nilai hazard rate pada Tabel 1 dan 2.

Keterangan : 𝑇𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚1 = (𝐻𝑎𝑧𝑎𝑟𝑑 𝑟𝑎𝑡𝑒1)−0.5. 𝑇𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚2 = (𝐻𝑎𝑧𝑎𝑟𝑑 𝑟𝑎𝑡𝑒2)−0.5

Titik Hazard rate1 Transform1 Titik Hazard rate2 Transform2

0 0,0041 15.61737619 0 0,0041 15.61737619 1 0,0041 15.61737619 1 0,0041 15.61737619 2 0,0125 8.94427191 2 0,0124 8.980265101 3 0,0169 7.692307692 3 0,0168 7.715167498 4 0,0085 10.84652289 4 0,0085 10.84652289 5 0,0086 10.78327732 5 0,0086 10.78327732 6 0,0087 10.72112535 6 0,0087 10.72112535 7 0,0132 8.703882798 7 0,0131 8.737040567 8 0,0089 10.5999788 8 0,0089 10.5999788 9 0,0181 7.432941462 9 0,0178 7.49531689 10 0,0351 5.337605127 10 0,0344 5.39163866 11 0,0215 6.819943395 11 0,0214 6.83585927 12 0,0048 14.43375673 12 0,0048 14.43375673 13 0,0122 9.053574604 13 0,0121 9.090909091 14 0,0123 9.016696347 14 0,0122 9.053574604 15 0,015 8.164965809 15 0,0149 8.192319205 16 0,0127 8.873565094 16 0,0125 8.94427191 17 0,0102 9.90147543 17 0,0102 9.90147543 19 0,0156 8.00640769 19 0,0155 8.032193289 20 0,0185 7.352146221 20 0,0183 7.39221271 21 0,0134 8.638684256 21 0,0133 8.671099695 22 0,0419 4.885319687 22 0,041 4.938647983 23 0,0258 6.225728064 23 0,0254 6.274558051 24 0,1518 2.566635012 24 0,132 2.752409413 26 0,2984 1.830630065 26 0,2639 1.946616073 27 0,2917 1.851534401 27 0,2514 1.994423411 28 0,3521 1.68526029 28 0,3149 1.782024496 29 0,2241 2.112414168 29 0,2034 2.217300351 30 0,45 1.490711985 30 0,368 1.648451183

33

RIWAYAT HIDUP

Penulis dilahirkan di Langsa, Aceh pada tanggal 02 Oktober 1992 sebagai anak keempat dari pasangan Bapak Muhammad, SH dan Ibu Mardhiah, SPd. Tahun 2010 penulis lulus dari SMA Negeri 1 Langsa dan pada tahun yang sama penulis diterima sebagai mahasiswa di Institut Pertanian Bogor melalui jalur Beasiswa Utusan Daerah (BUD) di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam. Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Kalkulus 2 program S1 pada semester genap tahun ajaran 2011/2012, asisten mata kuliah Metode Statistika pada semester ganjil tahun ajaran 2012/2013, asisten mata kuliah Persamaan Diferensial Biasa pada semester genap tahun ajaran 2012/2013, asisten mata kuliah Analisis Numerik pada semester ganjil tahun ajaran 2013/2014, dan asisten mata kuliah Proses Stokastik Dasar semester genap tahun ajaran 2013/2014. Penulis juga aktif berorganisasi sebagai staff divisi Human Resource Development (HRD) di SERUM-G FMIPA pada tahun 2012. Panitia pesta sains tahun 2011, 2012, dan 2013. Penulis juga pernah meraih prestasi Juara II Lomba Kalkulus Se IPB tahun 2011, Juara III Lomba Karsa Cipta FMIPA IPB tahun 2012, Juara Regional Jabodetabek ON MIPA bidang Matematika 2013, Peserta ON MIPA Tingkat Nasional di Yogyakarta tahun 2013, Juara 1 Kompetisi Statistika Dasar tahun 2013, dan peraih medali perak bidang matematika pada ajang ON MIPA Tingkat Nasional tahun 2014.