PENERAPAN METODE PERBAIKAN ASM PADA MASALAH TRANSPORTASI TAK SEIMBANG DALAM PENDISTRIBUSIAN
SEMEN PADANG DI PT. MEGA ELTRA CABANG MEDAN
SKRIPSI
SINTYA SURYA NINGSIH 160803091
PROGRAM STUDI S-1 MATEMATIKA DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PEGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2020
PENERAPAN METODE PERBAIKAN ASM PADA MASALAH TRANSPORTASI TAK SEIMBANG DALAM PENDISTRIBUSIAN
SEMEN PADANG DI PT. MEGA ELTRA CABANG MEDAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
SINTYA SURYA NINGSIH 160803091
PROGRAM STUDI S-1 MATEMATIKA DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PEGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2020
PERNYATAAN ORISINALITAS
PENERAPAN METODE PERBAIKAN ASM PADA MASALAH TRANSPORTASI TAK SEIMBANG DALAM PENDISTRIBUSIAN
SEMEN PADANG DI PT. MEGA ELTRA CABANG MEDAN
SKRIPSI
Saya menyatakan bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Oktober 2020
Sintya Surya Ningsih 160803091
ii
PENERAPAN METODE PERBAIKAN ASM PADA MASALAH TRANSPORTASI TAK SEIMBANG DALAM PENDISTRIBUSIAN
SEMEN PADANG DI PT. MEGA ELTRA CABANG MEDAN
ABSTRAK
Masalah transportasi adalah masalah pendistribusian barang dari beberapa sumber (supply) ke beberapa tujuan (demand) dengan tujuan untuk meminimumkan biaya pendistribusian. Masalah transportasi sering terjadi pada dunia bisnis, salah satunya terdapat pada PT. Mega Eltra Cabang Medan yang mendistribusikan produk Semen Padang, Cat Sigma, Pupuk Pusri dan Obat-obatan Pertanian ke beberapa daerah di Provinsi Sumatera Utara. Permasalahan yang dihadapi oleh perusahaan tersebut adalah besarnya biaya pendistribusian produk Semen Padang yang disebabkan adanya masalah transportasi tak seimbang atau ketidakseimbangan antara jumlah persediaan dengan jumlah permintaan. Metode Perbaikan ASM adalah salah satu metode transportasi untuk memecahkan masalah transportasi tak seimbang dengan iterasi yang lebih sedikit. Berdasarkan hasil penelitian ini maka diperoleh bahwa biaya distribusi dengan menggunakan metode Perbaikan ASM Rp 481.995.000, sebelumnya perusahaan PT. Mega Eltra Cabang Medan harus mengeluarkan biaya distribusi sebesar Rp 594.050.000. Sehingga perusahaan tersebut mengalami penurunan biaya distribusi sebesar 18,862%.
Kata Kunci: Masalah Transportasi, Transportasi Tak Seimbang, Metode Perbaikan ASM
iii
APPLICATION OF THE REVISED VERSION OF ASM METHOD IN UNBALANCED TRANSPORTATION PROBLEMS IN DISTRIBUTION
SEMEN PADANG AT PT. MEGA ELTRA CABANG MEDAN
ABSTRACT
Transportation problem is a problem of distributing goods from several sources (supply) to several destinations (demand) with the aim of minimizing distribution costs. Transportation problems often occur in the business world, one of which is at PT. Mega Eltra Cabang Medan which distributes Semen Padang products, Sigma Paint, Pusri Fertilizers and Agricultural Medicines to several areas in North Sumatra Province. The problem faced by this company is the high cost of distributing Semen Padang products due to unbalanced transportation problems or an imbalance between the amount of supply and the amount of demand. The Revised Version of ASM Method is one of the transportation methods to solve the problem of unbalanced transportation in fewer iterations. Based on the results of this study, it was found that the distribution costs using the Revised Version of ASM Method were Rp. 481,995,000, previously the company PT. Mega Eltra Cabang Medan must pay a distribution fee of Rp. 594,050,000. So that the company experienced a decrease in distribution costs by 18.862%.
Keywords: Transportation Problems, Unbalanced Transportation, Revised Version of ASM Method
iv
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Allah SWT Yang Maha Pemurah dan Maha Penyayang, dengan limpah karunia-Nya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Penerapan Metode Perbaikan ASM pada Masalah Transportasi Tak Seimbang dalam Pendistribusian Semen Padang PT.
Mega Eltra Cabang Medan. Penulis mengucapkan terima kasih kepada semua pihak yang telah membantu dan membimbing penulis dalam penyusunan skripsi ini. Ucapan terima kasih penulis sampaikan kepada:
1. Bapak Prof. Dr. Runtung, S.H., M.Hum. selaku rektor Universitas Sumatera Utara dan seluruh jajaran rektorat Universitas Sumatera Utara.
2. Bapak Prof. Dr. Kerista Sebayang, M.S. selaku Dekan FMIPA USU, Ibu Dr. Nursahara Pasaribu, M.Sc. selaku Wakil Dekan I FMIPA USU, Bapak Drs. Parapat Gultom, MSIE, Ph.D selaku Wakil Dekan II FMIPA USU dan Bapak Saharman Gea, S.Si., M.Si. Ph.D selaku Wakil Dekan III FMIPA USU.
3. Bapak Dr. Suyanto, M.Kom dan Bapak Drs. Rosman Siregar, M.Si selaku Ketua Departemen dan Sekretaris Departemen Matematika FMIPA USU dan seluruh dosen Departemen Matematika FMIPA USU serta seluruh Staf Administrasi Departemen Matematika FMIPA USU.
4. Ibu Dr. Esther Sorta Mauli Nababan, M.Sc selaku dosen pembimbing yang telah memberikan bimbingan dan pengarahan kepada penulis sehingga skripsi ini dapat diselesaikan.
5. Bapak Dr. Suyanto, M.Kom dan Bapak Dr. Syahriol Sitorus, S.Si., M.IT.
selaku dosen pembanding yang telah memberikan segala saran dan masukan dalam proses penyelesaian skripsi ini.
6. Bapak Dr. Syahriol Sitorus, S.Si., M.IT. selaku dosen penasehat akademik yang senantiasa membantu dan membimbing selama masa perkuliahan S1- Matematika.
7. Bapak Suparmin selaku pihak dari PT. Mega Eltra Cabang Medan yang telah mengizinkan dan membantu penulis untuk mengambil data di PT.
Mega Eltra Cabang Medan dalam menyelesaikan skripsi ini.
v
8. Orang tua penulis, Ayahanda Supriadi, dan Ibunda Poniseh, serta saudara maupun saudari penulis, Muhammad Syafriandi, Dendy Fadly Agustian, Siti Permata Sari, dan Dyan Cahya Meilani Poetri.
9. Seluruh teman-teman Matematika stambuk 2016, terkhusus kepada Dea, Dinna, Fini, Firza, Hafiza, Muthia, Nisa, Rani, Siti, Puput, Atun, dan Depi, yang telah berjuang bersama-sama, sebagai tempat betukar pikiran dalam mencari tempat penelitian dan memberikan dukungan serta semangat kepada penulis.
10. Serta pihak-pihak yang berpengaruh dalam proses penyelesaian skripsi ini yang tidak dapat penulis sebutkan satu persatu.
Semoga segala bentuk bantuan yang telah diberikan kepada penulis mendapat balasan yang lebih baik dari Allah SWT. Penulis memohon maaf apabila terdapat kesalahan dalam penulisan skripsi ini. Semoga skripsi ini dapat bermanfaat bagi pembaca.
Medan, Oktober 2020
Sintya Surya Ningsih 160803091
vi DAFTAR ISI
Halaman
PENGESAHAN SKRIPSI i
ABSTRAK ii
ABSTRACT iii
PENGHARGAAN iv
DAFTAR ISI vi
DAFTAR TABEL viii
DAFTAR GAMBAR x
DAFTAR LAMPIRAN xi
BAB 1 PENDAHULUAN
1.1 Latar Belakang 1
1.2 Rumusan Masalah 3
1.3 Batasan Masalah 3
1.4 Tujuan Penelitian 4
1.5 Manfaat Penelitian 4
BAB 2 TINJAUAN PUSTAKA
2.1 Linear Programming 5
2.2 Karakteristik-karakteristik dalam Linear
Programming 5
2.3 Masalah Transportasi 6
2.4 Model Transportasi 8
2.4.1 Masalah Transportasi Seimbang 9 2.4.2 Masalah Transportasi Tak Seimbang 9
2.5 Metode Transportasi 10
2.6 Metode Perbaikan ASM 12
BAB 3 METODE PENELITIAN
3.1 Waktu dan Tempat 16
3.2 Metode Penalitian 16
3.3 Kerangka Peneltian 18
BAB 4 HASIL DAN PEMBAHASAN
4.1 Pengumpulan Data 19
4.1.1 Data Persediaan Semen Padang 19 4.1.2 Data Permintaan Semen Padang 19 4.1.3 Data Biaya Distribusi dari Gudang ke Toko
Konsumen 20
4.2 Pengolahan Data 21
4.3 Perhitungan Metode Pemecahan Masalah 26
4.4 Analisis Hasil Perhitungan 47
BAB 5 KESIMPULAN DAN SARAN
vii
5.1 Kesimpulan 50
5.2 Saran 50
DAFTAR PUSTAKA 51
LAMPIRAN 52
viii
DAFTAR TABEL
Nomor
Tabel Judul Halaman
2.1 Tabel Transportasi 7
4.1 Data Kapasitas Persediaan Semen Padang Tahun 2019 19 4.2 Data Penyaluran Semen Padang Tahun 2019 20 4.3 Data Biaya Transportasi dari Gudang ke Toko Konsumen
Tahun 2019 20
4.4 Data Kapasitas Persediaan, Permintaan, dan Biaya Distribusi Semen Padang dari Gudang ke Toko Konsumen Tahun 2019
23 4.5 Tabel Permasalahan Transportasi
4.6 Tabel Masalah Transportasi Tak Seimbang 23 4.7 Tabel Masalah Transportasi Seimbang dengan Penambahan
Dummy 26
4.8 Hasil Reduksi Kolom 29
4.9 Penggantian Nilai Dummy dengan Nilai Reduksi Terbesar 29
4.10 Hasil Reduksi Baris 31
4.11 Hasil Reduksi Kolom 32
4.12 Hasil Penetapan Indeks e 33
4.13 Hasil Pengalokasian (1) 33
4.14 Hasil Pengalokasian (2) 34
4.15 Hasil Pengalokasian (3) 34
4.16 Hasil Pengalokasian (4) 35
4.17 Hasil Pengalokasian (5) 35
4.18 Hasil Pengalokasian (6) 36
4.19 Hasil Pengalokasian (7) 36
4.20 Hasil Pengalokasian (8) 37
4.21 Hasil Pengalokasian (9) 37
4.22 Perbaikan Tabel Transportasi 38
4.23 Perbaikan Tabel Transportasi dengan Menggunakan Biaya
yang Telah Direduksi 39
4.24 Hasil Pengulangan Reduksi Baris 40
4.25 Hasil Pengulangan Reduksi Kolom 41
4.26 Hasil Pengulangan Reduksi Baris 42
4.27 Hasil Pengulangan Penetapan Indeks e 43
4.28 Hasil Pengulangan Pengalokasian (1) 43
4.29 Hasil Pengulangan Pengalokasian (2) 44
ix
4.30 Hasil Pengulangan Pengalokasian (3) 44
4.31 Hasil Pengulangan Pengalokasian (4) 45
4.32 Hasil Akhir Pengalokasian dengan Persediaan dan
Permintaan yang Telah Terpenuhi 45
4.33 Perbaikan Tabel Transportasi 46
x
DAFTAR GAMBAR
Nomor
Gambar Judul Halaman
2.1 Gambaran Umum Model Transportasi 7
3.1 Kerangka Penelitian 18
4.1 Jaringan Transportasi dari Gudang ke Toko Konsumen 22 4.2 Gambar Penyelesaian Masalah Transportasi dengan
Program POM for Windows 47
xi
DAFTAR LAMPIRAN
Nomor
Lampiran Judul Halaman
1 Surat Izin Pengambilan Data 52
2 Surat Konfirmasi Izin Pengambilan Data 53
3 Data Persediaan Semen Padang Periode Januari 2019 –
Desember 2019 54
4 Data Penyaluran Semen Padang Periode Januari 2019 –
Desember 2019 55
5 Data Biaya Transportasi Pengiriman Semen Padang
Periode Januari 2019 – Desember 2019 56
6 Daftar Biaya Pendistribusian Semen Padang PT. Mega Eltra Cabang Medan Periode Januari 2019 – Desember 2019
57
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Permasalahan transportasi dapat diselesaikan dengan metode transportasi. Terdapat beberapa metode untuk menyelesaikan masalah transportasi baik yang menggunakan solusi fisibel awal kemudian menggunakan solusi akhir maupun yang tanpa menggunakan fisibel awal. Beberapa metode yang menggunakan fisibel awal yaitu Metode Pojok Barat Laut (North West Corner Method), Metode Biaya Terendah (Least Cost Method), dan Metode VAM (Vogel Approximation), kemudian menggunakan solusi akhir untuk menguji optimalitas yaitu Metode Batu Loncat (Stepping Stone), atau Metode MODI (Modified Distribution) (Winston, 2004).
Kelemahan dari serangkaian metode tersebut adalah memiliki dua proses penyelesaian dan dipandang kurang efisien.
Perkembangan ilmu pengetahuan maju sangat pesat sehingga para ahli dapat menemukan metode-metode transportasi baru yang lebih efisien dan sederhana untuk memecahkan masalah transportasi. Dalam perhitungannya metode-metode tersebut langsung didapatkan solusi optimum tanpa harus mencari solusi fisibel awalnya terlebih dahulu atau disebut dengan metode langsung. Beberapa metode langsung telah berhasil memberikan solusi optimal pada masalah transportasi seimbang, sedangkan untuk masalah transportasi tak seimbang belum tentu menghasilkan solusi optimal.
Salah satu metode langsung adalah Metode ASM. Metode ini diperkenalkan oleh Abdul Quddoos, Dr. Shakeel Javaid, dan Prof. Mohd Masood Khalid. Quddoos et al.
(2012) dalam jurnalnya berjudul A New Method for Finding an Optimal Solution for Transportation Problems menyimpulkan bahwa karakteristik dari metode ASM ini menitikberatkan pada nilai hasil reduksi yang bernilai nol, lanjut ke penetapan indeks pada angka nol, hingga pengalokasian dari indeks terkecil. Metode ASM ini telah berhasil memberikan solusi optimal pada masalah transportasi seimbang tetapi tidak memberikan solusi optimal pada masalah tak seimbang. Quddoos et al. (2016) melakukan penelitian kembali yang berjudul A Revised Version of ASM-Method for Solving Transportation Problem. Dari hasil penelitian tersebut dapat disimpulkan
bahwa metode perbaikan ASM pada masalah transportasi tak seimbang terdapat Initial Basic Feasible Solution (IBFS) yang sangat dekat ke solusi optimum.
Sehingga dengan adanya metode perbaikan ASM dapat memberikan solusi optimal pada masalah transportasi tak seimbang. Pada metode perbaikan ASM terdapat algoritma berupa penambahan baris atau kolom dummy dimana biaya pada baris atau kolom dummy tersebut bernilai nol sehingga sangat berpengaruh terhadap hasil reduksi. Maka harus diberikan penambahan algoritma untuk mengoptimalkan angka nol yang muncul pada baris atau kolom dummy.
Masalah transportasi sering terjadi pada dunia bisnis. Terbukti bahwa saat ini perusahaan melebarkan sayapnya untuk meningkatkan hasil produksinya agar mendapatkan keuntungan yang maksimal dalam mengirimkan hasil produksinya dengan waktu yang tepat dan biaya angkutan yang minimum. Dalam hal ini perusahaan memerlukan suatu strategi pemecahan suatu masalah transportasi yang bisa memberikan solusi optimal berupa peningkatan keuntungan yang berguna untuk meminimumkan total biaya pendistribusian dengan tetap memenuhi kebutuhan permintaaan barang dikalangan konsumen berdasarkan persediaan barang yang tersedia.
PT. Mega Eltra merupakan sebuah perusahaan yang bergerak dalam bidang perdagangan, antara lain melakukan perdagangan lokal. Dalam menjalankan usahanya PT. Mega Eltra mempunyai cabang di berbagai daerah seperti Bandar Lampung, Bandung, Banjarmasin, Makassar, Medan, Padang, Palembang, Pekanbaru, Semarang dan Surabaya. Pada cabang PT. Mega Eltra yang terletak di Medan mempunyai kegiatan mendistribusikan produk Semen Padang, Cat Sigma, Pupuk Pusri dan Obat-obatan Pertanian ke beberapa daerah di Provinsi Sumatera Utara. Dalam mendistribusikan produk ke berbagai daerah sebagai salah satu bagian dari operasional perusahaan, tentunya membutuhkan jumlah biaya transportasi yang tidak sedikit.
Perencanaan yang matang sangat diperlukan agar biaya transportasi yang dikeluarkan seefisien mungkin dan tidak menjadi permasalahan yang dapat menguras biaya besar. Permasalahan yang dihadapi oleh perusahaan tersebut adalah besarnya biaya pendistribusian produk Semen Padang di PT. Mega Eltra dari beberapa gudang kebeberapa toko konsumen yang disebabkan adanya masalah transportasi tak
seimbang atau ketidakseimbangan antara jumlah persediaan dengan jumlah permintaan. Untuk itu diperlukan metode yang tepat dalam mendistribusikan produk dari sejumlah gudang ke beberapa tempat tujuan distribusi sehingga akan dapat meminimumkan biaya pendistribusian.
Berdasarkan uraian tersebut, maka penulis memberi tulisan ini dengan judul
“Penerapan Metode Perbaikan ASM pada Masalah Transportasi Tak Seimbang dalam Pendistribusian Semen Padang PT. Mega Eltra Cabang Medan”.
1.2 Rumusan Masalah
Masalah pada penelitian ini adalah penyelesaian masalah transportasi tak seimbang dalam pendistribusian Semen Padang di PT. Mega Eltra Cabang Medan untuk meminimumkan biaya transportasi dengan menggunakan Metode Perbaikan ASM.
1.3 Batasan Masalah
Adapun batasan masalah dalam penelitian adalah sebagai berikut:
1. Penelitian hanya difokuskan pada masalah transportasi tak seimbang dalam pendistribusian Semen Padang.
2. Data yang digunakan adalah data sekunder yang diperoleh PT. Mega Eltra Cabang Medan periode Januari 2019 sampai Desember 2019, yaitu:
a. Data jumlah permintaan Semen Padang.
b. Data jumlah persediaan Semen Padang.
c. Data biaya pendistribusian Semen Padang.
3. Lalu lintas yang dilalui lancar.
4. Pengiriman hasil produksi dikirim menggunakan alat transportasi darat yaitu truk dan alat pengangkutan tersebut tersedia setiap saat.
5. Tidak dipertimbangkan adanya faktor acak seperti bencana alam dan lain sebagainya.
6. Diasumsikan harga BBM konstan.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah untuk mendapatkan gambaran mengenai penggunakan Metode Perbaikan ASM dalam mencari solusi optimal pada masalah transportasi tak seimbang dalam pendistribusian Semen Padang pada PT. Mega Eltra Cabang Medan.
1.5 Manfaat Penlitian
Adapun manfaat yang diharapkan dari penelitian adalah sebagai berikut:
1. Menambah wawasan dan informasi dalam bidang operasi riset yang berhubungan dengan masalah transportasi tak seimbang menggunakan Metode Perbaikan ASM.
2. Sebagai bahan referensi bacaan untuk penelitian sejenisnya.
3. Sebagai bahan pertimbangan bagi perusahaan dalam mengambil kebijakan pada masalah transportasi tak seimbang.
BAB 2
TINJAUAN PUSTAKA
2.1 Linear Programming
Linear programming adalah suatu model penyelesaian optimal pada masalah keputusan dengan cara menentukan terlebih dahulu fungsi tujuan seperti memaksimalkan keuntungan atau meminimumkan biaya dan kendala-kendala yang ada ke dalam model matematis persamaan linear (Sitorus. 1997).
Menurut Frederick S. Hiller dan Gerald J. Lieberman, linear programming merupakan suatu model matematis untuk menggambarkan masalah yang dihadapi.
Linear berarti bahwa semua fungsi matematis dalam model merupakan fungsi-fungsi linear. Pemrograman merupakan sinonim untuk kata perencanaan. Linear programming mencakup perencanaan kegiatan-kegiatan untuk mencapai suatu hasil yang optimal, yaitu suatu hasil yang mencerminkan tercapainya sasaran tertentu yang paling baik menurut model matematis di antara alternatif-alternatif yang mungkin, dengan menggunakan fungsi linier (Wijaya. 2013).
2.2 Karakteristik-karakteristik dalam Linear Programming
Menurut Bu’ulolo (2017) karakteristik-karakteristik yang biasa digunakan untuk menyelesaiakan persoalan program linier dalam membangun model dari suatu formula akan digunakan yaitu:
1) Variabel Keputusan
Variabel keputusan adalah variabel yang menguraikan secara lengkap keputusan- keputusan yang akan dibuat.
2) Fungsi Tujuan
Fungsi tujuan merupakan fungsi dari variabel keputusan yang akan dimaksimumkan (untuk pendapatan atau keuntungan) atau diminimumkan (untuk ongkos atau biaya).
3) Pembatas
Pembatas merupakan kendala yang dihadapi, sehingga kita tidak bisa menentukan harga-harga variabel keputusan secara sembarang.
4) Pembatas Tanda
Pembatas tanda adalah yang menjelaskan apakah variabel keputusannya diasumsikan hanya berharga nonnegatif atau variabel keputusan boleh berharga positif, boleh juga negatif.
2.3 Masalah Transportasi
Transportasi merupakan bentuk khusus dari program linier yang digunakan untuk memecahkan masalah yang berhubungan dengan transportasi (pengangkutan) yaitu masalah pendistribusian barang dari beberapa tempat persediaan ke beberapa tempat permintaan. Tujuan utama transportasi adalah menentukan banyaknya barang yang optimal yang akan diangkut dari beberapa sumber (persediaan atau supply) ke beberapa tujuan (permintaan atau demand) sehingga meminimumkan total biaya pendistribusian.
Masalah transportasi timbul ketika seseorang mencoba menentukan cara pengiriman (pendistribusian) suatu jenis barang dari beberapa sumber (lokasi penawaran) ke beberapa tujuan (lokasi permintaan). Untuk itu perusahaan harus mampu mengatur biaya operasional yaitu biaya yang digunakan antara pengeluaran dan pemasukan perusahaan. Semakin besar rentang antara pemasukan dan pengeluaran, maka semakin besar pula keuntungan yang diperoleh dengan harapan pemasukan lebih besar dari pengeluaran (Aminuddin. 2005).
Menurut He D et al. (2014) dalam masalah transportasi yaitu pola pengiriman optimal antara sumber atau pusat persediaan dan tujuan atau pusat permintaan harus ditentukan. Misalkan sumber m adalah menyediakan n tujuan dengan produk tertentu. Terdapat sebagai jumlah produk yang tersedia di sumber i, dan sebagai jumlah produk yang diperlukan di tujuan j. Selanjutnya, biaya pengiriman satu unit produk dari sumber i ke tujuan j diasumsikan sebagai , dan terdapat adalah jumlah yang dikirim dari sumber i ke tujuan j. Jika biaya pengiriman diasumsikan proporsional dengan jumlah yang dikirim dari setiap sumber ke setiap tujuan sehingga untuk meminimalkan total biaya pengiriman ternyata menjadi masalah program linier.
Karakteristik permasalahan transportasi yaitu terdapat sejumlah sumber dan sejumlah tujuan tertentu. Komoditas atau produk yang didistribusikan dari sumber dan diminta oleh tujuan besarnya sesuai permintaan atau kapasitas sumber. Biaya
pengiriman setiap unit satuan komoditas dari sumber ke tujuan besarnya tertentu (Hermansyah et al. 2016).
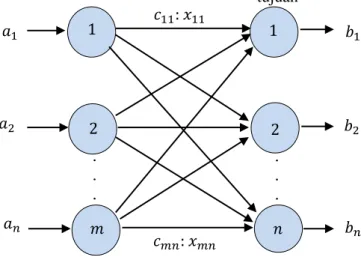
Masalah umum transportasi direpresentasikan oleh gambar berikut:
Gambar 2.1 Gambaran Umum Model Transportasi
Masalah umum direpresentasikan oleh Gambar 2.1. Ada m sumber dan n tujuan setiap sumber atau tujuan direpresentasikan dengan sebuah node. Panah menyatakan rute yang menghubungkan sumber dan tujuan. Panah (m,n) yang menggabungkan sumber m ke tujuan n membawa dua informasi yaitu biaya transportasi per unit (cmn) dan jumlah yang dikirim (xmn). Jumlah pasokan pada sumber adalah am dan jumlah kebutuhan tujuan di n adalah bn. Tujuan model menentukan xmn yang tidak diketahui yang akan meminimalkan total biaya transportasi yang memenuhi batas pasokan dan kebutuhan. Pomodelan masalah transportasi dapat disusun pada tabel berikut:
𝑐11: 𝑥11
sumber tujuan
𝑎1 1 𝑏1
𝑐𝑚𝑛: 𝑥𝑚𝑛
1
2 2
𝑚 𝑛
Unit 𝑎2 pasokan
𝑏2 Unit kebutuhan
𝑏𝑛 𝑎𝑛
. . . . . .
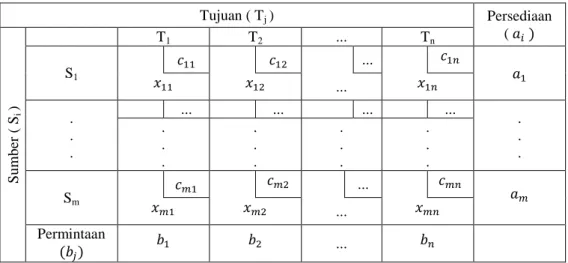
Tabel 2.1 Tabel Transportasi
Tujuan ( Tj ) Persediaan
(
Sumber ( Si )
T1 T2 ... Tn
S1 11 12
... 1
11 12 ... 1 1
. . .
... ... ... ...
. . . .
. .
. . .
. . .
. . .
Sm
1 2 ...
1 2 ...
Permintaan
1 2 ...
Keterangan:
Si = sumber ke i, Tj = tujuan ke j,
ai = persediaan ke i,
bj = permintaan ke j,
c
ij = biaya transportasi barang dari sumber i ke tujuan jx
ij= banyak barang yang diangkut dari sumber i ke tujuan jm i 1 , 2 , 3 ,...,
n j 1 , 2 , 3 ,...,
2.4 Model Masalah Transportasi
Misalkan terdapat m sumber dan n tujuan. Suatu barang x akan diangkut dari sumber 1 2 ke tujuan 1 2 dengan biaya per unit sebesar , maka jumlah barang sebesar dikirimkan dari sumber pusat ke pusat tujuan . Model transportasi secara umum sebagai berikut:
Minimum:
∑ ∑
1 1
(2.1)
dengan kendala:
∑ 1 2
1
(2.2)
∑ 1 2
1
(2.3)
, 1 2 , 1 2 .
2.4.1 Masalah Transportasi Seimbang
Masalah transportasi seimbang (balanced) adalah masalah biaya angkutan barang dimana jumlah barang yang disediakan dari tempat asal sama dengan jumlah barang yang diminta di tempat tujuan, yaitu:
∑ ∑ (2.4)
2.4.2 Masalah Transportasi Tak Seimbang
Masalah transportasi tak seimbang (unbalanced) adalah suatu masalah transportasi dimana jumlah permintaan lebih besar dari pada jumlah persediaan atau jumlah peersediaan lebih kecil dari pada jumlah permintaan, yaitu:
∑ ∑ (2.5)
Pada masalah tak seimbang dapat diseimbangkan dengan cara menambahkan dummy sebesar, yaitu:
∑ ∑ (2.6)
atau
∑ ∑ (2.7)
Berikut adalah definisi dan teorema yang berkaitan dalam masalah transportasi (Septiana et al. 2017) :
Definisi 1. Himpunan alokasi { 1 2 1 2 } yang memenuhi kendala pada masalah tranportasi disebut solusi optimal.
Definisi 2. Solusi fisibel dikatakan solusi optimal jika meminimumkan total biaya
transportasi.
Untuk menjamin masalah transportasi mempunyai solusi fisibel maka transportasinya harus seimbang, seperti diberikan teorema sebagai berikut ini.
Teorema 3. (Eksistensi) Masalah transportasi memiliki solusi fisibel jika dan hanya jika merupakan masalah transportasi seimbang, yaitu ∑ 1 ∑ 1 .
Untuk menjamin setiap masalah transportasi memiliki solusi optimal, diberikan teorema sebagai berikut ini.
Teorema 4. Untuk sebarang solusi optimal masalah transportasi ( 1) merupakan solusi optimal dari masalah transportasi (P).
Teorema 4 akan digunakan untuk menunujukkan Teorema 5 sebagai berikut.
Teorema 5. Jika { | 1 2 1 2 } solusi fisibel dari masalah transportasi (P) dan , untuk semua i dan j, dimana dan adalah bilangan riil sedemikian sehingga minimum dari masalah transportasi ( 1) bernilai 0, maka { | 1 2 1 2 } adalah solusi optimal dari masalah transportasi (P).
2.5 Metode Transportasi
Model transportasi merupakan suatu metode yang digunakan untuk mengatur pendistribusian dari sumber-sumber yang menyediakan produk yang sama ke tempat- tempat yang membutuhkan secara optimal (Siswanto. 2007).
Metode transportasi kelompok kasus program linier yang menyelesaikan masalah pengiriman produk dari sumber (misalnya kandang) ke tujuan (misalnya gudang). Tujuannya adalah untuk menentukan jadwal pengiriman dengan meminimalkan total biaya pengiriman yang memenuhi batas permintaan dan kebutuhan. Model transportasi dapat digunakan untuk memecahkan masalah-masalah dunia bisnis lainnya seperti masalah periklanan, pembelanjaan modal, analisis lokasi, keseimbangan lini perakitan, perencanaan dan penjadwalan produksi, dan penilaian personal (Sari et al. 2013).
Terdapat beberapa metode untuk menyelesaikan masalah transportasi baik yang menggunakan solusi fisibel awal kemudian solusi akhir maupun tidak
menggunakan solusi fisibel awal. Beberapa metode untuk mencari solusi fisibel awal antara lain Metode Pojok Barat Laut (North West Corner Rules), Metode Biaya Terkecil (Least Cost), dan Metode VAM (Vogel Approximation). Kemudian solusi akhir menggunakan Metode Batu Loncatan (Stepping Stone) atau metode MODI (Modified Distribution Method). Kelemahan dari serangkaian metode tersebut adalah harus dicari solusi fisibel awal. Metode ini dipandang kurang efisien.
Kemudian muncul metode langsung, yaitu tanpa harus mencari solusi fisibel awal, misalnya Metode Zero Neigbourning, Metode Zero Suffix, Metode Zero Point, Metode Exponential Approach, Metode ASM dan sebagainya. Karakteristik dari metode-metode tersebut memperhatikan pada angka 0 (nol) hasil reduksi baris dan kolom dari sel biaya. Pada metode Zero Neigbourning dan Zero Suffix dihitung nilai rata-rata sekitar angka 0 yang bukan bernilai 0, kemudian pengalokasian bergantung pada nilai rata-rata terbesar. Sedangkan pada metode Zero Point diperhatikan permintaan dan persediaan pada sel dengan biaya tereduksi 0 yang bersangkutan.
Berbeda dengan metode Exponential Approach, metode ini menetapkan penalti eksponensial pada setiap sel biaya yang bernilai 0. Penalti eksponensial adalah banyaknya angka 0 pada baris ke-i dan kolom ke-j selain angka 0 yang terpilih.
Pengalokasian pada sel dengan penalti eksponensial terkecil. Jika terdapat penalti ekponensial terkecil yang sama, maka pengalokasian bergantung pada rata-rata permintaan dan persediaan terkecil untuk sel yang bersesuaian. Hampir serupa dengan metode Exponential Approach, metode ASM juga menetapkan indeks penalti e untuk setiap sel- ij yang bernilai 0, yang mana indeks penalti e adalah banyaknya angka 0 pada baris ke- i dan kolom ke- j dan tidak termasuk angka 0 yang terpilih pada sel- ij . Pengalokasian pada sel dengan indeks penalti terkecil. Jika terdapat indeks penalti terkecil yang sama, maka pengalokasian bergantung pada hasil penjumlahan dari biaya tereduksi pada baris ke-i dan kolom ke-j dari sel- ij yang bersangkutan dengan hasil penjumlahan terbesar. Jika masih terjadi kesamaan, maka memilih sel- ij (sel yang memiliki indek e terkecil yang sama) yang memiliki rata- rata persediaan dan permintaan terkecil.
2.6 Metode Perbaikan ASM
Metode ASM merupakan metode langsung untuk menyelesaikan masalah transportasi. Metode ini diperkenalkan oleh Abdul Quddoos, Dr. Shakeel Javaid, dan Prof. Mohd Masood Khalid yang selanjutnya disingkat menjadi ASM.
Metode ASM adalah salah satu metode optimasi masalah transportasi yang langsung menguji keoptimalan dari tabel transportasi. Metode ASM memberikan solusi optimal secara langsung dengan iterasi yang lebih sedikit untuk masalah transportasi. Karena metode ini menghabiskan lebih sedikit waktu dan sangat mudah untuk dimengerti dan diterapkan, maka akan menjadi sangat membantu untuk pengambilan keputusan yang menangani masalah permintaan dan persediaan (Quddoos et al. 2012).
Algoritma metode ASM (Quddoos et al. 2012):
1. Menyusun tabel transportasi dari masalah transportasi yang diberikan.
2. Mengurangi biaya setiap baris pada tabel transportasi dengan biaya minimum masing-masing baris dan kemudian mengurangi biaya setiap kolom dengan nilai minimum masing-masing kolom.
3. Sekarang akan ada setidaknya satu nol di setiap baris dan setiap kolom dalam matriks biaya yang telah dikurangi. Pilih nol pertama, perhatikan ( i, j ) nol yang dipilih, hitung jumlah total nol (tidak termasuk nol yang dipilih) di baris i dan kolom j . Kemudian pilih nol selanjutnya dan hitung jumlah total nol pada baris dan kolom dengan cara yang sama. Ulangi untuk semua nol pada matriks biaya.
4. Sekarang pilih nol dari sejumlah nol yang telah terhitung pada langkah 3 yang minimum dan berikan jumlah maksimum yang mungkin pada sel. Jika terjadi seri untuk beberapa nol yang terhitung dari langkah 3, pilih salah satu nol. Alokasikan jumlah yang mungkin untuk sel tersebut.
5. Setelah melakukan langkah 4, hapus baris dan kolom untuk perhitungan lebih lanjut dimana persediaan dari sumber tertentu habis atau permintaan untuk tujuan tertentu terpenuhi.
6. Periksa apakah hasil perhitungan matriks terdapat minimal satu nilai nol di setiap baris dan di setiap kolom. Jika tidak, ulangi langkah 2, jika sebaliknya ke langkah 7.
7. Mengulangi langkah 3 sampai langkah 6 sampai seluruh permintaan terpenuhi dan seluruh persediaan habis.
Metode ASM memberikan solusi optimal untuk menyelesaikan masalah transportasi seimbang yang telah ditunjukkan oleh Quddoos et al. pada tahun 2012.
Algoritma pada metode ASM ini menitikberatkan pada hasil reduksi yang bernilai nol dari reduksi baris dan reduksi kolom. Selanjutnya menetapkan indeks dari angka 0 pada setiap baris dan kolom, dilanjutkan dengan pengalokasian sebesar mungkin dari jumlah persediaan dan permintaan pada indeks terkecil. Namun selama dalam penelitian, Quddoos et al temui sedikit masalah dimana metode ASM tidak langsung memberikan solusi optimal tetapi memberikan Initial Basic Feasible Solution (IBFS) terbaik yang mana sangat dekat ke solusi optimal. Satu dasar masalah yang ditemui adalah masalah transportasi tak seimbang. Untuk mengatasi masalah ini, Quddoos et al menghadirkan revisi metode ASM pada tahun 2016 yang dikenal dengan sebutan Metode Perbaikan ASM. Solusi dari Metode Perbaikan ASM ini adalah adanya penambahan algoritma yaitu penambahan sel dummy. Sel dummy ini berfungsi untuk membuat tabel transportasi tak seimbang menjadi seimbang. Selanjutnya, untuk melakukan reduksi, tergantung dari penambahan baris atau kolom dummy.
Jika baris dummy yang ditambahkan, maka dilakukan reduksi kolom terlebih dahulu setelah itu reduksi baris, begitu pula sebaliknya. Dan untuk algoritma selanjutnya sama seperti algoritma metode ASM sebelumnya yaitu menetapkan indeks dari angka 0 pada setiap baris dan kolom (termasuk baris/kolom dummy) dan dilanjutkan dengan pengalokasian sebesar mungkin dari jumlah persediaan dan permintaan (termasuk sel dummy yang ditambahkan) pada indeks terkecil. Sehingga pada Metode Perbaikan ASM ini memberikan solusi optimal untuk masalah transportasi tak seimbang. Dan Metode Perbaikan ASM ini tetap mempunyai algoritma yang sederhana dan mudah dipahami.
Metode perbaikan ASM merupakan metode langsung yang merupakan perbaikan dari metode ASM. Kelebihan dari metode ini adalah dapat digunakan untuk menyelesaikan masalah transportasi tak seimbang dan memberikan solusi optimal. Metode ini juga dapat digunakan baik untuk kasus minimum maupun kasus maksimum (Solikhin. 2017).
Berikut adalah lemma yang berkaitan tentang masalah transportasi untuk mencari solusi maksimum dan solusi minimum (Septiana et al. 2017) :
Lemma 6. Diberikan ∑ 1∑ 1 , maka – ).
Berikut adalah teorema yang berkaitan dengan masalah transportasi tak seimbang dengan menggunakan metode perbikan ASM (Septiana et al. 2017) : Teorema 7. Solusi yang diperoleh dengan metode perbaikan ASM untuk sebarang masalah transportasi tak seimbang 2 merupakan solusi optimal.
Berikut adalah algoritma Metode Perbaikan ASM (Quddoos et al. 2016):
1. Menyusun tabel transportasi dari masalah transportasi. Periksa apakah masalahnya seimbang atau tidak. Jika masalah seimbang, langsung ke tahap 4, jika tidak, lanjut ke tahap 2.
2. Jika masalah tidak seimbang, kemudian salah satu dari dua kasus berikut kemungkinan terjadi:
a. Jika total persediaan melebihi total permintaan, masukkan kolom dummy tambahan pada tabel transportasi untuk menyerap kelebihan persediaan. Biaya transportasi untuk sel di kolom dummy ini diatur ke ‘M’ dimana M > 0 adalah sangat besar tetapi batas nilai positif. Atau
b. Jika total permintaan melebihi total persediaan, masukkan baris dummy tambahan pada tabel transportasi untuk memenuhi kelebihan permintaan. Biaya transportasi untuk sel di baris dummy ini diatur ke ‘M’ dimana M > 0 adalah sangat besar tetapi batas nilai positif.
3. Setelah masalah seimbang karena adanya penambahan dummy, kemudian salah satu dari dua kasus berikut kemungkinan terjadi:
a. Di kasus (a) pada langkah 2, identifikasi elemen terendah dari setiap baris dan kurangi dari setiap elemen dari masing-masing baris dan kemudian yang dihasilkan tabel, identifikasi elemen terendah dari setiap kolom dan kurangi dari setiap elemen dari masing-masing kolom dan lanjut ke langkah 5. Atau b. Di kasus (b) pada langkah 2, identifikasi elemen terendah dari setiap kolom
dan kurangi dari setiap elemen dari masing-masing kolom dan kemudian yang
dihasilkan tabel, identifikasi elemen terendah dari setiap baris dan kurangi dari setiap elemen dari masing-masing baris dan lanjut ke langkah 5.
4. Identifikasi elemen terendah dari setiap baris dan kurangi dari setiap elemen dari masing-masing baris dan setelah dihasilkan tabel, identifikasi elemen terendah dari setiap kolom dan kurangi dari setiap elemen dari masing-masing kolom.
5. Dalam tabel yang telah dikurangi, setiap baris dan setiap kolom memiliki setidaknya satu nol. Sekarang, pilih nol pertama (katakan 0) dan hitung jumlah nol (tidak termasuk nol yang dipilih) di baris dan kolom dan catat sebagai tanda dari nol yang telah dipilih. Ulangi proses ini untuk semua nol pada tabel transportasi.
6. Pilih sel yang mengandung nol yang mana nilai yang bertanda adalah minimum dan berikan jumlah maksimum yang memungkinkan pada sel tersebut. Jika terjadi seri untuk beberapa nol di langkah 5, pilih salah satu nol dari beberapa nol tersebut di baris dan kolom maksimum. Sediakan jumlah maksimum yang mungkin untuk sel tersebut.
7. Hapus baris atau kolom untuk dipertimbangkan lebih lanjut dimana persediaan dari sumber tertentu habis (atau permintaan untuk tujuan tertentu terpenuhi). Jika pada tahap apapun, kolom permintaan telah terpenuhi dan baris persediaan telah habis, kemudian hapus hanya satu kolom (atau baris) dan baris (atau kolom) yang tersisa diberikan persediaan (atau permintaan) nol dalam perhitungan lebih lanjut.
8. Sekarang periksa apakah tabel yang telah dikurangi mengandung setidaknya satu nol di setiap baris dan setiap kolom. Jika ini tidak terjadi, ulangi langkah 4, jika sebaliknya ke langkah 9.
9. Ulangi langkah 5 sampai langkah 8 sampai semua permintaan terpenuhi dan persediaan habis.
BAB 3
METODE PENELITIAN
3.1 Waktu dan Tempat
Metode pengumpulan data yang dilakukan dengan studi pustaka dengan mengumpulkan data sekunder baik data yang dimiliki oleh perusahaan, jurnal atau sumber-sumber lainnya dan field research data yang diperoleh dengan hasil wawancara terhadap pemimpin perusahaan.
Penelitian dilaksanakan di pengumpulan PT. Mega Eltra Cabang Medan berlokasi di Komplek Multatuli Indah Blok AA No. 52 Medan yang terhitung mulai 09 September 2020 – 16 September 2020 sesuai dengan izin.
3.2 Metode Penelitian
Adapun langkah penyelesaiannya sebagai berikut:
1. Membuat tabel transportasi.
Dengan mengamati data yang ada pada tabel transportasi terhadap keseimbangan masalah transportasi.
2. Membuat ulang tabel transportasi seimbang
Dengan menambahkan dummy pada baris atau kolom dengan biaya awal 0.
3. Reduksi tabel transportasi dengan dummy
1. Jika baris dummy yang ditambahkan, maka ke langkah ke-4. Kemudian mengganti biaya dummy dengan biaya terbesar dari hasil reduksi baris.
Selanjutnya ke langkah ke-5 kemudian langkah ke-4.
2. Jika kolom dummy yang ditambahkan, maka ke langkah ke-5. Kemudian mengganti biaya dummy dengan biaya terbesar dari hasil reduksi kolom.
Selanjutnya ke langkah ke-4 kemudian langkah ke-5.
4. Reduksi Baris
Mengurangi setiap entri baris dengan masing-masing biaya terkecilnya, yaitu
.
5. Reduksi kolom
Mengurangi setiap entri kolom dengan masing-masing biaya terkecilnya, yaitu
.
6. Penetapan indeks e
Menetapkan indeks e untuk setiap sel ij yang bernilai nol, yang mana indeks e adalah banyaknya angka nol pada baris ke-i dan kolom ke-j dan tidak termasuk angka nol yang terpilih pada sel-ij.
7. Pengalokasian indeks e
Memilih angka 0 dengan indeks e terkecil dan mengalokasikan sel dengan jumlah terbesar yang mungkin dengan melihat persediaan dan permintaan sel yang bersangkutan. Jika terdapat indeks e terkecil yang sama (lebih dari satu), maka menghitung masing-masing jumlah pada baris ke-i dan kolom ke-j dari sel-ij yang bersangkutan (sel yang memiliki indeks e terkecil yang sama) dan mengalokasikan sebesar mungkin pada sel dengan hasil penjumlahan terbesar.
Jika masih terjadi kesamaan, maka memilih sel-ij (sel yang memiliki indeks e terkecil yang sama) yang memiliki rata-rata persediaan dan permintaan terkecil.
8. Perbaikan tabel transportasi
Membuat tabel transportasi baru untuk perhitungan selanjutnya dengan mengabaikan baris atau kolom yang permintaan atau persediaannya telah terpenuhi. Mengecek apakah tabel transportasi baru memiliki paling sedikit satu angka nol pada setiap baris dan kolom. Jika tidak terdapat, kembali ke langkah ke- 4.
9. Mengulangi langkah ke-6 sampai langkah ke-8 sedemikian sehingga semua permintaan terpenuhi dan semua persediaan habis.
.
3.3 Kerangka Penelitian
Adapun kerangka penelitian dalam pembuatan penulisan ini sebagai berikut:
Studi Pendahuluan
Penentuan Rumusan dan Batasan Masalah Penetuan Tujuan Penelitian
Studi Lapangan Studi Pustaka
Pengumpulan data jumlah persediaan produk, jumlah permintaan produk dan biaya pendistribusian semen padang oleh PT. Mega Eltra Cabang Medan
Reduksi tabel transportasi
Perbaikan tabel transportasi Membuat jaringan transportasi Membuat tabel permasalahan transportasi
Reduksi baris Reduksi kolom
Penetapan indeks pada setiap sel yang bernilai 0 Pengalokasian sel
Solusi Optimal Kesimpulan dan Saran Membuat tabel transportasi
Mengamati data terhadap transportasi masalah keseimbangan
Membuat ulang tabel transportasi dengan menambahkan dummy Membuat model persamaan
Perhitungan pemecahan masalah dengan menggunakan metode perbaikan ASM
BAB 4 PEMBAHASAN
4.1 Pengumpulan Data
Lokasi pengumpulan data di PT. Mega Eltra Cabang Medan yang berlokasi di Komplek Multatuli Indah Blok AA No. 52 Medan. Data yang dikumpulkan adalah data distribusi Semen Padang pada bulan Januari sampai Desember tahun 2019.
4.1.1 Data Persediaan Semen Padang
PT. Mega Eltra Cabang Medan dalam kegiatan pendistribusian Semen Padang memiliki beberapa gudang penyimpanan untuk memenuhi permintaan konsumen.
Data lokasi gudang dan kapasitas persediaan Semen Padang di masingmasing gudang pada tahun 2019 dapat dilihat pada Tabel 4.1.
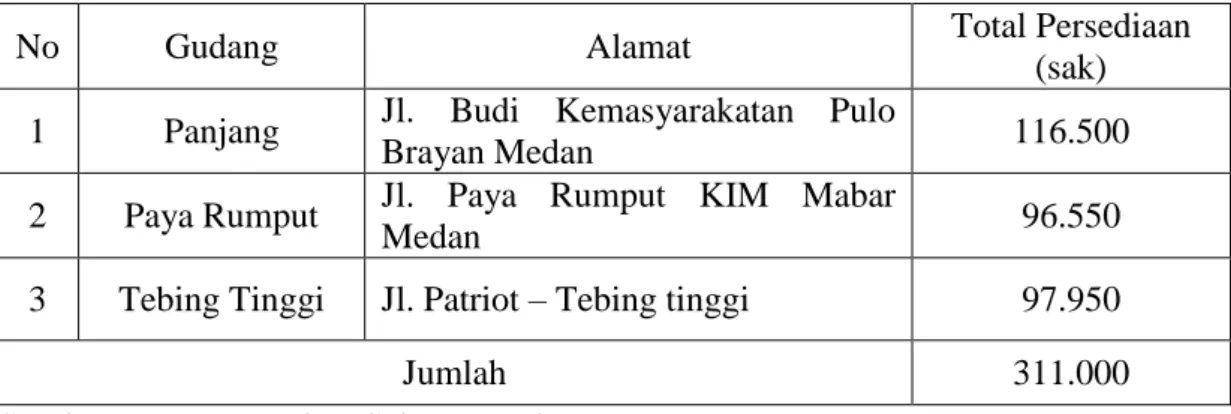
Tabel 4.1 Data Kapasitas Persediaan Semen Padang Tahun 2019
Sumber: PT. Mega Eltra Cabang Medan
4.1.2 Data Permintaan Semen Padang
Data permintaan merupakan data Semen Padang yang didistribusikan oleh PT. Mega Eltra Cabang Medan kepada konsumen pada tahun 2019. Data permintaan Semen Padang dari masing-masing gudang ke toko konsumen pada tahun 2019 dapat dilihat pada Tabel 4.2.
No Gudang Alamat Total Persediaan
(sak) 1 Panjang Jl. Budi Kemasyarakatan Pulo
Brayan Medan 116.500
2 Paya Rumput Jl. Paya Rumput KIM Mabar
Medan 96.550
3 Tebing Tinggi Jl. Patriot – Tebing tinggi 97.950
Jumlah 311.000
Tabel 4.2 Data Penyaluran Semen Padang Tahun 2019
Sumber: PT. Mega Eltra Cabang Medan
4.1.3 Data Biaya Distribusi dari Gudang ke Toko Konsumen
Data biaya distribusi dari gudang ke toko konsumen adalah biaya yang berhubungan dengan pengangkutan Semen Padang. Biaya distribusi yang dikeluarkan oleh perusahaan adalah biaya pengiriman Semen Padang tiap sak dari
gudang ke toko konsumen.
Pendistribusian Semen Padang ke toko konsumen menggunakan jasa angkutan darat yaitu truk. Data biaya distribusi dari gudang ke toko konsumen tahun 2019 dapat dilihat pada Tabel 4.3.
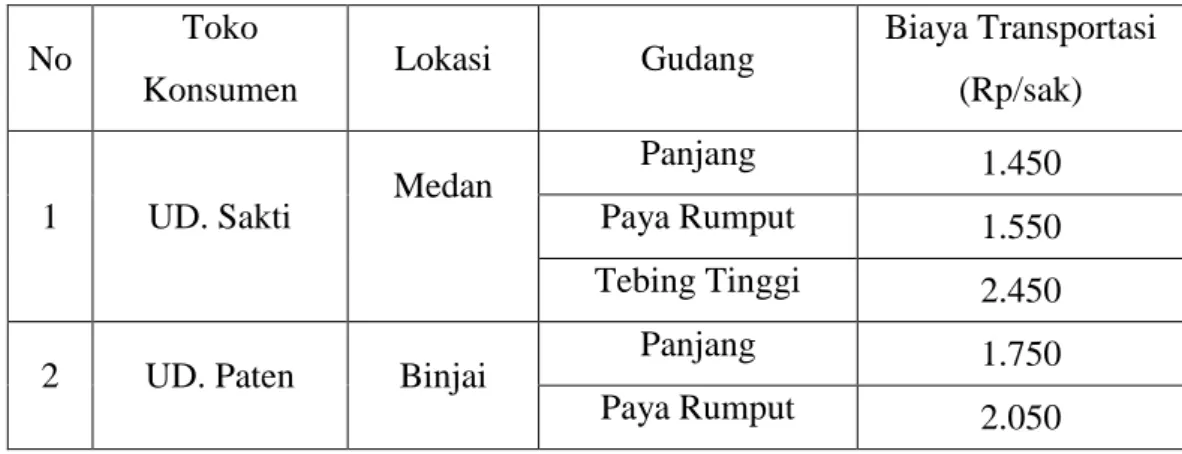
Tabel 4.3 Data Biaya Distribusi dari Gedung ke Toko Konsumen Tahun 2019
No Toko
Konsumen Lokasi Gudang Biaya Transportasi (Rp/sak)
1 UD. Sakti Medan Panjang 1.450
Paya Rumput 1.550
Tebing Tinggi 2.450
2 UD. Paten Binjai Panjang 1.750
Paya Rumput 2.050
Gudang
Toko Konsumen UD.
Sakti (sak)
UD.
Paten (sak)
UD.
Utama B (sak)
UD.
Indo-mas (sak)
UD.
Jecky (sak)
PT.
Nidya Karya (sak)
PT.
Waskita Karya
(sak)
UD.
Harco (sak) Panjang 19000 17000 20000 17000 4000 11000 - 12000
Paya
Rumput 15000 9000 22000 17000 5000 8000 7000 12000 Tebing
Tinggi 12000 5000 14000 37000 7000 17000 12000 - Jumlah 46000 31000 56000 71000 16000 36000 19000 24000
Tebing Tinggi 2.250
3 UD. Utama B Indrapura
Panjang 1.550
Paya Rumput 1.750
Tebing Tinggi 2.050
4 UD. Indo-mas Kisaran
Panjang 2.250
Paya Rumput 2.550
Tebing Tinggi 1.550
5 UD. Jecky Siantar
Panjang 2.250
Paya Rumput 2.750
Tebing Tinggi 1.150
6 UD. Nidya Karya
Tebing Tinggi
Panjang 1.750
Paya Rumput 2.050
Tebing Tinggi 1.050
7 UD. Waskita Karya
Tebing Tinggi
Panjang 2.150
Paya Rumput 2.250
Tebing Tinggi 950
8 UD. Harco Kabanjahe
Panjang 2.050
Paya Rumput 2.250
Tebing Tinggi 1.250 Sumber: PT. Mega Eltra Cabang Medan
4.2 Pengolahan Data
Pengolahan data pada penelitian ini akan dilakukan melalui beberapa tahap. Data- data yang telah diperoleh dari PT. Mega Eltra Cabang Medan dituliskan menjadi jaringan transportasi dan tabel transportasi, tujuan pembuatannya adalah untuk meringkas dan menyajikan dengan jelas data-data tersebut.
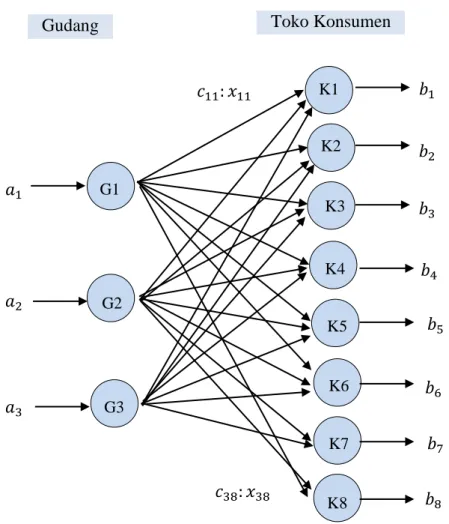
Gambar 4.1 Jaringan Transportasi dari Gudang ke Toko Konsumen
Berdasarkan jaringan transportasi diatas dapat dilihat bahwa terdapat 22 unit kegiatan distribusi dari 3 gudang ke 8 toko konsumen. Tabel 4.4 merupakan tabel transportasi pengolahan data kapasitas persediaan, data permintaan, dan data biaya distribusi Semen Padang dari masing-masing gudang ke masing-masing toko konsumen tahun 2019.
G2 G1
K2
K7 K1
G3
K6 K5 K4 K3
K8
Gudang Toko Konsumen
𝑎1
𝑎3 𝑎2
𝑏1
𝑏4 𝑏2
𝑏3
𝑏6 𝑏7 𝑏8 𝑏5 𝑐11: 𝑥11
𝑐38: 𝑥38
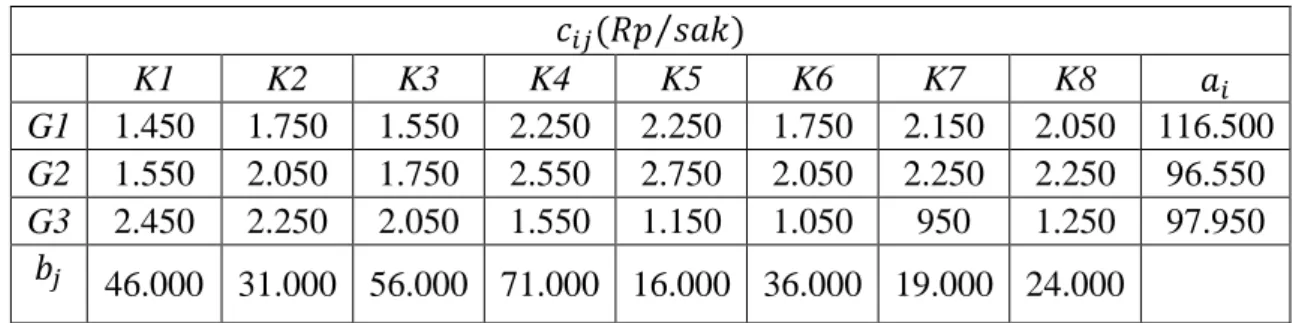
Tabel 4.4 Data Kapasitas Persediaan, Permintaan,dan Biaya Distribusi Semen Padang dari Gudang ke Toko Konsumen Tahun 2019
⁄
K1 K2 K3 K4 K5 K6 K7 K8
G1 1.450 1.750 1.550 2.250 2.250 1.750 2.150 2.050 116.500 G2 1.550 2.050 1.750 2.550 2.750 2.050 2.250 2.250 96.550 G3 2.450 2.250 2.050 1.550 1.150 1.050 950 1.250 97.950
46.000 31.000 56.000 71.000 16.000 36.000 19.000 24.000
Tabel 4.5 Tabel Permasalahan Transportasi
⁄
K1 K2 K3 K4 K5 K6 K7 K8
G1 1.450 1.750 1.550 2.250 2.250 1.750 2.150 2.050
116.500
G2 1.550 2.050 1.750 2.550 2.750 2.050 2.250 2.250
96.550
G3
2.450 2.250 2.050 1.550 1.150 1.050 950 1.250
97.950 46.000 31.000 56.000 71.000 16.000 36.000 19.000 24.000
Keterangan:
G1= Gudang 1 (Panjang) G2= Gudang 2 (Paya Rumput) G3= Gudang 3 (Tebing Tinggi) K1 = Konsumen 1 (UD. Sakti) K2 = Konsumen 2 (UD. Paten) K3= Konsumen 3 (UD. Utama B) K4= Konsumen 4 (UD. Indo-mas) K5= Konsumen 5 (UD. Jecky) K6= Konsumen 6 (PT. Nidya Karya) K7 = Konsumen 7 (PT. Waskita Karya) K8 = Konsumen 8 (UD. Harco)
= Persediaan ke i, = 1,2,3 = Permintaan ke j, = 1,2,3, … ,8
= Biaya transportasi barang dari gudang i ke konsumen j = 1,2,3
= 1,2,3, … ,8
Diketahui pada tabel 4.5 bahwa permasalahan transportasi tidak seimbang, dimana total jumlah persediaan lebih besar dibandingkan total jumlah permintaan.
Total jumlah persediaannya yaitu sebesar 311.000 sedangkan total jumlah permintaan yaitu sebesar 299.000.
Data yang diperoleh pada tabel 4.5 akan diformulasikan ke dalam model persamaan (2.1) sebagai berikut:
Minimumkan:
∑ ∑
1 1
= 11 11 + 12 12 + 13 13 + 14 14 + 15 15 + 16 16 + 17 17 +
18 18 + 21 21 + 22 22 + 23 23 + 24 24+ 25 25 + 26 26 +
27 27 + 28 28 + 31 31 + 32 32 + 33 33 + 34 34 + 35 35+
36 36 + 37 37 + 38 38
Persamaan berdasarkan data yang diperoleh:
Minimumkan:
∑ ∑
8
1 3
1
= 11 11 + 12 12 + 13 13 + 14 14 + 15 15 + 16 16 + 17 17 +
18 18 + 21 21 + 22 22 + 23 23 + 24 24+ 25 25 + 26 26 +
27 27 + 28 28 + 31 31 + 32 32 + 33 33 + 34 34 + 35 35+
36 36 + 37 37 + 38 38
= 1 45 11 + 1 75 12 + 1 55 13 + 2 25 14 + 2 25 15 + 1 75 16 + 2 15 17 + 2 5 18 + 1 55 21 + 2 5 22 + 1 75 23 + 2 55 24+
2 75 25 + 2 5 26 + 2 25 27 + 2 25 28 + 2 45 31 + 2 25 32 + 2 5 33 + 1 55 34 + 1 15 35+ 1 5 36 + 95 37 + 1 25 38
Dengan kendala menggunakan persamaan (2.2) sebagai berikut:
∑
1
∑
8
1
1 45 11 + 1 75 12 + 1 55 13 + 2 25 14 + 2 25 15 + 1 75 16 + 2 15 17 + 2 5 18 116.500
1 55 21 + 2 5 22 + 1 75 23 + 2 55 24+ 2 75 25 + 2 5 26 + 2 25 27 + 2 25 28 96 55
2 45 31 + 2 25 32 + 2 5 33 + 1 55 34 + 1 15 35+ 1 5 36 + 95 37 + 1 25 38 96 95
∑
1
∑
3
1
1 45 11 1 55 21 2 45 31 46 1 75 12 2 5 22 2 25 32 31 1 55 13 1 75 23 2 5 33 56 2 25 14 2 55 24 1 55 34 71 2 25 15 2 75 25 1 15 35 16 1 75 16 2 5 26 1 5 36 36 2 15 17 2 25 27 95 37 19 2 5 18 2 25 28 1 25 38 12
untuk semua i dan j Keterangan:
= banyak barang yang diangkut dari gudang i ke konsumen j
4.3 Perhitungan Metode Pemecahan Masalah
Data yang telah diperoleh akan langsung diselesaikan dengan menggunakan Metode Perbaikkan ASM.
Tahap 1
Membuat tabel transportasi.
Tabel 4.6 Tabel Masalah Transportasi Tak Seimbang
⁄
K1 K2 K3 K4 K5 K6 K7 K8
G1
1.450 1.750 1.550 2.250 2.250 1.750 2.150 2.050
116.500
G2
1.550 2.050 1.750 2.550 2.750 2.050 2.250 2.250
96.550
G3 2.450 2.250 2.050 1.550 1.150 1.050 950 1.250
97.950 46.000 31.000 56.000 71.000 16.000 36.000 19.000 24.000
Berdasarkan Tabel 4.5 terdapat jumlah persediaan (∑ 311 dan jumlah permintaan (∑ 299 , sehingga diperoleh ∑ ∑ . Hal ini dapat dinyatakan bahwa permasalahan pada penulisan ini tidak seimbang. Selanjutnya membuat ulang tabel transportasi dengan dilakukan penambahan dummy.
Tahap 2
Membuat ulang tabel transportasi. Jika ∑ ∑ maka akan dilakukan suatu tujuan penambahan dummy pada kolom untuk menyerap kelebihan yang terjadi sebesar yaitu ∑ ∑ 311 299 12 .
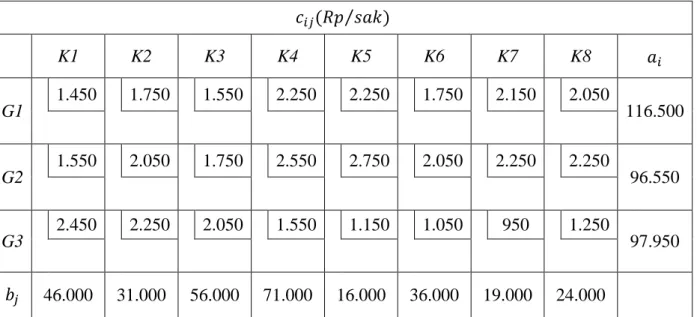
Tabel 4.7 Tabel Masalah Transportasi Seimbang dengan Penambahan Dummy
⁄
K1 K2 K3 K4 K5 K6 K7 K8 dummy
G1
1.450 1.750 1.550 2.250 2.250 1.750 2.150 2.050 0
116.500
G2
1.550 2.050 1.750 2.550 2.750 2.050 2.250 2.250 0
96.550
G3
2.450 2.250 2.050 1.550 1.150 1.050 950 1.250 0
97.950
46.000 31.000 56.000 71.000 16.000 36.000 19.000 24.000 12.000 311.000
Karena ∑ ∑ maka penambahan dummy dilakukan pada kolom permintaan. Berdasarkan persamaan (2.6) maka kolom dummy akan dilakukan penambahan sebesar yaitu ∑ ∑ 311 299 12 , kemudian permasalahan menjadi seimbang sehingga ∑ ∑ .
Tahap 3
Reduksi kolom dilakukan setelah penambahan dummy pada kolom permintaan, dengan cara mengurangi setiap entri kolom dengan masing-masing biaya terkecil .
Pada 1 biaya terkecilnya terletak pada 11 1 45 , sehingga
11 11 11 1 45 1 45
21 21 11 1 55 1 45 1
31 31 11 2 45 1 45 1
Pada 2 biaya terkecilnya terletak pada 12 1 75 , sehingga
12 12 12 1 75 1 75
22 22 12 2 5 1 75 3
32 32 12 2 25 1 75 5
Pada 3 biaya terkecilnya terletak pada 13 1 55 , sehingga
13 13 13 1 55 1 55
23 22 12 1 75 1 55 2
33 32 12 2 5 1 55 5
Pada 4 biaya terkecilnya terletak pada 34 1 55 , sehingga
14 14 34 2 25 1 55 7
24 24 34 2 55 1 55 1
34 34 34 1 55 1 55
Pada 5 biaya terkecilnya terletak pada 35 1 15 , sehingga
15 15 35 2 25 1 15 1 1
25 25 35 2 75 1 15 1 6
35 35 35 1 55 1 15
Pada 6 biaya terkecilnya terletak pada 36 1 5 , sehingga
16 16 36 1 75 1 5 7
26 26 36 2 5 1 5 1
36 36 36 1 5 1 5
Pada 7 biaya terkecilnya terletak pada 37 95 , sehingga
17 17 37 2 15 95 1 2
27 27 37 2 25 95 1 3
37 37 37 95 95
Pada 8 biaya terkecilnya terletak pada 38 1 25 , sehingga
18 18 38 2 5 1 25 8
28 28 38 2 25 1 25 1
38 38 38 1 25 1 25 Maka diperoleh tabel berikut
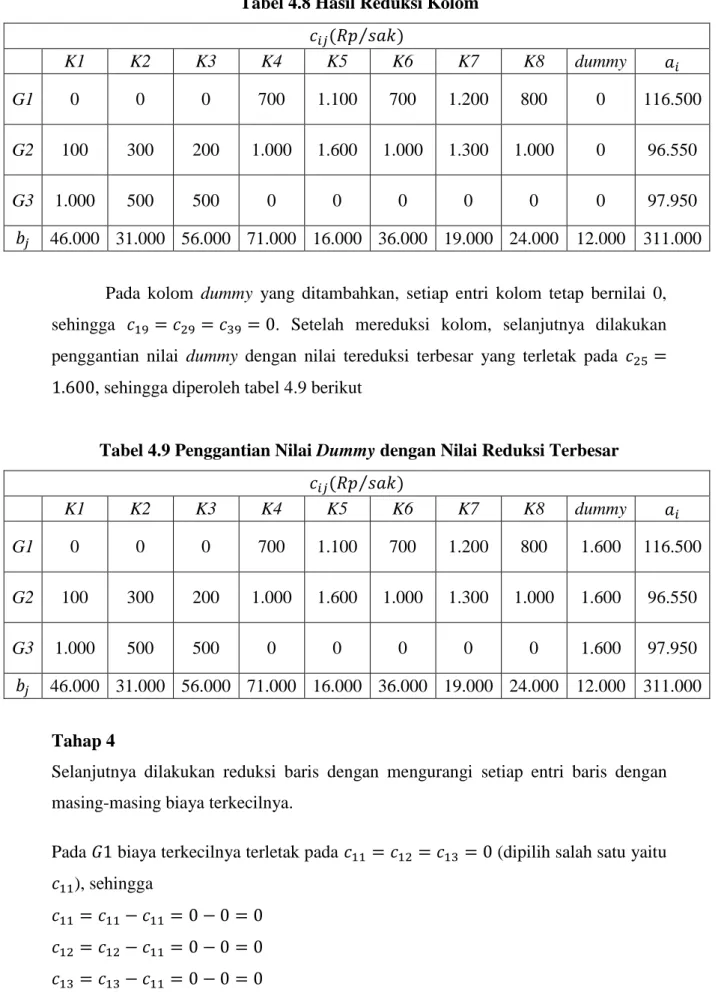
Tabel 4.8 Hasil Reduksi Kolom
⁄
K1 K2 K3 K4 K5 K6 K7 K8 dummy
G1 0 0 0 700 1.100 700 1.200 800 0 116.500
G2 100 300 200 1.000 1.600 1.000 1.300 1.000 0 96.550
G3 1.000 500 500 0 0 0 0 0 0 97.950
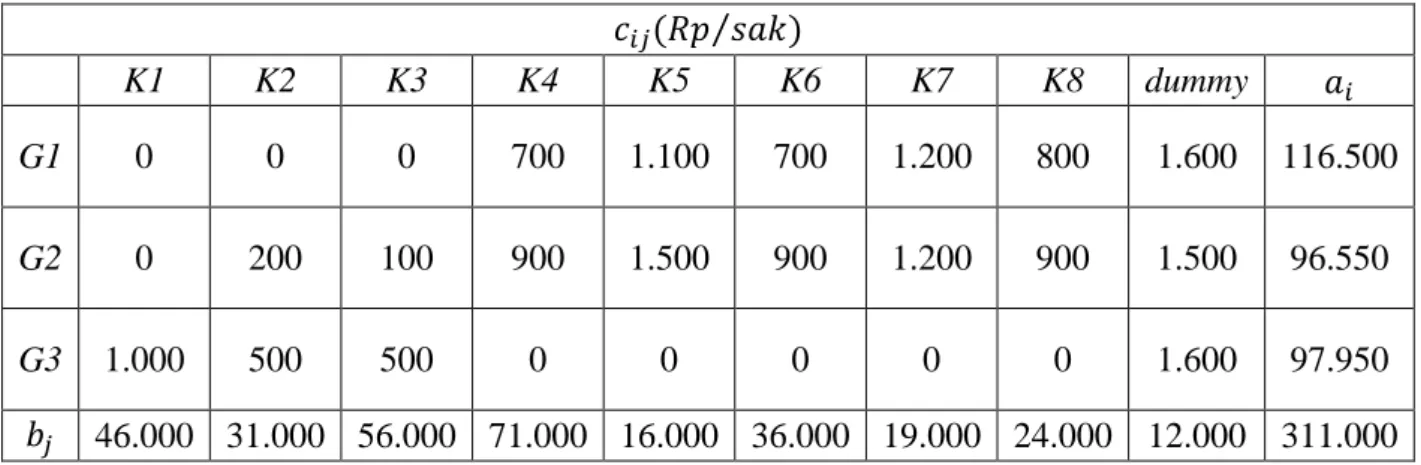
46.000 31.000 56.000 71.000 16.000 36.000 19.000 24.000 12.000 311.000 Pada kolom dummy yang ditambahkan, setiap entri kolom tetap bernilai 0, sehingga 19 29 39 . Setelah mereduksi kolom, selanjutnya dilakukan penggantian nilai dummy dengan nilai tereduksi terbesar yang terletak pada 25 1 6 , sehingga diperoleh tabel 4.9 berikut
Tabel 4.9 Penggantian Nilai Dummy dengan Nilai Reduksi Terbesar
⁄
K1 K2 K3 K4 K5 K6 K7 K8 dummy
G1 0 0 0 700 1.100 700 1.200 800 1.600 116.500
G2 100 300 200 1.000 1.600 1.000 1.300 1.000 1.600 96.550
G3 1.000 500 500 0 0 0 0 0 1.600 97.950
46.000 31.000 56.000 71.000 16.000 36.000 19.000 24.000 12.000 311.000
Tahap 4
Selanjutnya dilakukan reduksi baris dengan mengurangi setiap entri baris dengan masing-masing biaya terkecilnya.
Pada 1 biaya terkecilnya terletak pada 11 12 13 (dipilih salah satu yaitu
11), sehingga
11 11 11
12 12 11
13 13 11