BAB II TINJAUAN PUSTAKA

BAB II

TINJAUAN PUSTAKA

2.1 Teori Gravitasi Newton

Beberapa teori dapat membandingkan ketelitian ramalannya dengan teori gravitasi universal Newton. Ramalan mekanika benda angkasa untuk posisi planet sesuai dengan pengamatan. Penemuan Neptunus dan Ceres adalah diantara kesuksesan spektakuler yang memberikan dukungan untuk ketelitian teori ini. Tetapi teori Newton tidak sempurna : ramalan gerak untuk planet dalam (inner) menyimpang sedikit dari nilai yang di amati.

Dalam kasus merkurius kelebihan presesi perihelion sebanyak 43 detik-sudut per abad.

Penyimpangan kecil ini diamati melalui perhitungan oleh Le Verrier pada 1845 dan diperhitungkan kembali oleh Newcomb pada 1882. Penjelasan dari presesi adalah salah satu kesuksesan awal dari teori gravitasi relativistik Einstein. (Hans C. Ohanian, 1976)

Walaupun teori Newton tidak sempurna, teori ini adalah suatu pendekatan yang

luar biasa dalam limit kasus gerak pada kecepatan rendah dan dalam suatu medan

gravitasi lemah. Setiap teori relativistik gravitasi harus sesuai dengan teori Newton dalam

limit kasus ini. Oleh karena itu, akan dimulai dengan suatu penjelasan singkat beberapa

aspek dari teori Newton yang telah beliau kemukakan dalam tulisanya seperti hukum

gravitasi Newton yang diaplikasikan untuk memprediksi dan menghitung secara teliti

gerak planet, bulan, satelit dan objek lain di alam semesta ini.

2.1.1 Hukum Gravitasi Universal Newton

Hukum gravitasi Newton bersama dengan hukum gerak Newton telah diaplikasikan untuk memprediksi dan menghitung secara teliti gerak planet, bulan, satelit, dan objek lain di alam semesta. Berdasarkan Newton, hukum yang menentukan interaksi gravitasi adalah

”Gaya tarik gravitasi antara setiap dua benda di alam semesta secara langsung sebanding pada perkalian massanya dan berbanding terbalik terhadap kuadrat jarak antara kedua benda ”. Jika salah satu massa berada pada titik asal dan yang lain berada pada suatu jarak radial r , maka persamaan gaya mengambil bentuk matematika :

𝐅 = − 𝐺𝑚𝑚 ^′

𝑟 ² 𝐫� (2.1)

dengan G = 6,67 x 10 ^-11 N m ² /Kg ² , 𝐫� adalah vektor satuan. Gaya gravitasional termasuk gaya sentral yaitu gaya yang bergantung pada jarak radial dan beraksi sepanjang arah radial. (Atam P. Arya, 1990)

Berdasarkan hukum Newton, gravitasi adalah aksi pada suatu jarak: massa pada suatu titik beraksi secara langsung dan seketika pada massa lain, bahkan walaupun massa tersebut tidak bersentuhan dengannya. Newton mempunyai rasa khawatir yang serius tentang tarik-menarik khayal yang demikian dari massa yang jauh dan menyarankan bahwa interaksi akan disampaikan oleh material medium. Pandangan modernnya adalah bahwa gravitasi beraksi secara lokal melalui medan: suatu massa pada suatu titik menghasilkan suatu medan, dan medan ini beraksi pada massa apapun yang berhubungan dengannya. Medan gravitasi mungkin dipandang sebagai material medium yang dicari Newton; medan adalah material karena memiliki suatu rapat energi. Gambaran interaksi dengan memakai medan lokal mempunyai keuntungan lanjutan yang membimbing pada teori relativistik yang mana efek gravitasional merambat pada kecepatan berhingga.

Dalam sistem tata surya, teori Newton adalah suatu penaksiran yang luar biasa.

Persamaan gaya (2.1) dapat diturunkan dari suatu energi potensial

𝑉(𝑟) = − 𝐺𝑚𝑚′

𝑟 (2.2)

Pada umumnya, dapat dikatakan bahwa efek relativistik akan menjadi kecil, jika energi potensial jauh lebih kecil dari energi massa diam dan kecepatannya jauh lebih kecil daripada kecepatan cahaya. Untuk suatu massa m yang bergerak dengan kecepatan v sekitar suatu pusat massa 𝑚′ kita dapat menggambarkan kondisi ini sebagai

|𝑉| ≪ 𝑚𝑐 ² dan 𝑣 ≪ 𝑐

Dimana 𝑐 adalah kecepatan cahaya. Perhatikan bahwa pembentuk kondisi adalah ekuivalen pada 𝑟 ≫ 𝐺𝑚 ^′ /𝑐 ² . Oleh karena itu, penyimpangan dari teori Newton diharapkan menjadi sangat kecil jika jarak dari pusat massa cukup besar dan kecepatannya cukup rendah. Untuk matahari, dengan suatu massa 𝑚 ^′ = 𝑀 _⊙ ≅ 2 × 10 ³³ 𝑔 , dengan 𝐺𝑚 ^′ /𝑐 ² ≅ 2 𝐾𝑚 dan kondisi 𝑟 ≫ 2 𝑘𝑚 adalah dengan jelas sangat memuaskan, bahkan untuk komet dengan suatu perihelion yang begitu dekat terhadap permukaan matahari. (Hans C. Ohanian, 1976)

2.1.2 Potensial Gravitasi

Medan gravitasi yang kita pandang sebagai pembawa interaksi didefenisikan sebagai gaya persatuan massa,

𝐠(𝐫) = 1

𝑚 𝐅 (𝐫) (2.3)

Potensial gravitasi yang bersesuaian didefenisikan sebagai 𝛷(𝐫) ≡ 1

𝑚 𝑉 (𝐫) = − � 𝐺𝑚 _𝑖

|𝐫 − 𝐫 𝑖 |

𝑖

(2.4)

Defenisi ini membuat potensial negatif, seperti yang diperkirakan untuk suatu gaya tarik.

Potensial gravitasi kadang-kadang didefenisikan dengan tanda yang berlawanan dari

persamaan (2.4), tetapi lebih baik untuk dipilih tanda ini dengan menganalogikannya terhadap elektrostatik. Untuk distribusi massa kontinu seperti persamaan dibawah ini :

𝛷(𝐫) = − � 𝐺 𝜌(𝐫 ^′ )

|𝐫 − 𝐫 ^′ | 𝑑 ³ 𝑟 ^′ (2.5)

Dengan 𝜌(𝐫 ^′ ) adalah rapat massa. Persamaan (2.5) menyatakan bahwa Φ mematuhi persamaan poisson

∇ ² 𝛷(𝐫) = +4 𝜋 𝐺𝜌(𝐫) (2.6)

2.2 Prinsip Relativitas

Pada intinya, teori relativitas Einstein (baik teori relativitas khusus maupun teori relativitas umum) adalah teori fisika modern dari ruang dan waktu, yang telah mengganti konsep ruang dan waktu absolut Newton dengan ruang-waktu.

Semula dalam fisika, relativitas berarti penghapusan ruang absolut, suatu penyelidikan yang telah dikenal sebagaimana yang diinginkan sejak Newton. Dan ini tentu saja apa yang disempurnakan dua teori Einstein : relativitas khusus, teori ruang waktu datar, menghapuskan ruang mutlak dalam peranan Maxwellian sebagai ‘eter’ yang membawa medan elektromagnetik, dan khususnya gelombang cahaya, sedangkan relativitas umum, teori ruang-waktu lengkung, menghapuskan ruang waktu mutlak juga dalam peranan Newtonian-nya mengenai standar ada dimana-mana dan tidak dapat dipengaruhi dari gerak seragam atau diam. Anehnya, dan tidak secara terencana tetapi agak sebagai satu hasil sampingan yang tidak dapat dihindarkan, teori Einstein juga menghapuskan konsep waktu mutlak Newton.

Defenisi yang lebih modern dan positif dari relativitas telah disusun dari teori

relativitas yang sebenarnya. Berdasarkan pandangan ini, relativitas dari setiap teori fisika

menggambarkan dirinya sendiri dalam grup transformasi yang menentukan hukum teori

invariant dan oleh karena itu menggambarkan kesimetrian, sebagai contoh ruang dan

waktu dari teori ini. Maka seperti yang akan dilihat, mekanika Newton memiliki relativitas yang disebut grup Galilean, relativitas khusus memiliki relativitas dari grup Poincaré (atau grup Lorentz), relativitas umum memiliki relativitas grup lengkap transformasi ruang-waktu. Dan berbagai ilmu kosmologi memiliki relativitas simetri yang bermacam-macam dengan skala besar alam semesta yang dipercaya. Bahkan suatu teori yang hanya berlaku pada ruang Euclidean mutlak, memberikan bahwa secara fisik homogen dan isotropik, akan memiliki relativitas, yang dinamakan grup rotasi dan translasi. (Wolfgang Rindler, 2006)

2.2.1 Hukum Newton Dan Kerangka Inersial

Ketika menggambarkan fenomena fisika di bumi, biasanya digunakan sistem koordinat dengan titik asal pada pusat bumi. Tetapi, sistem koordinat ini tidak ideal untuk menggambarkan gerak planet disekitar matahari. Sistem koordinat dengan titik asal pada pusat matahari lebih natural. Karena matahari bergerak sekitar pusat galaksi, tidak ada yang spesial tentang sistem koordinat dengan titik asal pada pusat matahari.

Kerangka acuan fundamental Newton disebut ‘ruang mutlak’. Sifat geometri dari ruang ini diberikan oleh geometri Euclidean biasa. Ruang ini dapat didekati oleh sistem koordinat kartesian. Kerangka acuan non-rotasi yang diam, atau yang bergerak secara seragam dalam ruang mutlak disebut kerangka acuan Galilean. Dengan memilih titik asal dan orientasi, sistem telah ditetapkan. Newton juga mengenalkan waktu universal yang berdetik pada laju yang sama pada semua posisi dalam ruang. (Grøn Ø., Hervik S., 2007)

Relatif terhadap kerangka acuan Galillean, semua mekanika berkelakuan berdasarkan tiga hukum Newton:

(i) Partikel bebas bergerak dengan vektor kecepatan konstan.

𝐮 = 𝑑𝐫

dengan r adalah vektor posisi.

(ii) Vektor gaya pada suatu partikel sama dengan hasil kali massanya dengan vektor percepatan : F = m.a

(iii) Gaya dari aksi dan reaksi adalah sama dan berlawanan; sebagai contoh, jika partikel A memberikan gaya F pada partikel B, maka B memberikan suatu gaya –F pada A.

Hukum fisika biasanya dinyatakan relatif terhadap kerangka acuan, yang mengijinkan kuantitas fisika seperti kecepatan, medan listrik dan lain-lain, untuk didefinisikan. Diantara kerangka yang lebih disukai adalah kerangka tegar yang inersial.

Selanjutnya hukum Newton diaplikasikan didalamnya.

Hukum pertama Newton menyajikan untuk memilih kerangka inersial di antara kerangka tegar : kerangka tegar disebut kerangka inersial jika partikel bebas bergerak tanpa percepatan relatif terhadapnya. Dan selama kehadirannya, hukum Newton digunakan secara sama dalam semua kerangka inersial. Bagaimanapun, Newton mempostulatkan keberadaan dari ruang mutlak dimana dia berpikir pusat massa dari sistem tata surya adalah dalam keaadaan diam dan baginya, ini adalah daerah utama untuk mekanikanya. Bahwa hukum-hukum yang secara sama sah dalam semua kerangka acuan lain yang bergerak secara seragam terhadap ruang mutlak (kerangka inersial) adalah teorema yang menarik baginya. (Wolfgang Rindler, 2006)

2.2.2 Relativitas Newton

Dengan mengingat bahwa suatu kerangka inersial adalah suatu kerangka tegar yang mana hukum pertama Newton berlaku. Anggap kerangka S pada Gambar 2.1 adalah inersial.

Karena, menurut transformasi Galileo kecepatan tetap dalam S bertransformasi ke

kecepatan konstan dalam 𝐒′, dapat dilihat bahwa semua partikel bebas dalam S bergerak secara seragam dalam 𝐒′, yang oleh karena itu juga inersial. Dengan kata lain, hanya kerangka yang bergerak secara seragam relatif ke S yang dapat menjadi inersial. Untuk titik tetap dalam setiap kerangka inersial adalah partikel bebas potensial, sehingga semuanya harus bergerak secara seragam relatif terhadap S.

S v (x,y,z,t)

(x’,y’,z’,t’)

Y’

X’

y x vt x’

x

z Z’ S’

O O’

Gambar 2.1 Kerangka S′ Bergerak dengan Kecepatan Konstan Terhadap Kerangka S. (Ronald Gautreau, 2002)

Dalam transformasi koordinat Galilean, hubungan antara pengukuran (𝑥, 𝑦, 𝑧, 𝑡) milik O dengan pengukuran (𝑥 ^′ , 𝑦 ^′ , 𝑧 ^′ , 𝑡 ^′ ) milik O’ untuk sebuah kejadian tertentu dipeoleh dengan mengkaji gambar (2.1) diatas adalah :

𝑥 ^′ = 𝑥 − 𝑣𝑡 ; 𝑦 = 𝑦 ^′ ; 𝑧 ^′ = 𝑧 𝑑𝑎𝑛 𝑡 = 𝑡′ (2.7)

Sekarang, dari invariansi percepatan dapat dilihat bahwa semua yang dibutuhkan agar tiga hukum Newton invarian diantara kerangka inersial adalah (i) suatu aksioma bahwa massa m adalah invarian, dan (ii) aksioma bahwa setiap gaya adalah invarian.

Kedua asumsi ini tentu saja bagian dari teori Newton. Menghasilkan sifat dari mekanika

Newton bahwa hal ini berlaku sama pada semua kerangka inersial yang disebut relativitas

Newtonian (atau Galilean). (Wolfgang Rindler, 2006)

Dalam mekanika Newton, dianggap bahwa massa inersial dari benda tidak bergantung pada kecepatan benda. Maka massa benda di S sama seperti di 𝐒′. Sehingga gaya 𝐅′, diukur dalam 𝐒′ adalah

𝐅 ^′ = 𝑚 𝑑𝐮 ^′

𝑑𝑡 ^′ = 𝑚 𝑑𝐮

𝑑𝑡 = 𝐅 (2.8)

Oleh karena itu, gaya di 𝐒′ sama seperti di S. Hasil ini mungkin digambarkan dengan mengatakan bahwa hukum kedua Newton invarian dibawah transformasi Galliean; yaitu ditulis dalam cara yang sama dalam setiap kerangka acuan Galilean (inersial). Dengan kata lain, prinsip relatvitas Newtonin (Galilean) menyatakan bahwa ‘setiap sistem mekanika akan berkelakuan dalam cara yang sama dalam semua kerangka Galilean (inersial)’. (Grøn Ø., Hervik S., 2007)

2.3 Teori Relativitas Umum Einstein

Untuk setiap sistem fisis, setiap hukum yang menghubungkan besaran fisis tidak akan bergantung kepada sistem pemilihan sistem koordinat. Hal ini berarti, persamaan gerak sistem akan memiliki bentuk yang tetap (tidak berubah) di dalam semua sistem koordinat. Persamaan yang tidak berubah bentuknya terhadap transformasi koordinat dikatakan memiliki sifat kovarian terhadap transformasi tersebut. Sifat inilah yang menyebabkan tensor banyak digunakan untuk menelaah suatu sistem fisis.

Tensor adalah besaran yang merupakan perluasan dari vektor, seperti halnya

vektor merupakan perluasan dari besaran skalar. Tensor memiliki komponen-komponen

seperti halnya vektor. Besaran vektor sangat penting dalam fisika karena ia menyatakan

objek dengan kaedah-kaedah yang tetap sama meskipun kerangka acuan yang dipilih

berubah-ubah. Perubahan kerangka acuan memang menyebabkan nilai komponen tensor

berubah pula, namun kaedah-kaedah yang berlaku bagi komponen tensor tetap tidak

berubah.

Teori relativitas umum adalah salah satu teori fisika modern yang cukup besar peranannya dalam menerangkan struktur ruang waktu dan jagad raya. Teori ini adalah teori yang indah memiliki daya pikat ramalan terhadap gejala alam yang cukup menarik, namun memiliki persyaratan matematika berupa analisis tensor. Karena itu akan disajikan analisis tensor sebagai jembatan untuk memahami teori relativitas umum.

2.3.1 Analisis Tensor

Tensor adalah besaran yang merupakan perluasan besaran vektor seperti halnya vektor adalah perluasan besaran skalar. Yang terakhir disebut ini adalah besaran yang hanya ditentukan oleh angkanya saja, seperti harga barang, ukuran panjang, suhu dan lain-lain.

Sedangkan vektor adalah besaran yang selain ditentukan oleh besar (angkanya) dan juga oleh arahnya. Misalnya kecepatan, kekuatan tarik, gaya, dan lain-lain. Sebagai contoh bila kita mengatakan tiupan angin yang berkecepatan sepuluh kilometer per jam, maka kita harus menyebut pula angin itu bertiup dari mana kemana, misalnya dari arah barat ke timur. Jadi faktor arah juga harus disertakan untuk melengkapi pernyataan kecepatan.

Begitu juga dengan gaya, kita harus menyebut pula kemana arah dorongannya.

Sedangkan tensor lebih luas dari vektor, yaitu besaran yang selain ditentukan oleh besar (angkanya) dan arahnya juga ditentukan oleh sejumlah faktor lain.

Semua sifat-sifat vektor yang telah dikenal akan dimiliki juga oleh tensor dan

penggunaan tensor juga didalam fisika, umumnya akan membuat hukum-hukum fisis

yang mempunyai bentuk yang lebih umum dan sederhana. Besaran tensor sangat penting

dalam geometri karena mereka menyatakan objek geometri yang sebagaimana diketahui

pada hakikatnya tetap sama walaupun sistem koordinat yang kita pilih untuk menyatakan

objek geometri tersebut dalam ungkapan analisis atau koordinat. (Hans. J. Wospakrik,

1972). Untuk setiap sistem fisis, setiap hukum yang menghubungkan besaran fisis tidak

akan bergantung kepada pemilihan sistem koordinat. Hal ini berarti, persamaan gerak

sistem (baik zarah maupun medan) akan memiliki bentuk yang tetap (tidak berubah)

didalam semua sistem koordinat. Persamaan yang tidak berubah bentuknya terhadap transformasi koordinat dikatakan memiliki sifat kovarian terhadap transformasi tersebut.

Sifat inilah yang menyebabkan tensor banyak digunakan untuk menelah sistem fisis.

Didalam analisis tensor ada tiga indeks yang digunakan, yang jika semua indeks berada diatas disebut dengan tensor kontravarian, sebaliknya jika semua indeks berada dibawah disebut dengan tensor kovarian dan apabila indeks berada diatas dan dibawah disebut dengan tensor campuran. Jumlah indeks menyatakan rank dari tensor.

Teori Relativitas Umum (TRU) merupakan teori fisika modern yang cukup besar peranannya dalam menerangkan struktur ruang waktu dan jagad raya. Teori ini merupakan salah satu teori yang indah, memiliki daya pikat ramalan terhadap gejala alam yang cukup menarik, namun memiliki persyaratan matematik berupa analisis tensor, karena itulah sangat dibutuhkan analisis tensor sebagai jembatan untuk memahami teori relativitas umum. Namun demikian, tensor juga dapat dibedakan berdasarkan hukum transformasi yang dimilikinya yaitu :

1. Vektor Kontravarian

Fungsi 𝐵 ^𝑝 dalam sistem koordinat (𝑦 1 , 𝑦 2 , … , 𝑦 𝑛 ) disebut vektor kontravarian jika pada suatu transformasi koordinat 𝑈 _𝑛 → 𝑈 _𝑛 , sehingga fungsi 𝐵 ^𝑝 akan ditransformasikan menjadi

𝐵 ^𝑝 → 𝐵� ^𝑝 = � 𝜕𝑦� _𝑝

𝜕𝑦 _𝑞 𝐴 ^𝑞 , 𝑝 = 1, 2, … , 𝑛

𝑛 𝑞=1

dimana 𝐵� ^𝑝 merupakan fungsi dalam sistem koordinat (𝑦 ₁ , 𝑦� ₂ , … , 𝑦� _𝑛 ).

𝐵� ^𝑝 = 𝜕𝑦� _𝑝

𝜕𝑦 𝑞 𝐵 ^𝑞 (2.9)

disebut komponen vektor kontravarian atau tensor kontravarian rank satu.

2. Vektor Kovarian

Fungsi 𝐵 _𝑝 dalam sistem koordinat (𝑦 ₁ , 𝑦 ₂ , … , 𝑦 _𝑛 ) disebut vektor kovarian jika pada suatu transformasi koordinat 𝑈 _𝑛 → 𝑈 _𝑛 , sehingga fungsi 𝐵 _𝑝 akan ditransformasikan menjadi

𝐵 𝑝 → 𝐵� 𝑝 = � 𝜕𝑦 _𝑞

𝜕𝑦� 𝑝 𝐵 𝑞 , 𝑝 = 1, 2, … , 𝑛

𝑛 𝑞=1

dimana 𝐵� _𝑝 merupakan fungsi dalam sistem koordinat (𝑦� ₁ , 𝑦� ₂ , … , 𝑦� _𝑛 ).

𝐵� _𝑝 = 𝜕𝑦 𝑞

𝜕𝑦� _𝑝 𝐵 _𝑞 (2.10)

disebut komponen vektor kovarian atau tensor kovarian rank satu atau order satu.

3. Invarian

Suatu fungsi 𝐵 = 𝐵 (𝑦 1 , 𝑦 2 , … , 𝑦 𝑛 ) disebut invarian jika pada suatu transformasi koordinat 𝑈 _𝑛 → 𝑈 _𝑛 , sehingga fungsi 𝐵 akan ditransformasikan menjadi

𝐵 (𝑦 𝑛 ) → 𝐵� (𝑦� 𝑛 ) = 𝐵 (𝑦 𝑛 ) (2.11)

4. Tensor Campuran

Dalam konsep tensor, suatu tensor campuran adalah tensor yang bukan jenis kovarian kuat maupun kontravarian kuat. Fungsi 𝐵 _𝑞 ^𝑝 dalam sistem koordinat (𝑦 ₁ , 𝑦 ₂ , … , 𝑦 _𝑛 ) disebut tensor campuran yang memiliki komponen kontravarian rank satu dan komponen kovarian rank satu. Jika pada suatu transformasi koordinat 𝑈 𝑛 → 𝑈 𝑛 , maka fungsi 𝐵 _𝑞 ^𝑝 ditransformasikan menjadi

𝐵 _𝑞 ^𝑝 → 𝐵� _𝑞 ^𝑝 = � � 𝜕𝑦� 𝑝

𝜕𝑦 _𝑟

𝜕𝑦 _𝑠

𝜕𝑦� _𝑞

𝑛 𝑟=1 𝑛 𝑠=1

𝐵 𝑠 𝑟 , 𝑝, 𝑞 = 1, 2, … , 𝑛

dimana 𝐵� _𝑞 ^𝑝 merupakan fungsi dalam sistem koordinat (𝑦� ₁ , 𝑦� ₂ , … , 𝑦� _𝑛 ). Diperoleh 𝐵� _𝑞 ^𝑝 = 𝜕𝑦� 𝑝

𝜕𝑦 𝑟

𝜕𝑦 _𝑠

𝜕𝑦� 𝑞 𝐵 𝑠 𝑟 (2.12)

yang menyatakan komponen tensor campuran.

Dengan menggunakan defenisi dari tensor campuran di atas akan ditunjukkan bahwa 𝛿 _𝑝 ^𝑝 juga merupakan suatu tensor campuran. Sekarang perhatikan persamaan transformasi berikut

𝛿̅ _𝑞 ^𝑝 = 𝜕𝑦� _𝑝

𝜕𝑦 𝑟

𝜕𝑦 𝑠

𝜕𝑦� 𝑞 𝛿 𝑠 𝑟 𝛿̅ _𝑞 ^𝑝 = 𝜕𝑦� _𝑝

𝜕𝑦 𝑟

𝜕𝑦 𝑟

𝜕𝑦� 𝑞

𝛿̅ _𝑞 ^𝑝 = 𝛿 _𝑞 ^𝑝 (2.13)

dimana 𝛿 _𝑞 ^𝑝 = { _{0, 𝑝≠𝑞} ^{1, 𝑝=𝑞} dan 𝛿̅ _𝑞 ^𝑝 = { ^{1, 𝑝 = 𝑞} _{0, 𝑝 ≠ 𝑞} . Jadi diketahui bahwa 𝛿 _𝑞 ^𝑝 merupakan tensor campuran dengan kontravarian dan kovarian masing-masing ber-rank satu atau biasa dinamakan dengan delta kronecker.

2.3.1.1 Transformasi Koordinat

Misalkan koordinat-koordinat tegak lurus (x, y, z) dari sebarang titik dinyatakan sebagai fungsi-fungsi sehingga

𝑥 = 𝑥(𝑢 1 , 𝑢 2 , 𝑢 3 ), 𝑦 = 𝑦(𝑢 1 , 𝑢 2 , 𝑢 3 ), 𝑧 = 𝑧(𝑢 1 , 𝑢 2 , 𝑢 3 ) (2.14)

Andaikan bahwa bentuk di atas dapat dipecahkan untuk 𝑢 ₁ , 𝑢 ₂ , 𝑢 ₃ dalam 𝑥, 𝑦, 𝑧, yakni

𝑢 ₁ = 𝑢 ₁ (𝑥, 𝑦, 𝑧), 𝑢 ₂ = 𝑢 ₂ (𝑥, 𝑦, 𝑧), 𝑢 ₃ = 𝑢 ₃ (𝑥, 𝑦, 𝑧) (2.15)

Fungsi-fungsi dalam persamaan (2.14) dan (2.15) dianggap tunggal dan memiliki turunan-turunan yang kontinu sehingga kaitan (𝑥, 𝑦, 𝑧) dengan (𝑢 1 , 𝑢 2 , 𝑢 3 ) adalah tunggal.

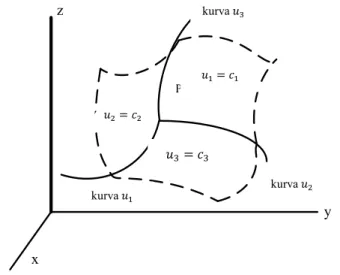
Misalkan diketahui sebuah titik P dengan koordinat-koordinat tegak lurus (𝑥, 𝑦, 𝑧) maka dari persamaan (2.14) dapat diasosiasikan suatu himpunan koordinat-koordinat (𝑢 1 , 𝑢 ₂ , 𝑢 ₃ ) yang tunggal yang disebut koordinat-koordinat kurvilinier dari P. Himpunan persamaan (2.14) dan (2.15) mendefenisikan suatu transformasi koordinat.

y x

z

Gambar 2.2 Kurva-kurva dan garis koordinat. (J. D. Anand, 2003)

Selanjutnya, akan didefenisikan transformasi koordinat menyangkut sistem koordinat lain dengan dimensi yang lebih tinggi. Untuk itu perlu diketahui terlebih dahulu mengetahui ruang dengan sebarang dimensi dan membahas sifat-sifat transformasi daripada ruang tersebut.

Sebuah ruang berdimensi n, dimana n adalah sembarang bilangan bulat positif, adalah merupakan himpunan daripada susunan yang teratur,

𝑥 = (𝑥 ₁ , 𝑥 ₂ , … , 𝑥 _𝑛 ) (2.16)

kurva 𝑢

1

P

kurva 𝑢

2

kurva 𝑢

3

𝑢

3

= 𝑐

3

𝑢

₁

= 𝑐

₁

𝑢

2

= 𝑐

2

dan yang memenuhi sifat-sifat daripada sebuah ruang vektor. Komponen sebuah vektor dalam ruang berdimensi n tersebut akan dinyatakan dengan indeks tertentu. Suatu kurva di dalam sebuah ruang berdimensi n adalah himpunan dari titik-titik x yang memenuhi n buah persamaan, yaitu 𝑥 _𝛼 = 𝑥 _𝛼 (𝑡), dimana t adalah parameter dan 𝛼 = 1, 2, … , 𝑛. Jika 𝑅 _𝑛 dianggap sebagai subruang dari 𝑅 𝑁 (n < N) maka 𝑅 𝑛 ditunjukkan oleh

𝑥 _𝛼 = 𝑥 _𝛼 �𝑡 ₁ , 𝑡 _2, … , 𝑡 _𝑛 � dengan 𝑡 _𝑖 , 𝑖 = 1, 2, … , 𝑛 menyatakan n buah parameter dan 𝛼 = 1, 2, … , 𝑛.

Kemudian diberikan sistem koordinat mencakup ruang tersebut, yaitu 𝑥 ₁ , 𝑥 ₂ , 𝑥 ₃ , 𝑥 ₄ yang membentuk sistem koordinat di 𝑅 _𝑛 . Setiap 𝑥̅ = (𝑥 ₁ , 𝑥 ₂ , … , 𝑥 _𝑛 ) menyatakan titik pada ruang 𝑅 𝑛 . Misalkan ada transformasi dari suatu sistem koordinat ke sistem yang lain maka bentuk perubahan koordinatnya dinyatakan sebagai berikut:

𝑥 ₁ ^′ = 𝑥 ₁ ^′ (𝑥 1 , 𝑥 2 , 𝑥 3 , 𝑥 4 ) 𝑥 ₂ ^′ = 𝑥 ₂ ^′ (𝑥 1 , 𝑥 ₂ , 𝑥 ₃ , 𝑥 ₄ ) . . . . . . . . .

𝑥 _𝑛 ^′ = 𝑥 _𝑛 ^′ (𝑥 ₁ , 𝑥 ₂ , … , 𝑥 _𝑁 )

Dengan demikian, diferensial untuk 𝑑𝑥 ₁ , 𝑑𝑥 ₂ , 𝑑𝑥 ₃ , 𝑑𝑥 ₄ dapat ditulis sebagai berikut:

𝑑𝑥 ₁ ^′ = 𝜕𝑥 ₁ ^′

𝜕𝑥 1 𝑑𝑥 1 + 𝜕𝑥 ₁ ^′

𝜕𝑥 2 𝑑𝑥 2 + 𝜕𝑥 ₁ ^′

𝜕𝑥 3 𝑑𝑥 3 + 𝜕𝑥 ₁ ^′

𝜕𝑥 4 𝑑𝑥 4

𝑑𝑥 ₂ ^′ = 𝜕𝑥 ₂ ^′

𝜕𝑥 ₁ 𝑑𝑥 1 + 𝜕𝑥 ₂ ^′

𝜕𝑥 ₂ 𝑑𝑥 2 + 𝜕𝑥 ₂ ^′

𝜕𝑥 ₃ 𝑑𝑥 3 + 𝜕𝑥 ₂ ^′

𝜕𝑥 ₄ 𝑑𝑥 4

. . . . . . . . . 𝑑𝑥 𝑛 ′ = 𝜕𝑥 𝑛 ′

𝜕𝑥 1 𝑑𝑥 1 + 𝜕𝑥 𝑛 ′

𝜕𝑥 2 𝑑𝑥 2 + … + 𝜕𝑥 𝑛 ′

𝜕𝑥 𝑁 𝑑𝑥 𝑁

Atau dapat juga disederhanakan menjadi

𝑑𝑥 _𝑛 ^′ = � 𝜕𝑥 _𝜇 ^′

𝜕𝑥 _𝛼 𝑑𝑥 _𝛼

𝑁 𝛼=1

(2.17) dengan 𝜇 = 1,2,3,4, … , 𝑛

2.3.2 Koordinat Kurvalinier

2.3.2.1 Koordinat Kurvalinier Ortogonal

Jika diperhatikan pada Gambar 2.2 permukaan-permukaan 𝑢 1 = 𝑐 1 , 𝑢 2 = 𝑐 2 , 𝑢 3 = 𝑐 3

dimana 𝑐 ₁ , 𝑐 2 , 𝑐 3 adalah konstanta, disebut permukaan-permukaan koordinat, dan setiap pasangan permukaan-permukaan ini berpotongan melalui kurva-kurva yang disebut kurva-kurva dan garis-garis koordinat (Gambar 2.2). Bila permukaan-permukaan koordinat ini berpotongan tegak lurus, maka sistem koordinatnya disebut ortogonal.

Kurva-kurva koordinat 𝑢 ₁ , 𝑢 ₂ 𝑑𝑎𝑛 𝑢 ₃ dari sistem kurvalinear ini analog dengan sumbu- sumbu koordinat (𝑥, 𝑦, 𝑧) dalam sistem koordinat tegak lurus.

2.3.1.2 Vektor Satuan dalam Sistem Koordinat Kurvalinier

Misalkan 𝑟 = 𝑥�𝑖 + 𝑦�𝑗 + 𝑧̂𝑘 adalah vektor kedudukan dari sebuah titik P. maka persamaan (2.14) dapat ditulis sebagai 𝑟 = 𝑟(𝑢 ₁ , 𝑢 ₂ , 𝑢 ₃ ). Sebuah vektor singgung pada kurva 𝑢 1 di P (dengan 𝑢 ₂ dan 𝑢 ₃ adalah konstanta) adalah

𝜕𝑟

𝜕𝑢 ₁ , 𝜕𝑟

𝜕𝑢 ₂ , 𝜕𝑟

𝜕𝑢 ₃ (2.18)

masing-masing adalah vektor singgung terhadap kurva dengan koordinat: 𝑢 ₁ , 𝑢 ₂ , 𝑢 ₃ . Maka vektor-vektor satuan dalam masing-masing arah koordinat kurvalinier ini adalah:

ê 1 = 𝜕𝑟 𝜕𝑢 1

� 𝜕𝑟 𝜕𝑢 ₁ � = 1 ℎ 1

𝜕𝑟

𝜕𝑢 1 , ê 2 = 𝜕𝑟 𝜕𝑢 2

� 𝜕𝑟 𝜕𝑢 ₂ � = 1 ℎ 2

𝜕𝑟

𝜕𝑢 2 , ê 3 = 𝜕𝑟 𝜕𝑢 3

� 𝜕𝑟 𝜕𝑢 ₃ � = 1 ℎ 3

𝜕𝑟

𝜕𝑢 3 (2.19)

dengan

ℎ ₁ = � 𝜕𝑟

𝜕𝑢 ₁ �, ℎ ₂ = � 𝜕𝑟

𝜕𝑢 ₂ � , ℎ ₃ = � 𝜕𝑟

𝜕𝑢 ₃ �

adalah panjang vektor-vektor singgung yang bersangkutan atau disebut juga sebagai faktor skala.

Uraian di atas memberikan bentuk pernyataan untuk sistem koordinat ortogonal yang ditinjau dengan berlaku syarat:

ê 1 . ê 2 = ê 2 . ê 3 = ê 3 . ê 1 = 0 (2.20)

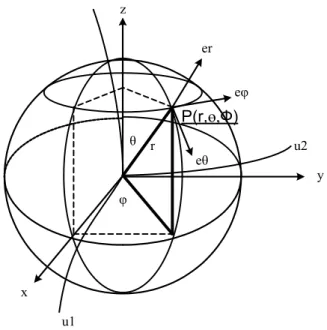
yang ketiga vektor satuan ê ₁ , ê ₂ , ê ₃ ini membentuk himpunan vektor satuan koordinat kurvalinier (Gambar 2.3). Dalam hal seperti ini penggunaan sistem koordinat kurvalinier yang sesuai seperti koordinat bola ternyata mengalihkan persoalan menjadi sederhana untuk ditangani.

2.3.2.3 Koordinat Kurvalinier Umum

z

y

x u1

u2 er

eφ

eθ θ

φ r

P(r,ө,Ф)

Gambar 2.3 Sistem koordinat kurvalinier bola. (Melly Frizha, 2012)

Dari 𝑟 = 𝑟(𝑢 1 , 𝑢 2 , 𝑢 3 ) kita peroleh 𝑑𝑟 = _𝜕𝑢 ^𝜕𝑟

1

𝑑𝑢 ₁ + _𝜕𝑢 ^𝜕𝑟

2

𝑑𝑢 ₂ + _𝜕𝑢 ^𝜕𝑟

3

𝑑𝑢 ₃ = ℎ 1 𝑑𝑢 1 ê 1 + ℎ 2 𝑑𝑢 2 ê 2 + ℎ 3 𝑑𝑢 3 ê 3

Maka diferensial dari panjang busur 𝑑𝑠 ditentukan dari 𝑑𝑠 ² = 𝑑𝑟 . 𝑑𝑟. Untuk sistem ortogonal,

𝑑𝑠 ² = ℎ ₁ ² 𝑑𝑢 ₁ ² + ℎ ₂ ² 𝑑𝑢 ₂ ² + ℎ ₃ ² 𝑑𝑢 ₃ ² 𝑑𝑠 ² = � ℎ _𝑖 ²

3 𝑖=1

𝑑𝑥 _𝑖 ² (2.21)

Untuk sistem-sistem kurvalinier yang tak ortogonal maka bentuk 𝑑𝑠 ² tidak akan memiliki bentuk yang sederhana seperti sebelumnya. Tapi secara umum dapat dituliskan sebagai berikut:

𝑑𝑠 ² = 𝑔 11 𝑑𝑥 ₁ ² + 𝑔 12 𝑑𝑥 1 𝑑𝑥 2 + 𝑔 13 𝑑𝑥 1 𝑑𝑥 3 + 𝑔 21 𝑑𝑥 2 𝑑𝑥 1 + 𝑔 22 𝑑𝑥 ₂ ² + 𝑔 23 𝑑𝑥 2 𝑑𝑥 3 + 𝑔 31 𝑑𝑥 3 𝑑𝑥 1 + 𝑔 32 𝑑𝑥 3 𝑑𝑥 2 + 𝑔 33 𝑑𝑥 ₃ ³

dimana komponen 𝑔 _𝑖𝑗 pada persamaan merepresentasikan koefisien-koefisien yang muncul dalam perhitungan 𝑑𝑥 ² + 𝑑𝑦 ² + 𝑑𝑧 ² . Bentuk 𝑑𝑠 ² dapat juga disederhanakan menjadi

𝑑𝑠 ² = � � 𝑔 _𝑖𝑗 𝑑𝑥 _𝑖 𝑑𝑥 _𝑗

3 𝑗=1 3 𝑖=1

(2.22)

Dalam bentuk matriks dapat dituliskan dengan

𝑑𝑠 ² = (𝑑𝑥 1 𝑑𝑥 2 𝑑𝑥 3 ) � 𝑔 11 𝑔 12 𝑔 13

𝑔 21 𝑔 22 𝑔 23

𝑔 ₃₁ 𝑔 ₃₂ 𝑔 ₃₃ � � 𝑑𝑥 ₁ 𝑑𝑥 ₂

𝑑𝑥 ₃ � (2.23)

Persamaan (2.23) adalah representasi 𝑔 _𝑖𝑗 lainnya yang dinyatakan dalam bentuk matriks.

2.3.3 Prinsip Ekuivalensi

Salah satu ciri kerangka inersial adalah suatu partikel diam akan tetap diam bila tidak ada gaya yang bekerja padanya. Biasanya gravitasi dianggap gaya, tetapi gravitasi memiliki sifat yang unik, karena semua partikel dan energi akan terkena gravitasi, dan semua partikel yang memiliki kecepatan awal yang sama akan memiliki lintasan yang sama dalam medan gravitasi, tak bergantung pada susunan internal partikelnya. Untuk gaya- gaya lain seperti gaya elektromagnetik, interaksi kuat, interaksi lemah beberapa partikel ada yang kena dan ada yang tidak. Misalnya gaya elektromagnetik hanya terkena pada partikel bermuatan.

Pada partikel netral tidak terkena gaya ini, jadi untuk gaya-gaya ini selalu dapat didefinisikan secara eksperimen bagaimana lintasan partikel yang tidak terkena gaya.

Tetapi tidak halnya untuk gravitasi, tidak ada partikel untuk membedakan lintasan partikel yang tidak terkena medan gravitasi (karena semua pasti terkena dan tidak ada yang terbedakan). Tetapi ada kerangka dimana partikel-partikel memiliki kecepatan yang seragam. Kerangka ini jatuh bebas dalam medan gravitasi dan semua partikel bebas akan memiliki kecepatan relatif sama terhadapa kerangka ini.

Ketika Newton merumuskan hukum gerak dan hukum gravitasinya, ia

mendefenisikan massa inersial dan massa gravitasi. Massa inersial diukur berdasarkan

ukuran kelembaman suatu benda terhadap gaya dorong atau gaya tarik yang bekerja,

sedangkan massa gravitasi diukur berdasarkan pengaruh gaya gravitasi pada benda

tersebut. Para eksperimentalis sejak zaman Newton hingga pertengahan abad ke-20 telah

berusaha membuktikan kesetaraan antara kedua jenis massa tersebut. Dengan percobaan

yang paling terkenal adalah percobaan Eotvos yang membuktikan bahwa kedua massa

tersebut setara. Berdasarkan bukti eksperimen tersebut, akhirnya Einstein menyimpulkan

dalam postulatnya yang terkenal dengan nama Prinsip Ekuivalensi Massa bahwa,”Gaya

gravitasi dan gaya inersial yang bekerja pada benda tunggal adalah sama dan tidak

terbedakan (indistinguisable) satu sama lain”. Konsekuensinya adalah bahwa tidak ada lagi kerangka acuan inersial.

2.3.4 Prinsip Kovariansi Umum

Akibat prinsip ekuivalensi massa yang menyebabkan tidak adanya kerangka acuan inersial, maka prinsip relativitas khusus menyatakan bahwa hukum-hukum fisika berlaku sama pada kerangka acuan inersial tidaklah berlaku umum. Oleh karena itu, Einstein merumuskan postulat keduanya yang terkenal dengan nama Prinsip Kovariansi Umum yang menyatakan bahwa,”Semua hukum-hukum fisika berlaku sama pada semua kerangka acuan tanpa kecuali”. Konsekuensinya adalah setiap besaran fisika haruslah dinyatakan dalam bentuk umum dan tidak bergantung pada koordinat dimana ia didefenisikan. Artinya semua besaran fisika harus dinyatakan dalam bentuk tensor.

Seperti telah dinyatakan sebelumnya dalam relativitas khusus, hukum-hukum gerak dinyatakan dalam bentuk yang invarian terhadap transformasi Lorentz dengan konsekuensi diperkenalkannya konsep ruang dan waktu dimensi 4 dengan metrik Minkowski. Generalisasinya, teori relativitas umum menyatakan bahwa hukum-hukum fisika harus invarian terhadap transformasi umum dengan konsep ruang-waktu 4 dimensi.

2.3.5 Kelengkungan Ruang-Waktu

Menurut Einstein, ruang dan waktu bersifat relatif. Ruang tergantung pada pengamatnya.

Ruang merupakan semacam hubungan antara benda-benda yang diukur dengan cara-cara

tertentu. Dengan demikian apabila pengukurannya dilakukan dengan cara yang berbeda,

maka hasilnyapun akan berbeda. Waktu juga bersifat relatif karena hasil pengukuran

terhadap hubungan-hubungan yang menyangkut waktu tergantung pada pengertian

keserampakan, karena apabila sesuatu terjadi, misalnya ledakan, maka kuatnya bunyi

ledakan akan berbeda di berbagai tempat. Selanjutnya H.A. Lorentz membuat suatu teori“

persamaan transformasi” yang melukiskan hubungan antara cara-cara pengukuran jarak – juga cara-cara pengukuran waktu – yang menyangkut dua pengamat yang mempunyai kerangka acuan yang berbeda dan berada dalam keadaan bergerak secara lurus, yang saling mendekati.

Di sini didapatkan sebenarnya jarak merupakan sekedar ukuran untuk menentukan ruang, demikianpun dengan transformasi dengan waktu dan hubungannya dengan ruang tidak akan pernah diketahui waktu secara tepat apabila tidak memperhitungkan koordinat ruang dan sebaliknya tidak akan diketahui ruang dari suatu obyek bila tidak memperhitungkan koordinat waktu. Sesungguhnya tidak ada waktu yang bersifat mandiri/mutlak, tidak ada ruang yang terpisah dari waktu atau waktu yang terpisah dari ruang yang ada hanyalah ruang-waktu. Akhirnya mulai saat ini kita harus memandang ruang dan waktu secara kontinum, jalin-menjalin secara tidak terpisahkan yang satu tidak mungkin ada tanpa yang lainnya. Keduanya merupakan satu kesatuan yang menyebabkan timbulnya segenap kenyataan. Dengan demikian waktu, ruang merupakan sekedar matra dari ruang-waktu.

Dari teori relativitas khusus, baik waktu atau ruang adalah bergerak relatif terhadap gerak pengamat dengan interval panjang dan waktu diukur oleh seorang pengamat secara umum tidak sama dengan interval panjang dan waktu yang diukur oleh pengamat yang berbeda. Karena panjang dan waktu relatif dan keduanya bergantung pada gerak relatif pada lintasan yang sama maka perlu untuk menyatakan kembali bahwa ruang berdimensi 3 dan 1 dimensi waktu tidak terpisah, dan lebih dari itu juga keduanya merupakan komponen yang setara dari suatu ruang-waktu 4 dimensi yang tunggal. Untuk menggambarkannya memang sulit tapi kita masih dapat merepresentasikannya secara matematis dengan menggunakan pertimbangan persamaan yang sesuai.

Beberapa contoh penggambaran kelengkungan ruang-waktu ditunjukkan pada Gambar 2.4 yang mengilustrasikan ruang datar berimensi 1 yang berupa garis lurus.

Untuk melengkungkannya, harus dibengkokkan pada arah yang lain. Tapi, kelengkungan

yang ditunjukkan dalam 1 dimensi tidak cukup dan memerlukan 2 dimensi untuk mengilustrasikannya lebih lanjut. Gambar 2.5 menyajikan suatu ruang 2 dimensi dan ilustrasi bagaimana ruang itu dilihat jika dibengkokkan.

(a)

(b)

Gambar 2.4 Ruang 1 dimensi (a) yang datar (b) yang lengkung. (Rinto Anugraha, 2005)

(a) (b)

Gambar 2.5 Ruang 2 dimensi (a) yang datar (b) yang lengkung. (Rinto Anugraha, 2005)

2.4 Asas Kesetaraan

Dalam teori kerelativan umum Albert Einstein mengemukakan asas kesetaraan, yang

merintis jalan pencetusan teori kerelativan umum lima tahun kemudian. Teori ini pada

dasarnya menyatakan,” bahwa semua hukum fisika bersifat mutlak atau tak ubah terhadap

setiap pengamat, termasuk yang bergerak dengan percepatan. Salah satu hukum fisika

sederhana untuk menyatakan ini, yakni “hukum kelembaman”. Menurut hukum ini,

apabila semua gaya yang bekerja pada semua benda yang meniadakan pengaruh, maka

benda tersebut akan berada pada keadaan diam atau bergerak dengan kecepatan yang arah atau besarnya tetap.

Einstein mengemukakan asas kesetaraan pada tahun 1911 yang mengatakan bahwa: dalam sistem pengamatan yang jatuh bebas dalam gaya berat (sistem ketaklemabaman), hukum fisika tetap berlaku seperti halnya dalam sistem pengamatan tanpa medan gaya berat (Sistem kelembaman) dan bahwa gaya kelembaman (atau khayal) setara dengan gaya berat. Karena gaya kelembaman bergantung pada massa ukuran dan gaya berat bergantung pada massa ukuran berat , maka asas kesetaraan diatas mengungkapkan bahwa kedua jenis massa ini sebenarnya adalah setara, atau lebih tegas lagi sama besar.

2.4.1 Asas kesetaraan dan geodesik ruang waktu lengkung

Asas kesetaraan Einstein dengan demikian mempertegas kembali hasil percobaan Galileo Galilei mengenai peristiwa jatuh bebas, bahwa semua benda bergerak dengan percepatan yang sama dibawah pengaruh gaya berat, yakni percepatan gaya berat, yang sama sekali tidak bergantung pada massanya masing-masing. Jadi dapat kita lihat bahwa gerak benda yang secara geometri dinyatakan oleh geodesik ruang waktu lengkung, padanan fisikanya adalah gerak dibawah pengaruh medan gaya berat. Nah, karena melengkungnya ruang waktu mengakibatkan geodesiknya berupa garis lengkung dan dipihak lain percepatan gaya berat disebabkan oleh gaya berat.

Maka pada tahun 1916, Albert Einstein mengemukakan dalam teori kerelatifan

umumnya bahwa hadirnya medan gaya berat di alam ini sebagai akibat melengkunghya

ruang waktu. Bila didalam teori gaya berat Newton yang menyatakan gaya berat Newton

melalui hukum gaya beratnya, maka dalam teori kerelatifan umum yang secara geometri

adalah teori tentang geometri ruang waktu lengkung, medan gaya berat dinyatakan

melalui komponen-komponen tensor metrik dari kuadrat metrik 𝑑𝑠 ² .

Ketergantungan tensor metrik ini pada titik dalam ruang waktu tidaklah dipilih seenaknya, melainkan harus memenuhi suatu aturan atau persamaan medan Einstein yang sangat terkenal dalam teori kerelatifan umumnya. Persamaan ini adalah merupakan suatu persamaan tensor yang menyatakan hubungan antara penyebaran materi disuatu pihak dan kelengkungan ruang waktu yang dinyatakan melalui tensor Riemannya dipihak lain. Jadi didalam persamaan medan Einstein memperlihatkan bahwa setiap benda bermassa mengakibatkan ruang waktu disekitarnya melengkung, yang didalam fisikanya dinyatakan bahwa disekitar benda bermassa akan timbul medan gaya berat atau gravitasi.

(Hans. J. W, 1978 )

2.4.2 Metrik Schwarzschild

Karl Schwarzschild adalah seorang ilmuan astronomi Jerman yang pertama kali memecahkan persamaan medan gravitasi Einstein secara eksak pada tahun 1916, yang dimaksud dengan pemecahan medan gravitasi Einstein adalah beliau mendapatkan komponen-komponen tensor metrik 𝑔 dari kuadrat metriknya 𝑑𝑠 ² ruang waktu lengkung yang memenuhi hubungan antara persamaan medan Einstein. Metrik yang didapat Schwarzschild ini dalam teori kerelatifanya disebut dengan metrik Schwarzschild.

Schwarzschild juga mempunyai hubungan yang sangat erat dengan teori lubang hitam.

Lubang hitam adalah sebuah pemusatan massa yang cukup besar sehingga menghasilkan gaya gravitasi yang sangat besar.

Gaya gravitasi yang sangat besar ini mencegah apapun lolos darinya kecuali

melalui perilaku terowongan kuantum. Medan gravitasi begitu kuat sehingga kecepatan

lepas di dekatnya mendekati kecepatan cahaya. Tak ada sesuatu, termasuk radiasi

elektromagnetik yang dapat lolos dari gravitasinya, bahkan cahaya hanya dapat masuk

tetapi tidak dapat keluar atau melewatinya, dari sini diperoleh kata “hitam”. Istilah lubang

hitam telah tersebar luas, meskipun ia tidak menunjuk ke sebuah lubang dalam arti biasa,

tetapi merupakan sebuah wilayah di angkasa dimana semua tidak dapat kembali. Secara

teoritis, lubang hitam dapat memliki ukuran apa pun, dari mikroskopik sampai ke ukuran alam raya yang dapat diamati.

Teori adanya lubang hitam pertama kali diajukan pada abad ke-18 oleh John Michell and Pierre-Simon Laplace, selanjutnya dikembangkan oleh astronom Jerman bernama Karl Schwarzschild pada tahun 1916 dengan berdasar pada teori relativitas umum dari Albert Einstein, dan semakin dipopulerkan oleh Stephen William Hawking.

Pada saat ini banyak astronom seperti charis yang percaya bahwa hampir semua galaksi dialam semesta ini mengelilingi lubang hitam pada pusat galaksi. John Archibald Wheeler pada tahun 1967 yang memberikan nama Lubang Hitam sehingga menjadi populer di dunia bahkan juga menjadi topik favorit para penulis fiksi ilmiah. Kita tidak dapat melihat lubang hitam, akan tetapi kita bisa mendeteksi materi yang tertarik/tersedot ke arahnya.

Dengan cara inilah, para astronom mempelajari dan mengidentifikasikan banyak lubang hitam di angkasa lewat observasi yang sangat hati-hati sehingga diperkirakan di angkasa dihiasi oleh jutaan lubang hitam.

Lubang Hitam tercipta ketika suatu objek tidak dapat bertahan dari kekuatan tekanan gaya gravitasinya sendiri. Banyak objek (termasuk matahari dan bumi) tidak akan pernah menjadi lubang hitam. Tekanan gravitasi pada matahari dan bumi tidak mencukupi untuk melampaui kekuatan atom dan nuklir dalam dirinya yang sifatnya melawan tekanan gravitasi. Tetapi sebaliknya untuk objek yang bermassa sangat besar, tekanan gravitasilah yang menang.

Massa dari lubang hitam terus bertambah dengan cara menangkap semua materi

didekatnya. Semua materi tidak bisa lari dari jeratan lubang hitam jika melintas terlalu

dekat. Jadi objek yang tidak bisa menjaga jarak yang aman dari lubang hitam akan

terhisap. Berlainan dengan reputasi yang disandangnya saat ini yang menyatakan bahwa

lubang hitam dapat menghisap apa saja disekitarnya, lubang hitam tidak dapat menghisap

material yang jaraknya sangat jauh dari dirinya. Dia hanya bisa menarik materi yang

lewat sangat dekat dengannya.

Kita dapat mengambil salah satu contoh bayangkan matahari kita menjadi lubang hitam dengan massa yang sama. Kegelapan akan menyelimuti bumi dikarenakan tidak ada pancaran cahaya dari lubang hitam, tetapi bumi akan tetap mengelilingi lubang hitam itu dengan jarak dan kecepatan yang sama dengan saat ini dan tidak terhisap masuk kedalamnya. Bahaya akan mengancam hanya jika bumi kita berjarak 10 mil dari lubang hitam, hal ini masih jauh dari kenyataan bahwa bumi berjarak 93 juta mil dari matahari.

Lubang hitam juga dapat bertambah massanya dengan cara bertubrukan dengan lubang hitam yang lain sehingga menjadi satu lubang hitam yang lebih besar.

2.4.2.1 Teori Relativitas Umum dalam Metrik Schwarzschild

Penerapan Teori Relativitas Umum dalam persamaan gravitasi Einstein yang mengabaikan tetapan kosmologi yang dirumuskan sebagai berikut :

𝑅 _µ𝑣 − 1

2 𝑔 ^µ𝑣 𝑅 = − � 8𝜋𝐺

𝑐 ⁴ � 𝑇 _µ𝑣 (2.24)

Dengan persamaan diatas akan diterapkan untuk menelaah beberapa gejala alam. Pertama kali akan diturunkan solusi persaam gravitasi Einstein untuk objek statik bermassa M yang diletakkan pada pusat koordinat dengan pemilihan koordinat empat dimensi berupa tiga dimensi koordinat ruang polar ( r , 𝜃 , 𝜙 ) dan satu dimensi koordinat waktu (t), yang dikenal sebagai solusi Schwarzschild.

Berikut ini akan diturunkan metrik yang mendiskripsikan medan gravitasi isotropik statik. Agar lebih mudah diperoleh, metrik ruang waktu 4 dimensi ( 3 dimensi ruang dan 1 dimensi waktu ) akan dirumuskan dalam wakilan koordinat bola. Dalam koordinat bola, 3 koordinatnya adalah

𝑥 ^𝑚 = (𝑥 ¹ , 𝑥 ² , 𝑥 ³ ) = ( r , 𝜃 , 𝜙 ) (2.25)

Metrik ruang waktu datar dalam wakilan koordinat bola diberikan oleh

Dalam mengikuti penulisan Weinberg, nilai c sementara diisikan sama dengan 1 sehingga metrik diatas menjadi

𝑑𝑠 ² = −𝑑𝑡 ² + 𝑑𝑟 ² + 𝑟 ² 𝑑𝜃 ² + 𝑟 ² 𝑠𝑖𝑛 ² 𝜃𝑑𝜙 ² (2.27)

Selanjutnya akan ditinjau metrik untuk medan gravitasi isotropik statik. Tensor metrik untuk medan tersebut, yang dalam hal ini untuk komponen 𝑔 _𝑡𝑡 dan 𝑔 _𝑟𝑟 hanya merupakan fungsi radial 𝑟. Bentuk metriknya menjadi

𝑑𝑠 ² = −𝐵(𝑟)𝑑𝑡 ² + 𝐴(𝑟)𝑑𝑟 ² + 𝑟 ² (𝑑𝜃 ² + 𝑠𝑖𝑛 ² 𝜃𝑑𝜙 ² ) (2.28)

Dimana metrik diatas akan kembali ke metrik Minkowski jika sumber medan gravitasi dilenyapkan. Dari metrik diatas, komponen tensor metrik kovarian yang tak lenyap adalah

𝑔 𝑡𝑡 = −𝐵(𝑟), 𝑔 𝑟𝑟 = 𝐴(𝑟), 𝑔 𝑟𝑟 , 𝑔 𝜃𝜃 = 𝑟 ² , 𝑔 𝜙𝜙 = 𝑟 ² 𝑠𝑖𝑛 ² 𝜃 (2.29)

Mengingat 𝑔 µ𝑣 bersifat diagonal, komponen tensor metrik kontravarian bernilai 𝑔 ^𝑡𝑡 = − 1

𝐵(𝑟) , 𝑔 ^𝑟𝑟 = 1

𝐴(𝑟) , 𝑔 ^𝜃𝜃 = 1

𝑟 ² , 𝑔 ^𝜙𝜙 = 1

𝑟 ² 𝑠𝑖𝑛 ² 𝜃 (2.30)

Selanjutnya determinan matriks yang menyajikan komponen tensor metrik adalah g yang bernilai

𝑔 = −𝐴(𝑟)𝐵(𝑟) 𝑟 ⁴ 𝑠𝑖𝑛 ² 𝜃 (2.31)

2.4.2.2 Medan gravitasi dalam ruang waktu Schwarzschild like

Medan gravitasi adalah manifestasi dari kelengkungan ruang waktu. Ruang waktu datar

artinya tidak ada medan gravitasi. Medan gravitasi dalam ruang waktu Schwarzschild-like

seperti medan gravitasi statik non-rotasi yang meliputi metrik Schwarzschild-De Sitter,

metrik Reissner-Nordstrom-De Sitter (Nailul Hasan, 2005). Secara umum penulisan

elemen garis keempat metri tersebut sering ditulis dalam koordinat (t , r , 𝜃 , 𝜙 ) atau

dalam bentuk persamaanya seperti persamaan berikut :

𝑑𝑠 ² = 𝐴(𝑟)𝑐 ² 𝑑𝑡 ² − 𝐴(𝑟) ⁻¹ 𝑑𝑟 ² − 𝑟 ² 𝑑𝜃 ² − 𝑟 ² 𝑠𝑖𝑛 ² 𝜃𝑑𝜙 ² (2.32)

Dimana kita tau

𝐴(𝑟) = �1 −

^𝑅𝑠_𝑟

� (2.33)

Untuk metrik Schwarzschild, menggambarkan ruang waktu disekitar sebuah sumber massa yang statik, yang tak berotasi dan tak bermuatan. Misalkan sebuah bintang masif yang tak berotasi dan tak bermuatan, sebagai salah satu contoh matahari. Maka untuk persaamaan metrik Reissner-Nordstrom adalah

𝐴(𝑟) = �1 − ^𝑅 _{𝑟 +}

^𝑠

^𝑞 _𝑟

₂²

� (2.34)

Persaaman metrik diatas menggambarkan ruang waktu disekitar sebuah sumber massa bermuatan yang statik, tak berotasi. Maka untuk persamaan metrik De-Sitter adalah

𝐴(𝑟) = �1 − ^Ʌ _3𝑟

²

� (2.35)

Dan untuk persamaan metrik Schwarzschild-De Sitter adalah

𝐴(𝑟) = �1 − ^𝑅 _𝑟

^𝑠

− ^Ʌ _3𝑟

²

� (2.36)

Sedangkan persamaan sebuah metrik untuk Reissner-Nordstrom-De Sitter adalah 𝐴(𝑟) = �1 − ^𝑅 _{𝑟 +}

^𝑠

^𝑞 _𝑟

₂²

− Ʌ

3 𝑟 ² � (2.37)

Sedangkan ruang waktu yang menggambarkan disekitar sebuah sumber massa bermuatan yang statik, dan tak berotasi adalah

𝑅 _𝑠 = ^2𝐺𝑀 _𝑐

₂

dan 𝑞 ² = _4𝜋𝜀 ^𝐺𝑞

²

0

𝑐

⁴

(2.38)

Dengan G adalah konstanta gravitasi Newton, sedangkan M adalah massa sumber medan

gravitasi, q adalah muatan sumber medan gravitasi, 𝜀 0 adalah permitivitas ruang hampa.