Nur Alfiani Santoso, Respatiwulan, dan Nughthoh Arfawi Kurdhi Program Studi Matematika FMIPA UNS
Abstrak. Proses percabangan merupakan suatu proses stokastik dimana setiap
in-dividu bereproduksi secara random dan tidak terkait dengan interaksi antar indi-vidu yang lain. Pada proses percabangan hanya terdapat satu indiindi-vidu sebagai in-duk pada waktu ke-0 dengan banyaknya individu baru yang lahir sebagai variabel random. Banyaknya individu baru yang lahir dapat memenuhi karakteristik suatu distribusi tertentu, salah satunya distribusi Poisson yang merupakan pengembangan dari distribusi binomial dengan probabilitas suksespkecil dan banyak populasiN be-sar. Proses percabangan dapat menggunakan fungsi pembangkit salah satunya fungsi pembangkit probabilitas (p.g.f) dari distribusi tertentu. Tujuan penelitian ini adalah menurunkan ulang dan menerapkan proses percabangan menggunakan fungsi pem-bangkit probabilitas pada distribusi Poisson. Pada proses percabangan menggunakan fungsi pembangkit dapat ditentukan nilai rata-rata dan nilai variansi untuk menge-tahui bagaimana pola pemusatan dan pola penyebaran dari banyaknya individu baru yang lahir. Nilai rata-rata dan variansi terbagi menjadi dua kategori yaitu untuk setiap individu dan untuk setiap genarasi. Dari penerapan diperoleh nilai banyaknya individu baru yang meningkat setiap kenaikan waktu sehingga kesuksesan penyebaran penyakit influenza tinggi.
Kata kunci : proses percabangan, distribusi Poisson, rata-rata, variansi
1. PENDAHULUAN
Kesehatan manusia dapat terganggu apabila terinfeksi penyakit. Penyakit terbagi menjadi penyakit menular dan penyakit tidak menular. Pada penye-baran penyakit menular proses penyepenye-barannya perlu diketahui oleh masyarakat agar dapat dilakukan pencegahan. Matematika dapat digunakan sebagai sarana mengetahui bagaimana pola penyebaran penyakit menular menggunakan proses percabangan. Proses percabangan adalah suatu proses stokastik dimana setiap individu bereproduksi secara random dan tidak terikat dengan interaksi antar individu yang lain. Feller [3] menyatakan bahwa salah satu contoh proses perca-bangan adalah mutasi genetik. Dalam setiap gen yang dibawa oleh makhluk hidup terdapat kemungkingan untuk muncul kembali pada keturunannya, melalui beberapa tahap penghapusan dan penambahan yang terjadi dalam selang waktu tertentu.
mutasi genetik. Menurut Walpole [7] distribusi probabilitas dengan dua kemu-ngkinan hasil dari n percobaan dinamakan distribusi binomial. Pada kejadian binomial dengan percobaan n besar dan probabilias sukses p kecil kondisi mu-lai mengikuti karakteristik distribusi Poisson. Salah satu karakteristik distribusi Poisson yaitu banyaknya hasil percobaan terjadi pada interval waktu tertentu dan tidak saling bergantung, dengan probabilitas sukses p kecil memungkinkan nilainya mendekati 0. Hal ini diperjelas oleh Bain dan Engelhardt [2] yang menya-takan bahwa distribusi Poisson merupakan pengembangan dari distribusi bino-mial dengan jumlah percobaan n besar dan nilai probabilitas sukses pkecil, oleh karena itu distribusi Poisson digunakan untuk menghitung nilai probabilitas suatu kejadian dalam selang waktu tertentu. Dalam suatu distribusi dapat ditentukan beberapa fungsi pembangkit.
Menurut Reluga [5], fungsi pembangkit memiliki peran yang penting kare-na secara tidak langsung merangkum dasar-dasar pengurutan dan operasi pen-carian untuk menyederhanakan bahasa matematika. Dalam mempelajari proses percabangan digunakan fungsi pembangkit probabilitas (p.g.f) selanjutnya di-cari nilai rata-rata dan variansi dari p.g.f untuk mengetahui bagaimana pola pemusatan dan pola penyebaran data. Untuk mempermudah pengamatan, pro-ses percabangan dengan fungsi pembangkit probabilitas pada distribusi Poisson diterapkan pada penyakit influenza.
2. PROSES PERCABANGAN
Menurut Taylor dan Karlin [6], untuk mempertahankan keturunannya su-atu makhluk hidup memproduksi keturunan dengan jumlah yang random, misal banyaknya keturunan berupa variabel random ξ dengan distribusi probabilitas
P r{ξ =k}=pk untuk k = 0,1,2, . . .,
dengan nilai pk≥0 dan ∑
∞
k=0pk=1.
Diasumsikan setiap individu lahir tidak bergantung antar individu yang lain dan memiliki waktu hidup yang sama. Banyaknya keturunan pada generasi ke-n
disebut denganXn. Pada proses menentukan banyaknya keturunan pada generasi ke-n menggunakan konsep percabangan. Asumsi penting yang digunakan dalam proses percabangan menurut Allen [1] adalah
(1) probabilitas individu memiliki keturunan (p) bernilai sama untuk setiap individu,
Proses percabangan merupakan suatu karakteristik rantai Markov sehing-ga karakteristik tersebut dapat diterapkan untuk mengetahui jumlah keturunan pada generasi ke-n+ 1 yaitu
Xn+1 =ξ1(n)+ξ2(n)+. . .+ξX(n)n.
Misalkan Z(t) merupakan banyaknya seluruh keturunan pada waktu t de-ngan proses kelahiran berasal dari satu induk sehingga asumsi proses percabade-ngan saatt=0 terpenuhi. Individu yang berperan sebagai induk memiliki rentang hidup yang diasumsikan sebagai variabel random τ dan jumlah keturunan yang lahir pada generasi ke-n adalahXn. Selanjutnya, banyaknya keturunan yang lahir pa-da waktu t adalah jumlahan dari individu yang berada pada proses selanjutnya
t ≥τ. Untuk setiap keturunan lahir pada waktu t dituliskan
Z(t) =
{ ∑X
n
i=1X(i) n≥τ 1, n < τ .
3. PROSES PERCABANGAN PADA DISTRIBUSI POISSON
Proses percabangan dimulai dengan individu tunggal pada waktu ke-0 yang kemudian disebut induk. Variabel random yang digunakan adalah banyaknya keturunan dari induk, banyaknya seluruh keturunan pada waktu ke-tdinotasikan denganZ(t), nilainya dapat diperoleh dari akumulasi nilaiXndimanaXnadalah banyaknya keturunan pada generasi ke-n, nilai Xn merupakan akumulasi dari ni-laiξX(n)n denganξ
(n)
Xn adalah banyaknya keturunan dari satu individu pada generasi
ke-n. Jika pola banyaknya keturunan dari induk mengikuti karakteristik suatu distribusi maka proses percabangan dapat menggunakan fungsi pembangkit pro-babilitas.
Menurut Allen [1] fungsi pembangkit probabilitas (p.g.f) dari suatu variabel randomξadalah fungsi gabungan himpunan bilangan real dengan notasiPξ yang didefinisikan dengan
Pξ(t) =E(tξ) =
∞
∑
k=0
pktk, (3.1)
untuk nilai t ∈R.
Distribusi Poisson merupakan salah satu distribusi bersifat diskret pengem-bangan dari distribusi binomial dengan fungsi distribusi probabilitas (p.d.f.) dari distribusi Poisson adalah
f(x) = λx
e−λ
dengan λ=rata-rata distribusi. Nilai p.g.f dari distribusi Poisson dapat diten-tukan dengan mensubstitusikan persamaan (3.2) ke dalam persamaan (3.1). Ni-lai p.g.f dapat digunakan untuk menentukan nilai rata-rata dan variansi dari banyaknya hasil proses percabangan, jika ∑∞
k=0pk = 1. Nilai rata-rata dan vari-ansi ξn yang memenuhi adalah
µξ=E(ξ) =
∞
∑
k=0
kpk, (3.3)
dan
σ2ξ =E[(ξ−µξ)2] =
∞
∑
k=0
k2pk−µ2ξ. (3.4)
Pada generasi ke-n nilai rata-rata dan variansi dari ξn didefinisikan sebagai
µn=E(ξXn) = µ
n untukn = 0,1,2, . . ., (3.5)
dan
σn2 =
{ σ2µn−1
(µn −1)
µ−1 , µ̸= 1
nσ2, µ= 1. (3.6)
4. HASIL DAN PEMBAHASAN
4.1. Proses Percabangan pada Distribusi Poisson. Proses percabangan adalah suatu proses stokastik dimana setiap individu bereproduksi secara random dan tidak terkait dengan interaksi antar individu yang lain. Menurut Taylor dan Karlin [6], seluruh makhluk hidup perlu mempertahankan keturunan dengan cara bereproduksi, misal banyaknya keturunan yang lahir merupakan variabel random
ξ. Diasumsikan setiap individu lahir tidak bergantung antar individu yang lain dan memiliki waktu hidup yang sama. Banyaknya keturunan pada generasi
ke-n disebut Xn. Karakteristik proses stokastik dapat terlihat dengan jelas pada variabel random banyaknya keturunan yang lahirξyang bergantung pada waktu, sehingga karakteristik rantai markov dapat diterapkan untuk mengetahui jumalah keturunan yang lahir pada generasi ke-n+ 1 di tampilkan dalam persamaan
Xn+1 =ξ1(n)+ξ2(n)+. . .+ξX(n)n, (4.1)
denganξ1(n)adalah banyaknya keturunan yang lahir dari individu 1 pada generasi ke-n. Jumlah keturunan yang lahir pada generasi ke-n+ 1 merupakan jumlahan dari banyaknya keturunan yang lahir dari individu ke-1 sampai individu ke-Xn pada generasi ke-n. Jumlah seluruh keturunan yang lahir sampai generasi ke-n
dinyatakan dengan Zn dan ditampilkan pada persamaan
Z(t) =
{ ∑X
n
i=1X(i) n≥τ
Feller [3] menjelaskan beberapa contoh penerapan proses percabangan yang dapat diterapkan dalam kehidupan, dari beberapa contoh yang dijelaskan pat diketahui bahwa banyaknya keturunan yang lahir tiap satuan waktu da-pat mendekati karakteristik suatu distribusi tertentu, salah satu distribusi yang banyak ditemukan dalam kehidupan adalah distribusi Poisson. Distribusi Pois-son adalah distribusi bersifat diskret yang merupakan pengembangan dari dis-tribusi binomial. Fungsi densitas probabilitas (p.d.f) dari distribusi Poisson di-tunjukkan pada persamaan (3.2). Untuk mengetahui pola pemusatan dan pola penyebaran banyaknya individu lahir dapat digunakan p.g.f distribusi Poisson. Nilai p.g.f diperoleh dengan subtitusi persamaan (3.2) dalam persamaan (3.1) sehingga diperoleh
Pξ(t) =E[tξ] =
∞
∑
k=0
pktk
= e−λ(1−t)
.
Nilai rata-rata dan variansi dapat ditentukan menggunakan nilai p.g.f, menggunakan persamaan (3.3) untuk rata-rata dan persamaan (3.4) untuk vari-ansi.
Nilai rata-rata
µξ =E(ξ) =
∞
∑
k=0
kpk
= λ,
nilai Variansi
σξ2 = E[ξ2]−E[ξ]2 =λ.
Selain mengetahui nilai p.g.f, rata-rata dan variansi dari ξ dapat pula di-cari nilai p.g.f, rata-rata dan variansi dari Xn yang merupakan jumlahan dari banyaknya keturunan baru yang lahir dari setiap individu pertama sampai indi-vidu ke-n−1 menggunkan nilaip.g.f, rata-rata dan variansi dari ξ. Nilai p.g.f
Pn(t) = P[P[· · ·[P(t)]· · ·]]
= e−λ+λPn−1
,
rata-rata pada generasi ke-n dicari menggunakan persamaan (3.5)
µn=E(ξXn) = µ
n
variansi pada generasi ke-n dicari menggunakan persamaan (3.6)
σ2n = {
λ2n −λn
λ−1 , λ̸= 1
nλ, λ= 1. (4.4)
4.2. Penerapan. Pada penerapan ini data penyebaran penyakit influenza yang digunakan mengacu pada Longiniet.al [4] dengan banyaknya populasiN = 2000 individu yang berada pada kawasan tertentu dan memiliki kemungkinan ter-tular influenza dengan nilai rata-rata penularanλ= 1.9. Waktu yang dibutuhkan untuk penyebaran virus influenzat = 4 hari. Data penyebaran penyakit influenza berkarakteristik distribusi Poisson denganpadalah probabilitas seorang individu tertular penyakit influenza sebesar 0.5. Pada penelitian ini dicari banyaknya in-dividu baru yang tertular penyakit influenza, ukuran populasi yang diwakili oleh rata-rata dan variansi, diambil sampel sampai generasi ke-10. Dengan
bantu-an software Mathematica 8.0 diperoleh banyaknya individu baru yang terbentuk
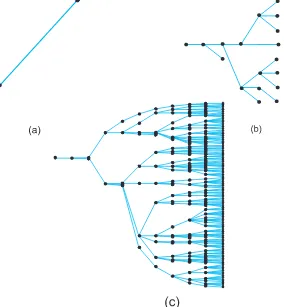
[image:6.595.164.448.406.713.2]dari satu individu induk untuk data berdistribusi Poisson, diambil sampel gambar pada pada generasi ke-1, 5, dan 10 yang disajikan dalam Gambar 1.
Gambar 1. Banyaknya individu pada (a) generasi ke-1, (b) generasi ke-5 dan,
Dari Gambar 1 (a) banyaknya individu baru yang tertular penyakit influenza dalam kurun waktu 4 hari sebanyak satu individu. Pada Gambar 1 (b) banyaknya individu baru yang tertular penyakit influenza pada generasi ke-5 dari satu induk dengan waktu setiap generasi 4 hari atau 20 hari kemudian sebanyak 8 individu. Pada Gambar 1 (c) banyaknya individu baru yang tertular penyakit influenza pada generasi ke-10 dari satu individu induk dengan waktu setiap generasi 4 hari atau 40 hari kemudian sebanyak 165 individu. Dari Gambar 1 dapat dilihat bahwa banyaknya individu baru yang tertular di setiap generasi mengalami peningkatan. Ukuran populasi dari data penyebaran penyakit influenza yang diterapkan dalam proses percabangan perlu diketahui agar dapat dilakukan analisis. Uku-ran populasi dapat diwakili dengan rata dan variansi dari data. Nilai rata-rata dan variansi dapat dicari menggunakan p.g.f dari distribusi Poisson sesuai persamaan 4.3 dan 4.4. Data banyaknya individu baru yang tertular penyakit influenza, rata-rata dan variansi sampai generasi ke-10 ditampilkan pada Tabel 1.
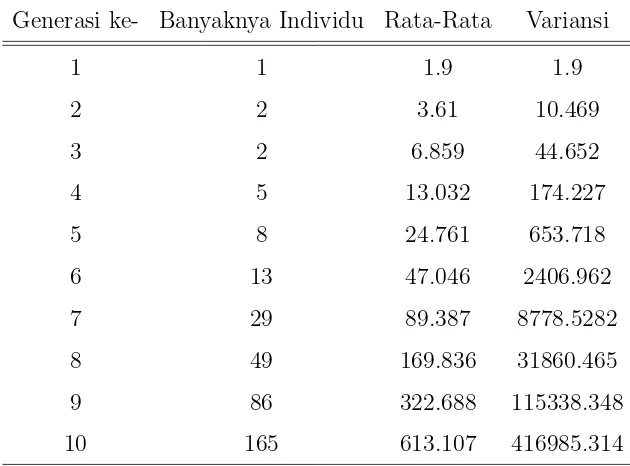
Tabel 1. Data banyaknya individu baru yang tertular penyakit influenza, rata-rata dan
variansi
Generasi ke- Banyaknya Individu Rata-Rata Variansi
1 1 1.9 1.9
2 2 3.61 10.469
3 2 6.859 44.652
4 5 13.032 174.227
5 8 24.761 653.718
6 13 47.046 2406.962
7 29 89.387 8778.5282
8 49 169.836 31860.465
9 86 322.688 115338.348
10 165 613.107 416985.314
Dari Tabel 1 dapat dilihat banyaknya individu baru yang tertular penyakit influenza serta perubahan rata-rata dan variansi di setiap generasi. Banyaknya individu yang tertular influenza dari generasi ke generasi mengalami peningkatan.
5. KESIMPULAN
(1) Proses percabangan untuk mengetahui banyaknya individu pada generasi tertentu dituliskan pada persamaan (4.1) dan jumlah seluruh individu baru sampai generasi tertentu dituliskan pada persamaan (4.2).
(2) Penerapan dengan nilai parameter yang mengacu pada Longini [4] menge-nai penyebaran penyakit influenza merupakan proses percabangan meng-gunakan fungsi pembangit probabilitas pada distribusi Poisson dengan banyaknya individu baru yang tertular penyakit influenza mengalami pen-ingkatan dalam setiap penpen-ingkatan generasi artinya kesuksesan penye-baran penyakit influenza cukup besar.
Daftar Pustaka
[1] Allen, L. J. S.,An Introduction to Stochastic Processes with Applications to Biology, Pren-tice Hall, Upper Saddla River, N.J., 2003.
[2] Bain, L. J. and M. Engelhardt., Introduction to Probability and Mathematical statistics, Duxbury, 1992.
[3] Feller, W., An Introduction to Probability Theory and Its Applications, Eugene Higgins Professor of Mathematics, Princenton University, 1950.
[4] Longini, I. M.,M. E. Halloran, A. Nizam and Y. Yang, Containing Pandemic Influenza with Antiviral Agents, American Journal of Epidemilogy 159(2004), 625-626.
[5] Reluga, T. C., Branching Process and Noncommuting Random Variables in Population Biology, Canadian Applied Mathematics Quarterly17(2009), 394-395.
[6] Taylor, Howard. M. and S. Karlin,An Introduction to Stochastic Modelling : revised
edi-tion, United States of America, 1994.
[7] Walpole, R. E., R. H. Myers, S. L. Myers, and K. Ye,Probability Statistics for Engineers