BAB II KAJIAN TEORI
A. Kajian Teori
1. Pembelajaran Matematika di SMP
Menurut Sugihartono (2012: 81), pembelajaran adalah suatu upaya yang dilakukan secara sengaja oleh pendidik untuk menyampaikan ilmu pengetahuan, mengorganisasi, dan menciptakan sistem lingkungan dengan berbagai metode sehingga siswa dapat melakukan kegiatan belajar secara efektif dan efisien serta dengan hasil yang optimal. Dalam UU Nomor 20 Tahun 2003 tentang Sistem Pendidikan Nasional pasal 1 ayat 20 disebutkan bahwa pembelajaran adalah proses interaksi pendidik dengan peserta didik dan sumber belajar pada suatu lingkungan belajar. Erman Suherman (2001: 8) menyatakan pembelajaran merupakan upaya penataan lingkungan yang memberi nuansa agar program belajar tumbuh dan berkembang secara optimal. Menurut Asep Jihad dan Abdul Haris (2008: 11), pembelajaran merupakan kombinasi dua aspek, belajar dan mengajar, belajar yaitu apa yang harus dilakukan oleh siswa dan mengajar yaitu apa yang harus dilakukan oleh guru.
Menurut Eveline Siregar dan Hartini Nara (2014: 13), ciri-ciri pembelajaran, antara lain:
a. merupakan upaya sadar dan disengaja, b. pembelajaran harus membuat siswa belajar,
d. pelaksanaannya terkendali, baik dari segi waktu, proses, isi, maupun hasilnya.
Reys, dkk (Erman Suherman, 2001:19), mendefinisikan matematika sebagai kajian tentang pola dan hubungan, suatu jalan atau pola berpikir, suatu seni, suatu bahasa, dan suatu alat. Menurut Johnson dan Rising (Erman Suherman, 2001: 19), matematika adalah pola berpikir, pola mengorganisasikan, serta pembuktian yang logis. Matematika itu adalah bahasa yang menggunakan istilah yang didefinisikan dengan jelas, cermat dan akurat, representasinya dengan simbol dan padat, lebih berupa bahasa simbol mengenai ide daripada mengenai bunyi.
Berdasarkan pengertian pembelajaran dan matematika, dapat disimpulkan bahwa pembelajaran matematika adalah upaya yang dilakukan secara sengaja oleh pendidik agar terjadi interaksi antara pendidik dengan peserta didik dan sumber belajar pada suatu lingkungan belajar tertentu untuk menelaah tentang pola dan hubungan, suatu jalan atau pola berpikir, suatu seni, suatu bahasa, dan suatu alat.
Pembelajaran matematika yang cocok diterapkan di SMP adalah pembelajaran yang sesuai dengan matematika sekolah. Ebutt dan Straker (Marsigit dkk, 2015: 235), mendefinisikan matematika sekolah sebagai berikut.
a. Matematika sebagai kegiatan penelusuran pola dan hubungan b. Matematika sebagai kreativitas yang memerlukan imajinasi
d. Matematika sebagai alat berkomunikasi 2. Karakteristik Siswa SMP
Piaget (Erman Suherman, 2001: 39) mengatakan bahwa karakteristik anak terbagi menjadi empat tahap perkembangan kognitif yaitu:
a. Tahap Sensori Motor (Sensory Motoric Stage)
Usia pada tahap sensori motor yaitu dari lahir sampai umur sekitar 2 tahun. Bagi anak yang berada pada tahap ini, pengalaman diperoleh melalui perbuatan fisik (gerakan anggota tubuh) dan sensori (koordinasi alat indera).
b. Tahap Pra Operasi (Pre Operational Stage)
Tahap pra operasional dimulai dari umur 2 tahun sampai dengan sekitar umur 7 tahun. Tahap ini adalah tahap persiapan untuk pengorganisasian operasi konkret. Istilah operasi yang digunakan oleh Piaget di sini adalah berupa tindakan-tindakan kognitif, seperti mengklasifikasikan sekumpulan objek (classifying), menata letak benda-benda menurut urutan tertentu (seriation), dan membilang (counting).
c. Tahap Operasi Konkret (Concrete Operational Stage)
Tahap operasi konkret dimulai dari sekitar umur 7 tahun sampai dengan sekitar umur 11 tahun. Umumnya anak-anak pada tahap ini telah memahami operasi logis dengan bantuan benda-benda konkret. Pada tahap ini anak memiliki kemampuan untuk mengklasifikasi, kemampuan memandang suatu objek dari sudut pandang yang berbeda
secara objektif, dan kemampuan berpikir reversible yaitu belum dapat memikirkan dua aspek atau lebih secara bersamaan.
d. Tahap Operasi Formal (Formal Operation Stage)
Tahap operasi formal dimulai dari sekitar umur 11 tahun dan seterusnya. Tahap operasi formal merupakan tahap akhir dari perkembangan kognitif secara kualitas. Anak pada tahap ini sudah mampu melakukan penalaran dengan menggunakan hal-hal yang abstrak dan tanpa harus berhadapan dengan objek atau peristiwanya langsung. Penalaran yang terjadi dalam struktur kognitifnya telah mampu hanya dengan menggunakan simbol-simbol, ide-ide, abstraksi, dan generalisasi. Ia telah memiliki kemampuan-kemampuan untuk melakukan operasi-operasi yang menyatakan hubungan diantara hubungan-hubungan dan memahami konsep promosi.
Siswa SMP di Indonesia berusia sekitar 12 sampai 15 tahun. Berdasarkan tahap perkembangan kognitif yang dikemukakan Piaget, siswa SMP berada pada tahap operasi formal. Anak pada tahap operasi formal sudah mampu melakukan penalaran dengan menggunakan hal-hal yang abstrak, tanpa harus berhadapan dengan objek atau peristiwanya langsung. Hasil penelitian yang dilakukan oleh Ashfeen Yousaf dan Tenzilla Khan (2014: 240) menunjukkan bahwa belum semua siswa SMP sudah memasuki tahap operasi formal. Siswa diberikan 3 macam aktivitas pada penelitian ini, yaitu inkuiri pertama, kedua, dan ketiga. Pada aktivitas
sudah masuk pada tahap operasi formal adalah 23,33%. Sedangkan pada aktivitas inkuiri kedua tentang Combinatorial Reasoning
sudah masuk pada tahap operasi formal adalah 10%. Kemudian pada aktivitas inkuiri ketiga tentang Proportional Reasoning % siswa masih berada pada tahap operasi konkret.
3. Pendekatan Pendidikan Matematika Realistik
Pendekatan Pendidikan Matematika Realistik (PMR) atau Realistic Mathematics Education mengacu pada pendapat Freudhental yang mengatakan bahwa matematika harus dikaitkan dengan realitas dan merupakan aktivitas manusia. Menurut Freudhental (Erman Suherman, 2001: 125), matematika bukan merupakan suatu subjek yang siap saji untuk siswa, melainkan matematika merupakan suatu pelajaran yang dinamis dan dapat dipelajari dengan cara mengerjakannya.
Menurut Treffers (Ariyadi Wijaya, 2012: 21), karakteristik Pendidikan Matematika Realistik, yaitu:
a. Penggunaan Konteks
Konteks atau permasalahan realistik pada pembelajaran matematika dengan Pendidikan Matematika Realistik digunakan sebagai titik awal pembelajaran matematika. Konteks pada Pendidikan Matematika Realistik tidak harus berupa masalah dalam dunia nyata. Konteks yang dimaksud bisa dalam bentuk permainan, penggunaan alat peraga atau hal yang lainnya selama hal tersebut bermakna dan dapat dibayangkan oleh siswa.
Penggunaan konteks dalam pembelajaran dapat menarik siswa untuk terlibat secara aktif melakukan eksplorasi permasalahan dalam pembelajaran. Manfaat penggunaan konteks dalam pembelajaran yaitu mengarahkan siswa untuk mengembangkan berbagai metode strategi penyelesaian masalah yang bisa digunakan. Selain itu, penggunaan konteks di awal pembelajaran dapat meningkatkan motivasi dan ketertarikan siswa dalam belajar matematika.
b. Penggunaan Model untuk Matematisasi Progresif
Model pada Pendidikan Matematika Realistik digunakan dalam melakukan matematisasi secara progresif. R. Soedjadi (2007: 4) menyatakan bahwa matematisasi progresif adalah upaya untuk mengarahkan kepada pemikiran matematika yang berawal dari masalah kontekstual dan akan berakhir dengan matematika formal. Treffers (Yenny B. Widjaja dan Andre Heck, 2003: 5) membedakan dua jenis matematisasi, yaitu matematisasi horisontal dan matematisasi vertikal. Matematisasi horisontal adalah proses menguraikan konteks atau masalah realistik ke dalam sistem matematika. Matematisasi vertikal adalah pengorganisasian sistem matematika itu sendiri, seperti menemukan cara pintas, generalisasi metode, dam membuat hubungan antara konsep-konsep dan strategi.
Penggunaan model berfungsi sebagai jembatan dari pengetahuan matematika yang bersifat konkret menuju pengetahuan matematika
dibedakan menjadi 2 macam, yaitu model of dan model for. Model of merupakan istilah untuk model yang menggambarkan situasi konteks. Model for adalah istilah untuk model yang sudah mengarah pada pencarian solusi secara matematis.
c. Pemanfaatan Hasil Konstruksi Siswa
Siswa ditempatkan sebagai subyek belajar dalam pembelajaran dengan pendekatan Pendidikan Matematika Realistik. Dalam pembelajaran dengan pendekatan Pendidikan Matematika Realistik, siswa memiliki kebebasan untuk menentukan strategi pemecahan masalah, sehingga diharapkan akan diperoleh strategi yang bervariasi. Hasil kerja dan konstruksi siswa selanjutnya digunakam untuk landasan pengembangan konsep matematika.
d. Interaktivitas
Proses belajar bukan hanya merupakan proses individu namun juga merupakan suatu proses sosial. Proses belajar siswa akan lebih bermakna ketika siswa dapat saling berinteraksi satu sama lain untuk mengomunikasikan gagasan dan hasil kerja mereka. Interaksi dalam pembelajaran bermanfaat dalam mengembangkan kemampuan kognitif dan afektif siswa secara simultan.
e. Keterkaitan
Konsep-konsep matematika tidak bersifat parsial, namun banyak konsep-konsep matematika yang memiliki keterkaitan. Keterkaitan yang dimaksud adalah hubungan antara beberapa topik dalam suatu
pembelajaran. Ketika siswa belajar konsep baru, siswa mengingat dan menggunakan konsep yang telah dipelajari sebelumnya (Erman Suherman, 2001: 19). Oleh karena itu, sebaiknya konsep-konsep matematika tidak dikenalkan kepada siswa secara terpisah. Dengan keterkaitan ini, diharapkan siswa dapat mengenal dan membangun lebih dari satu konsep matematika secara bersamaan.
Berdasarkan karakteristik Pendidikan Matematika Realistik, dapat disimpulkan bahwa pembelajaran matematika yang menggunakan pendekatan Pendidikan Matematika Realistik dapat menjembatani proses belajar siswa dari tahap konkret menuju tahap formal. Hal ini ditunjukkan dengan pembelajaran diawali dengan pemberian konteks atau masalah realistik. Kemudian konteks atau masalah realistik tersebut diuraikan ke dalam sistem matematika yang selanjutnya diarahkan ke bentuk formal melalui tahapan matematisasi progresif.
Menurut Treffers dan Goffree (Erman Suherman, 2001: 129) bahwa masalah kontekstual dalam pembelajaran dengan pendekatan Pendidikan Matematika Realistik, berguna untuk mengisi sejumlah fungsi, antara lain: a. pembentukan konsep,
b. pembentukan model, c. keterterapan
Menurut Murdani dkk (2013: 26), langkah-langkah pembelajaran dengan pendekatan Pendidikan Matematika Realistik adalah sebagai berikut.
a. Memahami masalah kontekstual b. Menyelesaikan masalah kontekstual
c. Membandingkan dan mendiskusikan jawaban d. Menyimpulkan
4. Perangkat Pembelajaran
Perangkat pembelajaran adalah suatu atau beberapa persiapan yang disusun oleh guru baik secara individu maupun kelompok (KKG atau MGMP) agar pelaksanaan dan evaluasi pembelajaran dapat dilakukan secara sistematis dan memperoleh hasil seperti yang diinginkan (Nazarudin, 2007:111). Hal ini menunjukkan bahwa perangkat pembelajaran disusun untuk memudahkan tercapainya tujuan pembelajaran. Perangkat pembelajaran meliputi silabus, Rencana Pelaksanaan Pembelajaran (RPP), Lembar Kegiatan Siswa (LKS), dan instrumen evaluasi, media pembelajaran, dan buku ajar. Namun dalam penelitian ini, perangkat pembelajaran dibatasi pada RPP dan LKS.
a. Rencana Pelaksanaan Pembelajaran (RPP)
Rusman (2010: 5) menyatakan bahwa RPP merupakan penjabaran silabus untuk mengarahkan kegiatan belajar peserta didik dalam upaya mencapai Kompetensi Dasar. Menurut Suyono dan Hariyanto (2015: 255), RPP adalah rencana pembelajaran yang
dikembangkan secara rinci dari suatu materi pokok yang mengacu pada silabus. E. Mulyasa (2013: 154) menyatakan bahwa RPP merupakan perencanaan jangka pendek untuk memperkirakan dan meproyeksikan tentang apa yang akan dilakukan guru dalam pembelajaran dan pembentukan kompetensi peserta didik. Berdasarkan pendapat-pendapat di atas, dapat disimpulkan bahwa RPP adalah rancangan proses pembelajaran yang di dalamnya berisi tentang kegiatan guru dan siswa yang digunakan sebagai acuan dalam pembelajaran agar dapat mencapai kompetensi dasar.
Menurut Permendiknas No 41 tahun 2007, komponen-komponen RPP terdiri dari:
1) Identitas Mata Pelajaran
Identitas mata pelajaran, meliputi: satuan pendidikan, kelas, semester, program/program keahlian, mata pelajaran atau tema pelajaran, jumlah pertemuan.
2) Standar Kompetensi
Standar Kompetensi merupakan kualifikasi kemampuan minimal peserta didik yang menggambarkan penguasaan pengetahuan, sikap, dan keterampilan yang diharapkan dicapai pada setiap kelas dan/atau semester pada suatu mata pelajaran.
3) Kompetensi Dasar
Kompetensi Dasar adalah sejumlah kemampuan yang harus dikuasai peserta didik dalam mata pelajaran tertentu sebagai rujukan penyusunan indikator kompetensi dalam suatu pelajaran. 4) Indikator Pencapaian Kompetensi
Indikator pencapaian kompetensi adalah perilaku yang dapat diukur dan/atau diobservasi untuk menunjukkan ketercapaian Kompetensi Dasar tertentu yang menjadi acuan penilaian mata pelajaran. Indikator pencapaian kompetensi dirumuskan dengan menggunakan kata kerja operasional yang dapat diamati dan diukur, yang mencakup pengetahuan, sikap, dan keterampilan.
5) Tujuan Pembelajaran
Tujuan pembelajaran menggambarkan proses dan hasil belajar yang diharapkan dicapai oleh peserta didik sesuai dengan Kompetensi Dasar.
6) Materi ajar
Materi ajar memuat fakta, konsep, prinsip, dan prosedur yang relevan, dan ditulis dalam bentuk butir-butir sesuai dengan rumusan indikator pencapaian kompetensi.
7) Alokasi waktu
Alokasi waktu ditentukan sesuai dengan keperluan untuk pencapaian Kompetensi Dasar dan beban belajar.
8) Metode Pembelajaran
Metode pembelajaran digunakan oleh guru untuk mewujudkan suasana belajar dan proses pembelajaran agar peserta didik mencapai Kompetensi Dasar atau seperangkat indikator yang telah ditetapkan. Pemilihan metode pembelajaran disesuaikan dengan situasi dan kondisi peserta didik, serta karakteristik dari setiap indikator dan kompetensi yang hendak dicapai pada setiap mata pelajaran.
9) Kegiatan pembelajaran
Kegiatan pembelajaran meliputi kegiatan pendahuluan, inti, dan penutup.
a) Pendahuluan
Pendahuluan merupakan kegiatan awal pembelajaran yang ditujukan untuk membangkitkan motivasi peserta didik. Kegiatan guru pada pendahuluan, meliputi:
(1) Menyiapkan peserta didik untuk mengikuti pembelajaran, baik secara psikis maupun fisik.
(2) Memberikan apersepsi
(3) Menyampaikan tujuan pembelajaran
(4) Menyampaikan cakupan materi dan uraian kegiatan sesuai dengan silabus.
b) Inti
Kegiatan Inti merupakan kegiatan utama dalam proses pembelajaran untuk mencapai kompetensi dasar. Kegiatan pembelajaran dilakukan secara interaktif, inspiratif, menyenangkan, menantang, memotivasi peserta didik untuk berpartisipasi aktif, serta memberikan ruang yang cukup bagi prakarsa, kreativitas, dan kemandirian sesuai dengan bakat, minat, dan perkembangan fisik, serta psikologis peserta didik (Rusman: 2012: 7). Kegiatan inti terbagi menjadi 3 kegiatan, yaitu eksplorasi, elaborasi, dan konfirmasi. Menurut Suyono dan Hariyanto (2015: 260), rincian dari kegiatan eksplorasi, elaborasi, dan konfirmasi sebagai berikut.
(1) Eksplorasi
Kegiatan guru pada eksplorasi, meliputi:
(a) Melibatkan peserta didik untuk mencari informasi yang luas dan dalam terkait materi yang akan dipelajari (b) Menggunakan berbagai pendekatan, metode, media,
dan sumber belajar
(c) Memfasilitasi interaksi anatara peserta didik dengan guru, peserta didik lain, maupun lingkungan
(d) Melibatkan peserta didik secara aktif dalam kegiatan pembelajaran
(2) Elaborasi
Kegiatan guru pada elaborasi, meliputi:
(a) Membiasakan peserta didik untuk membaca dan menulis dengan kegiatan atau tugas-tugas tertentu yang bermakna
(b) Memfasilitasi peserta didik agar memunculkan gagasan baru melalui pemberian tugas, diskusi, dan lain-lain (c) Memberikan kesempatan kepada siswa untuk
menganalisis, memecahkan masalah, dan bertindak tanpa rasa takut
(3) Konfirmasi
Kegiatan guru pada konfirmasi, meliputi: (a) Memberikan umpan balik positif dan penguatan
(b) Memberikan konfirmasi terhadap hasil eksplorasi dan elaborasi
(c) Mengarahkan peserta didik untuk melakukan refleksi (d) Memfasilitasi peserta didik untuk memperoleh
pengalaman yang bermakna dalam mencapai kompetensi
c) Penutup
Kegiatan penutup ditujukan untuk mengakhiri pembelajaran. Kegiatan guru pada penutup, meliputi:
(1) Membuat simpulan atau rangkuman pembelajaran bersama peserta didik
(2) Melakukan penilaian
(3) Memberikan umpan balik terhadap proses dan hasil pembelajaran
(4) Merencanakan kegiatan tindak lanjut
(5) Menyampaikan materi pembelajaran pada pertemuan berikutnya
10) Penilaian hasil belajar
Prosedur dan instrumen penilaian proses dan hasil belajar disesuaikan dengan indikator pencapaian kompetensi dan mengacu kepada Standar Penilaian.
11) Sumber belajar
Penentuan sumber belajar didasarkan pada Standar Kompetensi dan Kompetensi Dasar, serta materi ajar, kegiatan pembelajaran, dan indikator pencapaian kompetensi.
Prinsip-prinsip penyusunan RPP menurut Permendiknas Nomor 41 Tahun 2007, antara lain:
1) memperhatikan perbedaan individu peserta didik; 2) mendorong partisipasi aktif peserta didik;
3) mengembangkan budaya membaca dan menulis; 4) memberikan umpan balik dan tindak lanjut; 5) keterkaitan dan keterpaduan;
6) menerapkan teknologi informasi dan komunikasi.
Dalam penelitian ini, acuan yang digunakan dalam pengembangan RPP adalah prinsip-prinsip penyusunan RPP menurut Permendiknas Nomor 41 tahun 2007.
b. Lembar Kegiatan Siswa (LKS)
Suyono dan Hariyanto (2015: 262) menyatakan bahwa Lembar Kegiatan Siswa (LKS) adalah lembaran-lembaran yang berisi tugas yang harus dikerjakan oleh siswa. Menurut Das (2004: 1), LKS merupakan salah satu sarana pembelajaran yang dapat digunakan guru untuk meningkatkan aktivitas siswa dalam proses belajar-mengajar. Menurut Hendro Darmodjo dan Jenny R.E. Kaligis (1992: 40), manfaat LKS dalam pembelajaran antara lain :
1) memudahkan guru dalam mengelola proses belajar mengajar, 2) memudahkan guru mengarahkan siswanya untuk dapat menemukan
konsep-konsep melalui aktivitasnya sendiri atau dalam kelompok kerja,
3) memudahkan guru memantau keberhasilan siswa untuk mencapai sasaran belajar.
LKS dikatakan berkualitas baik apabila memenuhi syarat didaktik, konstruksi, dan teknik (Hendro Darmodjo dan Jenny R.E. Kaligis, 1992: 41).
1) Syarat Didaktik
LKS harus memenuhi syarat didaktik, artinya LKS harus memenuhi asas-asas belajar mengajar yang efektif, yaitu:
a) memperhatikan adanya perbedaan individual;
b) tekanan pada proses untuk menemukan konsep-konsep;
c) memiliki variasi stimulus melalui berbagai media dan kegiatan siswa;
d) dapat mengembangkan kemampuan komunikasi sosial, emosional, moral, dan estetika pada diri siswa;
e) pengalaman belajarnya ditentukan oleh tujuan pengembangan pribadi siswa dan bukan ditentukan oleh materi bahan pelajaran.
2) Syarat Konstruksi
Syarat konstruksi adalah syarat-syarat yang berkaitan dengan penggunaan bahasa, susunan kalimat, kosa-kata, tingkat kesukaran, dan kejelasan yang pada hakikatnya haruslah tepat guna dalam arti dapat dimengerti oleh pengguna yaitu siswa. Syarat-syarat konstruksi meliputi:
a. menggunakan bahasa yang sesuai dengan tingkat kedewasaan siswa;
b. menggunakan struktur kalimat yang jelas;
c. memiliki tata urutan pelajaran yang sesuai dengan tingkat kemampuan siswa;
d. hindarkan pertanyaan yang terlalu terbuka;
e. tidak mengacu pada buku sumber yang di luar kemampuan keterbacaan siswa;
f. menyediakan ruangan yang cukup untuk memberi keleluasaan pada siswa untuk menuliskan jawaban atau menggambar pada LKS;
g. menggunakan kalimat yang sederhana dan pendek; h. menggunakan lebih banyak ilustrasi daripada kata-kata;
i. dapat digunakan untuk semua siswa, baik yang lamban maupun yang cepat;
j. memiliki tujuan belajar yang jelas serta bermanfaat sebagai sumber motivasi;
k. mempunyai identitas untuk memudahkan administrasinya. 3) Syarat Teknis
a) Menggunakan huruf cetak dan tidak menggunakan huruf Latin atau Romawi.
b) Menggunakan huruf tebal yang agak besar untuk topik, bukan huruf biasa yang diberi garis bawah.
c) Menggunakan tidak lebih dari 10 kata dalam satu baris.
d) Menggunakan bingkai untuk membedakan kalimat perintah dengan jawaban siswa.
Menurut Hermawan (Endang Widjajanti, 2010: 5), LKS yang baik adalah LKS yang memenuhi aspek-aspek penilaian sebagai berikut.
1) Aspek Pendekatan Penulisan
Aspek pendekatan penulisan meliputi, penekanan pada keterampilan proses, penghubungan materi dengan aplikasinya pada kehidupan, dan pengajakan siswa untuk aktif dalam kegiatan pembelajaran.
2) Aspek Kebenaran Konsep
Aspek kebenaran konsep meliputi, kesesuaian konsep dengan konsep sebenarnya dan kesesuaian alur materi dengan materi prasyarat.
3) Aspek Kedalaman Konsep
Aspek kedalaman konsep meliputi, keberadaan latar belakang, seperti sejarah penemuan konsep, teorema, rumus, dan lain sebagainya, dan kesesuaian kedalaman materi dengan kompetensi siswa.
4) Aspek Keluasan Konsep
Aspek keluasan Konsep meliputi, kesesuaian keluasan konsep dengan materi pokok, keberadaan hubungan antara konsep dengan kehidupan sehari-hari, dan keberadaan informasi yang disajikan mengikuti perkembangan zaman.
5) Aspek Kejelasan Kalimat
Aspek kejelasan kalimat meliputi, kemudahan kalimat untuk dipahami dan ketidakberadaan interpretasi atau makna ganda pada kalimat.
6) Aspek Kebahasaan
Aspek kebahasaan meliputi, penggunaan bahasa baku dan keinteraktifan bahasa yang digunakan.
7) Aspek Penilaian Hasil Belajar
Aspek penilaian hasil belajar, meliputi pengukuran tiga aspek kemampuan, yaitu kemampuan kognitif, afektif, dan psikomotorik, dan pengukuran kemampuan siswa berdasarkan pada standar kompetensi.
8) Aspek Kegiatan Siswa
Aspek kegiatan siswa meliputi, keberadaan kegiatan yang memberikan pengalaman belajar secara langsung pada siswa, mendorong siswa untuk menyimpulkan konsep, dan sesuai denngan materi pelajaran.
9) Aspek Keterlaksanaan
Aspek keterlaksanaan meliputi, keberadaan kegiatan yang sesuai dengan alokasi waktu dan dapat dilaksanakan oleh siswa. 10) Aspek Penampilan Fisik
baca siswa, dan keberadaan desain yang meliputi konsistensi, format, organisasi, dan daya tarik
Dalam penelitian ini, acuan yang digunakan dalam pengembangan LKS adalah syarat-syarat LKS yang baik menurut Hendro Darmodjo dan Jenny R. E. Kaligis, yaitu syarat didaktik, teknis, dan konstruktif, dan aspek kebenaran konsep, kedalaman konsep dan keluasan konsep menurut Hermawan.
5. Materi Bangun Ruang Sisi Datar
Materi pembelajaran dalam penelitian ini adalah materi pokok Bangun Ruang Sisi Datar untuk siswa SMP kelas VIII semester 2 yang mengacu pada lampiran Permendiknas No 22 tahun 2006 mengenai standar isi.
Tabel 2. Standar Kompetensi dan Kompetensi Dasar Materi Bangun Ruang Sisi Datar
Standar Kompetensi (SK) Kompetensi Dasar (KD)
Geometri dan Pengukuran
5. Memahami sifat-sifat kubus, balok, prisma, limas, dan bagian-bagiannya, serta menentukan ukurannya
5.1. Mengidentifikasi sifat-sifat kubus, balok, prisma dan limas serta bagian-bagiannya
5.2. Membuat jaring-jaring kubus, balok, prisma dan limas
5.3. Menghitung luas permukaan dan volume kubus, balok, prisma dan limas
Secara rinci materi yang merupakan penjabaran SK dan KD di atas disajikan sebagai berikut.
Bangun ruang adalah bangun yang dibentuk oleh bangun datar dan mempunyai isi. Bangun ruang dibedakan menjadi bangun ruang sisi datar dan bangun ruang sisi lengkung. Bangun ruang sisi datar meliputi kubus,
balok, prisma, dan limas. Bangun ruang sisi lengkung meliputi tabung, kerucut, dan bola. SK dan KD di atas hanya mencakup bangun ruang sisi datar, yaitu kubus, balok, prisma, dan limas.
a. Kubus
1) Pengertian dan Unsur-Unsur Kubus
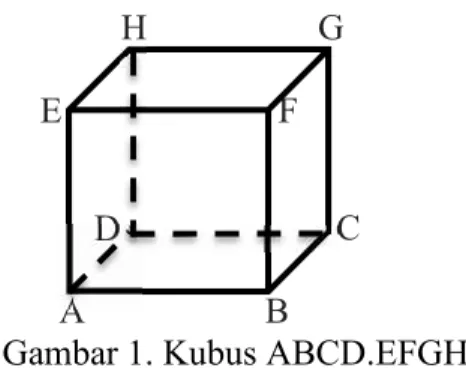
Kubus adalah bangun ruang yang dibentuk oleh 6 persegi yang mempunyai ukuran sama.
H G E F
D C A B
Gambar 1. Kubus ABCD.EFGH
Gambar diatas merupakan kubus ABCD.EFGH, yang mempunyai unsur-unsur sebagai berikut.
a) Sisi kubus, yaitu bangun datar yang membentuk kubus. Kubus
mempunyai 6 sisi. Semua sisi kubus berbentuk persegi, yang meliputi ABCD (sisi bawah/alas), ABFE (sisi depan), BCGF (sisi samping kanan), CDHG (sisi belakang), ADHE (sisi samping kiri), dan AFGH (sisi atas). Sisi-sisi yang sejajar, antara lain: ABCD dan EFGH, ABFE dan CDHG, BCGF dan ADHE. Sedangkan sisi yang saling tegak lurus adalah sisi-sisi yang tidak sejajar, yaitu ABCD dan ABFE, ABCD dan
CDHG, BCGF dan EFGH, CDHG dan EFGH, CDHG dan ADHE, ADHE dan EFGH.
b) Rusuk kubus, yaitu perpotongan antara dua sisi. Kubus mempunyai 12 rusuk, yang terdiri dari rusuk AB, BC, CD, AD, AE, BF, CG, DH, EF, FG, GH, dan EH. Terdapat 3 hubungan antar rusuk, yaitu :
(1) Sejajar, contohnya AB dan CD, BF dan CG, EH dan FG.
(2) Berpotongan, contohnya dan , dan , dan
.
(3) Bersilangan , contohnya dan , dan CD, BF dan
EH.
c) Titik sudut kubus, yaitu titik potong antara tiga rusuk. Terdapat 8 titik sudut pada kubus ABCD.EFGH antara lain: A, B, C, D, E, F, G, dan H.
d) Diagonal sisi, yaitu ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu sisi. AF, BE, AC, BD, BG, CF, CH, DG, EG, FH, AH, dan DE merupakan diagonal sisi kubus. Banyaknya diagonal sisi pada suatu kubus adalah 12. e) Diagonal ruang kubus, yaitu ruas garis yang menghubungkan
dua titik sudut yang berhadapan dan tidak pada satu sisi yang sama. Diagonal ruang pada kubus ABCD.EFGH ada 4, yaitu AG, BH, CE, dan DF.
f) Bidang diagonal kubus, yaitu daerah yang dibatasi dua diagonal bidang yang sejajar dan 2 rusuk kubus yang sejajar serta keduanya memotong kedua diagonal bidang. Suatu kubus memiliki 6 bidang diagonal, yaitu ACGE, BDHF, BGHA, CFED, AFGD, dan BEHC.
(a) (b) (c)
Gambar 2. (a) Diagonal Sisi Kubus, (b) Diagonal Ruang Kubus, (c) Bidang Diagonal Kubus
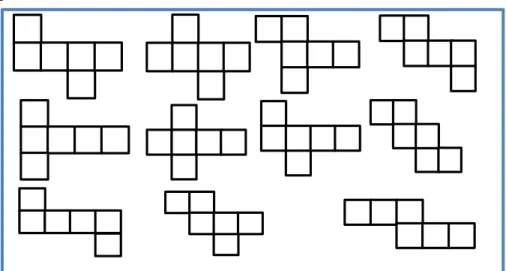
2) Jaring-Jaring Kubus
Jaring-jaring kubus merupakan rangkaian persegi yang dapat dibentuk menjadi suatu kubus. Jaring-jaring kubus disajikan pada gambar berikut.
r
3) Luas Permukaan Kubus
Luas permukaan kubus adalah jumlah luas semua sisi kubus. Luas permukaan kubus dapat diperoleh dengan menghitung luas jaring-jaring. Rumus luas permukaan kubus yaitu
4) Volume Kubus
Volume merupakan ukuran untuk menyatakan isi bangun ruang. Volume kubus adalah banyak kubus satuan yang dapat menempati suatu kubus. Gambar di samping menunjukkan volume kubus. Rumus volume kubus yaitu V= .
Gambar 4. Model Volume Kubus
b. Balok
1) Pengertian dan Unsur-Unsur Balok
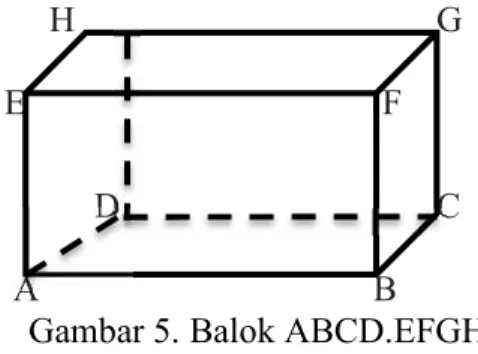
Balok adalah bangun ruang yang dibentuk oleh tiga pasang persegi panjang yang sejajar dengan bentuk dan ukuran sama. H G
E F D C A B
Gambar 5. Balok ABCD.EFGH
Gambar diatas merupakan balok ABCD.EFGH, yang mempunyai unsur-unsur sebagai berikut.
a) Sisi balok, yaitu bangun datar yang membentuk balok. Balok mempunyai 6 sisi, yang meliputi ABCD (sisi bawah/alas), ABFE(sisi depan), BCGF (sisi samping kanan), CDHG (sisi belakang), ADHE (sisi samping kiri), dan AFGH (sisi atas). Sisi-sisi yang sejajar, antara lain: ABCD dan EFGH, ABFE, dan CDHG, BCGF dan ADHE. Sedangkan sisi-sisi yang saling tegak lurus adalah sisi-sisi yang tidak sejajar, yaitu ABCD dan ABFE, ABCD dan BCGF, ABCD dan CDHG, ABCD dan ADHE, ABFE dan BCGF, ABFE dan EFGH, ABFE dan ADHE, BCGF dan CDHG, BCGF dan EFGH, CDHG dan EFGH, CDHG dan ADHE, ADHE dan EFGH.
b) Rusuk balok, yaitu perpotongan antara dua sisi. Balok mempunyai 12 rusuk, yang terdiri dari rusuk AB, BC, CD, AD, AE, BF, CG, DH, EF, FG, GH, dan EH. Terdapat 3 hubungan antar rusuk, yaitu:
(1) Sejajar, contohnya AB dan CD, BF dan CG, FG dan EH.
(2) Berpotongan, contohnya AB dan , BF dan FG, AD dan .
(3) Bersilangan , contohnya dan , FG dan CD, CG dan
AD.
c) Titik sudut balok, yaitu titik potong antara tiga rusuk. Terdapat 8 titik sudut pada balok ABCD.EFGH antara lain: A, B, C, D,
d) Diagonal sisi balok, yaitu ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu sisi. AF, BE, AC, BD, BG, CF, CH, DG, EG, FH, AH, dan DE merupakan diagonal sisi balok. Banyaknya diagonal sisi pada suatu balok adalah 12.
e) Diagonal ruang balok, yaitu ruas garis yang menghubungkan dua titik sudut yang berhadapan dan tidak pada satu sisi yang sama. Diagonal ruang pada balok ABCD.EFGH ada 4, yaitu AG, BH, CE, dan DF.
f) Bidang diagonal balok, yaitu daerah yang dibatasi dua diagonal bidang yang sejajar dan 2 rusuk balok yang sejajar serta keduanya memotong kedua diagonal bidang. Suatu balok memiliki 6 bidang diagonal, yaitu ACGE, BDHF, BGHA, CFED, AFGD, dan BEHC.
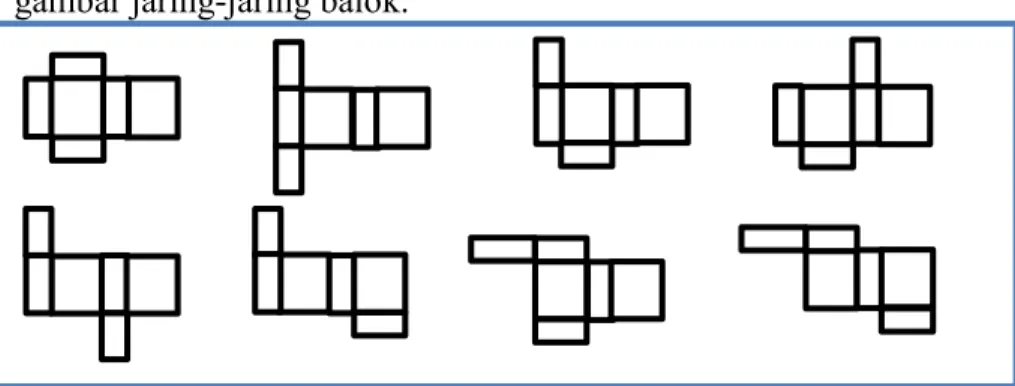
2) Jaring-Jaring Balok
Jaring-jaring balok merupakan rangkaian persegi panjang yang dapat dibentuk menjadi balok. Berikut merupakan contoh gambar jaring-jaring balok.
3)Luas Permukaan Balok
Luas permukaan balok adalah jumlah luas semua sisi balok. Luas permukaan balok dapat diperoleh dengan menghitung luas jaring-jaring. Rumus luas permukaan balok yaitu:
L= 4) Volume Balok
Volume balok adalah banyak kubus satuan yang dapat menempati suatu balok. Rumus luas volume balok, yaitu:
V= 2. Prisma
a) Pengertian dan Unsur-Unsur Prisma
Prisma adalah adalah bangun ruang yang dibentuk oleh dua bidang sejajar yang mempunyai bentuk dan ukuran sama, serta persegi panjang yang memotong dua bidang tersebut menurut garis-garis sejajar. F C E D B A Gambar 7. Prisma
a) Sisi prisma, yaitu bangun datar yang membentuk prisma. Sisi-sisi prisma ABC.DEF terdiri dari ABC (Sisi-sisi bawah/alas), DEF (sisi atas), dan sisi tegak yang meliputi ABED, BCFE, ACFD. b) Rusuk prisma, yaitu perpotongan antara dua sisi prisma.
Rusuk-rusuk prisma ABC.DEF, meliputi: 2) rusuk alas, yaitu AB, BC, dan AC, 3) rusuk atas, yaitu DE, EF, dan DF, 4) rusuk tegak, yaitu AD, BE, dan CF.
c) Titik sudut prisma, yaitu titik potong antara tiga rusuk. Terdapat 6 titik sudut pada prisma ABC.DEF antara lain: A, B, C, D, E, dan F.
Berdasarkan bentuk alasnya, terdapat prisma segitiga, prisma segiempat, prisma segilima, dan seterusnya. Banyaknya titik sudut, sisi, dan rusuk untuk setiap prisma berbeda-beda. Untuk lebih jelas, perhatikan tabel berikut.
Tabel 3. Banyaknya Titik Sudut, Sisi, dan Rusuk Prisma Nama Bangun Bentuk
Alas Banyaknya Titik Sudut Banyaknya Sisi Banyaknya Rusuk
Prisma segitiga Segitiga 6 5 9
Prisma segiempat Segiempat 8 6 12
Prisma segilima Segilima 10 7 15
Prisma segi enam Segienam 12 8 18
Prisma segi-n Segi-n b) Jaring-Jaring Prisma
Jaring-jaring prisma merupakan rangkaian segi banyak dan persegi panjang yang dibentuk menjadi suatu prisma. Jaring-jaring prisma segitiga ditampilkan pada gambar berikut.
Gambar 8. Jaring-Jaring Prisma
c) Luas Permukaan Prisma
Luas permukaan prisma adalah jumlah luas semua sisi prisma. Luas permukaan prisma diperoleh:
karena luas alas dan luas atas selalu sama, maka
d) Volume Prisma
Perhatikan ilustrasi berikut.
artimath.wordpress.com Gambar 9. Model Volume Prisma Berdasarkan ilustrasi di atas diperoleh:
= 2
= =
= 3. Limas
a) Pengertian dan Unsur-Unsur Limas
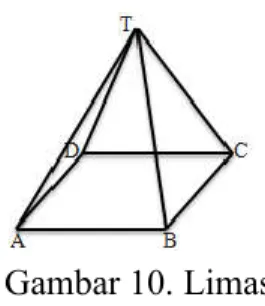
Limas adalah bangun ruang yang dibentuk oleh suatu segi n dan segitiga-segitiga yang banyaknya n. Perhatikan gambar di bawah ini.
Gambar 10. Limas
Gambar di atas merupakan limas T.ABCD yang mempunyai unsur-unsur sebagai berikut.
a) Sisi limas, yaitu bangun datar yang membatasi limas. Sisi-sisi limas T.ABCD terdiri dari ABCD (sisi bawah/alas) dan sisi tegak yang meliputi TAB, TBC, TCD, TAD.
b) Rusuk limas, yaitu perpotongan antara dua sisi limas. Rusuk-rusuk limas T.ABCD, meliputi:
(1) rusuk alas, yaitu AB, BC, CD, dan AD, (2) rusuk tegak, yaitu TA, TB, TC, dan TD.
c) Titik sudut limas, yaitu titik potong antara tiga rusuk. Terdapat 5 titik sudut pada limas T.ABCD antara lain: A, B, C, D, dan T. titik sudut T merupakan titik puncak limas.
Berdasarkan bentuk alasnya, terdapat limas segitiga, limas segiempat, limas segilima, dan seterusnya. Banyaknya titik sudut, sisi, dan rusuk untuk setiap limas berbeda-beda. Untuk lebih jelas, perhatikan tabel berikut.
Tabel 4. Banyaknya Titik Sudut, Sisi, dan Rusuk Limas Nama Bangun Bentuk Alas Banyaknya
Titik Sudut
Banyaknya Sisi
Banyaknya Rusuk
Limas segitiga Segitiga 4 4 6
Limas segiempat
Segiempat 5 5 8
Limas segilima Segilima 6 6 10
Limas segienam
Segienam 7 7 12
Prisma segi-n Segi-n b) Jaring-Jaring Limas
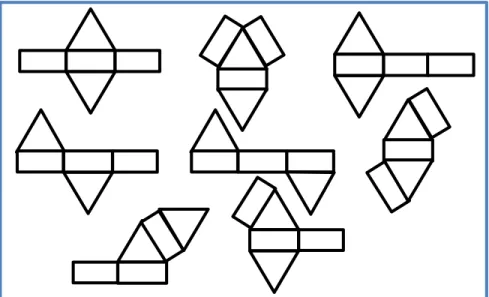
Jaring-jaring limas merupakan rangkaian segibanyak dan segitiga-segitiga yang dapat dibentuk menjadi suatu limas. Jaring-jaring limas segiempat ditampilkan pada gambar berikut.
c) Luas Permukaan Limas
Luas permukaan limas adalah jumlah luas semua sisi limas. Luas permukaan limas dapat diperoleh dengan menghitung luas jaring-jaring. Gambar berikut merupakan jaring-jaring limas.
Gambar 12. Jaring-Jaring Limas Segiempat
L =
L =
L = + d) Volume Limas
Perhatikan ilustrasi berikut.
6 6
6. Pengembangan Perangkat Pembelajaran
Pengembangan perangkat pembelajaran dilakukan dengan mengacu pada desain pengembangan perangkat pembelajaran. Salah satu desain pengembangan dalam menyusun perangkat pembelajaran yaitu model pengembangan ADDIE. Model ADDIE merupakan singkatan dari Analysis, Design, Development, Implementation, dan Evaluation. Model ADDIE dikembangkan oleh Dick dan Carry untuk merancang sistem pembelajaran. Menurut Endang Mulyatiningsih (2012: 200), model pengembangan ADDIE terdiri dari lima tahapan, yaitu analisis (analysis), perancangan (design), pengembangan (development), implementasi (implementation), dan evaluasi (evaluation).
a. Analisis (Analysis)
Tahap analisis merupakan tahapan dalam penelitian pengembangan yang dilaksanakan sebelum tahap perencanaan. Kegiatan utama pada tahap ini adalah menganalisis perlunya pengembangan perangkat pembelajaran dan menganalisis syarat-syarat dan kelayakan pengembangan perangkat pembelajaran. Tahap analisis dilaksanakan agar perangkat pembelajaran yang dikembangkan sesuai dengan karakteristik siswa, tujuan belajar, materi pembelajaran, dan lingkungan belajar. Tahap analisis meliputi kegiatan analisis kompetensi, karakteristik siswa, dan kebutuhan.
b. Perancangan (Design)
Tahap design merupakan tahap merancang konsep produk secara rinci. Kegiatan pada tahap ini meliputi pembuatan rancangan produk yang mengacu pada Standar Proses dan hasil pada tahap analisis.
c. Pengembangan (Development)
Tahap pengembangan dalam model ADDIE berisi kegiatan merealisasikan produk. Pada tahap ini produk dikembangkan sesuai dengan rancangan yang telah disusun pada tahap perancangan. Pada penelitian ini produk yang dikembangkan adalah perangkat pembelajaran berupa RPP dan LKS.
d. Implementasi (Implementation)
Tahap implementasi merupakan tahap mengujicobakan produk yang telah dikembangkan pada situasi yang nyata, yaitu di kelas. Hasil pada tahap ini akan menghasilkan data yang akan digunakan untuk mengukur kualitas produk.
e. Evaluasi (Evaluation)
Pada tahap ini dilakukan pengukuran terhadap ketercapaian produk. Data-data yang diperoleh pada tahap implementasi diolah untuk mengukur kualitas produk.
Selain mengacu pada model pengembangan, perangkat pembelajaran yang dikembangkan perlu memperhatikan kriteria kualitas. Perangkat
pembelajaran dinyatakan berkualitas apabila memenuhi tiga kriteria, yaitu kevalidan, kepraktisan, dan keefektifan (Nieveen, 1999: 127).
a. Kevalidan
Aspek kevalidan adalah kriteria kualitas perangkat pembelajaran dilihat dari sisi materi. Menurut Nieveen (1999: 127), perangkat pembelajaran dapat dikatakan valid jika materi yang terdapat dalam perangkat pembelajaran memenuhi validitas isi dan validitas konstruk. Validitas isi berarti materi yang terdapat dalam perangkat pembelajaran sesuai dengan kurikulum yang berlaku. Validitas konstruk berarti semua komponen dalam perangkat pembelajaran saling terkait.
Kevalidan pada perangkat pembelajaran yang dikembangkan didasarkan pada penilaian oleh para ahli. Para ahli, dalam penelitian ini adalah dosen Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta.
b. Kepraktisan
Menurut Nieveen (1999: 127), perangkat pembelajaran dapat dikatakan praktis jika mudah digunakan oleh guru dan siswa dalam proses pembelajaran, sehingga perangkat pembelajaran yang dikembangkan sebaiknya sesuai dengan kebutuhan dan harapan di lapangan. Kepraktisan perangkat pembelajaran didasarkan pada angket respon. Angket respon digunakan untuk mengetahui tanggapan
seberapa mudah penerapan perangkat pembelajaran tersebut. Angket respon tersebut terdiri dari angket respon siswa dan guru. Selain itu, kepraktisan juga dinilai berdasarkan keterlaksanaan pembelajaran, yaitu berapa persen pembelajaran yang terlaksana sesuai dengan RPP yang telah dikembangkan. Perangkat pembelajaran dapat dikatakan praktis jika persentase keterlaksanaan pembelajaran lebih dari 80%. c. Keefektifan
Menurut Nieveen (1999: 127), perangkat pembelajaran yang dikembangkan dapat dikatakan efektif jika siswa mengapresiasi proses pembelajaran yang berdampak pada tes formatif kelompok sasaran yang diinginkan. Apresiasi siswa yang tinggi akan meningkatkan pencapaian siswa dalam belajar. Dengan kata lain, perangkat pembelajaran dapat dikatakan efektif jika persentase ketuntasan hasil belajar siswa besar, yaitu lebih dari 60%.
B. Penelitian yang Relevan
Penelitian yang relevan dengan penelitian ini adalah penelitian yang dilakukan oleh Febriana Nurrokhmah dari Universitas Negeri Yogyakarta
Pendekatan Matematika Realistik untuk Meningkatkan Kemampuan
Hasil penelitian ini menunjukkan bahwa berdasarkan penilaian ahli dan guru matematika, perangkat pembelajaran memenuhi kriteria valid. dengan rata-rata skor untuk RPP 4,05 dari skor maksimal 5,00 dan memiliki kualifikasi
baik, sedangkan rata-rata skor untuk LKS 4,03 dari skor maksimal 5,00 dan memiliki kualifikasi baik. Selain itu, berdasarkan hasil pengisisan angket respon siswa dan guru diperoleh hasil perangkat pembelajaran memenuhi kriteria praktis dengan rata-rata skor angket respon siswa 4,06 dengan kualifikasi baik dan rata-rata skor angket respon guru 4,58 dengan kualifikasi sangat baik dengan masing-masing skor maksimal 5,00. Hasil ini menunjukkan bahwa perangkat pembelajaran yang dikembangkan dengan pendekatan Pendidikan Matematika Realistik pada materi teorema Pythagoras memenuhi kriteria valid dan praktis.
Penelitian yang relevan lainnya adalah penelitian yang dilakukan oleh Ilma Triwindari dari Universitas Negeri Yogyakarta tahun 2014 yang RPP dan LKS Materi Lingkaran dengan Pendekatan Matematika Realistik . Hasil dari penelitian ini adalah RPP dan LKS yang dikembangkan dengan pendekatan Matematika Realistik pada materi lingkaran memenuhi kriteria valid, praktis, dan efektif. RPP memenuhi kriteria valid dengan rata-rata skor 80,44% dari skor maksimal. LKS memenuhi kriteria valid dengan rata-rata skor 81,78% dari skor maksimal.
C. Kerangka Berpikir
Matematika merupakan salah satu mata pelajaran yang wajib ada dalam kurikulum sekolah dan wajib dikuasai siswa. Namun pada kenyataannya, masih banyak siswa yang belum menguasai materi matematika. Hal ini
tidak dirancang dengan baik, sehingga siswa mengalami kesulitan untuk memahaminya. Pembelajaran matematika yang dirancang di lapangan lebih banyak menekankan kepada hal-hal yang abstrak.
Rancangan pembelajaran diwujudkan dalam perencanaan pembelajaran. Perencanaan pembelajaran merupakan hal penting yang mempengaruhi tercapainya tujuan pembelajaran. Apabila perencanaan pembelajaran disusun dengan baik, maka tujuan pembelajaran akan tercapai secara optimal. RPP merupakan salah satu komponen perencanaan pembelajaran, sehingga RPP menentukan ketercapaian tujuan dalam proses pembelajaran. Namun kenyataan di lapangan menunjukkan bahwa RPP yang disusun oleh guru belum memfasilitasi siswa untuk menemukan pengetahuannya sendiri.
Perencanaan pembelajaran yang baik adalah perencanaan yang sesuai dengan karakteristik siswa agar dapat memfasilitasi siswa dalam menguasai materi pembelajaran. Karakteristik siswa SMP menurut Piaget adalah siswa SMP sudah masuk pada tahap operasi formal. Namun pada kenyataannya sebagian siswa baru sampai tahap operasi konkret. Oleh karena itu perlu adanya pembelajaran yang dapat menjembatani siswa dari tahap operasi konkret menuju tahap operasi formal. Salah satu pendekatan yang bisa digunakan untuk mendesain pembelajaran seperti itu adalah Pendidikan Matematika Realistik.
Pendidikan Matematika Realistik merupakan pendekatan pembelajaran yang menggunakan konteks atau masalah realistik sebagai titik awal pembelajaran. Kemudian siswa diberikan kegiatan untuk melakukan
matematisasi dan menemukan konsep. Matematisasi merupakan kegiatan yang mengarahkan siswa dari konteks menuju ke bentuk formal suatu konsep. Beberapa kegiatan dilakukan secara berkelompok sehingga muncul interaksi antar siswa. Selanjutnya hasil konstruksi siswa digunakan sebagai landasan untuk pengembangan konsep. Selain itu, pembelajaran dengan pendekatan Pendidikan Matematika Realistik memfasilitasi keterkaitan antar topik dalam suatu pembelajaran, sehingga memudahkan siswa untuk menemukan konsep baru.
Berdasarkan uraian tersebut, disusun perangkat pembelajaran dengan pendekatan Pendidikan Matematika Realistik pada materi bangun ruang sisi datar kelas VIII SMP/MTs. Gambar berikut merupakan kerangka berpikir dalam penelitian ini.
Gambar 14. Skema Kerangka Berpikir Obyek dari geometri ruang
merupakan benda-benda pikiran yang sifatnya abstrak.
Menurut Piaget, siswa SMP sudah masuk pada tahap operasi formal.
Bangun Ruang merupakan salah satu obyek dari geometri ruang, sehingga materi bangun ruang bersifat abstrak.
Pada kenyataannya, sebagian besar siswa SMP belum memasuki tahap operasi formal dan baru sampai pada tahap operasi konkret
Perangkat pembelajaran dengan pendekatan Pendidikan Matematika Realistik pada materi bangun ruang sisi datar yang valid, praktis, dan
efektif.
Kegiatan Pembelajaran dengan pendekatan Pendidikan Matematika Realistik, yang meliputi langkah-langkah:
1. memahami masalah kontekstual, 2. menyelesaikan masalah kontekstual,
3. membandingkan dan mendiskusikan jawaban, 4. menyimpulkan.
Pembelajaran diawali dengam konteks atau permasalahan realistik
Penggambaran situasi konteks menggunakan model untuk melakukan matematisasi progresif
Keterkaitan antar konsep matematika
Interaktivitas Pemanfaatan hasil konstruksi siswa
D. Pertanyaan Penelitian
1. Bagaimana kevalidan perangkat pembelajaran dengan pendekatan matematika realistik materi bangun ruang sisi datar kelas VIII SMP/MTs? 2. Bagaimana kepraktisan perangkat pembelajaran dengan pendekatan
matematika realistik materi bangun ruang sisi datar kelas VIII SMP/MTs? 3. Bagaimana keefektifan perangkat pembelajaran dengan pendekatan