AFNI SULISTIANI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2007
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
AFNI SULISTIANI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2007
NIM
:
G 54103045
Menyetujui :
Pembimbing I
Dr. Ir. Siswadi, M.Sc.
NIP 130 938 651
Pembimbing II
Dr. Ir. Hadi Sumarno, MS.
NIP 131 430 804
Mengetahui :
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Prof. Dr. Ir. Yonny Koesmaryono, MS.
NIP 131 473 999
Demografi adalah ilmu yang mempelajari secara ilmiah tentang populasi manusia, terutama yang berhubungan dengan umur, struktur dan perkembangannya. Salah satu komponen utama demografi yang berpengaruh terhadap struktur dan jumlah penduduk adalah kematian. Angka Harapan Hidup (AHH) merupakan indikator kematian yang umum dipakai. Terdapat empat macam AHH yaitu AHH periode, AHH kohort, The Cross-Sectional Average Length of Life (CAL) dan Rata-rata AHH Kohort (RAK). Dengan menggunakan data angka kematian Amerika Serikat
1901-1991 diperoleh bahwa laju kematian sesaat , di mana a adalah umur dan t adalah
tahun, merupakan fungsi yang paling menggambarkan angka kematian Amerika Serikat. Fungsi tersebut digunakan untuk menghitung ke empat AHH tahun 1901-1991 dan dapat memprediksi AHH beberapa tahun ke depan. RAK adalah indikator yang baik digunakan untuk menghitung AHH dibandingkan dengan AHH periode dan CAL. RAK [ ] dan AHH kohort [ ]
dapat diduga melalui AHH periode [ ] dengan persamaan
dan 2 ( , )a t exp( 5.3377 0.0016a 0.0006a 0.0164 )t µ = − − + − ( ) RAK t ec(0, )t (0, ) p e t ( ) 1.7526 1.0765 p(0, ) RAK t = − + e t ec(0, )t =8.0697 1.0789+ ep(0, )t .
SUMARNO.
Demography is the scientific study of human populations, primarily with respect to their size, structure, and development. One of the prime demography components which influential to population structure and size is mortality. Life Expectancy (LE) is generally used as indicator of mortality. There are four kinds of LE i.e. period LE, cohort LE, The Cross-Sectional Average
Length of Life (CAL) and Average Cohort LE (ACLE). By using data of United States mortality in
1901-1991 we found that the force of mortality where is age and t is time, is the best
function for describing mortality rate in United States. That function is used to calculate the four kinds of LE in years 1901-1991 and predict LE in the future. ACLE is a good indicator for calculating LE compared to period LE and CAL. ACLE [
2
( , )a t exp( 5.3377 0.0016a 0.0006a 0.0164 )t
µ = − − + − a
( )
ACLE t ] and cohort LE [ ] can be estimated by using period LE [ ] with equation
(0, ) c e t (0, ) p e t ACLE t( )= −1.7526 1.0765+ ep(0, )t and . (0, ) 8.0697 1.0789 (0, ) c p e t = + e t
Pendidikan formal yang ditempuh penulis yaitu di SDN 05 Pagi Jakarta lulus pada tahun 1997, SLTPN 223 Jakarta lulus pada tahun 2000, SMUN 39 Jakarta lulus pada tahun 2003 dan pada tahun yang sama penulis diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor, melalui jalur SPMB (Seleksi Penerimaan Mahasiswa Baru).
Selama mengikuti perkuliahan, penulis pernah menjadi pengajar privat pada mata kuliah Kalkulus I (2005). Pada tahun 2007 penulis memenangi Sesi Poster Semester Genap 2006/2007 sebagai juara harapan II. Penulis juga aktif mengikuti beberapa kepanitian di antaranya Pesta Sains 2006 sebagai Koordinator Konsumsi Pusat, MUSWIL 2006 sebagai Divisi Dana Usaha, MISOTO 2006 sebagai Koordinator Voli, Seminar Sains 2006 sebagai Sekretaris, Lets Make Money + 2005 sebagai Sekretaris, MISOTO 2005 sebagai Koordinator Humas.
ini berhasil diselesaikan. Tema yang dipilih adalah Demografi dengan judul Penentuan Angka Harapan Hidup. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Terima kasih penulis ucapkan kepada :
Bapak Dr. Ir. Siswadi, M.Sc. dan Bapak Dr. Ir. Hadi Sumarno, MS. selaku dosen pembimbing yang telah memberi bimbingan, masukan, dorongan, nasihat serta segala bantuan sehingga tugas akhir ini dapat terselesaikan.
Ayah, ibu, kakak dan adik yang selalu memberi kasih sayang, perhatian dan dukungan moril atau materi.
Seseorang yang selalu memberikan inspirasi, semangat, doa, kasih sayang, perhatian, dukungan moril atau materi dan bantuan yang tidak pernah putus.
Semua staf dosen pengajar Departemen Matematika yang telah memberikan ilmu yang bermanfaat selama menuntut ilmu di Departemen Matematika.
Orang tua kedua di Bogor yang memberikan perhatian dan kegembiraan.
Sahabat yang selalu memberi kebahagiaan, semangat, tantangan, perhatian, dan bantuan. Sahabat dan teman seperjuangan Matematika ’40 yang tidak bisa disebutkan satu persatu.
Terima kasih atas segala persahabatan yang telah kita jalin selama empat tahun ini dan mohon maaf apabila ada kesalahan yang disengaja ataupun tidak disengaja serta terima kasih atas segalanya.
Penulis menyadari bahwa tulisan ini masih jauh dari kesempurnaan dan penulis sangat menghargai segala saran dan kritik yang membangun dari pembaca. Penulis juga mengharapkan tulisan ini dapat bermanfaat bagi semua pihak yang memerlukan. Terima kasih.
Bogor, Agustus 2007
DAFTAR ISI ... i
DAFTAR TABEL ... ii
DAFTAR GAMBAR ... iii
DAFTAR LAMPIRAN ... iv
I. PENDAHULUAN A. Latar Belakang ... 1
B. Tujuan ... 1
C. Bahan dan Metode ... 1
II. DEFINISI DAN NOTASI ... 1
III. MODEL DAN KARAKTERISTIKNYA A. AHH Kohort ... 5
B. AHH Periode ... 5
C. CAL ... 5
D. RAK ... 6
IV. PENERAPAN MODEL A. Penentuan Laju Kematian Sesaat ... 8
B. Penentuan Angka Harapan Hidup ... 10
V. KESIMPULAN ... 15
VI. DAFTAR PUSTAKA ... 16
DAFTAR TABEL
Halaman
Tabel 1 Nilai AHH periode, AHH kohort, CAL dan RAK tahun 1901-1991 ... 13
Tabel 2 Nilai prediksi AHH periode, AHH kohort, CAL dan RAK AS ... 13
Tabel 3 Pendekatan empirik untuk AHH periode ... 14
DAFTAR GAMBAR
Halaman Gambar 1 Daerah angka kematian yang digunakan dalam perhitungan AHH periode, AHH
kohort, dan CAL ... 6
Gambar 2 Daerah Angka Kematian RAK ... 7
Gambar 3 Laju kematian sesaat AS per umur per tahun dari 1901 sampai 1991... 8
Gambar 4 Kurva µ( , )a t Model I ... 9
Gambar 5 Kurva µ( , )a t Model II ... 9
Gambar 6 Kurva gabungan untuk t=0 ... 9
Gambar 7 Kurva gabungan untuk t=30... 9
Gambar 8 Kurva gabungan untuk t=60 ... 10
Gambar 9 Kurva gabungan untuk t=90... 10
Gambar 10 AHH periode, AHH kohort, CAL dan RAK menggunakan µ( , )a t yang paling sesuai dengan µ( , )a t AS... 13
DAFTAR LAMPIRAN
Halaman Lampiran 1 Tabel 4 Nilai µ( , )a t AS per umur per tahun 1901-1991 dan µ( , )a t Model II .. 18 Lampiran 2 Pembuktian t x t x x t
t
p
p
µ
+∂
= −
∂
... 20 Lampiran 3 Pembuktian f t( )=tpxµx t+ adalah fkp ... 21 Lampiran 4 Pembuktian 0 ... 22 0 exp[ ] x x = −∫
µ dy A A yPENDAHULUAN
Latar BelakangDemografi adalah kajian mengenai kependudukan yang menyangkut berbagai faktor seperti jumlah, struktur usia, kepadatan, kelahiran, kematian, pertumbuhan, serta variabel sosial dan ekonomi. Komponen utama demografi yang berpengaruh terhadap struktur dan jumlah penduduk adalah fertilitas (kelahiran), mortalitas (kematian), dan migrasi (perpindahan penduduk).
Mortalitas atau kematian dapat menimpa siapa saja, tua, muda, kapan, dan di mana saja. Kasus kematian terutama dalam jumlah banyak berkaitan dengan masalah sosial, ekonomi, adat istiadat maupun masalah kesehatan lingkungan. Tinggi rendahnya kematian diukur menggunakan indikator. Indikator ini berguna untuk memonitor kinerja pemerintah pusat maupun lokal dalam peningkatan kesejahteraan masyarakat. Indikator kematian yang umum dipakai adalah angka kematian kasar, angka kematian bayi, angka kematian balita, angka kematian anak, angka kematian ibu, dan angka harapan hidup.
Angka Harapan Hidup (AHH) pada suatu umur tertentu didefinisikan sebagai rata-rata tahun hidup yang akan dijalani oleh seseorang yang telah berhasil mencapai umur tersebut dalam situasi kematian yang berlaku di lingkungan masyarakatnya. Semakin tinggi kematian maka semakin rendah AHH. AHH dapat digunakan sebagai indikator pembangunan ekonomi. Semakin baik pembangunan ekonomi di suatu wilayah, maka semakin tinggi AHH.
AHH yang biasa dikenal adalah AHH periode dan AHH kohort. Nilai AHH periode bervariasi karena perubahan angka kematian. Sedangkan AHH kohort tidak dihitung sesering AHH periode karena untuk menghitung AHH kohort diperlukan data dalam jangka waktu bertahun-tahun hingga kohort melengkapi kematiannya. Kemudian
tahun 1986, Brouard memperkenalkan The
Cross-sectional Average Length of Life (CAL)
sebagai indikator kematian alternatif. CAL melengkapi AHH kohort atau AHH periode. Tetapi CAL tidak menyertakan kematian setelah periode tertentu. Sembilan tahun kemudian, Schoen dan Canudas-Romo memperkenalkan indikator kematian yang baru yaitu Rata-rata AHH Kohort (RAK). Indikator ini diharapkan dapat memberikan gambaran terbaik dari AHH.
Tujuan
Penulisan karya ilmiah ini bertujuan untuk mencari persamaan yang menggambarkan laju kematian sesaat, kemudian menghitung AHH periode, AHH kohort, CAL dan RAK dengan menggunakan persamaan tersebut.
Bahan dan Metode
Data yang digunakan adalah data angka kematian Amerika Serikat (AS) tahun 1901-1991
(WWW.demog.berkeley.edu/~bmd/states.html) Untuk mendapatkan laju kematian sesaat yang sesuai dengan data AS yang pertama dilakukan adalah mencoba beberapa model yang diperkirakan dapat merepresentasikan data tersebut. Kebermaknaan (significancy) dugaan parameter dalam model dan koefisien determinasi (yang disesuaikan banyaknya parameter) akan digunakan dalam pemilihan. Kemudian model terpilih tersebut akan digunakan untuk menghitung AHH periode, AHH kohort, CAL dan RAK. Untuk menunjukkan bahwa model terpilih tersebut menyesuaikan data dengan baik, diberikan nilai AHH periode dari pendekatan empirik. Selanjutnya dihitung Proportionate Error (PE) sebagai ukuran kecocokan data dengan model.
DEFINISI DAN NOTASI
Definisi 1 Penduduk [Population]Penduduk adalah jumlah orang yang mendiami suatu daerah pada waktu tertentu.
(Wirosuhardjo, 1980)
Definisi 2 Kelahiran Hidup [Birth Life]
Kelahiran hidup adalah peristiwa keluarnya bayi dari rahim ibunya, tanpa memperdulikan lama kehamilan, dan setelah
itu bayi bernafas atau menunjukkan tanda-tanda kehidupan yang lain seperti detak jantung, denyut nadi atau gerakan nyata yang disengaja, baik bila tali pusat dipotong atau masih melekat dengan plasenta.
Definisi 3 Kematian [Mortality]
Kematian adalah hilangnya semua tanda-tanda kehidupan secara permanen yang dapat terjadi setiap saat setelah kelahiran hidup.
(Wirosuhardjo, 1980)
Definisi 4 Dinamika Penduduk [Population
Dynamics]
Dinamika penduduk adalah proses perubahan secara terus menerus yang mempengaruhi penduduk seperti kelahiran, kematian dan perpindahan penduduk.
(Wirosuhardjo, 1980)
Definisi 5 Angka Pertumbuhan Penduduk [Population Growth Rate]
Angka pertumbuhan penduduk adalah angka yang menunjukkan peningkatan atau penurunan jumlah penduduk suatu daerah dari waktu ke waktu. Dalam angka ini semua konponen yang berhubungan dengan pertumbuhan penduduk seperti kelahiran, kematian dan migrasi diperhitungkan.
Angka pertumbuhan penduduk yang minus berarti jumlah penduduk yang ada pada suatu daerah mengalami penurunan yang bisa disebabkan oleh banyak hal. Pertumbuhan penduduk meningkat jika jumlah kelahiran dan perpindahan penduduk dari luar ke dalam lebih besar dari jumlah kematian dan perpindahan penduduk dari dalam ke luar.
(www.organisasi.org, 9 Agustus 2006)
Definisi 6 Umur Tepat [Exact Age]
Umur tepat adalah umur yang dihitung pada saat hari ulang tahun seseorang.
(Wirosuhardjo, 1980)
Definisi 7 Angka Kematian Menurut Umur [Age Spesific Death Rate]
Angka kematian menurut umur adalah jumlah kematian menurut kelompok umur tertentu dibagi jumlah penduduk dalam kelompok umur yang sama.
(Wirosuhardjo, 1980)
Definisi 8 Kohort [Cohort]
Kohort adalah sekelompok orang yang mempunyai pengalaman waktu yang sama (biasanya satu tahun) dari suatu peristiwa tertentu.
(Utomo, 1985)
Definisi 9 Periode [Period]
Periode adalah mengenai peristiwa yang terjadi pada sebagian penduduk atau keseluruhan selama satu waktu tertentu.
Misalnya angka kematian seluruh penduduk Indonesia dalam tahun 1990.
(Utomo, 1985)
Definisi 10 Kohort Kelahiran [Birth Cohort]
Kohort kelahiran adalah banyaknya kelahiran hidup yang terjadi dalam suatu periode tertentu.
(Wirosuhardjo, 1980)
Definisi 11 Angka Tahunan [Annual Rate]
Angka tahunan adalah periode dalam waktu 12 bulan.
(Wirosuhardjo, 1980)
Definisi 12 Bertahan Hidup [Survival]
Bertahan hidup adalah suatu kondisi terutama di mana seorang individu atau suatu kelompok tetap hidup setelah interval waktu yang ditentukan.
(Shrestha, 2006)
Definisi 13 Tabel Hayat [Life Table]
Tabel hayat adalah tabel yang menggambarkan ketahanan hidup dari kelahiran hidup.
(Brown, 1997)
Definisi 14 Angka Harapan Hidup [Life
Expectancy]
Angka harapan hidup pada suatu umur tertentu didefinisikan sebagai rata-rata tahun hidup yang akan dijalani oleh seseorang yang telah berhasil mencapai umur tersebut dalam situasi kematian yang berlaku di lingkungan masyarakatnya.
(Utomo, 1985)
Definisi 15 Umur Panjang [Longevity]
Umur panjang adalah lamanya hidup. “Rata-rata umur panjang” biasanya berkenaan dengan AHH.
(Shrestha, 2006)
Definisi 16 Notasi dan Rumus Satu variabel
• x adalah umur.
• Ax n+ adalah banyaknya orang yang bertahan hidup hingga umur x+n.
• adalah banyaknya orang yang meninggal antara umur
ndx
x dan x+n. • adalah peluang bertahan hidup dari
umur
tpx
x hingga x t+ .
• nqx adalah peluang seseorang berumur x
meninggal sebelum mencapai x+n. • mx adalah angka kematian umur x .
• adalah banyaknya tahun hidup yang dijalani antara umur
nLx
x dan x+n oleh penduduk berumur x .
• Tx adalah total waktu yang dijalani penduduk berumur x sampai akhir
hayatnya.
• ex adalah AHH umur x .
ndx =Ax−Ax n+ x t t x x p =A + A n x n x x d q = A x n n x s x L d + =
∫
A s x x x d m L = x y s y x x T L ∞ ∞ = =∑
=∫
A ds x x L T ∞ = x x x T e = Auntuk , notasi selanjutnya dapat ditulis sebagai berikut : 1 n= x d , px, qx, dan Lx. Dua variabel • a adalah umur. • t adalah tahun.
• adalah banyaknya orang yang bertahan hidup hingga tepat berumur pada tahun t.
( , )a t
A
a
• adalah banyaknya orang yang meninggal antara umur dan
( , )
nd a t
a a+n pada tahun . t
• adalah peluang bertahan hidup dari umur pada tahun t hingga
( , )
np a t
a a+n.
• adalah peluang seseorang berumur tepat tahun pada tahun meninggal sebelum mencapai
( , )
nq a t
a t
a+n. • adalah angka kematian umur
tahun . ( , )
m a t a
t
• adalah tahun hidup yang dijalani antara umur dan a oleh penduduk berumur pada tahun t.
( , )
nL a t
a +n
a
• adalah total waktu yang dijalani penduduk berumur pada tahun sampai akhir hayatnya.
( , )
T a t
a t
• adalah AHH umur pada tahun . ( , ) e a t a t ( , ) ( , ) ( , ) d a t m a t L a t = ( , ) ( , ) ( , ) nd a t =A a t −A a+n t ( , ) ( , ) ( , ) n n d a t q a t a t = A ( , ) ( , ) a n n a L a t s t ds + =
∫
A ( , ) n ( , ) ( , ) y a a T a t L y t s t ds ∞ ∞ = =∑
=∫
A ( , ) ( , ) ( , ) T a t e a t a t = Auntuk n=1, notasi selanjutnya dapat ditulis sebagai berikut :
( , )
d a t , q a t( , ), dan L a t( , ).
(Brown, 1997)
Definisi 17 Laju Kematian Sesaat [The
Force of Mortality] Diketahui dx=Ax−Ax+1 dan x x x d q = A dari definisi sebelumnya untuk , sehingga dapat ditulis :
1
n=
1
x x x x x
q A =d =A −A + , jika ukuran ini dipengaruhi oleh suatu periode waktu yang singkat, sepanjang ∆t, maka rumusnya akan menjadi : * x x t x x x q A ∆ =t ∆d =A −A +∆t atau * . x x t x x q t +∆ − = ∆ A A A di mana * x
q menotasikan angka kematian yang berlaku yang didasarkan pada aktivitas kematian dalam interval kecil dari x ke
x + t∆ . Jika kemudian kita limitkan
persamaan di atas dengan , kita mempunyai suatu ukuran yang dinamakan laju kematian sesaat (dinotasikan
0 t ∆ → x µ ), yaitu 0 lim . x x t x t x t µ +∆ ∆ → − = ∆ A A A didefinisikan bahwa 0 lim x t x x t t D +∆ ∆ → − = ∆ A A A (turunan dari A ), sehingga diperoleh x
x x x D µ =− A A = −DlnA x
untuk dua variabel : ( , )a t
µ = −Dln ( , )A a t
( , )a t
µ adalah laju kematian sesaat umur tahun .
a t
(Brown, 1997)
Definisi 18 Erfi (z)
Didefinisikan fungsi galat Erf (z) adalah
Erf (z) 2 0 2 z t e dt π − =
∫
Sehingga Erfi (z) adalah fungsi galat imajiner dengan rumus :
Erfi (z)= Erf (iz)/i
(Mathematica, 2005)
MODEL DAN KARAKTERISTIKNYA
Angka Harapan Hidup (AHH) pada suatu umur tertentu didefinisikan sebagai rata-rata tahun hidup yang akan dijalani oleh seseorang yang telah berhasil mencapai umur tersebut dalam situasi kematian yang berlaku di lingkungan masyarakatnya. AHH waktu lahir misalnya, merupakan rata-rata tahun hidup yang akan dijalani oleh bayi yang baru lahir. AHH umur lima tahun berarti rata-rata tahun hidup yang akan dijalani oleh mereka yang telah mencapai umur lima tahun. AHH pada suatu umur merupakan indikator yang baik untuk menunjukkan tingkat sosial ekonomi secara umum.
AHH umur x yang dinotasikan dengan ex
menyatakan rata-rata waktu yang akan dijalani setelah umur x . Secara khusus AHH didefinisikan sebagai total waktu yang dijalani banyaknya orang yang bertahan hidup dari umur x sampai akhir hayatnya dibagi dengan jumlah orang yang bertahan hidup hingga umur x .
x
L didefinisikan sebagai banyaknya tahun hidup yang dijalani antara umur x dan x+1 oleh A . Sebagai kemungkinan lain x Lx dapat
didefinisikan sebagai rata-rata banyaknya orang yang masih hidup antara umur x dan
1 +
x , di mana diberikan nilai rata-rata Ax t+
dari t=0 sampai dengan t=1. Sehingga Lx
dapat ditulis
1
0
x x t
L =
∫
A dt +sebagai hubungan yang tepat antara Lx dan x
A , di mana A diasumsikan kontinu dan nilai x
integralnya diasumsikan ada. Kemudian apabila diberikan x y y x T ∞ = =
∑
L dt akan diperoleh : 0 x x t T ∞ + =∫
ASehingga AHH dapat ditulis sebagai
0 x t x x dt e ∞ + =
∫
A AEkspresi ex dapat diperoleh dengan
menggunakan beberapa pendekatan yang berhubungan dengan statistik. Harapan waktu hidup yang akan dijalani orang yang berumur
x dinotasikan dengan ex, dan adalah
variabel acak untuk waktu hidup yang akan dijalani, kemudian
T
x
e adalah nilai harapan dari
T
, dinotasikan Ε( )T . Diketahui bahwa( ) t x x t
f t = p µ+ (Bukti di Lampiran 3) adalah fungsi kepekatan peluang dari
T
, sehingga nilai harapan dariT
diberikan oleh :0 0 [ ] ( ) µ ∞ ∞ + = =
∫
=∫
x t e E T tf t dt t px x tdt dengan menggunakan : t x t x x t t p pµ+ ∂ = − ∂ (Bukti di Lampiran 2) akan diperoleh : 0 0 0 | µ ∞ ∞ ∞ + = − + =∫
t pt x x tdt t pt x∫
tp dtx tp dtx 0 ∞∫
Sehingga ex dapat ditulis sebagai
0 0 0 x t x t x t x x x dt e p dt dt ∞ + ∞ ∞ + =
∫
=∫
=∫
A A A ADengan demikian dapat pula dirumuskan ragam dari
T
yaitu :2 2 0 ( ) t x x t ( )x Var T t pµ dt e ∞ + =
∫
− , dengan 2 2 ( ) [ ] ( [ ]) Var T =E T − E TSebelum memperkenalkan ukuran baru, akan dibahas indikator yang ada terlebih dahulu.
Indikator Kematian AHH Kohort
AHH kohort adalah AHH yang menggunakan angka kematian bukan dari satu tahun, tetapi dari serangkaian tahun di mana individunya akan mencapai umur tertinggi. AHH kohort mewakili satu kohort. AHH kohort pada kelahiran pada waktu dirumuskan oleh : t 0 ( , ) (0, ) (0, ) (0, ) (0, ) c c c c c a t da T t e t t t ω = =
∫
A A AAnggap Ac(0, )t =1, sehingga dapat dilihat bahwa adalah peluang bertahan hidup dari lahir hingga umur a untuk kohort kelahiran pada waktu dan
( , )
c a t
A
t ω adalah umur
tertinggi yang dicapai.
Dengan menggunakan rumus :
0 0 exp[ µ ] = −
∫
A A x x ydy (Bukti di Lampiran 4) akan diperoleh : ( , ) c a t A 0 (0, ) exp[ µ( , ) ] =A −∫
+ a c t x t x dx 0 exp[ µ( , ) ] = −∫
a x t+x dxSimbol c dalam persamaan di atas digunakan untuk menandai AHH kohort. Pada teks lainnya, simbol p digunakan untuk mengindentifikasi AHH periode.
AHH kohort mencerminkan kejadian nyata dari masing-masing individu. Meskipun dikatakan lebih baik untuk kenyataan, AHH kohort tidak dihitung sesering AHH periode karena untuk menghitung AHH kohort diperlukan data dalam jangka waktu bertahun-tahun lamanya hingga kohort melengkapi kematiannya. Selain itu, perusahaan asuransi jarang menggunakan indikator ini karena asuransi perlu mencari informasi dalam waktu yang singkat mengenai AHH seseorang. Di samping itu, AHH kohort tidak mendefinisikan secara tepat pertumbuhan penduduk karena angka pertumbuhan penduduk dipengaruhi oleh banyaknya kohort, dan perbandingan dari satu kohort kurang dapat menggambarkan dinamika penduduk seluruhnya. AHH kohort pada kelahiran pada waktu t−a dirumuskan oleh :
0 ( , ) (0, ) (0, ) (0, ) (0, ) c c c c c x t a dx T t a e t a t a t a ω − − − = = − −
∫
A A Adengan Ac( ,a t−a) adalah peluang bertahan hidup dari lahir hingga umur untuk kohort kelahiran pada waktu dengan
a − t a (0, − )=1 Ac t a . AHH Periode
AHH periode adalah AHH pada tahun yang diberikan menggunakan angka kematian sebenarnya atau harapan pada setiap umur untuk tahun tersebut. AHH periode pada kelahiran pada waktu dapat diekspresikan sebagai : t 0 ( , ) (0, ) (0, ) (0, ) (0, ) p p p p p a t da T t e t t t ω = =
∫
A A Adengan (0, )Ap t =1, sehingga adalah peluang bertahan hidup dari lahir hingga umur
. Peluang ini dirumuskan sebagai : ( , ) p a t A a ( , ) Ap a t 0 (0, ) exp[ µ( , ) ] =A −
∫
a p t x t dx 0 exp[ µ( , ) ] = −∫
a x t dxAHH periode menyediakan metode untuk meringkas kondisi sekarang ini karena data yang diperlukan tersedia dengan waktu yang tidak terlalu lama. Akan tetapi, AHH periode bervariasi karena angka kematian berubah dari waktu ke waktu.
CAL
The Cross-Sectional Average Length of Life (CAL) adalah gabungan dari
bermacam-macam kejadian kohort dalam suatu model sewaktu atau ukuran kematian yang menunjuk kepada satu periode dalam asumsi suatu penduduk mempunyai angka kelahiran konstan, tetapi kematian bervariasi pada setiap umur dan waktu. Indikator ini melengkapi AHH periode dan AHH kohort. CAL pada
kelahiran pada waktu t dirumuskan sebagai berikut : 0 ( , ) (0, ) ( ) (0, ) (0, ) c cal c c a t a da T t a CAL t t a t a ω − − = = − −
∫
A A Adengan Ac( ,a t−a) adalah peluang bertahan hidup dari lahir hingga umur untuk kohort kelahiran pada waktu dengan
a
−
(0, − )=1 Ac t a . Peluang Ac( ,a t−a) dapat dirumuskan sebagai : ( , − ) Ac a t a 0 (0, ) exp[ ( , ) ] a c t a µ x t a x dx =A − −
∫
− + 0 exp[ µ( , ) ] = −∫
a x t− +a x dxCAL menggabungkan kematian masa lalu
dengan kematian sekarang dari semua kohort.
Secara umum, CAL lebih rendah dari AHH
periode karena beberapa kematian populasi seumur pada masa lalu biasanya lebih besar dibanding kematian masa kini pada waktu t. Sehingga peluang bertahan hidup untuk menghasilkan CAL lebih rendah daripada
AHH periode. CAL juga tidak menyertakan
kematian setelah periode tertentu.
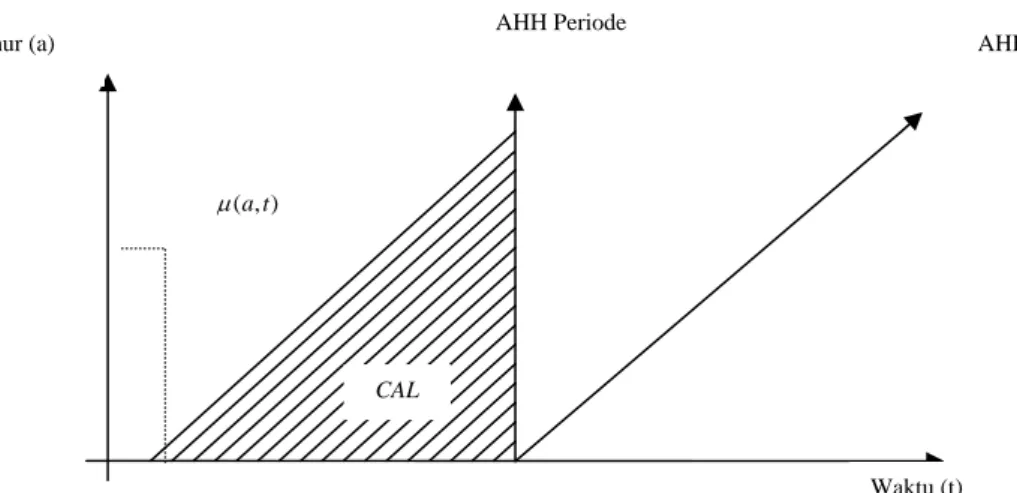
AHH Periode
Gambar 1 Daerah angka kematian yang digunakan dalam perhitungan AHH periode, AHH kohort, dan CAL.
(Guillot 2003)
Gambar 1 menunjukkan daerah angka kematian yang digunakan dalam perhitungan AHH periode pada kelahiran pada waktu [ ], AHH kohort pada kelahiran pada waktu [ ] , dan The Cross-Sectional Average Length of Life (CAL) pada waktu
[ ]. t
(0, )
pe
t
te
c(0, )
t
t( )
CAL t
RAK : Indikator Kematian Baru
Pada tahun 2005, Schoen dan Canudas-Romo memperkenalkan indikator kematian baru yang mencakup rata-rata AHH dari kohort yang hidup pada waktu yang diberikan. Pendekatan secara langsung : Schoen dan Canudas-Romo merinci rata-rata terboboti dari AHH kohort dengan kohort kelahiran
[ ]. Bobot diperlukan karena tidak beralasan untuk memberikan tekanan yang sama antara anggota populasi yang baru lahir dan anggota populasi masing-masing umur yang bertahan hidup hingga umur tinggi. Pada setiap umur, bobot yang diajukan adalah peluang bertahan hidup sebenarnya dari umur
tersebut, yaitu . Misalkan
− t a ec(0,t−a) ( , ) c a t−a A
( )
RAK t
menandai rata-rata AHH kohort pada kelahiran pada waktu t dan dirumuskan sebagai berikut : ( ) RAK t 0 0 (0, ) ( , ) a a d − − ) ( , c c c e t a t a da a t a ω ω = −∫
∫
A A 0 (0, ) ( , ) ( ) c c e t a a t a da CAL t ω − − =∫
A 0 (0, ) ( , ) c CAL e t a C a t a da ω =∫
− −di mana CCAL( ,a t−a) adalah distribusi kepadatan dari peluang bertahan hidup kohort,
( , ) ( , ) ( ) c CAL a t a C a t a CAL t − − =A .
Nilai dari
RAK t
( )
adalah rata-rata dari AHH kohort dalam tahun yang diboboti oleh peluang bertahan hidup sebenarnya dari umur tertentu. Untuk mencari RAK,t
Umur (a) AHH Kohort
( , )a t
µ
CAL
diperlukan AHH dari semua kohort, data ini tidak tersedia dengan cepat karena perlu menunggu kohort untuk melengkapi kematiannya. Sekalipun begitu, data kohort yang diperlukan tidak dapat dihindari lagi, karena ukuran yang dimaksud digunakan untuk menentukan rata-rata AHH.
RAK menyediakan ukuran yang tepat dan jelas secara konsep karena didasarkan dari
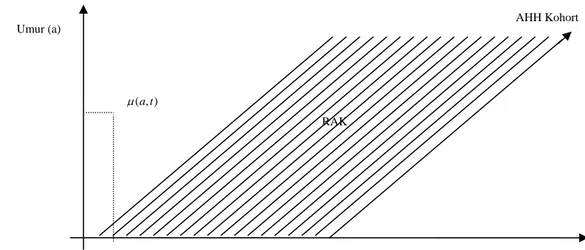
AHH kohort. Gambar di bawah ini menunjukkan daerah angka kematian yang digunakan dalam perhitungan rata-rata AHH kohort pada waktu [t
RAK t
( )
] .AHH Kohort U
Gambar 2 Daerah angka kematian RAK.
RAK mur (a)
Waktu (t) ( , )a t
PENERAPAN MODEL
Penentuan Laju Kematian SesaatLaju kematian sesaat umur x (µ ) x
diperoleh dari data angka kematian umur x
( ) dengan menggunakan asumsi laju kematian sesaat adalah konstan (
x m
x
µ =µ). Sehingga dapat dibuktikan bahwa mx=µx.
Bukti : Apabila diketahui x x x d m L = dan (Lampiran 3) maka diperoleh : 1 0 x x t x t d =
∫
A +µ +dt x m x x d L = 1 0 1 0 x t x t x t dt dt µ + + + =∫
∫
A A 1 0 1 0 x t x t dt dt µ + + =∫
∫
A A 1 0 1 0 x t x t dt dt µ + + =∫
∫
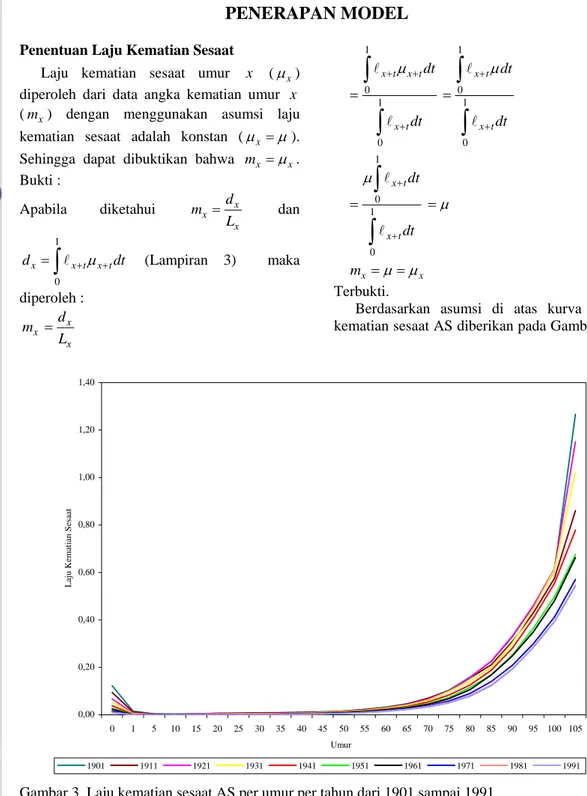
A A µ = x x m = =µ µ Terbukti.Berdasarkan asumsi di atas kurva laju kematian sesaat AS diberikan pada Gambar 3.
0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 0 1 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 Umur L aju Ke ma tia n Se sa at 1901 1911 1921 1931 1941 1951 1961 1971 1981 1991
Gambar 3 Laju kematian sesaat AS per umur per tahun dari 1901 sampai 1991
Kurva ini menggambarkan laju kematian sesaat AS per umur per tahun yang dinotasikan dengan µ( , )a t antara tahun 1901 sampai 1991. Berdasarkan kurva di atas pada tahun t selang umur 0-5 tahun µ( , )a t
mengalami penurunan. Hal ini dikarenakan tingginya angka kematian anak di bawah lima tahun yang disebabkan kegagalan proses kelahiran, lemahnya daya tahan tubuh anak, penyakit bawaan orang tua, dan kondisi
kesehatan lingkungan tempat tinggalnya. Selang umur 5-60 tahun µ( , )a t mengalami kenaikan yang tidak terlalu besar karena manusia melakukan penyesuaian daya tahan tubuh terhadap lingkungan sekitar. Sedangkan untuk umur di atas 60 tahun µ( , )a t
mengalami kenaikan yang cukup besar karena faktor penyakit dan daya tahan tubuh manusia yang semakin menurun. Secara umum,
( , )a t
penurunan yang artinya indikator kesehatan di AS dari tahun ke tahun semakin baik.
Gambar 3 mempunyai bentuk kurva seperti fungsi kuadratik, untuk mendapatkan
( , )a t
µ yang paling sesuai dengan data, dicoba model kuadratik untuk fungsi µ( , )a t , yaitu :
¾ Model I
2 ( , )a t a a t
µ = +α β +γ + ε
Dari hasil analisis regresi diperoleh : ˆ 0.1238 α = (p−value=0.000), , ˆ 0.0085 β = − (p−value=0.000) ˆ 0.0001 γ = (p value− =0.000), ˆ 0.0009 ε = − (p value− = 000) , 0. dengan koefisien determinasi
dan yang disesuaikan ( adjusted) . 2 0.818 R = 2 R R2 2 0.816 a R =
Kurva yang diperoleh dari model tersebut diberikan pada Gambar 4.
-0,20 -0,10 0,00 0,10 0,20 0,30 0,40 0 10 20 30 40 50 60 70 80 90 100 Umur L aju Ke ma tia n Se sa at t=0 t=1 t=2 t=3 t=4 t=5 t=6 t=7 t=8 t=9
Gambar 4 Kurva ( , )µ a t Model I Dari kurva di atas, Model I dapat menghasilkan µ( , )a t yang negatif. Hal ini tidak mungkin terjadi, oleh karena itu fungsi kuadratik tidak dapat digunakan untuk mendekati ( , )µ a t AS.
¾ Model II
2 ( , )a t exp( a a t) µ = α β+ +γ +ε Dari hasil analisis regresi diperoleh :
ˆ 5.3377 α = − (p−value=0.000), , ˆ 0.0016 β = − (p−value=0.778) ˆ 0.0006 γ = (p−value= 000) ,0. ˆ 0.0164 ε = − (p−value= 000) , 0. dengan R2 =0.880 dan Ra2 =0.878. Nilai µ( , )a t untuk dan {0,1, 5,10,15,...,105} a= {0,10, 20, 30,..., 90} t= Model II disajikan dalam Tabel 4 (Lampiran 1). Kurva yang diperoleh dari model tersebut diberikan pada Gambar 5. 0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50 0 1 5 101520253035 4045 5055606570 7580859095100 105 Umur L aju K em atia n S es aa t t=0 t=10 t=20 t=30 t=40 t=50 t=60 t=70 t=80 t=90
Gambar 5 Kurva ( , )µ a t Model II
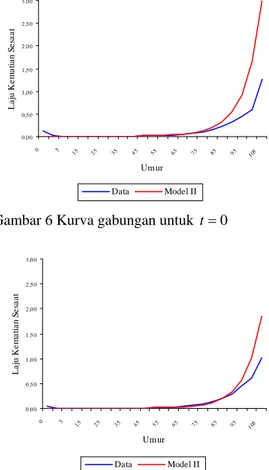
Berikut ini akan dibandingkan kurva laju kematian sesaat AS dengan Model II untuk tertentu. t 0 ,0 0 0 ,5 0 1 ,0 0 1 ,5 0 2 ,0 0 2 ,5 0 3 ,0 0 0 5 15 25 35 45 55 65 75 85 95 105 Um ur L a ju K e ma tia n S e sa a t Data Model II
Gambar 6 Kurva gabungan untuk t=0
0 ,0 0 0 ,5 0 1 ,0 0 1 ,5 0 2 ,0 0 2 ,5 0 3 ,0 0 0 5 15 25 35 45 55 65 75 85 95 105 Um ur L a ju K e ma tia n S e sa a t Data Model II
0,00 0,50 1,00 1,50 2,00 2,50 3,00 0 5 15 25 35 45 55 65 75 85 95 105 Umur L aju Ke ma tia n Se sa at Data Model II
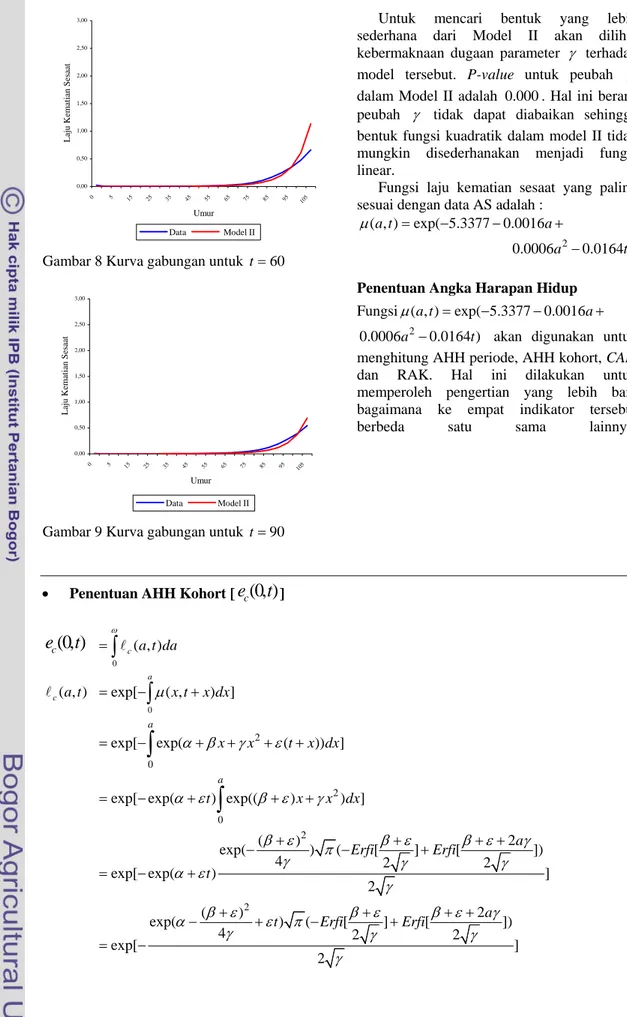
Gambar 8 Kurva gabungan untuk t=60
0,00 0,50 1,00 1,50 2,00 2,50 3,00 0 5 15 25 35 45 55 65 75 85 95 105 Umur L aju Ke ma tia n Se sa at Data Model II
Gambar 9 Kurva gabungan untuk t=90
Untuk mencari bentuk yang lebih sederhana dari Model II akan dilihat kebermaknaan dugaan parameter γ terhadap model tersebut. P-value untuk peubah γ dalam Model II adalah . Hal ini berarti peubah
0.000
γ tidak dapat diabaikan sehingga bentuk fungsi kuadratik dalam model II tidak mungkin disederhanakan menjadi fungsi linear.
Fungsi laju kematian sesaat yang paling sesuai dengan data AS adalah :
( , )a t exp( 5.3377 0.0016a
µ = − − +
2
0.0006a −0.0164 )t Penentuan Angka Harapan Hidup
Fungsi ( , )µ a t =exp( 5.3377 0.0016− − a
2
+
t
0.0006a −0.0164 ) akan digunakan untuk menghitung AHH periode, AHH kohort, CAL, dan RAK. Hal ini dilakukan untuk memperoleh pengertian yang lebih baik bagaimana ke empat indikator tersebut berbeda satu sama lainnya.
• Penentuan AHH Kohort [
e
c(0, )
t
](0, )
ce
t
0 ( , ) c a t da ω =∫
A ( , ) c a t A 0 exp[ ( , ) ] a x t x dx µ = −∫
+ 2 0 exp[ exp( ( )) ] a x x t x d α β γ ε = −∫
+ + + + x dx 2 0exp[ exp( ) exp(( ) ) ]
a t x x α ε β ε γ = − +
∫
+ + 2 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ exp( ) ] 2 a Erfi Erfi t β ε π β ε β ε γ γ γ γ α ε γ + + + + − − + = − + 2 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 a t Erfi Erfi β ε β ε β ε γ α ε π γ γ γ γ + + + − + − + = − +(0, )
ce
t
0 ( , ) c a t da ω =∫
A 2 0 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 a t Erfi Erfi da ω α β εγ ε π β εγ β ε γ γ γ + + + + − + − + =∫
−• Penentuan AHH Periode [
e
p(0, )
t
](0, )
pe
t
0 ( , ) p a t da ω =∫
A ( , ) Ap a t 0 exp[ µ( , ) ] = −∫
a x t dx 2 0 exp[ exp( ) ] a x x t dx α β γ ε = −∫
+ + + 2 0exp[ exp( ) exp( ) ]
a t x x α ε β γ = − +
∫
+ dx 2 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ exp( ) ] 2 a Erfi Erfi t β π β β γ γ γ γ α ε γ + − − + = − + 2 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 a t Erfi Erfi β β β γ α ε π γ γ γ γ + − + − + = −(0, )
pe
t
0 ( , ) ω =∫
Ap a t da 2 0 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 a t Erfi Erfi da ω α βγ ε π βγ β γ γ + − + − + =∫
− γ• Penentuan CAL [
CAL(t)
]( )
CAL t
0 ( , ) c a t a da ω =∫
A − ( , ) c a t−a A 0 exp[ ( , ) ] a x t a x dx µ = −∫
− + 2 0 exp[ exp( ( )) ] a x x t a x d α β γ ε = −∫
+ + + − + x 2 0exp[ exp( ( )) exp(( ) ) ]
a
t a x x dx
α ε β ε γ
2 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ exp( ( )) ] 2 a Erfi Erfi t a β ε π β ε β ε γ γ γ γ α ε γ + + + + − − + = − + − 2 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 a a β ε t Erfi β ε Erfi β ε γ α ε ε π γ γ γ γ + + + − − + − + = − +
( )
CAL t
0 ( , ) c a t a da ω =∫
A − 2 0 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 a a t Erfi Erfi da ω β ε β ε β ε γ α ε ε π γ γ γ γ + + + + − − + − + =∫
−• Penentuan RAK [RAK t( )]
( ) RAK t 0 (0, ) ( , ) ( ) c c e t a a t a da CAL t ω − − =
∫
A(0,
−
)
ce
t a
0 ( , ) ω =∫
Ac x t−a dx 2 0 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] 2 x a t Erfi Erfi dx ω β ε β ε β ε γ α ε ε π γ γ γ γ + + + + − − + − + =∫
− ( ) RAK t 0 (0, ) ( , ) ( ) c c e t a a t a da CAL t ω − − =∫
A ( ) RAK t 2 0 0 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 ( ( exp[ ] ) 2 x a t Erfi Erfi dx ω ω β ε β ε β ε γ α ε ε π γ γ γ γ + + + + − − + − + =∫ ∫
− 2 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 exp[ ] ) 2 a a t Erfi Erfi da β ε β ε β ε γ α ε ε π γ γ γ γ + + + + − − + − + − 2 0 ( ) 2 exp( ) ( [ ] [ ]) 4 2 2 ( exp[ ] ) 2 a a t Erfi Erfi da ω α ε β εγ ε π β εγ β ε γ γ γ + + + + − − + − + −∫
Rumus empat indikator di atas kemudian dievaluasi untuk ω=110 dengan
menggunakan
pengintegralan numerik dalam Mathematica
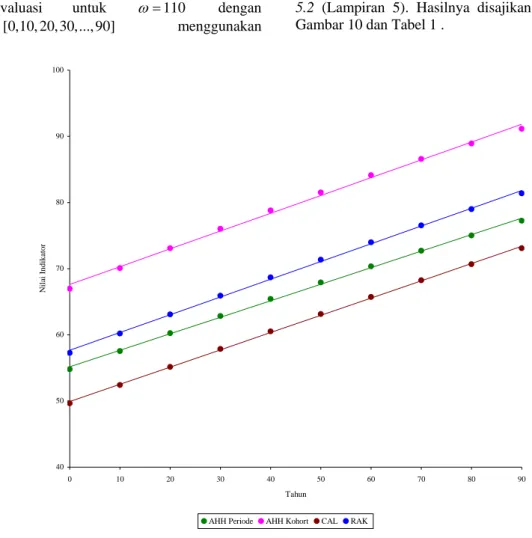
5.2 (Lampiran 5). Hasilnya disajikan dalam Gambar 10 dan Tabel 1 .
[0,10, 20, 30,..., 90] t∈ 40 50 60 70 80 90 100 0 10 20 30 40 50 60 70 80 9 Tahun N ila i I ndika to r 0
AHH Periode AHH Kohort CAL RAK
Gambar 10 AHH periode, AHH kohort, CAL dan RAK menggunakan µ( , )a t yang paling sesuai dengan µ( , )a t AS.
Tabel 1 Nilai AHH periode, AHH kohort, CAL dan RAK tahun 1901-1991
t AHH
Periode AHH
Kohort CAL RAK
0 (1901) 54.8072 66.9609 49.6524 57.2691 10 (1911) 57.5468 70.0748 52.4174 60.2 20 (1921) 60.2311 73.0913 55.157 63.0804 30 (1931) 62.8555 76.0068 57.863 65.9042 40 (1941) 65.4168 78.8183 60.5284 68.6661 50 (1951) 67.9129 81.522 63.1473 71.3614 60 (1961) 70.343 84.1126 65.7152 73.9861 70 (1971) 72.7068 86.5832 68.2284 76.5357 80 (1981) 75.0051 88.9256 70.6846 79.0059 90 (1991) 77.2389 91.1312 73.0819 81.3915
Gambar 10 menunjukkan bahwa pada tahun yang diberikan t, AHH kohort untuk kelahiran tahun tersebut adalah yang tertinggi dari empat indikator yang ada, diikuti RAK, AHH periode dan CAL. Nilai CAL yang
diperoleh kecil. Hal ini juga terjadi pada negara Inggris di mana CAL tahun 1910 ± 44 tahun dibanding dengan AHH periode ± 50 tahun (Schoen dan Canudas-Romo 2005).
Menggunakan laju kematian sesaat yang telah diperoleh, dapat diprediksi AHH periode, AHH kohort, CAL dan RAK untuk AS beberapa tahun ke depan. Misalkan akan diprediksi ke empat indikator tersebut untuk AS tahun 2001 sampai dengan 2021 (
s/d
100
t=
120
t= ). Prediksi tersebut dapat dilihat pada Tabel 2.
Tabel 2 Nilai prediksi AHH periode, AHH kohort, CAL dan RAK AS
t AHH
Periode AHH
Kohort CAL RAK
100 (2001) 79.4099 93.1921 75.4195 83.6873 110 (2011) 81.5198 95.1019 77.6971 85.8876 120 (2021) 83.5703 96.8571 79.9151 87.9869
Tabel 2 menunjukkan AHH kohort sebagai indikator tertinggi dibandingkan tiga indikator lainnya.
Persamaan garis masing-masing indikator adalah : (0, )* 55.1856 0.2494 p e t = + t t (0, )* 67.6144 0.2691 c e t = + ( )* 49.9130 0.2608 CAL t = + t ( )* 57.6593 0.2685 RAK t = + t
Dari persamaan garis tersebut, dicari hubungan AHH periode dengan RAK dan AHH kohort sehingga dapat diprediksi ke dua indikator tersebut untuk beberapa tahun ke depan menggunakan AHH periode karena AHH periode paling mudah diperoleh terutama dari ketersediaan data. Dengan substitusi persamaan ke persamaan
dan diperoleh : (0, ) * p e t ( ) * RAK t ec(0, ) *t # ( ) 1.7526 1.0765 p(0, ) * RAK t = − + e t # (0, ) 8.0697 1.0789 (0, ) * c p e t = + e t
Selanjutnya, diberikan nilai AHH periode dari pendekatan empirik serta dihitung
Proportionate Error (PE) sebagai ukuran
kecocokan data dengan model. PE dirumuskan dengan : 9 0 9 0 | i i| i i i Model Empirik PE Empirik = = − =
∑
∑
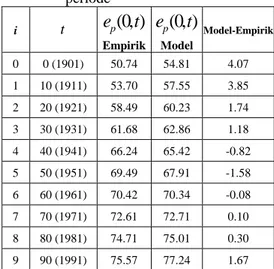
(Bloom, 1982) Bloom (1982) menyatakan bahwa model secara umum memberikan kecocokan yang baik dengan data apabila PE di bawah 10%.Tabel 3 Pendekatan empirik untuk AHH periode i t
e
p(0, )
t
Empirik(0, )
pe
t
Model Model-Empirik 0 0 (1901) 50.74 54.81 4.07 1 10 (1911) 53.70 57.55 3.85 2 20 (1921) 58.49 60.23 1.74 3 30 (1931) 61.68 62.86 1.18 4 40 (1941) 66.24 65.42 -0.82 5 50 (1951) 69.49 67.91 -1.58 6 60 (1961) 70.42 70.34 -0.08 7 70 (1971) 72.61 72.71 0.10 8 80 (1981) 74.71 75.01 0.30 9 90 (1991) 75.57 77.24 1.67Dari Tabel 3 diperoleh yang menunjukkan bahwa Model II menyesuaikan data dengan baik.
0.0235
PE=
KESIMPULAN
AHH kohort, CAL dan RAK suatu negara dapat dihitung apabila memiliki data angka kematian per umur per tahun secara lengkap. Negara Amerika Serikat memiliki data angka kematian tahun 1901-1991. Data tersebut digunakan untuk mendapatkan fungsi laju kematian sesaat yang sesuai. Hasil yang diperoleh : ( , )a t exp( 5.3377 0.0016a µ = − − + t 2 0.0006a −0.0164 ) di mana a adalah umur dan adalah tahun merupakan laju kematian sesaat yang paling menggambarkan angka kematian AS. Kemudian fungsi tersebut digunakan untuk menghitung AHH periode, AHH kohort, CAL dan RAK. Fungsi tersebut dapat pula digunakan untuk memprediksi ke empat indikator beberapa tahun ke depan.
t
Perhitungan AHH periode, AHH kohort,
CAL dan RAK menggunakan fungsi tersebut,
diketahui bahwa AHH kohort adalah indikator dengan nilai tertinggi. Karena indikator ini dapat dihitung setelah kohort melengkapi
kematiannya sehingga nilainya sesuai dengan kenyataan.
RAK adalah indikator yang baik digunakan untuk menghitung AHH dibandingkan dengan AHH periode dan CAL. Indikator ini menyediakan ukuran yang tepat dan jelas secara konsep karena didasarkan dari AHH kohort. Dalam model dinamika penduduk, RAK dapat diuji dengan model kematian yang berbeda dan hasilnya dibandingkan dengan indikator lainnya.
CAL menghasilkan nilai yang terkecil
karena kematian masa lalu lebih besar dibanding masa kini.
Mengikuti kondisi kematian di AS, RAK [ ] dan AHH kohort [ ] dapat diduga melalui AHH periode [ ] dengan persamaan : # ( ) RAK t ec(0, )t # (0, ) * p e t # ( ) 1.7526 1.0765 p(0, ) * RAK t = − + e t # (0, ) 8.0697 1.0789 (0, ) * c p e t = + e t
DAFTAR PUSTAKA
Ardana NKK. 2004. Panduan Penggunaan
Mathematica (Ed ke-1). Bogor: Departemen Matematika, FMIPA IPB.
Bloom DE. 1982. “What’s happening to the age at first birth in the United States? A study of recent cohorts”. Demography 19 (3): 351-370. Koleksi Jurnal HS-FMIPA-IPB.
Bongaarts J, G Feeney. 2002. “How long do we live?” Population and Development
Review 28(1): 13-29.
Brown RL. 1997. Introduction to The
Mathematics of Demography (Ed ke-3).
Connecticut : Actex Publications.
Draper NR, H Smith. 1992. Analisis Regresi
Terapan (Ed ke-2). Bambang S, penerjemah. Jakarta: PT Gramedia Pustaka Utama. Terjemahan dari: Applied
Regression Analysis.
Guillot M. 2003a. “The cross-sectional average length of life (CAL), A cross-sectional mortality measure that reflects the experience of cohorts”. Population
Studies 57(1): 41-54.
Hogg RV, JW McKean, AT Craig. 2005.
Introduction to Mathematical Statistics
(Ed ke-6). Upper Saddle River, NJ:
Pearson Education.
Lucas D et al. 1984. Pengantar
Kependudukan. Sumanto WB, R Saladi,
penerjemah. Yogyakarta: Gadjah Mada University Press.
Mathematica 5.2. Copyright 1988-2005 Wolfram Research, Inc. United States of
America.
Schoen R, VC Romo. 2005. “Changing mortality and average cohort life expectancy”. Demographic Research 13: 117-142.
Shrestha LB. 2005. Life Expectancy in The
United States. Order Code RL32792. [7
Des 2006].
Utomo B. 1985. Mortalitas: Pengertian dan
Contoh Kasus di Indonesia. Jakarta:
Proyek Penelitian Morbiditas dan Mortalitas UI.
Wirosuhardjo K et al. 1985. Kamus Istilah
Demografi. Jakarta: Pusat Pembinaan dan
Pengembangan Bahasa.
WWW.demog.berkeley.edu/~bmd/states.html.
Lampiran 1
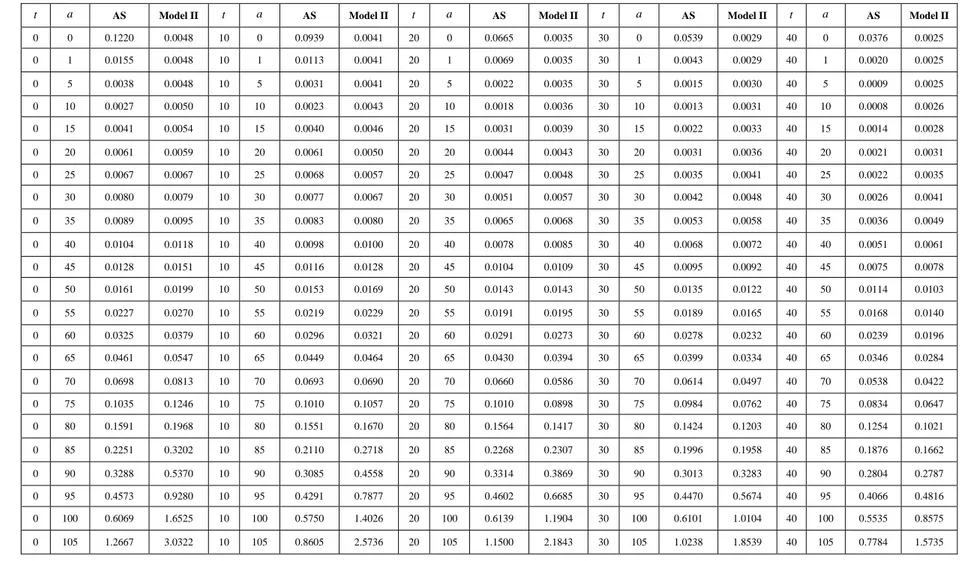
Tabel 4 Nilai ( , )µ a t AS per umur per tahun 1901-1991 dan ( , )µ a t Model II
t a AS Model II t a AS Model II t a AS Model II t a AS Model II t a AS Model II
0 0 0.1220 0.0048 10 0 0.0939 0.0041 20 0 0.0665 0.0035 30 0 0.0539 0.0029 40 0 0.0376 0.0025 0 1 0.0155 0.0048 10 1 0.0113 0.0041 20 1 0.0069 0.0035 30 1 0.0043 0.0029 40 1 0.0020 0.0025 0 5 0.0038 0.0048 10 5 0.0031 0.0041 20 5 0.0022 0.0035 30 5 0.0015 0.0030 40 5 0.0009 0.0025 0 10 0.0027 0.0050 10 10 0.0023 0.0043 20 10 0.0018 0.0036 30 10 0.0013 0.0031 40 10 0.0008 0.0026 0 15 0.0041 0.0054 10 15 0.0040 0.0046 20 15 0.0031 0.0039 30 15 0.0022 0.0033 40 15 0.0014 0.0028 0 20 0.0061 0.0059 10 20 0.0061 0.0050 20 20 0.0044 0.0043 30 20 0.0031 0.0036 40 20 0.0021 0.0031 0 25 0.0067 0.0067 10 25 0.0068 0.0057 20 25 0.0047 0.0048 30 25 0.0035 0.0041 40 25 0.0022 0.0035 0 30 0.0080 0.0079 10 30 0.0077 0.0067 20 30 0.0051 0.0057 30 30 0.0042 0.0048 40 30 0.0026 0.0041 0 35 0.0089 0.0095 10 35 0.0083 0.0080 20 35 0.0065 0.0068 30 35 0.0053 0.0058 40 35 0.0036 0.0049 0 40 0.0104 0.0118 10 40 0.0098 0.0100 20 40 0.0078 0.0085 30 40 0.0068 0.0072 40 40 0.0051 0.0061 0 45 0.0128 0.0151 10 45 0.0116 0.0128 20 45 0.0104 0.0109 30 45 0.0095 0.0092 40 45 0.0075 0.0078 0 50 0.0161 0.0199 10 50 0.0153 0.0169 20 50 0.0143 0.0143 30 50 0.0135 0.0122 40 50 0.0114 0.0103 0 55 0.0227 0.0270 10 55 0.0219 0.0229 20 55 0.0191 0.0195 30 55 0.0189 0.0165 40 55 0.0168 0.0140 0 60 0.0325 0.0379 10 60 0.0296 0.0321 20 60 0.0291 0.0273 30 60 0.0278 0.0232 40 60 0.0239 0.0196 0 65 0.0461 0.0547 10 65 0.0449 0.0464 20 65 0.0430 0.0394 30 65 0.0399 0.0334 40 65 0.0346 0.0284 0 70 0.0698 0.0813 10 70 0.0693 0.0690 20 70 0.0660 0.0586 30 70 0.0614 0.0497 40 70 0.0538 0.0422 0 75 0.1035 0.1246 10 75 0.1010 0.1057 20 75 0.1010 0.0898 30 75 0.0984 0.0762 40 75 0.0834 0.0647 0 80 0.1591 0.1968 10 80 0.1551 0.1670 20 80 0.1564 0.1417 30 80 0.1424 0.1203 40 80 0.1254 0.1021 0 85 0.2251 0.3202 10 85 0.2110 0.2718 20 85 0.2268 0.2307 30 85 0.1996 0.1958 40 85 0.1876 0.1662 0 90 0.3288 0.5370 10 90 0.3085 0.4558 20 90 0.3314 0.3869 30 90 0.3013 0.3283 40 90 0.2804 0.2787 0 95 0.4573 0.9280 10 95 0.4291 0.7877 20 95 0.4602 0.6685 30 95 0.4470 0.5674 40 95 0.4066 0.4816 0 100 0.6069 1.6525 10 100 0.5750 1.4026 20 100 0.6139 1.1904 30 100 0.6101 1.0104 40 100 0.5535 0.8575 0 105 1.2667 3.0322 10 105 0.8605 2.5736 20 105 1.1500 2.1843 30 105 1.0238 1.8539 40 105 0.7784 1.5735
Tabel 4 (Lanjutan)
t a AS Model II t a AS Model II t a AS Model II t a AS Model II t a AS Model
II 50 0 0.0276 0.0021 60 0 0.0238 0.0018 70 0 0.0159 0.0015 80 0 0.0106 0.0013 90 0 0.0083 0.0011 50 1 0.0012 0.0021 60 1 0.0009 0.0018 70 1 0.0007 0.0015 80 1 0.0005 0.0013 90 1 0.0004 0.0011 50 5 0.0005 0.0021 60 5 0.0004 0.0018 70 5 0.0004 0.0015 80 5 0.0003 0.0013 90 5 0.0002 0.0011 50 10 0.0005 0.0022 60 10 0.0004 0.0019 70 10 0.0004 0.0016 80 10 0.0003 0.0014 90 10 0.0003 0.0011 50 15 0.0010 0.0024 60 15 0.0010 0.0020 70 15 0.0010 0.0017 80 15 0.0008 0.0014 90 15 0.0008 0.0012 50 20 0.0014 0.0026 60 20 0.0013 0.0022 70 20 0.0014 0.0019 80 20 0.0011 0.0016 90 20 0.0011 0.0014 50 25 0.0014 0.0030 60 25 0.0014 0.0025 70 25 0.0013 0.0021 80 25 0.0012 0.0018 90 25 0.0012 0.0015 50 30 0.0017 0.0035 60 30 0.0017 0.0029 70 30 0.0015 0.0025 80 30 0.0014 0.0021 90 30 0.0016 0.0018 50 35 0.0025 0.0042 60 35 0.0024 0.0035 70 35 0.0021 0.0030 80 35 0.0018 0.0026 90 35 0.0020 0.0022 50 40 0.0039 0.0052 60 40 0.0037 0.0044 70 40 0.0032 0.0037 80 40 0.0026 0.0032 90 40 0.0027 0.0027 50 45 0.0061 0.0066 60 45 0.0059 0.0056 70 45 0.0051 0.0048 80 45 0.0040 0.0041 90 45 0.0038 0.0034 50 50 0.0097 0.0088 60 50 0.0091 0.0074 70 50 0.0078 0.0063 80 50 0.0064 0.0054 90 50 0.0057 0.0045 50 55 0.0143 0.0119 60 55 0.0134 0.0101 70 55 0.0119 0.0086 80 55 0.0101 0.0073 90 55 0.0090 0.0062 50 60 0.0213 0.0167 60 60 0.0207 0.0142 70 60 0.0180 0.0120 80 60 0.0155 0.0102 90 60 0.0143 0.0087 50 65 0.0315 0.0241 60 65 0.0298 0.0204 70 65 0.0263 0.0173 80 65 0.0237 0.0147 90 65 0.0221 0.0125 50 70 0.0470 0.0358 60 70 0.0438 0.0304 70 70 0.0389 0.0258 80 70 0.0353 0.0219 90 70 0.0323 0.0186 50 75 0.0729 0.0549 60 75 0.0678 0.0466 70 75 0.0586 0.0395 80 75 0.0533 0.0336 90 75 0.0496 0.0285 50 80 0.1148 0.0867 60 80 0.1061 0.0736 70 80 0.0903 0.0624 80 80 0.0814 0.0530 90 80 0.0776 0.0450 50 85 0.1684 0.1410 60 85 0.1681 0.1197 70 85 0.1397 0.1016 80 85 0.1259 0.0862 90 85 0.1226 0.0732 50 90 0.2523 0.2365 60 90 0.2474 0.2007 70 90 0.2083 0.1704 80 90 0.1928 0.1446 90 90 0.1916 0.1227 50 95 0.3645 0.4087 60 95 0.3489 0.3469 70 95 0.2988 0.2944 80 95 0.2838 0.2499 90 95 0.2856 0.2121 50 100 0.4966 0.7278 60 100 0.4804 0.6177 70 100 0.4109 0.5243 80 100 0.3915 0.4450 90 100 0.3933 0.3777 50 105 0.6748 1.3355 60 105 0.6625 1.1335 70 105 0.5703 0.9620 80 105 0.5421 0.8165 90 105 0.5448 0.6930
Lampiran 2 Diketahui : x t t x t t
p
x +∂
=
∂
∂
∂
A
A
dan x x xD
µ
=
−
A
A
Akan dibuktikan : t x t x x t tp
p
µ
+∂
= −
∂
Bukti : x x xD
µ
=
−
A
A
x xD
A
= −
A
µ
x x x t xµ
∂
= −
∂
A
A
x t x t x t tµ
+ +∂
= −
∂
A
A
+ x t x t x t t x xµ
+ +∂
−
=
∂
A
A
A
A
+ x t x t t x t x x t t xp
+µ
+p
µ
+∂
−
=
= −
∂
A
A
Terbukti.Lampiran 3 Diketahui : Ayµy = −DAy, n x n x x d q = A dan x t t x x p =A+ A Akan dibuktikan : ( )f t =tpxµx t+ adalah fkp Bukti :
yµ = −y D y
A A , diintegralkan masing-masing ruas terhadap y dengan x≤ ≤ + . y x n x n y y x dy µ +
∫
A x n y x D dy + =∫
− A | x n y x x n n x d + + = −A =A −A = x y t sehingga x n n x y y x d µ d + =∫
A atau 0 n ndx =∫
Ax t+µx t+d apabila diberikan n x n x x d q = A dan x t t x x p =A + A , diperoleh : nqx 0 n x t x t x dt µ + + =∫
A A 0 n tpxµx t+d =∫
tnqx adalah peluang seseorang berumur x meninggal sebelum mencapai x+n, jika n= ∞, maka
0 x t x x t q p dt 0 | tpx ∞ = − µ ∞ ∞ =
∫
+ = −∞px+0px = + =0 1 1 x p∞ peluang bertahan hidup dari umur x hingga x+ ∞ adalah 0 0px peluang bertahan hidup dari umur x hingga x adalah 1
Fungsi tpxµx t+ memenuhi syarat fkp di mana terdapat fungsi adalah fkp apabila
, dengan ( ) f t 0 ( ) 1 f t dt ∞ =
∫
f t( )≥0 Sehingga f t( )= tpxµx t+ adalah fkp. Terbukti.n y D y Lampiran 4 Diketahui lµ = − A 0 0 exp[ ] x x = −
∫
µydy A A ln y D y Akan dibuktikan : Bukti : µ = − A 0 0 ln x x ydy D ydy µ −∫
= − −∫
A 0 0 0 ln ln ln x x ydy x µ −∫
= A − A = A A 0 A Masing-masing ruas di eksponensialkan dan dikalikan dengan .0 0 0 0 exp[ ] exp[ln ] x x ydy x µ −
∫
= A = A A A A . Terbukti.Lampiran 5
Dimisalkan α =A, β =b, γ =g, ε = , u adalah laju kematian sesaat, l adalah peluang e
bertahan hidup dan E adalah AHH, perhitungan ke empat indikator dalam Mathematica 5.2 dirumuskan sebagai berikut.
• AHH kohort
In[1]:= uco=Exp[A+b x+g x^2+e (t+x)]
Out[1]=
A+bx+gx2+eHt+xL
In[2]:= lco=Exp[- Integrate[uco,{x,0,a}]]
Out[2]= − A−Hb+eL2 4g +et"#####πi k jjjj
jj−ErfiB2b+e"####gF+ErfiB
b+e+2ag 2"####g Fy { zzzz zz 2"####g In[3]:= Eco=Integrate[lco,{a,0,110}] Out[3]= · 0 110 − A−Hb+eL2 4g +et"#####πi k jjjj jj−ErfiB2b"####+egF+ErfiB b+e+2ag 2"####g Fy { zzzz zz 2"####g a In[4]:= A=-5.3377; b=-0.0016; g=0.0006; e=-0.0164; In[5]:= Eco=Integrate[lco,{a,0,110}] Out[5]= ‡0 110 −36.1801 −5.4727−0.0164tH0.43403+Erfi@20.4124H−0.018+0.0012aLDL a In[6]:= Kohort=Table[NIntegrate[lco,{a,0,110}],{t,0,90,10}] Out[6]= {66.9609,70.0748,73.0913,76.0068,78.8183,81.522,84.1126,86.5832,88.9256,91. 1312} • AHH periode
In[1]:= up=Exp[A+b x+g x^2+e t]
Out[1]=
A+et+bx+gx2
In[2]:= lp=Exp[- Integrate[up,{x,0,a}]]
Out[2]= − A− b2 4g+et"#####πi k jjjj jj−ErfiB2"####bgF+ErfiB b+2ag 2"####g Fy { zzzz zz 2"####g In[3]:= Ep=Integrate[lp,{a,0,110}]
Out[3]= · 0 110 − A− b4g2+et"##### πi k jjjj jj−ErfiB2"####bgF+ErfiB b+2ag 2"####g Fy { zzzz zz 2"####g a In[4]:= A=-5.3377; b=-0.0016; g=0.0006; e=-0.0164; In[5]:= Ep=Integrate[lp,{a,0,110}] Out[5]= ‡0 110 −36.1801 −5.33877−0.0164tH0.0368658+Erfi@20.4124H−0.0016+0.0012aLDL a In[6]:= Periode=Table[NIntegrate[lp,{a,0,110}],{t,0,90,10}] Out[6]= {54.8072,57.5468,60.2311,62.8555,65.4168,67.9129,70.343,72.7068,75.0051,77. 2389} • CAL
In[1]:= ucal=Exp[A+b x+g x^2+e (t-a+x)]
Out[1]=
A+bx+gx2+eH−a+t+xL
In[2]:= lcal=Exp[- Integrate[ucal,{x,0,a}]]
Out[2]= − A−ae−Hb+eL2 4g +et"#####πi k jjjj
jj−ErfiB2b+e"####gF+ErfiB
b+e+2ag 2"####g Fy { zzzz zz 2"####g In[3]:= Ecal=Integrate[lcal,{a,0,110}] Out[3]= · 0 110 − A−ae−Hb+eL2 4g +et"#####πi k jjjj jj−ErfiB2b"####+egF+ErfiB b+e+2ag 2"####g Fy { zzzz zz 2"####g a In[4]:= A=-5.3377; b=-0.0016; g=0.0006; e=-0.0164; In[5]:= Ecal=Integrate[lcal,{a,0,110}] Out[5]= ‡0
110 −36.1801 −5.4727+0.0164a−0.0164tH0.43403+Erfi@20.4124H−0.018+0.0012aLDL a
In[6]:= cal=Table[NIntegrate[lcal,{a,0,110}],{t,0,90,10}]
Out[6]={49.6524,52.4174,55.157,57.863,60.5284,63.1473,65.7152,68.2284,70.6846,73.0 819}
•
RAK
In[1]:= uco=Exp[A+b x+g x^2+e (t-a+x)]
Out[1]=
A+bx+gx2+eH−a+t+xL
Out[2]= − A−ae−Hb+eL2 4g +et"#####πi k jjjj
jj−ErfiB2b+e"####g F+ErfiB
b+e+2gx 2"####g Fy { zzzz zz 2"####g In[3]:= Eco=Integrate[lco,{x,0,110}] Out[3]= · 0 110 − A−ae−Hb+eL2 4g +et"#####πi k jjjj jj−ErfiB2b"####+egF+ErfiB b+e+2gx 2"####g Fy { zzzz zz 2"####g x
In[4]:= ucal=Exp[A+b x+g x^2+e (t-a+x)]
Out[4]= A+bx+gx2+eH−a+t+xL In[5]:=lcal=Exp[- Integrate[ucal,{x,0,a}]] Out[5]= − A−ae−Hb+eL2 4g +et"#####πi k jjjj
jj−ErfiB2b+e"####gF+ErfiB
b+e+2ag 2"####g Fy { zzzz zz 2"####g
In[6]:= rak=(Integrate[Eco lcal ,{a,0,110}])/(Integrate[lcal,{a,0,110}])
Out[6]= i k jjjj jjjj jjjj jjjj jjjj jjj · 0 110 − A−ae−Hb+eL2 4g +et"#####πi k jjjj
jj−ErfiB2b+e"####gF+ErfiB
b+e+2ag 2"####g Fy { zzzz zz 2"####g · 0 110 −
A−ae−Hb+e4gL2+et"#####
πi
k jjjj
jj−ErfiB2b+e"####gF+ErfiB
b+e+2gx 2"####g Fy { zzzz zz 2"####g x a y { zzzz zzzz zzzz zzzz zzzz zzz ì i k jjjj jjjj jjjj jjjj jjjj jjj · 0 110 −
A−ae−Hb+e4gL2+et"#####
πi k jjjj jj−ErfiB2b"####+egF+ErfiB b+e+2ag 2"####g Fy { zzzz zz 2"####g a y { zzzz zzzz zzzz zzzz zzzz zzz In[7]:= A=-5.3377; b=-0.0016; g=0.0006; e=-0.0164;
Out[8]=
J‡
0
110 −36.1801 −5.4727+0.0164a−0.0164tH0.43403+Erfi@20.4124H−0.018+0.0012aLDL
‡ 0 110 −36.1801 −5.4727+0.0164a−0.0164tH0.43403+Erfi@20.4124H−0.018+0.0012xLDL x aN ì J‡ 0
110 −36.1801 −5.4727+0.0164a−0.0164tH0.43403+Erfi@20.4124H−0.018+0.0012aLDL
aN In[9]:= rak=Table[(NIntegrate[Eco
lcal,{a,0,110}])/(NIntegrate[lcal,{a,0,110}]),{t,0,90,10}]
Out[9]={57.2691,60.2,63.0804,65.9042,68.6661,71.3614,73.9861,76.5357,79.0059,81.39 15}