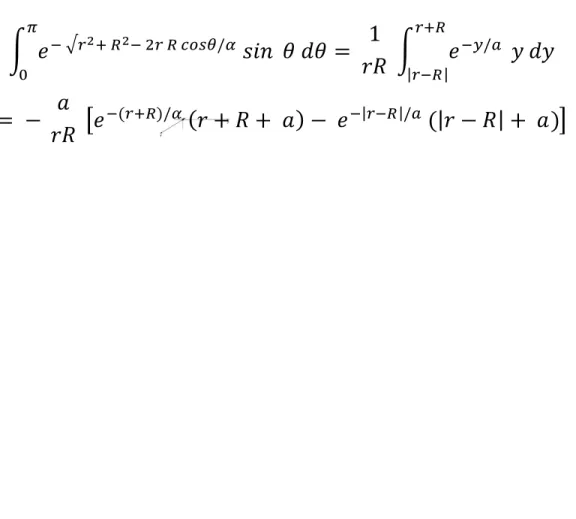BAB I BAB I PENDAHULUAN PENDAHULUAN 1.1 Latar Belakang 1.1 Latar Belakang
Salah satu masalah dalam mekanika kuantum adalah menentukan energi suatu Salah satu masalah dalam mekanika kuantum adalah menentukan energi suatu sistem yang pada dasarnya dapat dilakukan dengan cara menyelesaikan persamaan sistem yang pada dasarnya dapat dilakukan dengan cara menyelesaikan persamaan Schrodinger. Untuk sistem sederhana seperti partikel dalam kotak, gerak harmonis satu Schrodinger. Untuk sistem sederhana seperti partikel dalam kotak, gerak harmonis satu dimensi atau sistem atom hidrogen penyelesaian persamaan Schrodinger telah pernah dimensi atau sistem atom hidrogen penyelesaian persamaan Schrodinger telah pernah dilakukan dan tidak membutuhkan kalkulasi yang terlalu rumit. Namun untuk sistem dilakukan dan tidak membutuhkan kalkulasi yang terlalu rumit. Namun untuk sistem yang terdiri atas banyak partikel seperti pada atom berelektron banyak atau pada suatu yang terdiri atas banyak partikel seperti pada atom berelektron banyak atau pada suatu molekul penyelesaian persamaan Schrodinger untuk sistem tersebut tidak sederhana molekul penyelesaian persamaan Schrodinger untuk sistem tersebut tidak sederhana atau bahkan merupakan sesuatu yang sangat rumit. Untuk itu pada makalah ini akan atau bahkan merupakan sesuatu yang sangat rumit. Untuk itu pada makalah ini akan membahas salah satu metode aproksimasi (pendekatan) dengan metode vari
membahas salah satu metode aproksimasi (pendekatan) dengan metode vari asi.asi.
Metode variasi adalah salah satu cara untuk menemukan pendekatan ke Metode variasi adalah salah satu cara untuk menemukan pendekatan ke eigenstate energi terendah atau keadaan dasar. Ide dasar dari metode ini adalah harga eigenstate energi terendah atau keadaan dasar. Ide dasar dari metode ini adalah harga ekspekstasi dari operator energi H yang disebut energi rata, tentunya energi ekspekstasi dari operator energi H yang disebut energi rata, tentunya energi rata-rata ini terkait dengan fungsi keadaan yang digunakan. Energi rata-rata-rata-rata ini harus lebih rata ini terkait dengan fungsi keadaan yang digunakan. Energi rata-rata ini harus lebih besar atau sama dengan keadaan energi terendah dari sistem. Karena energi terendah besar atau sama dengan keadaan energi terendah dari sistem. Karena energi terendah sebagai batas bawah dari harga ekspektasi maka memungkinkan untuk memilih fungsi sebagai batas bawah dari harga ekspektasi maka memungkinkan untuk memilih fungsi
gelombang “coba” (trial) yang mengandung sejumlah parameter dan meminimasi harga
gelombang “coba” (trial) yang mengandung sejumlah parameter dan meminimasi harga
ekspektasi dengan metoda variasi. Dasar metode variasi adalah memilih sebuah fungsi ekspektasi dengan metoda variasi. Dasar metode variasi adalah memilih sebuah fungsi gelombang yang tergantung pada satu atau lebih parameter dan menemukan nilai-nilai gelombang yang tergantung pada satu atau lebih parameter dan menemukan nilai-nilai parameter ini dengan nilai harapan energi serendah mungkin.
parameter ini dengan nilai harapan energi serendah mungkin.
1.2 Tujuan 1.2 Tujuan
Makalah ini membahas bagaimana metode variasi digunakan dalam mekanika Makalah ini membahas bagaimana metode variasi digunakan dalam mekanika kuantum. Dimana metode variasi ini didasari oleh teorema yang menyatakan operator kuantum. Dimana metode variasi ini didasari oleh teorema yang menyatakan operator Hemiltonian H sebagai operator penentu energi terendah E
Hemiltonian H sebagai operator penentu energi terendah Eminmin
1.3 Batasan Masalah 1.3 Batasan Masalah
Bagaimana metode variasi digunakan dalam mekanika kuantum disertai dengan Bagaimana metode variasi digunakan dalam mekanika kuantum disertai dengan contoh kasus.
BAB II BAB II
TINJAUAN PUSTAKA TINJAUAN PUSTAKA
2.1
2.1 Teorema VariasiTeorema Variasi
Jika kita ingin menghitung energi keadaan dasar E
Jika kita ingin menghitung energi keadaan dasar Egguntuk sistem yang digambarkanuntuk sistem yang digambarkan
dalam Hamiltonian H, tapi tidak bisa memecahkan persamaan Schrodinger (bergantung dalam Hamiltonian H, tapi tidak bisa memecahkan persamaan Schrodinger (bergantung waktu). Pilihlah beberapa fungsi normalisasi
waktu). Pilihlah beberapa fungsi normalisasi
..Misalkan terdapat persamaan eigen dan fungsi gelombang umum yaitu : Misalkan terdapat persamaan eigen dan fungsi gelombang umum yaitu :
Persamaan eigenPersamaan eigen H H nn
E E nn nn Fungsi gelombangFungsi gelombang nn
N N n n C C
Dengan demikian sembarang nilai energi rata-rata untuk suatu fungsi eigen Dengan demikian sembarang nilai energi rata-rata untuk suatu fungsi eigen ternormalisasi tertentu tidak mungkin lebih besar dari energi rata-rata tingkat dasarnya. ternormalisasi tertentu tidak mungkin lebih besar dari energi rata-rata tingkat dasarnya. Secara matematis dituliskan
Secara matematis dituliskan Teorema:
Teorema:
⟨⟨||||⟩⟩〈〈〉〉
(1)(1)Persamaan diatas adalah harga ekspetasi dari H dalam keadaan
Persamaan diatas adalah harga ekspetasi dari H dalam keadaan
yang merupakanyang merupakan kepastian energi keadaan dasar. Tentu saja, jikakepastian energi keadaan dasar. Tentu saja, jika
hanya berlaku untuk satu keadaanhanya berlaku untuk satu keadaan eksitasi, sehinggaeksitasi, sehingga
〈〈〉〉
melebihimelebihi
; tetapi teorema mengatakan bahwa kondisi yang; tetapi teorema mengatakan bahwa kondisi yang sama untuk sembarangsama untuk sembarang
..Metode variasi ini didasari oleh teorema jika telah diketahui bahwa operator Metode variasi ini didasari oleh teorema jika telah diketahui bahwa operator Hemiltonian H adalah operator penentu energi terendah E
Hemiltonian H adalah operator penentu energi terendah Egg maka untuk sistem yangmaka untuk sistem yang
fungsi gelombangnya
fungsi gelombangnya berlaku :berlaku :
** H H
d d
E E ggDan untuk sembarang fungsi
Dan untuk sembarang fungsi gelombang ternormalisasigelombang ternormalisasi yang kondisi ikatannya sesuaiyang kondisi ikatannya sesuai dengan kondisi ikatan
dengan kondisi ikatan maka berlakulah :maka berlakulah :
** H H d d
E E gg ternormalisasiternormalisasi (2)(2) DenganDengan adalah fungsi gelombang partikel yang sesungguhnya sedangadalah fungsi gelombang partikel yang sesungguhnya sedang adalahadalah fungsi gelombang
fungsi gelombang aproksimasiaproksimasi atauatau fungsi var fungsi variasiiasi
Untuk membuktikan teorema tersebut maka suatu fungsi dapat diekspansi Untuk membuktikan teorema tersebut maka suatu fungsi dapat diekspansi menjadi kombinasi linear yang suku-sukunya merupakan fungsi eigen. Untuk itu menjadi kombinasi linear yang suku-sukunya merupakan fungsi eigen. Untuk itu
k k k a (3)Dan karena adalah fungsi eigen maka padanya berlaku :k
k k
k E
H (4)
Substitusi pers. (3) ke ruas kiri pers. (2) membuat ruas kiri ini menjadi : H d a H a jd k j j k k
*
* *
Dengan menggunakan persamaan eigen (4) maka ruas kiri pers. (2) menjadi :
k j j j j k k a E d a d H * * *Karena a j , ak dan Ek adalah bukan fungsi maka mereka dapat dikeluarkan dari tanda
integral, sehingga :
k j k j kj j j k j k j j k a E d a a E a d H * * * *Perlu diingat bahwa kj berharga 1, jika k = j dan 0 jika k
j sehingga ruas kiri pers. (2) menjadi :
k k k k a E a d H * * (Boleh juga dinyatakan
j j j j a E a d H * * ) Karena ak *ak
ak 2 maka
k k k E a d H 2 * (5)Mengingat Egadalah tingkat energi terendah maka Ek pasti > Egsehingga :
k g k k k k E a E a d H 2 2 * atau
k k a E d H 1 2 * (6)Karena adalah ternormalisasi maka
* d
1, dan jika ekspansi pers (3) dimasukkan ke dalam kondisi normalisasi ini maka :2 * * * * 1
k j k j k k kj j k j k j k a d a a a a d (7) Jika
2
1 k ka , dimasukkan pada pers. (6) maka diperoleh :
Dengan demikian pers.(2) sudah terbukti. Teorema dengan pernyataan seperti pada pers. (2) adalah jika ternormalisasi. Bagaimana jika tidak ternormalisasi? Fungsi yang tidak ternormalisasi akan menjadi ternormalisasi jika dikalikan dengan suatu bilangan yaitu A yang disebut faktor normalisasi sehingga pers. (8) menjadi :
H d
E gA2 * (9)
Harga A dapat dihitung dari sifat fungsi ternormalisasi yaitu A2
d *
1, jadi pers. (3) dapat ditulis : g E d d H
* * (10)Keberhasilan penggunaan metode variasi ini ditentukan oleh kemampuan memformulasi berdasarkan data boundary condition.
Fungsi disebut fungsi variasi dan integral (2) atau integral (10) disebut integral variasional. Untuk dapat memperoleh aproksimasi yang bagus terhadap energi ground state Eg maka harus mencoba beberapa fungsi variasi yang memberikan hasil
terendah tetapi tidak lebih rendah dari Eg yang sesungguhnya (yaitu Eg yang diperoleh
melalui eksperimen). Salah satu cara untuk mengetahui bahwa fungsi variasi yang kita gunakan adalah salah jika fungsi variasi itu menghasilkan integral variasional yang lebih rendah dari Egmanakala harga Egsesungguhnya dari sistem itu telah diketahui.
Jika diambil 1 sebagai fungsi gelombang ground state yang sesungguhnya,
dengan demikian :
1
1
E g
H
(11)Jika secara kebetulan dapat membuat fungsi variasi yang sama dengan 1, maka dengan
menggunakan pers. (11) ke dalam pers. (2) akan terlihat bahwa integral variasional tepat sama dengan Eg. Jadi fungsi gelombang keadaan dasar menghasilkan integral
variasional terendah untuk suatu sistem. Dalam praktek orang sering memasukkan beberapa parameter ke dalam fungsi variasi untuk memperoleh integral variasional yang semakin mendekati energi keadaan dasar yang sesungguhnya.
Contoh Kasus
Contoh 1 : (Osilator Harmonik)
Anggap kita ingin mencari keadaan energi dasar untuk osilator harmonik satu dimensi:
2 2 2 2 2 2 1 2 dx m x d m H
Jawab :Prosedur pertama yaitu mencari fungsi sembarang untuk digunakan sebagai fungsi eigen ternormalisasi, misalkan kita pilih fungsi.
2
)
( x
Aebx Normalisasikan fungsi tersebut (cari A yang cocok) melalui syarat normalisasi berikut dimana b adalah konstanta:
| |
∫
| |
Selanjutnya mencari masing-masing rata-rata energi potensial dan energi kinetik dari Hamiltoniannya.
〈〉〈〉〈〉
Energi kinetik rata-rata :
〈〉
| |
(
)
Energi potensial rata-rata :
〈〉
| |
Hamiltonian total : b m m b H 8 2 2 2
Minimalisasikan H terhadap b:〈〉
Substitusikan nilai b yang didapat ke Hamiltonian, sehingga diperoleh :
Contoh 2 :
Misalkan kita ingin mencari keadaan energi dasar potensial fungsi delta:
Jawab:
Dan lagi, kita tahu jawabannya:
. Sebelum A, kita gunakan fungsi percobaan gaussian. Kita siap menentukann normalisasi dan menghitung〈〉
〈〉| |
Dengan jelas,
〈〉
Dan kita tahu bahwa ini menghasilkan
untuk semua b. Meminimalisasi itu,〈〉
√
Sehingga
〈〉
Tentu saja sedikit lebih tinggi dari
, karena
> 2 Contoh 3 :Turunkan fungsi variasi jika fungsi eksaknya merupakan fungsi partikel dalam kotak satu dimensi yang panjangnya l dengan kondisi batas berharga 0 jika x = 0 dan x = l. Aproksimasilah Eg.
Jawab :
Fungsi harus mempunyai sifat-sifat tersebut. Bentuk paling sederhana untuk yang memenuhi sifat-sifat tersebut adalah :
) (l x x
Karena tidak ada pernyataan bahwa ternormalisasi maka tidaklah menggunakan pers. (2). Tetapi pers.(10) dengan operator Hemilton H = -(P2 /2m) d2 /dx2 (dimana energi potensial partikel dalam kotak satu dimensi adalah 0 untuk di dalam kotak). Pembilang ruas kiri pers. (10) adalah :
dx x lx dx d x lx m P dx x l x dx d x l x m P dt H l l ) ( ) ( 2 ) ( ) ( 2 2 0 2 2 2 2 0 2 2 2 *
m l P 6 3 2 Penyebut ruas kiri pers.(10):
30 ) ( 5 0 2 2 * l x d x l x dt l
Jika disubsitusikan pada pers. (10) diperoleh :
l l dx x l x d 0 5 2 2 * 30 ) ( Jika disubstitusikan pada pers. (10) diperoleh :
g E m l h 2 2 2 4 5
Contoh 3. Temukan ikatan paling atas energi keadaan dasar sumur persegi tak hingga satu dimensi, menggunakan fungsi percobaan gelombang segitiga.
Gambar 1. Fungsi gelombang segitiga percobaan untuk sumur persegi tak hingga
| |
| |
Dalam kasus ini
Seperti yang digambarkan pada Gambar 2. Sekarang, turunan dari tahapan fungsi adalah fungsi delta.
Gambar 2. Turunan dari fungsi gelombang pada Gambar 1.
Dan karena
〈〉
*+
*+
Eksak keadaan dasar adalah
, sehingga teorema kerja 12 >
2.2 Keadaan Dasar HeliumAtom helium pada Gambar 3 berisi dua elektron dalam orbit mengelilingi nukleus yang berisi dua proton (sama dengan neutron, mereka tidak sesuai seperti yang kita
harapkan). Hamiltonian sistm ini (mengabaikan struktur halus dan koreksi yang kecil) adalah
|
|
(12)Masalah kita adalah menghitung keadaan energi dasar,
sejumlah besar energi yang akan melepaskan dua electron. (Diberikan
yang mudah untuk menggambarkan“energi ionisasi” yang diperlukan untuk menghilangkan satu electron)
telah dihitung sangat akurat dalam laboratorium:
eV (eksperimen) (13)Nilai ini akan kita peroleh secara teoritis.
Gambar 3. Atom Helium
Adalah suatu hal yang aneh jika suatu masalah yang penting dan mudah tidak
mempunyai solusi yang eksak. Kesalahan tersebut dating dari tolakan electron-elektron.
|
|
(14)Jika kita abaikan bentuk tersebut, jangkauan H menjadi Hamiltonian Hiddrogen bebas (hanya dengan muatan nuklir 2e diganti dengan e); sehingga solusi eksak adalah fungsi gelombang hidrogenik:
(15)Energi totalnya adala 8E1= -109 eV. Ini dimulai dari jalan yang panjang -79 eV.
Untuk mendapatkan pendekatan yang baik untuk
, kita aplikasikan metoda variasi, menggunakan
sebagai fungsi gelombang percobaan. Ini adalah pilihan terbaik karena fuungsi eigennya sebagian besar Hamiltonian.Sehingga
〈
〉
〈
〉
(17)dimana
〈
〉
|
|
(18)Gambar 4. Pemilihan koordinat untuk integral
Langkah awal kita adalah mengintegralkan
; dengan tujuan
sudah ditentukan, dan sekarang kita orientasikan pada system koordinat
sehingga sumbu polar berada sepanjang
(lihat Gambar 4). Dengan menggunakan hukum kosinus,|
|
(19)dan karena
|
|
(20)Integral
terhadap (2
); integral
adalah
|
|
|{
(21) Sehingga
(22)Itu mengikuti bahwa
〈
〉
sama dengan
Integral angular adalah mudah (4
), dan integral
menjadi
Akhirnya
〈
〉
(23)Dan energi totalnya
〈
〉
(24)Tidak terlalu jelek(ingat, nilai eksperimen adalah -79 eV). Tapi kita bisa membuat yang lebih baik.
Jika kita berfikir lebih realistis bahwa fungsi percobaan
(yang terdiri dari dua electron yang tidak saling berinteraksi)? Dengan mengabaikan pengaruh electron lainnya, kita bisa mengatakan satu electron membentuk awan bermuatan negative sebagai perisai nucleus sehingga electron lainnya dianggap sebagai muatan efektif inti (Z=2).Pendapat ini kita gunakan pada bentuk fungsi percobaan
(25)Kita cobakan Z sebagai parameter variasi, dengan mengambil nilai
〈〉
minimum.Fungsi gelombang ini adalah keadaan eigen dari Hamiltonian tak pertubasi (mengabaikan tolakan electron), tapi dengan Z = 2, pada keadaan Coulumb. Kembali kita tulis H dengan mengikuti:
|
|
(26)Harga ekspektasi H otomatis adalah
〈
〉
〈
〉
(27)disini (1/r) adalah ekspektasi nilai 1/r dalam satu partikel hidrogenik keadaan dasar
(tapi dengan nilai muatan atom Z); sehingga〈
〉
(28)Nilai ekspektasi
sama dengan persamaan 23, kecuali disini ada nilai Z = 2〈
〉
(29)Mengambil semuanya bersamaan, kita temukan
〈
〉
(30)Berdasarkan metoda variasi, kuantitas melebihi
untuk beberapa nilai Z. Yang terendah diatas ikatan ketika〈〉
diminimalkan:〈〉
Dari ini kita ikuti bahwa
(31)Ini adalah hasil yang rasional, ini mengatakan pada kita bahwa electron lainnya berada di luar nucleus, mengurangi efef muatan dengan 2 diperoleh 1,69. Mengambil nilai ini untuk Z, kita peroleh
〈
〉
(32)Keadaan dasar Helium telah diukur dengan ketelitian yang tinggi, menggunakan fungsi gelombang percobaan yang lengkap dengan memperbaiki beberapa parameter. Nilainya sudah mendekati eksperimen dengan selisih 2%.
Contoh Kasus Contoh 1 :
Mengambil nilai
=-79,0 eV untuk energi keadaan dasar Helium, hitunglah energi ionisasi (energi untuk melepas 1 elektron). Petunjuk: pertama hitung energi keadaan dasar ion He+, dengan satu electron mengorbit inti, lalu kurangi untuk dua energi.Jawab:
He+ adalah ion hidrogenik; Energi keadaan dasarnya adalah (2)2(
−
13.6 eV), atau−
54.4 eV. (
’)
Sehingga
- (
’)
79.0
−
54.4 = 24.6 eV untuk menghilangkan satu electron. Contoh 2 :Aplikasikan metoda tersebut untuk H- dan Li+ (masing-masing punya dua electron, seperti Helium, tapi nilai Z = 1 dan Z = 3). Carilah muatan efektif, dan hitunglah ikatan terbaik diatas
untuk masing-masing kasus. Catatan: Dalam kasus ini H- harus dicari dulu〈〉
> -13,6 eV.Jawab:
Tahap awalnya kita anggap inti proton dengan Z0. Mengabaikan tolakan
elektron-elektron, sehingga
Dan energinya adalah 2Z02E1
〈
〉
menjadi 1/a Maka〈
〉
Dan nilai
〈〉[
]
Jika kita perisai satu-satu perubahan itu adalah (Z - 2) digantikan dengan ( Z
−
Z 0).〈〉
〈〉
Sehingga:
= 1 (H-) ;
, muatan efktif kurang dari 1, seperti yang diharapkan〈〉
= 2 (He) ;
〈〉
= 3 (Li+) ;
〈〉
2.3 Molekul Ion Hidrogen
Aplikasi klasik lainnya untuk metoda variasi adalah prinsip ion molekul hydrogen H2+, yang berisi satu electron dan dua proton dalam medan Coulumb seperti terlihat
pada Gambar 5. Kita bisa mengasumsikan momen yang berlaku pada proton dalam posisi berjarak R satu sama lain, walaupun satu dari yang paling penting dari perhitungan ini untuk menentukan nilai R yang sebenarnya, Hamiltoniannya adalah
(33)dimana
dan
adalah jarak electron terhadap proton. Strategi awal penyelesaian ini adalah menentukan fungsi gelombang percobaan, dan menggunakan metoda variasi untuk mendapatkan ikatan pada energi keadaan dasar.Untuk menentukan fungsi gelombang percobaan, gambaran ion atom hydrogen dalam keadaan dasar adalah
dan lalu membawa proton jauh dan memakunya di bawah jarak R. Jika nilai R lebih besar dari radius Bohr (a), fungsi gelombang electron tidak akan berubah banyak. Tapi kita akan mencoba dua proton dalam persamaan dasar, sehingga electron mempunyai kemugkinan yang sama berasosiasi dengan lainnya. Fungsi gelombang percobaan yang ditawarkan adalah:
(35)
Gambar 5. Molekul Ion Hidrogen H2+
Tugas pertama kita adalah menormalisasi fungsi percobaan:
||
| |
(36)
Integral satu dua adalah 1 (karena
telah dinormalisasi); yang ketiga lebih rumit.
(37)Mengambil koordinat proton 1 dan 2 pada sumbu z, pada jarak R seperti Gambar 5, kita punya:
(38)dan selanjutnya
(39)Integral
dalam (2
). Untuk melakukan integral
√
sehingga
kemudian
||
[
||
|| ]
Gambar 6. Koordinat untuk perhitungan persamaan 37
Lalu integral r kita dapatkan
Dengan mengevaluasi integral, kita dapatkan
(40)I disebut integral overlap/ tumpang tindih; digunakan untuk mengukur jumlah
overlap
(perhatikan dengan nilai 1 untuk R
0 dan o saat R
. I dalambentuk factor normalisasi adalah
| |
(41)Selanjutnya kita harus menghitung nilai ekspetasi H dari keadaan percobaan
.Dimana
= -13,6 eV pada keadaan energi dasar dari atom hidrogn dan r2sama denganmeletakkan r1
[
]
Ini mengikuti bahwa:
〈〉
| |
〈
〉
〈
〉
(42)
Nilai direct integral/ integral langsung
〈
〉
(43)Dan exchange integral/ pertukaran integral,
〈
〉
(44)Hasilnya adalah
(45)dan
(46)Mengambil semuanya bersamaan, dan nilai
kita simpulkan bahwa:〈〉
(47)Berdasarkan metoda variasi, keadaan energi dasar kecil dari
〈〉
. Sehingga hanya energi electron dengan energi potensial yang berasosiasi dengan tolakan proton-proton.
Sehingga energi total system dalam -
dan ekspresi fungsi dari
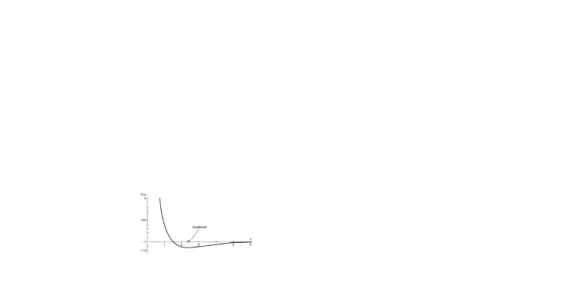
, kecildari
Fungsi yang diplot pada Gambar 7. Ikatananya terlihat, untuk grafik di bawah -1, mengindikasikan energi lebih sedikit dari atom netral ditambah proton bebas (-13,6 eV). Kesetimbangan jarak proton sekitar 2.4 jari-
jari Bohr atau 1.27Ǻ
Gambar 7. Plot fungsi F(x) persamaan 49
Contoh Kasus Contoh 1 :
Evaluasi D dan X pada persamaan 43 dan 44. Cek jawabannya pada persamaan 45 dan 46. Jawab:
〈
〉 〈
〉
√
√
| |
||
||
|
|
|
}
,
-
[
]
pers 7.45〈
〉
√
√
||
||
,
-
|
|
pers 7.46 Contoh 2 :Misalkan kita menggunakan tanda minus pada fungsi gelombang percobaan, persaman 35.
[
]
Tanpa menggunakan integral baru, cari F(x) dan buktikan kalau tidak ada ikatan.
Jawab:
〈〉
Grafik (dengan tanda plus untuk perbandingan) tidak ada nilai minimum, dan tetap di atas -1, menunjukkan bahwa energi lebih besar daripada proton dan atom yang dipisahkan. Oleh karena itu, tidak ada bukti ikatan di sini.
BAB III PENUTUP
Ide dasar dari metode variasi adalah harga ekspekstasi dari operator energi H memberikan energi rata-rata, energi rata-rata ini harus lebih besar atau sama dengan keadaan energi terendah dari sistem. Karena energi terendah sebagai batas bawah dari
harga ekspektasi maka memungkinkan untuk memilih fungsi gelombang “coba” (trial)
yang mengandung sejumlah parameter dan meminimasi harga ekspektasi dengan cara variasi.
Fungsi yang tidak ternormalisasi akan menjadi ternormalisasi jika dikalikan dengan suatu bilangan A yang disebut faktor normalisasi 2
*
1E d H
A dan harga A dihitung dari sifat fungsi ternormalisasi yaitu A2
d * 1DAFTAR PUSTAKA
Griffiths D.J. 1995. Introduction to quantum mechanics. Prentice Hall. Inc
Koichi Ohno, 2004, Buku Teks Kimia Kuantum Online, Terjemahan Bambang Prijamboedi, Iwanami Publishing Company
Sugihartono I, Prinsip Variasi Dalam Mekanika Kuantum , Jurusan Fisika FMIPA UNJ, Jakarta
Triyanta, 2000, Fisika Kuantum ; Disampaikan pada Lokakarya Perbaikan Mutu Mata kuliah Fisika Kuantum dan Fisika Statistik, FMIPA Unand, Padang
Nouredine Zettili, 2009, Quantum Mechanics Concepts and Applications, Second Edition, John Wiley and Sons, Ltd, Publication