sehingga dari tabel 3.1 diperoleh nilai rata-rata sebagai berikut:

(1)

BAB III

FUNGSI DISTRIBUSI DATA A. Distribusi Data dan Histogram

Pengambilan data berulang akan memperoleh serentetan data hasil pengukuran. Serentetan data tersebar atau terdistribusi disekitar nilai perkiraan terbaiknya. Semakin banyak data yang diperoleh dari hasil pengukuran akan membingungkan pada saat pencatatan dan menampilkan karena kondisi data tidak urut nilainya. Cara mengatasi kesulitan ini menggunakan distribusi atau histogram. Sebagai contoh, pengukuran jarak dari lensa sampai banyangan (x) diperoleh data yang terdistribusi sebagai berikut: 26,24,26,28,23,24,25,24,26,25

Data agar mudah dicatat ditampilkan mengunakan histogram. Tahap pertama untuk menampilkan data dalam bentuk histogram adalah mengurutkan data dari terkecil ke terbesar. Data hasil pengukuran jarak lensa kebayanga dapat ditampilkan menjadi: 23,24,24,24,25,25,26,26,26,28. pencatatan data ini akan lebih baik dibuat secara sederhanan. Sebagai contah pencatatan data 26,26,26 yang ditulis sebanyak tiga kali disederhanakan. Kita dapat mencatat nilai 26 dan jumlah ditemukannya nilai tersebut secara bersama-sama. Pencatatan data ditampilkan dalam Tabel 3.1

Tabel 3.1: tabel frekuensi data

Nilai (xk) 23 24 25 26 27 28 Frekuensi (nk) 1 3 2 3 0 1

Pada tabel 3.1, nilai data ditunjukan dengan notasi (xk), dengan k = 1,2,3,.... Notasi (xk) untuk menunjukan variasi perbedaan nilai yang ditemukan. Notasi (nk) menujukan jumlah frekuensi nilai xk ditemukan, dengan k = 1,2,3,....

Nilai rata-rata dari data yang diperoleh dapat dihitung mengunakan persamaan sebagai berikut:

N

X

N i i





1 _,

(2)

10

28

26

25

24

23 





x

Penghitungan nilai rata-rata juga dapat dilakukan menggunakan persamaan sebagai berikut:

N

n

x

N k k k





1 _,

sehingga perhitungan diperoleh hasil sebagi berikut:

10 )

1

28 (

)

3

26 (

)

2

25 (

)

3

24 (

)

1

23 (





















x

Distribusi data hasil pengukuran dapat ditampilkan secara gafik dalam histogram. Pada pembuatan grafik dalam bentuk histogram data yang diplot adalah nilai nk dengan nilai xk.

Contoh pembuatan grafik dalam bentuk histogram seperti ditunjukan oleh gambar 11. grafik yang ditnjukan gambar 11 juga sisebut dengan bar histogram.

Gambar 11: Historgam dari 10 pengukuran panjang. Sumbu vertikal menujukan banyaknya data nilai pengukuran xi .

xk nk 22 23 24 25 26 27 28 1 2 3 4

(3)

Kadang kala, Hasil pengukuran dipenoleh nilai yang tidak bulat. Contoh data hasil pengukuran jarak lensa dengan jarak banyangan yang tersebut sebelumnya merupakan data yang nilainya bulat. Data yang berupa bilangan tidak bulat lebih cocok dibuat tepat dibuat dalan range nilai kedalam bilangan yang sesuai dengan interval. Contoh data pengukuran jarak lensa dengan bayangan adalah: 26,4; 23,9; 25,1; 24,6;22,7;23,8;25,1;23,9;25,3;25,4. data ini akan lebih cocok ditampilkan dalam bentuk interval data. Tabel 2 menunjukkan intelval data dan banyaknya data yang ada dalam interval tersebut.

Tabel 3.2: Interval data pengamatan

Interval 22-23 23-24 24-25 25-26 26-27 27-28

Banyaknya data 1 3 1 4 1 0

Gambar 12: interval histogram yang menunjukan bagian dari pengukuran.

Pengambilan data yang semakin banyak akan mengakibatkan tampilan data dalam grafik lebih halus dan teratur. Data yang jumlahnya bayak dapat dibuat interval histogram yang semakin sempit. Semakin sempitnya interval, histogram akan semakin halus dan teratur. Gambar 14 menunjukan histogram dari data pengukuran yang jumlahnya banyak.

xk nk 22 23 24 25 26 27 28 1 2 3 4

(4)

Gambar 14: Histogram dengan jumlah data yang banyak

Kurva yang terbentuk dari gambar 14 merupakan kurva kontinue. Semakin sempit lebar histogram maka semakin halus kurva yang terbentuk. Kurva kontinue ini membentuk fungsi tertentu (

f

(x

)

).

Gambar 15: kurva distribusi f(x).(a) setelah banyak pengukuran, bagian yang berada diantara x dan x + dx adalah daerah f(x)dx potongan sempit. (b) bagian yang berada diantara

x = a dan x = b adalah daerah yang menaungi.

Daerah yang berada di daerah di antara nilai hasil pengukuran a dan b adalah

dx

x

f

b a



(

)

. Luas daerah dibawah kurva

f

x

dx

b a



(

)

merupakan jumlah pengukuran yang berada pada interval nilai a dan b. Pada jumlah pengukuran yang besar,



f

(

x

)

dx

adalah peluang pengukuran tunggal x akan memberikan hasil antara x sampai dengan x+ dx. secara

sama, integral

f

x

dx

b a

(5)

berada pada x = a dan x = b. Apabila daerah pengukuran dari





sampai dengan





maka peluang hasil pengukuran adalah sama dengan 1



   



1 )

( dx

x

f

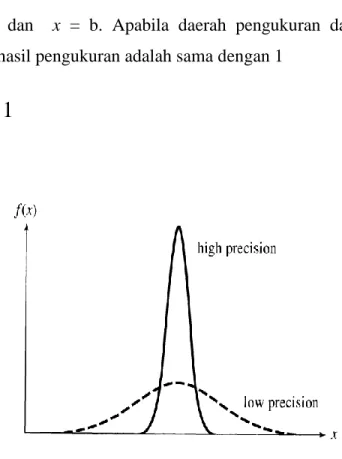
Gambar 16: dua grafik distribusi, pertama untuk presisi yang tinggi dan yang kedua untuk presisi yang rendah.

B. Distribusi Normal

Perbedaan tipe pengukuran mempunyai perbedaan curva distribusi. Tidak semua curva distribusi mempunyai bell shape yang simetri. Distribusi binomila dan poisson sebagai contoh distibusi yang tidak simetry. Namun demikian, banyak pengukuran yang memiliki kurva bell shape yang simetri untuk pembatasan distribusinya.

Fungsi matematis yang mendiskripsikan kurva bell shape disebut distribusi normal atau distribusi gauss. Bentuk Fungsi ini ditunjukan sebagai berikut

2 2 2 x

e

 (3.1)

Ketika nilai x = 0, fungsi gauss bernilai 1. Nilai x yang bergerak dari salah satu arah

menjauh dari nilai nol (0), 2 2

2 

x

(6)

(sempit), dan lambat apabila



lebar. Semakin menjauh perubahan nilai x dari nol maka persamaan 2 2 2 x

e



mengecil kearah nol.

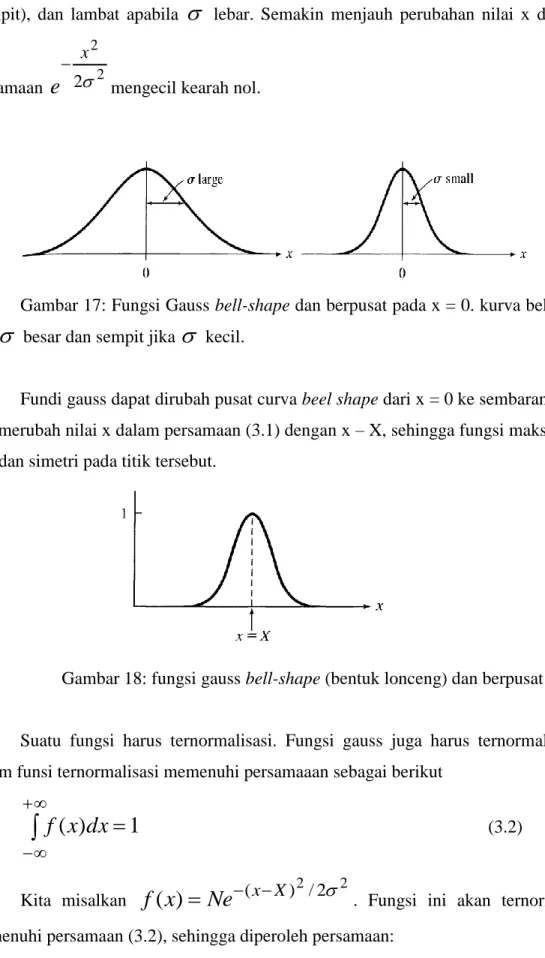
Gambar 17: Fungsi Gauss bell-shape dan berpusat pada x = 0. kurva bell-shape lebar jika



besar dan sempit jika



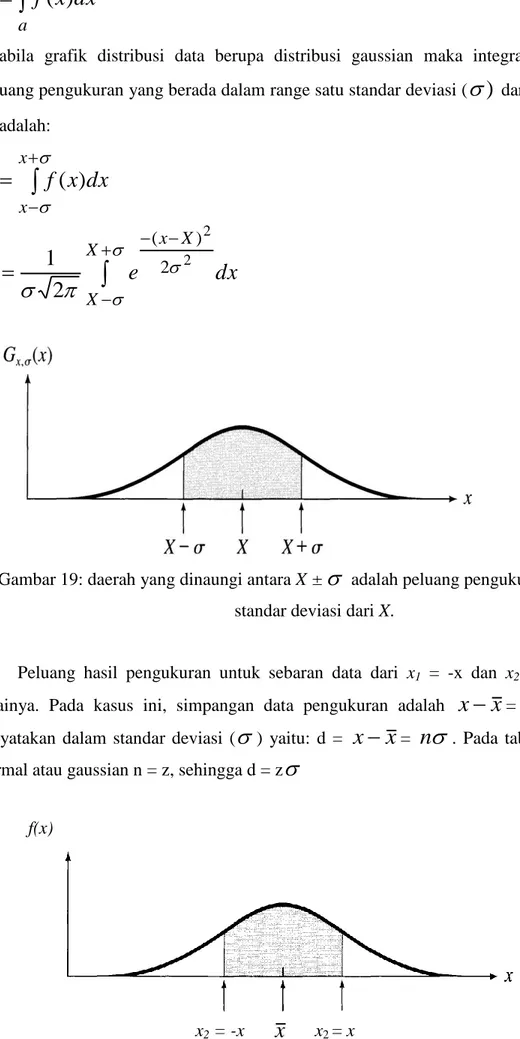
kecil.

Fundi gauss dapat dirubah pusat curva beel shape dari x = 0 ke sembarang titik x = X. kita merubah nilai x dalam persamaan (3.1) dengan x – X, sehingga fungsi maksimum pada x = X dan simetri pada titik tersebut.

Gambar 18: fungsi gauss bell-shape (bentuk lonceng) dan berpusat pada X

Suatu fungsi harus ternormalisasi. Fungsi gauss juga harus ternormalisasi. Secara umum funsi ternormalisasi memenuhi persamaaan sebagai berikut



   



1 )

( dx

x

f

(3.2) Kita misalkan 2 2_/₂ ) (

)

(

x

Ne

x X 

f



  . Fungsi ini akan ternormalisasi jika memenuhi persamaan (3.2), sehingga diperoleh persamaan:

(7)

1 )

(



( )2/2 2









        

dx

Ne

dx

x

f

x X  (3.3)

Perhitungan persamaan 3.3 akan lebih sederhana apabila nilai x-X diubah menjadi y dan dari casus persamaan ini dy = dx sehingga diperoleh



    

_

1

2 2_/₂

dy

e

N

y  (3.4) kemudian mensubtitusi



y

= z ( dalam casus ini dy =



dz), sehingga diperoleh



    

_

1

2 / 2

dz

e

N



z , untuk nilai /2

2 

2





    

dz

e

z

Hasil akhir perhitungan diperoleh



    

_

_

_



e

2/2

dz

N

2 N

z (3.5)

Berdasarkan persamaan 3.4 dan 3.5 diperoleh

N



2 



1

, sehingga nilai





2

1 

N

Dapat kita simpulkan, fungsi Gaus atau normal yang ternormalisasi adalah sebagai berikut:

2 2 2 ) (

2

1 )

(







X x

e

x

f

 



(3.6) Dengan x = besaran fisika yang diukur

X = nilai benar x yang dicari

f = frekuensi perolehan nilai x dalam pengukuran





2

1

= nilai maksimum f



= parameter percobaan yang berkaitan dengan kehalusan alat ukur yang digunakan

(8)

Nilai

x

diperoleh setelah melakukan banyak percobaan. Nilai

x

diperoleh dengan persamaan sebagai berikut:





  



xf

x

dx

x

(

)

, sehingga untuk distrbusi Gauss nilai

x

ditunjukan oleh:

dx

xe

x

X x



     



2 2 2 ) (

2

1

_





(3.7)

Jika kita subtitusikan y = x – X atau x = y + X, kemudian dx=dy maka integral pada persamaan (3.7) menjadi dua bagian.

)

(

2

1

2 2 2 2 2 2

_dy

_X

_e

_dy

ye

x

y y



        





 





(3.8) Nilai 2

0

2 2





    

dy

ye

y  _dan 2

_

₂

_

2 2





    

dy

e

y , sehingga persamaam 3.8

dapat diperoleh hasil sebagai berikut:









2 .

.

2

1 X

x



sehingga hasil akhir diperoleh

x



X

Nilai standar deviasi (



_x) diperoleh dari persamaan berikut ini:

dx

x

f

x

x2



(

)

2

(

)

   







, dengan cara perhitungan yang sama dengan

perhitungan

x

diperoleh nilai



_x2





2.

C. Integral kebolehjadian dan tingkat kepercayaan

Batas distribusi (f(x)) dari pengukuran beberapa besar x menggambarkan peluang perolehan dari nilai x. Secara kushus, peluang pengukuran yang memberikan hasil dalam range a≤x≤b ditunjukan aleh persamaan 3.8.

(9)





b a

dx

x

f

P

(

)

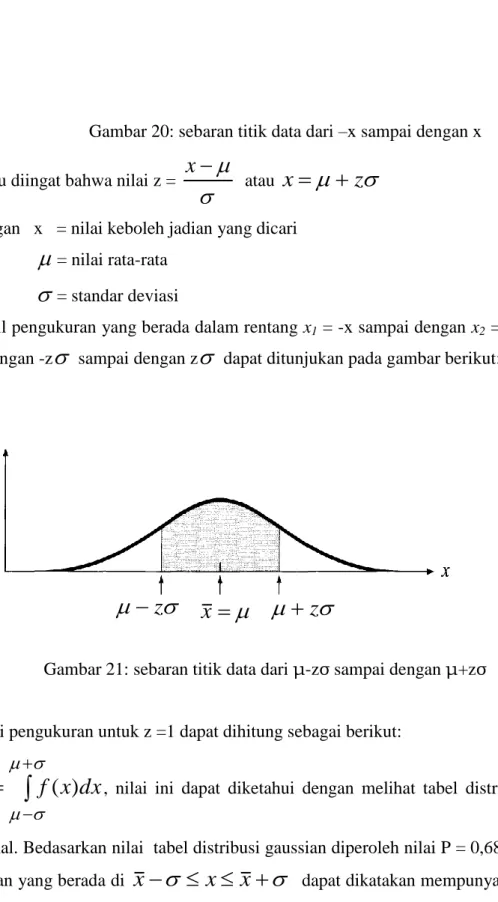
(3.8)

Apabila grafik distribusi data berupa distribusi gaussian maka integral dapat dihitung. peluang pengukuran yang berada dalam range satu standar deviasi (



)

dari nilai sebenarnya X adalah:

dx

e

dx

x

f

P

X X X x x x



     



    





2 2 2 ) (

2

1 )

(

Gambar 19: daerah yang dinaungi antara X ±



adalah peluang pengukuran dalam satu standar deviasi dari X.

Peluang hasil pengukuran untuk sebaran data dari x1 = -x dan x2 = x dapat dicari nilainya. Pada kasus ini, simpangan data pengukuran adalah

x



x

= d. Nilai d dapat dinyatakan dalam standar deviasi (



) yaitu: d =

x



x

=

n



. Pada tabel nilai distribusi normal atau gaussian n = z, sehingga d = z



x2 = x

x

x2 = -x

(10)

Gambar 20: sebaran titik data dari –x sampai dengan x

Perlu diingat bahwa nilai z =







x

atau

x







z



dengan x = nilai keboleh jadian yang dicari



= nilai rata-rata



= standar deviasi

Hasil pengukuran yang berada dalam rentang x1 = -x sampai dengan x2 = x yang sudah diganti dengan -z



sampai dengan z



dapat ditunjukan pada gambar berikut:

Gambar 21: sebaran titik data dari μ-zσ sampai dengan μ+zσ Nilai pengukuran untuk z =1 dapat dihitung sebagai berikut:



 



   

dx

x

f

P

(

)

, nilai ini dapat diketahui dengan melihat tabel distribusi gaussian atau normal. Bedasarkan nilai tabel distribusi gaussian diperoleh nilai P = 0,68 = 68%. Hasil pengukuran yang berada di

x







x



x





dapat dikatakan mempunyai peluang atau keboleh jadian 68 %. Hasil suatu pengukuran biasanya dituliskan dalam bentuk

x



s

_x.







z





x







z

f(x)

(11)

Biasanya sx =



, sehingga hasil ukur yang dinyatakan dengan

x



s

_x memiliki kebolehjadian pengukuran sebesar 68%. Nilai sx bisa sajatidak =



, tetapi sx bisa bernilai



2

,

3 

,

4 

, dan seterusnya. Nilai z yang digunakan untuk mengetahui peluang hasil pengukuran. Kebolehjadian dari masing-masing nilai z dapat dilihat pada tabel 3.3.

Gamabr 22: keboleh jadian untuk nilai z = 1











x







f(x) P = 68% untuk z=1

(12)