I PENDAHULUAN II LANDASAN TEORI

I PENDAHULUAN

Latar Belakang

Sekolah merupakan salah satu bagian penting dalam pendidikan. Oleh karena itu sekolah harus memperhatikan bagian-bagian yang ada di dalamnya. Salah satu bagian penting yang tidak dapat dipisahkan dalam sekolah adalah masalah penjadwalan mata pelajaran. Oleh sebab itu perlu dibuat sebuah penjadwalan mata pelajaran berkualitas yang memuaskan guru, murid dan sekolah. Salah satu sekolah yang mempunyai masalah penjadwalan mata pelajaran adalah Sekolah Menengah Pertama (SMP).

Pada setiap SMP mata pelajaran yang diajarkan sesuai dengan kurikulum yang berlaku. Mata pelajaran yang diajarkan ada yang nantinya diujikan dalam Ujian Akhir Nasional (UAN), untuk selanjutnya kita sebut sebagai mata pelajaran inti (primary) dan ada pula mata pelajaran yang tidak diujikan dalam UAN, melainkan hanya diujikan oleh sekolah masing-masing atau biasa disebut Ujian Akhir Sekolah (UAS), untuk selanjutnya kita sebut sebagai mata pelajaran biasa (nonprimary). Begitu pula dengan gurunya, ada yang mengajar mata pelajaran inti, ataupun mata pelajaran biasa, namun ada pula yang mengajar keduanya. Setiap guru mempunyai

preferensi hari dan periode waktu dalam memberikan mata pelajaran yang akan diajarkannya. Atas dasar perbedaan di atas, masalah penjadwalan mata pelajaran akan dibuat.

Masalah penjadwalan mata pelajaran di sini dapat dimodelkan sebagai masalah pemrograman linear integer (Integer Linear Programing/ILP). ILP adalah masalah optimisasi dengan fungsi objektif dan kendala yang linear serta variabel integer.

Karya ilmiah ini merupakan rekonstruksi dari karya ilmiah T Birbas, S Daskalaki, dan E Housos (1997) yang berjudul “Timetabling for Greek high schools”. Dalam karya ilmiah ini akan diperlihatkan formulasi dan penyelesaian masalah penjadwalan mata pelajaran menggunakan bantuan software LINGO 8.0.

Tujuan

Tujuan penulisan karya ilmiah ini adalah menunjukan peranan pemrograman linear integer dalam menentukan penjadwalan mata pelajaran Sekolah Menengah Pertama yang memenuhi preferensi mata pelajaran dan preferensi guru.

II LANDASAN TEORI

Dalam menyelesaikan masalah penjadwalan mata pelajaran pada karya ilmiah ini digunakan suatu model ILP untuk proses penyelesaiannya. Supaya lebih memahami dalam pembuatan model ILP dan proses penyelesaiannya, beberapa definisi dan teori yang terkait dengan ILP perlu dijelaskan terlebih dahulu. Berikut ini akan dijelaskan definisi dan teori yang digunakan

Fungsi Linear dan Pertidaksamaan Linear Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear.

Definisi 1 (Fungsi Linear)

Suatu fungsi f(x1,x2,...,xn) dalam variabel-variabel x x₁, ₂,...,x adalah suatu _n fungsi linear jika dan hanya jika untuk suatu

himpunan konstanta c c₁, ₂,...,c , dapat ditulis _n sebagai; . ... ) ,..., , (x1 x2 xn c1x1 c2x2 cnxn f = + + + (Winston, 2004) Sebagai gambaran, f x x( ,_{1 2})=3x₁+5x₂ merupakan fungsi linear, sementara

2 3

1 2 1 2

( , )

f x x =x x bukan fungsi linear. Definisi 2 (Pertidaksamaan Linear)

Untuk sembarang fungsi linear )

,..., , (x1 x2 xn

f dan sembarang bilangan b , pertidaksamaan f(x1,x2,...,xn)≤b dan b x x x f( 1, 2,..., n)≥ adalah pertidaksamaan linear. (Winston, 2004)

Pemrograman Linear

Pemrograman linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut.

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel x_i, pembatasan tanda menentukan x_i harus taknegatif (xi ≥0).

(Winston, 2004) Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar PL)

Suatu pemrograman linear didefinisikan mempunyai bentuk standar sebagai berikut: min z = cTx

terhadap Ax = b

x≥ 0. (1) di mana b

≥

0. Dengan x dan c berupa vektor berukuran n, vektor b berukuran m, sedangkan A berupa matriks berukuran m x n yang disebut juga matriks kendala.

(Nash & Sofer, 1996) Solusi Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimal bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947, dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.

Pada masalah PL (1), vektor x yang memenuhi kendala Ax=b disebut solusi PL (1). Misalkan matriks A dapat dinyatakan sebagai A=

(

B N

)

, dengan B adalah matriks berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran m× −(n m) yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala.

Dalam hal ini matriks B disebut matriks basis untuk PL (1).

Misalkan x dapat dinyatakan sebagai vektor =    B N x x

x , dengan x adalah vektor B variabel basis dan x adalah vektor variabel _N nonbasis, maka Ax=b dapat dinyatakan sebagai :

(

)

  =     B N x Ax B N x . =Bx + NxB N =b (2)

Karena matriks B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2)

B

x dapat dinyatakan sebagai:

- .

= -1 -1

B N

x B b B Nx (3) Definisi 4 (Solusi Basis)

Solusi dari suatu masalah PL disebut solusi basis jika memenuhi syarat berikut: a) Solusi tersebut memenuhi kendala pada

masalah PL.

b) Kolom-kolom dari matriks kendala yang berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.

(Nash & Sofer, 1996) Definisi 5 (Solusi Fisibel Basis)

Vektor x disebut solusi fisibel basis jika x merupakan solusi basis dan x≥0.

(Nash & Sofer, 1996) Ilustrasi solusi basis dan solusi fisibel basis diberikan dalam Contoh 1.

Contoh 1

Misalkan diberikan masalah LP sebagai berikut 1 2 1 2 3 1 2 4 1 5 min -3 - 2 terhadap -2 3 - 2 8 5 z x x x x x x x x x x = + + = + + = + = 0 , 1, ..., 5 i x ≥ i= . (4) Dari masalah LP (4) diperoleh:

2 1 1 0 0 3 1 2 0 1 0 , 8 1 0 0 0 1 5 −         = −_{ } =_{ }         A b . Misalkan dipilih

(

x3 x4 x5

)

dan

(

x1 x2

)

, = T = T B N x x

1 0 0 0 1 0 0 0 1     =_{ }     B .

Dengan menggunakan matriks basis di atas didapatkan

(

0 0

)

, −

(

3 8 5

)

. = T = 1 = T N B x x B b (5) Solusi (5) merupakan solusi basis, karena memenuhi kendala pada LP (4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (5), yaitu B bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (5) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

Hal yang juga penting dalam konsep pemrograman linear untuk model ini adalah daerah fisibel dan solusi optimal yang didefinisikan sebagai berikut.

Definisi 6 (Daerah Fisibel)

Daerah fisibel untuk suatu LP adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada LP tersebut.

(Winston, 2004) Definisi 7 (Solusi Optimal)

Untuk masalah maksimisasi, solusi optimal suatu LP adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimal suatu LP adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston, 2004) Pemrograman Integer

Pemrograman integer (Integer Programing/IP) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

(Garfinkel & Nemhauser, 1972) Definisi 8 (Linear Programming Relaksasi)

Linear Programming relaksasi atau sering disebut LP-relaksasi merupakan suatu pemrograman linear yang diperoleh dari suatu

IP dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.

Untuk masalah maksimisasi, nilai optimal fungsi objektif LP-relaksasi lebih besar atau sama dengan nilai optimal fungsi objektif IP, sedangkan untuk masalah minimisasi, nilai optimal fungsi objektif LP-relaksasi lebih kecil atau sama dengan nilai optimal fungsi objektif IP.

(Winston, 1995) Metode Branch-and-Bound

Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimal dari masalah ILP digunakan software LINGO 8.0 yaitu sebuah program yang didesain untuk aplikasi riset operasi dalam membangun dan menentukan solusi model linear, nonlinear, dan optimisasi integer dengan salah satu prinsip pemecahannya berdasarkan metode branch and bound.

Branch and bound adalah algoritma umum untuk mencari solusi optimal dari berbagai masalah optimasi. Metode ini pertama kali diperkenalkan oleh A.H. Land dan A.G. Doig pada tahun 1960.

Prinsip dasar metode ini adalah memecah daerah fisibel suatu masalah LP-relaksasi dengan membuat subproblem-subproblem. Ada dua konsep dasar dalam algoritme branch and bound.

1. Branching

Branching adalah proses membagi-bagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.

2. Bounding

Bounding adalah suatu proses untuk mencari/menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimal pada subproblem yang mengarah ke solusi, di sini dilakukan LP-relaksasi pada ILP.

Metode branch and bound diawali dengan menyelesaikan LP-relaksasi dari suatu masalah integer programming. Jika semua nilai variabel keputusan solusi optimal sudah berupa integer, maka solusi tersebut merupakan solusi optimal ILP. Jika tidak, dilakukan pencabangan dan penambahan batasan pada LP-relaksasinya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa nilai fungsi objektif optimal untuk ILP ≤ nilai fungsi objektif optimal untuk LP-relaksasi (masalah maksimisasi), sehingga nilai fungsi objektif optimal LP-relaksasi merupakan batas

atas bagi nilai fungsi objektif optimal untuk masalah ILP. Diungkapkan pula oleh Winston (2004) bahwa nilai fungsi objektif optimal untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimal untuk masalah ILP asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem sudah memenuhi kendala integer pada masalah ILP, artinya semua variabelnya sudah bernilai integer.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound.

1)Langkah 0

Didefinisikan z sebagai batas bawah dari nilai fungsi objektif (solusi) ILP yang optimal. Pada awalnya ditetapkan z =−∞ dan i=0.

2)Langkah 1

Subproblem LP dipilih sebagai bagian _{( )i} masalah berikutnya untuk dipecahkan. Subproblem LP diselesaikan. _{( )i}

a) Jika LP terukur dan solusi PL yang _{( )i} ditemukan lebih baik maka batas bawah z diperbarui. Jika tidak, bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah dipecahkan, maka proses dihentikan.

b) Jika LP tidak terukur, proses _{( )i} dilanjutkan ke langkah 2 untuk melakukan pencabangan LP . _{( )i} Suatu subproblem dikatakan terukur (fathomed) jika terdapat kondisi sebagai berikut.

1. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimal untuk ILP.

2. Subproblem tersebut menghasilkan suatu solusi optimal dengan semua variabelnya bernilai integer. Jika solusi optimal ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimal dan nilai fungsi objektifnya menjadi batas bawah nilai fungsi objektif optimal bagi masalah ILP pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimal untuk masalah ILP.

3. Nilai fungsi objektif optimal untuk subproblem tersebut tidak melebihi batas bawah saat itu, maka subproblem ini dapat dieliminasi. 3). Langkah 2

Dipilih salah satu variabel x_j yang nilai optimalnya adalah x*_j yang tidak memenuhi batasan integer dalam solusi LPi. Bidang

1 ] [ ]

[x*_j <x_j < x*_j + disingkirkan dengan membuat dua subproblem PL, yaitu x_j <[x*_j] dan x_j >[x*_j]+1, sehingga diperoleh kendala subproblem baru sebagai berikut:

• Subproblem baru 1: kendala subproblem lama + kendala *

[ ]

j j

x ≤ x

• Subproblem baru 2: kendala subproblem lama + kendala x_j ≥[x*_j] 1+

dengan [x*_j] didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan

.

* j

x Selanjutnya kembali ke langkah 1. (Winston, 1975) Untuk memudahkan pemahaman metode branch-and-bound diberikan contoh sebagai berikut.

Contoh 2 (Metode Branch-and-Bound) Misalkan diberikan masalah ILP sebagai berikut : max z=4x₁+7x₂ terhadap 1 2 1 2 7 5 9 45 x x x x + ≤ + ≤

x

i

≥

0

, i = 1, 2. (6)

Setelah diselesaiakan menggunakan software LINGO 8.0 didapatkan solusi optimal LP-relaksasi dari masalah ILP (6) adalah x₁=4.5 , x₂ =2.5, dan z=35.5 (lihat Lampiran 2). Batas atas nilai optimal fungsi objektif masalah ini adalah 35.5. Daerah fisibel LP-relaksasi masalah (6) ditunjukkan pada Gambar 1. Solusi optimal berada pada titik perpotongan dua garis yang berasal dari kendala pertidaksamaan masalah (6).

Gambar 1 Daerah fisibel untuk LP

relaksasi dari masalah IL

Langkah berikutnya adalah memartisi daerah fisibel LP-relaksasi

bagian berdasarkan variabel yang berbentuk pecahan (non integer). Karena nilai dari kedua variabel yang diperoleh bukan

dipilih salah satu variabel untuk dasar pencabangan. Misalkan dipilih

dasar pencabangan. Jika masalah

diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:

• Subproblem 2: Subproblem 1 ditambah kendala x₂ ≤2;

• Subproblem 3: Subproblem 1 ditambah kendala x₂≥3.

Secara grafis dapat dilihat pada gambar di bawah ini.

Gambar 2 Daerah fisibel untu Subproblem 2 dan Subproblem 3

Setiap titik (solusi) fisibel dari IP ( termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan Subproblem 3 dikatakan dicabangkan oleh

Daerah fisibel untuk LP-LP (6).

Langkah berikutnya adalah memartisi relaksasi menjadi dua bagian berdasarkan variabel yang berbentuk ). Karena nilai dari kedua variabel yang diperoleh bukan integer, maka dipilih salah satu variabel untuk dasar angan. Misalkan dipilih x₂ sebagai dasar pencabangan. Jika masalah LP-relaksasi diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan 2 Subproblem 2: Subproblem 1 ditambah Subproblem 3: Subproblem 1 ditambah Secara grafis dapat dilihat pada gambar di

Daerah fisibel untuk Subproblem 2 dan Subproblem 3.

Setiap titik (solusi) fisibel dari IP (6) rah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan Subproblem 3 dikatakan dicabangkan oleh x₂.

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih Subpr

solusi optimal untuk Subproblem 2 1 5

x = ,x₂ =2, dan z=34 2). Semua variabel bernilai

memenuhi kendala bilangan bulat), maka tidak perlu dilakukan pencabangan di Subproblem 2. Solusi dari

menjadi batas bawah yaitu sama dengan 3 Saat ini Subproblem yang belum diselesaiakan adalah Subproblem 3. Solusi optimal untuk Subproblem 3 adalah

2 3

x = , dan z=35.4 (lihat Karena solusi optim

bukan solusi integer dan masih mempunyai kemungkinan solusi lebih besar dari batas bawah, maka dipilih pencabangan pada Subproblem 3 pada x ₁,

dua subproblem lagi.

• Subproblem 4: Subproblem 3 ditambah kendala x₁≤3

• Subproblem 5: Subproblem 3 ditambah kendala x₁≥4

Sekarang dipilih Subproblem yang belum diselesaikan yaitu Subproblem 4 Subproblem 5. Subproblem 5 takfisibel ( Lampiran 2), maka subproblem ini tidak dapat menghasilkan solu

Subprolem yang belum diselesaiakan adalah Subproblem 4. Setelah diselesaiakan solusi optimal yang didapatkan untuk Subproblem 4 adalah x₁=3, x₂ =3.3, dan

dari subproblem 4 tidak integer

dari batas bawah, maka dipilih pencabangan pada Subproblem 4 sehingga diperoleh subproblem baru lagi

• Subproblem 6: Subproblem 4 ditambah kendala x₂ ≤3

• Subproblem 7: Subproblem 4 ditambah kendala x₂ ≥4

Solusi optimal untuk Subproblem 6 adalah 1 3

x = , x₂ =3, z=33 (lihat Lampiran Solusi optimal untuk Subproblem 6 memenuhi solusi integer, akan tetapi solusi pada Subproblem ini lebih kecil (tidak lebih dari batas bawah sehingga solusi pada Subproblem 6 tidak menjadi batas bawah baru. Subproblem 7 menghasilkan solusi optimal x₁ =1.8, x₂ =4

Lampiran 2). Solusi dari Subproblem 7 tidak integer dan lebih baik dari batas bawah, maka pada Subproblem ini dilakukan pencabangan lagi sehingga diperoleh Subproblem baru lagi

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih Subproblem 2, optimal untuk Subproblem 2 adalah 34 (lihat Lampiran emua variabel bernilai integer (solusinya memenuhi kendala bilangan bulat), maka tidak perlu dilakukan pencabangan di . Solusi dari Subproblem 2 menjadi batas bawah yaitu sama dengan 34.

Saat ini Subproblem yang belum diselesaiakan adalah Subproblem 3. Solusi Subproblem 3 adalah x₁=3.6,

(lihat Lampiran 2). optimal Subproblem 3

dan masih mempunyai kemungkinan solusi lebih besar dari batas bawah, maka dipilih pencabangan pada , sehingga diperoleh Subproblem 4: Subproblem 3 ditambah Subproblem 5: Subproblem 3 ditambah ubproblem yang belum diselesaikan yaitu Subproblem 4 atau Subproblem 5. Subproblem 5 takfisibel (lihat maka subproblem ini tidak apat menghasilkan solusi optimal. Subprolem yang belum diselesaiakan adalah Subproblem 4. Setelah diselesaiakan solusi optimal yang didapatkan untuk Subproblem 4 , dan z=35.3. Solusi integer dan lebih baik maka dipilih pencabangan sehingga diperoleh Subproblem 6: Subproblem 4 ditambah Subproblem 7: Subproblem 4 ditambah Solusi optimal untuk Subproblem 6 adalah (lihat Lampiran 2). Solusi optimal untuk Subproblem 6 memenuhi akan tetapi solusi pada ebih kecil (tidak lebih baik) dari batas bawah sehingga solusi pada Subproblem 6 tidak menjadi batas bawah baru. Subproblem 7 menghasilkan solusi

4

= , z=35.2 (lihat ). Solusi dari Subproblem 7 tidak dan lebih baik dari batas bawah, maka pada Subproblem ini dilakukan pencabangan lagi sehingga diperoleh Subproblem baru lagi

• Subproblem 8: Subproblem 7 ditambah kendala x₁≤1

• Subproblem 9: Subproblem 7 ditambah kendala x₁≥2

Penyelesaian dari Subproblem 9 menghasilkan solusi yang takfisibel (lihat Lampiran 2), maka subproblem ini tidak dapat menghasilkan solusi optimal. Subproblem 8 menghasilkan solusi optimal

1 1

x = , x₂ =4.4, z=35.1 (lihat Lampiran 2). Solusi dari Subproblem 8 tidak integer dan lebih baik dari batas bawah, maka pada Subproblem ini dilakukan pencabangan lagi sehingga diperoleh Subproblem baru lagi

• Subproblem 10: Subproblem 8 ditambah kendala x₂≤4

• Subproblem 11: Subproblem 8 ditambah kendala x₂≥5

Subproblem 10 menghasilkan solusi optimal x₁=1, x₂ =4, z=32. Subproblem ini menghasilkan solusi integer, akan tetapi solusi yang dihasilkan pada subproblem ini tidak lebih baik dari batas bawah sehinggga solusi pada Subproblem 10 tidak menjadi batas bawah baru. Subproblem 11 menghasilkan solusi optimal x₁=0, x₂ =5,

35

z= . Solusi pada Subproblem ini menghasilkan solusi integer dan lebih baik dari batas bawah sehingga solusi pada Subproblem 11 menjadi batas bawah baru. Karena sudah tidak ada lagi subproblem baru yang dapat dibuat maka tidak perlu dilakukan pencabangan lagi. Dengan demikian, solusi optimal pada contoh 2 adalah x₁*=0,

2* 5

x = , z=35 .

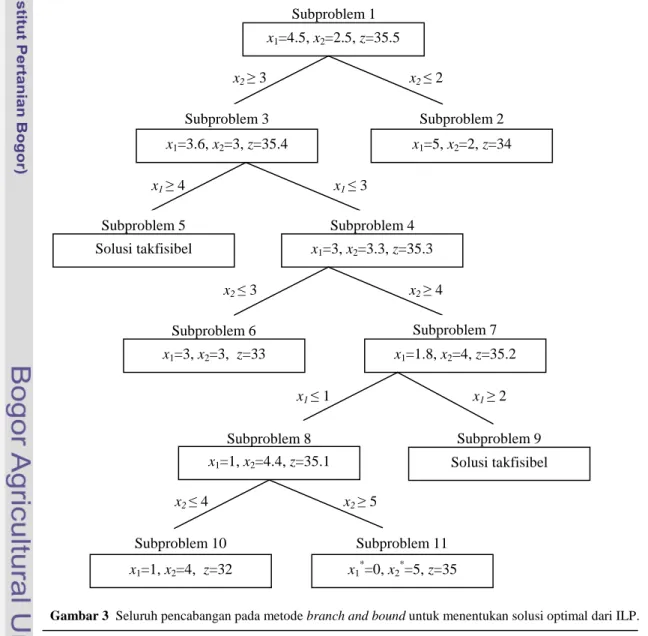
Secara keseluruhan pencabangan semua Subproblem untuk masalah ILP pada contoh 2 ditunjukan pada gambar di bawah ini.

Gambar 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi optimal dari ILP.

Subproblem 10 x1=1, x2=4, z=32 Subproblem 11 x1*=0, x2*=5, z=35 Subproblem 9 Solusi takfisibel Subproblem 8 x1=1, x2=4.4, z=35.1 x2 ≥ 5 x2 ≤ 4 Subproblem 2 x1=5, x2=2, z=34 Subproblem 1 x1=4.5, x2=2.5, z=35.5 x2 ≥ 3 x2 ≤ 2 Subproblem 3 x1=3.6, x2=3, z=35.4 x1 ≥ 4 x1 ≤ 3 Subproblem 5 Solusi takfisibel Subproblem 4 x1=3, x2=3.3, z=35.3 x2 ≥ 4 x2 ≤ 3 Subproblem 6 x1=3, x2=3, z=33 Subproblem 7 x1=1.8, x2=4, z=35.2 x1 ≥ 2 x1 ≤ 1