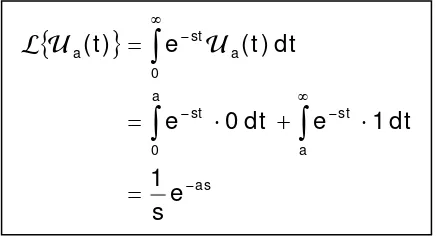BAB 4 : TRANSFORMASI LAPLACE - Transformasi Laplace.pdf

BAB 4 : TRAN SFORM ASI LAPLACE

4 .1 . Pe n da h u lu a n

Pem bicar aan t ent ang Tr ansfor m asi Laplace t idak lepas dar i beber apa konsep, di ant ar anya : kekonver genan, int egr al, kekont inuan fungsi dan per sam aan difer ensial, khususnya Masalah Syar at Bat as ( Boundar y Value Pr oblem ).

Hingga saat ini, Tr ansfor m asi Laplace m er upakan suat u alat ( m et ode) am puh unt uk m enyelesaikan Masalah Syar at Bat as. Hal ini ak an lebih t er lihat j ika m asalah syar at bat as t er sebut m em uat fungsi- fungsi t akkont inu ( discont inuous) at au fungsi-fungsi per iodik .

Secar a um um , di dalam bab ini akan dit inj au Tr ansfor m asi Laplace dan sifat - sifat nya, I nver s Tr ansfor m asi Laplace dan Tr ansfor m asi Der ivat if. I nver s Tr ansfor m asi dan Tr ansfor m asi Der ivat if sangat ber per an di dalam penyelesaian suat u per sam aan difer ensial. Pada bagian t er apan akan dit inj au suat u m odel Masalah Syar at Bat as unt uk lendut an balok dan sist em pegas- m assa.

Tu j u a n I n st r u k sion a l Kh u su s :

4 .2 . Tr a n sfor m a si La pla ce

( )

₌

∫

∞ −

( )

0 st

dt t f e s

F D e fin isi 1

Jika f fungsi t er definisi unt uk t > 0, m ak a fungsi F yang didefinisikan :

sedem ikian hingga int egr al t er sebut ada, disebut Tr ansfor m asi Laplace fungsi f.

Tr ansfor m asi Laplace disim bolkan dengan { .} . Dengan dem ikian m aka { f} = F yait u { f( t ) } = F( s) .

4 .3 . Tr a n sfor m a si La pla ce Fu n gsi- Fu n gsi

Se de r h a n a

Ber ikut t r ansfor m asi laplace fungsi- fungsi seder hana :

1. f( t ) = 1, t > 0 m aka

{ }

( )

( )

s 1 1 s 1 dx e s 1 dt 1 e t

f

0 x 0

st _{⋅ = = Γ =}

= ∞

∫

−

∫

∞ −



2. f( t ) = t , t > 0 m aka

( )

{ }

₂

( )

₂

0 x 2 0

st

s 1 2 s

1 dx x e s

1 dt t e t

f =

∫

=

∫

= Γ =

∞ − ∞

−



3. f( t ) = tp , t > 0, p> 0, m aka

( )

{ }

(

p 1

)

s 1 s

dx s x e dt t e t

f

1 p 0

p x 0

p

st _{ = Γ +}

     =

= ∞ − ∞ − ₊

∫

∫



Akibat :

1 p s

! p

( )

{ }

( )

a s

1 dx

e a s

1 dt

e dt e e t

f

0 x 0

t a s 0

at st

− = −

= =

=

∫

∞ − ∞

∫

− − ∞

∫

−



5. f( t ) = sin at , t > 0, a k onst ant a, m aka

( )

{ }

( )

parsial egralan

int peng dengan

, a s

a

e d at sin lim s 1 dt

at sin e lim dt

at sin e t

f

2 2

M 0

st M

M 0

st M

0 st

+ =

     − = =

=

∫

∫

∫

−

∞ → −

∞ → ∞

−



6. f( t ) = cos at , t > 0, a konst ant a, m aka

( )

{ }

( )

parsial egralan

int peng dengan

, a s

s

e d at cos lim s 1 dt

at cos e

lim dt at cos e

t f

2 2

M 0

st M

M 0

st M

0 st

+ =

     − = =

=

∫

∫

∫

−

∞ → −

∞ → ∞

−



1. f kont inu pada t it ik dalam ( int er ior point ) t iap- t iap subint er val t er sebut , dan

D e fin isi 2 :

Fungsi f dikat akan k ont inu sepot ong- sepot ong ( piecew ise cont inuous) pada int er val I , j ika I dapat dipar t isi m enj adi sej um lah ber hingga subint er val, sedem ikian hingga :

2. lim it f( t ) ber hingga ( finit e), unt uk t m endekat i m asing- m asing t it ik uj ung t iap- t iap subint er val.

1. f kont inu sepot ong- sepot ong pada int er val 0t < Te or e m a 1

Diket ahui fungsi f dengan sifat :

2. Tedapat konst ant a c, M> 0 dan t0> 0, sedem ikian hingga

| f( t ) |Mect , t > t0

Cat at an



Fungsi f yang m em enuhi syar at no 2 pada t eor em a 1 biasa disebut fungsi dengan sifat eksponent ial t ingkat c.

:



Teorem a t er sebut m enyat akan syar at cukup eksist ensi t r ansfor m asi laplace suat u fungsi, t et api t idak m enyebut kan syar at per lu dar i eksist ensi t er sebut . Hal ini ber ar t i suat u fungsi yang t idak m em enuhi salah sat u syar at t eor em a it u m asih dim ungk inkan m em punyai t r ansfor m asi laplace.

Te or e m a 2 :

Jika f1 dan f2 m asing- m asing fungsi yang m em punyai

t r ansfor m asi laplace dan c1, c2 m asing- m asing konst ant a

sebar ang, m ak a :

{ c1f1( t ) + c2f2( t ) } =c1{ f1( t ) } +c2{ f2( t ) }

( )

( )

{

}

(

( )

( )

)

( )

(

)

(

( )

)

( )

( )

( )

{ }

f t c

{ }

f

( )

t c

dx t f e c dx t f e c

dx t f c e dx t f c e

dx t f c t f c e t

f c t f c

2 2 1

1

0

2 st 2 0

1 st 1

0

2 2 st 0

1 1 st 0

2 2 1

1 st 2

2 1

1

 



+ =

+ =

+ =

+ =

+

∫

∫

∫

∫

∫

∞ − ∞

−

∞ − ∞

− ∞

− Bukt i



(

)

(

2 2

)

2

2 2

a 4 s s

a 2

a 4 s 2

s s

2 1

+ =

+ −

= Cont oh

4 .4 . I n ve r s Tr a n sfor m a si La pla ce

Dar i definisi t r ansfor m asi laplace t elah diket ahui :

{ f( t ) } = F( s)

I nver s t r ansfor m asi laplace ber lak u sebaliknya, yait u: 

- 1_{{ F( s) } = f( t ) .}

{

} (

₂ 2 ₂

)

2

a 4 s s

a 2 at

sin

+ =



Cont oh :

Kar ena , m aka

(

)

sin at

a 4 s s

a

2 2

2 2

2

1 ₌

   

 

+ −



Te or e m a 3 :

Jika F1 dan F2 m asing- m asing t r ansfor m asi laplace suat u

fungsi dan c1, c2 m asing- m asing konst ant a sebar ang, m aka - 1_{{ c}

1F1( s) + c2F2( s) } =c1- 1{ F1( s) } +c2- 1{ F2( s) } .

Te or e m a 4 :

Jika F adalah t r ansfor m asi laplace fungsi f dan a konst ant a sebar ang, m ak a : - 1{ F( s- a) } =eat- 1{ F( s) } .

( )

s e f

( )

t dt

{ }

f

( )

t F

0

st ₌  = ∞

∫

−

Bukt i

(

s a

)

e f

( )

t dt e e f

( )

t dt

{

e f

( )

t

}

F at

0

at st 0

t ) a s

( _{= =} 

=

−

∫

∫

∞ − ∞

−

− _{, sehingga}

(

)

{

}

(

)

16 ) 3 s ( 1 3 s 3 s F dengan , 3 s F 16 ) 3 s ( 1 3 s 16 ) 9 s 6 s ( 1 s 25 s 6 s 1 s 2 1 -2 1 -2 1 -2 1 -+ + − + = + + =       + + − + =       + + + + =       + + +     Cont oh

[

cos4t sin4t

]

e 16 s 2 16 s s e 16 s 2 s e 2 1 3t -2 1 -2 1 -3t -2 1 -3t -− =             + −       + =       + − =   

Bedakan j ika fungsi pem bilang dapat difakt or kan, seper t i cont oh ber ikut :

(

3t 4t

)

1 -1 -1 -1 -2 1 -e e 7 3 4 s 1 3 s 1 7 3 4 s 7 / 3 3 s 7 / 3 ) 4 s ) ( 3 s ( 3 12 s s 3 − − =             + −       − =       + − − =       + − =       − +      Cont oh

Te or e m a 5 :

{

f(t) g(t)

}



{ } { }

f(t)  g(t)

 ∗ =

( Te or e m a Kon volu si)

Jika f dan g m asing- m asing fungsi kont inu sepot ong-sepot ong pada set iap int er val t er t ut up [ 0,b] dan t er dapat bilangan r eal M dan N sedem ikian hingga | f( t ) |Meαt dan | g( t ) |Neαt , unt uk suat u konst ant a α dengan t∈[ 0,b] , m ak a

dengan τ τ − τ =

∗g(t)

∫

f( )g(t )d ) t ( f t 0

( )

₌ ∞

∫

− τ

( )

_{τ τ} 0 s d f e s F Bukt i :

Dengan asum si F( s) ={ f( t ) } dan G( s) ={ g( t ) }

Diam bil : dan

∫

( )

∞ ρ − _{ρ ρ} = 0 s d g e G( s) diper oleh:

( ) ( )

( )

( )

      ρ ρ       τ τ =

∫

∞ − τ ∞

∫

− ρ 0 s 0 s d g e d f e s G s F

( ) ( )

( ) (

)

( ) (

)

( ) (

)

      τ τ − τ =       τ τ − τ = τ τρ ρ + τ = τ τ − τ = ρ τ ρ τ =

∫

∫

∫

∫ ∫

∫ ∫

= τ ∞ = τ= − ∞ = τ= − ∞ ∞ ρ + τ − t 0 0 t t 0 st 0 t t 0 st 0 0 ) ( s d t g f dt d t g f e t koordinat sist em ke koordinat sist em dari t . subst dengan , dt d t g f e d d g f e 

Ter bukt i 

) t ( g ) t ( f ∗ Cat at an

Teorem a 5 di at as j uga m enyat akan :

- 1_{{ F( s) G( s) } =}

Sifa t k om u t a t if : f(t) ∗g(t) = g(t) ∗f(t)

) t ( f ) t ( g d ) t ( g ) ( g t , d ) ( g ) t ( f d ) t ( g ) ( f ) t ( g ) t ( f t 0 0 t t 0 ∗ = ρ ρ − ρ = τ − = ρ ρ ρ ρ − − = τ τ − τ = ∗

∫

∫

∫

Selanj ut nya unt uk { f( t ) } = F( s) dan { g( t ) } = G( s) , m aka ber dasar kan t eor em a konvolusi diper oleh

{

f(t) ∗g(t)

}

=F(s)G(s) ⇔ - 1

{

F(s)G(s)

}

= f(t) ∗g(t)



(

)

( ) ( )

{

}

( )

( )

t cos 1 d 1 sin

kom ut at if sebab

, ) t ( f ) t ( g

) t ( g ) t ( f

1 s

1 s

G dan s 1 s F dengan ,

s G s F

1 s

1 s 1 1

s s

1

t 0

2 1

-2 1 -2

1

-− = τ ⋅ τ =

∗ =

∗ =

+ = =

=

   

 

+ =

   

 

+

∫

  

Cont oh

4 .5 . D e r iva t if Tr a n sfor m a si

Pada bagian ini akan dit ur unkan suat u r um usan dar i der ivat if suat u hasil t r ansfor m asi.

Diper hat ik an :

( )

₌

∫

∞ −

( )

0

st_{f t dt} e

s F

⇔

( )

( )

e f

( )

t dt

( )

t e f

( )

t dt

{

( t)f

( )

t

}

ds

d dt

t f e ds

d s F ds

d

0

st 0

st 0

st _{= = − = −}

=

∫

∫

∫

∞

− ∞

− ∞

− _

Ser upa dengan car a di at as, dapat diper oleh j uga

( )

( )

t e f

( )

t dt

( )

t e f

( )

t dt

{

( t) f

( )

t

}

ds

d s F ds

d 2

0

st 2 0

st 2

2

− = −

= −

=

∫

∞ −

∫

∞ − _

Secar a um um , unt uk n= 1,2,3,... m aka F

( )

s

{

( t) f

( )

t

}

ds

d n

n n

{

}

(

_{2 2}

)

2 2 2 a s as 2 a s a ds d at sin t + =       + − =  Cont oh

4 .6 . Tr a n sfor m a si D e r iva t if da n M a sa la h Sya r a t

Ba t a s

Te or e m a 6 :

Diket ahui f( t ) fungsi kont inu dan f’( t ) kont inu sepot ong-sepot ong pada int er val 0tT. Jika | f( t ) |Mect unt uk t > T dengan M dan c m asing- m asing suat u k onst ant a, m aka

{ f’( t ) } = s{ f( t ) } – f( 0)

        + + +         + +         + = + + + = ′ + + ′ + ′ = ′

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

− − − − − − − − − − − − − T T st T T st T T st T T st T 0 st T 0 st T T st T T st T 0 st T T st T T st T 0 st T 0 st N N 2 1 2 1 1 1 N 2 1 1 N 2 1 1 dt ) t ( f e s ) t ( f e dt ) t ( f e s ) t ( f e dt ) t ( f e s ) t ( f e ) t ( df e ... ) t ( df e ) t ( df e dt ) t ( f e ... dt ) t ( f e dt ) t ( f e dt ) t ( f e  Bukt i

Kar ena f’( t ) kont inu sepot ong- sepot ong pada int er val 0tT, m aka t er dapat bilangan bulat posit if N sedem ikian hingga f’( t ) kont inu pada sub- sub int er val : 0< t < T1, T1< t < T2, ...,

TN< t < T. Diper oleh :

∫

∫

∫

∫

∫

− − − − − − − − − − − + − =         + − + +         + − +         + − = ′ T 0 st sT T T st N sT sT T T st 1 sT 2 sT T 0 st 1 sT T 0 st dt ) t ( f e s ) 0 ( f ) T ( f e dt ) t ( f e s ) T ( f e ) T ( f e dt ) t ( f e s ) T ( f e ) T ( f e dt ) t ( f e s ) 0 ( f ) T ( f e dt ) t ( f e N N 2 1 1 2 1 1 

Selanj ut nya, kar ena | e- sTf( T) || e- sTMecT| = Me- ( s- c) T, m aka

{ }

f (t) 0 f(0) s

{ }

f(t)

dt ) t ( f e s ) 0 ( f ) T ( f e lim dt ) t ( f e dt ) t ( f e s ) 0 ( f ) T ( f e lim dt ) t ( f e lim 0 st sT T 0 st T 0 st sT T T 0 st T   ′ = − + ⇔ + − = ′ ⇔       + − = ′

∫

∫

∫

∫

∞ − − ∞ → ∞ − − − ∞ → − ∞ →

Ter bukt i . 

Bent uk um um t eor em a 6 yait u t r ansfor m asi laplace unt uk t ur unan ke- n fungsi f( t ) dinyat akan oleh t eor em a 7 ber ikut :

Te or e m a 7 :

Diket ahui fungsi f( t ) dengan f( n- 1)( t ) kont inu dan f( n)( t ) kont inu sepot ong- sepot ong pada int er v al 0tT. Jika | f( k )( t ) |Mect , k= 0,1,2,...,n- 1 unt uk t > T dengan M dan c m asing- m asing suat u konst ant a, m aka :

{ f( n)( t ) } = sn{ f( t ) } – sn- 1f( 0) – sn- 2f’( 0) – sn- 3f” ( 0) –... – f( n- 1)( 0)

1. Tent ukan penyelesaian y” + 4y’+ 3y= 0, j ika y( 0) = 3 dan y’( 0) = 1

Cont oh

⇔ _{ y” } + 4{ y’} + 3{ y} = 0 Penyelesaian:

{ y” + 4y’+ 3y } = { 0}

⇔ s2{ y} –sy( 0) –y’( 0) + 4[ s{ y} –y( 0) ] + 3{ y} = 0 ⇔ s2{ y} –3s–1+ 4[ s{ y} –3] + 3{ y} = 0

⇔ [ s2+ 4s+ 3]{ y} –3s–13= 0 ⇔ _{ y} =

(

3s +13

)

(s2 +4s +3)

⇔

{

(

)

}

   

 

+ + + − =

+ + +

=

) 1 s (

5 )

3 s (

2 )

3 s 4 s ( 13 s 3

y -1 2 -1

⇔ y = - 2e- 3t+ 5e- t

2. Tent ukan penyelesaian y” + y= 2t , j ik a y(π 4) = π 2 dan y’( π 4) = 2−√2

⇔ s2{ y} –sy( 0) –y’( 0) +{ y} = Penyelesaian:

{ y” + y } = { 2t }

2 s 2

⇔ [ s2+ 1]{ y} –sA–B= 2 s2 , dengan A= y( 0) dan B= y’( 0)

⇔ _{ y} = B

1 s

1 A

1 s

s )

1 s ( s

2

2 2

2

2 ₊ + ₊ + ₊

⇔ _{ y} = B

1 s

1 A

1 s

s 1

s 1 s

1

2 _{2 2 2 2}

+ + + +    

 

+ −

Dengan subst it usi y (π 4) = π 4 dan y’( π 4) = 2−√2 diper oleh nilai A= B= 1.

3. Jika x= f( t ) dan y= g( t ) , selesaikanlah sist em per sam aan difer ensial :

   = − − ′ = + − ′ t t e 4 y x 2 y e 8 y 3 x 6 x

dengan syar at x( 0) = - 1 dan y( 0) = 0.

{

}

{ }

{

}

{ }

   = − − ′ = + − ′ t t e 4 y x 2 y e 8 y 3 x 6 x     Penyelesaian: ⇔ ⇔

{ }

{ }

{ }

{ } { }

{ }

   − = − − − − = + − − ) 1 s ( 4 y x 2 ) 0 ( y y s ) 1 s ( 8 y 3 x 6 ) 0 ( x x s       ⇔

{ }

{ }

{ }

{ } { }

{ }

   − = − − − − = + − + ) 1 s ( 4 y x 2 0 y s ) 1 s ( 8 y 3 x 6 1 x s       ⇔

{ }

{ }

{ }

{ }

   − = + − − = + ) 1 s ( 4 y 1) -( s x 2 -) 1 s ( ) s 9 ( y 3 x 6) -( s     ⇔

{ }

4 s 1 1 s 2 1 s 2 3 6 s 1 s ) 1 s ( 4 3 ) 1 s ( ) s 9 ( x − + − − = − − − − − − − = 

{ }

4 s 3 2 1 s 3 2 1 s 2 3 6 s ) 1 s ( 4 2 ) 1 s ( ) s 9 ( 6 s y − + − − = − − − − − − − − = 

4 .7 . Fu n gsi Un da k da n Fu n gsi Pe r iodik

  

> < =

a t , 1

a t , 0 ) t ( a



D e fin isi 3 :

Unt uk set iap bilangan r eal a0, Fungsi Undak Sat uan ( unit st ep funct ion) a didefinisikan :

Gr afik fungsi undak sat uan adalah :

Tr ansfor m asi Laplace fungsi undak sat uan adalah

{

}

as

a st a

0 st 0

a st a

e s 1

dt 1 e dt 0 e

dt ) t ( e

) t (

−

∞ − −

∞ −

=

⋅ +

⋅ =

=

∫

∫

∫



 

) t ( c )

t ( c ) t ( c

n 2

1 2 a n a

a

1 +  ++  D e fin isi 4 :

Suat u fungsi f disebut fungsi undak j ika t er dapat bilangan-bilangan r eal c1 , c2 ,…, cn dan bilangan- bilangan r eal non

negat if a1 , a2 ,…, an sedem ikian hingga :

f( t ) =

a

1

o

t

Tr ansfor m asi Laplace fungsi undak adalah

{ }

{

}

{

}

{

}

{

}

(

as

)

n s

a 2 s a 1

a n a

2 a

1

a n a

2 a

1

n 2

1

n 2

1

n 2

1

e c e

c e

c s 1

) t ( c

) t ( c

) t ( c

) t ( c )

t ( c ) t ( c )

t ( f

− −

− _{+ + +}

=

+ + +

=

+ + +

=



 

  

 



 

  

Cont oh :

1.

Tent ukan t r ansfor m asi laplace fungsi- fungsi undak ber ikut :

      

≥ < ≤ −

< ≤

< <

=

5 t , 2 3

5 t 2 , 1

2 t 1 , 3

1 t 0 , 0 )

t (

f

2.

    

≥ < ≤ −

< < =

4 t , 2 3

4 t 1 , 1

1 t 0 , 3 )

t ( g

1. Kar ena f( t ) = 00( t ) + ( 3- 0)1( t ) + ( - 1- 3)2( t ) + (+ 1)5( t )

Penyelesaian:

= 31( t ) - 42( t ) + ₂5 5( t )

m aka :

{ }

(

5s

)

2 5 s 2 s

e e

4 e 3 s 1 ) t (

f = − − − + −



2. Kar ena g( t ) = 30( t ) + ( - 1- 3)1( t ) + (+ 1)4( t )

= 30( t ) - 41( t ) + ₂5 4( t )

m aka :

{ }

(

s ₂5 4s

)

e e

4 3 s 1 ) t (

g = − − + −



t r ansfor m asi laplace fungsi sem acam ini, t er lebih dulu dit inj au t r ansfor m asi laplace suat u fungsi t r anslasi.

Jika fungsi f( t ) , t > 0 dit r anslasi sej auh a sepanj ang sum bu t , m aka diper oleh fungsi t r anslasi a( t ) f( t - a) , yait u :

  

≥ −

< < =

−

a t , ) a t ( f

a t 0 , 0 )

a t ( f ) t ( a



Tr ansfor m asi Laplace fungsi t r anslasi a( t ) f( t - a) dapat dicar i

sebagai ber ik ut :

{

}

{ }

f(t) e

dt ) t ( f e e du ) u ( f e e

a t u dengan ,

du ) u ( f e e

dt ) a t ( f e dt 0 e

dt ) a t ( f ) t ( e

) a t ( f ) t (

as

0 st as 0

su as 0

su sa

a st a

0 st 0

a st a

  



−

∞ − − ∞

− − ∞

− −

∞ − −

∞ −

=

= =

− = =

− +

⋅ =

− =

−

∫

∫

∫

∫

∫

∫

Jika diam bil g( t ) = f( t - a) , m aka diper oleh :

{

(t)g(t)

}

{

(t)f(t a)

}

e as

{ }

f(t) e as

{

g(t a)

}

a

a = − = = +

−

− _{ }

  



Dengan dem ikian j ika diket ahui g fungsi kont inu sepot ong-sepot ong :

t

f( t )

t a

     ≥ < ≤ < < = b t , ) t ( g b t a , ) t ( g a t 0 , ) t ( g ) t ( g 3 2 1

m aka diper oleh

(

g (t) g (t)

)

(t)

(

g (t) g (t)

)

(t) ) t ( ) t ( g ) t (

g = ₁ ₀ + ₂ − ₁ _a + ₃ − ₂ _b

⇔

(

g(t)

)

= 

(

g₁(t)₀(t) +

(

g₂(t) −g₁(t)

)

_a(t) +

(

g₃(t) −g₂(t)

)

_b(t)

)

⇔

( )

g(t)

(

g (t)

)

e

(

g (t a) g (t a)

)

e bs

(

g₃(t b) g₂(t b)

)

1 2

as

1 + + − + + + − +

= _ − _ − _     π > π < < = t , t t 0 , t sin ) t ( f Cont oh

Tent ukan t r ansfor m asi laplace fungsi :

(

)

(

t sint

)

(t) t sin ) t ( t sin t ) t ( t sin t , t t 0 , t sin ) t ( f 0 π π − + = − + =    π > π < < =    Penyelesaian:

m aka :

( )

(

)

(

(

)

)

(

)

(

)

(

)

    + + π + + + = + π + + + = π + − π + + + = − + = π − π − π − π 1 s 1 s s 1 e 1 s 1 t sin t e 1 s 1 ) t sin( t e 1 s 1 ) t ( t sin t t sin ) t ( f 2 2 s 2 s 2 s 2      

g1( t )

g2( t )

g3( t )

t

a

Ber ikut akan dit ent ukan t r ansfor m asi laplace unt uk suat u fungsi per iodik f dengan per ioda P:

D e fin isi 5 :

Suat u fungsi f disebut fungsi per iodik j ika t er dapat bilangan r eal posit if P ( disebut per ioda fungsi f) , sehingga ber laku :

f( t + P) = f( t ) , unt uk set iap t .

Cont oh gr afik suat u fungsi per iodik seper t i gam bar ber ik ut :

{ }

( )_{f(u P)du , dengan u P t}

e dt ) t ( f e

dt ) t ( f e dt ) t ( f e

dt ) t ( f e )

t ( f

0

P u s P

0 st

P st P

0 st 0

st

= + +

+ =

+ =

=

∫

∫

∫

∫

∫

∞ + − −

∞ − −

∞ −



{ }

f( t ) e

dt ) t ( f e

t P u dengan ,

du ) u ( f e e dt ) t ( f e

sP P

0 st

0 su sP P

0 st



− −

∞ − − −

+ =

= + +

=

∫

∫

∫

diper oleh :

{ }

∫

−

− −

= P

0 st

sP e f(t)dt e

1 1 )

t ( f



Tent ukan t r ansfor m asi laplace fungsi per iodik yang r um usan Cont oh

  

< ≤ −

< ≤ =

4 t 2 , 1

2 t 0 , 1 )

t ( f

{ }

) e 1 ( s

e 1

s e s

e e

1 1

dt ) 1 ( e dt 1 e e

1 1

dt ) t ( f e e 1

1 )

t ( f

s 2 s 2

4 2 st 2

0 st s

4

4 2

st 2

0 st s

4 4 0

st s 4

− −

− −

−

− −

− − −

+ − =

    

  

+ −

− =

   

 

− ⋅ +

⋅ −

= − =

∫

∫

∫



Penyelesaian:

kar ena per ioda fungsi f adalah P= 4, m aka

4 .8 . Te r a pa n

) x ( w dx

y d EI

4 4

= Model Lendut an Balok

Akan dit ent ukan penyelesaian m odel lendut an balok:

unt uk keadaan :



kedua uj ung dit um pu j epit ( em bedded) , yait u : y( 0) = 0, y’( 0) = 0, y ( L) = 0 dan y’( L) = 0

w ( x) = w0



beban m er at a sepanj ang balok , yait u w ( x) = w0

( konst an) . ket er angan:

y( x) = lendut an balok di posisi sej auh x dar i uj ung kir i w ( x) = beban di posisi sej auh x dar i uj ung k ir i

EI = konst ant a kekakuan lent ur ( flexur al r egidit y ) L = panj ang balok

{ }

0 4

4

w dx

y d

EI 

 =

   

 

Penyelesaian:

, dengan EI dan w0 konst ant a

⇔

[

{ }

]

s w ) 0 ( y ) 0 ( y s ) 0 ( y s ) 0 ( y s y s

EI 4 ₋ 3 ₋ 2 ′ ₋ ′′ ₋ ′′′ ₌ 0

⇔

{ }

s EI w ) 0 ( y ) 0 ( y s y

s4 ₋ ′′ ₋ ′′′ ₌ 0

⇔

{ }

EI w s

1 ) 0 ( y s

1 ) 0 ( y s

1

y 0

5 4

3 ′′ + ′′′ + =



⇔

4 0 3 2

0 5 4

3 1

-t EI 4!

w t ! 3

) 0 ( y t ! 2

) 0 ( y

EI w s

1 ) 0 ( y s

1 ) 0 ( y s

1 y

+ ′′′

+ ′′

=

   



 _{′′ + ′′′ +}

= _

...( i)

3 0 2

t 6EI

w t 2

) 0 ( y t ) 0 ( y

y′ = ′′ + ′′′ + ...( ii) subst it usi y ( L) = 0 ke per sam aan ( i) diper oleh :

4 0 3 2

L EI 4!

w L ! 3

) 0 ( y L ! 2

) 0 ( y

0 = ′′ + ′′′ +

⇔

24EI L w ) 0 ( y 6 L ) 0 ( y 2

L2 3 ₀ 4

− = ′′′ +

′′ ...( iii) dan subst it usi y’( L) = 0 ke per sam aan ( ii) diper oleh :

w )

0 (

y ′′′ ₊ +

⇔

6EI L w ) 0 ( y 2 L ) 0 ( y L

3 0 2

− = ′′′ +

′′ ...( iv) dar i per sam aan ( iii) dan ( iv) diper oleh nilai y” ( 0) dan y” ’( 0) , yait u :

EI 12

L w

2 L L

6 L 2 L

2 L ) EI 6 ( L w

6 L ) EI 24 ( L w )

0 ( y

2 0 2

3 2

2 3

0

3 4

0

= −

−

=

′′

EI 2

L w

2 L L

6 L 2 L

) EI 6 ( L w L

) EI 24 ( L w 2 L ) 0 (

y 0

2 3 2

3 0

4 0 2

− = −

−

= ′′′

Akhir nya, dengan subst it usi nilai- nilai y ” ( 0) dan y” ’( 0) t er sebut ke per sam aan ( i) , diper oleh per sam aan lendut an :

(

2 2

)

0 2

(

)

2

2 0

4 0 3

0 2 2 0

x L x EI 24

w x

Lx 2 L x EI 24

w

x EI 24

w x

EI 12

L w x EI 24

L w y

− =

+ −

=

+ −

=

...( v)

M a ca m Tu m pu a n Cat at an:

Kondisi syar at bat as pada beber apa m acam t um puan balok ( y= lendut an, y’= sudut put ar , y’’= m om en lent ur dan y’’’= gaya geser) .

Sya r a t ba t a s ga m ba r Tum puan seder hana

( sim ply suppor t ed) y= 0 dan y’’= 0 Bebas ( fr ee) y’’= 0 dan y’’’= 0

Jika konst ant a pegas A dan B m asing- m asing k1 dan k2,

m aka ber dasar kan Hukum Hook dan Hukum I I New t on diper oleh m odel get ar an sist em :

Sist em Pegas- Massa

Diket ahui dua m assa m1 dan m2 t er hubung dengan pegas A

dan B ( m assa pegas diabaikan) seper t i gam bar ber ikut .

) x x ( k dt

x d m

) x x ( k x k dt

x d m

1 2 2 2

2 2 2

1 2 2 1 1 2

1 2 1

− −

=

− +

− =

⇔

0 x k x k dt

x d m

0 x k x ) k k ( dt

x d m

2 2 1 2 2

2 2 2

2 2 1 2 1 2

1 2 1

= +

−

= −

+ +

...( vi)

Akan diselesaikan cont oh per sam aan ( v i) unt uk m1= m2= 1, k1= 6 dan k2= 4

yait u :

x1= 0

x2= 0

k1

k2

x1

x2

m1

m2

A

0 x 4 x 4 dt x d 0 x 4 x 10 dt x d 2 1 2 2 2 2 1 2 1 2 = + − = − +

...( v ii)

dengan syar at

1 dt ) 0 ( dx , 0 ) 0 ( x 1 dt ) 0 ( dx , 0 ) 0 ( x 2 2 1 1 − = = = = ...( viii) 0 x 4 x 4 dt x d 0 x 4 x 10 dt x d 2 1 2 2 2 2 1 2 1 2 =       + − =       − +   Penyelesaian:

Jika per sam aan ( v ii) diam bil t r ansfor m asi laplace, diper oleh

Am bil X (s)

dt x d dan ) s ( X dt x d 2 2 2 2 1 2 1 2 =       =       

 diper oleh

0 ) s ( X 4 ) s ( X 4 ) 0 ( x ) 0 ( sx ) s ( X s 0 ) s ( X 4 ) s ( X 10 ) 0 ( x ) 0 ( sx ) s ( X s 2 1 2 2 2 2 2 1 1 1 1 2 = + − ′ − − = − + ′ − −

Subst it usi syar at ( viii) diper oleh

4 .9 . Pe r in t a h - Pe r in t a h

M ATH EM ATI CA

Ber ikut cont oh- cont oh per int ah MATHEMATI CA unt uk m enghit ung t r ansfor m asi Laplace :

 Tr ansfor m asi Laplace

In[1]:= LaplaceTransform[t,t,s]

Out[1]=

In[2]:= LaplaceTransform[t^7,t,s]

Out[2]=

In[3]:= LaplaceTransform[Sin[4t],t,s]

Out[3]=

In[4]:= LaplaceTransform[Exp[a t],t,s]

Out[4]=

In[5]:= f=(t-1)Exp[2t]

Out[5]=

In[6]:= LaplaceTransform[f,t,s]

Out[6]=

 I nver s Tr ansfor m asi Laplace

In[7]:=

Out[8]=

In[9]:=

Out[9]=

 Fungsi Undak Sat uan

In[10]:=LaplaceTransform[UnitStep[t-2],t,s]

Out[10]=

 Menyelesaikan Per sam aan Difer ensial Cont oh 1:

0 y dt

y d

2 2

= +

m enyelesaikan per sam aan difer ensial

In[1]:=eq=D[y[t],t,t]+y[t]0

Out[1]= Penyelesaian:

In[2]:=sub=LaplaceTransform[eq,t,s]

Out[2]=

In[3]:=ys=Solve[sub,LaplaceTransform[y[t],t,s]]

Out[3]=

In[4]:=yt=InverseLaplaceTransform[ys[[1,1,2]],s,t]

Out[4]=

Per int ah “ys[[1,1,2]]” pada I n[ 4] adalah unt uk m engam bil suku pada Out [ 3], yait u ♦ angka 1 per t am a ar t inya langkahi kur ung paling luar

pada Out [ 3]

♦ angka 1 kedua ar t inya langkahi kur ung selanj ut nya ♦ angka 2 ar t inya m engam bil suku kedua pada Out [ 3]

Cont oh 2: m enyelesaikan Masalah syar at bat as y” + 4y’+ 3y= 0

dengan

y( 0) = 3 dan y’( 0) = 1

Out[1]= Penyelesaian:

In[1]:= eq=D[y[t],t,t]+4D[y[t],t]+3y[t]0

In[2]:=sub=LaplaceTransform[eq,t,s]

Out[2]=

In[3]:=sub2=sub/.{y[0]3,y'[0]1}

Out[3]=

In[4]:=ys=Solve[sub2,LaplaceTransform[y[t],t,s]]

Out[4]=

In[5]:=yt=InverseLaplaceTransform[ys[[1,1,2]],s,t]

SOAL- SOAL LATI H AN

1. Selesaikan Tr ansfor m asi Laplace ber ikut a.

L

_{{ ( t - 1) e}2t_}

b. 

{

t e3t cos2t

}

c. 

{

t2 sinh(t)

}

d. 

{

cosh(at)cos(at)

}

e. 

{

sinh(at)sin(at)

}

f.

L

_{{ f( t ) } = ...}

j ika

  

π ≥

π < ≤ =

2 t , 0

2 t 0 , t sin )

t ( f

g.

{

3

}

t 1∗

 = ...

h. 

{

e−t _∗et cost

}

_{= ...}

2. Selesaikan I nver s Tr ansfor m asi ber ikut a.

   

 

− +s 12 s

3

2 1

-L

b.

   

 

+ +

+ −

7 s 4 s

2 s 2 1



c.

   

 

+ +

4 2 1

-2) ( s

1) ( s

L

d.

   

 

−

−2s 1

- _e

4 s

1

L

3. Gunakan Tr ansfor m asi Laplace unt uk m enyelesaikan Masalah Syar at Bat as ber ikut :

( c) . y” + 16y= f( t ) , y ( 0) = 0, y’( 0) = 1 j ika

  

π ≥

π < ≤ =

t , 0

t 0 , t 4 cos )

t ( f

4. Tent ukan t r ansfor m asi laplace dar i beban pada balok dengan panj ang L ( lihat gam bar )

5. Gunakan Tr ansor m asi Laplace unt uk m enyelesaikan per sam aan lendut an balok :

( )

x

w

dx

y

d

EI

4 4

=

dengan syar at : y( 0) = y( L) = y’( 0) = y’( L) = 0 Jika diket ahui :

• Panj ang balok L= 1m

• Angka kekakuan lent ur EI = 1/ 3 • Beban w ( x) = 8N ( beban m er at a)

6. Selesaikan lagi soal no.5 dengan beban sebagai ber ik ut

   

< ≤

< ≤ −

=

L x 2 L , 0

2 L x 0 , L

x 2 1 ) x ( w

w0

o

L

7. Selesaikan lagi soal no.5 dengan beban w ( x) seper t i pada gam bar soal no.4

8. Selesaikan sist em per sam aan difer ensial ber ikut ( a) . Or der ( t ingkat ) 1:

2 1

2

2 1 1

x 5 x dt dx

x x 5 dt dx

+ =

+ =

dengan syar at :

7 ) 0 ( x , 3 ) 0 (

x₁ = − ₂ =

( b) . Tingkat 2 :

t 1 2

2 2

2 1

2 1 2

e 4 x 4 dt

x d

x 3 x dt

x d

− =

+ =

dengan syar at :

2 dt

) 0 ( dx , 1 ) 0 ( x

3 dt

) 0 ( dx , 2 ) 0 ( x

2 2

1 1

= =

= =

( c) . Tingkat 3

0 dt

x d 2 x 2 dt dx

t sin 6 dt

x d x 4 dt dx

3 2 3 1

1

3 2 3 1 1

= −

+

= +

−

dengan syar at :

0 dt

) 0 ( x d , 0 dt

) 0 ( dx

0 ) 0 ( x , 0 ) 0 ( x

2 2 2 2

2 1

= =

9. Tent ukan t r ansfor m asi Laplace fungsi- fungsi per iodik dengan gr afik seper t i gam bar ber ikut :

( i) .

( ii) .

a

b 2b 3b

1