Unitary Root-MUSIC with a Real-Valued
Eigendecomposition: A Theoretical and Experimental
Performance Study
Marius Pesavento, Alex B. Gershman
, Senior Member, IEEE
, and Martin Haardt
, Senior Member, IEEE
Abstract—A real-valued (unitary) formulation of the popular root-MUSIC direction-of-arrival (DOA) estimation technique is considered. This Unitary root-MUSIC algorithm reduces the com-putational complexity in the eigenanalysis stage of root-MUSIC because it exploits the eigendecomposition of a real-valued covari-ance matrix. The asymptotic performcovari-ance of Unitary root-MUSIC is analyzed and compared with that of conventional root-MUSIC. The results of this comparison show identical asymptotic prop-erties of both algorithms in the case of uncorrelated sources and a better performance of Unitary root-MUSIC in scenarios with partially correlated or fully coherent sources. Additionally, our simulations and the results of sonar and ultrasonic real data processing demonstrate an improved threshold performance of Unitary root-MUSIC relative to conventional root-MUSIC. It can be then recommended that, as a rule, the Unitary root-MUSIC technique should be preferred by the user to the conventional root-MUSIC algorithm.
Index Terms—Array processing, direction-of-arrival estimation, Unitary root-MUSIC.
I. INTRODUCTION
T
HE PROBLEM of reducing the computational complexity of eigenstructure methods via real-valued formulations has recently drawn a considerable attention in the literature [1]–[7]. In [1], Huarng and Yeh presented a real-valued variant of spectral MUSIC based on a unitary transformation. In [2], Zoltowski et al. developed real-valued beamspace root-MUSIC. Linebarger et al. [3] proposed efficient algo-rithms for real-valued SVD updating. Based on a unitary transformation [1], Haardt and Nossek developed a unitary ESPRIT algorithm [4]—an efficient variant of ESPRIT [8] exploiting the centro-Hermitian property of the forward–back-ward covariance matrix. Later, Haardt formulated efficient multidimensional extensions of the unitary ESPRIT technique [5]. In [6], Gershman and Haardt employed Unitary ESPRIT with an eigenvalue-based reliability test to develop a new algorithm based on the estimator bank scheme [9]. In [7], Gershman and Stoica developed a unitary variant of MODE.Manuscript received January 15, 1999; revised October 19, 1999. This work was supported in part by the Natural Sciences and Engineering Research Council (NSERC) of Canada. The associate editor coordinating the review of this paper and approving it for publication was Dr. Brian M. Sadler.
M. Pesavento and A. B. Gershman are with the Communications Research Laboratory, Department of Electrical and Computer Engineering, McMaster University, Hamilton, Ont., Canada L8S 4K1 (e-mail: [email protected]).
M. Haardt is with Siemens AG, Munich, Germany. Publisher Item Identifier S 1053-587X(00)03298-0.
In this paper, a unitary formulation of the root-MUSIC algorithm [10] is considered. First, the exact equivalence of this algorithm to the forward–backward (FB) root-MUSIC is proven. We stress, however, that the implementations of these two techniques are different. In particular, Unitary root-MUSIC has a simpler implementation than FB root-MUSIC because the former exploits the eigendecomposition of a real-valued matrix. Then, the asymptotic performance of the Unitary root-MUSIC algorithm is studied. We show that in situations with uncorrelated signal sources, the asymptotic performances of the Unitary and conventional root-MUSIC algorithms are identical. However, in correlated (or coherent) source sce-narios, the asymptotic performance of Unitary root-MUSIC is shown to be better than that of conventional root-MUSIC. This performance improvement is due to the forward–backward averaging effect. In the final part of our paper, simulation and experimental results are presented. In particular, the conven-tional and Unitary root-MUSIC techniques are tested using real sonar and ultrasonic sensor array data.
Sometimes, forward–backward averaging has been found to cause a certain degradation of asymptotic performances of direction finding techniques [14]. Interestingly, Unitary root-MUSIC does not suffer from such a degradation. Addi-tionally, our simulations demonstrate that Unitary root-MUSIC outperforms conventional root-MUSIC [10] in the threshold domain. Similar results on the threshold performance were ob-served in the real data processing experiments. As both Unitary and conventional root-MUSIC algorithms are applicable to the same array configuration [uniform linear arrays (ULA’s)], we conclude that, as a rule, Unitary root-MUSIC should be preferred by the user to conventional root-MUSIC.
II. ARRAYSIGNALMODEL ANDCOMPLEX-VALUED COVARIANCEMATRICES
Let a ULA be composed of sensors, and let it re-ceive ( ) narrowband sources impinging from the directions . Assume that there are snapshots available. The array observation vector is modeled as [2], [13]
(1)
where is the matrix of the signal
direction vectors
(2)
is the steering vector. In addition
vector of source waveforms; vector of white sensor noise; wavelength;
interelement spacing; transpose.
The conventional (forward-only) estimate of the covariance ma-trix [2], [11]
(3)
is given by [11], [12]
(4)
where
source waveform covariance ma-trix;
identity matrix; noise variance; Hermitian transpose.
The matrix is centro-Hermitian if
(5)
where is the exchange matrix with ones on its antidiagonal and zeros elsewhere, and stands for complex conjugate. The matrix (3) is known to be centro-Hermitian if and only if is a diagonal matrix, i.e., when the signal sources are uncorrelated [4]. However, to “double” the number of snapshots and decor-relate possibly cordecor-related source pairs in the case of an arbitrary matrix , the centro-Hermitian property is sometimes forced by means of the so-called FB averaging [1], [3], [4]
(6)
The FB matrix (6) is often used in various direction-finding methods [1], [3]–[7], [14], [17], [18] instead of the conventional (forward-only) sample covariance matrix (4). It can be readily shown that
(7)
where
(8)
diag
(9)
III. REAL-VALUEDCOVARIANCEMATRIX
We introduce the real-valued covariance matrix as [1], [3], [4]
(10)
and the real-valued sample covariance matrix as
(11)
where is any unitary, column conjugate symmetric
matrix. According to [3], any matrix is column conjugate symmetric if
(12)
For example, the following sparse matrices [1], [3], [4]
(13)
can be chosen for arrays with an even and odd number of sen-sors, respectively, where the vector .
Interestingly, the matrix (11) can be also obtained via the for-ward-only covariance matrix
Re (14)
IV. UNITARYROOT-MUSIC
Let the eigendecompositions of the matrices (3), (7), and (10) be defined in a standard way [3]
(15) (16) (17)
where
diag
diag
diag
and the subscripts and stand for signal- and noise-subspace, respectively. In turn, the eigendecompositions of the sample co-variance matrices (4), (6), and (11) can be defined as
(18) (19) (20)
diag
Writing the characteristic equation for the matrix (6) as , we obtain that
(21)
Equation (21) can be identified as the characteristic one for the real-valued covariance matrix (11). Hence, the eigenvectors and eigenvalues of the matrices (6) and (11) are related as
(22) (23)
The conventional root-MUSIC polynomial is given by
(24)
(25)
where
(26)
, and . Similarly to (24) and (25), the FB root-MUSIC polynomial can be used:
- (27)
(28)
A simple manipulation with the use of (22) yields
-should be exploited for the polynomial rooting in (30). The re-lationship between the former and new manifolds follows from the expression for the real-valued true covariance matrix (10)
(33) (34)
where
(35)
Let us term the polynomial (31) as the Unitary root-MUSIC polynomial since it exploits the eigendecomposition of the real-valued matrix (11) instead of that of the complex matrices (4) or (6). From (29)–(31), it is clear that the FB and Unitary root-MUSIC polynomials are identical. Hence, the performance of Unitary root-MUSIC does not depend on a particular choice of the unitary column conjugate symmetric matrix , although (13) seems to be a very good choice because the matrix (11) can be obtained from the matrix (6) with a very low computa-tional cost. However, although both polynomials
-and - are proven to be identical, the computation of the coefficients of - is a simpler operation [if implemented via the real-valued eigendecomposition (20)] be-cause the real-valued eigendecomposition has a reduced com-putational complexity than the complex one, approximately by a factor of four [2]. Since the polynomial rooting is a much sim-pler operation than the eigendecomposition, we can conclude that the overall computational cost of Unitary root-MUSIC is about four times lower than that of conventional root-MUSIC as in (24) and (25). We also stress that this conclusion cannot be extended to the unitary spectral MUSIC technique [1] because the main computational cost of spectral MUSIC is due to the exhaustive spectral search rather than the eigendecomposition.
We end this section with a few remarks on a substantial difference between the Unitary root-MUSIC algorithm (31) and the popular beamspace root-MUSIC technique presented by Zoltowski et al.[2]. The latter algorithm is entirely based on the centered array assumption (which is not easy to satisfy in certain practical applications), whereas the unitary algorithm (31) does not require such an assumption. Furthermore, to come up with the real-valued computations, the algorithm [2] ignores the complex part of the beamspace covariance matrix, thereby ignoring some useful information contained in its complex part. Finally, since the Unitary root-MUSIC algorithm is equivalent in the performance to FB root-MUSIC, it can be applied to scenarios with pairwise coherent sources, whereas beamspace root-MUSIC is inapplicable to such scenarios.
V. PERFORMANCEANALYSIS
The asymptotic performance of conventional spectral MUSIC has been studied by many authors, e.g., Kaveh and Barabell [15], Stoica and Nehorai [16], and others. The perfor-mance of conventional root-MUSIC has been studied by Rao and Hari [13]. FB spectral MUSIC has been analyzed by Pillai and Kwon [17] and Rao and Hari [18]. To our knowledge, in the existing literature, there is no performance analysis of either Unitary or FB root-MUSIC. It should be noted that the FB covariance matrix (6) has different statistical properties than the forward-only matrix (4) and, therefore, in the general case, the performance of FB direction-finding algorithms may differ severely from that of their forward-only prototypes [14].
Let us introduce the “eigenvector error” vector
(36)
Then, the following lemma holds [5], [19].
Lemma 1: The signal-subspace eigenvector estimation er-rors (36) are asymptotically (for a large number of snapshots ) jointly Gaussian distributed with zero means and covariance matrices given by
Cov
(37)
where
(38)
Im (39)
, and denotes the Kronecker delta.
Applying directly the results derived in [13], we obtain that the DOA estimation mean square error (MSE) of Unitary root-MUSIC is given by
(40)
where
(41)
and
Re
Re (42)
where
(43)
(44)
Using the results of Lemma 1, after manipulations outlined in Appendix A, we obtain that
Re
(45)
In Appendix B, it is proven that
(46)
Therefore, we can rewrite (40) as
(47)
Using (22) and (23), we obtain the final expression for the DOA estimation MSE
(48)
where . Comparing (48) with the results derived by Rao and Hari [13, Eqs. (26) and (28)], we obtain that the only difference between the MSE’s of the conventional and Unitary root-MUSIC algorithms is that our expression (48) for the Unitary root-MUSIC MSE contains the eigenvectors and eigenvalues of the FB covariance matrix (7), whereas the aforementioned expressions in [13] contain the eigenvectors and eigenvalues of the conventional covariance matrix (3). From (7)–(9), it follows that in uncorrelated source scenarios , and therefore, we conclude that the asymptotic performances of the Unitary and conventional root-MUSIC algorithms are identical for uncorrelated sources. However, in situations with partially correlated or coherent sources, the asymptotic performance of Unitary root-MUSIC is better than that of conventional root-MUSIC due to the forward–backward averaging effect. Although this fact is not proven analytically for the general case of arbitrary correlation, it is clearly demon-strated in the next section by means of comparison of analytical and simulation results.
VI. SIMULATIONS
In our simulations, we assumed a ULA of ten omnidirectional sensors with the half-wavelength interelement spacing and two equally powered narrowband sources with the DOA’s
esti-mation root-mean-square errors (RMSE’s) have been compared with the stochastic Cramér–Rao bound (CRB) [20] and with the results of our theoretical (asymptotic) analysis.
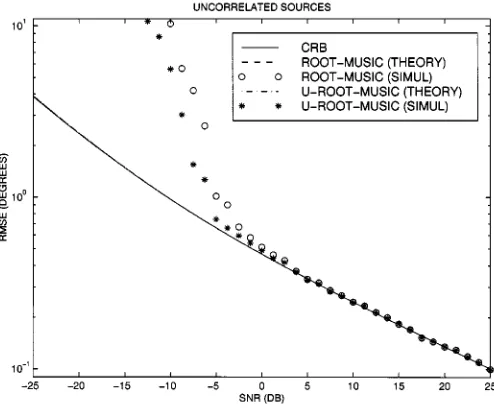
In the first example, we assumed two uncorrelated sources and snapshots. Fig. 1 displays the results for con-ventional and Unitary root-MUSIC versus the SNR. Note that in this figure, the theoretical performance and CRB curves are nearly identical (i.e., they merge into one curve).
In the second example, we assumed two uncorrelated sources with the fixed SNR dB. Fig. 2 shows the results for the conventional and Unitary root-MUSIC algorithms versus the number of snapshots . Again (as in Fig. 1), the theoretical and CRB curves merge here into one curve.
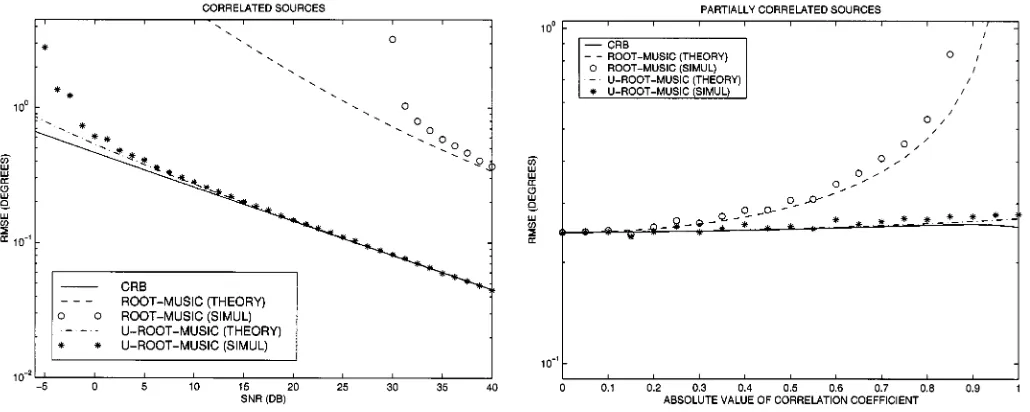
In the third example, has been taken, and two cor-related sources have been assumed with the absolute value of the correlation coefficient equal to 0.99 and zero intersource phase in the first sensor. The results for conventional and Uni-tary root-MUSIC versus the SNR are plotted in Fig. 3.
In the fourth example, we assumed two correlated sources with the same parameters again, and the fixed SNR dB has been taken. Fig. 4 displays the results for the conventional and Unitary root-MUSIC techniques versus the number of snapshots
.
In the last example, we assumed the fixed SNR dB and and considered two correlated sources. Fig. 5 shows the results for conventional and Unitary root-MUSIC versus the absolute value of the correlation coefficient.
From Figs. 1–5, we observe that there is an excellent corre-spondence of the theoretical curves and experimental points at a high SNR and a large . In the first two examples with the un-correlated sources (Figs. 1 and 2), the asymptotic performances of both algorithms are identical. However, from the last three ex-amples with the correlated sources (Figs. 3–5), we see that the Unitary root-MUSIC algorithm has a superior asymptotic per-formance. In particular, Fig. 5 demonstrates the difference in the performances of the Unitary and conventional root-MUSIC al-gorithms in the situation where the sources become more and more correlated. Moreover, from our figures, it clearly follows that both for correlated and uncorrelated source scenarios, Uni-tary root-MUSIC has a lower SNR threshold and better finite-sample performance than conventional root-MUSIC.
VII. REALDATAEXAMPLES
To compare the conventional and Unitary root-MUSIC algo-rithms further, experimental sonar and ultrasonic ULA data have been used. In this section, we describe the data sets and present the results of real data processing.
A. Sonar Data
The experimental site was located in the Bornholm Deep, which is to the east from Bornholm island in the Baltic Sea. The experiments were conducted by STN Atlas Elektronik, Bremen, Germany, in October 1983. A horizontal ULA of 15 hydrophones was towed by a surface ship. The strongest moving broadband source was given by another (cooperating) ship. The sources originating from at least two other (non-cooperating) moving ships have been also detected [21]. The
Fig. 1. Comparison of the performances of the conventional and Unitary root-MUSIC algorithms versus the SNR in the first example. Note that the theoretical and CRB curves merge.
Fig. 2. Comparison of the performances of the conventional and Unitary root-MUSIC algorithms versus N in the second example. Note that the theoretical and CRB curves merge.
sea depth at the experimental site was about 60–65 m. The towed receiving array had the interelement spacing
m, and the sampling frequency was Hz after lowpass filtering with a cut-off of 256 Hz. The narrowband snapshots with the 4-Hz bandwidth have been formed from this broadband data after a DFT at the frequency bin Hz. The sequence of covariance matrices has been estimated using nonoverlapping sliding windows with 4 s duration each.
Fig. 3. Comparison of the performances of the conventional and Unitary root-MUSIC algorithms versus the SNR in the third example.
Fig. 4. Comparison of the performances of the conventional and Unitary root-MUSIC algorithms versusNin the fourth example.
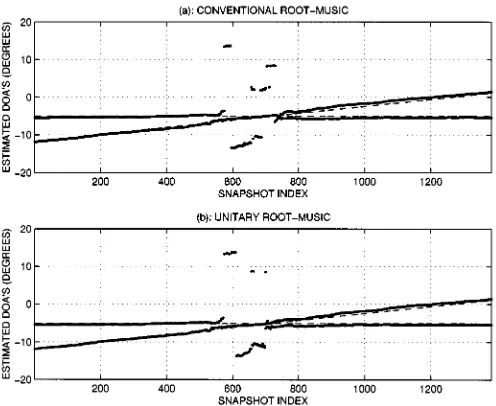
nearly identical performance. In particular, both of them are able to resolve closely spaced sources. Although some performance degradation of the unitary algorithm relative to the conventional one may be expected in the presence of array calibration errors, our experimental results demonstrate to us that this degradation is negligible.
B. Ultrasonic Data
The employed ultrasonic data were recorded at University of Wyoming Source Tracking Array Testbed (UW STAT) [22]. These narrowband six-element array data are available on the World Wide Web at
http://www.eng.uwyo.edu/elec-trical/array.html and have been used as benchmark
data in [7], [22], and [23]. They have the carrier frequency of 40 kHz and the signal bandwidth of 200 Hz. The receiving ULA with the interelement spacing has been used.
Fig. 5. Comparison of the performances of the conventional and Unitary root-MUSIC algorithms versus the absolute value of correlation coefficient in the fifth example.
Fig. 6. Comparison of the conventional and Unitary root-MUSIC algorithms using real sonar data.
Fig. 7. Comparison of the conventional and Unitary root-MUSIC algorithms using real ultrasonic data.
than for the conventional one. This fact demonstrates the supe-rior threshold performance of Unitary root-MUSIC.
VIII. CONCLUSION
The revalued (unitary) formulation of the root-MUSIC al-gorithm has been addressed. Unitary and FB root-MUSIC poly-nomials have been shown to be exactly identical, but the Unitary root-MUSIC technique has been proven to enjoy simpler im-plementation than the conventional and FB root-MUSIC tech-niques. Closed-form expressions for the large sample mean-square estimation errors of Unitary root-MUSIC have been de-rived. These expressions have been compared with the well-known results for conventional root-MUSIC, and it has been shown that Unitary root-MUSIC performs asymptotically sim-ilarly to or better than conventional root-MUSIC. Additionally, our simulations and real sonar and ultrasonic data examples have verified the better threshold performance of Unitary root-MUSIC. As both the Unitary and conventional root-MUSIC al-gorithms are applicable to the same array configuration (ULA), it can be concluded that, as a rule, Unitary root-MUSIC should be preferred by the user to conventional root-MUSIC.
APPENDIX A PROOF OF(45)
For the sake of notational simplicity, denote and . Then
Re (49)
where
(50)
(51)
Inserting (37) into (50) and exploiting the property , we obtain that
(52)
It is straightforward to show that the function (38) has the fol-lowing invariance properties:
(53)
Taking into account (53), rearranging the elements in (52), and exchanging the indexes in this equation, we obtain that
(54)
and therefore, (52) can be simplified to
(55)
After similar manipulations, (51) can be simplified to
(56)
Inserting (55) and (56) into (49), we prove (45).
APPENDIX B PROOF OF(46)
From (26), (32), and (41), it follows that
where
diag (58)
From (26), we have
(59)
In addition, according to (12) and (22)
(60)
Using (12), (22), (32), (57), (59), and (60), and denoting and , we can transform the left side of (46) in the following manner:
(61)
where . Now, to complete the proof of (46), it remains to be shown that
(62)
To prove (62), let us use (12) and (57) and the following identi-ties:
(63) (64)
Then, we have
(65)
With (65), the proof of (46) is completed.
REFERENCES
[1] K. C. Huarng and C. C. Yeh, “A unitary transformation method for angle of arrival estimation,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 39, pp. 975–977, Apr. 1991.
[2] M. D. Zoltowski, G. M. Kautz, and S. D. Silverstein, “Beamspace root-MUSIC,”IEEE Trans. Signal Processing, vol. 41, pp. 344–364, Jan. 1993.
[3] D. A. Linebarger, R. D. DeGroat, and E. M. Dowling, “Efficient direc-tion-finding methods employing forward–backward averaging,”IEEE Trans. Signal Processing, vol. 42, pp. 2136–2145, Aug. 1994. [4] M. Haardt and J. A. Nossek, “Unitary ESPRIT: How to obtain increased
estimation accuracy with a reduced computational burden,”IEEE Trans. Signal Processing, vol. 43, pp. 1232–1242, May 1995.
[5] M. Haardt, “Efficient one-, two-, and multidimensional high-resolution array signal processing,” Ph.D. dissertation, Tech. Univ. Munich, Mu-nich, Germany, 1997.
[6] A. B. Gershman and M. Haardt, “Improving the performance of Unitary ESPRIT via pseudo-noise resampling,”IEEE Trans. Signal Processing, vol. 47, pp. 2305–2308, Aug. 1999.
[7] A. B. Gershman and P. Stoica, “On unitary and forward–backward MODE,”Digital Signal Process., vol. 9, no. 2, pp. 67–75, Apr. 1999. [8] R. Roy and T. Kailath, “ESPRIT—Estimation of signal parameters via
rotational invariance techniques,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 37, pp. 984–995, July 1989.
[9] A. B. Gershman, “Pseudo-randomly generated estimator banks: A new tool for improving the threshold performance of direction finding,”IEEE Trans. Signal Processing, vol. 46, pp. 1351–1364, May 1998. [10] A. J. Barabell, “Improving the resolution performance of
eigenstruc-ture-based direction-finding algorithms,” inProc. ICASSP, Boston, MA, May 1983, pp. 336–339.
[11] P. Stoica and K. C. Sharman, “Novel eigenanalysis method for direction estimation,”Proc. Inst. Elect. Eng. F, vol. 137, pp. 19–26, Feb. 1990. [12] , “Maximum likelihood methods for direction-of-arrival
estima-tion,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 38, pp. 1132–1143, July 1990.
[13] B. D. Rao and K. V. S. Hari, “Performance analysis of root-MUSIC,”
IEEE Trans. Acoust., Speech, Signal Processing, vol. 37, pp. 1939–1949, Dec. 1989.
[14] P. Stoica and M. Jansson, “On forward–backward MODE for array signal processing,”Digital Signal Process., vol. 7, no. 4, pp. 239–252, Oct. 1997.
[15] M. Kaveh and A. Barabell, “The statistical performance of MUSIC and the minimum-norm algorithms in resolving plane waves in noise,”IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-34, pp. 331–340, Apr. 1986.
[16] P. Stoica and A. Nehorai, “MUSIC, maximum likelihood and Cramér–Rao bound,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 37, pp. 720–741, May 1989.
[17] S. U. Pillai and B. H. Kwon, “Performance analysis of MUSIC-type high resolution estimators for direction finding in correlated and coherent scenes,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 37, pp. 1176–1189, Aug. 1989.
[18] B. D. Rao and K. V. S. Hari, “Weighted subspace methods and spa-tial smoothing: Analysis and comparison,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 41, pp. 788–803, Feb. 1993.
[19] G. M. Kautz and M. Zoltowski, “Performance analysis of MUSIC em-ploying conjugate symmetric beamformers,”IEEE Trans. Signal Pro-cessing, vol. 43, pp. 737–748, Mar. 1995.
[20] P. Stoica and A. Nehorai, “Performance study of conditional and uncon-ditional direction-of-arrival estimation,”IEEE Trans. Acoust., Speech, Signal Processing, vol. 38, pp. 1783–1795, Oct. 1990.
[21] C. F. Mecklenbräuker, A. B. Gershman, and J. F. Böhme, “Broadband ML-approach to environmental parameter estimation in shallow ocean at low SNR,”Signal Process., to be published.
[22] J. W. Pierre, E. D. Scott, and M. P. Hays, “A sensor array testbed for source tracking algorithms,” inProc. ICASSP, Munich, Germany, 1997, pp. 3769–3772.
[23] A. B. Gershman and J. F. Böhme, “A pseudo-noise approach to direction finding,”Signal Process., vol. 71, pp. 1–13, Nov. 1998.
Marius Pesavento was born in Werl, Germany, in 1973. He received the M.S. (Diploma) degree in electrical engineering from Ruhr University, Bochum, Germany, in 1999.
Alex B. Gershman (M’97–SM’98) was born in Nizhny Novgorod, Russia, in 1962. He received the M.S. (Diploma) and Ph.D. degrees in radiophysics from the Nizhny Novgorod State University, in 1984 and 1990, respectively.
From 1984 to 1989, he was with the Ra-diotechnical and Radiophysical Institutes, Nizhny Novgorod. From 1989 to 1997, he was with the Institute of Applied Physics of Russian Academy of Science, Nizhny Novgorod, as a Senior Research Scientist. From the summer of 1994 until the begin-ning of 1995, he held a Visiting Research Fellow position at the Swiss Federal Institute of Technology, Lausanne. From 1995 to 1997, he held an Alexander von Humboldt Fellow position at the Ruhr University, Bochum, Germany. From 1997 to 1999, he was a Member of Staff at the Department of Electrical Engineering at Ruhr University. Since 1999, he has been with the Department of Electrical and Computer Engineering, McMaster University, Hamilton, Ont., Canada, as an Associate Professor. His research interests are in the area of signal processing and include statistical signal and array processing, adaptive beamforming and smart antennas, signal parameter estimation and detection, spectral analysis, high-order statistics, and signal processing applications to underwater acoustics, wireless communications, seismology, and radar. He has published more than 100 journal and conference papers on these topics.
Dr. Gershman was a recipient of the 1993 International Union of Radio Science (URSI) Young Scientist Award, the 1994 Outstanding Young Scientist Presidential Fellowship (Russia), the 1994 Swiss Academy of Engineering Science and Branco Weiss Fellowships (Switzerland), and the 1995–1996 Alexander von Humboldt Fellowship (Germany). He is listed in severalWho’s Who in the WorldandWho’s Who in Science and Engineeringeditions. He is an Associate Editor of IEEE TRANSACTIONS ONSIGNALPROCESSINGand a Member of the Sensor Array and Multichannel Signal Processing Technical Committee of the IEEE Signal Processing Society.
Martin Haardt (S’90–M’98–SM’99) was born in Germany on October 4, 1967. He received the Dipl.-Ing. (M.S.) degree from the Ruhr University, Bochum, Germany, in 1991 and the Dr.-Ing. (Ph.D.) degree from the Munich University of Technology, Munich, Germany, in 1996, both in electrical engineering.
From 1989 to 1990, he was a Visiting Scholar at Purdue University, West Lafayette, IN, sponsored by a fellowship of the German Academic Exchange Service (DAAD). From 1991 to 1993, he worked for Corporate Research and Development, Siemens AG, Munich, Germany, conducting research in the areas of image and biomedical signal processing. From 1993 to 1996, he was a Research Associate with the Institute of Network Theory and Circuit Design at the Munich University of Technology, where his research was focused on smart antennas. In 1997, he joined Siemens Mobile Networks, Munich, where he was responsible for strategic research for third-generation mobile radio systems. Since 1998, he has been serving as Director of International and University Projects in the Chief Technical Office of Siemens Communication on Air. He also teaches at the Munich University of Technology and is a contributing author toThe Digital Signal Processing Handbook,(Boca Raton, FL: CRC and Piscataway, NJ: IEEE, 1998). His current research interests include wireless communications, array and digital signal processing, and numerical linear algebra.