Mekanika Benda Langit

(1)

Bab I

Masalah

Masalah Dua

Dua Benda

Benda

Gerak planet mengitari Matahari. Satelit yang mengelilingi Bumi dan bintang-bintang Gerak planet mengitari Matahari. Satelit yang mengelilingi Bumi dan bintang-bintang yang mengitari

yang mengitari pusat Galaksi, diatur oleh gaya sentral yang bekerja pusat Galaksi, diatur oleh gaya sentral yang bekerja sepanjang garis lurus yangsepanjang garis lurus yang menghubungkan benda langit terhadap sumber gaya tersebut. Aturan untuk menerangkan gaya menghubungkan benda langit terhadap sumber gaya tersebut. Aturan untuk menerangkan gaya sentral ini lazim

sentral ini lazim disebut hukum gravitasi disebut hukum gravitasi Newton, “ Gaya tarik Newton, “ Gaya tarik menarik antara dua titik menarik antara dua titik massamassa adalah berbanding langsung

adalah berbanding langsung dengan hasil kali dengan hasil kali massa mereka smassa mereka serta berbanding terbalik erta berbanding terbalik dengandengan jarak kuadratnya”. Dinyatakan dalam

jarak kuadratnya”. Dinyatakan dalam pernyataan, Hukum Newtonpernyataan, Hukum Newton

2 2 2 2 1 1 r r m m m m G G F F

==

−−

→ → (1-1) (1-1) Dengan

Dengan G = G = konstanta gravitkonstanta gravitasiasi m

mii massa massa ke – ke – ii

r jarak m

r jarak m11 ke m ke m22

Satuan yang dipilih mengikuti aturan berikut; Satuan yang dipilih mengikuti aturan berikut; 1.

1. Jika m Jika m dalam gram dalam gram dan r dan r dalam sentimdalam sentimeter maka eter maka G=6,67 10G=6,67 10-8-8 cgs cgs 2.

2. Jika m Jika m dalam massa dalam massa matahari dan r matahari dan r dalam satuan dalam satuan astronomi astronomi maka nilai maka nilai G adalah G adalah 0,0172020,017202 (disebut konstanta Gauss, simbol, k)

(disebut konstanta Gauss, simbol, k)

1.1

1.1 Vektor

Vektor

Didefinisikan

Didefinisikan vektor vektor posisi, posisi, r, r, vector vector kecepatan kecepatan v v dan dan vector vector percepatan percepatan a, a, sebagaisebagai

2 2 2 2 ,, dt dt r r d d dt dt dv dv a a dt dt dr dr vv

==

→ → (1-2) (1-2) Vektor satuan

Vektor satuan dalam arah dalam arah r dan sr dan sudutudut

θθ

dinyatakan dinyatakan dalam dalam simbol simbol UUr r dan U dan Uθθ

dalam hal ini hubungan antara U

dalam hal ini hubungan antara Ur r dan U dan Uθθ adalah; adalah;

,, r r r r U U θθ θ θ θ _θ_θ θ _θ_θ θθ θ θ → → • • → → → → • • →→

=

= −

(1-3)(1-3) Vektor U

Vektor Ur r tegak lurus U tegak lurus Uθθ ,selain itu dari gabungan persamaan vektor diatas dapat ditulis ,selain itu dari gabungan persamaan vektor diatas dapat ditulis

kembali; kembali; → → → → → →

++

==

r r U U r r θ θ U U _θ_θ dt dt dr dr vv _r_r (1-4)(1-4) 2 2 2 2 2 2 (( )) r r ((22 )) d d r r a a r r r r U U r r r r U U dt dt θ θ θ θ θ θ θ θ → → •••• →→ •• •• •• →→

=

= =

= −

−

+

+ ++

(1-5)(1-5)

(2)

Ilustrasi vektor ini diragakan dalam Gb 1-1 berikut ini Ilustrasi vektor ini diragakan dalam Gb 1-1 berikut ini

Gb. 1-1 Titik massa m bergerak dalam pengaruh Gb. 1-1 Titik massa m bergerak dalam pengaruh gaya sentral yang berpusat pada titik O gaya sentral yang berpusat pada titik O

1.2

1.2 Momentum lin

Momentum linier, mome

ier, momentum sudut,

ntum sudut, momen dan

momen dan gaya

gaya

Berikut didefinisikan beberapa besaran vector; Berikut didefinisikan beberapa besaran vector; Momentum linier (vektor) : massa kali kecepatan Momentum linier (vektor) : massa kali kecepatan

→ → → →

==

mmvv p p (1-6)(1-6) Momentum sudut (

Momentum sudut (vektor) adalah vektor) adalah jarak kali momentum jarak kali momentum linierlinier

→ → → → → →

==

r r xm xmvv L L (1-7)(1-7)

Momen/Torque/torka(vektor): jarak kali gaya Momen/Torque/torka(vektor): jarak kali gaya

(3)

Ilustrasi vektor ini diragakan dalam Gb 1-1 berikut ini Ilustrasi vektor ini diragakan dalam Gb 1-1 berikut ini

Gb. 1-1 Titik massa m bergerak dalam pengaruh Gb. 1-1 Titik massa m bergerak dalam pengaruh gaya sentral yang berpusat pada titik O gaya sentral yang berpusat pada titik O

1.2

1.2 Momentum lin

Momentum linier, mome

ier, momentum sudut,

ntum sudut, momen dan

momen dan gaya

gaya

Berikut didefinisikan beberapa besaran vector; Berikut didefinisikan beberapa besaran vector; Momentum linier (vektor) : massa kali kecepatan Momentum linier (vektor) : massa kali kecepatan

→ → → →

==

mmvv p p (1-6)(1-6) Momentum sudut (

Momentum sudut (vektor) adalah vektor) adalah jarak kali momentum jarak kali momentum linierlinier

→ → → → → →

==

r r xm xmvv L L (1-7)(1-7)

Momen/Torque/torka(vektor): jarak kali gaya Momen/Torque/torka(vektor): jarak kali gaya

(4)

==

r r x xF F N N (1-8)(1-8) Gaya Newton; Gaya Newton; dt dt dv dv m m dt dt r r d d m m F F ₂₂ 2 2 →→ → → → →

==

(1-9)(1-9)

Turunkan momentum sudut terhadap waktu t, diperoleh; Turunkan momentum sudut terhadap waktu t, diperoleh;

→ → → → → → → → → → → → → → → → → →

==

∗∗ N N F F x x r r )) v v x x r r (( dt dt d d m m dt dt )) v v xm xm r r (( d d dt dt dL dL L L (1-10)(1-10) Tinjau

Tinjau suatu suatu titik titik massa massa m, m, bergerak bergerak dengan dengan percepatan percepatan konstan konstan a, a, sepanjang sepanjang garis garis lurus.lurus. Gaya yang bekerja pada titik massa m akan menghasilkan kerja W sebesar;

Gaya yang bekerja pada titik massa m akan menghasilkan kerja W sebesar;

∫∫

==

)) (( )) 0 0 (( 0 0 t t vv S S t t vv S S vdv vdv m m Fds Fds W W (1-11)(1-11)

atau dapat ditulis kembali sebagai atau dapat ditulis kembali sebagai

)) (( 2 2 1 1 )) (( )) ((ss W W ss mm vv22 vv₀₀22 W W

−−

==

−−

(1-12)(1-12) Jadi kerja

Jadi kerja yang dilakukan untuk yang dilakukan untuk memindahkan titik memindahkan titik massa m massa m dari posisi dari posisi awal awal ss00 pada pada

kedudukan

kedudukan s pada s pada saat t saat t adalah perubahan energi adalah perubahan energi kinetis tkinetis titik mitik massa tersebut assa tersebut dalam selangdalam selang waktu (t-t

waktu (t-t00 ). Fungsi kerja W(s) dapat diganti dengan fungsi skalar yang lain ,yaitu energi ). Fungsi kerja W(s) dapat diganti dengan fungsi skalar yang lain ,yaitu energi

potensial V(s) dimana

potensial V(s) dimana V(s) = - W(s). Dengan perkataan lain (1-12) dapat V(s) = - W(s). Dengan perkataan lain (1-12) dapat dinyatakan dinyatakan sebagaisebagai

E E ss V V mv mv ss V V mv mv

++

==

++

(( ))

==

2 2 1 1 )) (( 2 2 1 1 0 0 2 2 0 0 2 2 (1-13) (1-13) Dalam hal

Dalam hal ini E ini E merupakan energi total merupakan energi total sistem. Pernyataan sistem. Pernyataan ini menunjukkan bilini menunjukkan bila energia energi kinetis mengecil maka energi potensial akan membesar demikian pula sebaliknya. Untuk lebih kinetis mengecil maka energi potensial akan membesar demikian pula sebaliknya. Untuk lebih jelas

jelas perhatikan perhatikan contoh contoh berikut. berikut. Misalkan Misalkan ada ada dua dua titik titik massa massa M M dan dan m m yang yang berada berada dalamdalam pengaruh gaya sentral berjarak

(5)

Gb1.2

Gb1.2 Perpindahan titik Perpindahan titik massa m massa m dari posisi dari posisi SS00 ke posisi S ke posisi S

Gaya gravitasi yang bekerja pada m adalah; Gaya gravitasi yang bekerja pada m adalah;

2 2 ss Mm Mm G G F F

==

−−

(1-14)(1-14)

Kerja yang dilakukan oleh F untuk memindahkan titik massa m sejauh ds adalah; Kerja yang dilakukan oleh F untuk memindahkan titik massa m sejauh ds adalah;

ds ds ss Mm Mm G G ss dW dW (( ))

==

−−

₂₂ (1-15)(1-15)

Jika pada saat; Jika pada saat;

tt11=t=t00

→

ss11 = = r r dan vdan v11 = v = v00 tt22=t=t

→

ss22 = = s s dan vdan v22 = v = v Maka diperoleh ; Maka diperoleh ;

∫∫

==

−−

ss ss vv vv ds ds ss Mm Mm G G mvdv mvdv 0 0 0 0 2 2 (1-16)(1-16) atau ; atau ; 0 0 2 2 0 0 2 2 2 2 1 1 2 2 1 1 ss Mm Mm G G mv mv ss Mm Mm G G mv mv

−−

==

−−

(1-17)(1-17)

(6)

Jika partikel diletakkan pada s

→ ∞

, ganti s0 dengan r, maka diperoleh r Mm G mv mv2

=

₀2

−

2 1 2 1 (1-18)

Energi potensial pada jarak r, didefinisikan

r Mm G r

V ( )

=

−

(1-19)

Dalam hal ini, V(r) adalah kerja yang dilakukan untuk memindahkan titik massa m dari kedudukan r, keposisi tak terhingga, keadaan ini dikenal sebagai potensial titik massa M terhadap m, lazim dinyatakan dalam bentuk;

r M G r

U ( )

=

−

(1-20)

Pernyataan diatas menunjukkan bahwa gaya gravitasi pada kedua titik massa yang berjarak r satu sama lain adalah;

r U r Mm G F → →

−

=

₂ (1-21)

Gabungkan (1-20) dengan (1-21) diperoleh;

r U dr dU m F → →

−

=

(1-22)

Perlu diingat bahwa besaran U-fungsi skalar dan F menyatakan fungsi vektor dalam hal ini

→ → → →

+

=

F x F _y F _z

F terdiri dari komponen pada sumbu x,y dan z

1.3 Potensial bola padat

Salah satu hal penting dalam membicarakan persamaan gerak sistim dua benda adalah potensial benda padat yang diterima oleh suatu titik massa m. Bumi kita berbentuk elipsoid, dalam telaah ini dianggap merupakan bola padat sempurna dengan distribusi massa yang homogen. Untuk itu tinjaulah suatu irisan bola padat seperti yang diperlihatkan pada gambar 1-3

(7)

Gb.1-3 Irisan seperdelapan bola padat. Potensial bola padat M terhadap titik massa m. Massa total M, se-olah olah terkonsentrasi pada pusat bola

Untuk menurunkan sifat potensial suatu bola padat misalkan, a menyatakan radius bola, d

σ

elemen luas kulit bola,

ρ

density dan m-massa satu satuan yang diletakkan pada posisi (0,0,h), sedangkan p-jarak d

σ

dari massa m. gaya tarik gravitasi antara elemen kulit bola dan titik massa m dapat dinyatakan sebagai;

2 p

d G

dF

=

−

ρ σ (1-23)

dalam hal ini

d

σ

= a2 sin

ϕ

d

ϕ

d

θ

(1-24)

Karena bentuk bola ini simetri maka komponen elemen vektor yang sejajar terhadap bidang xy akan saling meniadakan. Sedangkan komponen dalam arah sumbu z dapat dijumlahkan, jadi gaya total yang diterima oleh satu satuan massa m adalah;

∫

=

−

=

ρ σ Cosα p d G dF F _z _z ₂ (1-25) tetapi; p2 = a2 + h2 –2ah Cos

ϕ

(1-26)

(8)

sedangkan;

p aCos h

Cosα

=

−

(1-27)

Gabungkan persamaan (1-26) dengan (1-27) kita peroleh;

ph p a h Cos 2 2 2 2

₋

₊

=

α (1-28)

dari pernyataan (1-26) dapat diturunkan; pdp = ah Sin

ϕ

d

ϕ

jadi persamaan (1.24) dapat ditulis sebagai; σ pdpd θ

h a d

=

Oleh sebab itu gaya total sepanjang sumbu z dapat dinyatakan kembali dalam bentuk;

∫∫

ρ

−

+

θ

−

=

R 2 2 2 2 2 z adpd h p 2 ) p a h ( G F (1-29)

dalam hal ini, R adalah himpunan pasangan terurut (p,

θ

), dengan sifat yang dapat ditulis sebagai; R=

{

(p,

θ

)

|

h-a

≤

p

≤

h+ a, 0

≤ θ ≤

2

π }

. Integral (1-29) memberikan solusi;

2 2 4 h a G F _z

=

−

π ρ (1-30)

Persamaan (1-30 ) menyatakan gaya total yang diterima oleh titik massa m dari seluruh permukaan bola. Sedangkan gaya total yang diterima massa m dari kulit bola setebal da

adalah; da h a G dF ₂ 2 4π ρ

−

=

(1-31)

Dengan demikian gaya total dari seluruh isi bola adalah;

da h a G F r 2 2 0 4π

∫

ρ

−

=

(1-32)

Massa total bola adalah ;

da a M r

∫

=

0 2 4π ρ (1-33)

(9)

Gabungkan (1-32) dengan (1-33) diperoleh; 2 h M G F

=

−

(1-34)

Persamaan ini menunjukkan bahwa untuk bola padat homogen dengan distribusi kerapatan yang simetri, gaya gravitasi itu se-olah olah hanya disebabkan oleh massa bola yang

terkonsentrasi pada pusatnya. Bentuk umum yang dikenal ialah bila notasi h kita ganti dengan r dan mengingat relasi

r U F

∂

=

maka potensial U dari bola homogen tersebut dapat ditulis sebagai;

r GM

U

=

(1-35)

Dalam hal ini M massa total bola dan r jarak titik massa m, ke pusat bola tersebut

1.4 Persamaan gerak dua titik massa

Tinjau dua titik massa m1 dan m2 yang terletak pada jarak r 1 dan r 2 dari pusat koordinat seperti

yang ditunjukkan oleh Gb 1-4

Gb.1-4 Dua titik massa m1 dan m2 pada posisi r 1 dan r 2 . Titik P

menyatakan pusat massa sistim dan r jarak m1 dan m2

Untuk mempelajari gerak dari sistem dua benda ini kita mulai dengan melihat kembali hukum gravitasi Newton. Persamaan gerak sistem dapat dinyatakan dalam bentuk dua pasang

(10)

1. Gaya gravitasi oleh m1 terhadap m2 ; 1 2 21 2 r m m F G U r → = − uuur (1-36)

2. Gaya gravitasi oleh m2 terhadap m1 ;

2 1 12 2 r m m F G U r → = uuur (1-37)

Jika kedua persamaan (1-36) dan (1-37) kita jumlahkan maka akan memberikan

12 21 0

F + F =

uuur uuur

, dapat juga ditulis dalam bentuk lain; m r m r ₁ 1 ₂ 2 0

•• ••

→ →

+

=

Dengan melakukan dua kali integrasi terhadap pernyataan ini, diperoleh;

2 1 2 2 1 1 → → → →

+

=

+

m r c t c r m (1-38)

Dalam hal ini konstanta vektor c1 dan c2 berasal dari dua kali integrasi persamaan diatas.

Selain itu pusat massa dapat diturunkan dari definisi;

2 1 1 ₂ 1 2 1 2 c t c m r m r R m m M → → → → →

₊

=

+

(1-39)

dalam hal ini M = m1 + m2 . Jadi jelas bahwa persamaan ini adalah suatu persamaan garis

lurus, dengan perkataan lain pusat massa bergerak menurut suatu garis lurus sebagai fungsi dari waktu t. Untuk menentukan gerak relatif m1 dan m2 terhadap pusat massa tulislah;

1 1 r R r → → → ′ = + dan r 2 R r 2 → → → ′ = + dengan r 1 → ′ dan r 2 →

′ menyatakan vektor posisi m1 dan m2 terhadap pusat

massa. Dari gambar diatas vektor yang menghubungkan m1 dan m2 memenuhi kaedah;

2 1 2 1

r r r r r → → → → →

′ ′

= − = − (1-40)

Karena persamaan pusat massa(1-39) adalah linier maka turunan kedua dari vektor pusat massa adalah vektor nol

R O •• → →

=

maka diperoleh r ₁ r ₁ •• •• → →

′

=

dan r ₂ r ₂ •• •• → →

′

(11)

1 2 2 1 1 1 3 ( ) m m r r m r G r •• → → →

′ ′

₋

′=

(1-41)

hal yang sama berlaku pula;

1 2 2 1 2 2 3 ( ) m m r r m r G r •• → → →

′ ′

−

′ = −

(1-42) Karena; 2 1 1 2 1 1 2 2 m r m r m r m r O •• •• •• •• → → → → →

′

+

= + =

(1-43) maka r 2 →

′ dapat dieliminasi dari pernyataan (1-42), hasilnya;

1 2 1 1 1 3 1 2 (1 ) m m m m r G r r m •• → →

′

= −

+

′

(1-44)

Hal yang sama untuk (1-42) dengan mengeliminasi

→

' 1

r diperoleh hasil sebagai berikut;

1 2 2 2 2 3 2 1 (1 ) m m m m r G r r m •• → →

′

= −

+

′

(1-45)

Dengan mengingat bahwa M = m1 + m2 maka persamaan (1-44) dan (1-45) dapat dinyatakan

dalam bentuk; 1 3 1 M r G r r •• → →

′

= −

′

dan r ₂ G M ₃ r ₂ r •• → →

′

= −

′

(1-46)

Selanjutnya akan diambil sebagai pusat koordinat adalah titik massa m1 seperti yang

(12)

Gb. 1-5 Kedudukan titik massa m1 dan m2 dalam sistim koordinat

kartesis,sebagai pusat koordinat dipilih titik massa m1

Konsekuensi dari adanya gaya gravitasi, massa yang lebih kecil akan mempunyai jarak yang lebih besar ke titik pusat massa dibandingkan dengan massa yang lebih besar, dalam hal m1

jauh lebih besar dari m2 , maka m1 akan menjadi pusat gaya sentral. Pernyataan (1-46) dapat

diubah dalam bentuk yang lebih umum. Dengan menggabungkan bentuk persamaan (1-46) diperoleh; 2 1 3 ( 2 1) M r r G r r r •• •• → → → →

′ ′

− =

′ ′

−

atau r G M ₃ r r •• → →

′

= −

′

(1-47)

Ini adalah persamaan yang menunjukkan vektor percepatan m2 relatif terhadap m1. Vektor

posisi

→

r bila dinyatakan dalam bentuk kartesis x,y dan z menjadi;

→ → → →

+

=

x i y j zk

r dalam hal ini , ,

→ →

j

i dan

→

k adalah vektor satuan pada sumbu x,y dan z. Persamaan (1-47) dapat diuraikan dalam bentuk kartesis yaitu;

2 2 2 3/ 2 ( ) x GMx x y z •• −

=

−

+ +

2 2 2 3/ 2 ( ) y GMy x y z •• −

=

−

+ +

(1-48) 2 2 2 3/ 2 ( ) z GMz x y z •• −

=

−

+ +

(13)

Ketiga bentuk persamaan (1-48) menyatakan percepatan titik massa m2 relatif terhadap m1

yang bekerja dalam arah sumbu x,y dan z. Selanjutnya kalikan bentuk ,

x y

•• ••

dan z

••

dari persamaan (1-48) dengan x,y dan z kemudian jumlahkan maka akan diperoleh pernyataan ; 0 y x x y •• ••

−

=

0 z y y z •• ••

−

=

(1-49) 0 x z z x •• ••

−

=

Integrasikan ketiga persamaan (1-49) terhadap waktu dt memberikan;

1 x y y x a • •

−

=

2 y z z y a • •

−

=

(1-50) 3 z x x z a • •

−

=

Simbol a1,a2, dan a3 pada pernyataan (1-50) adalah konstanta integrasi. Kalikan masing-masing

pernyataan diatas berturut-turut dengan z, x dan y, selanjutnya kita jumlahkan maka diperoleh; 0 z a y a x a₁

+

₂

+

₃

=

(1-51)

Bentuk persamaan (1-51) dalam ilmu ukur analitik dikenal sebagai persamaan bidang datar yang melalui titik pusat koordinat x = 0, y = 0 dan z = 0. Dengan lain perkataan m2 bergerak

pada satu bidang lintasan yang melalui titik massa m1 dan m2

1.5 Konstanta Luas, Momentum Sudut dan Energi

Berbagai sifat penting dapat kita turunkan dari pengaruh gaya sentral yang bekerja pada titik massa, dari persamaan (1-47) dapat diturunkan hubungan berikut;

3 M r G r r •• → →

= −

lakukan perkalian vektor dengan

→ r maka diperoleh; 2 2 r xm r r xm v •• • → → → →

=

atau 2 2 3 ( ) 0 Mm d G r x r r xm v r dt •• → → → →

−

=

(1-52)

(14)

dengan lain perkataan, momentum sudut

→ →

→

=

r xm v

L ₂ selama m2 bergerak melintasi m1 adalah

konstan, boleh juga dikatakan bahwa

→

L tidak berubah arah selama m2 melintasi m1 atau

→

L

selalu ortogonal (tegak lurus) terhadap bidang dimana

→

r dan v

→

berada.

Selanjutnya tinjau pernyataan momentum sudut berikut, dalam berbagai bentuk yang identik;

→ → →

=

r xm v L ₂ (1-53) 2 L r xm r • → → →

=

(1-54) 2( r ) L r xm r U r U θ _θ → → • → • →

=

+

(1-55) 2 2 L L m r θ U → • →

=

(1-56)

Dimana (r,

θ

) adalah koordinat polar pada bidang orbit dan U L

→

adalah vektor satuan yang tegak lurus terhadap U r

→

dan θ

→

U dengan demikian U L

→

selalu tegak lurus pada bidang orbit. Selanjutnya misalkan, h r 2θ

•

=

dalam hal ini h menyatakan dua kali luas daerah yang disapu oleh radius vektor r persatuan waktu. Karena L adalah konstan maka dapat dikatakan

2 h r θ

•

=

adalah suatu konstanta, secara analitik pernyataan ini merupakan pengejawantahan hukum Kepler II, kadangkala h disebut juga konstanta Kepler. Kemudian,dari bentuk persamaan; 2 2 3 Mm r m v G r • _→

→

= −

, bila kita ambil perkalian skalar terhadap

→

v , maka diperoleh uraian sebagai berikut; 2 2 3 Mm m v v G r v r • → → →

→

• =

−

•

(1-57)

atau dapat juga ditulis dalam bentuk lain;

) 1 ( ) 2 1 ( ₂ 2 ₂ r dt d GMm v m dt d

=

(1-58)

Akibatnya, bila diintegrasikan terhadap waktu dt, diperoleh;

E r Mm G v m₂ 2

−

2

=

2 1 (1-59)

(15)

Dalam hal ini E adalah konstanta integrasi yang menyatakan energi total sistim. Makna dari persamaan (1-59) memperlihatkan bahwa energi total sistim tidak berubah terhadap waktu dan merupakan jumlah energi kinetik (bentuk pertama ruas kiri) dan energi potensial (bentuk kedua dari ruas kiri).

1.6 Orbit dalam bentuk polar

Dalam bentuk komponen radial dan transversal pernyataan tentang hukum Newton dapat ditulis dalam bentuk berikut;

2 2 (r r U ) _r (2r r U ) G U M _r r θ θ θ θ •• • → • • •• → →

−

+ +

=

−

(1-60)

Persamaan ini tentu harus memenuhi pasangan;

2 2 (r r ) G M r θ •• •

−

= −

(1-61) (2r θ r θ )U θ 0 • • •• →

+

=

(1-62)

Pernyataan (1-61) diatas dapat ditulis kembali dalam bentuk berikut;

2 2 (r r ) G M 0 r θ •• •

−

+

=

(1-63)

Untuk menyederhanakan persamaan (1-63) ambillah pemisalan berikut;

GM

=

dan

u

r

=

1 . Substitusi kedua besaran ini kedalam pernyataan (1-63) diperoleh;

2 2 2 h u d u d μ θ

+

=

(1-64)

Penyelesaian persamaan diferensial tingkat dua ini merupakan penjumlahan solusi bentuk homogen dan solusi khusus hasilnya adalah;

2 ) ( h ACos u

=

θ

−

ω

+

(1-65)

atau dapat juga ditulis dalam bentuk

1 ) ( 2 2

+

−

=

ω θ μ μ Cos Ah h r (1-66)

(16)

A dan

ω

merupakan konstanta integrasi. Bila kita bandingkan dengan pernyataan irisan kerucut dalam bentuk polar;

) ( 1

+

θ

−

ω

=

eCos p r (1-67)

Maka diperoleh kesimpulan bahwa; μ 2 h p

=

dan 2 Ah e μ

=

(1-68)

Dalam hal ini e dan p akan menentukan bentuk dan jenis irisan kerucut. Simbol e dikenal sebagai eksentrisitas, yaitu besaran yang menunjukkan jenis irisan kerucut. Harga e selalu positif, sedangkan r selalu bergantung pada nila

ω

dan

θ

. Apabila kita tinjau ketentuan berikut; 1) Nilai

ω

=

θ

maka e p r

+

=

1 dan ini merupakan jarak r minimum yang dapat dicapai oleh titik massa m2 terhadap m1 dalam lintasannya, diberi simbol r p

2) Nilai

ω

-

θ

= 1800 maka e p r

−

=

1 kita lihat bahwa ini adalah jarak maksimum titik massa m2 terhadap m1 dalam orbitnya, diberi simbol r a.

Tinjau pula bila pada ketentuan diatas kita ambil nilai e untuk bermacam macam harga; a) Eksentrisitas e =0 maka r p = r a titik terjauh sama besarnya dengan jarak titik terdekat.

Bentuk lintasan seperti ini adalah suatu lingkaran b) Eksentrisitas e =1 maka;

2

p

r _p

=

dan r a

→ ∞

titik terjauh berlokasi ditak terhingga.

Bentuk lintasan seperti ini dikenal sebagai suatu parabola

c) Eksentrisitas berada diantara 0 dan 1, 0 < e <1, maka; r p < p dan

r a > 0

d) Eksentrisitas e > 1 maka r p < p dan r a < 0

Masing-masing bentuk pernyataan c) dan d) dalam ilmu ukur analitik dikenal berturut-turut sebagai lintasan elips dan hiperbola. Bentuk lintasan dalm uraian a), b), c) dan d) diragakan dalam Gb 1.6

Lintasan berbentuk elips mendominasi gerak dan lintasan anggota Tata Surya kita. Apabila gaya sentral menguat orbit berkecendrungan menjadi lingkaran, namun jika gaya sentral melemah maka lintasan akan menuju ke eksentrisitas yang lebih besar. Ketika kecepatan orbit sama atau lebih besar dari 2 kecepatan lingkaran maka benda langit tersebut akan lepas dari Tata Surya kita. Itulah sebabnya mengapa planet dengan temperatur tinggi tidak mempunyai atmosfer. Kecepatan thermal partikel telah melewati kecepatan lepasnya. Makin besar jarak partikel dari permukaan Bumi, semakin tinggi pula peluangnya untuk lepas. Berbeda dengan

(17)

menjadi lebih renggang, temperatur meningkat dengan bertambahnya ketinggian dan mencapai maksimum pada lapisan teratasnya yang disebut stratopause.

Gb 1-6 Gerak m2 melintasi m1 dalam berbagai bentuk lintasan (a) lingkaran, (b) parabola, (c)

elips dan (d) hiperbola. Massa m2 bergerak melintasi m1 dalam pengaruh gaya sentral

yang mengarah ke massa m1

Satelit buatan maupun alami(natural) bergerak dalam orbit elips, demikian pula anggota Tata Surya kita namun ada beberapa yang bergerak dalam orbit hiperbolik misalnya gerak batu meteor. Beberapa contoh benda langit yang bergerak dalam lintasan hiperbolik antara lain, komet Iras Araki dan komet Kohoutek

Andaikan dalam geraknya, titik massa m2 mempunyai lintasan berbentuk elips dan misalkan

juga a menyatakan setengah sumbu panjang elips, maka hubungan setengah sumbu panjang dengan jarak terjauh dan terdekat m2 terhadap m1 dapat ditulis 2a = r a + r p. Akibat pernyataan

ini nilai parameter p tersebut harus memenuhi hubungan p= a(1-e2 ) . Sehingga persamaan irisan kerucut (1-50) dapat ditulis lagi sebagai;

) ( 1 ) 1 ( 2 ω θ

−

+

−

=

eCos e a r (1-69)

Energi total sistem dapat kita hubungkan untuk berbagai nilai eksentrisitas e, demikian pula sebaliknya. Untuk keperluan ini tulis kembali pernyataan energi dalam bentuk;

0 1 2

₋

₂

₋

₌

E Mm G v

(18)

kita peroleh pernyataan; 0 2 1 2 2 2 2h u

−

m u

−

E

=

m μ (1-70)

Ini merupakan persamaan kuadrat dalam bentuk variabel u, sehingga akar dari persamaan kuadrat ini adalah,

2 2 2 2 2 12 2 1 m Eh h h u μ μ μ

_±

₊

=

(1-71)

Nilai maksimum akan berbentuk;

2 2 2 2 2 max 2 1 m Eh h h u μ μ μ

+

=

(1-72)

sedangkan nilai minimum adalah;

2 2 2 2 2 min 2 1 m Eh h h u μ μ μ

+

−

=

(1-73)

Tetapi dari bentuk polar yang telah diturunkan pada paragraf sebelumnya;

2 ) ( h ACos u

=

θ

−

ω

+

,

nilai maksimum terjadi bila

θ

-

ω

= 00 dan nilai minimum terjadi bila selisih nilai

θ

-

ω

= 1800 dan kedua pernyataan ini setara dengan;

2 max

h A

u

=

+

(1-74)

Bandingkan pernyataan (1-74) ini dengan pernyataan (1-72), kesimpulan yang diperoleh adalah; 2 2 2 2 2 1 m Eh h A μ μ

+

=

(1-75) Tetapi nilai , ₂ h e

A

=

oleh sebab itu eksentrisitas dapat juga dinyatakan sebagai fungsi dari energi total sistim, bentuk persamaannya adalah;

(19)

2 2 2 2 1 m Eh e μ

+

=

(1-76)

Dari pernyataan ini jelaslah bahwa bila;

a) Energi total sistem E = 0 , maka e = 1 jadi orbit berbentuk suatu parabola b) Energi total sistem E < 0 , maka e < 1 jadi orbit berbentuk suatu elips

c) Energi total sistem E > 0 , maka e > 1 jadi orbit berbentuk suatu hiperbola

Untuk lintasan yang berbentuk elips, konstanta kecepatan luas h dapat ditentukan atau dinyatakan dalam elemen orbit, yaitu;

) 1 ( e2 a p

=

−

atau (1 2) 2 e a h

−

=

μ (1-77)

Bentuk kedua (1-60) dapat juga ditulis sebagai;

2 2

(1 )

h r θ GMa e

•

=

−

(1-78)

Selanjutnya ingin ditentukan kecepatan m2 dalam geraknya melintasi m1 dalam orbit yang

eliptis. Untuk itu gabunglah pernyataan (1- 76) dengan (1-78) maka diperoleh;

) 2 ( ₂ 2 2 2 μ m Eh GMa h

=

−

atau a m E 2 2

−

=

(1-79)

Pernyataan (1-79) memperlihatkan semakin besar setengah sumbu panjang lintasan, semakin kecil pula energi total sistem. Selanjutnya bila energi total E ini disubstitusikan kedalam persamaan energi, maka kita peroleh;

) 2 1 1 ( 2 2 a r GM V

=

−

(1-80)

Persamaan ini menunjukkan bahwa jika a = r, kecepatan tersebut merupakan kecepatan orbit lingkaran, jika a →

∞

memperlihatkan kecepatan lepas/parabola

Andaikan K menyatakan luas daerah yang disapu oleh radius vektor r, dalam satu periode P, dengan demikian daerah yang disapu persatuan waktu oleh radius vektor r adalah

dt dK , yang memenuhi pernyataan; 2 2 dK 1 1 (1 ) dt 2r θ 2 GMa e •

=

−

(1-81)

(20)

Integrasikan dalam selang waktu dt dari 0 sampai t, maka diperoleh; 0 2 ) 1 ( 2 1 K

=

GMa

−

e t

+

K (1-82)

K 0 adalah konstanta integrasi yang dapat ditentukan. Dengan mengingat bahwa K= 0 bila t =

0, maka dalam satu periode t = P, luas daerah yang disapu adalah P

dt dK

dan ini sama dengan luas elips, yaitu

π

ab. Jadi dapat dinyatakan bahwa;

P e GMa ab (1 ) 2 1

₋

2

=

π (1-83)

Selanjutnya dari rasio setengah sumbu pendek dan sumbu panjang elips; (1 ) a

b 2

e

−

=

maka

tempo yang diperlukan oleh m2 untuk melengkapi satu putaran adalah;

GM a3/2

2

P

=

π (1-84)

Pernyataan ini menunjukkan bahwa bila setengah sumbu panjang membesar maka periode akan membesar, demikian pula sebaliknya jika setengah sumbu panjang elips mengecil maka tempo yang diperlukan oleh partikel untuk melengkapi orbitnya mengecil pula. Bentuk diatas dapat juga ditulis dalam bentuk lain yaitu;

GM a 2 3 2 4 P

₌

π (1-85)

Karena ruas kanan suatu konstanta maka dapat disimpulkan bahwa dalam sistem dua benda rasio ₃

2

P

a selalu tetap dan pernyataan ini tidak lain merupakan pengejawantahan hukum

Kepler ketiga yang dikenal sebagai hukum harmoni. Dalam sistim Tata Surya simbol M menyatakan jumlah massa Matahari + massa pengikutnya(misalnya; planet, asteroid,komet). Bila diambil P dalam tahun dan a dinyatakan dalam satu satuan astronomi, maka untuk planet Bumi, ruas kanan persamaan diatas bernilai satu. Untuk keperluan peraktis yang tidak memerlukan ketelitian yang tinggi, pernyataan (1-85) dapat digunakan buat menghitung jarak satelit terhadap bumi, bila periode satelit diketahui. Demikian juga untuk jarak planet dalam Tata Surya. Syarat yang harus dipenuhi adalah;

(21)

1 2 n 3 3 3 1 2 P P P tan n kons a

=

a

= .… =

a

=

(1-86)

Persamaan ini dikenal dengan jargon persamaan harmonik. Berikut diberikan beberapa contoh penerapan hukum Kepler.

a) Menentukan waktu dan kecepatan awal yang diperlukan oleh sebuah roket untuk mencapai Bulan

Sebuah roket dapat dianggap sebagai benda langit yang bergerak dari satu titik ke titik yang lain dalam ruang. Semua hukum Kepler diandaikan dipenuhi oleh gerak roket.

Untuk menyelesaikan persoalan ini kita berpegang pada kenyataan bahwa titik perige roket terletak dipermukaan Bumi. Sedangkan apoge adalah titik targetnya, yaitu Bulan. Teknologi roket, faktor gangguan bersifat gravitasional maupun non-gravitasonal tidak diperhitungkan, sehingga untuk estimasi awal mengenai tempo yang diperlukan oleh roket untuk mencapai Bulan dapat dihitung dari hukum gerak dua-benda yang telah kita ketahui

Gb.1-7 Lintasan roket dari permukaan Bumi bergerak menuju Bulan dalam bentuk lintasan setengah elips. Gerak roket dianggap taat pada kaedah hukum Kepler. Bumi bergerak mengitari Matahari. Bulan bergerak mengelilingi Bumi, sekaligus melakukan rotasi

Dari gambar 1-7 di atas jelas terlihat bahwa sumbu panjang lintasan roket, ar yang berbentuk

elips tidak lain dari setengah sumbu panjang lintasan Bulan, a b dengan lain perkataan ar = a b/2

dengan demikian Jika kita misalkan PR periode roket yaitu tempo yang diperlukan roket untuk

melengkapi satu kali putaran mengelilingi Bumi dan PB periode Bulan yaitu, tempo yang

diperlukan Bulan untuk melengkapi putarannya mengelilingi Bumi yaitu 27,32 hari. Maka dapat dinyatakan bahwa;

P P 2 2 3 2 B 3 2 R B R P P

=

→

=

(1-87)

(22)

Jadi PR = 9,65 hari. Ini merupakan tempo yang diperlukan roket tadi untuk melengkapi satu

kali lintasannya. Dengan demikian tempo yang diperlukan untuk mencapai Bulan adalah setengah PR atau 4,83 hari. Selanjutnya untuk menentukan kecepatan yang diperlukan guna

mencapai Bulan kita lakukan hal berikut;

1) Pada titik perige yang terletak dipermukaan Bumi, jarak roket dari pusat gaya sentral (pusat Bumi); ) 1 ( 1 ) e -a(1 R 2 0 a e e r _p

=

−

+

=

2) Ganti r dengan r p dari persamaan energi, diperoleh;

⎥

⎦

⎤

⎢

⎣

⎡ +

=

0 2 1 2 V R e GM

Bandingkan kecepatan roket untuk mencapai Bulan, V, terhadap kecepatan lepas partikel dari gaya tarik Bumi Ve

⎥⎦

⎤

⎢⎣

⎡ +

=

2 1 2 2 e V V e atau eV _e 2 1 V

=

+

Kita tahu bahwa kecepatan lepas partikel dari Bumi dengan massa M adalah

det / 2 , 11 2 V 0 e km R GM

=

Kecepatan ini cukup besar, Itulah sebabnya kenapa Bumi masih mempunyai atmosfer. Partikel tidak akan dapat lepas dari gravitasi Bumi, apabila kecepatan kinetiknya lebih kecil dari kecepatan lepas ini. Jadi kecepatan awal roket yang diperlukan untuk mencapai Bulan bergantung pada desain orbit yang diinginkan. Tabel 1-1 berikut meragakan kecepatan awal V

yang dibutuhkan untuk berbagai nilai eksentrisitas

Tabel 1-1 Kecepatan roket untk menuju Bulan dalam berbagai nilai eksentrisitas No e V(km/det) Ket

1. 0 7.920 Lingkaran 2. 0.1 8.306 Elips 3. 0.2 8.675 Elips 4. 0.3 9.030 Elips 5. 0.4 9.371 Elips 6. 0.5 9.699 Elips

(23)

7. 0.6 10.018 Elips

8. 0.7 10.326 Elips

9. 0.8 10.625 Elips

10. 0.9 10.916 Elips 11. 1 11.200 Parabola

Dalam bentuk yang lebih rinci grafik e versus V dan sebaliknya diragakan dalam gambar 1-8 berikut;

Gb 1-8 Profil desain orbit yang dinyatakan oleh eksentrisitas versus kecepatan dalam kilometer/detik yang dibutuhkan roket untuk mencapai Bulan

b) Menentukan periode revolusi planet

Asteroid Pallas mempunyai jarak rerata(rata-rata) dari Matahari 2,77 SA. Ingin d itentukan selang waktu yang diperlukan untuk melakukan satu kali putaran mengelilingi Matahari. Untuk menyelesaikan soal ini, mula-mula dihitung dulu periode revolusi dan jarak

Matahari dari Hukum Kepler III, yaitu;

3 2 3 1 2 1 2 2 3 2 2 2 3 1 2 1 P P a a P P a a

=

→

=

Andaikan P1 dan a1 menyatakan harga P dan a untuk sistem Bumi-Matahari, sedangkan P2

dan a2 nilai P dan a untuk sistim Pallas dan Matahari, jadi dapat kita hitung yaitu 3 2 2

=

(2,73) P atau P = 4,61 tahun 0 0.2 0.4 0.6 0.8 1 1.2 1 7 13 19 25 31 37 43 49 55 61 67 73 79 85 91 97 0 2 4 6 8 10 12 e v/s V V v/s e

(24)

c) Menghitung periode lintasan satelit

Diketahui Satelit ke III Jupiter mengitari planet induk dalam jarak 14,9 R dan tempo yang diperlukan untuk melengkapi satu kali putar adalah 7 hari 3 jam dan 7 menit. Persoalan yang ingin diselesaikan adalah ingin dicari berapa waktu yang diperlukan oleh Satelit ke-V dan Satelit ke VIII untuk melengkapi lintasannya, bila masing-masing satelit jaraknya dari planet induk adalah 2,52 R dan 3, 28 R. Dalam hal ini R menyatakan jari-jari planet.

Untuk menyelesaikan soal ini dapat kita gunakan hukum Kepler III, yaitu

3 3 2 3 3 2 2 2 3 1 2 1 P P P a a a

=

Jadi bila kita misalkan P1, a1, P2, a2 dan P3, a3, masing-masing menunjukkan periode revolusi

dan setengah sumbu panjang elips dari satelit ke-III, ke-V dan ke VIII. Kita peroleh persamaan berikut; 2 2 2 3 2 3 3 3 P P (7,13) (14, 9) = (2, 52) = (3, 28)

dari pernyataan ini kita peroleh periode satelit ke-V dan ke VIII sebagai berikut; i) Satelit ke-V periodenya 11 jam 54 menit

ii) Satelit ke VIII periodenya 736 hari

Selain itu apabila periode dan setengah sumbu panjang lintasannya yang berbentuk elip

diketahui, dari hukum harmonik dapat juga kita gunakan untuk menghitung massa planet dari pernyataan; 2 2 1 3 1 P 4 a GM π

=

Dalam hal ini, P menyatakan periode satelit dan M massa planet, a jarak satelit ke planet induknya. Jika P dan a dalam c.g.s maka G adalah 6,68 10-8

d) Menentukan perubahan massa roket yang berpindah dari orbit lingkaran ke lintasan parabola

Sifat dan bentuk lintasan sebuah roket ditentukan oleh kedudukan awal dan kecepatan roket itu sendiri. Impuls yang ditimbulkan sebagai akibat dari pelepasan sebagian massanya menyebabkan roket bergerak dengan kecepatan tertentu yang bergantung pada kecepatan dorong, dalam hal ini kita menganggap kecepatan dorong Vg selalu tetap. Selanjutnya

misalkan pula;

mo = massa awal (massa diam) roket

mf = massa akhir setelah sebagian materi dilepaskan untuk mendorong gerak roket

V = kecepatan relatif roket tersebut terhadap suatu sistem kerangka acuan yang kita pilih.

Dari hukum kekekalan momentum diketahui bahwa perubahan momentum pada saat roket bergerak adalah sama dengan perubahan momentum yang diberikan oleh massa yang terlempar. Kita hanya meninjau kasus yang ideal, gesekan dengan angkasa dan gaya ganggu lainnya diabaikan selama proses ini berlangsung, demikian pula dengan teknologi

(25)

teknologinya. Roket dianggap sebagai objek ideal yang memenuhi semua syarat sebagai benda langit

Gb 1-9 Ilustrasi perubahan momentum sebuah roket yang bergerak dengan gaya dorong

Akibat massa yang dilepaskan timbul momentum sebesar dp1 yang mendorong roket bergerak

maju ke depan dengan perubahan momentum dp2

Hukum kekekalan momentum(lihat gambar 1-9) memberikan;

1 2 0 g 0

dm dV

dp dp V m

dt dt

+ = → + = (1-88)

Bentuk ini dapat juga kita tulis dalam pernyataan

m dm V

dV

=

−

_g (1-89)

dalam hal ini Vg adalah kecepatan dorong massa yang dilepaskan oleh roket. Selanjutnya

tinjau syarat batas sebagai berikut;

i) Sebelum didorong pada saat t = 0 kecepatan roket V0 , sedangkan massa total roket

adalah m0

ii) Sesudah didorong pada saat t, kecepatan roket adalah V ′ dan massanya mf

Gunakan syarat batas ini pada pernyataan (1-89) diperoleh;

∫

=

−

f m m g t

m

dm

V

dV

0 0 (1-90)

(26)

jadi dapat kita tulis; ) ( 0 g f V V Exp m m

−

=

(1-91)

dalam hal ini besaran V = −V ′ V 0

Kita lihat bahwa perbandingan massa akhir dan massa awal mengikuti suatu bentuk persamaan eksponensial, jika Vg >> V maka mf = m0, atau massa tersisa m = mf – m0 = 0,

dengan kata lain semua massa akan digunakan untuk mendorong roket tersebut. Selanjutnya masalah berikut dapat kita selesaikan.

Ilustrasi : Sebuah roket mula-mula bergerak dalam lintasan berbentuk lingkaran dengan kecepatan 5 km/det. Kemudian lintasan roket tersebut diubah menjadi parabola dengan kecepatan dorong Vg =2,8 km/det. Berapa prosen massa awal yang harus dipergunakan untuk

membuat lintasan parabola ?

Penyelesaian Kecepatan lingkaran h R GM V _c

+

=

Kecepatan parabola (kecepatan lepas)

h R GM V _e

+

=

2

Dalam hal ini M = M0+m, karena massa roket jauh lebih kecil dari massa Bumi, maka M = M0

sedangkan R dan h, masing-masing menyatakan radius Bumi dan tinggi objek dari permukaan Bumi, kedua pernyataan diatas jika digabung menjadi V _e

=

2V _c substitusi harga

G dan M serta radius Bumi R maka Vc dapat dihitung. Karena diberikan Vc = 5 km/det, soal

diatas dengan mudah dapat kita selesaikan, sebab telah diketahui;

0 e c ( 2 1) c

V V V V V = − = − = ′ − V =2,07 km/det

dari pernyataan (1-91) dapat dilihat bahwa rasio massa akhir dan massa awal roket tersebut adalah; 8 , 2 / 07 , 2 0 −

=

e m m_f

(27)

jadi massa yang habis terlempar adalah; m = m0 - mf = 0,524 m0 atau kira-kira 52,4% dari

massa awal

Dalam Tabel 1-2 diperlihatkan perbandingan massa mf /m0 untuk berbagai kecepatan dorong,

pada saat roket mengubah lintasan dari lingkaran ke bentuk parabola, sebagai fungsi ketinggian h. Tabel ini meragakan bahwa roket yang diluncurkan pada posisi ketinggian h<0,1 R dari permukaan Bumi akan kehilangan semua massanya walaupun kecepatan lontarnya kita perbesar. Makin tinggi roket dari permukaan Bumi massa yang harus dibuang semakin kecil. Untuk h= 2R dan Vg = 4 km/det massa yang harus dilemparkan oleh roket untuk membentuk

lintasan parabola paling sedikit adalah 40% dari massa awal

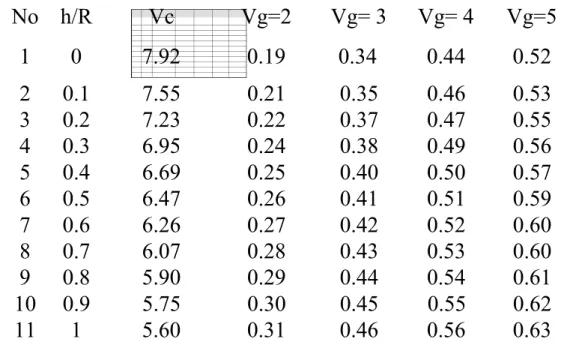
Tabel 1-2 Rasio mf /m0 untuk berbagai kecepatan dorong Vg dalam km/det,

sebagai fungsi dari h/R. Kolom tiga menunjukkan kecepatan lingkaran. Vc dalam km/det

No h/R Vc Vg=2 Vg= 3 Vg= 4 Vg=5 1 0 7.92 0.19 0.34 0.44 0.52 2 0.1 7.55 0.21 0.35 0.46 0.53 3 0.2 7.23 0.22 0.37 0.47 0.55 4 0.3 6.95 0.24 0.38 0.49 0.56 5 0.4 6.69 0.25 0.40 0.50 0.57 6 0.5 6.47 0.26 0.41 0.51 0.59 7 0.6 6.26 0.27 0.42 0.52 0.60 8 0.7 6.07 0.28 0.43 0.53 0.60 9 0.8 5.90 0.29 0.44 0.54 0.61 10 0.9 5.75 0.30 0.45 0.55 0.62 11 1 5.60 0.31 0.46 0.56 0.63

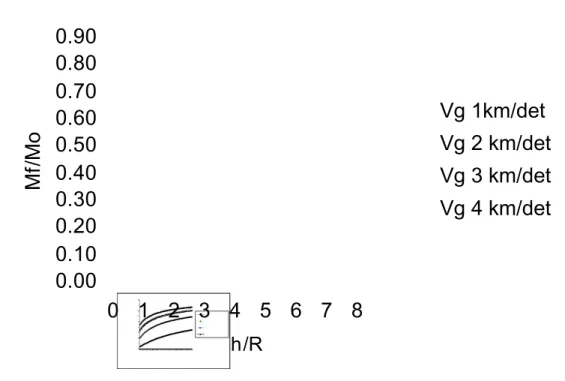
Relasi antara rasio massa final dan massa awal versus rasio ketinggian satelit terhadap radius bumi untuk berbagai Vgdiperlihatkan pada gambar 1-10 berikut

Pernyataan ( ) 0 g f V V Exp m m

−

=

memberikan beberapa kesimpulan antara lain;

a) Jika

g V

V

→ ∞

maka mf << m0 artinya massa yang dibuang m = mf - m0

∼

m0, tidak

diperlukan melemparkan massa untuk mendorong roket b) Jika 0

g V

V

→

maka mf

∼

m0 artinya massa yang dibuang m = mf - m0

∼

0, semua massa

(28)

.

Gb 1-10 Jumlah massa yang hilang sebagai fungsi ketinggian satelit dari permukaan Bumi untuk berbagai kecepatan dorong

Grafik diatas meragakan bahwa pada nilai Vg yang membesar maka rasio antara massa

final dan massa awal semakin kecil dan grafik berkecendrungan berimpit. Artinya pada kecepatan dorong yang sangat besar pembahasan rasio massa awal terhadap massa final tidak lagi signifikan. Pada jarak h

≥

8R, gradient cendrung mendekati nol, dengan perkataan lain titik stasioner dicapai pada nilai h

∼

8R

0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 0 1 2 3 4 5 6 7 8 h /R M f / M o Vg 1km/det Vg 2 km/det Vg 3 km/det Vg 4 km/det

(29)

1. Aplikasi Hukum Harmonik untuk menentukan massa planet

Mars mempunyai dua buah satelit Phobos dan Deimos. Jika diketahui Deimos bergerak mengelilingi Mars dengan jarak a=23490 km dan periode revolusinya P=30jam 18 menit. Berapakah massa planet Mars bila dinyatakan dalam satuan massa Matahari ?. Jika Periode revolusi Phobos 7jam39menit, berapakah jaraknya dari Mars?

Penyelesaian

Gunakan hukum harmonik;

3 1 2 2 2 ( ) 4 G m m a P π

+

=

Nyatakan dulu besaran dalam Satuan Astronomi untuk jarak, tahun untuk waktu dan Massa Matahari untuk massa planet/satelit , agar G/4

π

2 = 1

No Satelit P a(km) a(SA) P(Tahun)

1 Deimos 30h18m=1d2625 23490 0.000157 0,00351

2 Phobos 7h39m=0d31875 ? ? 0,0008848

Massa satelit (m2) dapat diabaikan terhadap massa planet m1

Dari Deimos; 3 2 mars a m P

=

→

Mmars = 3.148 10 -7 massa matahari

Selanjutnya nyatakan periode dan setengah sumbu panjang Deimos sebagai P1 dan a1

sedangkan untuk Phobos adalah P2 dan a2 maka kita peroleh;

(

)

(

)

(

)

3 3 3 3 1 2 2 2 2 2 2 1 2 0.000157 0.00351 0.0008848 a a a P

=

P

→

=

→

a2 = 6.265610 -5

(30)

2. Gerak satelit melewati meridian pengamat

Pada jam 20:00 WIB, ketika Ahmad sedang berada di Observatorium Bosscha Lembang ia melihat sebuah satelit melewati meridian dengan latar belakang Centaurus. Jika satelit itu mempunya periode 10 jam. Pukul berapa satelit itu akan melewati kembali meridian Ahmad apakah masih dengan latar belakang Centaurus ?, dapatkah Ahmad melihatnya ?

Penyelesaian

Soal ini dapat diselesaikan dengan mengambil analogi. Satelit sebagai planet luar dan Bumi adalah planet dalamnya. Pusat Bumi sebagai Matahari. Hubungan periode sinodis dan sideris planet luar adalah;

1 1 1

Sin Sid P

=

P _⊕

−

P

Dalam hal satelit bumi berevolusi lebih cepat dari rotasi Bumi, hubungan diatas menjadi;

1 1 1

Sin Sid

P

=

P

−

P_⊕ dalam soal ini periode revolusi/sideris satelit = 10 jam

Sedangkan periode revolusi Ahmad = 24 jam Jadi, dapat dihitung

1 1 1 Sin Sid P

=

P

−

P_⊕ jadi sin 1 1 1 7 17 .14 10 24 120 h Sin P P

= − = → =

24 jam Satelit

(31)

Dengan perkataan lain. Satelit akan melewati meridian yang sama pada jam (20h+17h.14)-24h=13h.14, atau jam 13:08:24 bukan dengan latar belakang Centaurus, karena siang hari jadi sulit untuk diamati dengan mata bugil.

3. Gerak Sputnik

Berapakah tinggi h, dari sebuah satelit geostasioner. Hitunglah periode yang dibutuhkn Sputnik I(diluncurkan tahun 1957) dengan ketinggian orbit h=200 kilometer dari permukaan Bumi, agar ia menjadi satelit geostasioner

Penyelesaian

Satelit geostasioner adalah satelit yang selalu berada pada satu titik yang tetap di langit terhadap titik yang ada di Bumi;

Rotasi Bumi, P= 24 jam = 1440 menit

Kec lingkaran titik massa m yang terletak di Bumi

R GM

V_c

=

= 7,9 km/det periode Satelit dekat Bumi;

84 9 , 7 40000 V R 2 P c s

=

π

=

menit

Dari Hukum Kepler III

→

₃ 2 3 1 2 2 2 1 3 2 2 2 3 1 2 1 a a P P a P a P

=

→

=

jadi dapat ditulis kembali

Bumi 3 / 2 R R 84 1440

=

⎥⎦

⎤

⎢⎣

⎡

_→

R=6,7 R Bumi

Jadi jarak satelit stasioner dari pusat Bumi adalah 6,7 radius Bumi atau h = 5,7 R Bumi

Untuk kasus Sputnik, diketahui ketinggiannya dari permukaan Bumi h= 200 kilometer, jadi jaraknya dari pusat Bumi R=R bumi+200

Jadi agar Sputnik menjadi satelit geostasioner haruslah;

S Sputnik 2 / 3 Bumi P P R R

=

⎥

⎦

⎤

⎢

⎣

⎡

→

84 P 6370 200 6370 Sputnik 2 / 3

=

⎥⎦

⎤

⎢⎣

⎡

+

→

PSputnik = 88 menit = 1h 28m

(32)

Sputnik akan selalu berada diatas sebuah titik di permukaan Bumi bila periodenya 1 jam 28 menit

4

. Satelit yang berubah lintasan

Sebuah satelit bergerak dengan orbit lingkaran, dengan jejari R 1 mengitari Bumi.

Sesaat kemudian sebuah roket kecil pada satelit dihidupkan untuk mengubah arahnya sehingga menjadi elips. Perubahan ini mengakibatkan satelit kehilangan setengah momentum sudutnya tetapi energi total tetap konstan. Berapakah jarak titik terdekat (perige)dan titik terjauh (apoge) satelit ini dari pusat Bumi, bila dinyatakan sebagai fungsi dari R 1 ?

Penyelesaian

Mula-mula orbit berbentuk lingkaran dan momentum sudutnya;

1 1 1 C C R GM mR R mV L

=

Kemudian orbit menjadi elips kecepatan lingkaran VC menjadi kecepatan elips, V

mVR

L

=

→

L

_C

2

1 =

→

1 1 1 1

2

2 R

GM

R

V

R

V

R

V

m

mVR

=

_C

→

=

_C

=

(1)

Hukum kekekalan energi ketika orbit satelit berujud lingkaran dan berjarak R 1dari pusat gaya

sentral di titik O dan pada suatu titik sembarang S, ketika orbitnya berubah menjadi elips dan berjarak R dari pusat gaya sentral, menyatakan;

(33)

R GMm mV 2 1 R GMm mV 2 1 2 1 2

C

−

=

−

atau dapat juga ditulis sebagai;

2 C 2 C 2 C 1 2 C 2 V R GM 2 V 2 V R GM 2 R GM 2 V R GM 2 V

=

+

−

=

+

−

=

−

(2) Gabungkan (1) pada (2) 2 2 2 1

2

C

R

V

C

GM

V

R

−

=

⎟

⎠

⎞

⎜

⎝

⎛

(3)

Jabarkan kembali(3) dan nyatakan GM sebagai fungsi kecepatan lingkaran VC

0

2

1

2

1

2

1 2 1 1 2 2 1 2

=

⎥

⎦

⎤

⎢

⎣

⎡

−

+

⎟

⎠

⎞

⎜

⎝

⎛

→

=

⎥

⎦

⎤

⎢

⎣

⎡

+

⎟

⎠

⎞

⎜

⎝

⎛

R

V

R

V

C C (4)

Cari R dari persamaan diatas, setelah dimodifikasi kita peroleh;

0

8

4

0

4

8

4

2 1 1 2 2 1 2 2 1

+

−

=

→

_R

−

_RR

+

_R

=

R

RR

R

(5)

Dari rumus “abc” kita peroleh nilai R

1 2 1 2 1 1 12

3

2

1

8

16

64

8 R

R

⎟

⎠

⎞

⎜

⎝

⎛ ±

=

−

±

=

(6)

Jarak maksimum adalah titik Apoge R A dan jarak minimum adalah, perige R P dari satelit;

1 1

3

2

1

3

2

1

1 R

R

P A

⎟

⎠

⎞

⎜

⎝

⎛ −

=

⎟

⎠

⎞

⎜

⎝

⎛ +

=

(7)

Selain itu bisa dihitung setengah sumbu panjang elips, a dan eksentrisitas e,

1

2a a R

R

R_A

+

_P

=

→

=

(34)

5. Problem tentang elongasi maksimum dan minimum

Jika, a menyatakan setengah sumbu panjang dan e, menyatakan eksentrisitas telah diketahui bahwa Bumi mempunyai, a=1 SA dan e =0,017. Sedangkan Merkurius mempunyai a = 0,39 SA dan e = 0,206. Pertanyaannya hitunglah elongasi maksimum dan elongasi minimum planet Merkurius?

Penyelesaian

Dari hubungan goniometri pada gambar diatas kita ketahui;

SB

SP

Sin

=

1

ϕ

menjadi maksimum bila

SB minimum(Bumi di Perihelium) dan SP1 maksimum (Merkurius di Aphelium)

ϕ

menjadi minimum bila

SB maksimum(Bumi di Aphelium) dan SP1 minimum (Merkurius di Perihelium) Dari hukum Kepler kita ketahui bahwa nilai ekstrim jarak sebuah planet adalah;

(

e

)

a

R

_A

=

1 +

(

e

)

a

R

_P

=

1 −

Jadi untuk

ϕ

maksimum maka;

(

)

(

)

1

0

017

0 47847059

206

0

1

39

0

1

1 ,

)

,

(

)

,

(

,

₌

−

+

=

−

+

=

B B M M

e

a

e

a

Sin

ϕ

→ϕ

=280,6

Jadi untuk

ϕ

minimum maka;

(

)

(

)

1

0

017

0 30448377

206

0

1

39

0

1

1 ,

)

,

(

)

,

(

,

=

+

−

=

+

−

=

B B M M

e

a

e

a

Sin

ϕ

→ϕ

=170,7

(35)

6. Problem tentang keubahan orbit akibat tekanan radiasi Matahari

Diketahui sebuah wahana bergerak mengitari Matahari. Pada saat berada di perihelium wahana menerima energi matahari persatuan luas persatuan waktu sebesar F1 sedangkan ketika di aphelium 0,25 F1. Akibat tekanan radiasi yang berubah-ubah setengah sumbu panjangnya a= 2 SA, mengalami pengurangan sebesar 0.001 SA/priode.

Berapakah a) eksentrisitas

b) perubahan periodenya setiap kali mengitari Matahari

Penyelesaian a) Di perihelium 2 4 4 p p p p L L F r r F π π

=

→ =

Di Aphelium

(

)

2 4 4 4 0.25 a a a a p p L L L L F r r F F F π π π π

=

→

=

Kita ketahui; 4 (1 ) (1 ) (1 ) (1 ) 2 (1 ) (1 ) (1 ) (1 ) p a p p F r a e e e e r a e e F e e

+

=

→

=

→

=

−

Atau 2(1-e)=(1+e) jadi e= 1/3

b) 32 3 12

2

P a

= → Δ =

P a a

Δ

Dengan memasukkan a = 2 dan

Δ

a=0.001 maka kita peroleh 0.002

P

→ Δ =

tahun/periode

7. Problem tentang kecepatan dan periode orbit elips

Sebuah satelit bergerak dalam orbit eliptik dengan setengah sumbu panjang a. satelit dapat dianggap sebagai partikel yang bergerak dalam pengaruh gaya gravitasi Bumi. Jika kecepatannya di perigee adalah VPdan di Apogee , VA. Buktikan periode orbitnya adalah

(36)

2 P A P A a 1 e (V V ) P V V

π

−

+

=

Penyelesaian

Momentum sudut adalah konstant, jadi berlaku

(

)

P A xmV

=

2a

−

x mV A P P P A 2aV xV V V V

⎡

⎤

= ⎢

₊

⎥

⎣

⎦

Konstanta luas 2 P 1 1 d 1 d 1 h x x x xV 2 2 dt 2 dt 2

θ

⎛

θ

⎞

=

_⎜

_⎟

=

⎝

⎠

Luas elips = periode x konstanta luas;

(

A P

)

2

(

A P

)

P A P A P ab V V a 1 e V V 1 ab P xV P 2 aV V V V

π

+

π

−

+

⎛

⎞

π

=

_⎜

_⎟

→

=

⎝

⎠

8. Problem gerak dibawah pengaruh gaya sentral yang berbanding terbalik

dengan jarak pangkat-4

(37)

Sebuah partikel dilempar dengan kecepatan ₁ 3 2 V 3a

μ

=

dengan sudut tertentu terhadap

radius vektor dari pusat gaya sentral

4

f r

μ

=

persatuan massa. Pertanyaannya; a) tentukan energi potensialnya EP ?

b) tunjukkan persaman lintasannya berbentuk r a

(

1 Sin

)

2

=

+

θ

c) buktikan periodenya; 5 3 3a P 8 2

π

=

μ

Penyelesaian

a) Energi potensial dan gaya ;

0 4 3 dV f V fdr dr V dr _r _3r

μ

= → =

∫ ∫

=

− +

Syarat batas, jika r

→ ∞

maka V0 = 0

Jadi energi potensialnya adalah _P

3

E

3r

μ

= −

(38)

2 1 ₃ 1 V C 2 _3r

μ

−

=

Untuk r = a maka 3 3 1 2 C C 0 2 3a 3a

⎛

μ

⎞

μ

− = → =

⎜

⎟

⎝

⎠

Jadi energi total pada jarak r sembarang adalah;

2 2 3 3 1 2 V 0 V 2 _3r _3r

μ

− = → =

(1) tetapi ; 2 2 2 2 2 2 2 2 dr d dr d 2 d d dr 2 V r r r dt dt d dt dt dt d

⎡

⎤

θ

⎛ ⎞ ⎛ ⎞ ⎛

⎞

⎛ ⎞ ⎛ ⎞ ⎛ ⎞

_⎢

_⎥

=

_{⎜ ⎟ ⎜ ⎟ ⎜}

+

=

_⎟

+

_{⎜ ⎟ ⎜ ⎟ ⎜ ⎟}

=

+

θ

⎝ ⎠ ⎝ ⎠ ⎝

⎠

⎝ ⎠ ⎝ ⎠ ⎝ ⎠

⎢

_⎣

⎥

_⎦

(2)

Momentum sudut persatuan massa = konstanta luas h ,

dengan h r 2 d dt

θ

⎛ ⎞

=

_{⎜ ⎟}

⎝ ⎠

(3)

jadi gabungkan (3), (2) ke pernyataan (1), kita peroleh

2 ₄ 2 3 2 2 dr 2 r 2 r r d _{3r h} _3h

⎡

_{⎛ ⎞}

⎤

_μ

⎢

_{⎜ ⎟}

+

⎥

=

θ

⎝ ⎠

⎢

⎥

⎣

⎦

(4)

Tetapi momentum sudut pada jarak, r = a adalah,

1 ₃ 2 2 h aV a 3a 3a

μ

=

, substitusi besaran ini kedalam persamaan (4), diperoleh;

2 2 2 2 dr dr dr ar ar d d _{ar r} _{ar r}

⎛ ⎞ = − → θ =

→ θ =

⎜ ⎟

_θ

⎝ ⎠

₋

∫

₋

sehingga 2ArcSin 2r a ₀ a a

−

⎛

⎞

θ

=

_⎜

_⎟

+ θ

⎝

⎠

Syarat batas bila

θ = → =

0 r a jadi

θ

0 = 0

Persamaan gerak partikel adalah;

(

)

2r a a Sin r 1 Sin a 2

−

θ

=

→ = + θ

(39)

c) Luas daerah yang disapu persatuan waktu;

(

)

2 2 dA 1 d 1 a r dA 1 Sin d dt 2 dt 2 2

θ

⎡

⎤

=

→ =

_⎢

+ θ θ

_⎥

⎣

⎦

jadi ½ luas daerah yang ditempuh adalah

2 2 2 0 a 3 a A 1 2Sin Sin d 8 16 π

π

⎡

⎤

=

∫

_⎣

+ θ + θ θ

_⎦

=

Jadi periode partikel tersebut adalah;

2 5 2A 3 a 3a 3 3a P 2 h 16 2 8 2

⎛

_π

⎞

_π

=

⎜

_⎜

⎟

_⎟

=

μ

⎝

⎠

9. Problem gerak satelit yang diganggu oleh tekanan radiasi matahari dan

gaya gravitasi asteroid

Sebuah satelit mengelilingi Matahari, berbentuk bola dan dianggap sebagai benda hitam sempurna(black body). Satelit ini secara berkesinambungan memberikan informasi tentang suhu permukaannya(temperatur efektif) ke stasiun pengontrol di Bumi. Suhu tertinggi yang tercatat di permukaannya 5000 K, sedangkan temperatur minimumnya 4500K. Pertanyaannya;

a) Tentukanlah eksentrisitas e, dan setengah sumbu panjang orbitnya, a dan periode P

b) Andaikan ketika di aphelium tiba-tiba ada asteroid lewat sehingga impulse yang diterimanya menyebabkan ia terlepas dari gaya tarik gravitasi Matahari, berapakah kecepatannya ?

Penyelesaian

a) Benda hitam mempunyai sifat;

Energi yang diterima, Ein = Energi yang dipancarkan kembali, Eout Ein = Luas penampang bola kali fluks matahari(solar constant) Eout = Luas permukaan bola kali

σ

T4

Misal;

L0=luminositas matahari, r- jarak matahari ke satelit,

(40)

2 0 2 4 in L E R r

⎡

⎤

= π

_⎢

_⎥

π

⎣

⎦

(1) 2 4 4 out E

= π σ

R T (2)

Dari syarat benda hitam maka persamaan (1) = pernyataan (2), diperoleh

1/ 2 0 4 4 L r T

⎡

⎤

= ⎢

⎥

πσ

⎣

⎦

(3)

Dari pernyataan ini jelas terlihat bahwa temperatur minimum akan dicapat apabila r maksimum (pada titik aphelium), sedangkan pada titik perihelium temperatur akan menjadi maksimum

Misal;

rp – jarak perihelium, Tp – temperatur efektif di perihelium ra - jarak aphelium, Ta – temperatur efektif di aphelium

Jadi

(

)

(

)

2 4 2 4 2 1 9 0,81 1 10 p _a _a a _p _p r T T a e r _T _T a e

−

_{⎡ ⎤}

=

→

=

_{⎢ ⎥}

=

+

⎣ ⎦

(4) atau e=0,105

sumbu panjang elips= ra+rp

2a = ra + 0,81 ra = 1,81ra atau a = 0,905 ra (5)

Hitung jarak aphelium ra dari (3) dengan data yang diberikan pada daftar konstanta maka kita peroleh; 1/ 2 1/ 2 ₂₆ 11 0 4 8 4 3,86 10 1,14969 10 4 4 3,14 5, 67 10 450 L r T −

⎡

⎤

⎡

⎤

×

=

_⎢

_⎥

=

⎢

⎥

=

×

πσ

× × × ×

⎣

⎦

⎢

_⎣

⎥

_⎦

meter

atau dalam SA, jarak apheliumnya adalah ra = 0,766 SA Dengan demikian setengah sumbu panjang satelit,

(41)

jadi periodenya adalah; P= a3/2 = 0.58 tahun

Substitusi data dari daftar konstanta; Kecepatan lepas; 11 30 11 2 2 6, 67 10 1,99 10 1,14969 10 esc a GM V r −

× ×

=

×

atau Vesc= 48052,28852 m/s = 48.05 km/s

10. Problem tentang lepasnya galaksi

Suatu gugus galaksi mengisi suatu bola dengan jejari R dan rapat massa rata-rata

ρ

. Semua galaksi dianggap mempunyai rapat massa seragam. Ada sebuah galaksi bermassa M yang terletak dipermukaan bola. Pertanyaannya;

a. Tuliskan persamaan energi galaksi tersebut

b. Dalam model big-bang tentang asal muasal alam semesta, kecepatan galaksi mengarah radial dan menjauhi pusat bola. Kecepatannya adalah V=HR dimana H=(15km/s)/(106 ly) adalah konstanta Huble. Berapakah

ρ

agar galaksi yang ada pada kulit bola tersebut bisa lepas ?

Penyelesaian

Soal ini bisa dianggap sebagai two-body problem dua massa M dan m. Persamaan energi system adalah 2 2 mV R GMm E E E _t

=

_k

+

_p

=

−

+

Galaksi bisa lepas dari gugusnya bila

R GM V mV R GMm E _t 0 2 2 0 2 2

=

→

=

+

−

→

=

atau G H R M R G R GM R H π ρ ρ π 8 3 3 4 2 2 2 3 2 2

⎥⎦

_→

₌

⎤

⎢⎣

⎡

=

Gunakan satuan cgs G=6,6710-8 H=15km/s/106 tahun cahaya=1,58410-18/s

(42)

Jadi

ρ

= 4,5 10 gram/cm

11. Gosip tentang terlihatnya Mars sebesar Bulan

Beberapa waktu yang lalu media gosip memberitakan planet Mars akan terlihat sebesar Bulan. Pertanyaannya berapakah diameter sudut maksimum planet Mars yang bisa kita amati?. Sebagai acuan ambil setengah sumbu panjang dan eksenrtisitas Bumi dan Mars masing-masing (a=1 SA, e = 0,017) dan (a=1,5 SA, e = 0,093) sedangkan jejari Mars, adalah R= 3393,4 kilometer

Penyelesaian

Posisi terdekat Mars adalah pada saat oposisi. Misalkan d, menyatakan jarak terdekat Mars ke Bumi pada saat oposisi (Mars di perihelium dan Bumi di aphelium);

) e 1 ( a ) e 1 ( a d

=

_M

−

_B

+

=1,5(1-0,093)- (1+0,017)=0,3435 SA = 51,525 106 km Diameter linier Mars = 6786,8 km

Jadi diameter sudut Mars

α

= 0 ,0075 27",1689 2 360 52510 , 51 8 , 6786 o 6

π

=

Bandingkan dengan diameter sudut Bulan

α

=30’=1800” jadi rasionya cuma 0,15 diameter sudut Bulan. Tidak benar Mars terlihat sebesar Bu lan

Soal Latihan

1) Sebuah satelit bergerak dalam

orbit berbentuk lingkaran mengelilingi Bumi. Tentukan jarak satelit tersebut dari pusat bola Bumi jika periodenya;

a) 1.5 kali periode Bulan b) 2 kali periode Bulan

c) 0.05 kali periode Bulan

Jaw: a) 2,42 108 meter, b) 6,09 108 meter, c) 5,2 107 meter

2) Sebuah satelit dengan massa 1000 kg berada pada ketinggian 400 km dari permukaan Bumi. satelit bergerak dalam orbit lingkaran. Berapakah

a) Kecepatan orbitnya b) Energi kinetiknya

c) Momentum sudutnya

Jaw: a) 7,68 m/s tangent terhadap orbit; b) 2,95 1010 J ; c) 5,2 1013 kg m2/s tegak lurus terhadap orbit

3) Ada satelit yang bergerak dengan periode 90 menit dan tingginya tetap sebesar 280 km dari permukaan Bumi. Agar satelit ini menjadi geosinkron/geostasioner berapakah seharusnya