Diktat Teknik Pengaturan

TEKNIK PENGATURAN

Oleh:

Mohammad Dhandhang Purwadi

UNTUK KALANGAN SENDIRI

JURUSAN TEKNIK MESIN, FAKULTAS TEKNIK UNIVERSITAS NASIONAL

Kata Pengantar

Puji syukur kehadhlirat Allah SWT, karena dengan berkah, rahmat dan hidayah-Nya diktat ini dapat diselesaikan.

Tujuan utama dari penulisan diktat ini adalah untuk membantu mahasiswa dalam memahami isi perkuliahan Teknik Pengaturan. Dengan adanya diktat ini diharapkan mahasiswa dapat mengefisiensikan proses dan waktu pema-haman terhadap materi yang disampaikan oleh dosen yang bersangkutan di depan kelas tanpa kehilangan waktu untuk mencatat.

Dalam diktat ini dibahas masalah teknik pengaturan yang mendasar, se-hingga pembaca akan dapat mengikuti isi buku ini dengan mudah. Persoalan teknik pengaturan yang lebih kompleks dan canggih, pembahasannya dapat diperoleh dari buku teks yang lengkap dan tersedia diperpustakaan universi-tas.

14 Juli 2002 Penulis

Daftar Isi

1 Pendahuluan 7

2 Transformasi Laplace dan Kebalikannya 10

2.1 Variabel dan Fungsi Kompleks . . . 11

2.2 Transformasi Laplace (Laplace Transform) . . . 11

2.3 Transformasi Laplace Balik (Invers Laplace Transform) . . . . 12

2.4 Metode Ekspansi Fraksional . . . 13

2.4.1 Kutup (pole) dan Zero . . . 14

2.4.2 Ekspansi Fraksional Dengan Kutup Berbeda . . . 15

2.4.3 Ekspansi Fraksional Dengan Kutup Kembar . . . 17

2.5 Contoh Penggunaan Transformasi Laplace . . . 19

3 Fungsi Alih 22 4 Diagram Blok 27 4.1 Diagram Blok Sistem Untai Tertutup. . . 27

4.2 Prosedur Menggambar Diagram Blok. . . 29

4.3 Penyederhanaan Diagram Blok . . . 31

5 Analisis Respons Transien 36 5.1 Sistem Orde 1. . . 37

5.1.1 Respons sistem orde 1 terhadap fungsi undak satuan . . 37

5.1.2 Respons sistem orde 1 terhadap fungsi ramp satuan . . 38

5.1.3 Respons sistem orde 1 terhadap fungsi impuls satuan . 40 5.2 Sistem Orde 2. . . 40

5.2.2 Respons sistem orde dua terhadap fungsi impuls satuan 46 5.2.3 Respons sistem orde dua terhadap fungsi ramp satuan . 47 5.2.4 Spesifikasi respons transien . . . 48 5.2.5 Spesifikasi respons transien dalam sistem orde dua . . . 50 5.3 Stabilitas, Kriteria Stabilitas Routh . . . 53 5.3.1 Analisis stabilitas dalam bidang kompleks . . . 54 5.3.2 Kriteria stabilitas Routh. . . 54

6 Analisis Tempat Kedudukan Akar 61

6.1 Tempat kedudukan akar . . . 63 6.2 Cara menggambar tempat kedudukan akar. . . 66

Daftar Gambar

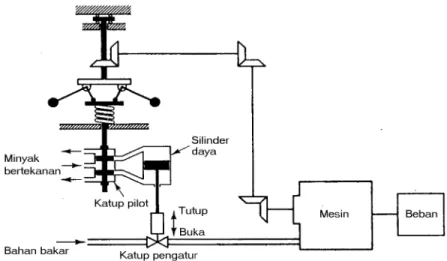
1 Sistem pengatur kecepatan gubernur . . . 8

2 Sistem pengendali kedudukan satelit . . . 23

3 Struktur sistem suspensi kendaraan bermotor . . . 25

4 Contoh diagram blok . . . 28

5 Contoh diagram blok untai tertutup . . . 29

6 Sistem peredam getaran roda sepeda motor . . . 31

7 Pembuatan diagram blok . . . 32

8 Aturan penyederhanaan diagram blok . . . 33

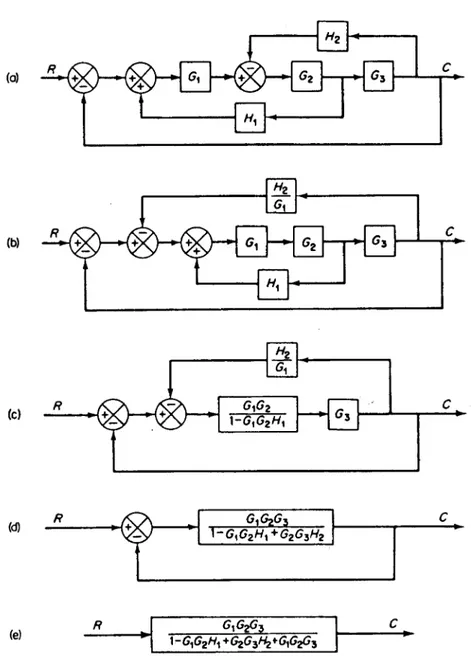
9 Contoh penyederhanaan diagram blok . . . 34

10 Contoh diagram blok sistem orde 1 . . . 37

11 Grafik respons transien sistem orde 1 terhadap masukan undak satuan . . . 39

12 Bentukfisik dan diagram blok sistem servomekanika . . . 40

13 Grafik respons transien sistem orde 2 terhadap masukan undak satuan . . . 44

14 Spesifikasi respons transien terhadap fungsi undak satuan . . . 49

15 Spesifikasi respons transien terhadap fungsi undak satuan sis-tem orde 2. . . 51

16 Metode perhitunganβ . . . 52

17 Daerah stabil dan tak stabil pada koordinat kompleks . . . 55

18 Diagram blok suatu sistem untai tertutup . . . 61

19 Tempat kedudukanzerodan kutup dari persamaan (85) . . . . 65

20 Langkah ke-1 dan ke-2 menggambar tempat kedudukan akar. . 68

22 Langkah 1—5 menggambar tempat kedudukan akar . . . 75 23 Gambar lengkap tempat kedudukan akar . . . 77

Daftar Tabel

1

Pendahuluan

Pengaturan suatu sistem mempunyai peranan penting dalam banyak bi-dang, diantaranya bidang rekayasa, sosial, ekonomi bahkan pemerintahan yang menyangkut berbagai aspek yang berkaitan secara canggih. Dalam bidang rekayasa (engineering), sistem pengaturan otomatis mempunyai peran yang sangat penting, misalnya dalam sistem pengendalian pesawat di luar angkasa, sistem pembidik misil taktis, sistem pilot pesawat terbang otomatis, sistem robotika. Contoh lain dapat pula berupa pengendalian tekanan, suhu dan kelembaban dalam bidang rekayasa proses.

Karena pengetahuan tentang proses dan teknik pengaturan dapat memper-baiki dan megoptimalkan kinerja dari suatu sistem, maka teknik pengaturan harus difahami secara baik oleh seorang ahli yang menggeluti bidang ilmu dan teknologi.

Sebelum mempelajari suatu ilmu, alangkah baiknya jika sebelumnya kita mengetahui sejarahnya, agar kita dapat lebih memahami duduk persoalannya mengapa ilmu tersebut dapat muncul kepermukaan dan dipakai oleh banyak orang. Secara historis, orang pertama yang menerapkan sistem pengaturan otomatis ialah James Watt. Pada abad delapan belas. Ilmuwan ini menerap-kan sistem pengaturan gubernur sentrifugal pada mesin uapnya untuk men-gatur kecepatan putaran mesin secara otomatis. Pada tahap berikutnya Mi-norsky, Hazen dan Nyquist mengembangkan teori tentang teknik pengaturan otomatis. Di tahun 1922 Minorsky yang bekerja dalam bidang pengendalian pesawat berhasil menunjukkan bahwa stabilitas sistem dapat ditentukan dari persamaan diferensial yang mewakili sistem tersebut. Nyquist pada tahun 1932 berhasil mengembangkan metode yang lebih sederhana dalam menen-tukan stabilitas suatu sistem untai tertutup berdasarkan pada respons untai

terbuka terhadap masukan berbentuk sinus (sinusoidal) yang tunak. Pada tahun 1934, Hazen Memperkenalkan istilah servomekanika untuk sistem pe-ngaturan posisi dan membahas tentang perancangan rilai servomekanika yang mampu menutup dan membuka sesuai dengan perubahan masukan.

Gambar 1: Sistem pengatur kecepatan gubernur

Hingga tahun 1940, metode respons-frekuensi dipakai oleh para ilmuwan untuk mendapatkan kinerja yang memuaskan dari disain sistem pengaturan untai tertutup linear. Pada awal tahun 1950-an, Evan berhasil mengem-bangkan metode tempat kedudukan akar (root locus). Baik metode respons-frekuensi maupun tempat kedudukan akar, keduanya adalah merupakan me-tode yang menjadi tulang punggung dari teori teknik pengaturan otomatis klasik. Pada tahun 1950, masalah pengaturan bergeser dari perancangan komponen sistem satu persatu menjadi perancangan keseluruhan sistem yang optimal. Perkembangan teknik pengaturan menuntut penyelesaian dari suatu sistem yang terdiri dari banyak masukan (input) dan luaran (output) dengan

keterkaitan yang sangat canggih.

Dengan tersediannya mesin penghitung (komputer) pada tahun 60-an jadikan teknik pengaturan otomatis modern semakin mampu untuk men-gatasi masalah yang canggih. Dengan tersedianya komputer digital yang se-makin murah, teknik pengaturan berkembang hingga melingkupi teknik pe-ngaturan dari sistem pepe-ngaturan yang kompleks baik yang bersifat determinis-tik maupun stokhasideterminis-tik, dan mempunyai kemampuan belajar serta beradaptasi secara mandiri. Bahkan dengan ketersediaan perangkat yang baik sekarang ini, teori pengaturan dapat bergerak dengan meniru sistem non-teknis, misalnya biologis, biomedis, ekonomi dan sosioekonomi.

Pada akhirnya penulis berharap agar diktat ini dapat dipergunakan seba-gai pegangan dasar dalam mempelajari teknik pengaturan. Dalam diktat ini hanya akan dibahas mengenai teori dari teknik pengaturan yang klasik yaitu meliputi teori respons-frekuensi dan tempat kedudukan akar. Diktat ini hanya memuat hal yang dasar dan dapat dipakai dengan mudah oleh mahasiswa S-1 yang telah mempelajari dasar matematika persamaan diferensial, transformasi Laplace, operasi matrik dasar.

2

Transformasi Laplace dan Kebalikannya

Dalam teknik pengaturan otomatis transformasi Laplace (Laplace trans-form) merupakan suatu metode operasional yang utama. Dengan transformasi Laplace kita dapat menyelesaikan persamaan diferensial linear dengan mudah tanpa melalui metode penyelesaian persamaan diferensial yang kadang-kadang menimbulkan pesoalan aljabar yang rumit, misalnya metode variasi parame-ter, faktor integrasi dan lain sebagainya.

Transformasi Laplace dapat mentransformasi fungsi umum (misalnya fungsi trigonometri, fungsi eksponensial dll.), operator diferensial, operator integral ke dalam bentuk persamaan aljabar biasa dalam variabel komplekss. Dengan demikian persamaan diferensial dapat ditransformasikan dengan transformasi Laplace menjadi persamaan aljabar biasa dalam variabel kompleks. Bila vari-abel tak bebas pada persamaan ini diselesaikan (dengan cara mengelompokkan variabel bebas di ruas kanan dan variabel tak bebas di ruas kiri), maka pe-nyelesaian dari persamaan diferensial dapat diperoleh dengan cara mentrans-formasi Laplace balik dari penyelesaian variabel tak bebas tersebut. Dalam mentransformasi Laplace dan transformasi baliknya telah tersedia tabel yang cukup seksama. Untuk ekspresi aljabar yang rumit, ekspresi tersebut dapat disederhanankan dengan teknik ekspansi fraksional. Beberapa keuntungan dari metode transformasi Laplace adalah:

1. Dengan tanpa menyelesaikan persamaan diferensial dari sistem yang dit-injau (setelah dilakukan transformasi Laplace), secara grafis dapat di-tentukan kinerja sistem yang bersangkutan.

2. Bila persamaan diferensial sistem telah dapat diselesaikan dengan me-tode transformasi Laplace, secara bersamaan akan dapat diperoleh

pe-nyelesaian baik komponen tunak (steady state) maupun transiennya (tran-sient).

2.1 Variabel dan Fungsi Kompleks

Transformasi Laplace akan mengubah fungsi riil (dalam teknik penga-turan biasanya fungsi waktut) menjadi fungsi kompleks,s. Variabel kompleks mempunyai dua komponen, yaitu komponen riilσ dan komponen imaginer ω. Karena itu variabel komplekss dapat ditulis sebagai

s=σ+jω. (1)

Fungsi kompleks,F(s), adalah fungsi dalam variabel kompleks s yang mem-punyai komponen riil Fx dan komponen imaginer Fy. Fungsi kompleks F(s) dapat ditulis dalam komponennya sebagai

F(s) =Fx+jFy, (2) besar (magnitude) dari F(s) adalah _|F(s)_|=qF2

x +Fy2 dan sudut dari F(s) adalah θ= tan−1(Fy/Fx). F(s) mempunyai konjugate ˜F(s) =Fx−jFy.

Fungsi kompleks yang sering dijumpai dalam sistem pengaturan linear adalah fungsi dalam variabel s yang tunggal dan unik (berbeda dari yang lain) untuk satu nilai stertentu.

2.2 Transformasi Laplace (Laplace Transform)

Secara matematis transformasi Laplace dapat didefinisikan sebagai beri-kut:

L[f(t)] =F(s) = Z _∞

0

dengan

f(t) : Suatu fungsi waktut yang riil,f(t) = 0 bilat <0,

s : Variabel kompleks,

L : Operator transformasi Laplace,

F(s) : Fungsi kompleks hasil transformasi dari f(t),

yang perlu diingat pada definisi di atas adalah transformasi Laplace darif(t) akan menghasilkan F(s). Dengan notasi matematis dapat ditulis: _L[f(t)] =

F(s)

2.3 Transformasi Laplace Balik (Invers Laplace Transform) Transformasi Laplace Balik dapat didefinisikan sebagai berikut:

L−1[F(s)] =f(t) = 1 2πj Z c+j∞ c−j∞ F(s)est ds, (4) dengan

F(s) : Suatu fungsi kompleks dalam s,

t : Variabel waktu yang bersifat riil,

L−1 _{: Operator transformasi Laplace balik,}

f(t) : Fungsi waktu hasil transformasi balik dari F(s).

Dalam transformasi Laplace balik, fungsi kompleks F(s) ditransformasi ba-lik ke fungsi dengan variabel riil (biasanya waktu t), f(t). Dengan notasi matematis dapat ditulis: _L−1_{[F(s)] =f(t).}

Untuk mempermudah operasi transformasi Laplace dan transformasi La-place balik, biasanya digunakan tabel berikut ini. Pada tabel ini hanya di-tampilkan transformasi dasar saja untuk selebihnya dapat dilihat pada buku-buku matematika acuan anda.

No f(t) F(s) 1 Impuls satuanδ(t) 1 2 Undak satuan l(t) 1_s 3 Ramp satuan _s12 4 tn−1 (n−1)! (n = 1,2,3,...) 1 sn 5 tn _{(n=1,2,3,...)} n! sn+1 6 e−at 1 (s+a) 7 1 (n−1)!t n−1_e−at _{(n=1,2,3,...)} 1 (s+a)n 8 sinωt ω s2_+ω2 9 cosωt _s2₊s_ω2

Selain tabel transformasi Laplace di atas, terdapat pula sifat-sifat transfor-masi Laplace yang berguna, beberapa diantaranya yang sering dipakai dalam analisis teknik pengaturan otomatis adalah sebagai berikut:

1 _L[Af(t)] =AF(s) 2 _L[f1(t) +f2(t)] =F1(s) +F2(s) 3 _L[f(_at)] =aF(as) 4 _L[d dtf(t)] =sF(s)−f(0) 5 _L[d2 dt2f(t)] =s2F(s)−sf(0)−f˙(0) 6 _L[R₀tf(t)dt] = F(s)_s

2.4 Metode Ekspansi Fraksional

Dalam persoalan analisis teknik pengaturan otomatis sering dijumpai hasil transformasi Laplace yang dapat ditulis dalam bentuk fraksional sebagai:

F(s) = B(s)

B(s) dan A(s) adalah berbentuk polinomial dalam variabel s, dan orde dari

B(s) lebih kecil dari padaA(s).

Bila timbul bentukF(s) seperti persamaan (5) di atas, maka biasanya ben-tuk tersebut dapat diekspansi atas beberapa suku dalam benben-tuk yang lebih mudah untuk ditransformasi-balikkan. Ekspansi tersebut adalah sebagai be-rikut,

F(s) =F1(s) +F2(s) +F3(s) +. . .+Fn(s). (6) Transformasi Laplace balik dari bentuk persamaan yang sudah terekspansi tersebut adalah:

L−1[F(s)] =_L−1[F1(s)] +L−1[F2(s)] +L−1[F3(s)] +. . .+L−1[Fn(s)] =f1(t) +f2(t) +f3(t) +. . .+fn(t) (7)

2.4.1 Kutup (pole) dan Zero

Sebelum melanjutkan pembahasan mengenai metode ekspansi fraksional, sebaiknya kita fahami lebih dahulu arti dari istilah kutup dan zero.

Dalam teknik pengaturan otomatis, akan sering dijumpai persoalan fungsi kompleks dengan bentuk umum seperti dalam persamaan (5), berikut ini adalah salah satu contoh bentuk persamaan (5).

F(s) = B(s)

A(s) =

K(s+z1)(s+z2). . .(s+zm) (s+p1)(s+p2). . .(s+pn)

(m < n) (8) Pada persamaan (8) di atas, F(s) berbentuk fraksional dengan pembilang

B(s) dan penyebut A(s) berupa polinomial. Pembilang B(s) berupa poli-nomial dalam z. Akar dari persamaan B(s) = 0 adalah (s1 = −z1), (s2 =

−z2),. . .(sm =−zm). Akar dari B(s) ini disebut zero. Jadi pada persamaan (8) terdapat m buah zero.

Akar dari persamaanA(s) = 0 (pada penyebut), yaitu (s1 = −p1), (s2 =

−p2),. . .(sn =−pn), disebut kutup (pole), dengan demikian pada persamaan (8) terdapat n buah kutub. Contoh dari bentuk fraksional yang sering di-jumpai adalah sebagai berikut:

F(s) = s+ 4

s2_{+ 3s+ 2}=

(s+ 4)

(s+ 1)(s+ 2) (9) pada persamaan ini terdapat satu buahzeroyaitus=₋4 dan dua buah kutup yaitu s=₋1 dan s=₋2.

Pada pembahasan berikutnya, akan banyak dijelaskan bahwa karakteristik atau sifat suatu sistem pengaturan otomatis akan sangat dipengaruhi oleh kondisi dan kedudukan dari kutup dan juga zero.

2.4.2 Ekspansi Fraksional Dengan Kutup Berbeda

Ekspansi fraksional dilakukan terhadap suatu fungsi kompleksF(s) den-gan tujuan agar diperoleh bentuk yang lebih sederhana sehingga transformasi Laplace balik dapat dilakukan dengan mudah.

Bila fungsi kompleksF(s) mempunyai kutup yang berbeda satu dan lain-nya, maka untuk ekspansi fraksional dapat digunakan metode sebagai berikut. Misalnya dalam persoalan teknik pengaturan ditemui fungsi kompleks F(s) yang dapat ditulis sebagai:

F(s) = B(s)

A(s) =

K(s+z1)(s+z2). . .(s+zm) (s+p1)(s+p2). . .(s+pn)

(m < n). (10) Bentuk fraksional ini sulit untuk ditransformasi Laplace balik, karena hanya terdiri dari satu suku dan komposisinya cukup kompleks. Agar transformasi Laplace balik mudah dilakukan bentuk fraksional ini dapat diubah menjadi beberapa suku yang sederhana:

F(s) = B(s) A(s) = a1 s+p1 + a2 s+p2 +. . . an s+pn . (11)

Persamaan (11) jauh lebih sederhana dari bentuk aslinya dan mudah untuk ditransformasi Laplace balikkan. Konstantaak (k= 1,2, . . . n) dapat dihitung dengan persamaan berikut.

ak = ∙ (s+pk) B(s) A(s) ¸ s=−pk (k= 1,2, . . . , n) (12) Dari uraian ekspansi fraksional di atas, jelas terlihat bahwa informasi nilai kutup-kutup (p1, p2, . . . pn) tetap terjaga, sedang nilai zero lebur dalam ak. Pada pembahasan kemudian, akan diketahui bahwa nilai kutup dari fungsi kompleks sebuah sistem pengaturan otomatis akan mempunyai arti penting yang berkaitan dengan sifat dari sistem yang bersangkutan.

Berikut ini diberikan contoh pemakaian ekspansi fraksional, bila fungsi kompleks F(s) mempunyai kutup yang berbeda.

Contoh : Gunakan metode ekspansi fraksional untuk menentukan transfor-masi Laplace balik dari fungsi kompleks F(s) berikut ini:

F(s) = s+ 4

s2_{+ 3s+ 2}=

(s+ 4) (s+ 1)(s+ 2) Ekspansi fraksional dari fungsi kompleks F(s) ini adalah

F(s) = (s+ 4) (s+ 1)(s+ 2) = a1 s+ 1+ a2 s+ 2

Berdasarkan persamaan (12) pada hal.16, a1 dan a2 dapat diperoleh sebagai berikut a1 = ∙ (s+ 1) s+ 4 (s+ 1)(s+ 2) ¸ s=−1 = ∙_{s+ 4} s+ 2 ¸ s=−1 = −1 + 4 −1 + 2 = 3 a2 = ∙ (s+ 2) s+ 4 (s+ 1)(s+ 2) ¸ s=−2 = ∙_{s+ 4} s+ 1 ¸ s=−2 = −2 + 4 −2 + 1 =−2

Jadi F(s) = 3 s+ 1+ −2 s+ 2= 3 s+ 1 − 2 s+ 2 L−1_{[F(s)] =} L−1 ∙ ₃ s+ 1 ¸ −L−1 ∙ ₂ s+ 2 ¸ f(t) = 3e−t₋2e−2t

2.4.3 Ekspansi Fraksional Dengan Kutup Kembar

Dalam suatu fungsi kompleks F(s) = B(s)_A(s), dapat saja terjadi akar-akar

A(s) = 0 mempunyai nilai sama atau kembar. Dalam hal ini dapat saja kem-bar dua, tiga, empat dst. Dengan kata lain fungsi F(s) dikatakan mempunyai kutup kembar berganda. Pada kondisi yang demikian itu, metode ekspansi fraksional yang telah dibahas di atas tidak dapat digunakan lagi. Bagaimana cara melakukan ekspansi fraksional pada fungsi kompleks yang memiliki kutup kembar, mari kita perhatikan penjelasan berikut ini.

Untuk lebih mudahnya, dalam menjelaskan ekspansi fraksional dengan kutup kembar, digunakan pembahasan dengan contoh. Berikut ini terdapat suatu fungsi kompleks F(s) yang dapat ditulis sebagai:

F(s) = s

2_{+ 2s+ 3}

(s+ 1)3 , (13)

fungsi F(s) di atas mempunyai tiga buah kutup yang sama, yaitu s=₋1. Fungsi F(s) pada persamaan (13) diekspansikan dalam tiga suku (sesuai dengan jumlah kutupnya) sebagai

F(s) = B(s) A(s) = b3 (s+ 1)3 + b2 (s+ 1)2 + b1 (s+ 1) (14) Nilai dari b1, b2, b3 harus kita tentukan, caranya adalah sebagai berikut. Per-tama, kalikan kedua ruas persamaan (14) dengan (s+ 1)3 _{seperti langkah}

berikut. (s+ 1)3B(s) A(s) = (s+ 1) 3 b3 (s+ 1)3 + (s+ 1) 3 b2 (s+ 1)2 + (s+ 1) 3 b1 (s+ 1)(15) atau (s+ 1)3B(s) A(s) =b3+ (s+ 1)b2+ (s+ 1) 2_b 1 (16)

jika pada persamaan ini disubtitusikan langsung nilais=₋1 pada ruas kanan (ruas kiri disubtitusikan secara tak langsung), maka akan diperoleh

∙ (s+ 1)3 B(s) A(s) ¸ s=−1 =b3 (17)

dengan persamaan ini kita dapat menghitung nilai b3.

Berikutnya, bila ruas kanan persamaan (16) didiferensialkan terhadap s

secara langsung, dan ruas kirinya didiferensialkan secara tak langsung, akan diperoleh d ds ∙ (s+ 1)3B(s) A(s) ¸ =b2+ (s+ 1)b1 (18) Subtitusikan nilai s = ₋1 secara langsung pada ruas kanan dan secara tak langsung pada ruas kiri dari persamaan (18) akan diperoleh:

d ds ∙ (s+ 1)3B(s) A(s) ¸ s=−1 =b2 (19)

Sekarang kita peroleh persamaan untuk menghitung nilaib2. Persamaan untuk menghitungb1dapat diperoleh dengan cara mendeferensialkan lagi persamaan (18), hasilnya adalah d2 ds2 ∙ (s+ 1)3 B(s) A(s) ¸ = 2b1 ⇒ 1 2 ! ( d2 ds2 ∙ (s+ 1)3B(s) A(s) ¸ s=−1 ) =b1 (20)

Langkah selanjutnya adalah menerapkan persamaan untuk menghitung

b1, b2, b3 yang telah kita peroleh dari persamaan (14), hasilnya adalah:

b3 = ∙ (s+ 1)3 B(s) A(s) ¸ s=−1 = (s2+ 2s+ 3)s=−1= 2 b2 = d ds ∙ (s+ 1)3B(s) A(s) ¸ s=−1 = ∙ d ds ¡ s2+ 2s+ 3¢ ¸ s=−1 = (2s+ 2)_s=−1= 0 b1 = 1 2 ! ( d2 ds2 ∙ (s+ 1)3 B(s) A(s) ¸ s=−1 ) = 1 2 ½ d2 ds2 £ s2+ 2s+ 3¤_s=−1 ¾ = 1 2(2) = 1

Dengan lengkapnya nilai b1, b2, b3, persamaan (14) dapat ditulis menjadi:

F(s) = B(s) A(s) = 2 (s+ 1)3 + 0 (s+ 1)2 + 1 (s+ 1)

Bila persamaan ini ditransformasi Laplace balikkan, akan diperoleh:

L−1_{[F(s)] =} L−1 ∙ ₂ (s+ 1)3 ¸ +_L−1 ∙ ₀ (s+ 1)2 ¸ +_L−1 ∙ ₁ (s+ 1) ¸ f(t) =t2_e−t_{+ 0 +e}−t _{= (t}2_{+ 1)e}−t _t ≥0 2.5 Contoh Penggunaan Transformasi Laplace

Pada bagian ini akan diberikan contoh penggunaan transformasi Laplace dan kebalikannya untuk persoalan yang sering timbul dalam teknik pengaturan otomatis.

Contoh : Karakteristika sebuah sistem pengaturan otomatis diwakili dengan persamaan diferensial di bawah ini. Tentukan respons transienx(t) dari sistem pengaturan otomatis ini.

¨

pada persamaan di atas ¨x= d2

dt2x(t), x˙ =

d dtx(t).

Transformasi Laplace dari komponen penyusun persamaan diferensial ter-sebut adalah

L[x] =_L[x(t)] =X(s)

L[x˙] =s X(s)₋x(0) =s X(s)₋2

L[¨x] =s2X(s)₋s x(0)₋x˙(0) =s2X(s)₋2s₋3

Bila hasil transformasi Laplace disubtitusikan ke dalam persamaan diferensial sistem di atas, diperoleh:

[s2X(s)₋2s₋3] + 3 [s X(s)₋2] + 2X(s) = 0 s2_X(s) −2s₋3 + 3s X(s)₋6 + 2X(s) = 0 s2X(s) + 3s X(s) + 2X(s)−2s−3−6 = 0 s2X(s) + 3s X(s) + 2X(s) = 2s+ 3 + 6 (s2_{+ 3s+ 2)X(s) = 2s+ 3 + 6} X(s) = 2s+ 3 + 6 s2_{+ 3s+ 2} = 2s+ 9 (s+ 1)(s+ 2) Dengan menerapkan ekspansi fraksional, diperoleh

X(s) = 2s+ 9 (s+ 1)(s+ 2) = a1 s+ 1+ a2 s+ 2 pada persamaan inia1 dan a2 dapat diperoleh dengan:

a1= ∙ (s+ 1) 2s+ 9 (s+ 1)(s+ 2) ¸ s=−1 = ∙_{2s+ 9} s+ 2 ¸ s=−1 = −2 + 9 −1 + 2 = 7 a2= ∙ (s+ 2) 2s+ 9 (s+ 1)(s+ 2) ¸ s=−2 = ∙_{2s+ 9} s+ 1 ¸ s=−2 = −4 + 9 −2 + 1 =−5 X(s) = 7 s+ 1+ −5 s+ 2 = 7 s+ 1− 5 s+ 2

Respons transienx(t) dapat diperoleh dengan mentransformasi Laplace balik X(s), x(t) =_L−1_{[X(s)], yaitu:} x(t) =_L−1[X(s)] =_L−1 ∙ 7 s+ 1 ¸ −L−1 ∙ 5 s+ 2 ¸ = 7_L−1 ∙ ₁ s+ 1 ¸ −5_L−1 ∙ ₁ s+ 2 ¸ = 7e−t₋5e−2t

3

Fungsi Alih

Di dalam teori pengaturan, istilah fungsi alih (transfer function) biasanya digunakan untuk melukiskan sifat-sifat hubungan antara masukan dan luaran suatu komponen sistem maupun sistem secara keseluruhan yang dapat diek-spresikan sebagai persamaan diferensial linear dalam fungsi waktu.

Secara teoritis fungsi alih dari persamaan diferensial linear dalam fungsi waktu didefinisikan sebagai perbandingan atau rasio hasil transformasi La-place antara luaran (fungsi respons) dan masukan (fungsi pengendali) dibawah asumsi bahwa semua kondisi awal nol. Dengan persamaan matematis definisi fungsi alih G(s) dapat ditulis sebagai:

Fungsi alih =G(s) = L[Luaran]

L[Masukan] ¯ ¯ ¯

kondisi awal nol

(21) Bila sebuah sistem diwakili dengan persamaan diferensial linear dalam fungsi waktu sebagai berikut,

a0y(n)+a1y(n−1)+. . .+an−1y˙+any=b0x(m)+b1x(m−1)+. . .+bm−1x˙+bmx, (22) maka fungsi alihnya adalah:

Fungsi alih =G(s) = Y(s)

X(s) =

b0sm+b1sm−1+. . .+bm−1s+bm

a0sn+a1sn−1+. . .+an−1s+an

(23) Dengan menggunakan konsep fungsi alih, dinamika sistem yang berupa persamaan diferensial (persamaan (22) ) dapat dinyatakan dalam bentuk per-samaan aljabar biasa dalam variabels. Pada fungsi alih di atas pangkat tert-inggi dari variabel s pada penyebut adalah n, karena itu sistem pengaturan yang diwakili oleh fungsi alih tersebut dikatakan sebagai sistem orde-n.

Untuk mendapatkan fungsi alih dari sebuah sistem dapat diikuti langkah-langkah berikut ini:

1. Tulislah persamaan diferensial yang mewakili sifat dinamika sistem 2. Lakukan transformasi Laplace pada persamaan diferensial yang

dipero-leh dengan asumsi semua kondisi awal nol 3. Perbandingkan antara luaran dan masukan

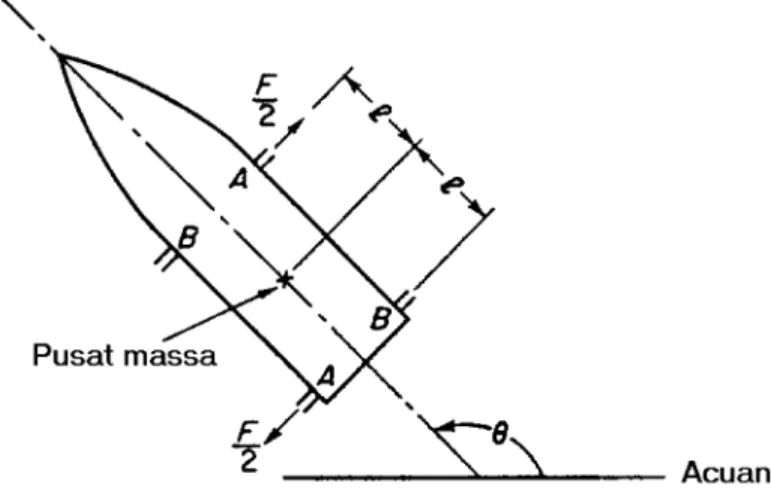
Contoh : Sebuah sistem pengendali kedudukan satelit di luar angkasa mem-punyai cara pengaturan kedudukan dengan cara penyemprotan roket seperti terlihat pada Gambar 2. Pada sistem pengendali satelit tersebut kemiringan satelitθdiatur dengan nosel roket A dan B yang bekerja secara sinkron. Sem-protan roket sebuah nosel A atau B masing-masing adalahF/2 dan menghasil kan torsi T = F

2`+ F

2`=F `. Perubahan torsi dengan waktu dinyatakan den-gan T(t), dan momen inersia pada titik pusat massanya adalah J. Tentukan fungsi alih dari sistem pengendali satelit ini.

Tahap 1: Berdasarkan hukum Newton untuk gaya dapat diperoleh persamaan:

Jd

2_θ(t)

dt2 =T(t).

Persamaan ini mewakili sistem pengendali satelit di atas.

Tahap 2: Transformasi Laplace dari persamaan sistem pengendali satelit ter-sebut dengan asumsi semua kondisi awal pada saatt= 0 bernilai nol diperoleh

J_L[d 2_θ(t)

dt2 ] =L[T(t)]

J ³s2Θ(s)₋sθ(0)₋θ(0)˙ ´=T(s),

karena semua kondisi awal nol, makaθ(0) = 0 danθ(0) = 0. Dengan demikian˙ persamaan diatas berubah menjadi:

J s2Θ(s) =T(s),

pada sistem pengendali satelit di atas, torsiT yang timbul karena gaya dorong nosel roket merupakan masukan, sedangkan hasil atau luarannya adalah perubahan sudut θ. Dengan demikian diperoleh fungsi alih yang tidak lain adalah perbandingan antara luaran dan masukan sebagai

Fungsi alih = [Luaran] [Masukan] =

Θ(s)

T(s) = 1

J s2

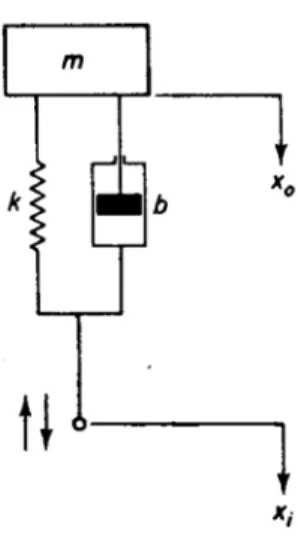
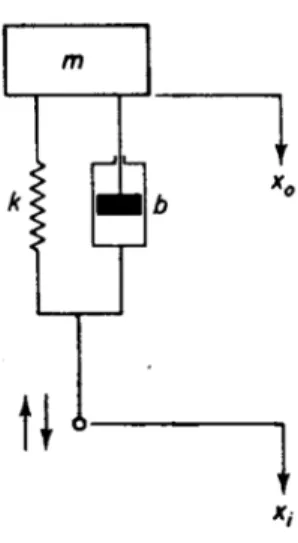
Contoh : Sebuah sistem suspensi kendaraan bermotor mempunyai struktur seperti Gambar 3. Pada sistem ini bekerja gaya gravitasi terhadap massamke arah vertikal (ke bawah). Gaya gravitasiFgrvakan mendapat perlawanan dari gaya pegas Fpgs dan gaya dari peredam kejut Fpkj. Besarnya masing-masing gaya tersebut dapat didefinisikan sebagai berikut:

Gambar 3: Struktur sistem suspensi kendaraan bermotor

dengan x˙o= dx_dto dan ¨xo= d

2_x

o

dt2 .

Komposisi kesetimbangan gaya yang bekerja pada suspensi diperoleh: Fgrv =Fpgs+Fpkj ⇒ mx¨o=−k(xo−xi)−b(x˙o−x˙i)

Bila persamaan kesetimbangan gaya di atas ditranformasi Laplace dengan menganggap semua kondisi awal sama dengan nol, akan diperoleh

m s2Xo(s) =−k(Xo(s)−Xi(s))−b(s Xo(s)−s Xi(s)) = (b s+k) (Xi(s)−Xo(s))

m s2_X

o(s) = (b s+k) (Xi(s)−Xo(s))

bila persamaan tersebut dibagi dengan Xi(s) pada kedua ruasnya (nilai per-samaan tidak akan berubah), akan diperoleh

m s2Xo(s) Xi(s)

= (b s+k)

Xi(s)

m s2Xo(s) Xi(s) = (b s+k) µ 1₋Xo(s) Xi(s) ¶ ⇒ X_Xo(s) i(s) = (b s+k) m s2 µ 1₋Xo(s) Xi(s) ¶ Xo(s) Xi(s) = (b s+k) m s2 − (b s+k) m s2 Xo(s) Xi(s) ⇒ Xo(s) Xi(s) +(b s+k) m s2 Xo(s) Xi(s) = (b s+k) m s2 µ 1 +(b s+k) m s2 ¶_X o(s) Xi(s) = (b s+k) m s2 ⇒ µ_{m s}2 m s2 + (b s+k) m s2 ¶_X o(s) Xi(s) = (b s+k) m s2 µ_{m s}2_{+b s+k} m s2 ¶_X o(s) Xi(s) = (b s+k) m s2 ⇒ Xo(s) Xi(s) = µ _{m s}2 m s2_{+b s+k} ¶_{(b s+k)} m s2 Xo(s) Xi(s) = (b s+k) m s2_{+b s+k}

Beberapa hal yang perlu dicatat tentang fungsi alih adalah:

• Fungsi alih adalah model matematis yang digunakan untuk mengkaji pengaruh masukan terhadap luaran dari persamaan diferensial suatu sistem.

• Fungsi alih adalah sifat unik yang dimiliki oleh sistem yang bersangku-tan, tidak bergantung terhadap besarnya masukan ataupun fungsi pe-ngendali.

• Di dalam fungsi alih telah terjalin satuan penting yang berkaitan dengan masukan dan luaran.

• Bila fungsi alih sistem telah diketahui, kita dapat mempelajari luaran sistem terhadap berbagai jenis masukan.

• Bila fungsi alih sulit untuk diturunkan secara matematis (teoritis), fungsi alih dapat diperoleh dengan cara eksperimen dengan cara memberi ma-sukan tertentu (yang telah diketahui) pada sistem dan mencatat perilaku luarannya.

4

Diagram Blok

Sebuah sistem pengaturan bisa terdiri dari beberapa komponen. Untuk menunjukkan fungsi dan kinerja dari setiap komponen dalam teknik penga-turan digunakan diagram yang disebut diagram blok. Pada bagian ini akan dibahas tentang bagaimana memperoleh diagram blok dari suatu sistem, dan bagaimana teknik yang harus digunakan dalam penyederhanaan diagram blok menjadi diagram yang mudah difahami dan dianalisis.

Diagram blok sebenarnya adalah suatu metode untuk merepresentasikan fungsi dari setiap komponen sistem dan arah aliran sinyal yang mengalir an-tara satu komponen ke komponen lain. Berbeda dengan metode matematis, metode grafis ini mempunyai suatu keuntungan yaitu bahwa aliran sinyal da-pat direpresentasikan dalam bentuk yang lebih realistis dan mudah difahami.

Dalam diagram blok terdapat komponen-komponen sebagai berikut:

• Blok, adalah suatu kesatuan yang mempunyai fungsi tertentu dan dis-imbolkan dengan kotak persegi panjang. Di dalam sebuah blok tertulis suatu fungsi yang menunjukkan fungsi alih dari komponen yang diwakili oleh blok tersebut. Lihat Gambar 4.

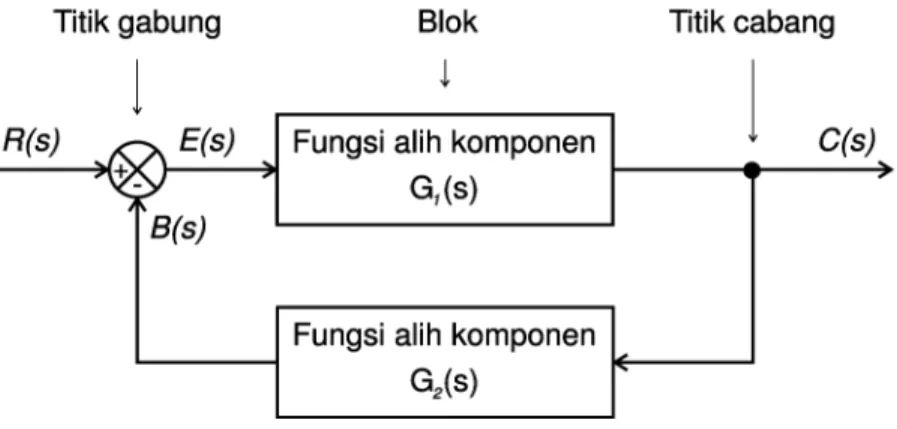
• Titik gabung, adalah suatu titik pertemuan antara beberapa aliran sinyal dengan operasi penjumlahan atau pengurangan. Lihat Gambar 4.

• Titik cabang, adalah suatu titik tempat terjadinya percabangan aliran sinyal. Lihat Gambar 4

4.1 Diagram Blok Sistem Untai Tertutup

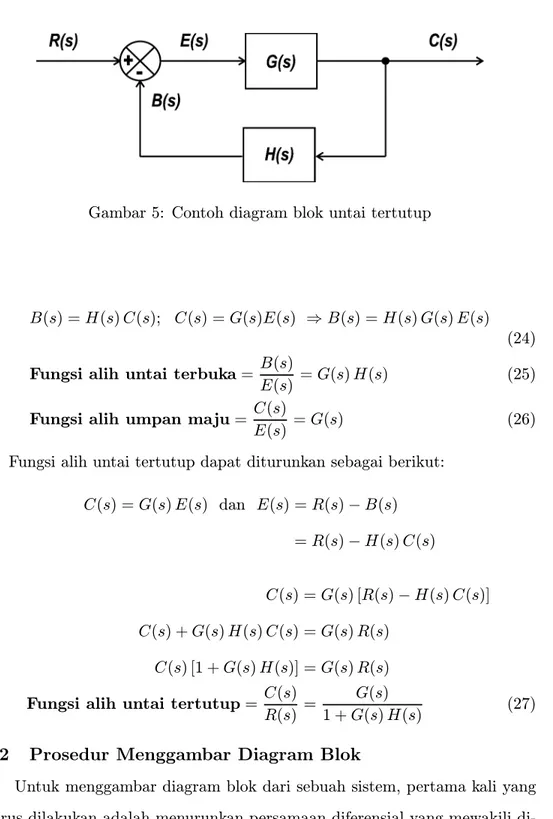
Gambar 5 hal.29 adalah salah satu contoh dari diagram blok dengan un-tai tertutup yang sering dijumpai. Pada contoh diagram blok tersebut sinyal

Gambar 4: Contoh diagram blok

luaran C(s) dipisahkan pada titik cabang dan diumpan-balikkan ke masukkan

R(s) melalui suatu titik gabung pengurangan. Sebelum diumpan-balikkan ke titik gabung terlebih dahulu dilalukan pada komponen dengan fungsi alih

H(s). Melalukan sinyal umpan-balik pada suatu komponen seperti ini adalah suatu hal yang sering dijumpai, karena dimensi sinyal output dan sinyal in-put biasanya berbeda. Dengan melalukan sinyal outin-put padaH(s) diharapkan sinyal output diubah dimensinya sehingga mempunyai dimensi yang sama den-gan sinyal input yang akan digabungkan. Perlu dicatat bahwa penggabunden-gan dua satuan dengan dimensi yang berbeda secara fisik tidak dapat dilakukan, misalnya penggabungan dua satuan seperti suhu dan tekanan. Pada gambar tersebut luaran C(s) diperoleh dengan cara mengalikan fungsi alih komponen

G(s) dengan masukkanE(s). Sedangkan sinyal kesalahan aktuasiE(s) adalah

E(s) =R(s)₋B(s), dan umpan baliknyaB(s) =H(s)C(s).

Dari Gambar 5 hal.29, dapat didefinisikan Fungsi alih untai terbuka, Fungsi alih umpan majudanFungsi alih untai tertutupsebagai berikut:

Gambar 5: Contoh diagram blok untai tertutup

B(s) =H(s)C(s); C(s) =G(s)E(s) _⇒B(s) =H(s)G(s)E(s) (24) Fungsi alih untai terbuka= B(s)

E(s) =G(s)H(s) (25) Fungsi alih umpan maju= C(s)

E(s) =G(s) (26) Fungsi alih untai tertutup dapat diturunkan sebagai berikut:

C(s) =G(s)E(s) dan E(s) =R(s)₋B(s) =R(s)₋H(s)C(s)

C(s) =G(s) [R(s)₋H(s)C(s)]

C(s) +G(s)H(s)C(s) =G(s)R(s)

C(s) [1 +G(s)H(s)] =G(s)R(s) Fungsi alih untai tertutup= C(s)

R(s) =

G(s)

1 +G(s)H(s) (27) 4.2 Prosedur Menggambar Diagram Blok

Untuk menggambar diagram blok dari sebuah sistem, pertama kali yang harus dilakukan adalah menurunkan persamaan diferensial yang mewakili

di-namika proses yang terjadi pada setiap komponen dari sistem tersebut. Kemu-dian persamaan tersebut ditransformasi Laplace dengan asumsi semua kondisi awal nol. Selanjutnya masing-masing persamaan yang telah ditransformasi La-place diekspresikan dengan satu blok. Pada akhir langkah, blok-blok tersebut digabungkan menjadi satu kesatuan diagram blok yang mewakili sistem secara kesatuan.

Secara garis besar langkah-langkah tersebut dapat ditulis sbb:

1. Tulis persamaan diferensial dinamika proses setiap komponen sistem 2. Transformasi Laplace-kan setiap persamaan diferensial dengan

mengam-bil asumsi bahwa kondisi awal (pada t= 0) bernilai nol

3. Ekspresikan setiap persamaan dengan diagram blok secara terpisah 4. Gabungkan seluruh blok diagram komponen menjadi satu kesatuan

Berikut ini akan dikemukakan salah satu contoh menggambar diagram blok. Gambar 6 hal.31 adalah bentuk model dari peredam getaran pada se-buah roda dari sepeda motor. Persamaan yang mendiskripsikan bekerjanya gaya-gaya pada komponen pegas, peredam kejut dan massam adalah sebagai berikut:

mx¨0=F

F =₋b(x˙0−x˙i)−k(x0−xi).

Gambar 6: Sistem peredam getaran roda sepeda motor

awal nol adalah:

m s2_X

0(s) =F(s) (28)

F(s) =₋b[s X0(s)−s Xi(s)]−k[X0(s)−Xi(s)]

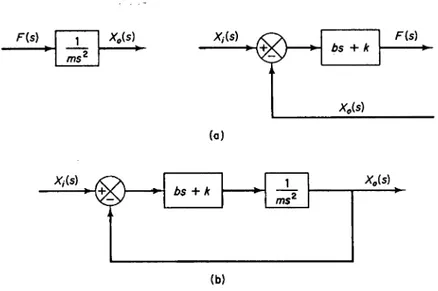
= (b s+k) [Xi(s)−X0(s)] (29) Diagram blok dari persamaan (28) dan (29) dapat dilihat pada Gambar 7(a). Gambar 7(b) adalah diagram blok hasil penggabungan dari diagram blok kom-penen pada Gambar 7(a)

4.3 Penyederhanaan Diagram Blok

Bila sistem pengaturan yang kita amati cukup kompleks dan rumit, maka diagram blok yang dihasilkan dengan cara yang telah dijelaskan, menjadi kom-pleks juga. Karena itu perlu adanya penyederhanaan diagram blok dengan diagram yang lebih sederhana dan mudah untuk difahami.

Gambar 7: Pembuatan diagram blok

Penyederhanaan yang dimaksud adalah, misalnya ada dua blok yang ter-pasang secara seri, maka kedua blok ini dapat disederhanakan menjadi satu blok. Beberapa hal yang harus diperhatikan dan diingat dalam menyeder-hanankan diagram blok adalah:

• Fungsi alih maju dari hasil penyederhanaan komponen harus tetap sama

• Fungsi alih melingkari untai yang ada harus tetap sama

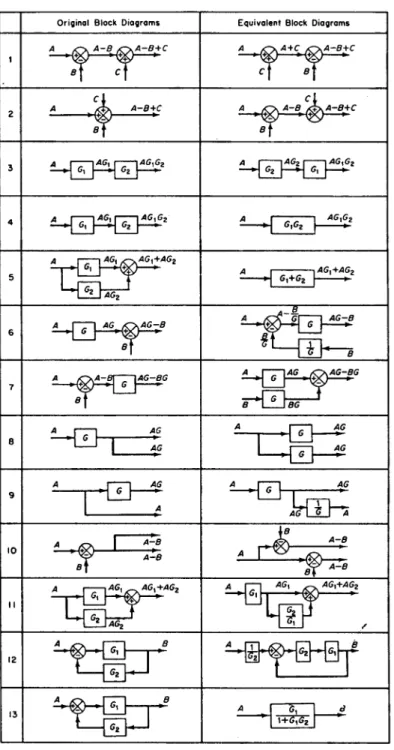
Dalam penyederhanaan diagram blok, terdapat beberapa aturan yang da-pat dipakai sebagai pedoman penyederhaan. Aturan tersebut dada-pat dilihat pada Tabel yang ditunjukkan dalam Gambar 8.

Sebagai contoh, Gambar 9 pada hal.34 menggambarkan bagaimana penye-derhanaan tersebut dapat dilakukan. Pada gambar (a), terlihat diagram blok yang sangat kompleks. Setelah dilakukan penyederhanaan, pada hasil akhir (gambar (e)) terlihat bahwa diagram blok hanya terdiri dari satu blok saja, yang merupakan fungsi alih dari seluruh sistem (pada awalnya diwakili oleh diagram blok yang rumit). Jadi jelas bahwa tujuan akhir dari penyederhanaan ini adalah mendapatkan fungsi alih dari keseluruhan sistem.

Proses penyederhanaan diagram blok pada Gambar 9 hal.34 secara ringkas dapat dijelaskan sebagai berikut:

1. Gambar (a) menunjukkan gambar asli dari sistem yang rumit

2. Dengan menggunakan aturan nomor 6 pada Gambar 8 yang dikenakan padaH2, dari gambar (a) dapat diubah menjadi (b)

3. Dengan menggunakan aturan nomor 13 pada Gambar 8 yang dikenakan pada G1, G2, dan H1 diperoleh gambar (c). Dengan aturan yang sama yang dikenakan pada H2

G1,

G1G2

1−G1G2H1 dan G3 diperoleh gambar (d). Se-lanjutnya aturan yang sama menghasilkan gambar (e)

5

Analisis Respons Transien

Dalam perancangan sebuah sistem, setelah dilakukan perancangan bentuk fisik dan model matematisnya dibuat maka dengan berbagai metode analisis, kinerja sistem dapat diselidiki.

Setelah perancangan sistem selesai, diperlukan suatu analisis mengenai kinerja sistem terhadap berbagai masukan. Tetapi pada kenyataannya di la-pangan, bagaimana bentuk masukan yang nyata tidak diketahui secara pasti. Karena itu untuk menguji respons transien (kinerja) sistem digunakan ma-sukkan berupa fungsi-fungsi sederhana yang dapat mewakili kondisi umum masukan yang nyata. Dengan cara ini dapat dilakukan evaluasi terhadap sis-tem yang telah dirancang dan selanjutnya perbaikan dapat dilakukan dengan lebih seksama berdasarkan pertimbangan dari hasil pengujian respons transien sistem.

Fungsi sederhana yang sering digunakan untuk menguji respons transien diantaranya adalahfungsi undak,fungsi ramp,fungsi percepatan,fungsi impuls dan fungsi sinus dlsb. Karena fungsi-fungsi tersebut sangat seder-hana, maka analisis respons transien dapat dilakukan dengan mudah dan re-latif cepat. Transformasi Laplace dari fungsi uji yang sangat sering digunakan adalah sebagai berikut:

Nama fungsi Transformasi Laplace Fungsi impuls satuan 1

Fungsi undak satuan 1 s

5.1 Sistem Orde 1

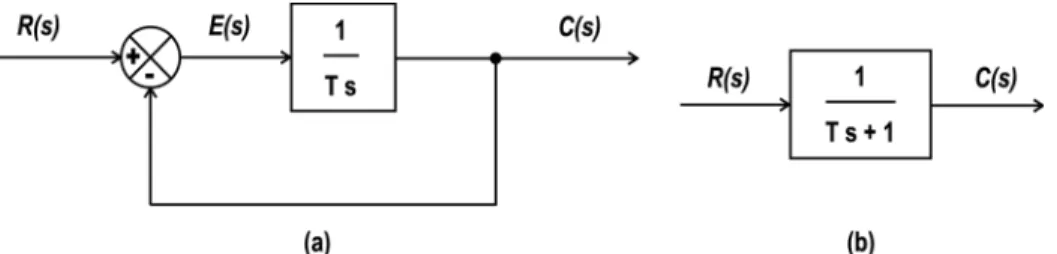
Contoh fisik dari sistem orde satu misalnya adalah rangkaian RC, sistem termal dlsb. Sebagai ilustrasi untuk sistem orde satu dapat dilihat diagram blok pada Gambar 10 berikut ini.

Gambar 10: Contoh diagram blok sistem orde 1

Fungsi alih dari Gambar 10 dapat diperoleh dari gambar (b) sebagai beri-kut:

C(s)

R(s) = 1

T s+ 1 (30)

Pada persamaan (30) terlihat bahwa pangkat tertinggi dari spada penyebut adalah satu, karena itu sistem di atas disebut sistem orde satu. Dalam pem-bahasan berikut ini, akan dibahas mengenai pengujian sistem orde 1 di atas dengan berbagai fungsi masukan agar diperoleh respons transien atau kinerja dari sistem.

5.1.1 Respons sistem orde 1 terhadap fungsi undak satuan

Dari tabel transformasi Laplace diperoleh bahwa transformasi Laplace fungsi undak satuan adalah 1_s. Dengan demikian bila sistem orde satu di atas diberi masukan fungsi undak satuan, maka R(s) = 1

dapat ditulis sebagai: C(s) = 1 T s+ 1R(s) = 1 T s+ 1 1 s (31)

Dengan menggunakan ekspansi fraksional, seperti pada persamaan (11) hal.15, diperoleh

C(s) = 1

s− T

T s+ 1. (32)

Respons transien sistem orde 1 terhadap masukan fungsi undak satuan dapat ditentukan dengan mentransformasi Laplace balik persamaan (32), yaitu:

L−1[C(s)] =_L−1[1 s− T T s+ 1] =_L−1[1 s]−L −1_[ T T s+ 1] c(t) = 1₋e−t/T (t_≥0). (33) Persamaan ini menunjukkan respons transien sistem orde 1 bila diberi ma-sukkan fungsi undak satuan. Keluaran pada kondisi awal dapat diperoleh den-gan memasukkan nilait= 0, yaituc(t) = 0 (e0_{= 1), dan keluaran pada kondisi} mendekati jenuh dapat diperoleh dengan memasukkan nilait=_∞. Pada saat

t = T, c(T) = 0.632. Dari fungsi respons ini dapat dilihat bahwa konstanta waktu T mempunyai peran terhadap kesigapan respons terhadap masukkan. Semakin kecil nilai T, respons sistem menjadi semakin cepat. Grafik fungsi

c(t) pada persamaan (33) dapat dilihat pada Gambar 11 di halaman 39

5.1.2 Respons sistem orde 1 terhadap fungsi ramp satuan Transformasi Laplace dari fungsi ramp satuan adalah 1

s2, dengan memberi masukkan R(s) = 1

s2 persamaan (30) dapat ditulis sebagai:

C(s) = 1 T s+ 1R(s) = 1 T s+ 1 1 s2. (34)

Gambar 11: Grafik respons transien sistem orde 1 terhadap masukan undak satuan

Penerapan metode ekspansi fraksional (persamaan (11) hal.15) pada persamaan (34) menghasilkan C(s) = 1 s2 − T s + T2 T s+ 1. (35) Transformasi Laplace balik dari persamaan ini akan menghasilkan respon tran-sien sebagai berikut.

L−1_{[C(s)] =} L−1_[1 s2 − T s + T2 T s+ 1] L−1_{[C(s)] =} L−1_[1 s2]−L −1_[T s] +L −1_[ T 2 T s+ 1] c(t) =t₋T +T e−t/T (t_≥0). (36) Sifat-sifat dari respons transien ini dapat diselidiki dengan menggambar grafik dari fungsi c(t).

5.1.3 Respons sistem orde 1 terhadap fungsi impuls satuan

Masukan untuk fungsi impuls satuan adalahR(s) = 1, maka persamaan (30) dapat ditulis sebagai:

C(s) = 1

T s+ 1R(s) = 1

T s+ 11. (37) Respons transien yang diperoleh dari persamaan (37)adalah

c(t) = 1

T e

−t/T _(t

≥0). (38)

5.2 Sistem Orde 2

Salah satu contohfisik dari sistem orde dua adalah sistem servomekanik seperti terlihat pada Gambar 12. Gambar (a) menunjukkan skemafisik rangka-ian servomekanik, gambar (b) adalah digram bloknya. Digram blok dari sistem servomekanik yang telah disederhanakan diperlihatkan pada gambar (c).

Dari diagram blok Gambar 12(c) diperoleh fungsi alih sistem sebagai be-rikut C(s) R(s) = K s(J s+B) +K = K J s2_{+B s+K} (39) dengan K = (K0K1K2)/(n Ra) : Konstanta

J = J0/n2 : Momen inersia pd poros luaran

B = [b0+ (K2K3/Ra)]/n2 : Koefisien friksi viskositas pd poros luaran Penyebut persamaan (39) menunjukkan bahwa pangkat tertinggi dari vari-abel s adalah 2 (dua), dengan demikian jelas sistem tersebut adalah sistem orde dua.

Kutup (lihat kembali penjelasan tentang kutup di halaman 14 ) dari fungsi alih untai tertutup persamaan (39) dapat berupa bilangan kompleks atau riil. Kutup persamaan tersebut akan berupa bilangan imaginer bilaB2

−4J K <0, dan bilangan riil bila B2

−4J K_≥0.

Dengan rumus ABC, penyebut dari persamaan (39) dapat difaktorisasi, sehingga persamaan (39) dapat ditulis sebagai

C(s) R(s) = K/J s2_{+B/J s+K/J} = ∙ K/J s+B/J₂ + q (B/J₂ )2₋K/J ¸∙ s+B/J_{2 −} q (B/J₂ )2₋K/J ¸ (40) Dalam sistem orde dua sering dipakai parameter-parameter yang berhu-bungan dengan konstanta B, J, dan K. Parameter yang akan didefinisikan berikut ini tidak dipakai pada sistem orde satu. Berikut ini adalah definisi dari parameter atenuasi(σ),frekuensi alam tak-teredam (ωn) danrasio redaman (ζ). K J =ω 2 n, B J = 2ζ ωn = 2σ (41)

Rasio redamanζ itu sendiri adalah perbandingan antararedaman nyata(B) dan redaman kritis (Bc = 2

√ J K), yaitu ζ = B Bc = B 2√J K (42)

Dengan mensubtitusikan parameter yang telah didefinisikan pada per-samaan (41) dan (42), fungsi alih sistem orde dua, perper-samaan (39) hal.41, dapat diubah menjadi:

C(s) R(s) = ω2 n s2_{+ 2ζω} ns+ωn2 (43) Kini fungsi alih sistem orde dua dapat dinyatakan dengan dua paramter, yaitu ωn dan ζ. Bila 0 < ζ < 1 kutup-kutup akan berada pada daerah tidak stabil (pada penjelasan berikutnya akan dibahas bahwa daerah tidak stabil adalah daerah yang berada disebelah kanan dalam bidang kompleks) dan sis-tem dalam kondisi teredam-kurang sehingga sistem akan berosilasi terus menerus. Untukζ = 1 danζ >1, sistem akan berada dalam kondisiteredam dan teredam-lebih. Pada kondisi ini sistem tidak berosilasi. Bila ζ = 0, respons transien dari sistem akan tidak berkesudahan (terus menerus ada dan tak berhenti, lihat Gambar 13 hal.44).

5.2.1 Respons sistem orde 2 terhadap fungsi undak satuan

Sekarang kita akan menentukan respon transien dari sistem orde dua terhadap masukan fungsi undak satuan (R(s) = 1

s) dengan bentuk matematis yang mewakilinya adalah fungsi alih persamaan (43). Tidak seperti sistem orde satu, pada sistem orde dua ini kita mempunyai tiga kemungkinan kondisi yaitu teredam-kurang 0 < ζ < 1, teredam kritis ζ = 1 dan teredam-lebih ζ > 1. Karena itu dalam menerapkan masukan fungsi undak satuan, ketiga kondisi tersebut harus diperhitungkan juga.

Teredam kurang (0<ζ<1):

Fungsi alih sistem pengaturan orde dua dapat ditulis kembali sebagai be-rikut. C(s) R(s) = ω2 n s2_{+ 2ζω} ns+ω2n = ω 2 n (s+ζωn+jωd)(s+ζωn−jωd) , (44) ωd = ωn √

1₋ζ2 _{adalah frekuensi alam teredam. Dengan memasukkan} fungsi undak satuan, R(s) = 1

s, persamaan (44) menjadi: C(s) = ω 2 n s2_{+ 2ζω} ns+ωn2 1 s = 1 s− s+ 2ζωn s2_{+ 2ζω} ns+ωn2 = 1 s− s+ζωn (s+ζωn)2+ωd2 −_(s+ζωζωn n)2+ωd2 (45) Transformasi Laplace balik dari persamaan ini adalah:

L−1[C(s)] =_L−1[1 s]−L −1_[ s+ζωn (s+ζωn)2+ωd2 ]_−L−1[ ζωn (s+ζωn)2+ωd2 ] c(t) = 1₋e−ζωnt _cosω dt−e−ζωnt ζωn ωd sinωdt = 1₋e−ζωnt µ cosωdt+ ζωn ωn √ 1₋ζ2 sinωdt ¶ = 1₋e−ζωnt µ cosωdt+ ζ √ 1₋ζ2 sinωdt ¶ = 1₋ e− ζωnt √ 1₋ζ2 sin à ωdt+ tan−1 √ 1₋ζ2 ζ ! (t_≥0) (46) Persamaan (46) adalah respons transien sistem orde dua terhadap masukan undak satuan. Dari persamaan ini diketahui bahwa frekuensi dari transien osilasi adalah frekuensi alam teredam ωd yang bervariasi dengan ζ. Ilustrasi yang menggambarkan respons transien sistem orde dua dengan berbagai nilai ζ dapat dilihat pada Gambar 13

Gambar 13: Grafik respons transien sistem orde 2 terhadap masukan undak satuan

Sinyal kesalahan (error) untuk sistem ini dapat diperoleh dari selisih antara masukan dan luaran, yaitu:

Kesalahan = Masukan₋Luaran

e(t) =r(t)₋c(t) =e−ζωnt µ cosωdt+ ζ √ 1₋ζ2sinωdt ¶ (t_≥0) (47) Bila persamaan ini digambar akan diperoleh grafik kesalahan yang berbentuk osilasi sinus teredam. Pada kondisi tunak dengan t=_∞ diperoleh e(_∞) = 0, dengan demikian pada kondisi tunak tidak ada kesalahan antara masukan dan

luaran atau dengan kata lain pada kondisi tunak luaran akan sesuai dengan masukan. Hal ini berlaku untuk 0 < ζ <1, bila ζ = 0 maka akan diperoleh

e(t) = cosωdt. Berarti sistem akan mempunyai kesalahan terus menerus dan berosilasi dengan modus sinusuidal, dari respons transien juga membuktikan hal ini, yaitu c(t) = 1₋cosωnt

Teredam kritis (ζ = 1):

Pada kasus ini dua kutup dari fungsi alih (C(s)/R(s)) mempunyai nilai yang hampir sama, karena itu dapat dilakukan pendekatan teredam kritis. Fungsi alih sistem orde dua pada kondisi teredam kritis dapat ditulis sbb:

C(s) R(s) = ω2 n s2_{+ 2ζω} ns+ωn2 = ω 2 n s2_{+ 2ω} ns+ωn2 = ω 2 n (s+ωn)2 , (48) bila pada masukan diberikan fungsi undak satuan (R(s) = 1

s), akan diperoleh: C(s) = ω 2 n (s+ωn)2s (49) Transformasi Laplace balik dari persamaan ini adalah

L−1[C(s)] =_L−1 ∙ _ω2 n (s+ωn)2s ¸ c(t) = 1₋e−ωnt_{(1 +ω} nt) (50)

Pada persamaan ini tidak muncul faktor sinusuidal, yang ada hanya modus eksponensial, jadi tidak akan ada osilasi. Grafik dari respons transien untuk sistem ini dapat dilihat pada Gambar 13 hal.44 dengan ζ = 1

Teredam lebih (ζ>1):

Dalam kasus ini dua kutup dari fungsi alih (C(s)/R(s)) mempunyai nilai negatip riil yang berbeda. Fungsi alih sistem orde dua pada kondisi teredam lebih dapat ditulis sbb:

C(s) R(s) = ω2_n s2_{+ 2ζω} ns+ωn2 = ω 2 n (s+ζωn+ωnpζ2_{−1)(s+ζωn−ωn}p_ζ2₋₁₎(51) bila pada masukan diberikan fungsi undak satuan (R(s) = 1

s), akan diperoleh: C(s) = ω 2 n (s+ζωn+ωn √ ζ2_−1)(s+ζω n−ωn √ ζ2₋₁₎ 1 s (52)

Transformasi Laplace balik dari persamaan ini akan diperoleh:

c(t) =1 + 1 2√ζ2_−1(ζ+√_ζ2₋₁₎e −(ζ+√ζ2_−1)ω nt − 1 2√ζ2_−1(ζ−√_ζ2₋₁₎e −(ζ−√ζ2_−1)ωnt =1 + ωn 2√ζ2₋₁ ⎛ ⎝ e−(ζ+ √ ζ2_−1)ω nt (ζ+√ζ2_−1)ω n − e−(ζ−√ζ2_−1)ω nt (ζ₋√ζ2_−1)ω n ⎞ ⎠ (t_≥0) (53) Pada persamaan ini tidak muncul modus sinusuidal, modus yang dominan adalah eksponensial, karena itu pada Gambar 13 hal.44 untuk ζ > 1 tidak terlihat adanya osilasi. Semakin besar nilai ζ dari satu, akan menghasilkan peluruhan eksponensial yang lebih cepat.

5.2.2 Respons sistem orde dua terhadap fungsi impuls satuan Transformasi Laplace dari fungsi impuls satuan adalah 1, jadiR(s) = 1. Fungsi alih sistem orde 2 setelah menerima masukan berbentuk fungsi impuls satuan dapat ditulis sebagai berikut:

C(s) = ω 2 n s2_{+ 2ζω} ns+ω2n R(s) = ω 2 n s2_{+ 2ζω} ns+ω2n (54) Transformasi Laplace balik dari persamaan (54) akan menghasilkan res-pons transien sebagai berikut:

0_≤ζ <1 c(t) = _√ ωn 1₋ζ2e −ζωnt_sinω n p 1₋ζ2_{t (55)}

ζ = 1 c(t) =ω_n2t e−ωnt ₍₅₆₎ ζ >1 c(t) = ωn 2√ζ2₋₁e −(ζ+√ζ2₋₁₎ ωnt− ωn 2√ζ2₋₁e −(ζ−√ζ2₋₁₎ ωnt (57)

5.2.3 Respons sistem orde dua terhadap fungsi ramp satuan Respons transien sistem orde dua terhadap fungsi ramp dapat diperoleh dengan metode langsung. Pada pembahasan ini akan dipelajari kesalahan tunak dari sistem orde dua yang diberi masukan fungsi ramp. Persamaan kesalahan tunak dapat ditulis sebagai berikut:

E(s) = J s

2_{+B s}

J s2_{+B s+K}R(s) (58) Tanpa menggunakan transformasi Laplace, dapat diperoleh e(t) sebagai beri-kut: e(t) = lim s→0s E(s) = lim s→0s J s2_{+B s} J s2_{+B s+K} 1 s2 = B K = 2ζ ωn (59) dengan ζ = B 2√KJ,ωn = q K J.

Hingga di sini telah dibahas mengenai respons transien dari suatu sistem orde dua terhadap masukan yang berupa fungsi undak satuan, impuls sat-uan dan ramp satsat-uan. Dari jenis respons transien ini, respons terhadap ma-sukan fungsi undak satuan mempunyai arti penting, yaitu dengan mengetahui respons transien terhadap fungsi undak satuan, secara matematis, respons

terhadap sembarang masukan dapat diketahui. Karena itu respons terhadap fungsi undak satuan sering dijadikan acuan dalam mengevaluasi disain sistem pengaturan dalam dunia industri.

5.2.4 Spesifikasi respons transien

Untuk kepraktisan di lapangan, banyak kasus menunjukkan bahwa sifat kinerja sistem pengaturan yang ditinjau dispesifikasikan dengan istilah-istilah yang mewakili suatu kuantitas dalam domain waktu (sebagai fungsi waktu atau yang berkaitan dengan waktu).

Pada kenyataannya, kebanyakan sistem pengaturan memperlihatkan sifat kinerja sebagai sistem osilasi teredam sebelum mencapai kondisi tunak (lihat Gambar 14 hal.49). Berkaitan dengan sifat ini (osilasi teredam), berikut ini akan dijelaskan beberapa definisi parameter karakteristika respons transien terhadap masukan fungsi undak satuan.

Definisi dari parameter yang sering dipakai pada sistem osilasi teredam dapat dijelaskan sebagai berikut. (Lihat Gambar 14 hal.49).

1. Waktu tunda (delay time), td : Waktu yang diperlukan oleh respons (fungsi respons) untuk mencapai setengah dari nilai akhir osilasi atau kondisi tunak (lihat td pada Gambar 14).

2. Waktu naik (rise time), tr : Waktu yang diperlukan oleh respons (fungsi respons) untuk naik 10% — 90%, 5% — 95%, atau 0% — 100% dari nilai akhirnya. Untuk sistem orde 2 teredam-kurang waktu naik yang dipakai mempunyai pengertian yaitu waktu untuk naik dari 0% — 100%. Untuk sistem teredam-lebih dipakai definisi waktu untuk naik dari 10% — 90%

Gambar 14: Spesifikasi respons transien terhadap fungsi undak satuan

3. Waktu puncak (peak time), tp : Waktu yang diperlukan oleh respons (fungsi respons) untuk mencapai puncak pertama dari overshoot. 4. Overshootmaksimum(maximum overshoot),Mp: Nilai puncak

mak-simum kurva respons yang diukur dari nilai satu. Bila nilai tunak dari respons tidak sama dengan satu, maka untuk parameter ini biasanya digunakan persen overshoot maksimum yang didefinisikan sebagai

Persenovershootmaksimum = c(tp)−c(∞)

c(_∞) ×100%. (60) Nilai ini menunjukkan stabilitas relatif dari sistem. Untuk jelasnya lihat

Mp pada Gambar 14.

5. Waktu settling (settling time),ts : Waktu yang diperlukan oleh kurva respons untuk mencapai dan terus berada pada rentang suatu nilai pre-sentasi absolut yang telah ditentukan (biasanya 2% = 0.02 atau 5% = 0.05) di sekitar nilai akhir atau nilai tunaknya.

5.2.5 Spesifikasi respons transien dalam sistem orde dua

Di atas telah dijelaskan mengenai spesifikasi respons transien dari suatu sistem osilasi teredam. Sistem dengan karakter osilasi teredam yang telah kita pelajari adalah sistem orde dua, dengan respons transiennya ditunjukkan oleh persamaan (46) hal.43.

Pada bagian ini akan diuraikan tentang contoh untuk mendapatkan waktu naik, waktu puncak, overshoot maksimum, waktu settling dari sistem orde yang respons transiennya ditunjukkan dalam persamaan (46) hal.43. Untuk mempermudah penjelasan pada bagian ini dicantumkan kembali Gambar 15 hal.51 yang memuat titik-titik dari spesifikasi respons transien.

Waktu naik, tr : Waktu naik dapat diperoleh dengan carac(tr) = 1, dengan cara ini persamaan (46) hal.43 dapat ditulis kembali sebagai

c(tr) = 1−e−ζωntr µ cosωdtr+ ζ √ 1₋ζ2 sinωdtr ¶ = 1 (61) atau e−ζωntr µ cosωdtr+ ζ √ 1₋ζ2 sinωdtr ¶ = 0 (62)

pada persamaan ini jelas pasti bahwa e−ζωntr

6

= 0, karena itu sebagai kon-sekuensinya adalah µ cosωdtr+ ζ √ 1₋ζ2 sinωdtr ¶ = 0 (63)

Gambar 15: Spesifikasi respons transien terhadap fungsi undak satuan sistem orde 2 atau ζ √ 1−ζ2 sinωdtr=−cosωdtr tanωdtr=− ζ √ 1₋ζ2 =₋ωd σ Jadi tr= 1 ωd tan−1 µ_ω d −σ ¶ = π−β ωd (64) β adalah suatu konstanta yang dapat ditentukan dengan Gambar 16 hal.52 berikut ini, yaitu β= tan−1

à ωn √ 1₋ζ2 σ ! = tan−1 µ_ω d σ ¶ .

Gambar 16: Metode perhitungan β

fungsi respons transienc(t) terhadap waktu,tdan kemudian nilai tersebut di nolkan (d dtc(t) = 0). d dtc(t) ¯ ¯ ¯ t=tp = (sinωdtp) ωn √ 1₋ζ2e −ζωdtp _{= 0 (65)}

Pada persamaan ini ωn/

√

1₋ζ2_{6= 0 dan e}−ζωdtp _{6= 0, karena itu}

sinωdtp = 0

ωdtp = 0,π,2π,3π. . . (66) Karena waktu puncak hanya berkaitan dengan puncakovershootyang pertama maka ωdtp=π tp= π ωd (67)

atau dengan kata lain t=tp =π/ωd. Dengan demikian dapat ditulis Mp =c(tp)−1 =₋e−ζωn(π/ωd) µ cosπ+√ ζ 1₋ζ2 sinπ ¶ =e−(σ/ωd)π_=e−(ζ/ √ 1−ζ2_)π (68) Persen overshootmaksimum adalah e−(σ/ωd)π_×100%.

Waktu settling,ts: Nilai dari waktu settlingdapat ditentukan sesuai dengan aturan toleransi yang digunakan (2% atau 5%), Masing-masing dapat dihitung dengan persamaan sebagai berikut:

ts= 4 ζωn

= 4

σ untuk aturan toleransi 2% (69)

ts= 3 ζωn

= 3

σ untuk aturan toleransi 5% (70) 5.3 Stabilitas, Kriteria Stabilitas Routh

Dari bagian terdahulu, telah dibahas bahwa untuk suatu sistem yang telah dirancang perlu diselidiki stabilitasnya, dengan melihat respons transiennya. Karena, seperti terlihat pada Gambar 13 hal.44, untuk nilai ζ = 0 respons transien sistem orde dua menunjukkan gejala tidak stabil. Dalam merancang suatu sistem pengaturan, sistem yang tidak stabil selalu dihindari, dan harus dicarikan upaya untuk menstabilkan sistem.

Selain dengan cara menyelidiki respons transien dari suatu sistem, sta-bilitas sistem dapat pula diketahui dengan metode Routh. Dengan metode ini, tanpa harus mencari serpons transien sistem, dengan hanya melihat ke-dudukan/posisi kutup dalam koordinat kompleks dapat ditentukan apakah sistem akan stabil atau tidak.

5.3.1 Analisis stabilitas dalam bidang kompleks

Stabilitas suatu sistem untai tertutup (closed-loop) linear dapat diten-tukan dari kedudukan atau lokasi kutup-kutupnya dalam koordinat kompleks. Apabila suatu sistem mempunyai kutub yang berada pada lokasi di sebelah kanan dari σ = 0 (sebelah kanan setengah koordinat kompleks), maka sistem tersebut akan menjadi tak-stabil. Untuk lebih jelas lihat Gambar 17 hal.55. Jika sistem mempunyai satu kutup atau lebih yang berada di sisi sebelah kanan, maka dengan berjalannya waktu kutup-kutup tersebut menjadi mode yang dominan, sehingga respons sistem akan berosilasi dan secara monoton amplitudo osilasi meningkat sehingga sistem menjadi sangat tidak stabil, dan kalau sistem dibiarkan beroperasi terus, pada suatu saat akan terdapat kom-ponen sistem yang rusak. Sebaliknya apabila semua kutup dari suatu sistem berada di sisi sebelah kiri, garisσ = 0, maka mode yang dominan akan menye-babkan amplitudo osilasi menurun secara monoton, hingga suatu saat respon sistem akan konvergen di suatu nilai tertentu. Sistem semacam ini akan stabil. Stabilitas sistem dengan kutup berada disebelah kiri tidak dijamin penuh bila letak kutup sangat dekat dengan sumbujω. Karena itu perlu adanya jarak tertentu dari sumbu jω yang dapat menjamin keamanan stabilitas sistem.

5.3.2 Kriteria stabilitas Routh

Kriteria stabilitas Routh adalah suatu metode untuk menentukan lokasi kutup (di sebelah kiri atau kanan garis σ = 0) tanpa harus melakukan fak-torisasi polinomial penyebut dari fungsi alih sistem.

Fungsi alih suatu sistem dapat berbentuk sebagai berikut:

C(s) R(s) = B(s) A(s) = b0sm+b1sm−1+. . .+bm−1s+bm a0sn+a1sn−1+. . .+an−1s+an (m_≤n) (71)

Gambar 17: Daerah stabil dan tak stabil pada koordinat kompleks

Bilanmempunyai nilai lebih dari dua, maka untuk mendapatkan kutup-kutup dari sistem diperlukan waktu yang lama dan berbelit-belit karena harus me-lakukan faktorisasi. Untuk mengatasi kesulitan ini, dapat digunakan metode Routh. Dengan kriteria stabilitas Routh, polinomial penyebut A(s) tidak perlu difaktorisasi, dan kriteria stabilitas Routh dapat menentukan apakah ada kutup yang berada disebelah kanan dari sistem koordinat kompleks atau tidak. Bagaimana kriteria Routh dapat menentukan stabilitas sistem, berikut ini dikemukakan prosedur dari Kriteria stabilitas Routh

1. Tuliskan polinomial penyebut dari fungsi alih, A(s), seperti bentuk be-rikut ini.

a0sn+a1sn−1+. . .+an−1s+an= 0 (72) dengan semua koefisien (a0. . . an) semuanya riil dan asumsi bahwa tidak

ada akar (kutub) bernilai nol (an 6= 0). Persamaan ini sering disebut sebagai Persamaan karakteristik.

2. Bila pada koefisien polinomial A(s) terdapat nilai nol atau negatip diantara satu atau lebih koefisien yang bernilai positip, maka terdapat akar dari polinomial tersebut yang imaginer dan mempunyai komponen rill positip (komponen riil positip selalu terletak di sebelah kanan garis σ = 0). Dengan demikian sistem akan mempunyai kutup yang terletak pada daerah tidak stabil pada Gambar 17 hal.55. Karena itu, untuk kasus seperti ini sistem pasti tak-stabil.

3. Apabila semua koefisien polinomial mempunyai nilai positip, maka untuk menentukan stabilitas, koefisien-koefisien tersebut disusun dalam ben-tuk matriks dengan aturan sebagai berikut: koefiesen b1. . . bn,c1. . . cn,

Tabel 1: Matrikulasi koefisien polinomial dalam kriteria Routh

sn _{: a} 0 a2 a4 a6 . . . sn−1 _{: a} 1 a3 a5 a7 . . . sn−2 _{: b} 1 b2 b3 b4 . . . sn−3 _{: c} 1 c2 c3 c4 . . . sn−4 _{: d} 1 d2 d3 d4 . . . .. . ... ... s2 _{: e} 1 e2 s1 _{: f} 1 s0 _{: a} n

berikut: b1= a1a2−a0a3 a1 ; b2= a1a4−a0a5 a1 ; b3= a1a6−a0a7 a1 . . . (73) c1= b1a3−a1b2 b1 ; c2= b1a5−a1b3 b1 ; c3= b1a7−a1b4 b1 . . . (74) d1= c1b2−b1c2 c1 ; d2= c1b3−b1c3 c1 . . . (75) .. . ...

menurut kriteria Routh, Jumlah akar dari persamaan (72) hal.55 (atau jumlah kutup dari persamaan (71) hal.54 ) yang berada pada daerah positip (sisi sebelah kanan) atau dearah tak-stabil sama jumlahnya den-gan banyaknya perubahan tanda yang terjadi pada koefisien-koefisien kolom pertama pada matrikulasi Tabel 1 (a0, a1, b1, c1, d1, . . . g1). Perlu diketahui, bahwa dalam hal ini, cukup tanda dari koefisien kolom per-tama saja yang perlu diketahui. Nilai absolutnya tidak mutlak untuk dihitung. Dengan demikian dapat difahami bahwa untuk menyelidiki stabilitas suatu sistem dengan kriteria Routh tidak memerlukan penye-lesaian fungsi alih secara lengkap, tetapi cukup dengan menyusun ma-trikulasi Routh dan menghitung perubahan tanda pada koefisien dalam kolom pertama. Dari prosedur 2 dan 3 dalam kriteria Routh, dapat dis-impulkan bahwa suatu sistem akan stabil bila dan hanya bila : Semua koefisien pada persamaan (72) hal.55 mempunyai nilai positip dan bila koefisien tersebut disusun dalam bentuk matrikulasi Tabel 1 hal.56 tidak terjadi perubahan tanda pada koefisien dalam kolom pertamanya.

ini.

s4+ 2s3+ 3s2+ 4s+ 5 = 0,

matrikulasi dari persamaan ini adalah :

s4 _{: 1 3 5} s3 _{: 2 4 0} s2 _: 2·3−1·4 2 = 1 2·5−1·0 2 = 5 s1 _: 1·4−2·5 1 s0 _{: 5}

pada matrikulasi di atas, baris s4 _{dan s}3 _{dapat diperoleh dari koefisien} polinomial secara langsung. Jika terdapat baris yang kehabisan koefisien dapat digantikan secara langsung dengan nol, pada contoh ini angka nol pada baris s3 _{di bawah angka 5 diperoleh dengan cara itu. Baris s}2 dan s1 _{diperoleh dengan menggunakan persamaan (73) dan (74).} Koe-fisien pada baris s0 _{diperoleh langsung dari koefisien polinomial. Hasil} perhitungan dari matrikulasi di atas dapat ditulis sebagai berikut:

s4 _{: 1 3 5} s3 _{: 2 4 0} s2 _{: 1 5} s1 _: −6 s0 _{: 5}

Pada hasil akhir ini, koefisien pada kolom pertama adalah (1,2,1,₋6,5). Tanda dari koefisien ini secara berurutan adalah (+,+,+,₋,+). Jadi terdapat dua kali perubahan tanda, yaitu pertama dari positip ke negatip dan yang kedua dari negatip ke positip. Dengan demikian sistem yang dianalisis ini mempunyai dua buah kutup yang berada di sisi kanan

(daerah tak-stabil) dari bidang kompleks, karena terdapat dua kali pe-rubahan tanda pada kolom pertama matrikulasi kriteria Routh. Untuk memperjelas cara menghitung perubahan tanda dapat dikaji contoh be-rikut ini

+ + + - - - :1_×perubahan_⇒ 1 kutup di sisi kanan + + - + + + :2_×perubahan_⇒ 2 kutup di sisi kanan + + - - + + :2_×perubahan_⇒ 2 kutup di sisi kanan + + - + + - :3_×perubahan_⇒ 3 kutup di sisi kanan + + - + - + :4_×perubahan_⇒ 4 kutup di sisi kanan - + - + - + :5_×perubahan_⇒ 5 kutup di sisi kanan Contoh : Berikut ini adalah contoh penggunaan kriteria Routh untuk menentukan rentang stabilitas sistem, dalam kasus stabilitas bersyarat. Tentukan batas nilai K dari sistem dengan fungsi alih berikut ini agar sistem tetap stabil.

C(s)

R(s) =

K

s(s2_{+s+ 1)(s+ 2) +K} persamaan karakteristik dari fungsi alih ini adalah

s(s2+s+ 1)(s+ 2) +K = 0

s4_{+ 3s}3_{+ 3s}2_{+ 2s+K = 0} matrikulasi koefisien Routh untuk persamaan ini adalah

s4 _{: 1 3 K} s3 _{: 3 2 0} s2 _: 7 3 K s1 _{: 2−} 9 7K s0 _{: K}

koefisien pada kolom pertama adalah (1,3,7 3,(2−

9

7K), K). Tanda dari koefisien tersebut adalah (+,+,+,?,?). ? menunjukkan bahwa tanda untuk koefisien yang bersangkutan bergantung nilaiK. Karena itu agar tidak terjadi perubahan tanda pada kolom pertamaK harus memenuhi syarat berikut: pada baris s1 : 2₋9 7K >0 → 2> 9 7K → 2_×7 9 > K → 14 9 > K pada baris s0 : K >0

dua syarat ini harus dipenuhi secara bersamaan. Bila keduanya diga-bungkan akan diperoleh

14

9 > K >0 atau 0< K < 14

9 .

Syarat di atas menunjukkan rentang nilaiKyang membuat sistem masih tetap stabil, karena syarat tersebut menjamin tidak akan terjadi peruba-han tanda pada kolom pertama matrikulasi koefisien Routh. Di luar rentang ini sistem akan mempunyai kutup di sebelah kanan (daerah tak-stabil) dan sistem berosilasi dan kemudian menjadi tak-stabil. Pada ni-laiK = 14

9, (secara matematis) sistem akan berosilasi dengan amplitodo yang tetap karena kolom pertama baris s1 _{mempunyai nilai nol (bukan} positip dan bukan pula negatip).

6

Analisis Tempat Kedudukan Akar

Pada bagian ini akan dijelaskan tentang suatu metode yang dikembangkan oleh W. R. Evans yang dapat membantu untuk menganalisis sistem dalam perancangannya. Metode tersebut dinamakanAnalisis tempat kedudukan akar(Root-Locus Analysis). Teknik analisis tempat kedudukan akar ini memu-ngkinkan kita untuk menghitung respons domain-waktu dengan lebih akurat dan dapat menghasilkan informasi tentang respons frekuensi secara langsung.

Gambar 18: Diagram blok suatu sistem untai tertutup

Untuk memahami fungsi dan kegunaan metode analisis tempat kedudukan akar, sebaiknya dimulai dengan suatu sistem untai tertutup tipikal yang di-gambarkan dengan diagram blok seperti yang terlihat pada Gambar 18 hal.61. Fungsi alih untai tertutup dari gambar tersebut adalah:

C(s)

R(s) =

G1(s) 1 +G1(s)H(s)

(76) Fungsi alih untai terbuka G1(s)H(s) (lihat persamaan (25) hal.29) dapat dit-ulis sebagai G1(s)H(s) =K G(s) =K B(s) A(s) = K(b0sm+b1sm−1+. . .+bm−1s+bm) a0sn+a1sn−1+. . .+an−1s+an ₍₇₇₎

pada persamaan ini fungsi alih untai tertutup di atas dapat ditulis kembali sebagai C(s) R(s) = G1(s) 1 +G1(s)H(s) = G1(s) 1 +K G(s) = G1(s) 1 +KB(s)_A(s) = G1(s)A(s) A(s) +K B(s) (78) dan persamaan karakteristik untuk fungsi alih untai tertutup ini dapat ditulis dalam berbagai bentuk (semua persamaan ini mempunyai nilai dan arti yang sama) sebagai berikut

1 +K G(s) = 0 (79) 1 +K B(s) A(s) = 0 (80) A(s) +K B(s) = 0 (81) G(s) =₋1 K (82)

Dari persamaan karakteristik ini jelas bahwa nilai kutup-kutup dari fungsi alih sistem untai tertutup di atas (persamaan (76) ) tergantung pada nilai K. Seperti telah diuraikan dalam contoh penggunaan kriteria Routh pada bagian sebelumnya yaitu dalam kasus stabilitas bersyarat, bahwa terdapat rentang nilai K tertentu yang akan menjadikan sistem dalam kondisi tetap stabil. Kasus tersebut menunjukkan bahwa nilai K akan mempengaruhi stabilitas. Hal yang sama terjadi pula pada sistem Gambar 18 hal.61.

Karena akar-akar persamaan karakteristik ( persamaan (79)_∼(82) ) akan berubah dengan bervariasinya nilaiK, maka Evans menyarankan kepada per-ancang sistem agar menggambar tempat-tempat kedudukan akar yang mung-kin pada saat K bervariasi dari 0 hingga _∞. Dengan cara ini diharapkan perancang secara grafis akan dapat menentukan rentang harga K yang tepat agar sistem tetap berfungsi dengan baik tanpa resiko adanya ketidakstabilan yang timbul kemudian dalam unjuk kerjanya karena berubahnya nilai K.

Dalam analisis tempat kedudukan akar, kita tidak perlu melakukan fak-torisasi terhadap persamaan karakteristik dari fungsi alih untai tertutup (1 +

K G(s) = 0) untuk dapat menyelesaikan persoalan stabilitas. Yang diperlukan dalam analisis tempat kedudukan akar adalahkutup atau zero dariG(s) = B(s)_A(s)

saja, bukan kutup dan zero dari fungsi alih untai tertutup C(s)_R(s) = G1

[1+K G(s)],

karena sebenarnya kutup dan zero dari G(s) semuanya adalah kutup-kutup

dari C(s)_R(s) yang tempat kedudukannya di dalam koordinat kompleks

mempun-yai arti dalam hal stabilitas sistem untai tertutup secara keseluruhan. 6.1 Tempat kedudukan akar

Sebelum memulai pembahasan lebih lanjut, sebaiknya kita simak dan fahami dahulu dua definisi yang sangat mendasar sehubungan dengan teknik analisis tempat kedudukan akar.

• Tempat Kedudukan Akar: adalah tempat kedudukan dari semua nilai s yang dapat memenuhi persamaan karakteristik 1 +KG(s) = 0 dengan parameter riil K berubah dari 0_{→ ∞}. Karena 1 +KG(s) = 0 adalah penyebut dari fungsi alih untai tertutup suatu sistem yang ditinjau, maka akar-akar pada tempat kedudukan tersebut merupakan kutup sistem untai tertutup.

Bila persamaan karakteristik 1 +KG(s) = 0 diubah menjadi G(s) = _−K1, untukK bernilai riil postip maka pastiG(s) akan bernilai riil negatip. Dengan kata lain, bila G(s) dinyatakan dalam bentuk polar yaitu dengan ekspresi

BesardanSudut, maka agar 1 +KG(s) = 0 terpenuhi, makaK dalam bentuk

polar haruslah mempunyai sudut fase yang berlawanan (kedua sudut fase akan membentuk sudut 180◦_{). Dari kenyataan ini dapat didefinisikan:}