ESTIMATOR CAMPURAN KERNEL DAN DERET FOURIER DALAM REGRESI NONPARAMETRIK (Studi Kasus: Pemodelan Persentase Penduduk Miskin di Indonesia)

(1)

1

TESIS – SS142501

ESTIMATOR CAMPURAN KERNEL DAN DERET

FOURIER DALAM REGRESI NONPARAMETRIK

(Studi Kasus: Pemodelan Persentase Penduduk Miskin

di Indonesia)

NGIZATUL AFIFAH NRP. 1315201002

DOSEN PEMBIMBING :

Dr. Drs. I Nyoman Latra, MS

Prof. Dr. Drs. I Nyoman Budiantara, M.Si

PROGRAM MAGISTER JURUSAN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH NOPEMBER

SURABAYA 2017

(2)

ii

(3)

THESIS – SS142501

MIXED ESTIMATOR OF KERNEL AND FOURIER

SERIES IN NONPARAMETRIC REGRESSION

(Case Study: Modeling Percentage of Poor People in Indonesia)

NGIZATUL AFIFAH NRP. 1315201002

SUPERVISOR :

Dr. Drs. I Nyoman Latra, MS

Prof. Dr. Drs. I Nyoman Budiantara, M.Si

PROGRAM OF MAGISTER DEPARTMENT OF STATISTICS

FACULTY OF MATHEMATICS AND NATURAL SCIENCES INSTITUT TEKNOLOGI SEPULUH NOPEMBER

SURABAYA 2017

(4)

(5)

ESTLMA TOR CAMPURAN KERNEL DAN DERET FOURIER DALAM REGRESI NONPARAMETRIK

(Studi Kasus: Pemodela~ Persentase Penduduk Miskin di Indonesia)

Tesis disusun untuk memenuhi sa1ah satu syarat memperoleh gelar Magister Sains (M.Si) di

Institut Tekno1ogi Sepuluh Nopember 01eh:

NGIZATUL AFIF AH

NRP. 1315 201 002

Disetujui oleh:

/

1. Dr. Dis. I Nyoman Latra, MS

NIP. 19811'130 197901 1 001

. . /

/ 1'/y

2. Prof Dr. Drs. I Nyoman Budiantara, M.Si NIP. 19650603 198903 1 003

~~

3. Dr. Ora. Ismaini Zain, M.Si

NIP. 19600525 198803 2 001

4. Dr. Bambang Widjanarko Otok, M.Si NIP. 19681124 199412 1 001

Tanggal Ujian : 9 Januari 2017 Peri ode Wisuda : Maret 2017

(Pembimbing I)

(Pembimbing II)

(Penguji)

Direktur Program Pasca Sarjana,

Prof. Ir. Djauhar Manfaat, M.Sc., Ph.D NIP.l9601202 198701 1 001

(6)

v

ESTIMATOR CAMPURAN KERNEL DAN DERET FOURIER

DALAM REGRESI NONPARAMETRIK

(Studi Kasus: Pemodelan Persentase Penduduk Miskin di Indonesia)

Nama Mahasiswa : Ngizatul Afifah

NRP : 1315201002

Dosen Pembimbing : Dr. Drs. I Nyoman Latra, MS

Prof. Dr. Drs. I. Nyoman Budiantara, M.Si

ABSTRAK

Terdapat tiga macam pendekatan dalam analisis regresi yaitu regresi parametrik, nonparametrik dan semiparametrik. Regresi nonparametrik memungkinkan variabel respon mengikuti kurva regresi nonparametrik yang berbeda satu variabel prediktor dengan variabel prediktor lainnya. Pada data berpasangan



v v₁_i, ₂_i,...,v_pi,t t₁_i, ₂_i,...,t_qi,y_i



, i1, 2,..., ,n diasumsikan mengikuti model regresi nonparametrik campuran





 

1 1 , p q i i j j s s j s v t     







 y μ v t ε g h ε.

dengan = ( , , … , )′ dan = , , … , . Komponen g_j

 

v_j

didekati dengan fungsi kernel dan komponen h_s

 

t_s didekati dengan fungsi deret fourier. Error ε diasumsikan berdistribusi normal dengan mean nol dan varian konstan. Estimator diperoleh dengan menggunakan metode optimasi Penalized Least Square (PLS).Hasil estimator fungsi yang diperoleh adalah:

 





ˆ  , ,M , a λ C Φ λ y

 

_{ }

1 ˆ j p j ji j v   



g V Φ y

 





, 1 ˆ _{, ,} _, s q M si s t M   



h S Φ λ y dan μˆΦ λ, ,M



v ti, i



 Z Φ λ



, ,M



y.

Matriks C

_

Φ λ, ,M

_

, S



Φ λ, ,M



dan Z



Φ λ, ,M



bergantung pada bandwidth, parameter penghalus dan parameter osilasi. Model regresi campuran nonparametrik kernel dan deret fourier diterapkan pada data persentase penduduk miskin di Indonesia tahun 2013, dimana variabel responnya adalah persentase penduduk miskin (y), variabel prediktor yang mengikuti kurva regresi kernel adalah rata-rata lama sekolah (v1) dan Angka Melek Huruf atau AMH (v2),

sedangkan variabel prediktor yang mengikuti kurva regresi deret fourier adalah Rata-rata Lama Sekolah (t1). Pemodelan ini menghasilkan R2 sebesar 62,78

persen dan MSE sebesar 23,370.

Kata kunci: Deret Fourier, Kernel, Persentase Penduduk Miskin, Regresi Nonparametrik Campuran.

(7)

vi

(8)

vii

MIXED ESTIMATOR OF KERNEL AND FOURIER SERIES

IN NONPARAMETRIC REGRESSION

(Case Study: Modeling Percentage of Poor People in Indonesia)

Name : Ngizatul Afifah

NRP : 1315201002

Supervisor : Dr. Drs. I Nyoman Latra, MS

Prof. Dr. Drs. I. Nyoman Budiantara, M.Si

ABSTRACT

There are three kinds of approaches in the regression analysis that is parametric, nonparametric and semiparametric regression. Nonparametric regression allows the response variable follow different nonparametric regression curve of the predictor variables with other predictor variables. In the pairs of data



v1i,v2i,...,vpi,t1i,t2i,...,tqi,yi



, i1, 2, ..., ,n is assumed to follow mixed nonparametric regression model:





 

1 1 , p q i i j j s s j s v t     

_



_

 y μ v t ε g h ε.

where = ( , , … , )′ and = , , … , . Component gj

 

vj

approached by kernel functions and components h_s

 

t_s approached by fourier series. Error ε assumed normal distribution with mean zero and constant variance. Mixed estimator is obtained using Penalized Least Square (PLS). The estimator function is:

 





ˆ  , ,M , a λ C Φ λ y

_{ }

1 ˆ j p j ji j v   



g V Φ y

 





, 1 ˆ _{, ,} _, s q M si s t M   



h S Φ λ y and μˆ_{Φ λ}_{, ,}_M



v t_i, _i



Z Φ λ



, ,M



y.

Matrixes ( , , ), S



Φ λ, ,M



and Z

_

Φ λ, ,M

_

depends on bandwidth, smoothing parameter and oscillation parameters. The mixed estimator of kernel and fourier series in nonparametric regression applied to the data the percentage of poor people in Indonesia in 2013, where the variable response is the percentage of poor people in Indonesia (y), the predictor variables that follow the curve of regression kernel is Mean Years School (v1) and Adult Literacy Rate (v2), while

the predictor variables that follow Fourier series is Unemployment Rate (t1). This

modeling produces R2 of 62,78 percent and MSE of 23.370.

Keywords: Fourier Series, Kernel, Mixed Nonparametric Regression, Percentage of Poor People.

(9)

viii

(10)

ix

KATA PENGANTAR

Puji dan syukur penulis hadiratkan kepada Allah SWT, karena atas segala rahmat dan ridho-Nya sehingga tesis yang diberi judul “Estimator Campuran Kernel dan Deret Fourier dalam Regresi Nonparametrik (Studi Kasus: Pemodelan Persentase Penduduk Miskin di Indonesia)” ini bisa terselesaikan. Tesis ini merupakan salah satu syarat untuk menyelesaikan pendidikan di Program Magister S2 Statistika ITS. Ada banyak pihak yang telah membantu dalam penulisan tesis ini, sehingga penulis ingin menyampaikan ucapan terima kasih kepada

1. Bapak Dr. Drs. I Nyoman Latra, MS dan Bapak Prof. Dr. Drs. I Nyoman Budiantara, M.Si selaku dosen pembimbing, yang telah bersedia meluangkan waktu untuk memberikan bimbingan, saran, dan ilmu yang sangat bermanfaat dalam penyelesaian tesis ini.

2. Ibu Dr. Ismaini Zain, M.Si. dan Bapak Dr. Bambang Widjanarko Otok, M.Si. selaku dosen penguji yang telah memberikan banyak saran dan masukan agar tesis ini menjadi lebih baik.

3. Bapak Dr. Suhartono, M.Sc. selaku Ketua Jurusan Statistika ITS dan Bapak Dr. rer. pol. Heri Kuswanto, M.Si. selaku Kaprodi Pascasarjana Statistika FMIPA ITS.

4. Bapak /Ibu dosen pengajar di Jurusan Statistika ITS, terima kasih atas semua ilmu berharga yang telah diberikan.

5. Bapak/Ibu staf dan karyawan di Jurusan Statistika ITS, terima kasih atas segala bantuan selama masa perkuliahan penulis

6. Kedua orang tua yang sangat penulis sayangi dan hormati, Ibu Suwaebah dan Bapak M. Abdul Djalal yang tidak pernah lelah mendaokan yang terbaik untuk penulis serta selalu memberi motivasi untuk tidak pernah menyerah. Terimakasih juga untuk kakak (Tatik Farikhah) dan adik (Azizatul Khakimah) yang selalu menjadi penyemangat penulis.

(11)

x

7. Semua teman-teman seperjuangan S2 Statistika ITS, terima kasih atas bantuan dan kebersamaan selama ini, khususnya Pencari Ilmu (Mbak Cinti, Mbak Tutus, Titin, Rizfani, Asmita, Rani, Maman dan Surya).

8. Semua teman-teman SKC (Fery, Nenah, Erti, Sofia dan Revi), The Sister (Mia, Dewi, Mbak Atik, Efa dan Rofik), Vian dan Arini yang selalu membantu penulis dalam setiap kesulitan.

9. Lembaga Pengelolala Dana Pendidikan (LPDP) yang telah memberikan dukungan finansial melalui beasiswa BPI tahun 2015-2017.

10.Serta, semua pihak yang telah membantu penulis, namun tidak dapat penulis sebutkan satu per satu.

Penulis menyadari bahwa tesis ini masih jauh dari sempurna, sehingga kritik dan saran sangat diharapkan. Semoga tesis ini dapat memberikan manfaat guna memperluas wawasan keilmuan pembacanya.

Surabaya, Januari 2017 Penulis

(12)

xi

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

LEMBAR PENGESAHAN... iii

ABSTRAK ... v

ABSTRACT ... vii

KATA PENGANTAR ... ix

DAFTAR ISI ... xi

DAFTAR TABEL ... xv

DAFTAR GAMBAR... xvii

DAFTAR LAMPIRAN ... xix

BAB 1 PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Perumusan Masalah ... 4

1.3 Tujuan Penelitian ... 4

1.4 Manfaat Penelitian ... 5

1.5 Batasan Masalah Penelitian ... 5

BAB 2 TINJAUAN PUSTAKA ... 7

2.1 Analisis Regresi ... 7

2.2 Regresi Parametrik, Nonparametrik dan Semiparametrik ... . 7

2.3 Regresi Nonparametrik Kernel ... 9

2.4 Regresi Nonparametrik Deret Fourier ... 12

2.5 Generalized Cross Validation (GCV) ... 15

2.6 Koefisien Determinasi R2 ... 16

2.7 Tinjauan Non Statistika ... . 16

2.7.1 Konsep dan Pengukuran Kemiskinan ... 16

(13)

xii

BAB 3 METODE PENELITIAN ... 19

3.1 Sumber Data ... 19

3.2 Variabel Penelitian ... 19

3.3 Definisi Operasional Variabel Penelitian ... 19

3.4 Tahapan Penelitian ... 20

BAB 4 HASIL DAN PEMBAHASAN ... 25

4.1 Model Regresi Campuran Nonparametrik Kernel dan Deret Fourier ... 25

4.2 Estimasi Kurva Regresi Nonparametrik Kernel dan Deret Fourier ... 27

4.3 Sifat Estimator Kurva Regresi ... 34

4.4 Pemilihan Bandwidth, Parameter Osilasi M, dan Parameter Penghalus Optimum ... 36

4.5 Aplikasi pada Data Kemiskinan ... 36

4.5.1 Analisis Deskriptif ... 37

4.5.2 Model Regresi Nonparametrik Campuran .... 40

4.5.2.1 Model dengan Komponen Deret Fourier 1 Parameter Osilasi ... 41

(14)

xiii

BAB 5 KESIMPULAN DAN SARAN ... 51

5.1 Kesimpulan ... 51

5.2 Saran... 52

DAFTAR PUSTAKA ... 53

LAMPIRAN ... 57

(15)

xiv

(16)

xv

DAFTAR TABEL

Halaman

Tabel 4.1 Statistik Deskriptif Variabel Respon dan Variabel Prediktor ... 37

Tabel 4.2 GCV dari Model-Model dengan 2 Kernel dan 1 Deret Fourier .... 39

Tabel 4.3 GCV dari Model-Model dengan 1 Kernel dan 2 Deret Fourier .... 39

Tabel 4.4 Variabel Prediktor dan Pendekatan yang Digunakan ... 40

Tabel 4.5 Perbandingan Nilai GCV Model Komponen Deret Fourier dengan M = 1 ... 41

Tabel 4.10 Perbandingan GCV untuk Pemilihan Parameter Osilasi M ... 46

Tabel 4.11 Estimasi Komponen Deret Fourier ... 46

(17)

xvi

(18)

xvii

DAFTAR GAMBAR

Halaman

Gambar 2.1 Scatter Plot Kernel ... 9

Gambar 2.2 Deret Fourier Non-Tren dengan M = 1 ... 13

Gambar 2.3 Deret Fourier Non-Tren dengan M = 3 ... 13

Gambar 2.4 Deret Fourier Tren menurun dengan M = 1 ... 13

Gambar 2.5 Deret Fourier Tren menurun dengan M = 3 ... 13

Gambar 2.6 Deret Fourier Tren naik dengan M = 1 ... 13

Gambar 2.7 Deret Fourier Tren naik dengan M = 3 ... 13

Gambar 3.1 Langkah-langkah Tahap Analisis untuk Tujuan Pertama ... 22

Gambar 3.1 Langkah-langkah Tahap Analisis untuk Tujuan Kedua ... 23

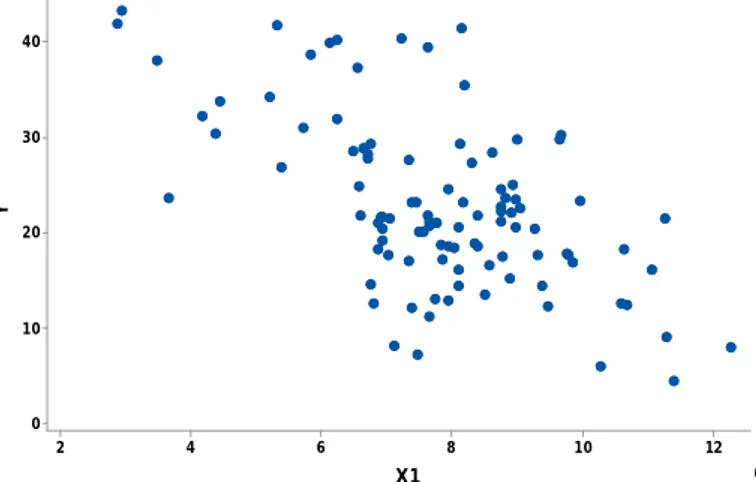
Gambar 4.1 Scatter Plot antara Persentase Penduduk Miskin (Y) dan Rata-Rata Lama Sekolah (X1) ... 37

Gambar 4.2 Scatter Plot antara Persentase Penduduk Miskin (Y) dan Tingkat Pengangguran Terbuka (X2) ... 38

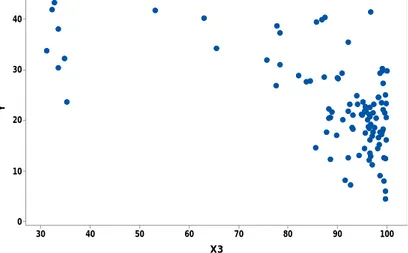
Gambar 4.3 Scatter Plot antara Persentase Penduduk Miskin (Y) dan Angka Melek Huruf (X3) ... 38

(19)

xviii

(20)

xix

DAFTAR LAMPIRAN

Halaman Lampiran 1 Data yang Digunakan ... 57 Lampiran 2 Syntax R Model Nonparametrik Campuran 2 Kernel dan

1 Fourier ... 60 Lampiran 3 Syntax R Model Nonparametrik Campuran 1 Kernel dan

(21)

xx

(22)

1

BAB 1

PENDAHULUAN

1.1Latar Belakang

Analisis regresi merupakan salah satu analisis dalam Statistika yang digunakan untuk menyelidiki pola hubungan fungsional antara dua atau lebih variabel. Dalam mengestimasi kurva regresi terdapat tiga pendekatan, yaitu pendekatan regresi parametrik, regresi nonparametrik dan regresi semiparametrik (Budiantara, Mariati, Ratnasari, Zain, Ratna, Sudiarsa, Mardianto, dan Hendayanti, 2015a). Identifikasi awal pola data dapat dilakukan dengan memanfaatkan pengalaman masa lalu atau menggunakan diagram pencar (scatter plot). Seringkali dalam praktek, bentuk pola hubungan fungsional antara variabel respon dan variabel prediktor tidak diketahui. Pada kondisi ini tentu model regresi parametrik kurang sesuai digunakan. Seiring dengan makin berkembangnya teknologi di bidang komputasi, model regresi nonparametrik semakin banyak digunakan. Model regresi nonparametrik baik digunakan untuk pola data yang tidak diketahui bentuknya. Regresi nonparametrik memiliki fleksibilitas yang tinggi, dimana data diharapkan mencari sendiri bentuk estimasi kurva regresinya tanpa dipengaruhi oleh subyektifitas peneliti (Eubank, 1999).

Model-model pendekatan regresi nonparametrik yang dikembangkan oleh penelitian sebelumnya mempunyai dua asumsi yang mendasar. Asumsi pertama yaitu pola dari masing-masing prediktor dalam model regresi nonparametrik multivariabel prediktor dianggap mempunyai pola yang sama, sedangkan asumsi yang kedua yaitu peneliti memaksakan menggunakan satu bentuk estimator model untuk setiap variabel prediktor. Dua asumsi yang digunakan dalam model regresi nonparametrik ini pada dasarnya hanya ada secara teoritis. Pada penelitian sebenarnya sering dijumpai kasus-kasus dimana terjadi pola data yang berbeda dari masing-masing variabel prediktor. Selain itu dengan hanya menggunakan satu bentuk estimator dalam mengestimasi kurva regresi nonparametrik multivariabel, berakibat estimator yang diperoleh tidak akan sesuai dengan pola data. Akibatnya, estimasi model regresi yang diperoleh tidak tepat

(23)

2

dan cenderung mempunyai error yang besar. Berdasarkan hasil-hasil penelitian di atas, Budiantara, Ratnasari, Ratna dan Zain (2015b) menyarankan penggunaan estimasi model kurva regresi yang sesuai dengan pola data.

Ada banyak jenis estimator dalam model regresi nonparametrik, seperti kernel, spline, polinomial lokal, wavelet dan deret fourier. Beberapa penelitian mengenai estimator kernel telah dilakukan oleh banyak peneliti seperti oleh Okumura dan Naito (2006), Yao (2007), Kayri dan Zirhlioglu (2009) serta Cheng, Paige, Sun dan Yan (2010). Penelitian mengenai estimator spline telah dilakukan oleh peneliti lain seperti Eubank (1999), Merdekawati dan Budiantara (2013) serta Darmawi dan Otok (2014). Penelitian tentang estimator polinomial lokal dilakukan oleh Su dan Ullah (2008), He dan Huang (2009), Filho dan Yao (2009) serta Qingguo (2010). Penelitian mengenai estimator wavelet antara lain dilakukan oleh Antoniadis, Bigot dan Sapatinas (2001), Amato dan De Canditiis (2001), serta Taylor (2009). Penelitian untuk estimator deret fourier dilakukan oleh peneliti antara lain Bilodeau (1992), Galtchouk dan Pergamenshchikov (2009) serta Ratnasari, Budiantara, Zain, Ratna dan Mariati (2015).

Estimator kernel adalah pengembangan dari estimator histogram. Estimator ini merupakan estimator linier yang mirip dengan estimator regresi nonparametrik yang lain, perbedaannya hanya karena estimator kernel terdapat

bandwidth (Eubank, 1999). Kelebihan dari estimator kernel adalah memiliki kemampuan yang baik dalam memodelkan data yang tidak mempunyai pola tertentu (Hardle, 1994). Selain itu, estimator kernel mempunyai sifat fleksibel, bentuk matematisnya mudah, dan dapat mencapai tingkat kekonvergenan yang relatif cepat. Dari segi komputasinya, metode kernel lebih mudah dilakukan dan mudah diimplementasikan.

Model regresi nonparametrik yang lain adalah deret fourier. Salah satu keunggulan pendekatan regresi nonparametrik dengan menggunakan deret Fourier adalah mampu mengatasi data yang mempunyai sebaran trigonometri, dalam hal ini adalah sinus dan cosinus. Pola data yang sesuai dengan pendekatan Fourier merupakan pola data yang berulang, yaitu pengulangan terhadap nilai variabel dependen untuk variabel independen yang berbeda-beda (Prahutama, 2013).

(24)

3

Model regresi nonparametrik dapat diterapkan di berbagai bidang keilmuan, salah satunya adalah bidang sosial. Pada bidang ini, model regresi nonparametrik dapat diterapkan untuk menganalisis masalah kemiskinan. Masalah kemiskinan merupakan masalah yang sangat serius yang dihadapi oleh negara-negara di dunia terutama negara-negara-negara-negara berkembang termasuk Indonesia. Pengentasan kemiskinan telah menjadi agenda global yang tercantum dalam tujuan Sustainable Development Goals (SDGs) yang ditetapkan oleh Perserikatan Bangsa-Bangsa (PBB)(United Nations, 2016).

Pada tahun 2013 persentase penduduk miskin di Indonesia mencapai 11,47 persen. Dari 33 provinsi di Indonesia, terdapat tujuh provinsi dengan persentase penduduk miskin yang tergolong tinggi dibandingkan provinsi-provinsi lainnya yaitu Papua, Papua Barat, Nusa Tenggara Timur, Maluku, Gorontalo, Bengkulu, dan Aceh berturut-turut yaitu 31,53 persen; 27,14 persen; 20,24 persen; 19,27 persen; 18,01 persen; 17,75 persen dan 17,72 persen (BPS, 2016a). Hal ini akan menjadi hal yang menarik untuk dipelajari lebih lanjut, dimana jika meninjau

scatter plot dari variabel-variabel yang berpengaruh terhadap persentase kemiskinan di ketujuh provinsi tersebut maka akan didapatkan bahwa sebagian variabel tersebut membentuk pola regresi kernel dan sebagian yang lain membentuk pola deret fourier.

Estimasi model kurva yang tepat yaitu estimasi yang sesuai dengan pola data, sehingga penelitian ini merujuk pada penggunaan model estimator campuran kernel dan deret fourier. Penelitian tentang estimasi campuran telah dilakukan oleh Sudiarsa, Budiantara, Suhartono dan Purnami, (2015), dalam hal ini fokus penelitian adalah pada estimator gabungan deret fourier dan truncated spline dalam regresi nonparametrik multivariabel, dimana estimator diperoleh melalui optimasi Penalized Least Square (PLS). Rory (2016) melakukan penelitian serupa mengenai regresi campuran nonparametrik spline truncated dan kernel untuk pemodelan data kemiskinan di Provinsi Papua dengan menggunakan optimasi

Ordinary Least Square (OLS). Purnomo (2016) melakukan penelitian terhadap estimator campuran kernel dan regresi spline truncated linier multivariabel dalam regresi nonparametrik di Provinsi Jawa Tengah. Metode optimasi yang digunakan adalah OLS. Rismal (2016) melakukan penelitian mengenai estimasi campuran

(25)

4

spline truncated dan kernel dalam regresi nonparametrik pada data Tingkat Pengangguran Terbuka (TPT) di Provinsi Jawa Barat. Dalam penelitian tersebut, metode optimasi yang digunakan adalah metode Maximum Likelihood Estimation

(MLE).

Berdasarkan uraian di atas, pokok permasalahan dalam model regresi nonparametrik ini adalah bagaimana bentuk estimator kurva regresi campuran nonparametrik kernel dan deret fourier. Metode optimasi yang digunakan adalah PLS, dimana dalam metode tersebut terdapat parameter penghalus yang baik digunakan untuk pada deret fourier. Pokok permasalahan selanjutnya adalah penerapan estimator kurva regresi campuran nonparametrik tersebut pada data riil, yaitu data persentase penduduk miskin di Indonesia.

1.2Perumusan Masalah

Dengan memperhatikan latar belakang yang telah diuraikan di atas, permasalahan yang dapat dirumuskan adalah sebagai berikut:

1. Bagaimana bentuk dan sifat estimator campuran kernel dan deret fourier dalam regresi nonparametrik?

2. Bagaimana memodelkan persentase penduduk miskin di Indonesia dengan menggunakan estimator campuran kernel dan deret fourier dalam regresi nonparametrik?

1.3Tujuan Penelitian

Berdasarkan perumusan masalah di atas, tujuan dari penelitian ini adalah sebagai berikut:

1. Mengkaji bentuk dan sifat estimator campuran kernel dan deret fourier dalam regresi nonparametrik.

2. Memodelkan persentase penduduk miskin di Indonesia dengan menggunakan estimator campuran kernel dan deret fourier dalam regresi nonparametrik.

(26)

5 1.4 Manfaat Penelitian

Manfaat yang ingin dicapai dari penelitian ini adalah sebagai berikut : 1. Mengembangkan wawasan keilmuan dan pengetahuan tentang regresi

nonparametrik kernel.

2. Mengembangkan wawasan keilmuan dan pengetahuan tentang regresi nonparametrik deret fourier.

3. Mengembangkan wawasan keilmuan dan pengetahuan tentang estimator campuran kernel dan deret fourier dalam regresi nonparametrik.

4. Mengetahui model estimasi persentase penduduk miskin dengan menggunakan estimator campuran kernel dan deret fourier dalam regresi nonparametrik yang dapat digunakan untuk memprediksi presentase kemiskinan di Indonesia.

1.5Batasan Masalah Penelitian

Dalam penelitian ini, ruang lingkup permasalahan dibatasi pada beberapa hal sebagai berikut.

1. Permasalahan persentase penduduk miskin dalam penelitian ini dibatasi pada persentase penduduk miskin di Provinsi Papua, Papua Barat, Nusa Tenggara Timur, Maluku, Gorontalo, Bengkulu, dan Aceh.

2. Estimator kernel yang digunakan dalam estimator campuran adalah estimator kernel Nadaraya-Watson dan fungsi kernel yang digunakan adalah Kernel Gaussian.

3. Estimator campuran kernel dan deret fourier diperoleh dengan menggunakan optimasi Penalized Least Square (PLS).

4. Metode yang digunakan dalam menentukan bandwidth optimum, parameter osilasi M dan paramater penghalus adalah metode Generalized Cross Validation (GCV).

5. Sifat estimator campuran yang akan dikaji adalah sifat bias dan sifat kelas estimator linier.

(27)

6

(28)

7

BAB 2

TINJAUAN PUSTAKA

2.1Analisis Regresi

Analisis regresi digunakan untuk mengetahui model pola hubungan antara variabel respon dan variabel prediktor. Diberikan n pasangan titik ( , ), = 1, . . . , dengan asumsi dan dihubungkan oleh model regresi

( ) , 1, 2,...,

i i i

y  t  i n (2.1)

Dimana adalah error random yang diasumsikan identik, independen dan berdistribusi normal dengan mean nol dan varian . Fungsi ( ) merupakan fungsi yang tidak diketahui pada titik , … , . Fungsi disebut fungsi regresi atau kurva regresi. Analisis regresi memiliki dua tujuan utama, pertama, memberikan cara mengeksplorasi hubungan antara variabel respon dan variabel prediktor dan yang kedua adalah membuat prediksi (Rory, 2016).

2.2Regresi Parametrik, Nonparametrik dan Semiparametrik

Model regresi umumnya dibagi ke dalam tiga pendekatan, yaitu model regresi parametrik, model regresi nonparametrik dan model regresi semiparametrik. Apabila bentuk kurva ( ) pada persamaan (2.1) diketahui, maka pendekatan model regresi ini dinamakan pendekatan model regresi parametrik. Apabila bentuk kurva ( ) tidak diketahui atau tidak terdapat informasi masa lalu yang lengkap tentang bentuk pola datanya, maka pendekatan model regresi yang digunakan adalah pendekatan model regresi nonparametrik. Dalam beberapa kasus, sebagian bentuk pola data diketahui, sedangkan untuk sebagian yang lain bentuk datanya tidak diketahui. Pada kasus ini, pendekatan model regresi yang disarankan adalah pendekatan model regresi semiparametrik (Rory, 2016).

Dalam regresi parametrik terdapat asumsi yang sangat kaku dan kuat yaitu bentuk kurva regresi diketahui, misalnya linier, kuadratik, kubik, polinomial derajat p, eksponen, dan lain-lain. Untuk memodelkan data menggunakan regresi linier, kudrat, kubik atau yang lain-lain, umumnya dimulai dengan membuat

(29)

8

scatterplot. Apabila scatter plot ini terdapat kecenderungan data mengikuti pola linier maka digunakan model regrsi (parametrik) linier, sebaliknya jika scatter plot data terdapat kecenderungan pola kuadratik maka digunakan model regresi (parametrik) kuadratik, dan seterusnya. Disamping memperhatikan pola kecenderungan data melalui scatter plot, peneliti dituntut dalam regresi paramaterik memiliki informasi di masa lalu yang detail tentang pola agar data diperoleh pemodelan yang baik (Budiantara, 2011).

Secara umum bentuk model regresi linear berganda dengan p variabel prediktor diberikan oleh persamaan (2.2) :

0 1 1 1 2 ... , 1, 2,...,

i i i p pi i

y    x  x   x  i  n (2.2)

Dimana y_i adalah variabel respon, ₀adalah konstanta, adalah koefisien variabel prediktor, dan ε_iadalah error dimana ε_i ~ N



0,2



.

Model regresi (2.2) dapat ditulis dalam bentuk matriks sebagai berikut :

 

y Xβ ε _(2.3)

dengan y_{adalah vektor dari variabel respon berukuran} × 1, merupakan matriks berukuran × ( + 1) dan adalah vektor parameter yang akan diestimasi berukuran (p1) 1 , ε_{adalah vektor}error random berukuran × 1 berdistribusi normal, independen dengan mean nol dan variansi 2I. Secara lengkap matriks dan vektor-vektor tersebut diberikan oleh:

11 12 1 0 1 1 21 22 2 1 2 2 31 32 3 1 2 1 1 1 , , , dan 1 p p p p n n n n np x x x y x x x y x x x y x x x                     _ _       _ _                   _ _ _ _             y X β ε          (2.4)

Estimator parameter-parameter model diperoleh berdasarkan berbagai metode yang telah dikenal dalam Statistika, yaitu Least Square atau Maximum Likelihood Estimator, jika digunakan metode least square didapat estimator parameter :

1

ˆ _₍ _ ₎ _

β X X X y (2.5) Regresi semiparametrik diperoleh dari gabungan antara komponen parametrik dan komponen nonparametrik. Dalam beberapa kasus, variabel respon

(30)

9

dapat memiliki hubungan linear dengan salah satu variabel prediktor, tetapi dengan variabel prediktor yang lain tidak diketahui bentuk pola hubungannya. Model regresi semiparametrik dirumuskan sebagai berikut :

( ) , 1, 2,3,...,

i i i i

y xβ z  i n (2.6)

i

y adalah variabel respon ke-i, x_iadalah komponen parametrik, ( )z_i adalah fungsi regresi nonparametrik, dan adalah random error, dimana ~N(0,σ ). 2.3Regresi Nonparametrik Kernel

Diberikan pasangan pengamatan independen ( , ), = 1, 2, . . . , dimana adalah variabel respon, sedangkan adalah variabel prediktor. Hubungan dan dapat dimodelkan secara fungsional dalam bentuk

( ) ,

i i i

y  g v  (2.7)

dimana kurva regresi g v( )_i merupakan kurva yang tidak diketahui bentuknya seperti pada Gambar 2.1.

Gambar 2.1. Scatter Plot Kernel

Menurut Hardle (1994), kurva g v( )_i pada model nonparametrik dapat diestimasi dengan pendekatan kernel yang didasarkan pada fungsi densitas kernel. Kurva g v( )_i pada model (2.7) dapat diestimasi menggunakan estimator kernel Nadaraya-Watson.

Model regresi kernel Nadaraya-Watson diperoleh dari meminimumkan fungsi



0



2 1 . n i i i v v N y  K        _ _  



(31)

10 Dengan demikian diperoleh

0 1 1 ˆ _, i n i n i i i v v K y v v K                    



Akibatnya:

 









 





1 1 1 1 1 1 ˆ , 2.8 n i i n i _i i n i i i K v v g v n y n K v v n W v y              



dimana g vˆ ( )_ adalah fungsi taksiran regresi kernel dan  merupakan lebar

bandwidth. Fungsi W vi( ) merupakan fungsi pembobot

 









1 1 1 n i i n i _i i K v v W v n K v v         



dimana K v v_



 _i



adalah fungsi kernel





1 i i v v K_ v v K        _ _  

Fungsi kernel adalah fungsi yang bernilai riil, kontinu, terbatas dan simetris dan intergralnya sama dengan satu atau

_

K z dz

 

1. Fungsi kernel dapat berupa kernel uniform, kernel segitiga, kernel epanechnikov, kernel kuadrat, kernel triweight dan kernel Gaussian (Widiardi, 2014) sebagai berikut:

1. Kernel uniform

 

1, 1 2 K z z         2. Kernel Triangle



K z

 

 1 z , z 1



3. Kernel Epanechnikov

 

3



1 2



, 1 4 K z z z          4. Kernel Quartic

 

15



1 2



2, 1 16 K z z z         

(32)

11 5. Kernel Triweight

 

35



1 2



3, 1 32 K z z z         

6. Kernel Gaussian

 

1 exp 1 2 , 2 2 K z z z       _ _           

Jika bentuk penjumlahan pada persamaan (2.8) dijabarkan dengan lebih lengkap, maka

 

1

 

1

 

1

 

1 1 2 2

ˆ ... _n _n

g v_ n W _ v y n W _ v y  n W _ v y

Karena berlaku untuk setiap = 1 sampai dengan = , maka jika persamaan untuk 1 sampai dengan digabungkan ke dalam bentuk matriks akan menjadi

 

1 1 1 1 ₁ ₁ ₂ ₁ ₁ ₁ 1 1 1 2 1 2 2 2 2 2 1 1 1 1 2 ˆ _... ˆ ... ... ˆ n n n n n n n n g v _{n W} _v _{n W} _v _{n W} _v _y g v n W v n W v n W v y n W v n W v n W v y g v  _ _ _                    _ _{ } _   _ _{ } _   _ _{ } _    _ _{ } _   _ _{ } _   __ _{ }_ _        

Jika dinotasikan ke dalam bentuk matriks akan menjadi

 

ˆ_ v   g V y (2.9) dimana

 

1 1 1 1 ₁ ₁ ₁ ₂ ₁ ₁ 1 1 1 2 2 1 2 2 2 2 1 1 1 1 2 2 ˆ _... ˆ ... ˆ , dan ... ˆ n n n n n n n g v _y _{n W} _v _{n W} _v _{n W} _v g v y n W v n W v n W v v y n W v n W v n W v g v  _ _ _                      _ _ _ _   _ _ _ _   _ _ _ _ _ _         _ _ _ _   _ _ __ __   g y V      

Vektor gˆ_

 

v berukuran × 1, vektor y berukuran × 1 dan matriks V

 



berukuran × .

Estimator kernel sangat sensitif pada pemilihan bandwidth  yang fungsinya mengontrol kemulusan kurva estimasi. Jika bandwidth  diperkecil maka bias akan turun, namun varian akan membesar, sebaliknya jika bandwidth 

diperbesar maka varian yang akan turun, namun bias akan membesar. Oleh karena itu, perlu adanya keseimbangan antara bias dan varian melalui pemilihan bandwidth  yang optimum (tidak terlalu kecil dan tidak terlalu besar).

(33)

12 2.4Regresi Nonparametrik Deret Fourier

Estimator Deret Fourier dalam regresi nonparametrik umumnya digunakan apabila data yang diselidiki polanya tidak diketahui dan ada kecenderungan berulang. Deret fourier merupakan polinomial trigonometri yang mempunyai fleksibelitas, sehingga dapat menyesuaikan diri secara efektif terhadap sifat lokal data. Deret Fourier baik digunakan untuk menjelaskan kurva yang menunjukkan gelombang sinus dan cosinus.

Pendekatan regresi nonparametrik Deret Fourier diperoleh dengan meminimumkan Penalized Least Squares (PLS), yaitu kriteria pendugaan yang menggabungkan Goodness of fit dengan kemulusan kurva dimana diantara keduanya dikontrol oleh suatu parameter pemulusan.

Apabila fungsi hC

_

0,

_

{ ;h hkontinu pada (0, )} maka ukuran kesesuaian kurva terhadap data adalah ∑ ( − ℎ( )) dan ukuran kekasaran kurva adalah ∫ ℎ ( ) . Estimator h diperoleh dengan meminimumkan PLS sebagai berikut:

 



 



 

_{ }





2 2 ₂ 1 0 0, 1 2 n i i h C i Min n y h t  h t dt             





 _(2.10)

 adalah parameter penghalus dan 0. Untuk nilai  yang sangat besar akan menghasilkan estimator kurva regresi yang sangat halus. Sebaliknya untuk nilai 

yang kecil akan memberikan estimator kurva regresi yang sangat kasar(Tripena, 2009). Karena h adalah fungsi yang kontinu maka h dapat dihampiri dengan fungsi T(t), dimana:

 

0 1 1 cos 2 M k k T t bt a a kt    

_

(2.11)

dimana, , , , = 1, 2, … , merupakan parameter-parameter model dan k

merupakan parameter osilasi. Bentuk pada persamaan (2.11) disebut deret fourier dengan tren, sedangkan persamaan (2.12) berikut disebut sebagai deret fourier non-tren yaitu: 0 1 1 ( ) cos 2 M k k T t a a kt   



(2.12)

(34)

13

Ilustrasi dari persamaan (2.11) dan persamaan (2.12) dapat dilihat pada gambar berikut:

Gambar 2.2 Deret Fourier Non-Tren dengan M = 1

Gambar 2.3 Deret Fourier Non- Tren dengan M = 3

Gambar 2.4 Deret Fourier Tren menurun dengan M = 1

Gambar 2.5 Deret Fourier Tren menurun dengan M = 3

Gambar 2.6 Deret Fourier Tren naik dengan M = 1

Gambar 2.7 Deret Fourier Tren naik dengan M = 3 0 2 4 6 8 10 -2 -1 0 1 2 3 4 t y 0 2 4 6 8 10 -1 0 -5 0 5 1 0 t y 0 2 4 6 8 10 -1 5 -1 0 -5 0 5 t y 0 2 4 6 8 10 -2 5 -2 0 -1 5 -1 0 -5 0 5 1 0 t y 0 2 4 6 8 10 2 4 6 8 1 0 1 2 t y 0 2 4 6 8 10 -1 0 -5 0 5 1 0 1 5 2 0 2 5 t y

(35)

14

Dari ilustrasi-ilustrasi di atas terlihat bahwa semakin besar nilai M maka semakin rapat kurva deret fourier yang terbentuk dan sebaliknya.

Untuk menyelesaikan persamaan (2.10) terlebih dahulu dicari nilai P(a) dengan

 



₂



2 0 4 2 1 2 (2.13) M k k P a T t dt k a     





Berdasarkan persamaan (2.11) diperoleh PLS:

 



 



 

_{ }







 







0 1 0 1 0 1 2 2 ₂ 1 0 0, 1 2 1 4 2 0 , , ,..., 1 1 1 1 , , ,..., 1 1 , , ,..., 2 1 cos 2 k k k n i i h C i n M M i i k i k b a a a R i k k b a a a R b a a a R Min n y T t T t dt Min n y bt a a kt k a Min n Min n n n    _                         _ _     _ _    _  _        _          







y Xa y Xa a Da y y a X y





















0 1 1 1 1 1 1 , , ,...,k 2 (2.14) b a a a R n Min n n n                         a X y a X X D a y y a X y a X X D a

dalam hal ini



0, 0,1 , 2 ,...,4 4 4



, ,1 ₀, ,...,₁

2 M diag M b a a a   _{ } _   D a dan 1 1 1 1 2 2 2 2 3 3 3 3

1 cos cos 2 cos

n n n n t t Mt t t t t Mt t t t Mt t t t Mt                  X           .

Matriks D berukuran (M 2) ( M 2), vektor a berukuran (M 2) 1 dan Matriks X berukuran n(M 2).

Misalkan n1y y 2n1a X y a   



n1X X D a



Q

 

a . Dengan menurunkan secara parsial Q a

 

terhadap a dan hasilnya disamakan dengan nol didapat:

 



1



1 1 ˆ  n   n .     a X X D X y (2.15)

(36)

15 Estimator untuk kurva regresihdiberikan oleh:

 

0

 

1 1 ˆ ˆ _ˆ _ˆ _cos 2 M i i k i k h t_ b  t a  a  kt    

_

(2.16)

Estimasi persamaan regresi h diberikan oleh:

 

ˆ _t _ˆ      h Xa S y (2.17) dimana

_{ }



1



1 1 n n          S X X X D X (Tripena, 2009).

2.5 Generalized Cross Validation (GCV)

Perolehan regresi kernel yang optimal bergantung pada bandwidth  sedangkan deret fourier bergantung pada parameter penghalus λ dan parameter osilasi M. Bandwidth  maupun parameter penghalus λ dan parameter M yang terlalu kecil akan menghasilkan kurva yang under-smoothing yaitu sangat kasar dan fluktuatif, demikian juga sebaliknya. Oleh karena itu perlu dipilih bandwidth

maupun parameter penghalus λ yang optimal. Salah satu metode untuk mendapatkan  dan λ adalah dengan metode Generalized Cross Validation

(GCV). Metode GCV merupakan modifikasi dari metode Cross Validation (CV). Metode ini mempunyai kelebihan yaitu tidak memerlukan pengetahuan tentang

2

,

 invarian terhadap transformasi dan bersifat optimal asimptotik (Herawati, 2011).

Pemilihan bandwidth  optimal pada komponen kernel menggunakan GCV adalah sebagai berikut.

 







1



2 , MSE GCV n tr      I - V (2.18)

dimana MSE

 

 pada persamaan (2.6) adalah

 

1



 





 



MSE  n _   

 y IV I V y dan matriks V

 

 seperti pada persamaan (2.9) (Eubank, 1999). Pemilihan penghalus λ yang optimal pada komponen deret fourier menggunakan GCV didefinisakan sebagai berikut:

(37)

16

 







1



2 MSE GCV n trace       I S (2.19)

dengan MSEn1y I



S

 









IS

 





y dan matriks S

 

 seperti pada persamaan (2.17) (Asrini dan Budiantara, 2014 serta Tripena, 2009). Nilai  dan

optimal diperoleh dari nilai GCV yang terkecil. 2.6Koefisien Determinasi R2

Salah satu tujuan analisis regresi adalah mendapatkan model terbaik yang mampu menjelaskan hubungan antara variabel prediktor dan variabel respon berdasarkan kriteria tertentu. Salah satu kriteria yang digunakan dalam pemilihan model terbaik adalah dengan menggunakan koefisien determinasi R . 2 Secara umum semakin besar nilai R2, maka semakin baik pula model yang didapatkan. Koefisien determinasi didefinisikan sebagai berikut :

2 SSE

R

SST



dimana = ∑ ( − ) dan =∑ ( − ). Besaran nilai R2 tidak pernah negatif dan batasannya adalah 0≤ ≤ 1 (Gujarati dan Porter, 2015) .

2.7Tinjauan Non Statistika

Pada bagian ini diuraikan mengenai konsep dan definisi kemiskinan, pengukuran kemiskinan serta faktor-faktor yang mempengaruhi kemiskinan. 2.7.1 Konsep dan Pengukuran Kemiskinan

Badan Pusat Statistik (BPS) menggunakan konsep kemampuan memenuhi kebutuhan dasar (basic needs approach) dalam mengukur kemiskinan. Dengan pendekatan ini, kemiskinan dipandang sebagai ketidakmampuan dari sisi ekonomi untuk memenuhi kebutuhan dasar makanan dan bukan makanan yang diukur dari sisi pengeluaran. Garis Kemiskinan (GK) merupakan penjumlahan dari Garis Kemiskinan Makanan (GKM) dan Garis Kemiskinan Non Makanan (GKNM). Penduduk yang memiliki rata-rata pengeluaran perkapita per bulan di (2.19)

(38)

17

bawah GK dikategorikan sebagai penduduk miskin, sedangkan persentase penduduk miskin adalah persentase penduduk yang berada di bawah GK (BPS, 2012).

Kemiskinan secara konseptual dapat dibedakan menjadi dua yaitu kemiskinan relatif (relative poverty) dan kemiskinan absolut (absolute poverty). Kemiskinan relatif merupakan kondisi miskin karena pengaruh kebijakan pembangunan yang belum mampu menjangkau seluruh lapisan masyarakat sehingga menyebabkan ketimpangan distribusi pendapatan. Standar minimum disusun berdasarkan kondisi hidup suatu negara pada waktu tertentu dan perhatian terfokus pada golongan penduduk “termiskin”, misalnya 20 persen atau 40 persen lapisan terendah dari total penduduk yang telah diurutkan menurut pendapatan/pengeluaran. Kelompok ini merupakan penduduk relatif miskin. Definisi kemiskinan absolut ditentukan berdasarkan ketidakmampuan untuk mencukupi kebutuhan pokok minimum seperti pangan, sandang, kesehatan, perumahan, dan pendidikan yang diperlukan untuk bisa hidup dan bekerja. Kebutuhan pokok minimum diterjemahkan sebagai ukuran finansial dalam bentuk uang (BAPPENAS, 2010).

2.7.2 Faktor-Faktor yang Mempengaruhi Persentase Penduduk Miskin Terdapat beberapa faktor yang mempengaruhi kemiskinan, salah satunya adalah pendidikan. Hubungan antara kemiskinan dan pendidikan sangat penting, karena pendidikan sangat berperan dalam mempengaruhi angka kemiskinan. Orang yang berpendidikan lebih baik akan mempunyai peluang yang lebih rendah menjadi miskin (BPS, 2012). Salah satu aspek yang dapat digunakan untuk mengukur tingkat pendidikan adalah rata-rata lama sekolah. Definisi dari rata-rata lama sekolah adalah jumlah tahun belajar penduduk usia 15 tahun ke atas yang telah diselesaikan dalam pendidikan formal (tidak termasuk tahun yang mengulang). Penghitungan rata-rata lama sekolah membutuhkan informasi tentang partisipasi sekolah, jenjang dan jenis pendidikan tertinggi yang pernah atau sedang diduduki, ijasah tertinggi yang dimiliki dan tingkat atau kelas tertinggi yang pernah atau sedang diduduki (BPS, 2011). Rata-rata lama sekolah

(39)

18

di Indonesia dari tahun 2011 hingga 2013 mengalami peningkatan yang relatif lambat, dimana pada tahun 2011 mencapai angka 7,94 sedangkan pada tahun 2013 mencapai 8,14. Rata lama sekolah yang ingin dicapai oleh pemerintah pada tahun 2014 adalah 8,25 tahun, untuk itu pemerintah harus tetap konsisten dalam menjalankan program-program dalam bidang pendidikan agar target yang diinginkan dapat tercapai (BPS, 2013a).

Angka Melek Huruf (AMH) merupakan aspek pendidikan selain rata-rata lama sekolah yang berpengaruh terhadap kemiskinan. Angka Melek Huruf (AMH) adalah proporsi penduduk usia 15 tahun ke atas yang mempunyai kemampuan membaca dan menulis huruf latin dan atau huruf lainya, tanpa harus mengerti apa yang dibaca/ditulisnya terhadap penduduk usia 15 tahun ke atas (BPS, 2011). Pada periode 2011-2013, AMH di Indonesia meningkat dari 92,99 persen menjadi 94,14 persen. Kenaikan AMH ini dapat diartikan juga sebagai penurunan Angka Buta Huruf (ABH). Hal ini berarti penduduk usia 15 tahun ke atas yang tidak memiliki kemampuan membaca dan menulis menurun menjadi 5,86 persen. Padahal pada tahun 2014, pemerintah menargetkan ABH dapat mencapai angka 4,18 persen (BPS, 2013a).

Faktor lain yang juga berpengaruh terhadap kemiskinan adalah pengangguran. Tingkat pengangguran terbuka (TPT) adalah persentase penduduk yang mencari pekerjaan, yang mempersiapkan usaha, yang tidak mencari pekerjaan, karena merasa tidak mungkin mendapatkan pekerjaan, yang sudah mempunyai pekerjaan tetapi belum mulai bekerja dari sejumlah angkatan kerja yang ada. TPT dapat menginterpretasikan angka pengangguran terbuka, dalam hal ini mereka yang tidak bekerja tidak mempunyai pekerjaan dan selanjutnya tidak akan mampu memenuhi kebutuhan hidupnya (BPS, 2011). TPT di Indonesia pada periode 2005-2013 mengalami penurunan yaitu dari angka 11,24 menjadi 6,17 (BPS, 2016b).

(40)

19

BAB 3

METODE PENELITIAN

3.1Sumber Data

Penelitian ini menggunakan data sekunder Tahun 2013 dari publikasi yang diterbitkan oleh Badan Pusat Statistika (BPS). Unit observasi merupakan seluruh kabupaten/kota yaitu sebanyak 102 Kabupaten/Kota di Provinsi Papua, Papua Barat, Nusa Tenggara Timur, Maluku, Gorontalo, Bengkulu, dan Aceh. 3.2Variabel Penelitian

Berdasar pada latar belakang dan tujuan penelitian, terdapat satu variabel respon dan empat variabel prediktor yang digunakan. Variabel-variabel tersebut adalah sebagai berikut :

Variabel Respon:

Y : Persentase penduduk miskin Variabel Prediktor

X1 : Rata-rata lama sekolah (RLS)

X2 : Tingkat Pengangguran Terbuka (TPT)

X3 : Angka Melek Huruf (AMH)

3.3Definisi Operasional Variabel Penelitian

Adapun definisi operasional dari variabel-variabel yang digunakan dalam penelitian ini adalah sebagai berikut :

a. Persentase Penduduk Miskin

Persentase penduduk miskin adalah persentase penduduk yang berada di bawah Garis Kemiskinan (GK).

b. Rata-Rata Lama Sekolah (RLS)

Rata-rata lama sekolah menggambarkan jumlah tahun yang digunakan oleh penduduk usia 15 tahun ke atas dalam menjalani pendidikan formal (tidak termasuk tahun yang mengulang).

(41)

20 c. Tingkat Pengangguran Terbuka (TPT)

Tingkat pengangguran terbuka adalah persentase penduduk yang mencari pekerjaan, yang mempersiapkan usaha, yang tidak mencari pekerjaan, karena merasa tidak mungkin mendapatkan pekerjaan, yang sudah mempunyai pekerjaan tetapi belum mulai bekerja dari sejumlah angkatan kerja yang ada. d. Angka Melek Huruf (AMH)

Angka Melek Huruf (AMH) adalah proporsi penduduk usia 15 tahun ke atas yang mempunyai kemampuan membaca dan menulis huruf latin dan atau huruf lainya, tanpa harus mengerti apa yang dibaca/ditulisnya terhadap penduduk usia 15 tahun ke atas.

3.4Tahapan Penelitian

Tahap awal penelitian adalah menyelesaikan tujuan pertama penelitian yaitu melakukan kajian estimator kurva regresi campuran nonparametrik kernel dan deret fourier dalam model regresi nonparametrik aditif. Langkah-langkah yang dilakukan adalah sebagai berikut.

1. Diberikan variabel respon yi dengan variabel prediktornya , , … ,

dan , , … , diasumsikan mengikuti model regesi nonparametrik

campuran:

( , ) , 1, 2,...,

i i i i

y  v t  i n

dimana = ( , , … , )′ dan = ( , , … , )′

2. Merancang model regresi nonparametrik aditif:

 

1 1 ( , ) p q i i j ji s si j s g v h t    

_



_

v t

dengan ∑ g ( ) merupakan komponen kernel dan ∑ ℎ ( ) merupakan komponen deret fourier.

3. Untuk = 1 sampai dengan = , fungsi g ( ) didekati oleh ( ).

4. Fungsi ℎ ( ) didekati oleh fungsi ( ), sehingga untuk = 1 sampai dengan = , ℎ ( ) didekati oleh ( ).

(42)

21

5. Mencari bentuk estimasi kurva regresi campuran menggunakan metode

Penalized Least Square (PLS) melalui optimasi :

 

_{ }





2 2 2 1 0 1 1 1 2 p q q j j s s s s s s j s s Min n v t   T t dt                  



_{ }

a y g T

6. Menyelesaikan optimasi Min Q



 



a a dimana

_{ }

 

_{ }



 

_{ }



2 2 2 1 0 1 1 1 2 p q q j j s s s s s s j s s Q n v t   T t dt       









 

a y g T

7. Mendapatkan estimasi campuran

 

1 1 ˆ ˆ( , ) ˆ p q i i j ji s si j s g v h t    

_



_

v t

Tujuan kedua dari penelitian ini adalah mengaplikasikan model estimasi campuran regresi kernel dan deret fourier pada regresi nonparametrik pada data persentase penduduk miskin di Indonesia. Untuk menyelesaikan tujuan kedua, dilakukan langkah-langkah sebagai berikut:

1. Membuat scatter plot data antara variabel respon dengan masing-masing variabel prediktor.

2. Melakukan analisis deskriptif data untuk mengetahui gambaran umum tentang data kemiskinan di Indonesia.

3. Menentukan variabel prediktor yang merupakan komponen-komponen nonparametrik yang didekati dengan fungsi kernel dan yang didekati dengan fungsi deret fourier.

4. Memodelkan kemiskinan di Indonesia dengan menggunakan pendekatan nonparametrik campuran kernel dan deret fourier.

5. Menentukan bandwith optimal, parameter osilasi M, dan parameter penghalus menggunakan metode GCV

6. Mendapatkan estimasi kurva regresi nonparametrik campuran kernel dan deret fourier

7. Menghitung nilai R2 8. Mengambil kesimpulan

(43)

22

Gambar 3.1 dan 3.2 menunjukkan urutan tahap analisis untuk tujuan pertama dan ke dua yang dilakukan pada penelitian ini.

Gambar 3.1 Langkah-langkah Tahap Analisis untuk Tujuan Pertama

Mencari bentuk estimasi kurva regresi campuran menggunakan metode PLS :

 



 



2 2 2 1 0 1 1 1 2 p q q j j s s s s s s j s s Min n v t   T t dt                  



_{ }

a y g T

Menghampiri g ( ) dengan ( ) untuk = 1 sampai dengan =

Menyelesaikan optimasi Min Q



 



a a

Merancang model regresi nonparametrik aditif:

 

1 1 ( , ) p q i i j ji s si j s g v h t    







v t

Mendapatkan estimasi campuran :

 

1 1 ˆ ˆ( , ) ˆ p q i i j ji s si j s g v h t    

_



_

v t

Membentuk model regresi nonparametrik campuran ( , ) , 1, 2,...,

i i i i

y  v t  i n

Menghampiri ℎ ( ) dengan ( ) dan untuk = 1 sampai dengan = , fungsi ℎ ( ) didekati oleh ( )

(44)

23

Gambar 3.2. Langkah-langkah Tahap Analisis untuk Tujuan Kedua Menentukan bandwith optimal, parameter osilasi M, dan

parameter penghalus menggunakan metode GCV Menentukan variabel prediktor yang merupakan komponen

nonparametrik kernel dan deret fourier Analisis deskriptif data

Menghitung nilai R2 Mengambil kesimpulan

Membuat plot data

Memodelkan data kemiskinan di Provinsi Papua, Papua Barat, Nusa Tenggara Timur, Maluku, Gorontalo, Bengkulu, dan Aceh

(45)

24

(46)

25

BAB 4

HASIL DAN PEMBAHASAN

Mengacu pada tujuan penelitian, bab ini akan melakukan kajian mengenai estimasi kurva regresi campuran nonparametrik kernel dan deret fourier. Hasil kajian diaplikasikan pada data kemiskinan di Indonesia tahun 2013. Bab ini terdiri dari lima subbab. Subbab 4.1 merupakan pengenalan bentuk model regresi campuran nonparametrik kernel dan deret fourier. Subbab 4.2 berisi kajian estimasi kurva regresi campuran nonparametrik kernel deret fourier. Subbab 4.3 merupakan kajian mengenai sifat dari estimator kurva regresi tersebut. Subbab 4.4 berisi pembahasan mengenai pemilihan bandwidth, parameter osilasi M, dan parameter penghalus optimum. Selanjutnya pada Subbab 4.5, estimasi model regresi campuran nonparametrik kernel dan deret fourier yang telah dibahas pada subbab-subbab sebelumnya, diaplikasikan pada data persentase penduduk miskin di Indonesia.

4.1 Model Regresi Campuran Nonparametrik Kernel dan Deret Fourier Diberikan data berpasangan



v v₁_i, ₂_i,...,v_pi, ,t t₁_i ₂_i,...,t_qi,y_i



, i1, 2,...,n yang memiliki hubungan diasumsikan mengikuti model regresi nonparametrik. Variabel-variabel v v₁_i, ₂_i,...,v_pi, ,t t₁_i ₂_i,...,t_qi merupakan variabel-variabel prediktor dan y_i merupakan variabel respon.Bentuk model regresi nonparametrik tersebut adalah









1 , 2 ,..., , 1, 2 ,..., , (4.1) i i i pi i i qi i i i i y  v v v t t t       v t 

dimana = ( , , … , )′ dan = , , … , . Bentuk kurva regresi ( , ) pada model (4.1) diasumsikan tidak diketahui serta kurva tersebut

smooth dalam arti kontinu dan differensiabel. Error random



_i berdistribusi normal dengan E

_{ }

i 0 dan

 

2

.

i

Var   Selain itu, kurva regresi 

_

v ti, i

_

diasumsikan bersifat additif, sehingga dapat ditulis dalam bentuk

(47)

26



i, i



g v1

 

1i g v2

 

2i ... gp

 

vpi h t1i

 

1i h2i

 

t2i ... hqi

 

tqi .

 v t         (4.2)

Bentuk pola hubungan variabel respon yi dengan masing-masing variabel prediktor v v₁_i, ₂_i,...,v_pi diasumsikan tidak diketahui atau tidak memiliki pola tertentu. Secara teoritis, kurva regresi g v₁

 

₁_i ,g₂

 

v₂_i ,...,g_p

 

v_pi dapat dihampiri dengan kurva regresi kernel. Sedangkan bentuk pola hubungan variabel respon yi dengan masing-masing variabel prediktor t t1i, 2i,...,tqi diasumsikan membentuk pola berulang atau musiman seingga kurva regresi

 

1i 1i , 2i 2i ,..., qi qi

h t h t h t dapat dihampiri dengan deret fourier. Dengan demikian, kurva regresi ( , ) disebut dengan kurva regresi campuran nonparametrik yang dikelompokkan menjadi dua komponen kurva regresi yaitu komponen kurva regresi kernel dan komponen deret fourier. Selanjutnya, persamaan (4.2) dapat ditulis menjadi





_{ }

 