PERBANDINGAN ESTIMATOR KERNEL DAN ESTIMATOR SPLINE DALAM MODEL REGRESI NONPARAMETRIK

PERBANDINGAN ESTIMATOR KERNEL DAN

ESTIMATOR SPLINE DALAM MODEL REGRESI

NONPARAMETRIK

I KOMANG GDE SUKARSA

1

, I GUSTI AYU MADE SRINADI

2

,

NI LUH AYU PUSPA LESTARI

3

1

Jurusan Matematika Universitas Udayana, sukarsakomang@yahoo.com

2

Jurusan Matematika Universitas Udayana, srinadiigustiayumade@yahoo.co.id

3

Alumni Jurusan Matematika Universitas Udayana, ayu.p.lestari3975@yahoo.com

Abstrak

Analisis regresi nonparametrik merupakan metode pendugaan kurva regresi yang digunakan jika tidak ada informasi sebelumnya tentang bentuk kurva regresi atau tidak terikat pada asumsi bentuk fungsi tertentu. Estimasi fungsi regresi nonparametrik dilakukan berdasarkan data pengamatan dengan menggunakan teknik pemulusan

(smoothing). Penelitian ini bertujuan untuk membandingkan estimator kernel dan

estimator spline pada data sekunder, yaitu data motorcycle. Hasil penelitian ini menunjukkan bahwa estimator kernel lebih baik dibandingkan estimator spline dalam mengestimasi kurva regresi nonparametrik. Dalam estimator kernel, estimasi dilakukan pada setiap titik data sehingga menghasilkan kurva yang lebih mulus, sedangkan spline merupakan potongan-potongan polinomial yang digabungkan bersama pada setiap titik knot.

Kata Kunci: Regresi Nonparametrik, Smoothing, Estimator Kernel, Estimator Spline, titik

knot

1. Pendahuluan

Misalkan X adalah variabel prediktor dan Y adalah variabel respon untuk n pengamatan berpasangan





x

_i

,

y

_i





n_i1, maka hubungan linear antara variabel prediktor dan variabel respon tersebut dapat dinyatakan sebagai berikut:

i i

i

m

x

y



(

)





,

i

=1,2,...,n (1) dengan



i adalah sisaan yang diasumsikan independen dengan mean nol dan variansi

2



, serta m(x_i)adalah fungsi regresi atau kurva regresi, Eubank [2].

Ada dua pendekatan yang digunakan untuk mengestimasi fungsi regresi, yaitu pendekatan parametrik dan pendekatan nonparametrik. Dalam pendekatan parametrik, bentuk hubungan antara variabel respon dengan variabel prediktor diketahui atau diperkirakan dari bentuk kurva regresi, misalnya diasumsikan membentuk pola linear, kuadratik, eksponensial, dan polinomial. Pada regresi parametrik yaitu model regresi linear, juga harus memenuhi asumsi yang ketat diantaranya sisaan berdistribusi normal dan memiliki variansi yang konstan. Transformasi sering dilakukan untuk mengatasi

pe-nyimpangan asumsi dalam model regresi linear sehingga diperoleh model regresi yang sesuai. Bentuk atau fungsi dipilih melalui teknik trial dan error sehingga penggunaan transformasi yang tepat akan membawa pada metode pendugaan yang relatif mudah, tetapi kesalahan penggunaan transformasi bisa juga membawa pada metode pendugaan dengan model yang lebih rumit, Neter et al [7]. Pendekatan kedua adalah pendekatan nonparametrik. Estimasi fungsi regresi nonparametrik dilakukan berdasarkan data pengamatan dengan menggunakan teknik pemulusan (smoothing). Terdapat beberapa teknik smoothing dalam model regresi nonparametrik antara lain histogram, estimator kernel, deret orthogonal, estimator spline, k-NN, deret fourier, dan wavelet, Eubank [2].

Macam-macam fungsi kernel meliputi kernel Uniform, Triangle, Epanechnikov,

Gaussian, kuartik, dan cosines, Hardle [4]. Dalam regresi kernel pemilihan parameter

pemulus (bandwidth) jauh lebih penting dibandingkan dengan memilih fungsi kernel. Fungsi kernel yang umum digunakan adalah kernel Gaussian dan kernel Epanechnicov, Hastie dan Tibshirani [5]. Kernel Triangle sering digunakan karena lebih mudah dan cepat dalam perhitungan, Mathsoft [6]. Sedang salah satu bentuk estimator spline yang sering digunakan adalah Penalized Spline, Ruppert [8].

Tujuan yang ingin dicapai dalam penelitian ini adalah membandingkan estimator kernel dan estimator spline dalam mengestimasi model regresi nonparametrik pada data sekunder berdasarkan kriteria MSE, RMSE, dan MAD.

2. Tinjauan Pustaka

2.1

Estimator Densitas Kernel

Estimator densitas kernel merupakan pengembangan dari estimator histogram. Estimator kernel diperkenalkan oleh Rosenblatt (1956) dan Parzen (1962) sehingga disebut estimator densitas kernel Rosenblatt-Parzen, Hardle [4].

Secara umum kernel

K

dengan bandwith h menurut Wand dan Jones [9] didefinisikan sebagai:        h x K h x K_h( ) 1 , untuk - x , h > (2) serta memenuhi:

(i) K(x)0, untuk semua x; (ii) _{ }

  1 ) ( dxx K ; (iii)  2 ( )  20    x K x dx  ; (iv)



   0 ) (x dx xK

maka estimator densitas kernel untuk fungsi densitas f(x)adalah:





            n i i i n i h h h x x K nh x x K n x f 1 1 1 ) ( 1 ) ( ˆ (3) Dari persamaan (3) terlihat bahwa

f

ˆ x

_h

(

)

tergantung pada fungsi kernel

K

dan parameter

Fungsi kernel Triangle dan Gaussian menurut Hardle [4] didefiniskan sebagai : a. Kernel Triangle : K(x) =



1 x



I



x 1



b. Kernel Gaussian : K(x) =

_{ }

_       2 2 1 exp 2 1 x  x

Dengan I adalah fungsi indikator.

Regresi kernel adalah teknik statistik nonparametrik untuk mengestimasi fungsi regresi m(x) pada model regresi nonparametrik y_i m(x_i)



_i.

Nadaraya dan Watson tahun 1964 mendefinisikan estimator regresi kernel sehingga disebut estimator Nadaraya-Watson, Hardle [4], yaitu :

       n i h i n i h i i x x K n y x x K n x m 1 1 ) ( 1 ) ( 1 ) ( ˆ atau mˆ x( )= i n i hi x y w



1 ) ( ;





                    _n i i i n i i i hi h x x K h x x K h x x K h h x x K h x w 1 1 ) ( 1 ) ( 1 ) (

Bandwidth (h) adalah parameter pemulus (smoothing) yang berfungsi untuk mengontrol kemulusan dari kurva yang diestimasi. Bandwith yang terlalu kecil akan menghasilkan kurva yang undersmoothing yaitu sangat kasar dan sangat fluktuatif, dan sebaliknya bandwith yang terlalu lebar akan menghasilkan kurva yang oversmoothing yaitu sangat mulus, tetapi tidak sesuai dengan pola data, Hardle [4]. Oleh karena itu, harus dilakukan pemilihan bandwidth yang optimal.

Salah satu metode untuk mendapatkan

h

optimal adalah dengan menggunakan kriteria Generalized Cross Validation (GCV), Eubank [2], yang didefinisikan sebagai berikut: 2 )) ( ( 1 ) (       _  h H I tr n MSE h GCV dengan MSE =



_  n i i h i m x y n 1 2 )) ( ( 1

Dalam hal ini, h optimal yang terpilih adalah nilai h yang memberikan nilai GCV(h) minimum, kurva regresi yang dihasilkan cukup mulus dan sesuai dengan pola data.

2.2

Estimator Penalized Spline

Fungsi spline dengan orde p adalah suatu fungsi myang dapat dinyatakan sebagai berikut:







         K k p k i k p p i p i i i x x x x x m 1 1 1 0 0 ... )

(      dengan K adalah banyaknya knot dan

        _ k k p k i p k i x x x x     , 0 , ) ( ) (

Dari bentuk matematis fungsi spline tersebut, dapat dikatakan bahwa spline merupakan potongan-potongan polinomial dimana segmen-segmen polinomial yang berbeda digabungkan bersama pada titik knot ₁,₂, ,_K untuk menjamin sifat kontinuitasnya.

                                                               ) ( ) 1 ( 1 0 1 2 1 2 1 2 2 2 2 1 2 1 1 1 1 2 1 1 1 2 1 ) ( ) ( 1 ) ( ) ( 1 ) ( ) ( 1 ) ( ) ( ) ( K p p p p K n p n p n n n p K p p p K p p n x x x x x x x x x x x x x x x x m x m x m                      sehingga m(X) X



Estimator penalized spline dari m( X)dapat dituliskan sebagai mˆ₍X₎Xˆ

Nilai



ˆ diperoleh dengan menggunakan Estimator Penalized Spline yaitu meminimumkan fungsi Penalized Least Square (PLS):





    K k p k n i yi m xi 1 2 ) ( 2 )) ( (   (4) dengan



adalah suatu parameter pemulus,

K

adalah jumlah knot, dan

p

adalah orde

polinomial.

Dengan meminimumkan fungsi PLS pada persamaan (4), sehingga diperoleh



ˆ, yaitu:



XTX D



1XTY

ˆ 



 

 Bentuk estimasi dari fungsi

m

ˆ X

(

)

menurut Wand dan Jones [9], secara matriks dituliskan

sebagai :



X X D



X Y X X mˆ( ) T  1 T

2.3

Pemilihan Parameter Pemulus (

_{) Optimal}

Parameter



merupakan pengontrol keseimbangan antara kecocokan terhadap data (goodness of fit) dan kemulusan kurva (penalty). Jika



besar maka estimasi fungsi yang diperoleh akan semakin mulus, namun kemampuan untuk memetakan data tidak terlalu baik. Sebaliknya, jika



kecil maka estimasi fungsi yang diperoleh akan semakin kasar, Fahrmeir dan Tuhtz [3]. Oleh karena itu, dalam memilih nilai



diharapkan nilainya optimal agar diperoleh estimasi fungsi yang mulus dan pemetaan data yang baik.

Suatu kriteria untuk  akan dibatasi pada kelas estimator linier, yaitu:

Y H m_  () dengan





T T X D n X X X H()   1

dimana untuk setiap  ada matriks pemulus H

 

 berukuran n × n dengan H

 

 simetri dan semidefinit positif. Identik dengan penentuan bandwith (h) optimal dalam estimator Kernel, untuk mendapatkan



optimal digunakan metode Generalized Cross Validation (GCV), Eubank [2] yang didefinisikan sebagai berikut:

2 1 _{[ ( )])} ( ) ( ) (    H I tr n MSE GCV   _ dengan



  _  n i i i m x y n MSE 1 2 1 _{( ( ))} ) ( 

2.4

Pemilihan Jumlah Knot Optimal

Jumlah knot

 

K merupakan banyaknya titik knot atau banyaknya titik dimana terjadi perubahan perilaku fungsi pada interval yang berbeda. Dengan knot ke-k adalah kuantil ke-j dari nilai tunggal variabel prediktor

 

x_i n_i1, dimana



1





K k

diurut dari K1 sampai dengan Kn_uniqp1, dimana n_uniq adalah banyaknya nilai tunggal dari variabel prediktor

 

x_i n_i1, sehingga jumlah knot (K) kurang dari jumlah pengamatan.

2.5

Ukuran Ketepatan Estimator

Untuk menentukan kebaikan suatu estimator dapat dilihat dari tingkat kesalahannya. Semakin kecil tingkat kesalahannya semakin baik estimasinya. Menurut Aydin [1], kriteria untuk menentukan estimator terbaik dalam model regresi nonparametrik, antara lain:

a. Mean Square Error (MSE), MSE =









    n i i i n i i y y n e n 1 2 1 2 1 _ˆ 1

b. Root Mean Square Error (RMSE), RMSE = MSE

c. Mean Absolute Deviation (MAD), MAD =

n y y n e n t i i n t t





    1 1 ˆ

Data yang digunakan dalam penelitian ini adalah data sekunder, hasil penelitian yang dilakukan oleh Schmidt, Mattern, dan Schuler pada tahun 1981 yaitu data simulasi tabrakan sepeda motor pada suatu Post Mortem Human Test Object (PTMO), Hardle [4] untuk melihat kurva hubungan antara percepatan setelah tabrakan dengan waktu setelah terjadinya tabrakan dengan estimator Kernel Gaussian. Variabel dalam penelitian ini adalah variabel prediktor (X) yaitu waktu (dalam milidetik) setelah simulasi tabrakan, dan variabel respon (Y) yaitu percepatan (g = 9,81 m/s2) setelah tabrakan yang disimulasikan.

Model regresi nonparametrik dalam penelitian ini, diestimasi menggunakan estimator kernel dengan fungsi kernel Triangle dan kernel Gaussian, serta estimator

penalized spline. Adapun langkah-langkah yang dilakukan adalah sebagai berikut:

(i) Mengestimasi kurva regresi nonparametrik dengan estimator kernel Triangle. (ii) Mengestimasi kurva regresi nonparametrik dengan estimator kernel Gaussian. (iii) Mengestimasi model regresi nonparametrik dengan estimator penalized spline. (iv) Membandingkan hasil estimasi antara estimator kernel dan estimator spline

berdasarkan kriteria MSE, RMSE, dan MAD, serta membandingkan plot estimasi kurva regresi bersama-sama dengan plot data.

3. Hasil

Gambaran umum data penelitian dapat dilihat pada Tabel 1 dan plot antara kedua variabel penelitian pada Gambar 1.

Tabel 1. Statistika Deskriptif Data Motorcycle

Variabel N Min Maks Mean Q2 Standar deviasi

Waktu (X) 133 2,4 57,6 25,18 23,4 13,132

Motorcycle Waktu (milidetik) P e rc e p a ta n ( g) 10 20 30 40 50 -1 0 0 -5 0 0 50

Gambar 1. Diagram Pencar Data Motorcycle

Gambar 1 menunjukkan bentuk kurva yang menggambarkan hubungan antara waktu (milidetik) dengan percepatan (g), yang sangat sulit diestimasi bila digunakan pendekatan regresi parametrik. Kurva regresi diestimasi menggunakan pendekatan regresi nonparametrik dengan estimator kernel dan estimator spline.

3.1 Estimasi Data Motorcycle dengan Estimator Kernel

Langkah-langkah yang dilakukan dalam mengestimasi kurva regresi nonparametrik menggunakan estimator kernel adalah menentukan fungsi bobot atau fungsi kernel dan ukuran bobot yaitu nilai bandwidth (h) yang optimal. Sebelum menentukan nilai

bandwidth (h), terlebih dahulu dipilih fungsi kernel yang akan digunakan, dalam

penelitian ini digunakan fungsi kernel Triangle dan kernel Gaussian.

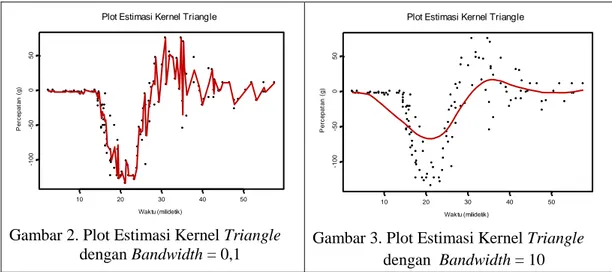
Nilai bandwidth yang terlalu kecil, misalkan h0,1 menghasilkan kurva regresi yang sangat kasar, seperti terlihat pada Gambar 2, sedangkan nilai bandwidth yang terlalu besar, misalkan h10 menghasilkan kurva regresi yang sangat mulus dan tidak sesuai dengan pola data, seperti terlihat pada Gambar 3.

Plot Estimasi Kernel Triangle

Waktu (milidetik) P e rc ep a ta n ( g ) 10 20 30 40 50 -1 0 0 -5 0 0 50

Gambar 2. Plot Estimasi Kernel Triangle

Plot Estimasi Kernel Triangle

Waktu (milidetik) P e rc ep a ta n ( g ) 10 20 30 40 50 -1 0 0 -5 0 0 50

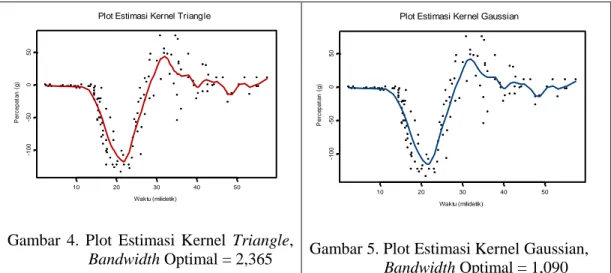
Berdasarkan kriteria GCV minimum, diperoleh nilai bandwidth (h) optimal untuk fungsi kernel Triangle sebesar 2,365 dan untuk fungsi kernel Gaussian sebesar 1,090.

Selanjutnya, dilakukan estimasi model regresi nonparametrik dengan estimator kernel Triangle pada bandwidth yang optimal. Estimasi model identik dengan menghitung nilai mˆ x( ) sehingga diperoleh nilai dugaan mˆ x( ) untuk kernel Triangle dan estimasi kurva regresi yang ditunjukkan pada Gambar 4. Demikian juga untuk fungsi kernel Gaussian, estimasi kurva regresi ditunjukkan pada Gambar 5.

Plot Estimasi Kernel Triangle

Waktu (milidetik) P e rc ep a ta n ( g ) 10 20 30 40 50 -1 0 0 -5 0 0 50

Gambar 4. Plot Estimasi Kernel Triangle,

Bandwidth Optimal = 2,365

Plot Estimasi Kernel Gaussian

Waktu (milidetik) P e rc ep a ta n ( g ) 10 20 30 40 50 -1 0 0 -5 0 0 50

Gambar 5. Plot Estimasi Kernel Gaussian, Bandwidth Optimal = 1,090

3.2 Estimasi Data Motorcycle dengan Estimator Spline

Kriteria yang digunakan untuk mendapatkan orde polinomial, jumlah knot, dan parameter pemulus () yang optimal adalah berdasarkan nilai GCV minimum. Hasil yang diperoleh dari output program S-plus yaitu GCV minimum bernilai 623,252 pada orde

)

( p = 1, jumlah knot (K)= 4 dengan titik knot yaitu ₁13,72, ₂20,56, ₃28,08,

28 , 39

4 

 , dan parameter pemulus ()0,305. Nilai ˆ yang diperoleh untuk spline orde 1 adalah sebagai berikut:

                         426 , 1 327 , 20 214 , 42 307 , 22 686 , 0 069 , 6 ˆ 

sehingga model dugaan untuk waktu terhadap percepatan dapat dituliskan sebagai:































     6,069 0,686 22,307 13,72 42,214 20,56 20,327 28,08 1,426 39,28 ) ( ˆ X X X X X X m

Plot Estimasi Spline Waktu (milidetik) P e rc ep a ta n ( g ) 10 20 30 40 50 -1 0 0 -5 0 0 50

Gambar 6. Plot Estimasi Spline Orde 1

3.3 Perbandingan Estimator Kernel dan Spline

Perbandingan estimasi kurva regresi antara estimator kernel dengan fungsi kernel

Triangle dan Gaussian, serta estimator spline secara bersama-sama dalam plot data,

ditunjukkan pada Gambar 7.

Plot Perbandingan Estimator Kernel dan Spline

Waktu (milidetik) P e rc e p a ta n ( g) 10 20 30 40 50 -1 0 0 -5 0 0 50 Triangle Gaussian Spline

Gambar 7. Plot Perbandingan Estimator Kernel dan Spline

Gambar 7 menunjukkan bentuk kurva regresi estimator kernel lebih mendekati bentuk plot data dibandingkan dengan bentuk kurva regresi estimator spline. Bentuk kurva regresi estimator spline terlihat setelah knot ke-3 tidak sesuai dengan pola data, hal ini disebabkan karena jumlah knot dan titik knot ditentukan berdasarkan sampel kuantil. Selain itu kurva regresi untuk estimator kernel lebih mulus dibandingkan dengan estimator spline, karena pada estimator kernel estimasi dilakukan pada setiap titik data, sedangkan spline merupakan potongan-potongan polinomial dimana segmen-segmen polinomial yang berbeda digabungkan bersama pada titik knot.

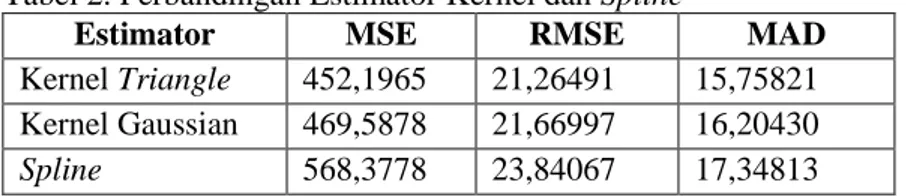
Gambar 7 juga memperlihatkan bahwa estimator kernel lebih baik dibandingkan dengan estimator spline dalam mengestimasi kurva regresi nonparametrik. Untuk mendukung kesimpulan ini, selanjutnya dilihat perbandingan nilai MSE, RMSE, dan MAD yang dihasilkan estimator kernel dan spline seperti tercantum pada Tabel 2. Walau kurva regresi kernel Triangle dan Gaussian hampir berimpit, berdasarkan nilai MSE, RMSE, dan MAD terlihat kernel Triangle lebih baik dari kernel Gaussian.

Tabel 2. Perbandingan Estimator Kernel dan Spline

Estimator MSE RMSE MAD

Kernel Triangle 452,1965 21,26491 15,75821 Kernel Gaussian 469,5878 21,66997 16,20430

Spline 568,3778 23,84067 17,34813

Nilai MSE, RMSE, dan MAD dari estimator spline lebih besar dibandingkan dengan estimator kernel Triangle dan kernel Gaussian. Hal ini juga menunjukkan bahwa estimator kernel lebih baik dibandingkan dengan estimator spline dan fungsi kernel

Triangle lebih baik dari kernel Gaussian dalam mengestimasi kurva regresi

nonparametrik untuk data motorcycle.

Daftar Pustaka

[1] Aydin, D, A Comparison of the Nonparametric Regression Models using Smoothing

Spline and Kernel Regression, World Academy of Science, Engineering and

Technology, 36, 253-257, 2007.

[2] Eubank, R., Spline Smoothing and Nonparametric Regression, Marcel Dekker,1988. [3] Fahrmeir, L. and G.Tuhtz, Multivariate Statistical Modelling Based on Generalized

Linier Models, Springer-Verlag, 1994.

[4] Hardle, W., Applied Nonparametric Regression, Cambridge University Press, 1994. [5] Hastie, T.J. and R.J. Tibshirani, Generalized Additive Models, Chapman and Hall,

1990.

[6] MathSoft, S-Plus Guide to Statistical and Mathematical Analysis, Version 3.2, A Division of Math Soft, Inc. Seattle, 1993.

[7] Neter,J., W. Wasserman dan M. H. Kutner, Model Linier Terapan Analisis Regresi

Linier Sederhana, Diterjemahkan oleh Bambang Sumantri, Jurusan Statistika

FMIPA IPB, 1997.

[8] Ruppert, D., Selecting the Number of Knots for Penalised Spline, Journal of Computational and Graphical Statistics 11, 735-757, 2002.