APLIKASI
SPLINE TRUNCATED
DALAM
REGRESI NONPARAMETRIK
SKRIPSI
FIKA KHAIRANI
120823020
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
APLIKASI
SPLINE TRUNCATEDDALAM
REGRESI NONPARAMETRIK
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat
mencapai gelar Sarjana Sains
FIKA KHAIRANI
120823020
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Aplikasi Spline Truncated dalam Regresi Nonparametrik
Kategori : Skripsi Nama : Fika Khairani Nomor Induk Mahasiswa : 120823020
Program Studi : Sarjana (S1) Matematika Ekstensi Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Diluluskan di Medan, Agustus 2015
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Dr. Open Darnius, M.Sc Prof. Dr. Tulus, M.Si
NIP. 19641041 199103 1 004 NIP. 19620901198803 1 002
Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
APLIKASI SPLINE TRUNCATED DALAM
REGRESI NONPARAMETRIK
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dari ringkasan yang masing-masing disebutkan sumbernya.
Medan, Agustus 2015
PENGHARGAAN
Tiada kata yang pantas diucapkan sebagai pembuka, selain ucapan syukur Penulis
kepada Allah SWT. Segala puji hanya bagi-Nya yang senantiasa memberikan
kesehatan dan nikmat kepada semua manusia, termasuk Penulis, sehingga
penyusunan skripsi dengan judul Aplikasi Spline Truncated dalam Regresi
Nonparametrik ini dapat diselesaikan dengan baik.
Terimakasih Penulis sampaikan kepada Bapak Prof. Dr. Tulus, M.Si
selaku dosen pembimbing 1 sekaligus Ketua Departemen di FMIPA USU dan
Bapak Dr. Open Darnius, M.Sc selaku dosen pembimbing 2 yang telah banyak
membantu dan meluangkan waktunya selama penyusunan skripsi ini. Terimakasih
kepada Bapak Dr. Faigiziduhu Bu’ulolo, M.Si dan Bapak Dr. Pasukat Sembiring,
M.Si selaku dosen penguji. Terimakasih juga kepada Ibu Dr. Mardiningsih, M.Si
selaku Sekretaris Departemen Matematika di FMIPA USU, Bapak Dr. Sutarman,
M.Sc selaku Dekan FMIPA USU, Pembantu Dekan FMIPA USU, seluruh Staf
Pengajar Departemen Matematika FMIPA USU, serta Pegawai FMIPA USU.
Mudah-mudahan Allah SWT senantiasa membalas kebaikan-kebaikan mereka.
Teruntuk keluarga tercinta, Ibunda Khairiyani, Ayahanda Sofian, adinda
Nurlia Hafni, Uswatun Khairi, Mifta Khairina, Muhammad Syafriansyah, dan
Muhammad Syafriandi, serta sahabat-sahabat terbaik Penulis, PS.Poemer,
terimakasih atas doa dan dukungan yang senantiasa diberikan sampai saat ini.
Mudah-mudahkan keberkahan, keridhoan, serta hidayah-Nya senantiasa
melimpahi kita semua.
Medan, Agustus 2015 Penulis,
APLIKASI SPLINE TRUNCATED DALAM REGRESI NONPARAMETRIK
ABSTRAK
Regresi spline truncated merupakan salah satu model dengan pendekatan
nonparametrik, yang merupakan modifikasi dari fungsi polinomial tersegmen.
Bentuk estimator spline sangat dipengaruhi oleh nilai parameter penghalus λ yang
pada hakekatnya adalah penentuan lokasi titik-titik knot. Penelitian ini bertujuan
untuk mengkaji penggunaan metode kuadrat terkecil dengan pendekatan matriks
dalam menentukan estimator regresi spline linier dua titik knot, serta menentukan
metode yang terbaik sebagai kriteria dalam penentuan titik knot yang optimal,
yakni MSE dan GCV. Dari hasil analisis dan pembahasan didapat bahwa estimator
regresinya dapat diselesaikan dengan metode kuadrat terkecil melalui pendekatan
matriks. Penggunaan metode kuadrat terkecil mengasumsikan bentuk fungsi
spline dan memberikan kemudahan interpretasi melalui model statistik.
Sedangkan dari hasil perhitungan data tegangan output sensor polimer diketahui
bahwa pemilihan model regresi spline terbaik dengan menggunakan metode
MSE(λ) sebesar 0,760617 dan GCV(λ) sebesar 1,188464. Setiap trial error hasil
minimal kedua metode bersama-sama secara konstan menunjukkan letak titik knot
yang sama. Hal ini menunjukkan bahwa kedua metode memiliki efektivitas yang
sama dalam menetukan letak titik knot yang optimal. Namun, jika dilihat dari nilai
yang dihasilkan, nilai MSE(λ) adalah nilai yang paling minimum dan bisa
dianggap sebagai metode yang terbaik karena efisien dan lebih mudah
penggunaanya dalam regresi spline linier.
SPLINE TRUNCATED APPLICATION IN NONPARAMETRIC REGRESSION
ABSTRACT
Spline truncated regression is one of the nonparametric approach model that has
been modified from segmented polynomial .The estimator form of spline is being
strongly influenced by λ as the value of smoothing parameter which is essentially
determining the location of knots. This research aims to examines the usage of the
least squares method with a matrix approach in order to determines estimator the
spline linear regression two knots well as to recognize the best method as the
criteria for the optimal knots, specifically MSE and GCV. As the result of this
research, it shows if the regression estimator can be solved with the least squares
method through a matrix approach. The usage of the least squares method assume
the form of spline functions and provide the easier interpretation way through
statistical models. Meanwhile from the data output voltage cencorship polymer, it
discovered that the selection of the best spline regression model using MSE (λ) is
equal to 0.760617 and GCV (λ) is equal to 1.188464. The minimum result of both
methods constantly showed the same knot point location in every trial error. It is
indicated if the result shows that both methods have the same effectiveness in
determining the optimal location of the point knots. However, refering to the
value result, the value of MSE (λ) is the minimum value and it could be
recognized as the best method since it is quite efficient and easier to be used in
spline linear regression.
DAFTAR ISI 2.7 Metode Kuadrat Terkecil 11
2.8 Matriks 12
2.8.1 Defenisi Matriks 12 2.8.2 Trace Matriks 13 2.8.3 Tranpos Matriks 13 2.8.4 Matriks Identitas 14 2.8.5 Matriks Idempoten 14 2.8.6 Matriks Simetri 14 2.8.7 Invers Matriks 15 2.8.8 Matriks Invertible 15
BAB 3 METODE PENELITIAN 16
3.1 Estimasi Model Spline dalam Regresi Nonparametrik 16 3.2 Menerapkan Model Spline pada Datauntuk Estimasi Pola
Hubungan Variabel Terikat dan Variabel Bebas 17
4.1.1 Persamaan Regresi Spline Linier
dengan Penurunan Terhadap 21 4.1.2 Persamaan Regresi Spline Linier
dengan Penurunan Terhadap 22 4.1.3 Pendekatan metode kuadrat terkecil
dengan metode matriks 24 4.1.4 Optimasi dengan MSE 25 4.1.5 Optimasi dengan GCV 26 4.2 Menerapkan Model Spline pada Data Simulasiuntuk
Estimasi Pola Hubungan Variabel Terikat dan
Variabel Bebas 27
4.2.1 Plot Antara Variabel Terikat dan Variabel Bebas 27 4.2.2 Estimasi Regresi Spline Linier 28 4.2.3 Pemilihan Model Regresi Spline Linier Terbaik 30 4.2.4 Pengujian Model Regresi Spline Linier Terbaik 31 4.2.5 Interpretasi Model Regresi Spline Truncated Linier 33
BAB 5 KESIMPULAN DAN SARAN 35
5.1 Kesimpulan 35
5.2 Saran 36
DAFTAR PUSTAKA
DAFTAR TABEL
Nomor Judul Halaman
Tabel
4.1 Ringkasan Nilai MSE dan GCV untuk Satu Titik Knot 28
4.2 Estimasi Model Regresi Spline Linier dengan Satu Titik Knot 29
4.3 Ringkasan Nilai MSE dan GCV untuk Dua Titik Knot 29
4.4 Estimasi Model Regresi Spline Linier dengan Satu Titik Knot 30
4.5 Titik Knot Optimum Satu dan Dua Titik Knot 30
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
2.1 Fungsi Spline Linier dengan Satu Titik Knot pada 8
4.1 Plot Pengaruh Waktu (menit) Terhadap Tegangan (mv) 27
4.2 Plot Normalitas Residual 32
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lampiran
1 Data Pengamatan Pengaruh Waktu (menit) Terhadap Tegangan
Output Sensor Polimer (milivolt) 38
2 Program Regresi Spline dengan Software Aplikasi Matlab
R2007b. 39
3 Nilai MSE dan GCV dari Percobaan Sebanyak p 45
4 Uji Simultan Model Regresi Spline Truncated Linier Terbaik
dengan Menggunakan SPSS 16.0 48
APLIKASI SPLINE TRUNCATED DALAM REGRESI NONPARAMETRIK
ABSTRAK
Regresi spline truncated merupakan salah satu model dengan pendekatan
nonparametrik, yang merupakan modifikasi dari fungsi polinomial tersegmen.
Bentuk estimator spline sangat dipengaruhi oleh nilai parameter penghalus λ yang
pada hakekatnya adalah penentuan lokasi titik-titik knot. Penelitian ini bertujuan
untuk mengkaji penggunaan metode kuadrat terkecil dengan pendekatan matriks
dalam menentukan estimator regresi spline linier dua titik knot, serta menentukan
metode yang terbaik sebagai kriteria dalam penentuan titik knot yang optimal,
yakni MSE dan GCV. Dari hasil analisis dan pembahasan didapat bahwa estimator
regresinya dapat diselesaikan dengan metode kuadrat terkecil melalui pendekatan
matriks. Penggunaan metode kuadrat terkecil mengasumsikan bentuk fungsi
spline dan memberikan kemudahan interpretasi melalui model statistik.
Sedangkan dari hasil perhitungan data tegangan output sensor polimer diketahui
bahwa pemilihan model regresi spline terbaik dengan menggunakan metode
MSE(λ) sebesar 0,760617 dan GCV(λ) sebesar 1,188464. Setiap trial error hasil
minimal kedua metode bersama-sama secara konstan menunjukkan letak titik knot
yang sama. Hal ini menunjukkan bahwa kedua metode memiliki efektivitas yang
sama dalam menetukan letak titik knot yang optimal. Namun, jika dilihat dari nilai
yang dihasilkan, nilai MSE(λ) adalah nilai yang paling minimum dan bisa
dianggap sebagai metode yang terbaik karena efisien dan lebih mudah
penggunaanya dalam regresi spline linier.
SPLINE TRUNCATED APPLICATION IN NONPARAMETRIC REGRESSION
ABSTRACT
Spline truncated regression is one of the nonparametric approach model that has
been modified from segmented polynomial .The estimator form of spline is being
strongly influenced by λ as the value of smoothing parameter which is essentially
determining the location of knots. This research aims to examines the usage of the
least squares method with a matrix approach in order to determines estimator the
spline linear regression two knots well as to recognize the best method as the
criteria for the optimal knots, specifically MSE and GCV. As the result of this
research, it shows if the regression estimator can be solved with the least squares
method through a matrix approach. The usage of the least squares method assume
the form of spline functions and provide the easier interpretation way through
statistical models. Meanwhile from the data output voltage cencorship polymer, it
discovered that the selection of the best spline regression model using MSE (λ) is
equal to 0.760617 and GCV (λ) is equal to 1.188464. The minimum result of both
methods constantly showed the same knot point location in every trial error. It is
indicated if the result shows that both methods have the same effectiveness in
determining the optimal location of the point knots. However, refering to the
value result, the value of MSE (λ) is the minimum value and it could be
recognized as the best method since it is quite efficient and easier to be used in
spline linear regression.
BAB 1
PENDAHULUAN
1.1Latar Belakang
Dalam Statistika, analisis regresi digunakan untuk melihat pengaruh variabel
bebas terhadap variabel terikat. Sebelum melakukan analisis lebih lanjut harus
dilihat terlebih dahulu pola hubungan variabel tersebut. Hal ini dapat dilakukan
melalui dua pendekatan yaitu pendekatan parametrik dan pendekatan
nonparametrik. Pendekatan parametrik atau biasa disebut dengan regresi
parametrik digunakan apabila diasumsikan bahwa bentuk model sudah ditentukan
atau pola data sudah diketahui bentuknya. Namun pada kenyataannya tidak semua
data diketahui pola hubungannya secara jelas atau bentuk model belum ditentukan.
Apabila teknik pendekatan parametrik tetap digunakan sebagai model pola data,
maka akan diperoleh hasil yang menyesatkan, sehingga pendekatan alternatif yang
digunakan adalah pendekatan nonparametrik atau biasa disebut regresi
nonparametrik. Regresi nonparametrik merupakan pendekatan regresi yang sesuai
untuk pola data yang tidak diketahui bentuknya, atau bisa dikatakan tidak terdapat
informasi apapun tentang bentuk dari fungsi regresi. Pendekatan nonparametrik
juga lebih fleksibel, hal ini dikarenakan tidak dibatasi oleh asumsi-asumsi seperti
halnya pada pendekatan parametrik.
Pada umumnya statistik nonparametrik sering digunakan pada uji-uji
hipotesis dan penggunaannya pada analisis regresi juga tidak dibahas secara
khusus, padahal banyak teknik estimasi yang bisa digunakan untuk mengestimasi
parameter-parameter model regresinya. Maka dalam hal ini dirasa perlu untuk
mempelajari penggunaan teknik estimasi dalam menentukan model regresi
nonparametrik. Salah satu teknik estimasi dalam regresi nonparametrik adalah
estimator spline. Spline adalah salah satu jenis piecewise polinomial, yaitu
memberikan fleksibilitas lebih dari polinomial biasa, sehingga memungkinkan
untuk menyesuaikan diri secara lebih efektif terhadap karakteristik lokal suatu
fungsi atau data. Spline juga mempunyai keunggulan dalam mengatasi pola data
yang cenderung naik/turun secara tajam, serta kurva yang dihasilkan relatif mulus.
Spline truncated adalah basis fungsi dalam spline yang merupakan model
polinomial yang tersegmen atau terbagi pada suatu titik fokus yang disebut knot.
Untuk memperoleh regresi spline yang optimal maka perlu dipilih lokasi knot
yang optimal pula. Masalah yang dihadapi dalam estimasi kurva adalah dalam
memilih parameter λ (pemulus) yang pada hakekatnya memilih lokasi titik-titik
knot juga.
Untuk nilai λ yang sangat besar akan menghasilkan bentuk kurva regresi
yang sangat halus. Sebaliknya untuk nilai λ yang kecil akan memberikan bentuk
kurva regresi yang sangat kasar, akibatnya pemilihan parameter penghalus
optimal merupakan hal yang sangat penting dalam regresi nonparametrik. Tujuan
dari pendekatan regresi nonparametrik, yakni ingin mendapatkan kurva mulus
yang mempunyai λ optimal menggunakan data amatan sebanyak n, maka
diperlukan ukuran kinerja atas estimator yang dapat diterima secara universal.
Ada banyak metode untuk menentukan parameter pemulus, beberapa di antaranya
adalah MSE (Mean Square Error) dan GCV (Generalized Cross Validation). Titik
knot optimal diperoleh dari nilai MSE dan GCV yang paling minimum. MSE
merupakan metode pemulus optimal yang paling sederhana, meskipun begitu
penggunaan MSE sangat jarang digunakan secara khusus untuk memilih titik knot
yang optimal, sedangkan GCV merupakan modifikasi dari CV (Cross Validation)
dan merupakan metode yang paling banyak dipakai dan disukai karena
kelebihannya yaitu memiliki sifat optimal asimtotik (Wahba, 1990, dalam
Oktaviana dan Budiantara, 2011).
Pada penelitian ini akan dibahas tentang penggunaan estimasi spline
truncated dalam menentukan model terbaik regresi nonparametrik dengan
penyelesaian optimal dan pemilihan parameter penghalus dengan menggunakan
1.2 Rumusan Masalah
Sesuai dengan latar belakang masalah yang telah diuraikan maka yang menjadi
pokok permasalahan dalam penelitian ini adalah bagaimana cara penggunaan
estimator spline dengan basis truncated dalam menentukan model regresi dengan
menggunakan MSE dan GCV sebagai metode pemulus optimal dalam menentukan
model regresi terbaik dan melihat metode mana yang menghasilkan nilai yang
paling minimum, serta penerapannya pada data.
1.3 Batasan Masalah
Dalam menentukan estimator spline digunakan basis fungsi truncated, dan untuk
menentukan nilai parameter-parameternya digunakan metode kuadrat terkecil
dengan pendekatan matriks, sedangkan metode yang dipakai untuk menentukan
parameter penghalus adalah metode MSE dan GCV. Adapun data yang digunakan
adalah data sekunder yang diperoleh dari Laboratorium Terpadu Departemen
Fisika Universitas Sumatera Utara, yakni pengaruh lama waktu (menit) yang
diberikan sebagai variabel bebas terhadap perubahan tegangan output sensor
polimer (mv) sebagai variabel terikat dan hanya akan mencari model regresi
spline linier terbaik dengan satu titik knot, dan dua titik knot menggunakan
metode MSE dan GCV. Untuk mengetahui apakah parameter penghalus memiliki
pengaruh terhadap model yang didapat atau tidak, digunakan uji hipotesis yaitu uji
simultan dan uji normalitas Kolmogorov-Smirnov.
1.4 Tujuan Penelititan
Sesuai dengan rumusan masalah yang dikemukakan sebelumnya, tujuan dari
penelitian ini adalah untuk mengkaji bentuk estimator spline dengan basis
truncated dalam menentukan model regresi dengan menggunakan MSE dan GCV
menentukan metode terbaik dalam menghasilkan nilai yang paling minimum,
serta penerapannya pada data.
1.5 Manfaat Penelitian
Penelitian ini dilakukan untuk menambah pengetahuan serta memperkaya literatur
mengenai analisis regresi nonparametrik sehingga dapat menjadi referensi untuk
penelitian selanjutnya, baik dalam penentuan estimator model regresi
nonparametrik ataupun penerapannya pada data rill.
BAB 2
LANDASAN TEORI
Dalam bab ini diuraikan beberapa tinjauan pustaka sebagai landasan teori
pendukung penulisan penelitian ini.
2.1 Analisis Regresi
Suatu pasangan peubah acak seperti (tinggi, berat) mempunyai suatu sebaran
peluang dua peubah (bivariate probability distribution). Bila ditaruh perhatian
pada ketergantungan suatu peubah acak Y terhadap suatu besaran atau kuantitas X
yang bervariasi namun bukan merupakan peubah acak, maka suatu persamaan
yang menghubungkan Y dan X disebut persamaan regresi (Draper dan Smith,
1966).
Analisis regresi merupakan metode yang banyak digunakan untuk
mengetahui hubungan antara sepasang variabel atau lebih. Misalkan Y adalah
variabel terikat dan X adalah variabel bebas, maka hubungan variabel X dan Y
dalam bentuk linier dapat dinyatakan sebagai berikut:
(2.1)
atau dapat ditulis dalam bentuk umum dengan lebih dari satu variabel :
(2.2)
keterangan: = variabel terikat
= variabel bebas
artinya, untuk suatu nilai X tertentu, nilai Y padanannya terdiri atas nilai
ditambah besaran yang membuat nilai menyimpang dari garis regresinya.
2.2 Regresi Nonparametrik
Regresi nonparametrik merupakan metode pendekatan regresi yang sesuai untuk
pola data yang tidak diketahui bentuk kurva regresinya atau tidak terdapat
informasi masa lalu yang lengkap tentang bentuk pola data. Menurut Eubank
(1988) dalam Tripena (2011) bentuk model regresi nonparametrik adalah sebagai
berikut:
(2.3)
dengan adalah variabel terikat sedangkan fungsi merupakan kurva regresi
yang tidak diketahui bentuknya, dan adalah variabel bebas, serta diasumsikan
berdistribusi . Pendekatan regresi nonparametrik memiliki fleksibilitas
yang tinggi, karena data yang diharapkan mencari sendiri bentuk estimasi kurva
regresinya tanpa dipengaruhi oleh faktor subyektifitas peneliti.
Ada beberapa teknik estimasi dalam regresi nonparametrik antara lain
pendekatan histogram, estimator spline, estimator Kernel, estimator deret
ortogonal, analisis Wavelet dan lain-lain. Spline adalah salah satu jenis piecewise
polinomial, yaitu polinomial yang memiliki sifat tersegmen. Sifat tersegmen ini
memberikan fleksibilitas lebih dari polinomial biasa, sehingga memungkinkan
untuk menyesuaikan diri secara lebih efektif terhadap karakteristik lokal suatu
fungsi atau data. Pendekatan estimator spline ada bermacam-macam antara lain
spline original, spline type M, spline relaxed, spline terbobot dan lain-lain.
Pendekatan spline mempunyai suatu basis fungsi. Basis fungsi yang biasa dipakai
antara lain spline truncated dan B-spline (Lyche dan Morken, 2004, dalam
Budiantara, 2006). Spline mempunyai kelemahan pada saat orde Spline tinggi,
perhitungan yang hampir singular, sehingga persamaan normal tidak dapat
diselesaikan (Schuemaker, 1981, dalam Budiantara, 2006).
Pengunaan spline difokuskan kepada adanya perilaku atau pola data, yang
pada daerah tertentu, mempunyai karakteristik yang berbeda dari daerah lain.
Pencocokan data dapat dilakukan dengan melihat titik-titik pada data yang
mengalami suatu perubahan ekstrim pada suatu daerah sehingga pola data pada
masing-masing daerah mengalami perbedaan.
2.3 Fungsi Spline Polynomial Truncated
Bentuk fungsi spline yang biasa dipergunakan adalah fungsi basis spline
polinomial truncated. } merupakan basis
untuk ruang spline berorde m (Budiantara, 2001, dalam Stepanus, 2011) dengan
fungsi sepenggal (truncated) adalah sebagai berikut:
(2.4)
Kr = knot ke-r yang memperlihatkan pola perubahan perilaku dari
Berdasarkan bentuk matematis fungsi spline, dapat dikatakan bahwa spline
merupakan model polinomial yang sepotong-sepotong (piecewise polynomial) dan
spline masih bersifat kontinu pada knot-knotnya. Knot diartikan sebagai suatu
titik fokus dalam fungsi spline, sehingga kurva yang dibentuk tersegmen pada titik
tersebut dan untuk setiap fungsi m, titik knot dapat dinyatakan dengan kombinasi
linier. Fungsi spline merupakan suatu gabungan fungsi polinomial dimana
penggabungan beberapa polinomial tersebut pada knot-knot dengan suatu cara
yang menjamin sifat kontinuitas. Spline adalah potongan polinomial mulus yang
masih memungkinkan memiliki sifat tersegmen (Eubank, 1988, dalam Tripena,
2011).
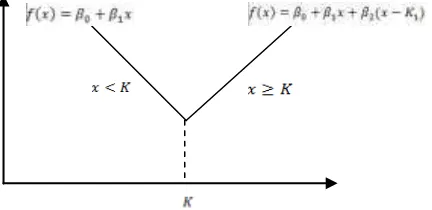
2.4 Fungsi Spline Linier
Fungsi spline linier merupakan fungsi spline dengan satu orde. Fungsi spline linier
dengan satu titik knot ( ) dapat disajikan dalam bentuk:
Fungsi ini dapat pula disajikan menjadi (Tripena, 2005, dalam Tripena, 2011):
Grafik spline linier satu titik knot pada dapat disajikan sebagai berikut:
2.5 Regresi Spline
Menurut Eubank (1988) dalam Tripena (2011), estimasi terhadap adalah
yakni estimator yang mulus. Dengan mempertimbangkan sifat-sifat fungsi
spline yang merupakan modifikasi dari regresi polinomial, maka untuk
mendapatkan model estimasi dari digunakan regresi spline.
Regresi spline adalah suatu pendekatan kearah pengepasan data dengan
tetap memperhitungkan kemulusan kurva. Regresi spline memungkinkan untuk
berbagai macam orde sehingga dapat dibentuk regresi spline linier, kuadrat, kubik
maupun orde m. Regresi spline linier biasanya diaplikasikan pada data dengan
pola yang masih sederhana sedangkan spline kuadrat dan kubik biasanya
diaplikasikan pada data dengan pola yang lebih kompleks.
Namun, dalam penyelesaiannya masalah utama menentukan model regresi
spline terbaik adalah letak titik knot yang optimal. Sasmitoadi (2005) dalam
Tripena (2011) menyebutkan bahwa terdapat 2 strategi untuk menyelesaikan
permasalahan yaitu pertama memilih banyaknya knot yang relatif sedikit,
sedangkan strategi yang kedua adalah kebalikannya, yakni menggunakan knot
yang relatif banyak.
2.6 Pemilihan Model Regresi Spline dengan yang Optimal
Pada pendekatan nonparametrik fitting kurva regresi dilakukan dengan
memperhatikan peubah dependen (y) secara terbatas di sekitar x pada selang
tertentu, tidak pada keseluruhan pengamatan x. Pada spline pendekatan dilakukan
pada segmentasi x untuk membangun fungsi s(x) dengan membagi pengamatan x
berdasarkan titik-titik x yang disebut knot. Pendekatan ini merupakan piecewise
polynomial, yaitu polinomial yang memiliki sifat tersegmen pada selang x yang
Dalam fungsi spline terdapat titik knot yang merupakan titik perpaduan
yang menunjukkan perubahan perilaku kurva pada selang berbeda, sehingga kurva
terbentuk tersegmen pada titik tersebut (Hardle, 1990, dalam Ismi, 2011).
Pemilihan λ (pemulus) optimal dalam Regresi spline pada hakekatnya
merupakan pemilihan lokasi titik knot. Pemilihan knot pada Regresi Spline
dilakukan secara trial error. Pemilihan knot ini sangat penting karena fungsi
spline sangat tergantung pada titik knot (Ismi, 2011)
Sesuai tujuan dari pendekatan regresi nonparametrik, yakni ingin
didapatkan kurva mulus yang mempunyai λ optimal menggunakan data amatan
sebanyak n, maka diperlukan ukuran kerja atas estimator. Ukuran kinerja atas
penduga kurva regresi dapat ditentukan dari MSE, fungsi loss dan fungsi resiko,
serta GCV. MSE merupakan ukuran kinerja yang paling sederhana, yaitu:
(2.6)
metode GCV mempunyai sifat optimal asimtotik (Wahba, 1990). Sementara
menurut Budiantara (2005, dalam Tripena, 2011), GCV merupakan modifikasi
dari Cross-Validation (CV) adalah metode untuk memilih λ yang meminimumkan.
Fungsi GCV sebagai berikut:
keterangan: GCV = Generelized Cross Validation
Kriteria dan diharapkan memiliki nilai yang minimum,
sehingga model regresi spline dapat dikatakan memiliki nilai yang optimal.
2.7 Metode Kuadrat Terkecil
Pada umumnya spline adalah suatu estimator yang diperoleh dengan
meminimumkan kuadrat terkecil terpenalti (penalized least square). Namun
penyelesaian optimasi ini secara matematika relatif sulit. Untuk mengatasi hal ini
maka digunakan optimasi kuadrat terkecil (least square) (Budiantara, 2007, dalam
Oktaviana dan Budiantara, 2011).
Metode kuadrat terkecil merupakan metode yang sangat lazim
dipergunakan dalam regresi linier. Metode ini digunakan untuk memperoleh
parameter koefisien dari persamaan regresi. Prinsip metode ini adalah
meminimumkan kuadrat residual.
Misalkan terdapat persamaan (2.1) dengan estimasi persamaan regresinya
sebagai berikut:
(2.8)
Keterangan: = penduga titik bagi
= penduga titik bagi
Nilai dan diperoleh dengan menggunakan metode kuadrat terkecil.
Metode kuadrat terkecil merupakan satu cara memperoleh dan dengan
meminimumkan jumlah kuadrat sisa.
(2.9)
syarat optimum adalah:
(210)
(2.11)
dari dua persyaratan optimum diperoleh persamaan normal sebagai berikut:
(2.12)
(2.13)
2.8 Matriks
2.8.1 Defenisi Matriks
Sianipar (2008) menyatakan bahwa, matriks ialah susunan berbentuk empat
persegi panjang dari elemen-elemen (bilangan-bilangan) yang terdiri dari
beberapa baris dan kolom dibatasi dengan tanda kurung, seperti bentuk:
Matriks A disebut matriks tingkat , atau disingkat matriks ,
karena terdiri dari m baris dan n kolom. Setiap disebut elemen (unsur) dari
matriks itu, sedang indeks i dan j berturut-turut menyatakan baris dan kolom. Jadi
elemen terdapat pada baris ke-i, kolom ke-j. Pasangan bilangan (m, n) disebut
dimensi (ukuran atau bentuk) dari matriks itu. Suatu matriks tidak mempunyai
harga numerik. Biasanya tanda kurang dapat dipakai seperti:
atau
Pada umumnya matriks disingkat dan dinyatakan dengan huruf besar,
sedang elemen-elemen matriks dengan huruf kecil. Untuk membeda-bedakan
matriks ditulis dengan atau misalnya untuk matriks
.
2.8.2 Trace Matriks
Jika , matriks disebut kuadrat atau disingkat n. Dalam hal ini
elemen-elemen disebut elemen pada. Jumlah
elemen-elemen pada diagonal suatu matriks disebut trace dari matriks itu yang disingkat
dengan , jadi:
2.8.3 Tranpos Matriks
Jika baris-baris dan kolom-kolom dari suatu matriks dipertukarkan
(baris pertama dengan kolom pertama dan seterusnya), maka diperoleh suatu
matriks yang disebut transpos yang disingkat atau . Jadi, bilamana:
2.8.4 Matriks Identitas
Hakim (1994) menyatakan bahwa suatu matriks bujur sangkar berordo n x n
dikatakan matriks identitas apabila elemen diagonalnya bernilai 1 dan elemen
lainnya bernilai nol. Matriks identitas berordo disimbolkan dengan In.
Beberapa matriks identitas adalah sebagai berikut:
,
Matrik identitas dapat pula dituliskan dalam bentuk sebagai berikut:
k, j= 1,2, …, n
2.8.5 Matriks Idempoten
Suatu matriks dikatakan matriks idempoten bila atau
2.8.6 Matriks Simetri
Matriks yang berukuran disebut matriks simetri jika dan hanya jika
untuk semua dan . teorema-teorema di bawah ini berhubungan dengan
transpos matriks.
6. Jika adalah matriks bujur sangkar, maka adalah matriks simetri.
2.8.7 Invers Matriks
Jika adalah matriks yang berukuran , maka invers matriks adalah
matriks yang berukuran yang disimbolkan dengan dengan sifat bahwa:
dan jelas bahwa adalah matriks identitas berukuran .
2.8.8 Matriks Invertible
Matriks disebut matriks invertible jika mempunyai invers.
BAB 3
METODE PENELITIAN
Adapun metodologi yang digunakan dalam penelitian ini adalah menggunakan
metode kepustakaan, yaitu dengan mengumpulkan dan membaca
informasi-informasi serta literatur yang berkaitan. Data yang digunakan dalam penelitian ini
berupa data sekunder yang diperoleh dari Laboratorium Terpadu Departemen
Fisika Universitas Sumatera Utara, yakni pengaruh lama waktu (menit) yang
diberikan sebagai variabel bebas terhadap perubahan tegangan output sensor
polimer (mv) sebagai variabel terikat. Sesuai dengan tujuan penelitian yang telah
dikemukakan, maka dalam metode penelitian ini terdapat dua pokok pembahasan,
yaitu kajian tentang penggunaan estimator spline dalam regresi nonparametrik dan
penerapannya pada data simulasi. Berikut akan dijelaskan langkah-langkah yang
dilakukan dalam metode penelitian ini.
3.1 Estimasi Model Spline dalam Regresi Nonparametrik
Dalam mengkaji penggunaan estimator spline dalam regresi nonparametrik
digunakan langkah-langkah sebagai berikut:
1. Membuat model regresi nonparametrik
2. Mendekati kurva regresi dengan fungsi spline truncated
3. Membuat model univariabel dengan K1, kombinasi (K1 dan K2),
dalam bentuk matriks
4. Membuat model regresi spline truncated nonparametrik dalam bentuk
matriks
5. Menentukan persamaan normal untuk nilai estimasi parameter-parameter
dengan metode kuadrat terkecil melalui pendekatan matriks
6. Membuat fungsi estimasinya
7. Pemilihan parameter pemulus dengan MSE
3.2. Menerapkan Model Spline pada Data untuk Estimasi Pola Hubungan
Variabel Terikat dan Variabel Bebas
Dalam menerapkan model spline pada data untuk estimasi pola hubungan variabel
dependen dan independen digunakan langkah-langkah sebagai berikut:
1. Membuat scatter plot antara variabel dependen dan independen.
2. Memodelkan variabel dependen dan variabel independen dengan
menggunakan spline linear (m= 1) dan dengan menggunakan satu titik knot,
dan dua titik knot.
3. Memilih model spline terbaik dengan memilih titik knot optimum dilihat
dari nilai MSE atau GCV yang paling minimum.
4. Berdasarkan model spline terbaik langkah berikutnya adalah membuat
persamaan regresi spline dan fungsi potongan (truncated).
5. Menguji signifikansi parameter model terbaik dengan uji hipotesis
simultan dan melakukan uji Kolmogorov-Smirnov untuk mengetahui
normalitas dari error random .
6. Membuat kurva estimasi regresi spline dan interpretasi model.
Dalam proses pengolahan data digunakan software aplikasi Matlab R2007b dan
BAB 4
ANALISIS DAN PEMBAHASAN
Dalam bab ini akan disajikan hasil analisis dari tujuan penelitian, yaitu mengenai
cara penggunaan estimator spline truncated. penggunaan MSE dan GCV sebagai
metode pemulus optimal serta penerapannya pada data.
4.1 Estimasi Model Spline dalam Regresi Nonparametrik
Misalkan adalah variabel terikat dan adalah variabel bebas, dengan banyak
data sebanyak maka hubungan variabel dan dalam regresi nonparametrik
dapat dinyatakan dalam bentuk umum sebagai berikut:
bentuk kurva regresi diasumsikan tidak diketahui, dimana saling bebas
dengan rata-rata nol dan variansi .
Berdasarkan persamaan (2.3) dan (2.5) jika dalam model kurva regresi
didekati dengan fungsi spline truncated, maka secara umum model regresi
nonparametrik spline truncated dengan derajat m dan N titik knot dapat ditulis
sebagai berikut:
(4.1)
Untuk memudahkan, fungsi spline truncated yang digunakan
diasumsikan univariabel, berorde satu dengan satu, dan dua titik knot, maka
persamaan (2.5) menjadi sebagai berikut:
apabila persamaan (4.2) diekspansi dengan menggunakan data sebanyak n dapat
disajikan sebagai berikut:
maka bentuk matriksnya dapat ditulis sebagai berikut:
fungsi spline satu titik knot (4.3)
dengan,
; ; ;
dan
Spline linier dengan 2 titik knot,
; untuk (4.4)
apabila persamaan (4.4) diekspansi dengan menggunakan data sebanyak n dapat
disajikan sebagai berikut:
maka bentuk matriksnya dapat ditulis sebagai berikut:
dengan,
; ; ;
dan
persamaan (4.3), dan (4.5) juga dapat disederhanakan secara umum menjadi:
(4.6)
dengan,
dan
Berdasarkan persamaan (4.2), dan (4.4) masing-masing regresi splinenya
dapat ditulis sebagai berikut:
(4.7)
(4.8)
Dengan menguraikan fungsi f dan memisahkan antara parameter dengan
variabel maka persamaan-persamaan tersebut secara umum berdasarkan
persamaan (4.6) dalam bentuk matriks dapat ditulis sebagai berikut:
(4.9)
dengan,
maka untuk memperoleh estimator pada persamaan (4.9), dilakukan optimasi
persamaan kuadrat dengan metode kuadrat terkecil melalui pendekatan matriks.
Pada materi matematika untuk meminimasi suatu fungsi terlebih dahulu harus
mencari turunan pertama dari fungsi tersebut, lalu dibuat sama dengan nol. Dalam
hal ini persamaan tersebut diturunkan terhadap .
4.1.1 Persamaan Regresi Spline Linier dengan Penurunan Terhadap
Penurunan terhadap :
⇔
⇔
penurunan terhadap :
Dari langkah-langkah penurunan dengan terhadap
didapat tiga persamaan yang dikenal sebagai persamaan normal, yaitu:
1. (4.10)
2. (4.11)
3.
(4.12)
4.1.2 Persamaan Regresi Spline Linier dengan Penurunan Terhadap
Penurunan terhadap :
⇔
penurunan terhadap :
penurunan terhadap :
Dari langkah-langkah penurunan dengan terhadap
didapat empat persamaan normal, yaitu:
1. (4.13)
2.
3.
(4.15)
4.
(4.16)
Untuk menentukan fungsi estimasi terlebih dahulu harus diperoleh nilai
estimator , maka dilakukan pendekatan menggunakan metode kuadrat terkecil
dengan metode matriks.
4.1.3 Pendekatan metode kuadrat terkecil dengan metode matriks
Dari persamaan normal yang telah diperoleh dapat dibentuk suatu persamaan
matriks sebagai berikut:
Untuk alasan kesederhanaan berlaku untuk semua , sesuai persamaan
(4.9) persamaan matriks di atas dapat ditulis sebagai berikut:
misalkan , maka:
(4.17)
keterangan: = estimator
Berdasarkan persamaan (4.17) diperoleh estimasi parameter-parameter
dengan menggunakan adalah matriks yang berukuran dan matriks yang
invertibel, dengan kata lain dapat dicari dengan menggunakan dan
(4.18)
atau secara umum dan ringkas persamaan normal dengan dan dapat
ditulis dengan algoritma matriks dari persamaan (4.9) estimasi koefisien
menggunakan metode kuadrat terkecil dilakukan dengan meminimumkan
terhadap . Untuk dengan menurunkan terhadap
dan menyamakan dengan nol sehingga diperoleh estimator:
(4.19)
sehingga diperoleh fungsi estimasinya, yaitu:
(4.20)
maka estimasi model regresinya, menjadi:
(4.21)
Memilih parameter penghalus merupakan hal yang sangat penting dalam
regresi nonparametrik. Pemilihan λ optimal dalam regresi spline pada hakekatnya merupakan pemilihan lokasi titik knot.
4.1.4 Pemilihan Parameter Pemulus dengan MSE
Ukuran kinerja atas estimator yang sederhana adalah kuadrat dari sisaan yang
dirata-rata. Berdasarkan persamaan (2.6) nilai MSE didapat setelah menyubsitusi
ke persamaan tersebut, dengan cara uji coba (trial error) titik-titik yang berada
di daerah pengamatan di sekitar x yang dijadikan sebagai dengan
memerhatikan titik-titik terdekat dengan daerah ekstrim. Hal ini berarti terdapat
nilai MSE sebanyak p untuk perlakuan . Sementara itu untuk dua titik knot,
mungkin. Kemudian dari nilai MSE sebanyak p dicari MSE yang paling minimum
4.1.5 Pemilihan Parameter Pemulus dengan GCV
Berdasarakan persamaan (2.7) nilai-nilai GCV diperoleh dari pembagian
nilai-nilai MSE dengan . bersifat simetris
dan idempoten. diperoleh dari fungsi estimasi pada persamaan
(4.19),
Keterangan: GCV = Generelized Cross Validation
4.2 Menerapkan Model Spline pada Data Simulasi untuk Estimasi Pola
Hubungan Variabel Terikat dan Variabel Bebas
Untuk menguji rumus-rumus dalam menentukan model regresi spline linier
terbaik yang telah dipaparkan sebelumnya, maka diperlukan data dalam
pengolahannya. Data yang digunakan adalah data sekunder yang diperoleh dari
Laboratorium Terpadu Departemen Fisika Universitas Sumatera Utara, yakni
pengaruh lama waktu (menit) yang diberikan sebagai variabel bebas terhadap
perubahan tegangan output sensor polimer (mv) sebagai variabel terikat.
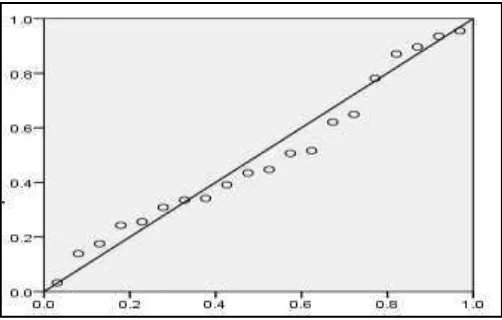
4.2.1 Plot Antara Variabel Terikat dan Variabel Bebas
Penyebaran data pengaruh lama waktu (menit) yang diberikan sebagai variabel
bebas terhadap perubahan tegangan output sensor polimer (mv) sebagai variabel
terikat dapat dilihat dari bentuk pola yang disajikan pada Gambar 4.1.
Berdasarkan Gambar 4.1 terlihat bahwa pola data mengalami
kecenderu-ngan naik secara tajam pada menit pertama (menit ke-5 sampai ke-25). Namun,
pada menit selanjutnya pola data mengalami kenaikan dan penurunan yang tidak
signifikan bila dibandingkan dengan beberapa menit pertama, meskipun
penurunan pola data terjadi hingga menit terakhir dan terdapat data yang konsisten
di beberapa menit. Hal ini menunjukkan bahwa, ada kecenderungan perubahan
waktu terhadap tegangan output sensor polimer untuk membentuk pola tertentu.
4.2.2 Estimasi Regresi Spline Linier
Dicobakan model spline linier dengan satu titik knot adalah:
Uji cobayang dilakukan dalam mencari titik knot menghasilkan titik knot
optimal yang bersesuaian dengan nilai MSE dan GCV minimum untuk model
spline linier dengan satu titik knot diberikan dalam tabel berikut:
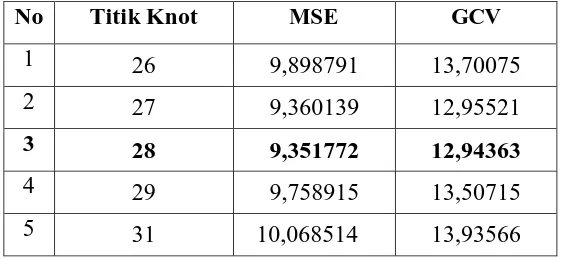
Tabel 4.1. Ringkasan Nilai MSE dan GCV untuk Satu Titik Knot
minimum untuk model spline linier dengan satu titik knot masing-masing sebesar
9,351772 dan 12,94363 yang berada pada titik knot K1= 28. Estimasi model
Tabel 4.2. Estimasi Model Regresi Spline Linier dengan Satu Titik Knot
Parameter Estimasi
281,4679
2,0891
-2,2178
Sehingga diperoleh estimasi model regresi spline linier dengan satu titik
knot K1= 28 yaitu:
Estimasi model regresi spline linier dengan satu titik knot dapat disajikan
pula dalam bentuk fungsi sepenggal (truncated) sebagai berikut:
Kemudian dicobakan model spline linier dengan dua titik knot adalah:
Titik knot optimal yang bersesuaian dengan nilai MSE dan GCV minimum
untuk model spline linier dengan dua titik knot diberikan dalam tabel berikut:
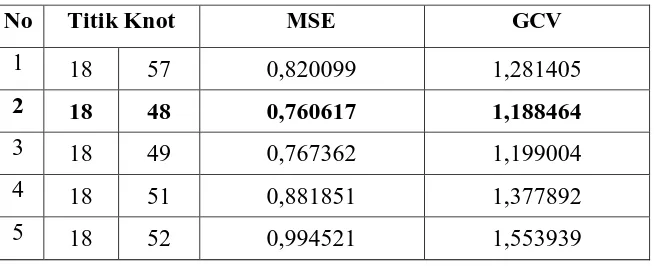
Tabel 4.3. Ringkasan Nilai MSE dan GCV untuk Dua Titik Knot
No Titik Knot MSE GCV
1 18 57 0,820099 1,281405
2 18 48 0,760617 1,188464
3 18 49 0,767362 1,199004
4 18 51 0,881851 1,377892
Berdasarkan Tabel 4.3 menunjukkan bahwa nilai MSE dan GCV yang
minimum untuk model spline linier dengan dua titik knot masing-masing sebesar
0,760617 dan 1,188464 yang berada pada titik knot K1= 18 dan K2=48. Estimasi
model regresi spline linier dengan dua titik knot dapat disajikan pada Tabel 4.4.
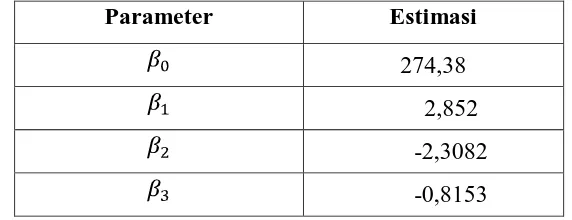
Tabel 4.4. Estimasi Model Regresi Spline Linier dengan Satu Titik Knot
Parameter Estimasi
274,38
2,852
-2,3082
-0,8153
Sehingga diperoleh estimasi model regresi spline linier dengan dua titik
knot K1= 18 dan K2=48 yaitu:
Estimasi model regresi spline linier dengan dua titik knot dapat disajikan
pula dalam bentuk fungsi sepenggal (truncated) sebagai berikut:
4.2.3 Pemilihan Model Regresi Spline Linier Terbaik
Dari kedua hasil trial error diambil knot yang optimum yang memiliki nilai MSE
dan GCV minimum. Nilai MSE dan GCV minimum untuk satu dan dua titik knot
disajikan pada Tabel 4.5.
Tabel 4.5. Titik Knot Optimum Satu dan Dua Titik Knot
Jumlah Knot Titik Knot MSE GCV
2 18 48 0,760617 1,188464
Berdasarkan Tabel 4.5 didapat titik knot (K) yang paling optimal dengan
nilai MSE dan GCV minimum masing-masing sebesar 0,760617 dan 1,188464
terletak pada K1 = 18 dan K2 = 48, sehingga model terbaik adalah model regresi
spline linier dengan dua titik knot sebagai berikut:
dengan fungsi sepenggalnya (truncated):
Model regresi spline linier dengan dua titik knot ini memiliki nilai
koefisien determinasi (R2) sebesar 0,995. Hal ini berarti bahwa variabel bebas
pemberian waktu tertentu mampu menerangkan sebesar 99,5% terhadap
perubahan tegangan output sensor polimer.
4.2.4 Pengujian Model Regresi Spline Linier Terbaik
Uji hipotesis untuk pemeriksaan model digunakan uji simultan, dengan rumus
hipotesis sebagai berikut:
H0 : (variabel bebas tidak mempengaruhi variabel terikat)
H1 : , paling tidak ada satu j di mana
dengan : H0 ditolak jika Fhitung≥ Ftabel, berarti H1 diterima
H1 ditolak jika Fhitung < Ftabel, berarti H0 diterima
dengan menggunakan software SPSS 16.0 dilakukan analisis variansi dan
Tabel 4.6. Analisis Variansi Model Spline Linier Dua Titik Knot
dengan dua titik knot (knot ke-18 dan 48) terdapat minimal satu koefisien regresi
yang memberikan pengaruh terhadap model dan cukup memadai sebagai model
pendekatan untuk data pengaruh waktu terhadap tegangan output sensor polimer.
Sedangkan untuk mengetahui bahwa error random berdistribusi normal
atau tidak, maka digunakan uji Kolmogorov-Smirnov sebagai uji asumsi dengan
hipotesis sebagai berikut:
H0 : error random berdistribusi normal
H1 : error random tidak berdistribusi normal
dengan menggunakan . Dari hasil output software SPSS 16.0 diperoleh
nilai Asimp. Sig(2-tailed) sebesar level of signifikan( ). Jadi H0
diterima dan H1 ditolak. Berarti error random berdistribusi normal. Plot
Gambar 4.2. Plot Normalitas Residual
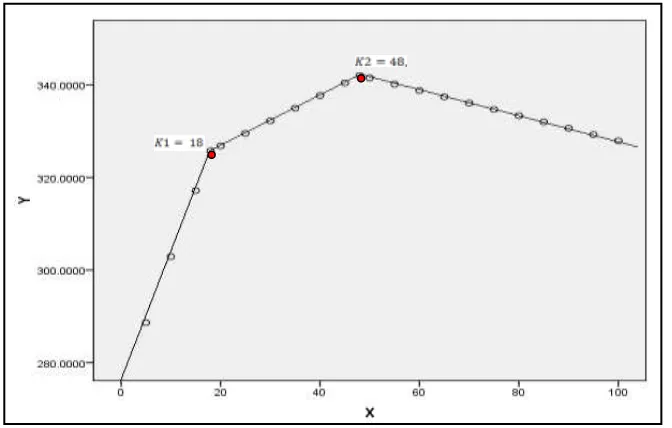
4.2.5 Interpretasi Model Regresi Spline Truncated Linier
Model regresi spline linier terbaik adalah dengan dua titik knot :
dengan fungsi sepenggalnya (truncated):
model spline disajikan dalam Gambar 4.2 berikut:
Gambar 4.3. Kurva Estimasi Regresi Spline Linier dengan Dua Titik Knot
Dari Gambar 4.3 terlihat bahwa kurva mempunyai slope baru pada
titik-titik amatan awal. Kurva regresi spline linier dengan dua titik knot sudah cukup
mampu membentuk pola yang sesuai dengan tingkat kemulusan kurva. Sedangkan,
maka jika terjadi penambahan waktu sebesar satu menit maka tegangan akan naik
sebesar 2,852 mv. Apabila percobaan berada pada penambahan waktu lebih dari
atau sama dengan sebesar 18 menit dan di kurang 48 menit, maka jika terjadi
penambahan waktu sebesar satu menit maka tegangan akan naik sebesar 0,5438
mv. Sementara percobaan yang berada pada waktu lebih dari atau sama dengan 48
menit jika terjadi penambahan waktu sebesar satu menit maka tegangan akan
BAB 5
KESIMPULAN DAN SARAN
5.1. Kesimpulan
Berdasarkan analisis dan pembahasan yang telah diuraikan pada bab sebelumnya,
maka dapat diperoleh kesimpulan:
1. Masalah utama pada regresi nonparametrik adalah adanya komponen
nonparametrik merupakan fungsi yang tidak diketahui bentuknya, yakni:
Penggunaan metode kuadrat terkecil mengasumsikan bentuk fungsi spline
truncated dan memberikan kemudahan interpretasi melalui model statistik.
2. Estimasi parameter model regresi nonparametrik spline linier dengan
menggunakan metode kuadrat terkecil melalui pendekatan matriks
diperoleh:
3. Penentuan lokasi knot yang berbeda, akan menghasilkan model regresi
spline linier yang berbeda dan dengan nilai MSE dan GCV yang berbeda
pula.
4. Dari hasil pengolahan data tegangan output sensor polimer diketahui
bahwa pemilihan model regresi spline terbaik dengan menggunakan
metode MSE(λ) sebesar 0,760617 dan GCV(λ) sebesar 1,188464. Setiap
trial error hasil minimal kedua metode bersama-sama secara konstan
menunjukkan letak titik knot yang sama. Hal ini menunjukkan bahwa
kedua metode memiliki efektivitas yang sama dalam menetukan letak titik
knot yang optimal. Namun, jika dilihat dari nilai yang dihasilkan, nilai
metode yang terbaik karena efisien dan lebih mudah penggunaannya untuk
model regresi spline linier dengan satu dan dua titik knot.
5. Model regresi spline linier terbaik dari satu dan dua titik knot adalah
dengan dua titik knot K1 = 18 dan K2 = 48 yaitu:
dengan fungsi sepenggalnya:
6. Dari uji hipotesis pada data dapat diambil kesimpulan bahwa model
regresi spline linier dengan titik knot K1 = 18 dan K2 = 48 cukup memadai
sebagai model pendekatan untuk data pengaruh waktu terhadap tegangan
output sensor polimer.
6.2. Saran
Karena keterbatasan peneliti dalam hal memperoleh referensi dan pemrograman
untuk perhitungan, pada penelitian ini masih banyak permasalahan yang belum
dikaji secara mendalam dan rinci. Oleh karena itu, beberapa hal yang dapat
disarankan pada penelitian selanjutnya adalah:
1. Pada penelitian ini hanya terbatas pada penggunaan regresi spline
truncated linier (orde satu) dan dua titik knot. Untuk penelitian selanjutnya
perlu dikaji lagi model regresi nonparametrik spline dengan orde kuadratik,
kubik atau polinomial derajat m, dengan penambahan knot lebih dari dua
serta dengan berbagai kombinasinya.
2. Pada penelitian ini data sekunder yang digunakan adalah univariabel.
Untuk penelitian selanjutnya perlu dikaji lagi regresi nonparametrik spline
dengan model yang lebih rumit seperti multivariabel dan semiparametrik.
3. Untuk penelitian selanjutnya dapat dibuat suatu program untuk mencari
digunakan, agar memudahkan perhitungan ketika menggunakan knot yang
banyak serta kombinasinya.
DAFTAR PUSTAKA
Budiantara, I.N. 2002. Aplikasi Spline Terbobot. Jurnal Teknik Industri, PETRA. Surabaya
Draper,N.R. dan H.Smith. 1992. Analisis Regresi Terapan. Jakarta: PT. Gramedia Utama
Ratno, D.S. dan Mustadjab, H.K. 1992. Analisis Regresi. Yogyakarta: Andi Offset
Herawati, Netty. 2011. Regresi Spline untuk P emodelan Bidang Kesehatan: Studi
Tentang Knot dan Selang Kepercayaan. Jurnal Jurusan
Matematika, FMIPA. Universitas Lampung.
Ismi, NS. 2011. P enerapan Spline Terboboti untuk Mengatasi Heteroskedastisitas
pada Regresi Nonparametrik. Jurnal Jurusan Matematika, FMIPA.
Universitas Brawijaya Malang.
Sianipar, Pangeran. 2008. Aljabar Linier. Medan: USU Press
Stefanus, N.T. dan Budiantara. 2011. Uji Hipotesis dalam Regresi Nonparametric Spline. Jurnal Jurusan Statistika, ITS.
Oktaviana, Dhina dan Budiantara, I.N. 2011. Regresi Spline Birespon untuk Memodelkan Kadar Gula Darah P enderita Diabetes Melitus.
Jurnal Jurusan Statistika. ITS.
Santosa, R. Gunawan. 2008. Aljabar Linier Dasar. Yogyakarta : Penerbit Andi
Tripena, A. 2011. Analisis Regresi Spline Kuadratik. Jurnal Jurusan MIPA, Fakultas Sains dan Teknik, UNSOED
Variabel Keterangan
X Waktu (menit)
Y Tegangan output sensor polimer (mv)
Diketahui oleh
Peneliti,
Muhammad Balyan
Lampiran 4. Uji Simultan Model Regresi Spline Truncated Linier Terbaik dengan Menggunakan SPSS 16.0
Input data variabel dari knot optimal dan ,
Variabel diberi label X
Variabel diberi label XK
Variabel diberi label XK2
Variabel diberi label Y
Kemudian klik Analyze > Regression > Linear sehingga muncul kotak kerja Linear Regression
Kemudian masukkan variabel X, XK, XK2 ke dalam kotak Independent, variabel Y ke dalam kotak Dependent
Klik Statistic sehingga muncul kotak kerja Linear Regression: Statistics
Klik Estimates, Model Fit
Lampiran 5. Uji Normalitas dengan Uji Kolmogorov-Smirnov
Input data dari knot optimal dan ,
Kemudian klik Analyze > Nonparametric Test > 1-Sample K-S sehingga muncul kotak kerja One-Sample Kolmogorov-Smirnov Test
Kemudian masukkan variabel e dan masukkan ke kotak kerja Test
Variable List
Klik Normal pada kotak kerja Test Distribution