BAB 2
LANDASAN TEORI
Dalam bab ini diuraikan beberapa tinjauan pustaka sebagai landasan teori pendukung penulisan penelitian ini.
2.1 Analisis Regresi
Suatu pasangan peubah acak seperti (tinggi, berat) mempunyai suatu sebaran peluang dua peubah (bivariate probability distribution). Bila ditaruh perhatian pada ketergantungan suatu peubah acak Y terhadap suatu besaran atau kuantitas X yang bervariasi namun bukan merupakan peubah acak, maka suatu persamaan yang menghubungkan Y dan X disebut persamaan regresi (Draper dan Smith, 1966).
Analisis regresi merupakan metode yang banyak digunakan untuk mengetahui hubungan antara sepasang variabel atau lebih. Misalkan Y adalah variabel terikat dan X adalah variabel bebas, maka hubungan variabel X dan Y dalam bentuk linier dapat dinyatakan sebagai berikut:
(2.1)
atau dapat ditulis dalam bentuk umum dengan lebih dari satu variabel :
(2.2)
artinya, untuk suatu nilai X tertentu, nilai Y padanannya terdiri atas nilai ditambah besaran yang membuat nilai menyimpang dari garis regresinya.
2.2 Regresi Nonparametrik
Regresi nonparametrik merupakan metode pendekatan regresi yang sesuai untuk pola data yang tidak diketahui bentuk kurva regresinya atau tidak terdapat informasi masa lalu yang lengkap tentang bentuk pola data. Menurut Eubank (1988) dalam Tripena (2011) bentuk model regresi nonparametrik adalah sebagai berikut:
(2.3)
dengan adalah variabel terikat sedangkan fungsi merupakan kurva regresi yang tidak diketahui bentuknya, dan adalah variabel bebas, serta diasumsikan berdistribusi . Pendekatan regresi nonparametrik memiliki fleksibilitas yang tinggi, karena data yang diharapkan mencari sendiri bentuk estimasi kurva regresinya tanpa dipengaruhi oleh faktor subyektifitas peneliti.
perhitungan yang hampir singular, sehingga persamaan normal tidak dapat diselesaikan (Schuemaker, 1981, dalam Budiantara, 2006).
Pengunaan spline difokuskan kepada adanya perilaku atau pola data, yang pada daerah tertentu, mempunyai karakteristik yang berbeda dari daerah lain. Pencocokan data dapat dilakukan dengan melihat titik-titik pada data yang mengalami suatu perubahan ekstrim pada suatu daerah sehingga pola data pada masing-masing daerah mengalami perbedaan.
2.3 Fungsi Spline Polynomial Truncated
Bentuk fungsi spline yang biasa dipergunakan adalah fungsi basis spline
polinomial truncated. } merupakan basis
untuk ruang spline berorde m (Budiantara, 2001, dalam Stepanus, 2011) dengan fungsi sepenggal (truncated) adalah sebagai berikut:
(2.4)
Secara umum, fungsi spline berorde m adalah sembarang fungsi yang dinyatakan sebagai berikut:
(2.5)
keterangan: s(x) = potongan polinomial berorde m pada subinterval (Kr, Kr+ 1) m = orde
N = banyaknya knot β = konstanta riil x = variabel bebas
Berdasarkan bentuk matematis fungsi spline, dapat dikatakan bahwa spline merupakan model polinomial yang sepotong-sepotong (piecewise polynomial) dan spline masih bersifat kontinu pada knot-knotnya. Knot diartikan sebagai suatu titik fokus dalam fungsi spline, sehingga kurva yang dibentuk tersegmen pada titik tersebut dan untuk setiap fungsi m, titik knot dapat dinyatakan dengan kombinasi linier. Fungsi spline merupakan suatu gabungan fungsi polinomial dimana penggabungan beberapa polinomial tersebut pada knot-knot dengan suatu cara yang menjamin sifat kontinuitas. Spline adalah potongan polinomial mulus yang masih memungkinkan memiliki sifat tersegmen (Eubank, 1988, dalam Tripena, 2011).
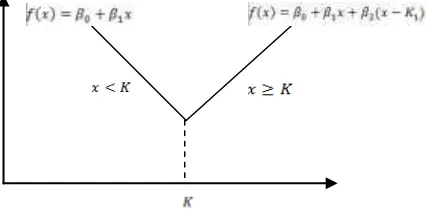
2.4 Fungsi Spline Linier
Fungsi spline linier merupakan fungsi spline dengan satu orde. Fungsi spline linier dengan satu titik knot ( ) dapat disajikan dalam bentuk:
Fungsi ini dapat pula disajikan menjadi (Tripena, 2005, dalam Tripena, 2011):
Grafik spline linier satu titik knot pada dapat disajikan sebagai berikut:
2.5 Regresi Spline
Menurut Eubank (1988) dalam Tripena (2011), estimasi terhadap adalah yakni estimator yang mulus. Dengan mempertimbangkan sifat-sifat fungsi spline yang merupakan modifikasi dari regresi polinomial, maka untuk mendapatkan model estimasi dari digunakan regresi spline.
Regresi spline adalah suatu pendekatan kearah pengepasan data dengan tetap memperhitungkan kemulusan kurva. Regresi spline memungkinkan untuk berbagai macam orde sehingga dapat dibentuk regresi spline linier, kuadrat, kubik maupun orde m. Regresi spline linier biasanya diaplikasikan pada data dengan pola yang masih sederhana sedangkan spline kuadrat dan kubik biasanya diaplikasikan pada data dengan pola yang lebih kompleks.
Namun, dalam penyelesaiannya masalah utama menentukan model regresi spline terbaik adalah letak titik knot yang optimal. Sasmitoadi (2005) dalam Tripena (2011) menyebutkan bahwa terdapat 2 strategi untuk menyelesaikan permasalahan yaitu pertama memilih banyaknya knot yang relatif sedikit, sedangkan strategi yang kedua adalah kebalikannya, yakni menggunakan knot yang relatif banyak.
2.6 Pemilihan Model Regresi Spline dengan yang Optimal
Dalam fungsi spline terdapat titik knot yang merupakan titik perpaduan yang menunjukkan perubahan perilaku kurva pada selang berbeda, sehingga kurva terbentuk tersegmen pada titik tersebut (Hardle, 1990, dalam Ismi, 2011).
Pemilihan λ (pemulus) optimal dalam Regresi spline pada hakekatnya merupakan pemilihan lokasi titik knot. Pemilihan knot pada Regresi Spline dilakukan secara trial error. Pemilihan knot ini sangat penting karena fungsi spline sangat tergantung pada titik knot (Ismi, 2011)
Sesuai tujuan dari pendekatan regresi nonparametrik, yakni ingin didapatkan kurva mulus yang mempunyai λ optimal menggunakan data amatan sebanyak n, maka diperlukan ukuran kerja atas estimator. Ukuran kinerja atas penduga kurva regresi dapat ditentukan dari MSE, fungsi loss dan fungsi resiko, serta GCV. MSE merupakan ukuran kinerja yang paling sederhana, yaitu:
(2.6)
keterangan: MSE = Mean Square Error
λ =
n = banyak data y = variabel dependen
= estimator pemulus
Menurut Wahba (1990) dan Wang (1998) dalam Oktaviana (2011), salah satu metode yang paling banyak dipakai dan disukai karena kelebihan yang dimilikinya adalah GCV. Dibanding metode lain, misal CV (Cross Validation), metode GCV mempunyai sifat optimal asimtotik (Wahba, 1990). Sementara menurut Budiantara (2005, dalam Tripena, 2011), GCV merupakan modifikasi dari Cross-Validation (CV) adalah metode untuk memilih λ yang meminimumkan. Fungsi GCV sebagai berikut:
keterangan: GCV = Generelized Cross Validation MSE = Mean Square Error
λ =
n = banyak data tr = trace
I = matriks identitas
= bersifat simetris dan idempoten
Kriteria dan diharapkan memiliki nilai yang minimum, sehingga model regresi spline dapat dikatakan memiliki nilai yang optimal.
2.7 Metode Kuadrat Terkecil
Pada umumnya spline adalah suatu estimator yang diperoleh dengan meminimumkan kuadrat terkecil terpenalti (penalized least square). Namun penyelesaian optimasi ini secara matematika relatif sulit. Untuk mengatasi hal ini maka digunakan optimasi kuadrat terkecil (least square) (Budiantara, 2007, dalam Oktaviana dan Budiantara, 2011).
Metode kuadrat terkecil merupakan metode yang sangat lazim dipergunakan dalam regresi linier. Metode ini digunakan untuk memperoleh parameter koefisien dari persamaan regresi. Prinsip metode ini adalah meminimumkan kuadrat residual.
Misalkan terdapat persamaan (2.1) dengan estimasi persamaan regresinya sebagai berikut:
(2.8)
Nilai dan diperoleh dengan menggunakan metode kuadrat terkecil. Metode kuadrat terkecil merupakan satu cara memperoleh dan dengan meminimumkan jumlah kuadrat sisa.
(2.9)
syarat optimum adalah:
(210) (2.11)
dari dua persyaratan optimum diperoleh persamaan normal sebagai berikut:
(2.12) (2.13)
2.8 Matriks
2.8.1 Defenisi Matriks
Sianipar (2008) menyatakan bahwa, matriks ialah susunan berbentuk empat persegi panjang dari elemen-elemen (bilangan-bilangan) yang terdiri dari beberapa baris dan kolom dibatasi dengan tanda kurung, seperti bentuk:
Matriks A disebut matriks tingkat , atau disingkat matriks , karena terdiri dari m baris dan n kolom. Setiap disebut elemen (unsur) dari matriks itu, sedang indeks i dan j berturut-turut menyatakan baris dan kolom. Jadi elemen terdapat pada baris ke-i, kolom ke-j. Pasangan bilangan (m, n) disebut dimensi (ukuran atau bentuk) dari matriks itu. Suatu matriks tidak mempunyai harga numerik. Biasanya tanda kurang dapat dipakai seperti:
atau
Pada umumnya matriks disingkat dan dinyatakan dengan huruf besar, sedang elemen-elemen matriks dengan huruf kecil. Untuk membeda-bedakan matriks ditulis dengan atau misalnya untuk matriks
.
2.8.2 Trace Matriks
Jika , matriks disebut kuadrat atau disingkat n. Dalam hal ini elemen-elemen disebut elemen pada. Jumlah elemen-elemen pada diagonal suatu matriks disebut trace dari matriks itu yang disingkat dengan , jadi:
2.8.3 Tranpos Matriks
Jika baris-baris dan kolom-kolom dari suatu matriks dipertukarkan (baris pertama dengan kolom pertama dan seterusnya), maka diperoleh suatu matriks yang disebut transpos yang disingkat atau . Jadi, bilamana:
2.8.4 Matriks Identitas
Hakim (1994) menyatakan bahwa suatu matriks bujur sangkar berordo n x n dikatakan matriks identitas apabila elemen diagonalnya bernilai 1 dan elemen lainnya bernilai nol. Matriks identitas berordo disimbolkan dengan In.
Beberapa matriks identitas adalah sebagai berikut:
,
Matrik identitas dapat pula dituliskan dalam bentuk sebagai berikut:
k, j= 1,2, …, n
2.8.5 Matriks Idempoten
Suatu matriks dikatakan matriks idempoten bila atau
2.8.6 Matriks Simetri
Matriks yang berukuran disebut matriks simetri jika dan hanya jika untuk semua dan . teorema-teorema di bawah ini berhubungan dengan transpos matriks.
1. .
2.
3. .
4. .
5. untuk r> 0.
2.8.7 Invers Matriks
Jika adalah matriks yang berukuran , maka invers matriks adalah matriks yang berukuran yang disimbolkan dengan dengan sifat bahwa:
dan jelas bahwa adalah matriks identitas berukuran .