Statistik dan Probabilitas 3

BAB II

TEKNIK SAMPLING

II.1. Pengertian Sampling dalam Industri

Dalam industri banyak pengukuran diambil dari basis data. Sebelum langkah diambil, data perlu dikumpulkan dahulu. Misalnya data yang diperlukan untuk mengontrol temperatur, tekanan, kecepatan dan waktu dalam usaha mempertahankan standar operasi dari peralatan. Data juga perlu untuk mengontrol nilai karakteristik dari bahan dan produk, misalnya tentang beratnya, besarnya, intensitasnya, kompisisi dari bahannya, dan sebagainnya. Akhirnya begitu juga mengenai efisiensi, produk, fraction defectives dan biaya dapat disebut data. Data itu menunjukkan situasi proses dari suatu produk, bukan merupakan kualitas dari lot (kumpulan).

Dalam banyak hal data itu diperoleh melalui sampling. Tentu saja tidak mungkin dilakukan pemeriksaan pada setiap produk, tetapi dengan pengambilan sampel dan kemudian dibuat estimasi untuk keseluruhan lot. Menurut Standard Industri Jepang (JISZ 8101 “Glosary of Term Used in Quality Control”) definisi sampel ialah bagian yang diambil dari suatu populasi untuk tujuan tertentu. Perhatikan gambar 2.1 sampel ditarik dari lot sutau produk yang sudah selesai untuk mempelajari karakteristik dari keseluruhan lot.

Sampel yang ditarik dari lini produksi (production line) untuk menentukan kondisi proses pada lini tersebut, mempertimbangkan metode proses yang akan datang, dan untuk memperoleh data sebagai dasar pengambilan langkah-langkah suatu tindakan.

Gambar 2.1

Jadi populasi merupakan grup yang memungkinkan dibuatnya perencanaan untuk mengambil langkah-langkah tindakan berdasarkan sampel atau data yang ditarik daripadanya.

Pada gambar 2.1 (a) ditunjukkan bahwa dalam hal langkah-langkah tindakan pada proses produksi, populasi dipertimbangkan dalam kondisi proses yang pasti. Produk dihasilkan oleh suatu proses pembuatan yang tidak terbatas (infinite population). Hal ini merupakan obyek dari kontrol proses dan analisis. Pada gambar 2.1 (b) ditunjukkan langkah-langkah kegiatan pada lot. Jumlah lot selalu terbatas, misalnya 100 ton batubara, atau 50 batang pensil. Populasinya dinamakan populasi terbatas (finite population). Hal ini merupakan objek dari inspeksi dan evaluasi kualitas. Oleh karena itu tujuan pengumpulan data dari sampel yang ditarik dari suatu populasi adalah untuk mengetagui lebih jauh tentang keadaan yang sebenarnya dari populasi itu, dan langkah-langkah selanjutnya dapat diambil dengan tepat.

II.2. Dasar Pemikiran Ststistik dan Sampling

Data yang dikumpulkan tidak seluruhnya sama, tetapi selalu mengandung dispersi. Data tak terbatas disebabkan oleh dispersi dalam proses pembuatan (manufaktur). Meskipun kondisi produksi ada dalam keadaan terkendali (state of control) bebrapa dispersi tidak dapat dihindari, misalnya dispersi diantara lot, diantara produk dalam lot yang sama, dan lain-lain.

Oleh karena dispersi itu terjadi pada suatu lot atau pada proses, jadi dispersi itu memperlihatkan suatu distribusi frekuensi. Ada beberapa cara pengukuran distribusi frekuensi. Apabila nilai rata-rata dan jumlah yang memperlihatkan dispersi (varians atau deviasi standar) dapat diketemukan, biasanya gambaran mengenai distribusi dapat ditentukan.

Apabila populasi menunjukkan distribusi frekuensi, random sampling (pengambilan sampel secara acak) dengan tepat harus tetap dipertahankan, artinya jangan sampai hanya memilih barang yang baik saja atau yang jelek saja, dan jangan mengambil sampel hanya dari satu bagian dari lot. Sampel harus benar-benar representatif ditarik dari suatu lot.

Untuk mengevaluasi suatu lot dapat dengan cara mengestimasi distribusi frekuensi lot tersebut, yaitu mengenai nilai rata-rata dan dispersi distribusi, akan tetapi pertimbangan ekonomi dan teknik sangat berat untuk memeriksa seluruh lot. Untuk mengatasinya dapat ditarik sampel dari lot tersebut, diukurnya dan kemudian diestimasi nilai rata-rata dan dispersinya. Hal ini berarti dalam sampling faktor-faktor ekonomis, teknis dan statistik harus benar-benar dipertimbangkan. Kondisi untuk sampling harus :

(1)Benar,

(2)Dapat dipercaya, (3)Cepat dan (4)Ekonomis.

Nilai data yang diambil dari sampel berbeda dengan nilai data dari populasi. Agar tidak membingungkan diberi simbol-simbol yang berbeda seperti pada tabel 2.1

Tabel 2.1

Populasi, sampel dan data

Populasi Sampel

Nilai rata-rata rata-rata populasi

µ rata-rata sampel X

Varians varians populasi

σ2

varians sampel S2 Deviasi Standar deviasi standar populasi

σ

deviasi standar populasi S

II.3. Random Sampling (Sampling Secara Acak) (1)Kondisi untuk random sampling

Suatu sampel dikatakan random, apabila setiap unit yang berada di dalam populasi mempunyai kesempatan yang sama (mempunyai probabilitas yang sama) untuk diikutsertakan dalam sampel yang bersangkutan.

Random sampling dari suatu populasi adalah tidak mudah. Misalmya memilih sampel secara random dari suatu yang terbungkus bukan saja sulit tetapi juga mahal. Pengambilan sampel dari 100.000 ton bijih besi halus

(2)Metode random sampling

a) Random Sampling Sederhana

Dengan menggunakan “Tabel Random Number” (lihat pada lampiran tabel)

Misalnya pengambilan sampel sebanyak 20 unit dari produk sebanyak 600 unit.

1. Berilah nomor urut unit dari 001 s/d 600

2. Tentukan secara random tempat mulainnya pemakaian tabel, yaitu kelompok ribuan, baris dan kolom. Misalnya pada ribuan ke-1, baris ke-20, dan kolom ke-18. jadi angka-angkanya adalah :

794 500 065 718 788 525 637 942 631 265 327 315 806 930 905 386 557 307

762 695 dan seterusnya sampai terkumpul

40 buah

3. batalkan nomor-nomor yang lebih besar dari 600. apabila nomor yang tidak dibatalkan muncul kedua kalinya, nomor itu harus dibatalkan

b) Sampling Sistematis

Misalkan akan ditarik 5 unit sampel dari 150 unit produk. Berilah nomor urut pruduk tersebut dari 1 s/d 150. interval pengambilan sampel adalah

30 1

, jika nomor pertama yang terpilih adalah 5, maka nomor berikutnya yang dipilih adalah :

II.4. Sampling Error

Bila diuji seluruh lot setelah dilakukan sampling dan diketemukan nilai sampel yang berbeda dibandingkan dengan nilai lot berarti telah terjadi sesuatu kesalahan (error). Kesalahan dapat dibagi dalam 2 kategori :

(1)Bias

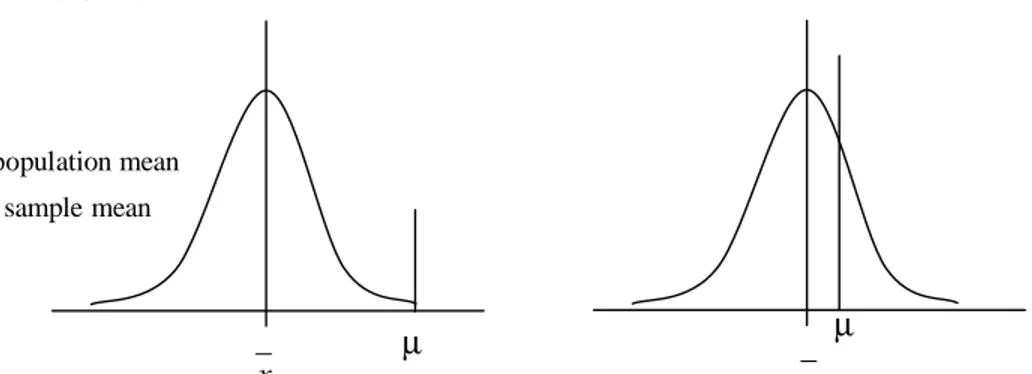
Bias terjadi bila terdapat perbedaan antara rata-rata sampel dan rata-rata populasi. Biasanya karena sampling yang kurang merata. Misalnya sampling pada bijih besi hanya pada bijih besi yang besar-besar saja. Keadaan ini sedapat mungkin harus dihindari. Perhatikan gambar 2.2 dibawah ini :

Gambar 2.2 Bias (2)Dispersi (ketelitian)

Nilai sampel yang diambil berulang-ulang dari suatu lot digambarkan dalam suatu histogram. Deviasi standar dari histogram itu menentukan tingkat ketelitian tertentu.

(3)Sampling Error

Bias yang tidak terkontrol, dispersi atau keduanya dan sampel yang tidak terkontrol akan mnyebabkan terjadinya error. Untuk mencapai tingkat kepercayaan, pengontrolan terhadap proses harus tetap dipertahankan. Hal-hal yang diperlukan adalah :

a) Analisis benyebab bias, dan jaminan ketelitian.

b) Adanya instruksi pengontrol penyebab terjadinya kesalahan. µ x µ = population mean x = sample mean µ x

c) Dibuatkannya instruksi tertentu yang dapat diikuti oleh pelaksana produksi.

d) Pengontrolan terhadap instrumen ukur dan peralatan.

II.5. Tipe-tipe Sampling

(1)Tipe random sampling

Mengambil sampel secara random dari keseluruhan lot (gambar 2.3)

Gambar 2.3 Random Sampling (2)Sampling dua tingkat

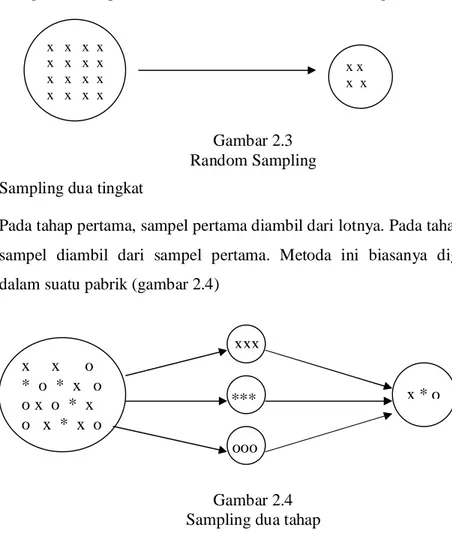
Pada tahap pertama, sampel pertama diambil dari lotnya. Pada tahap kedua sampel diambil dari sampel pertama. Metoda ini biasanya digunakan dalam suatu pabrik (gambar 2.4)

Gambar 2.4 Sampling dua tahap

(3)Stratified sampling

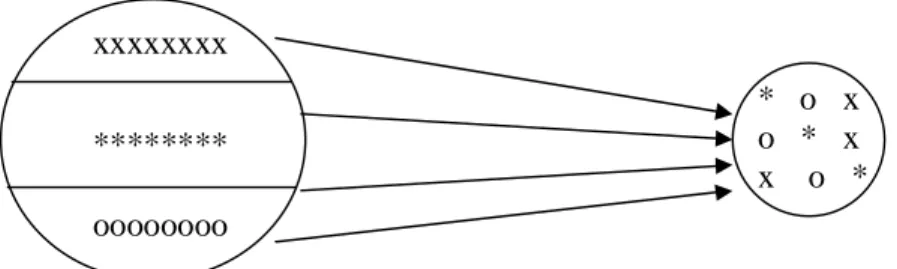
Lot dibagi dalam beberapa strata (lapisan) dan pada tiap-tiap strata diambil sampel. Setiap strata dianggap homogen (gambar 2.5)

x x x x x x x x x x x x x x x x x x x x xxx ooo *** x * o x x o * o * x o o x o * x o x * x o

Gambar 2.5 Stratified Sampling

(4)Cluster sampling

Pada suatu pabrik yang produknya dijadikan objek sampling, metode ini jarang digunakan. Jika metode ini tidak dilaksanakan dengan hati-hati dapat menurunkan ketelitian dan manimbulkan bias. Agar cara cluster ini berjalan dengan baiksemua bagian dari lot harus terwakili dalam proporsi yang sama. (gambar 2.6)

Gambar 2.6 Cluster Sampling (5)Selected sampling

Untuk mendapatkan nilai rata-rata dari suatu lot lebih baik melakukan sampling yang representatif dari seluruh lot. Suatu sampel dapat diambil dari suatu bagian khusus dan berdasarkan nilai dari sampel itu, nilai lot dapat diestimasi.

Misalnya selected sampel diambil pada waktu tertentu, pada sisi konveyor tertentu, dan sebagainya. Selected sampling relatif lebih tepat daripada sampel random sederhana dan metode ini adalah lebih mudah dan ekonomis meskipun tetap mengandung bias dari rata-rata populasi.

oooooooo ******** xxxxxxxx * o x o * x x o *

BAB III

DISTRIBUSI FREKUENSI

III.1. Pendahuluan

Data yang dikumpulkan biasanya tidak teratur. Salah satu cara untuk mengatur/menyusun/meringkaskan data ialah dengan membentuk distribusi frekuensi (frequency distribution). Distribusi frekuensi menurut jenis data dibagi dalam 2 golongan :

a) Distribusi frekuensi bilangan (numerical frequency distribution) Contoh Angka ujian 0.0 – 19.50 19.51 – 40.50 40.51 – 59.50 59.51 – 79.50 79.51 – 100.00 Jumlah Siswa 3 10 20 12 5 Jumlah 50

b) Distribusi frekuensi kategoris (categorical frequency distribution) Contoh : berdasarkan kemampuan produksi

Mesin gergaji Terzago tipe T-14 Terzago tipe F-30 Terzago tipe F-35 Frekuensi (buah) 30 35 25 Jumlah 90

III.2. Pembentukan Histogram

Data pada tabel 3.1 menunjukkan ketebalan (mm) dari 100 buah blok metal yang merupakan bagian-bagian dari suatu peralatan optik.

Tabel 3.1

Ketebalan blok metal (mm)

Data XL Xs 3.56° 3.46 3.48 3.50 3.42* 3.43 3.52 3.49 3.44 3.50 3.56 3.42 3.48 3.56° 3.50 3.52 3.47 3.48 3.46 3.50 3.56 3.38* 3.56 3.38 3.41 3.37* 3.47 3.49 3.45 3.44 3.50° 3.49 3.46 3.46 3.50 3.37 3.55° 3.52 3.44* 3.50 3.45 3.44 3.48 3.46 3.52 3.46 3.55 3.44 3.48 3.48 3.32 3.40 3.52° 3.34 3.46 3.43 3.30* 3.46 3.52 3.30 3.59 3.63° 3.59 3.47 3.38 3.52 3.45 3.48 3.31* 3.52 3.63 3.31 3.40* 3.54 3.46 3.51 3.48 3.50 3.68° 3.60 3.46 3.52 3.68 3.40 3.48 3.50 3.56° 3.50 3.52 3.46* 3.48 3.46 3.52 3.56 3.56 3.46 3.52 3.48 3.46 3.45 3.46 3.54° 3.54 3.48 3.49 3.41* 3.54 3.41 3.41 3.45 3.34* 3.44 3.47 3.47 3.41 3.48 3.54° 3.47 3.54 3.34

Keterangan : ° = nilai terbesar pada baris * = nilai terkecil pada baris

Pada tabel diatas dapat dilihat bahwa dengan N = 100 diperoleh nilai terbesar (XL) = 3,68 dan nilai terkecil (XS) = 3,30

Setelah data diatas digambarkan secara grafis akan tampak bentuk kecenderungannya. Dari sekian banyak macam grafik yang paling umum adalah histogram (gambar 3.1)

Cara membuat histogram (lihat tabel 3.1) (1)Hitung jumlah data

(2)Bagi data itu dalam 10 sub grup. Catat atau tandai nilai terbesar dan terkecil pada tiap sub grup. Kemuadian catat atau tandai nilai terkecil dan terbesar dari grup itu (dari keseluruhan).

Dalam hal ini nilai terbesar grup adalah XL = 3,66 dan terkecil XS = 3,30

(3)Range (R) dari seluruh data adalah R=x_L−x_S 3,68 – 3,30 = 0,38. Range dapat didistribusikan kedalam setiap kelas. Jumlah kelas ditentukan berdasarkan tabel 3.2

Tabel 3.2 Ketentuan jumlah kelas

Jumlah Data (N) Jumlah Kelas (K) 50 50 – 100 100 – 250 250 5 – 7 6 – 10 7 – 12 10 – 20

Untuk N = 100 dipilih K = 10 (atau 9) Interval Kelas : 0,038 10 38 , 0 = = − = K x x h L S

(4)Interval kelas (h) harus 2 angka dibelakang koma, atau unit pengukurannya adalah 0,01. Dengan demikian h dibulatkan menjadi 0,04 atau untuk mempermudah tentukan saja h = 0,05

(5)Batas kelas ditentukan untuk membuat histogram. Jika hasil pengukuran tepat dibatas kelas akan menyulitkan. Untuk menghindari itu unit batas diambil setengah dari unit pengukuran, jadi unit batas adalah 0,005. Lebar bar (batas kelas) menjadi 3,275 – 3,325 ; 3,325 – 3,375 dan selanjutnya lihat tabel 3.3

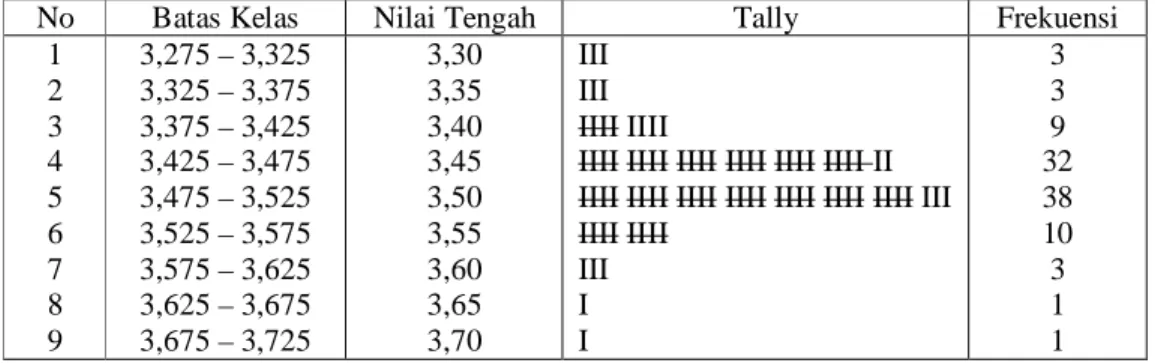
Tabel 3.3 Tabel Frekuensi

No Batas Kelas Nilai Tengah Tally Frekuensi 1 2 3 4 5 6 7 8 9 3,275 – 3,325 3,325 – 3,375 3,375 – 3,425 3,425 – 3,475 3,475 – 3,525 3,525 – 3,575 3,575 – 3,625 3,625 – 3,675 3,675 – 3,725 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 III III IIII IIII

IIII IIII IIII IIII IIII IIII II IIII IIII IIII IIII IIII IIII IIII III IIII IIII III I I 3 3 9 32 38 10 3 1 1

Berdasarkan tabel 3.3 histogram dapat dibuat seperti diperlihatkan pada gambar 3.1

Pada histogram harus dicantumkan tentang jumlah data (N), nomor mesin, nilai rata-rata (x), deviasi standar sampel (s), dan tarik pula garis limit spesifikasi bawah (lower specification limit, LSL) dan limit spesifikasi atas (upper specification limit, USL). Pada gambar 3.1 telah dicatat N = 100 ; x = 3,476 ; s = 0,065 ; LSL = 3,28 ; USL = 3,6 dan mesin no. 2

Gambar 3.1

Histogram ketebalan blok metal III.3. Nilai rata-rata

Yang dimaksud dengan nilai rata-rata disini adalah nilai rata-rata hitung. Nilai rata-rata inilah yang paling sering digunakan. Nilai rata-rata lain adalah nilai rata-rata ukur dan nilai rata-rata harmonis.

Nilai rata-rata adalah :

(1)Nilai disekitar sebaran data yang berupa angka-angka

(2)Suatu harga yang dapat dipakai untuk mewakili sekumpulan data (3)Ukuran tendensi pertengahan (measure of central tendency) Jenis nilai rata-rata hitung :

a) Rata-rata hitung data tak tersusun

Bila x1, x2, ..., xn terdiri dari n buah nilai dari variabel x, nilai

rata-ratanya : n x x x x x = 1+ 2 + 3 +...+ n Mesin no. 2 N = 100 x = 3,476 S = 0,065 mm 3,7 3,6 3,5 3,4 3,3 40 – 30 – 20 – 10 – LSL = 3,28 _{USL = 3,6}

atau :

∑

∑

= = = = n i i n i i _x n n x x 1 1 1

Cara lain yang lebih umum dengan menggunakan frekuensinya. Bila bilangan-bilangan x1, x2, ..., xn masing-masing terdapat sebanyak

f1, f2, ..., fn rata-rata hitungnya adalah :

n n n f f f x f x f x f x f x + + + + + + + = ... ... 2 1 3 3 2 2 1 1

b) Rata-rata hitung data tersusun

Dalam distribusi frekuensi nilai-nilai tidak diperhitungkan satu persatu melainkan dalam kelas-kelas. Pada umumnya nilai tengah kelas mewakili kelas itu (tabel 3.4)

Tabel 3.4 Nilai Tengah No Batas Kelas Nilai Tengah

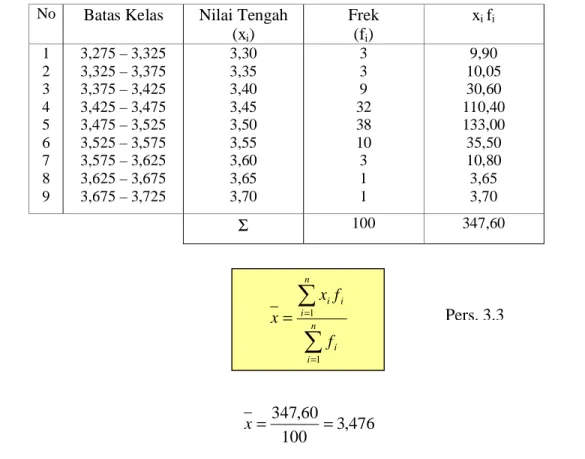
(xi) Frek (fi) xi fi 1 2 3 4 5 6 7 8 9 3,275 – 3,325 3,325 – 3,375 3,375 – 3,425 3,425 – 3,475 3,475 – 3,525 3,525 – 3,575 3,575 – 3,625 3,625 – 3,675 3,675 – 3,725 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3 3 9 32 38 10 3 1 1 9,90 10,05 30,60 110,40 133,00 35,50 10,80 3,65 3,70 Σ 100 347,60

∑

∑

= = = _n i i n i i i f f x x 1 1 476 , 3 100 60 , 347 = = x Pers. 3.1 Pers. 3.2 Pers. 3.3

Menghitung rata-rata hitung dengan cara duga Misalkan M = harga rata-rata duga

di = selisih antara nilai tengah kelas ke-i dengan M atau

di = xi – M ) (x M f d f_{i i} = _{i i} −

∑

f_id_i =

∑

(f_ix_i− f_iM)

∑

∑

fixi =M

∑

fi + fidi atau,

∑

fixi =nM +

∑

fidi sedangkan n x f x=

∑

i i atau nx=

∑

f_ix_i Jadi :

∑

+ =nM fidi x n atau

∑

+ = fidi n M x 1

Berdasarkan persamaan diatas dibuat tabel rata-rata duga (tabel 3.5) Tabel 3.5 Rata-rata duga No Nilai Tengah (xi) M di Frek (fi) fi di 1 2 3 4 5 6 7 8 9 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3,50 3,50 3,50 3,50 3,50 3,50 3,50 3,50 3,50 -0,20 -0,15 -0,10 -0,05 0,00 0,05 0,10 0,15 0,20 3 3 9 32 38 10 3 1 1 -0,60 -0,45 -0,90 -1,60 0,00 0,50 0,30 0,15 0,20 Σ 100 -2,40 476 , 3 024 , 0 50 , 3 ) 40 , 2 ( 100 1 50 , 3 + − = − = = x

Jenis nilai rata-rata lainnya adalah rata-rata ukur dan rata-rata harmonis Nilai rata-rata ukur :

∑

= = ∗ ∗ = n i i n x x x x U 1 2 1 ... atau ) log ... log (log 1 log x₁ x₂ x_n n U = + + +

∑

= = n i i x n U 1 log 1 log

Nilai rata-rata harmonis :

∑

= + + + = i n n x x x x n H 1 1 1 ) 1 ... ... 1 1 ( 1 1 2 1

∑

=      = n i xi n H 1 1

III.4. Ukuran Penyebaran

a) Range ; selisih antara nilai terkecil dan nilai terbesar dalam suatu deretan nilai

Contoh : 3,56 3,46 3,50 3,42 3,43 3,52 3,49 3,44 3,50 Range (R) = 3,56 – 3,42 = 0,14

b) Deviasi (simpangan) rata-rata

Diketahui sekumpulan data x1, x2, ..., xn mempunyai rata rata hitung 0,

jadi deviasi antara nilai-nilai itu dengan harga rata-ratanya adalah : (x1 - 0), (x2 - 0), ...,(xn - 0)

Harga mutlaknya adalah :

Pers. 3.6 Pers. 3.5

|x1 - 0|, |x2 - 0|, ...,|xn - 0| =

∑

= − n i i x x 1

Jadi deviasi (simpangan) rata-rata untuk : Data tidak tersusun

∑

− = x x n SR 1 _i Data tersusun

∑

− = f x x n SR 1 _{i i} Contoh Tabel 3.6

Simpangan rata-rata dengan harga mutlak No Kelas Nilai Tengah

(xi) Frek (fi) Nilai rata-rata (0) |xi - 0| fi |xi - 0| 1 2 3 4 5 6 7 8 9 10 3,275 – 3,325 3,325 – 3,375 3,375 – 3,425 3,425 – 3,475 3,475 – 3,525 3,525 – 3,575 3,575 – 3,625 3,625 – 3,675 3,675 – 3,725 3,725 – 3,775 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3,75 3 3 9 32 38 10 3 1 1 0 3,476 3,476 3,476 3,476 3,476 3,476 3,476 3,476 3,476 3,476 0,176 0,126 0,076 0,026 0,024 0,074 0,124 0,174 0,224 0,274 0,528 0,378 0,684 0,832 0,912 0,740 0,372 0,174 0,224 0,000 Σ 100 4,844

∑

− = f x x n SR 1 _{i i} 04844 , 0 100 844 , 4 = = SR

c) Deviasi Standar (standard deviation) 1. Data tak tersusun

Varians adalah pangkat 2 simpangan-simpangan anatara nilai-nilai pengamatan dengan rata-rata hitung dari kumpulan data itu.

Pers. 3.8.a

Varians :

∑

= − = n i i x x n s 1 2 2 ) ( 1

Untuk mengembalikan varians itu kepada ukuran simpangan, nilai varians itu harus diakar pangkat 2. nilai yang diperoleh disebut deviasi standar (s). Deviasi standar :

∑

= − = n i i n x x s 1 2 1 _{( )}

Cara khusus (short method) untuk memperoleh deviasi standar tanpa melalui perhitungan harga rata-rata lebih dahulu, sebagai berikut :

[

]

∑

= + − = n i i i x x x x n s 1 2 2 ) ( 2 1

∑

∑

= = + − = n i n i i i x x n x x n 1 2 1 2 ) ( 2 1 2 2 1 2 _{2( ) ( )} 1 x x x n n i i − + =

∑

= 2 1 2 _{( )} 1 x x n n i i − =

∑

= 2 1 1 2 1             − =

∑

∑

= = n x x n n i i n i i 2. Data tersusun Varians :

∑

= − = n i i i x x f n s 1 2 2 1 _{( )} Pers. 3.9 Pers. 3.10 Pers. 3.11 Pers. 3.12

Dengan :

n : jumlah pengamatan di dalam pecaran frekuensi k : jumlah kelas

xi : nilai tengah kelas ke-i

0 : harga rata-rata hitung fi : frekuensi kelas ke-i

Deviasi standar :

∑

= − = n i i i x x f n s 1 2 ) ( 1

Dengan cara yang sama dengan persamaan (3.10) dan (3.11), persamaan (3.13 dapat diubah menjadi :

2 1 1 2             − =

∑

=

∑

= n x f n x f s n i i i n i i i

Persamaan (3.14) ini dapat dipakai untuk menghitung nilai deviasi standar dengan tidak lebih dahulu menghitung nilai harga rata-rata hitung.

Disamping persamaan (3.10) dan (3.14) dapat digunakan persamaan (3.15) berikut : 2 1 1 2             − ∗ =

∑

=

∑

= n U f n U f i s n i i i n i i i Dengan :

i : selisih antara nilai tengah yang berdekatan

Ui : variabel dengan nilai -4, -3, -2, -1, 0, +1, +2, +3, +4 (letak 0

ditengah-tengah kelas)

Pers. 3.13

Pers. 3.14

Contoh :

Tabel 3.7

Nilai tengah dengan variabel U No. Nilai Tengah fi Ui Ui 2 fiUi fiUi2 1 2 3 4 5 6 7 8 9 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3 3 9 32 38 10 3 1 1 -4 -3 -2 -1 0 1 2 3 4 16 9 4 1 0 1 4 9 16 -12 -9 -18 -32 0 10 6 3 4 48 27 36 32 0 10 12 9 16 Σ 100 -48 190 2 100 48 100 190 05 , 0    − − = s 2304 , 0 9 , 1 05 , 0 − = s s = 0,0646

III.5. Median, Modus, Skewness Dan Kurtosis a) Median

Median adalah suatu nilai yang membagi dua suatu deretan nilai, sehingga banyak nilai dari bagian deretan itu sama. Dalam suatu deretan nilai 2, 6, 7, 9, 10, 13, 17 median deretan nilai itu adalah 9, jadi median itu merupakan rata-rata letak yaitu nilai yang terletak ditengah. Bagi deretan nilai yang genap misalnya 2, 6, 7, 9, 10, 13, 17, 18 mediannya adalah ½ (9 + 10) = 9,5

Sebelum menentukan median, deretan nilai harus disusun dahulu menurut urutan besar nilai-nilanya.

b) Median data tersusun

Bila n nilai dideretkan, median akan ditunjukkan oleh nilai yang ke-n/2. median dari distribusi frekuensi pada tabel 3.6 ditunjukkan oleh nilai yang ke 100/2 = 50. nilai yang ke-50 itu terdapat dikelas yang ke-5, karena di dalam kelas ke-1, ke-2, ke-3 dan ke-4 hanya terdapat 3 + 3 + 9 + 32 = 47 buah nilai saja. Didalam kelas ke-5 terdapat 38nilai. Dapat ditentukan

bahwa median itu ditunjukkan oleh nilai yang ke-3 dari nilai yang terdapat di dalam kelas ke-3 dari nilai yang terdapat di dalam kelas ke-5 itu jadi :

Median = 0,05 8 3 475 , 3 + ∗ = 3,475 + 0,004 = 3,479

Untuk hal yang umum :

i f s Bb Me M ∗ + = Dengan : Me : median

Bb : batas bawah median i : interval kelas

s : selisih antara nilai median dan frekuensi komulatif dari kelas-kelas dimuka (sebelum) kelas median

fM : frekuensi kelas median

c) Modus data tak tersusun

Merupakan bilangan terbanyak yang terdapat di dalam suatu kumpulan data

Contoh :

2, 2, 5, 6, 7, 7, 7, 9, 10, 11, 11 (modus = 7 uni modal) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 (modus = 0)

5, 6, 7, 8, 8, 8, 10, 11, 13, 13, 13, ,14 (modus = 8 dan 13 bi modal) d) Modus data tersusun

Ditentukan dalam persamaan :

i d d d B Mo ∗ + + = 2 1 1 1 Pers. 3.16 Pers. 3.17

Dengan : Mo : Modus

d1 : selisih antara frekuensi di dalam modus dan frekuensi di kelas yang

mendahuluinnya

d2 : selisih antara frekuensi di dalam kelas modus dan frejuensi di kelas

berikutnya i : interval modus

Pada Tabel 3.4 dapat dilihat bahwa : B1 : 3,475 d1 : 38 – 32 = 6 d2 : 38 – 10 = 28 i : 0,05 Jadi : Mo = 0,05 28 6 6 475 , 3       + + = 3,475 + 0,009 = 3,484

e) Kemiringan kurva (skewness)

Distribusi frekuensi berbentuk U terbalik atau lonceng dan simetris ditunjukkan pada gambar 3.1

Gambar 3.1 Distribusi normal pengukuran x fr ek u en si

x

Distribusi frekuensi yang lebih miring ke kanan dinamakan distribusi frekuensi dengan skewness negatif (gambar 3.2)

Gambar 3.2

Skewness negatif (0 < Mo)

Distribusi frekuensi dengan bentuk yang lebih miring ke kiri dinamakan distribusi frekuensi dengan skewness positif (gambar 3.3)

Gambar 3.3 Skewness positif (0 > Mo)

Makin tinggi derajat asimetri dari distribusi frekuensi makin besr pula penyimpangan antara tiga macam harga rata-rata (0, Me dan Mo), selisihnya dapat dijadikan ukuran bagi skewness. Ukuran kasar skewness adalah :

1. Skewness positif bila _{0 > Mo} 2. Skewness negatif bila 0 < Mo

Me Mo

x

Me Mo

Akan tetapi pemakaian selisih antara harga-harga rata-rata hitung dengan modus akan berubah dengan perubahan skala, sehingga ukuran kasar tersebut tidak berlaku.

Ukuran lain dengan mempergunakan persamaan koefisien skewness Pearson :

S Me x S_k = 3( − )

Jika Sk = 0 berarti kurva normal (simetris) Sk > 0 berarti skewness posistif Sk < 0 berarti skewness negatif

Skewness dapat pula diukur dengan ukuran momen :

3 3 1 ) ( S n x x f S_k =

∑

i− ×

Bentuk-bentuk skewness dapat dilihat pada gambar 3.4

Gambar 3.4

Bentuk-bentuk skewness untuk Sk > 0 ; Sk = 0 dan Sk < 0 f) Keruncingan kurva (kurtosis)

Kurtosis merupakan keruncingan distribusi frekuensi. Kurtosis terdiri dari 3 jenis, yaitu : leptokurtis (hampir runcing) ; platikurtis (hampir datar) dan mesokurtis (normal). Seperti ditunjukkan pada gambar 3.5

Sk = 0

Pers. 3.18

Sk < 0

Sk > 0

(a) (b) (c) Gambar 3.5

Distribusi (a) leptokurtis (b) platikurtis (c) mesokurtis Kurtosis dapat diukur dengan mempergunakan persamaan 3.19

3 1 ) ( 4 4 − × − =

∑

S n x x f K i i t

Bentuk-bentuk kurtosis dapat dilihat pada gambar 3.6

Gambar 3.6

Bentuk-bentuk kurtosis untuk Kt > 0 ; Kt = 0 dan Kt < 0

Jika Kt < 0 berarti kurva platikurtis (lebih tumpul daripada kurva normal) Jika Kt = 0 berarti kurva mesokurtis (normal)

Jika Kt > 0 berarti kurva leptokurtis (lebih runcing daripada kurva normal) Kt = 0

Kt < 0 Kt > 0

BAB IV

TEORI PROBABILITAS

IV.1.Pendahuluan

Hasil-hasil percobaan dapat dinyatakan dalam bentuk angka-angka atau golongan-golongan yang disebut outcome dari percobaan itu. Jika sebuah mata uang dilemparkan sebanyak 3 kali, outcome yang keluar mungkin berupa THT. H menunjukkan muka (head) dan T menunjukkan belakang (tail) dari mata uang itu. Untuk menganalisis suatu percobaan bukan outcome yang terjadi saja yang diperhatikan tetapi perlu diketahui pula hubungan antara semua outcome yang mungkin dihasilkan. Kumpulan semua outcome yang mungkin dihasilkan oleh suatu percobaan dinamakan sampel space dari percobaan tersebut. Setiap outcome yang menjadi anggota sari sampel space dinamakan titik sampel (sample point).

Definisi-definisi :

(1)Probabilitas (kemungkinan) adalah sesutau yang timbul apabila ada harapan akan terjadi atau akan tidak terjadi suatu peristiwa.

(2)Jika suatu peristiwa A mungkin terjadi di dalam m cara dari n kemungkinan, dan n kemungkinan itu mempunyai kesempatan yang sama untuk terjadi, sehingga probabilitas A sama dengan m/n atau :

n m A)= Pr(

(3)Jika dalam melakukan suatu deretan percobaan, perbandingan antara terjadi peristiwa A dengan jumlah kali percobaan itu dilakukan hampir sama dengan atau mendekati p dengan bertambah seringnya percobaan itu diulangi, probabilitas dari peristiwa sama dengan p, atau :

Pr(A) = p

Pers. 4.1

IV.2.Perhitungan Probabilitas

Jika dinyatakan suatu peristiwa dengan A dan titik-titik sampelnya a1, a2, ...,an

jadi :

∑

= = n i i a A 1 ) Pr( ) Pr(

Syarat-syarat perhitungan probabilitas :

(1)Jika A adalah peristiwa, dan bukan A atau Ac (komplemen A) adalah suatu peristiwa juga yang mempunyai probabilitas :

Pr(Ac) = 1 – Pr(A)

(2)Kalau A dan B merupakan dua buah peristiwa yang mutually exclusive

(dua peristiwa yang tidak mungkin terjadi serentak), diperoleh :

Pr(A atau B) = Pr(A∪B) = Pr(A) + Pr(B)

(3)Jika A dan B merupakan dua buah peristiwa yang bukan mutually exclusive, probabilitas terjadi peristiwa A atau B adalah sama dengan jumlah probabilitas-probabilitas dari peristiwa A dan peristiwa B dikurangi dengan probabilitas dari peristiwa A•B, atau :

Pr(A atau B) = Pr(A∪B) = Pr(A) + Pr(B) – Pr(A•B)

(4)Jika A dan B merupakan dua buah peristiwa yang bebas, maka :

Pr(A•B) = Pr(A∩B) = Pr(A) • Pr(B)

(5)Jika peristiwa A dan peristiwa B merupakan dua buah peristiwa yang tidak bebas, terjadinya kedua peristiwa itu secara serentak mempunyai probabilitas :

Pr(A dan B) = Pr(A∩B) = Pr(A) • Pr(B/A)

Pers. 4.3 Pers. 4.4 Pers. 4.5 Pers. 4.6 Pers. 4.7 Pers. 4.8

dengan :

Pr(B/A) = probabilitas B sesudah A terjadi atau probabilitas kondisional dari B

IV.3.Permutasi

Definisi : permutasi dari sejumlah obyek adalah penyusunan dari obyek-obyek tersebut dalam suatu urutan tertentu.

a) Permutasi dari n objek seluruhnya

Jumlah permutasi yang dapat dibuat dari n objek seluruhnya yang berbeda satu sama lain adalah n !, atau :

! n P_rn =

Contoh :

Dalam beberapa carakah 4 buah buku A, B, C dan D dapat disusun ? Jawab : n = 4

Permutasinya : P_rn =n! = 4 x 3 x 2 x 1 = 24 Jadi buku-buku itu disusun dalam 24 cara

b) Permutasi dari n objek yang tersedia dan diambil sebanyak r :

)! ( ! r n n P_rn − = dengan :

n = jumlah objek yang tersedia r = jumlah objek yang disusun contoh :

ada 4 buah buku A, B, C, dan D. Dalam berpa carakah buku-buku tersebut dapat disusun, jika setiap susunan berisi 2 buah buku ?

Jawab : n = 4 ; r = 2

Pers. 4.9.a

)! 2 4 ( ! 4 )! ( ! − = − = r n n P_rn 12 1 2 1 2 3 4 = × × × × =

Jadi buku itu dapat disusun dalam 12 cara

IV.4.Kombinasi

Definisi : Kombinasi dari sejumlah objek merupakan cara pemilihan objek-objek tersebut tanpa menghiraukan urutan (susunan) dari objek-objek-objek-objek yang bersangkutan. Jadi dalam hal objek A, B dan C. Susunan ABC BCA dan BAC merupakan kombinasi tetapi menurut permutasi susunan itu terdiri dari 3 permutasi.

a) Kombinasi dari n objek keseluruhan.

Banyaknya kombinasi dari suatu set yang terdiri dari n objek = 1 atau :

1 = n n C Contoh :

Suatu panitia harus terdiri dari 4 orang anggota. Calon anggota untuk panitia tersebut hanya 4 orang. Berpa carakah panitia tersebut dapat dibentuk, jika kedudukan anggota dalam panitia diabaikan perbedannya Jawab : panitia yang dapat dibentuk

1 =

n n

C cara

b) Kombinasi dari n objek tetapi tidak semua objek terpakai.

Jika jumlah objek yang satu sama lainnya berbeda, berjumlah n buah, dan yang diambil sebagai suatu kombinasi berisikan r buah diantaranya, jumlah kombinasi yang dapat dibuat adalah :

)! ( ! ! r n r n C_rn − = Pers. 4.10.a Pers. 4.10.b

Contoh – 1 ;

Berpakah kombinasi 3 buah buku dari 5 buah buku A, B, C, D dan E yang tersedia : Jawab : n = 5 ; r = 3 Kombinasinya = 10 )! 3 5 ( ! 3 ! 5 5 3 = − = C Contoh – 2 ;

Calon-calon untuk duduk dalam sebuah panitia berjumlah 8 orang, terdiri dari 5 pria dan 3 wanita. Berapa cara panitia dapat dibentuk ? Jawab : Pemilihan 3 pria dari 5 pria dapat dibentuk dalam

10 )! 3 5 ( ! 3 ! 5 5 3 = ₋ = C cara (n1)

Pemilihan 2 wanita dari 3 wanita dapat dibentuk dalam 3 )! 2 3 ( ! 2 ! 3 3 2 = − = C cara (n2)

Untuk menghitung keseluruhan cara yang dapat dibuat dalam pembentukan panitia tersebut yang terdiri dari pria dan wanita digunakan asaz perkalian permutasi. Dalam hal ini dengan n1 = 10 dan n2 = 3 ; P = n1 x n2 , jadi pembentukan panitia itu ada 10 x 3 cara = 30 cara.

Contoh – 3 ;

Calon-calon untuk duduk dalam sebuah panitia terdiri dari 5 pria dan 3 wanita. Persyaratannya pembentukan panitia tersebut harus terdiri dari paling sedikit 3 orang pria dan jumlah anggotanya 5 orang. Dengan berpa carakah panitia tersebut dapat dibentuk ?

Jawab :

Paling sedikit 3 pria merupakan syarat, jadi panitia dapat dibentuk dengan salah satu cara :

Jumlah cara yang dapat dibentuk = 30 cara (ditunjukkan dalam contoh 2) 2. Terdiri dari 4 pria dan 1 wanita

Jumlah cara yang dapat dibentuk = C₄5×C₁3

= )! 1 3 ( ! 1 ! 3 )! 4 5 ( ! 4 ! 5 − × − = 5 x 3 = 15 cara

3. Hanya terdiri dari 5 pria

Jumlah cara yang dapat dibentuk = 5 5 C = 1

Jadi jumlah cara yang dapat dibentuk yang terjadi dari paling sedikit 3 pria adalah :

BAB V

DISTRIBUSI PROBABILITAS, BINOMIAL, POISSON dan NORMAL

IV.5.Pendahuluan

Distribusi probabilitas bersamaan sekali dengan persamaan frekuensi relatif jika probailitasnya diulang sebanyak tidak berhingga, atau dapat dinyatakan dengan rumus :

Probabilitas =

_lim

(f /n)

n→∞

Dengan f/n sebagai frekuensi relatif.

Distribusi probabilitas mungkin berbentuk diskret atau kontinu. Distribusi probabilitas diskret ialah probabilitas yang variabel randomnya hanya mengambil nilai-nilai yang terisolasi satu dari yang lainnya. Distribusi probabilitas kontinu ialah distribusi yang variabel randomnya mengambil nilai-nilai yang kontinu. Distribusi Binomial merupakan distribusi diskret, dikembangkan dari percobaan Bernoulli. Distribusi Poisson juga merupakan distribusi diskret, digunakan untuk jumlah sampel yang lebih besar. Distribusi Normal merupakan distribusi yang kontinu. Pengalaman telah membuktikan bahwa sebagian besar dari variabel random yang kontinu di berbagai bidang aplikasi yang berbeda dan beraneka ragam, umumnya memiliki distribusi yang dapat didekati dengan distribusi normal atau dapat menggunakannya sebagai model teoritis.

IV.6.Distribusi Probabilitas

Suatu distribusi probabilitas dapat disusun berdasarkan pengalaman-pengalaman diwaktu yang lampauatau berdasarkan pertimbangan-pertimbangan teoritis.untuk memperjelas pengertian tentang distribusi probabilitas diskret diambil satu contoh, misalnya diamati banayaknya gambar (dinyatakan dengan H berarti head) yang keluar dari pelemparan 3 mata uang logam. Kemungkinan terjadinya gambar (H) dan tulisan (dinyatakan dengan T yang berarti tail) yaitu probabilitas munculnya H atau munculnya T adalah ½.

Tabel 5.1 Probabilitas munculnya H Titik Sampel ke No 1 2 3 Jumlah H Probabilitas titik sampel 1 T T T 0 1/8 2 3 4 T T H T H T H T T 1 1 1 1/8 1/8 1/8 5 6 7 H T H H H T T H H 2 2 2 1/8 1/8 1/8 8 H H H 3 1/8

Tabel 5.1 diatas dapat disederhanakan menjadi Tabel 5.2

Dengan memakai Tabel 5.2 ini dapat dilukiskan grafik distribusi probabilitas itu dalam bentuk histogram probabilitas (gambar 5.1) atau bentuk grafik lain

Tabel 5.2

Probabilitas f(x) dan probabilitas komulatif F(x) Banyaknya H x Frekuensi f Probabilitas f(x) Probabilitas Komulatif F(x) 0 1 2 3 1 3 3 1 1/8 3/8 3/8 1/8 1/8 4/8 7/8 8/8 Gambar 5.1 Histogram Probabilitas

Pada tabel 5.2 dapat dilihat pula hubungan antara f(x) dan fungsi distribusi probabilitas komulatif F(x), yaitu bahwa nilai F(x) sama dengan jumlah dari nilai-nilai f(x). Misalkan bahwa a adalah sebuah nilai yang dapat diambil oleh x maka dapat dinyatakan :

∑

= ( ) ) (a f x F 3/8 – 2/8 – 1/8 – f(x) Pers. 5.1

Dengan x ≤ a

Gambar 5.2 menunjukkan grafik distribusi probabilitas komulatif berdasarkan Tabel 5.2

Gambar 5.2 Grafik distribusi komulatif

Definisi : Suatu fungsi f(x) dapat disebut fungsi probabilitas yang diskret jika syarat-syarat berikut dipenuhi :

f(x) ≥ 0 dan,

∑

∞ = = 1 1 ) ( i i x f

Harga rata-rata hitung suatu variabel random dan diskret x yang fungsi probabilitasnya f(x) adalah :

∑

= = n i i if x x 1 ) ( µ dengan :

µ = harga rata-rata hitung

n = banyaknya nilai x yang mungkin

Varians (σ2_{) dari suatu variabel random x, yang fungsi probabilitasnya f(x)}

adalah : 8/8 – 7/8 – 4/8 – 1/8 – Pers. 5.2 Pers. 5.3

σ2 ₌

∑

= − n i i i f x x 1 2 ) ( ) ( µ atau σ2 ₌

∑

= − n i i i f x x 1 2 2 _{( )} µ

jadi deviasi standarnya adalah : σ ₌

∑

= − n i i i f x x 1 2 2 ) ( µ contoh :

Jika 2 buah dadu dilemparkan pada saat yang bersamaan, dan pelemparan dilakukan berulang kali dengan jumlah yang sangat banyak, ditanyakan jumlah mata dadu rata-rata setiap pelemparan (µ) dan deviasi standarnya (σ)

Penyelesaian :

Jika dilemparkan 2 buah dadu, kemungkinan jumlah mata dadu yang diperoleh adalah x dengan niali-nilai seperti di bawah ini :

x f(x) 1 0 = 0 2 (1, 1) = 1/36 3 (1, 2) ; (2, 1) = 2/36 4 (1, 3) ; (2, 2) ; (3, 1) = 3/36 5 (1, 4) ; (2, 3) ; (3, 2) ; (4, 1) = 4/36 6 (1, 5) ; (2, 4) ; (3, 3) ; (4, 2) ; (5, 1) = 5/36 7 (1, 6) ; (2, 5) ; (3, 4) ; (4, 3) ; (5, 2) ; (6, 1) = 6/36 8 (2, 6) ; (3, 5) ; (4, 4) ; (5, 3) ; (6, 2) = 5/36 9 (3, 6) ; (4, 5) ; (5, 4) ; (6, 3) = 4/36 10 (4, 6) ; (5, 5) ; (6, 4) = 3/36 11 (5, 6) ; (6, 5) = 2/36 12 (6, 6) = 1/36

Fungsi frekuensi jumlah mata dadu dari hasilpelemparan 2 buah dadu itu dikembangkan pada tabel 5.3 untuk mendapatkan nilai µ dan σ.

Pers. 5.4

Pers. 5.5

Tabel 5.3

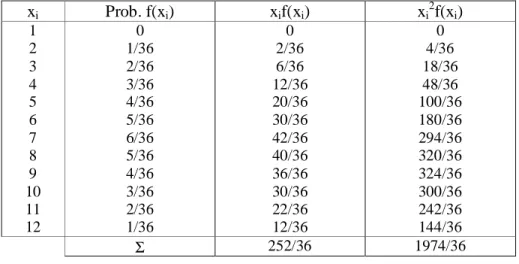
Nilai-nilai xif(xi) dan xi2f(xi)

dari hasil pelemparan 2 buah dadu

xi Prob. f(xi) xif(xi) xi2f(xi) 1 2 3 4 5 6 7 8 9 10 11 12 0 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36 0 2/36 6/36 12/36 20/36 30/36 42/36 40/36 36/36 30/36 22/36 12/36 0 4/36 18/36 48/36 100/36 180/36 294/36 320/36 324/36 300/36 242/36 144/36 Σ 252/36 1974/36 µ = 7 36 252 = σ2 ₌ 36 210 7 36 1974− 2 = σ _{= 2,415} 36 210 ₌

IV.7.Distribusi Binomial

Keistimewaan dari distribusi binomial adalah distribusi ini dapat dipakai untuk sangat banyak peristiwa. Distribusi binomial berdasarkan percobaan Bernoulli dengan ciri-ciri sebagai berikut :

(1)Setiap percobaan dirumuskan dengan sampel (S, G), yaitu setiap percobaan hanya memiliki 2 hasil, yaitu sukses (S) dan gagal (G).

(2)Pada setiap percobaan, probabilitas untuk sukses harus sama besar, biasanya dinyatakan dengan “p”.

(3)Setiap percobaan harus berdiri sendiri (independen event), yaitu terjadi atau tidak terjadinya peristiwa pertama tidak memberi akibat terhadap terjadi atau tidak terjadinya peristiwa berikutnya.

Misalnya pada pelemparan sebuah uang logam. Setiap pelemparan akan menghasilkan 1 diantara 2 kemungkinan, yaitu gambar dapat diumpamakan sukses dan diberi tanda H ; tulisan, dapat diumpamakan gagal dan diberi tanda T. Hasil seluruhnya dari pelemparan-pelemparan sebuah mata uang logam itu ditunjukkan tabel 5.4

Tabel 5.4

Probabilitas peristiwa dari pelemparan sebuah mata uang logam Mata Uang ke Jumlah Probabilitas Peristiwa

1 2 3 T H T T T H H T H H T T H T H H T H T H T T T H H H 3 2 2 2 1 1 1 0 0 1 1 1 2 2 2 3 (½)3 (½)0 1*(½)3 = 1/8 (½)2 (½)1 (½)2 (½)1 3*(½)2 (½)1 = 3/8 (½)2 (½)1 (½)1 (½)2 (½)1 (½)2 3*(½)1 (½)2 = 3/8 (½)1 (½)2 (½)0 (½)3 1*(½)3 = 1/8

Bila suatu percobaan Bernoulli terdiri dari n dengan probabilitas untuk sukses dan untuk gagal bagi setiap percobaan adalah masing-masing berturut-turut sebesar p dan q, fungsi probabilitasnya dinyatakan dengan notasi :

B(x | n,p) = Cn_xpxq(n−x) dengan : n x C = kombinasi x dari )! ( ! ! x n x n − q = 1 – p

Pada Tabel 5.4 dapat dilihat bahwa p = ½ dan n = 3. Dengan mempergunakan notasi persamaan 5.8 diperoleh Tabel 5.5

Tabel 5.5

Nilai-nilai B(x | n,p) dari pelemparan Sebuah mata uang logam x )! ( ! ! x n x n x n C_xn − =       = x (n x) q p − B(x | n,p) 1 2 3 4 = 2 x 3 0 1 )! 0 3 ( ! 0 ! 3 ₌ − (½)0 (½)3 1 8 1 3 )! 1 3 ( ! 1 ! 3 = − (½)1 (½)2 3 8 2 3 )! 2 3 ( ! 2 ! 3 = − (½)2 (½)1 3 8 3 1 )! 3 3 ( ! 3 ! 3 = − (½)3 (½)0 1 8 Σ 1

Angka-angka pada kolom 4 tabel 5.5 dapat dibaca langsung pada tabel Binomial untuk n = 3 dan p = 0,5. Rata-rata hitung : ( ) 0 x n x n x q p x n x − =

∑

      = µ

Kalau persamaan 5.9 diuraikan terus akan diperoleh :

µ = n.p Varians :

∑

_ −      − = 2 ( ) 2 ) ( pxq n x x n x µ σ

Kalau persamaan 5.11 diurakan terus akan diperoelh : σ2 _{= n.p.q}

Jadi deviasi standar :

σ _{= n ..pq}

Dari contoh diatas dapat dihitung : Rata-rata hitung : µ = n.p = 3 x 0,5 = 1,5 Varians : σ2 = n.p.q = 3 x 0,5 x 0,5 = 0,75 Pers. 5.9 Pers. 5.10 Pers. 5.11 Pers. 5.12 Pers. 5.13

Deviasi standar : σ = n ..pq = 0,75 = 0,866

IV.8.Distribusi Poisson

Menurut distribusi Binomial suatu sampel dengan ukuran (size) n mengandung cacat (defective) sejumlah x, probabilitas dari jumlah defective tersebut adalah :

B(x | n,p) = n x (n x)

xp q

C −

dengan :

p = fraksi cacat (defective fraction) q = (1 – p)

Dengan menghitung langsung atau mempergunakan tabel Binomial, nilai B(x) dengan segera dapat diketahui. Akan tetapi persamaan di atas akan menjadi sukar dalam penggunaannya nila n besar dan p kecil (p ≤ 0,1). Biasanya tabel Binomial hanya dibuat sampai dengan n = 100.

Untuk menghitung probabilitas jumlah defectives dari ukuran sampel n yang lebih besar dari 100 digunakan persamaan fungsi probabilitas Poisson :

P(x) = _{( )} ! ) ( np x e x np Dengan : e = exponential (e = 2,718) rata-rata hitung : µ = m = n.p varians : σ2 _{= m = n.p} deviasi standar : σ _{= m} = _np Contoh :

Dari suatu lot ditarik sampel dengan n = 200 yang ternyata mengandung defective 5%. Ini berarti P = 5 atau p = 0,05 • np = 200 x 0,05 = 10

Rata-rata hitung Varians Deviasi standar Pers. 5.14 Pers. 5.15 Pers. 5.16 Pers. 5.17

Bila sampel dari lot itu mengandung defectives x = 8, probabilitas adalah : P ( x=8 ) = ₁₀ 8 ) 718 , 2 ( ! 8 10 = 0,1126

Atau dapat digunakan tabel distribusi Poisson untuk np = x = 10 sebagai berikut

P (x=0) = 0,0000 P (x=5) = 0,0378 P (x=10) = 0,1251 P (x=1) = 0,0005 P (x=6) = 0,0631 P (x=11) = 0,1137 P (x=2) = 0,0023 P (x=7) = 0,0901 P (x=12) = 0,0948 P (x=3) = 0,0076 P (x=8) = 0,1126 P (x=13) = 0,0729 P (x=4) = 0,0189 P (x=9) = 0,1251 dan seterusnya

IV.9.Distribusi Normal

Distribusi Normal adalah salah satu jenis distribusi yang sering dipakai dalam statistik. Fungsi dari distribusi normal dinyatakan dalam persamaan :

2 2 2 ) (

2

1

)

(

σ µ

π

σ

− −

=

x

e

x

f

untuk -∞≤ x ≤∞ dengan :

e : bilangan tetap Euler = 2,718 π : 3,1415

µ : nilai rata-rata hitung σ _{: deviasi standar}

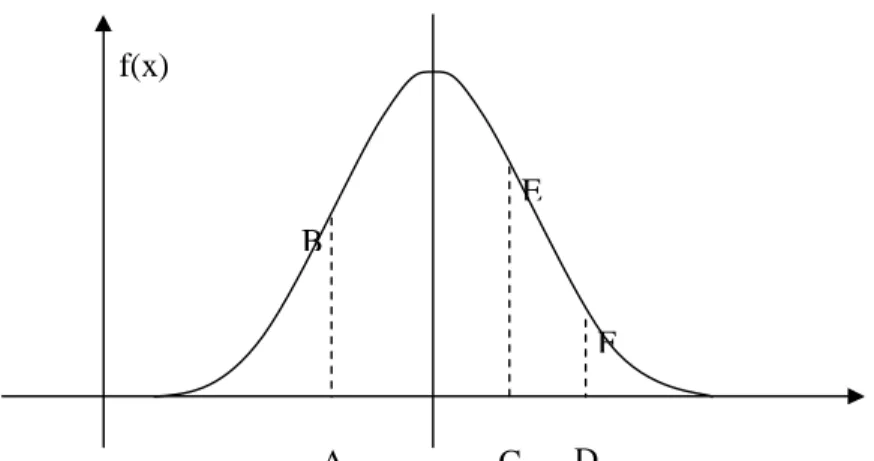
Grafik dari fungsi ini berbentuk lonceng (bell shape curve), merupakan kurva yang simetris terhadap garis vertikal melalui x = µ. Oleh karena x adalah suatu variabel random yang kontinu, setiap garis vertikal yang menghubungkan titik dari kurva normal itu dengan sumbu mendatar, demikian juga luas daerah dibawah kurva normal dan diatas sumbu mendatar dapat diasosiasikan dengan nilai probabilitas.

Pada gambar 5.3 dapat dilihat bahwa garis AB merupakan probabilitas dari x = A atau f(A).

Gambar 5.3 Kurva Normal

Luas daerah CEFD adalah probabilitas dari x antara C dan D. Luas daerah dibawah kurva normal adalah jumlah dari probabilitas untuk semua nilai x yang tentu saja sama dengan 1. Secara matematis dapat ditulis :

∫

∞ ∞ −

=

1

)

(

x

dx

f

Kalau integral ditarik sampai x = a, hasil integral itu sama dengan luas daerah di bawah kurva normal di sebelah kiri garis vertikal x = a yang sama dengan nilai dari fungsi distribusi komulatif f(x) untuk x = a atau f(a), jadi :

F(a) =

∫

∞ − a

dx

x

f

(

)

yang sama juga dengan P(x ≤ a) = F(a)

Jika a dan b merupakan 2 buah nilai x yang berbeda, dapat dituliskan : A B C E D F µµµµ f(x) Pers. 5.19 Pers. 5.20

P (a ≤ x ≤ b) =

∫

a b dx x f( ) = F(b) – F(a)

Dengan digunakannya persamaan 5.18 untuk membentuk kurva normal terlalu memerlukan banyak waktu. Cara itu dapat dihindari dengan digunakannya distribusi Normal Standar. Distribusi Normal Standar mempunyai µ = 0 dan σ _{= 1. Variabel random yang terdistribusi secara normal dinyatakan dengan z,} jadi : f (x) = 2 2 1

2

1

_z

e

−

π

untuk -∞≤ x ≤∞

Artinya setiap bagian dari luas daerah di bawah kurva normal yang lain dapat dinyatakan di dalam luas daerah di bawah kurva normal standar. Jadi luas daerah di bawah kurva normal standar telah dibuat daftarnya untuk nilai-nilai z, luas daerah di bawah kurva normal biasa di sebelah kiri nilai-nilai tertentu dapat dicari berdasarkan persamaan :

z = σ µ − x atau x = µ + z σ

Misalnya untuk z = +2 diperoleh x = µ + 2 σ. Dapat dilihat pada tabel distribusi normal, bahwa : F (z = +2) = F (x = µ + 2σ) = 0,9772

F (z = -2) = F (x = µ - 2σ) = 1 – F (z = +2z) = 1 - 0,9772 = 0,0228

Bila ingin diketahui luas daerah di bawah kurva normal untuk -2 ≤ z ≤ +2 yaitu untuk z diantara z = -2 dan z = +2 dapat dipergunakan persamaan 5.21

Pers. 5.21

Pers. 5.22

Pers. 5.23

P (-2 ≤ z ≤ +2) = F (z = +2) – F (z = -2) = 0,9772 – 0,0228 = 0,9544

Contoh soal

Spesifikasi diameter luar dari shaft seal suatu motor pompa adalah 1,515 inch s/d 1,525 inch. Rata-rata hitung populasi (µ) 1,5202 inch, dan deviasi standar (σ) 0,0020 inch. Berapa persen seal yang sesuai dengan spesifikasi ?

Penyelesaian : µ = 1,5202 σ = 0,0020 z = σ−µ x

limit atas untuk x = 1,525 : z = 0020 , 0 5202 , 1 525 , 1 − = +2,4 P (x ≥ 1,525) = P (z ≥ 2,4) = 0,0082

Gambar 5.4. Kurva Normal Standar dari shaft seal motor pompa limit bawah untuk x = 1,515 :

z = 0020 , 0 5202 , 1 515 , 1 − = -2,6

Oleh karena tabel distribusi normal hanya mempunyai nilai-nilai z yang posistif, jadi -2,6 harus dianggap posistif. Pada tabel diperoleh nilai 0,00466. nilai itu merupakan probabilitas untuk ukuran shaft seal kurang dari 1,5515 inch atau :

1,5202 in x Area equals 0,0082 1,525 in 1,515 in Area equals 0,00466 | -3 | -2 | -1 | 0 | +1 | +2 | +3 z

P (x ≤ 1,515) = P (z ≤ -2,6) = 0,00466

Jadi probabilitas diameter shaft seal yang sesuai dengan spesifikasi adalah : 1 – (0,0046 + 0,0082) = 0,98714

atau 98,714 %

BAB VI

DISTRIBUSI SAMPLING

IV.10. Pendahuluan

Pengambilan sampel bertujuan memperoleh keterangann mengenai populasi dengan mengamati hanya sebagian saja dari populasi itu. Pengambilan sampel dilaksanakan karena sering tidak mungkin dilakukan pengamatan terhadap seluruh anggota populasi atau sekalipun memungkinkan, tetap tidak praktis dan tidak efisien. Ada 3 tujuan utama dari pengambilan sampel. Ketiga tujuan itu menunjukkan juga jenis keterangan yang bagaimana yang dikehendaki dari penarikan sampel itu, yaitu penaksiran (estimation), pengujian hipotesis (testing of hypotheses) dan peramalan (prediction). Disamping ketiga tujuan itu tentu ada lagi beberapa tujuan lain, diantaranya penyelidikan apakah dua variabel itu mempunyai hubungan atau tidak.

VI.2.Distribusi Sampel Eksperimental

Enam buah bola dinomori dari 0 s/d 5 ditempatkan di dalam sebuah kotak. Dari dalam kotak itu secara random ditarik sampel-sampel yang terdiri dari 3 buah bola. Bilangan-bilangan yang menunjukkan nomor-nomor bola tersebut dianggap merupakan anggota-anggota sampel. Sesudah ditarik sebuah sampel dan dihitung harga rata-rata hitungnya, ketiga bola itu dikembalikan ke dalam kotak. Penarikan sampel dilakukan sebanyak 1.000 kali.

Hasil penarikan itu ditunjukkan oleh distribusi frekuensi pada tabel 6.1 distribusi frekuensi seperti ini dinamakan distribusi eksperimental

Tabel 6.1

Distribusi Sampel Eksperimental

x f f/n (f/n) x (f/n)( x)2 1,00 1,33 1,67 2,00 2,33 2,67 3,00 3,33 3,67 4,00 20 40 75 150 205 225 150 65 50 30 0,020 0,040 0,075 0,150 0,205 0,225 0,150 0,065 0,050 0,030 0,020 0,053 0,125 0,300 0,475 0,600 0,450 0,217 0,183 0,120 0,020 0,071 0,209 0,600 1,007 1,602 1,350 0,723 0,672 0,480 Σ 1.000 1 2,543 6,734 Rata-rata hitung : x = Σx (f/n) = 2,543 Deviasi standar : s = (x)2(f /n)−(x)2 = 0,53

Deviasi standar dari sebuah statistik seperti ini dinamakan standar error eksperimental dari statistik itu. Distribusi probabilitasnya dapat dilihat pada tabel 6.2

Tabel 6.2

Distribusi probabilitas dari populasi 6 buah bola x f(x) xf(x) (x - µ) (x - µ)2 f(x) 0 1 2 3 4 5 1/6 1/6 1/6 1/6 1/6 1/6 1/6 2/6 3/6 4/6 5/6 6/6 -2,5 -1,5 -0,5 +0,5 +1,5 +2,5 (6,25) 1/6 (2,25) 1/6 (0,25) 1/6 (0,25) 1/6 (2,25) 1/6 (6,25) 1/6 Σ 1 2,5 (17,50) 1/6

Dari tabel 6.2 diperoleh : Rata-rata hitung : µ = 2,5 Deviasi standar : σ = 6 5 , 17 _{= 1,7}

VI.3.Distribusi Sampel Teoritis

Distribusi sampel teoristis dari populasi yang terdiri dari 6 buah bola dapat dilihat pada tabel 6.3 yang hampir sama dengan tabel 6.1, hanya kolom frekuensi relatif diganti dengan kolom probabilitas. Pembentukan kolom probabilitas itu berdasarkan pertimbangan teoritis, bukan pertimbangan ekperimental. Banyaknya kombinasi yang beranggotakan n yang dapat dibentuk dari populasi yang terdiri dari N menurut persamaan 4.10 adalah :

)! ( ! ! n N n N n N C_nN − =       =

Jadi banyaknya kombinasi yang beranggotakan n = 3 buah bola yang dapat dibentuk dari sebuah populasi yang terdiri dari N = 6 buah bola adalah :

! 3 ! 3 ! 6 3 6 6 3 =      =

C = 20 sampel, terdiri dari :

Tabel 6.3

Kombinasi 3 dari 6 buah bola

Kombinasi x Kombinasi x Kombinasi x (0, 1, 2) (0, 1, 3) (0, 1, 4) (0, 1, 5) (0, 2, 3) (0, 2, 4) (0, 2, 5) 1,00 1,33 1,67 2,00 1,67 2,00 2,33 (0, 3, 4) (0, 3, 5) (0, 4, 5) (1, 2, 3) (1, 2, 4) (1, 2, 5) (1, 3, 4) 2,33 2,67 3,00 2,00 2,33 2,67 2,67 (1, 3, 5) (1, 4, 5) (2, 3, 4) (2, 3, 5) (2, 4, 5) (3, 4, 5) 3,00 3,33 3,00 3,33 3,67 4,00

Berdasarkan tabel 6.3 disusun tabel 6.4 seperti dibawah ini : Tabel 6.4

Probabilitas 3 dari 6 buah bola

x f Probabilitas x f Probabilitas 1,00 1,33 1,67 2,00 2,33 1 1 2 3 3 0,05 0,05 0,10 0,15 0,15 2,67 3,00 3,33 3,67 4,00 3 3 2 1 1 0,15 0,15 0,10 0,05 0,05 Σ 20 1,00

Setiap sampel mempunyai probabilitas yang sama (0,05). Untuk menghitung harga rata-rata hitung dan deviasi standar (standar error) dari distribusi sampel teoritis ini, dibuat dahulu tabel 6.5

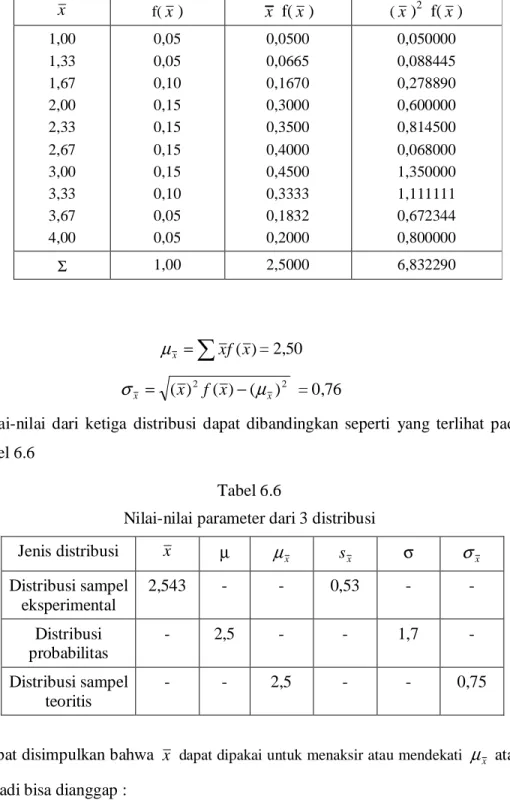
Tabel 6.5 Distribusi x f(x ) x f( x ) (x )2 f( x ) 1,00 1,33 1,67 2,00 2,33 2,67 3,00 3,33 3,67 4,00 0,05 0,05 0,10 0,15 0,15 0,15 0,15 0,10 0,05 0,05 0,0500 0,0665 0,1670 0,3000 0,3500 0,4000 0,4500 0,3333 0,1832 0,2000 0,050000 0,088445 0,278890 0,600000 0,814500 0,068000 1,350000 1,111111 0,672344 0,800000 Σ 1,00 2,5000 6,832290

∑

= xf(x) x µ = 2,50 2 2 ) ( ) ( ) ( _x x x f x

µ

σ

= − = 0,76

Nilai-nilai dari ketiga distribusi dapat dibandingkan seperti yang terlihat pada tabel 6.6

Tabel 6.6

Nilai-nilai parameter dari 3 distribusi

Jenis distribusi x µ

µ

_x s_x σ

σ

_x Distribusi sampel eksperimental 2,543 - - 0,53 - - Distribusi probabilitas - 2,5 - - 1,7 - Distribusi sampel teoritis - - 2,5 - - 0,75

Dapat disimpulkan bahwa x dapat dipakai untuk menaksir atau mendekati

µ

_x atau

x = µ_x= µ

Hubungan antara deviasi standar populasi (dari distribusi probabilitas) σ dan standard error

σ

_x adalah :

x σ = 1 − − N n N n σ

(sampel dari populasi yang kecil) atau :

x

σ

=

n

σ

(sampel dari populasi yang besar) dengan :

N = banyak anggota dari populasi n = banyak sampel yang ditarik

x

σ = standard error dari harga rata-rata hitung sampel teoritis σ = deviasi standar dari populasi

Pers. 6.1

Pers. 6.2

BAB VII

PENAKSIRAN & PENGUJIAN HIPOTESIS

IV.11. Pendahuluan

Ada 2 cara penaksiran yaitu : penaksiaran titik (point estimation) dan penaksiaran interval (interval estimation). Pada penaksiran titik dicoba langsung menaksir sebuah nilai; jadi bukan memakai sebuah interval sepotong garis maupun beberapa titik. Pada penaksiran interval, dalam teori pengambilan sampel, dimisalkan bahwa distribusi dari populasi yang diamati itu telah diketahui dan berdasarkan hal itu perhitungan probabilitas-probabilitas mengenai sampelnya dipersoalkan. Didalam praktek sebaliknya, yang diketahui ialah mengenai sampel yang ditarik dari suatu populasi dan berdasarkan sampel itu dicoba menarik kesimpulan-kesimpulan mengenai populasinya (parameter-parameternya). Penaksiran memakai teori pengambilan sampel ini adalah pencarian batas-batas interval dari parameter yang hendak ditaksir dengan probabilitas tertentu.

Dalam mencoba menyelidiki suatu persoalan sering digunakan suatu anggapan atau keterangan sementara mengenai gejala yang sedang diselidiki itu. Suatu populasi dapat dianggap mempunyai sifat tertentu. Anggapan itu mungkin salah atau juga benar. Anggapan seperti itu dinamakan hipotesis, sedangkan penyelidikan apakah hipotesis itu benar atau salah dinamakan pengujian hipotesis (testing of hypothesis). Jadi hipotesis adalah anggapan teoritis yang dapat dipertegas atau ditolak secara empiris.

IV.12. Penaksiaran 1. Penaksiran Titik

Penaksiran titik itu menginginkan agar suatu parameter ditaksir dengan memakai satu bilangan saja. Miaslkan yang ditaksir parameter-parameter µ, σ, atau ρ dengan memakai statistik-statistik x, s dan x/n

Jenis-jenis taksiran titik :

Bila ada satu parameter β dan penaksirnya b, penaksir b merupakan penaksir tak berpaling bila :

E(b) = β

dengan E(b) = pengharapan matematis dari b.

Harga rata-rata hitung sampel ( x) dan varians (s2_{) merupakan penaksir} tak berpaling untuk harga rata-rata hitung populasi (µ) dan varians populasi (σ2), jadi :

E(x) = µ E(s2) = σ2

s bukan penaksir tak berpaling bagi σ karena E(s) … σ, kalau E(s) = kσ dengan k = bilangan tetap, unbiased estimate bagi σ adalah s/k, karena :

E(s/k) = 1/k E(s) = σ b) Taksiran efisien

Jika parameter yang ditaksir dinyatakan dengan β dan statistik

2. Penaksiran Interval untuk sampel besar ( n > 30)

Penaksiran memakai teori pengambilan sampel ini adalah pencarian batas-batas interval dari parameter yang hendak ditaksir berada pada probabilitas tertentu.

Misalkan akan ditaksir harga rata-rata hitung suatu populasi (µ) yang anggotanya terdistribusi secara normal. Rata-rata hitung tersebut terletak diantara :

n

s

z

x

n

s

z

x

_α

µ

_α 2 1 2 1

≤

≤

+

−

dengan :

x = rata-rata hitung sampel s = standar deviasi sampel

α

2 1

z = faktor standar atau koefisien yang sesuai dengan interval keyakinan yang dipakai dalam pendugaan interval dan yang nilainya diberikan dalam tabel luas kurva normal.

Pers. 7.1

Pers. 7.2 Pers. 7.3

Pers. 7.4

Contoh

Diketahui : n = 100 s = 10

x = 160 confidence coeficient = 95% Ditanya :

*) Interval rata-rata hitung populasi Penyelesaian :

Gambar 7.1. Distribusi Normal Menurut tabel distribusi normal (lampiran-3) : 95% + 2,5% berarti _α 2 1 z = 1,96 dan - _α 2 1 z = -1,96 dan n s = 100 10 = 1 Jadi : 160 – 1,96 . 1 ≤µ≤ 160 + 1,96 . 1 158,04 ≤µ≤ 161,96

3. Penaksiran interval untuk sampel kecil (n < 30)

Untuk sampel kecil digunakan Tabel distribusi-t (lampiran). Contoh :

Diketahui : n = 16 x= 30 dan s = 8

Ditanyakan : Interval rata-rata hitung populasi bila confidence coeficient 99% Penyelesaian : α = 100% - 99% = 1% atau α = 0,001

½α = ½ x 0,01 = 0,005

Menurut tabel Distribusi-t, untuk t0,005 dan degree of freedom (df) = n-1 = 16 – 1 = 15 diperoleh _α

2 1

z = 2,947

Rata-rata hitungnya terletak diantara :

95% 2,5% 2,5% - _α 2 1 z + _α 2 1 z

n

s

z

x

n

s

z

x

_α

µ

_α 2 1 2 1

≤

≤

+

−

30 – 2,947 x 16 8 ≤µ≤ 30 + 2,947 x 16 8 24,106 ≤µ≤ 35,894

4. Menetukan besar minimum sampel

Perhatikan persamaan 7.5, bagian sebelah kanan adalah

n

s

z

x

_α

µ

≤

−

1₂

µ

α

≤

−

−

x

n

s

z

2 1 2 2

)

(

)

(

2 1

µ

σ

α

−

≤

∗

x

n

z

Karena x- µ = E merupakan kesalahan yang diperkenankan, diperoleh : 2 ) ( 2 1α ∗σ z ≤ nE2 Jadi : n ≥         _∗ E z )2 ( 2 1α σ

dengan σ = deviasi standar populasi (dianggap diketahui) Contoh :

Panjang pipa merupakan distribusi normal dengan σ = 20 cm. Berapa sampel minimal yang harus diambil agar kesalahan tidak melebihi 2 cm. Diketahui confidence coeficient 90%

Jawab : Pers. 7.6 90% 5% 5% - _α 2 1 z + _α 2 1 z

E = ( x- µ) = 2 cm σ = 20 cm

α = 100% - 90% = 10% ½α = ½ x 10% = 5%

Untuk luas daerah 90% + 5% = 95% diperoleh _α

2 1 z = 1,65 Menurut persamaan 7.6 n ≥         _∗ E z ₎2 ( 2 1α σ diperoleh : n ≥ _      _∗ 2 ) 20 65 , 1 ( 2 n ≥ 272,25

5. Penaksiran interval untuk deviasi standar Menggunakan persamaan : n z s 2 1+ 12α ≤σ≤ n z s 2 1− 12α Contoh :

Diketahui n = 200, deviasi standar sampel (s) = 15, confidence coeficient 99%. Buatkan penaksiran interval untuk deviasi standard populasi (σ) : Penyelesaian :

Lihat tabel distribusi Normal (lampiran III)

α = 100% - 99% = 1%

½α = ½ x 1% = 0,5% (level of significant)

Untuk luas daerah 99% + 0,5% = 99,5% atau confidence coeficient 0,995 diperoleh _α 2 1 z = 2,58 Jadi : 200 * 2 58 , 2 1 15 + ≤σ≤ 200 * 2 58 , 2 1 15 − Pers. 7.7

IV.13. Pengujian Hipotesis

1. Ukuran sampel besar ( n ≥ 30) Hipotesis yang akan diuji berupa :

Ho : µ = µo terhadap H1 : µ… µo (2 sisi)

Ho : µ = µo terhadap H1 : µ > µo (sisi kanan)

Ho : µ = µo terhadap H1 : µ < µo (sisi kiri)

Keterangan :

Ho = hipotesisi yang akan diuji (hipoteisis nol) H1 = hipotesisi alternatif

µ = rata-rata ukur sebenarnya dari populasi µo = suatu nilai yang telah ditetapkan

Caranya dengan : a) pengujian hipotesisi 2 sisi b) pengujian hipotesis 1 sisi kiri c) pengujian hipotesis 1 sisi kanan

a) Pengujian Hipotesis 2 sisi

Komposisi pengujian Ho : µ = µo H1 : µ… µo Fungsi penaksiran : zo = n s x−µ_o Pers. 7.8 acceptance region (diterima) - _α 2 1 z + _α 2 1 z _{Critical region} (ditolak) Critical region (ditolak)

Aturan pengujian : Tolak Ho bila zo > _α 2 1 z atau zo < _α 2 1 z Terima Ho bila - _α 2 1 z < zo < _α 2 1 z Contoh :

Suatu sampel yang terdiri dari 36 buah bola baja mempunyai x = 100 kg, µo = 110 kg dan s = 24 kg. Confidence coeficient 95%. Laksanakan

pengujian ! Penyelesaian :

Bila hipotesa x = 100 kg ternyata benar, berarti Ho diterima. Akan

tetapi bila hipotesa x = 100 kg ternyata salah, berarti Ho ditolak atau H1 diterima.

α = 100% - 95% = 5% ½α = ½ x 5% = 2,5%

Untuk luas daerah 95% + 2,5% = 97,5% diperoleh _α

2 1 z = 1,96 dan - _α 2 1 z = 1,96 zo = 36 24 110 100− ternyata z < - _α 2 1 z jadi Ho ditolak

atau H1 diterima, berarti ukuran sampel 36 karung itu tidak berasal dari

b) Pengujian Hipotesis 1 sisi kiri Komposisi pengujian : Ho : µ = µo H1 : µ < µo Fungsi penaksiran : zo = n s x−µ_o

Aturan pengujian : Tolak Ho bila z < _α

2 1 z Terima Ho bila z > _α 2 1 z Contoh :

Suatu sampel yang terdiri dari 36 buah bola baja mempunyai x = 100 kg, s = 24, µo = 115 dan confidence coeficient 95%. Laksanakan

pengujian terhadap µ < 115 kg Penyelesaian : Ho : µ = µo H1 : µ < 115 zo = 36 24 110 100− = -3,75 confidence coeficient 95% α = 100% - 95% = 5%

Jadi taraf nyata atau level of significance = 0,05 acceptance region (diterima) - _α 2 1 z Critical region (ditolak)

Menurut tabel distribusi normal (lampiran III) - zα = - 1,65

Peraturan pengujian : Tolak Ho jika z < -zα, ternyata z = -3,75 dan zα = -1,65 jadi Ho ditolak atau H1 diterima

c) Pengujian Hipotesis 1 sisi kanan

Komposisi pengujian : Ho : µ = µo H1 : µ > µo Fungsi penaksiran : zo = n s x−µ_o

Aturan pengujian : Tolak Ho bila z > _α

2 1 z Terima Ho bila z < _α 2 1 z Contoh ;

Ukuran sampel 36 karung, x = 100 kg, s = 24, confidence coeficient 95%. Adakan pengujian terhadap pernyataan µ > 95 kg

Penyelesaian : Ho : µ = µo H1 : µ > 95 zo = 36 24 95 100− = 1,25 confidence coeficient 95% acceptance region (diterima) + _α 2 1 z _{Critical region} (ditolak)

α = 100% - 95% = 5% = 0,05

Berdasarkan tabel Distribusi Normal (lampiran III) zα = 1,65

Peraturan pengujian Tolak Ho jika z > z_α Ternyata z < zα

Jadi Ho diterima atau H1 ditolak

2. Ukuran sampel kecil ( n< 30)

Pengujian hipotesis untuk ukuran sampel kecil digunakan Tabel Distribusi-t (lampiran IV).

t = n s x−µ_o

Contoh ;

Menurut iklan mobil A menempuh rata-rata 10 km untuk setiap 1 liter bensin yang dipakai. Untuk menguji benar tidaknya pernyataan tersebut telah diambil 10 buah mobil dan ternyata rata-rata hanya menempuh 9,7 km untuk setiap liter bensin dengan deviasi standar 0,4 km. Level of significance = 0,05

Penyelesaian :

Yang diuji hipotesisi nol (Ho) yang menyatakan bahwa µ = 10 terhadap hipotesis alternatif yang menyatakan bahwa µ < 10. ini adalah pengujian hipotesis 1 sisi kiri. Untuk degree of freedom (df) = 9 dan t0,05 pada tabel

Distribusi-t (lapiran IV) memberikan angka -1,933.

t = n s x−µ_o = 10 4 , 0 10 7 , 9 − = -2,37

Ternyata -2,37 < t0,05 , jadi Ho yang menyatakan µ = 10 ditolak, atau yang

menyatakan µ < 10 diterima.