BAB IV METODA RUNGE-KUTTA ORDE 4 PADA MODEL ALIRAN FLUIDA YANG TERGANGGU

BAB IV

METODA RUNGE-KUTTA ORDE 4 PADA MODEL

ALIRAN FLUIDA YANG TERGANGGU

Pada bab III, kita telah melakukan pengujian terhadap metoda Runge-Kutta orde 4 pada persamaan panas. Hasilnya, solusi analitik persamaan panas dapat dihampiri oleh solusi numerik dengan menggunakan metoda Runge-Kutta orde 4. Dengan bertolak pada hasil tersebut, pada bab ini, kita akan menggunakan metoda Runge-Kutta orde 4 untuk mencari solusi numerik dari suatu sistem persamaan diferensial parsial yang merupakan model linier masalah aliran fluida dimana solusi analitiknya tidak mudah untuk ditentukan.

Pada bab ini, kita akan membahas model aliran fluida yang akan ditinjau untuk memberikan gambaran fisisnya dan akan dibahas pula bagaimana menerapkan metoda Runge-Kutta orde 4 dalam mencari solusi analitiknya.

4.1 Model Aliran Fluida

Model aliran fluida yang akan ditinjau di sini berhubungan dengan model aliran fluida dimensi satu. Pada suatu saluran terbuka dengan dasarnya terdapat suatu gundukan kecil. Mula-mula, sebelum alirannya menabrak gundukan, alirannya adalah seragam yaitu simpangan permukaan dan kecepatannya konstan. Pada saat Aliran fluida tesebut mengalami gangguan yang disebabkan oleh adanya gundukan kecil pada dasar saluran, maka alirannya menjadi tidak seragam lagi. Hal ini dapat diamati dari simpangan yang terbentuk pada permukaan bebas fluida seperti pada Wiryanto [3].

Misalkan, kita pilih sistem koordinat kartesius dengan sumbu horisontal x sepanjang permukaan bebas dari fluida, maka simpangan fluida dapat dinyatakan sebagai y=η

(

x,t

)

dan dasar saluran sebagai y= −

(

h₀+h x

( )

)

di mana t adalah variabel waktu, h₀ adalah kedalaman dasar saluran dan h x

( )

adalah bentuk topografi gundukan. adalah kecepatan rata-rata awal aliran fluida, yang mewakili kecepatan fluida di titik-titik yang berada pada satu garis vertikal yang sama, pada

0

titik-titik pengamatan sebelum gundukan. Gambar 4.1 berikut merupakan sketsa dari kondisi di atas.

U

0

( )

, y=η x t 0 y=

a

b

0 y= −h

( )

(

0

)

y= − h +h x

Gambar 4.1 Sketsa kondisi aliran fluida

Berdasarkan paper Wiryanto [3], model matematika hasil perumusan kondisi fisis tersebut adalah suatu sistem persamaan diferensial parsial yang mempunyai bentuk

( )

t Fux F u x u hx Fh η + +ε ⎡_⎣ η + ⎤_⎦= − _x (31) 1 0 t x x u Fu Fη + + = (32)

dengan adalah kecepatan rata-rata aliran fluida yang merupakan rata-rata dari kecepatan fluida di titik-titik yang berada pada posisi x yang sama pada saat t tertentu. Sehingga, pada saat t tertentu, kecepatan fluida yang berada pada posisi x yang sama diwakili .

(

, u x t

)

( )

, u x t 0 a h

ε = adalah suatu besaran terkait dengan amplitudo a dan kedalaman dasar saluran . Sedangkan, parameter bilangan Froude didefinisikan sebagai

0

h

0 gh0

U , dengan g adalah percepatan gravitasi.

Dalam skripsi ini, kondisi fisis yang akan dipelajari adalah kondisi dimana awalnya aliran fluida, sebelum menabrak gundukan, adalah seragam yaitu kecepatan

dan simpangan permukaan fluidanya konstan. Sedangkan, kondisi pada batas-batas daerah pengamatan disamakan dengan kondisi awalnya.

4.2 Prosedur Numerik

Pada bab 2 sebelumnya, kita telah membahas formula Runge-Kutta orde 4 untuk persamaan diferensial biasa. Karena pada bab ini kita akan mencari solusi numerik dari suatu sistem persamaan diferensial, maka berikut ini akan diberikan bentuk umum dari formula Runge-Kutta orde 4 untuk sistem persamaan diferensial biasa.

Misalkan diketahui suatu sistem persamaan diferensial biasa

(

)

/ , , y = f t y z ,

(

)

/ , , z =g t y z .

Maka, formula Runge-Kutta orde 4 untuk sistem diatas adalah

(

1 1 2 3 1 2 2 6 n n 4

)

y ₊ = y + k + k + k +k (33)

(

1 1 2 3 1 2 2 6 n n z ₊ =z + l + l + l +l₄

)

(34) dimana

(

)

1 n, n, n k =hf t y z

(

)

1 n, n, n l =hg t y z 1 1 2 , , 2 2 n n n k l h k =hf t⎛_⎜ + y + z + ⎞_⎟ ⎝ 2⎠ 1 1 2 , , 2 2 n n n k l h l =hg t⎛_⎜ + y + z + ⎞_⎟ ⎝ 2⎠ 2 2 3 , , 2 2 n n n k l h k =hf t⎛_⎜ + y + z + ⎞_⎟ ⎝ 2⎠ 2 2 3 , , 2 2 2 n n n k l h l =hg t⎛_⎜ + y + z + ⎞_⎟ ⎝ ⎠

(

)

4 n , n 3, n k =hf t +h y +k z +l₃ 3 .

(

)

4 n , n 3, n l =hg t +h y +k z +l

Solusi numerik yang akan kita cari di sini adalah solusi numerik dari model linier aliran fluida di atas. Model linier tersebut diperoleh dengan mengabaikan suku-suku pada persamaan (31) dan (32) yang memuat ε yang kita anggap nilainya sangat kecil. Secara fisis, kondisi tersebut dapat diinterpretasikan bahwa besarnya simpangan maksimum dari permukaan fluida sangat kecil jika dibandingkan dengan kedalaman dari dasar saluran. Sehingga, model linier aliran fluida di atas mempunyai bentuk

t Fux Fhx η + = − (35) 1 0 t x x u Fu Fη + + = (36)

Kondisi-kondisi yang diberikan untuk mencari solusi numerik dari model linier di atas antara lain simpangan awal η

( )

x, 0 =0, dan kecepatan awal u x

( )

, 0 =1.

Untuk memudahkan dalam penjelasan metoda yang digunakan, kita tuliskan

( )

, t G u η = η

( )

, t u =H η u dengan

( )

, _{x x} G η u = −Fu −Fh (37)

( )

1 , _{x x} H u Fu F η = − − η . (38)

Misalkan interval

[

0, 50

]

adalah domain pengamatan dari model linier aliran fluida dan waktu pengamatan adalah . Domain pengamatan tersebut dibagi menjadi m buah titik diskrit dengan step size

0 t>

x

Δ dan interval waktu pengamatan dibagi menjadi n buah titik diskrit dengan step size Δt. Kita tuliskan x_j =x₀+ Δxj

t

dan t_i = + Δt₀ i untuk setiap i=1, 2,..., n dan j=1, 2,..., m. Selanjutnya, kita nyatakan simpangan permukaan dan kecepatan fluida di titik

(

x t_j, _i

)

berutrut-turut sebagai ηij ≅η

(

x tj, i

)

dan

( )

,

i

j j

u ≅u x ti .

Turunan parsial terhadap variabel x dihampiri dengan menggunakan metode beda pusat. Hampiran beda pusat untuk η_x adalah

1 1 2 i i j j x x η η η _≅ + − − Δ dan hampiran beda pusat untuk u adalah _x

1 1 2 i i j j x u u u x + − − ≅ Δ .

Berdasarkan diskritisasi domain, kita nyatakan Gij ≡G u

( )

i j i j dan .

Maka, bentuk persamaan (37) dan (38) menjadi

(

,

)

i i j j H ≡H η u 1 1 2 i i j j i j u u G F h x + − ⎛ − ⎞ = − _⎜⎜ + Δ ⎝ x⎠⎟⎟ (39) 1 1 1 1 1 2 2 i i i i j j j j i j u u H F x F x η η + − + − ⎛ − − ⎞ = −_⎜⎜ + Δ Δ ⎝ ⎠⎟⎟. (40)

Selanjutnya, turunan parsial terhadap variabel t pada persamaan (35) dan (36) dihampiri dengan menggunakan metoda Runge-Kutta orde 4. Maka, nilai η dan , i_j

untuk dan , ditentukan dengan menggunakan formula

i j u 1, 2,..., 1 i= n− j=1, 2,..., m

(

1 1 2 3 4 1 2 2 6 i i j j k k k k η+ ₌η _{+ + + +}

)

(41)

(

1 1 2 3 4 1 2 2 6 i i j j u+ =u + l + l + l +l

)

. (42) dengan

( )

1 i i j j k = ΔtG u = ΔtG

(

)

1 , i i i j j j l = ΔtH η u = ΔtH 1 2 2 i j l k = ΔtG u⎛_⎜ + ⎞_⎟ ⎝ ⎠ 1 1 2 , 2 2 i i j j k l l = ΔtH⎛_⎜η + u + ⎞_⎟ ⎝ ⎠ 2 3 2 i j l k = ΔtG u⎛_⎜ + ⎞_⎟ ⎝ ⎠ 2 2 3 , 2 2 i i j j k l l = ΔtH⎛_⎜η + u + ⎞_⎟ ⎝ ⎠

(

)

4 3 i j k = ΔtG u +l

(

)

4 3, i i j j l = ΔtH η +k u +l3 .

Berikut ini, diberikan contoh perhitungan untuk menentukan nilai k₂ dan . l₂

( )

1 1 2 2 2 i i j j l l k = ΔtG u⎛_⎜ + ⎞_⎟= Δt G u⎛_⎜ +G⎛_⎜ ⎞_⎟ ⎝ ⎠ ⎝ ⎝ ⎠ ⎞ ⎟ ⎠ ,

dimana

(

)

1 1 2 2 i j l G⎛ ⎞ =_{⎜ ⎟} G Δt ⎝ ⎠ H 1

( )

2 i j tG H = Δ . Jadi,

( )

2 1 2 i i j j k = Δt G⎛_⎜ + ΔtG H ⎞_⎟ ⎝ ⎠.

(

)

1 1 1 1 2 , , 2 2 2 2 i i i i j j j j k l k l l = ΔtH⎛_⎜η + u + _⎟⎞= ΔtH⎛_⎜ η u +⎛_⎜ ⎞_⎟ ⎝ ⎠ ⎝ ⎝ , ⎠ ⎞ ⎟ ⎠ . Karena H linier, maka

(

)

1 1 2 , , 2 2 i i j j k l l = Δt H⎛_⎜ η u + ⎜H⎛ ⎞_⎟⎞_⎟ ⎝ ⎠ ⎝ ⎠ dimana

(

)

1 1 1 1 1 , , 2 2 2 k l H⎛_⎜ ⎞ =_⎟ H ⎝ ⎠ k l 1

(

,

)

2 i i j j H tG tH = Δ Δ 1

(

,

)

2 i i j j tH G H = Δ Jadi,

(

)

2 1 , 2 i i j j l = Δt H⎛_⎜ + ΔtH G H ⎞_⎟ ⎝ ⎠ i j .

Dengan cara yang sama, kita peroleh

( )

(

(

)

)

3 1 , 2 2 i i i j j j t k = Δt G⎛_⎜ +Δ ⎛_⎜G H + ΔtG H G H ⎞_⎟⎟ ⎝ ⎠ ⎝ ⎠ i j ⎞

(

)

(

( ) (

)

)

3 , , 2 2 i i i i i j j j j j t t l = Δt H_⎜⎛ +Δ _⎜⎛H G H +Δ H G H H G H ⎞_⎟⎟ ⎝ ⎠ ⎝ , ⎠ i j ⎞

( )

(

(

)

)

(

(

( ) (

)

)

)

4 , , 2 2 i i i i i i i j j j j j j j t t k = Δt G_⎜⎛ + Δt G H_⎜⎛ +Δ _⎜⎛G H G H +Δ G H G H H G H ⎞_⎟⎟⎞_⎟ ⎝ ⎠ ⎝ ⎠ ⎝ , ⎠ ⎞

(

)

(

(

( ) (

)

)

4 , , 2 i i i i i j j j j j t l = Δt H⎛_⎜ + Δt H G H⎛_⎜ +Δ H G H H G H + ⎝ ⎝ , i j

(

(

(

,

)

)

,

(

( ) (

, ,

)

)

2 i i i i i j j j j j t H G H G H H G H H G H ⎞⎞ Δ ⎞⎞ ⎟ ⎟ ⎟⎟ ⎟ ⎠⎠⎠⎠.

Jika kita perhatikan, pada perhitungan , fungsi l₁ Hi_j akan melibatkan nilai-nilai ui_j−1,

, 1 i j

u ₊ ηi_j−1, dan ηi_j+1. Pada perhitungan , fungsi l₂ H G H

(

ij, ij

)

akan melibatkan nilai-nilai 2, , , i j u ₋ uij 2 i j u ₊ 2 i j η ₋ , η , dan ij 2 i j

η ₊ . Pada perhitungan , fungsi akan melibatkan u 3 l

( ) (

)

(

i_j , i_j,

)

H G H H G Hi_j i_j−3, ui_j−1, ui_j+1, ui_j+3, ηi_j−3, ηi_j−1, ηi_j+1, dan 3 i j

η ₊ . Pada perhitungan l , fungsi ₄ H G H G H

(

(

(

i_j, i_j

)

)

,H G H

(

( ) (

_ji ,H G Hi_j, i_j

)

)

)

akan melibatkan nilai-nilai u 4, , , i j− 2 i j u ₋ uij 2 i j u ₊ , 4 i j u ₊ , 4 i j η ₋ , 2 i j η ₋ , η , ij 2 i j η ₊ dan 4 i j η ₊ . Sehingga, untuk indeks waktu i = 1, 2, …n-1, perhitungan ηi_j+1 dan akan melibatkan sembilan buah nilai pada indeks waktu sebelumnya. Untuk lebih jelasnya, gambar 4.2 berikut ini merupakan “stencil” dari persamaan (41) dan (42).

1 i j u+ i+1, j i, j-4 i, j-3 i, j-2 i, j-1 i, j i, j+1 i, j+2 i, j+3 i, j+4

Gambar 4.2 Stencil dari skema Runge-Kutta orde 4 untuk masalah aliran fluida

Jika kita lihat dari stencil di atas maka untuk menghitung nilai ηi_j+1 akan melibatkan empat buah nilai di sebelah kiri dan kanan dari η . Hal yang sama juga i_j berlaku untuk menghitung nilai uij1

+

. Hal tersebut akan menimbulkan masalah jika kita akan menghitung nilai-nilai pada batas kiri dan kanan dari domain pengamatan atau nilai-nilai dengan indeks j= dan j m1 = . Untuk mengatasi masalah tersebut, kita gunakan arti fisis dari model aliran fluida yaitu dengan menetapkan 0 untuk nilai-nilai di luar domain pengamatan. Hal ini berarti bahwa keadaannya seragam tidak ada pengaruh dari gangguan.

Sehingga, solusi numerik yang akan kita cari adalah solusi dari

(

1 1 2 3 4 1 2 2 6 i i j j k k k k η+ ₌η _{+ + + +}

)

untuk i = 1, 2, …, n-1 dan j = 1, 2, …, m.

(

1 1 2 3 4 1 2 2 6 i i j j u+ =u + l + l + l +l

)

untuk i = 1, 2, …, n-1 dan j =1, 2, …, m. terhadap: kondisi awal 1 0 j η = , untuk j =1, 2, …, m 1 1 j u = , untuk j =1, 2, …, m kondisi batas 0 i j

η = , untuk i = 1, 2, …, n-1 dan j = -3, -2, -1, 0, m + 1, m + 2, m + 3, dan m + 4

1

i j

u = , untuk i = 1, 2, …, n-1 dan j = -3, -2, -1, 0, m + 1, m + 2, m + 3, dan m + 4.

4.3 Hasil Numerik

Pada sub bab ini, skema numerik yang telah kita bentuk digunakan untuk mengamati terbentuknya gelombang pada permukaan bebas fluida akibat adanya gundukan pada dasar saluran. Hasil-hasil numerik yang akan ditampilkan di sini menggunakan gundukan berbentuk

( )

(

)

2 0.1 28 1 h x x − =

− + yang ditempatkan pada

[

20, 35

]

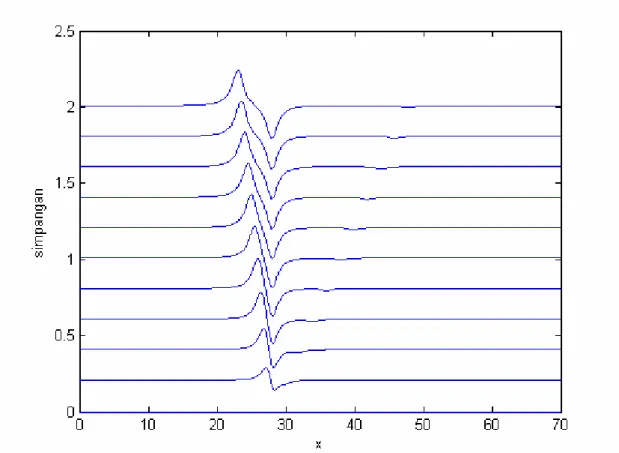
, dan . Gambar 4.3, 4.4 dan 4.5 berikut ini merupakan plot

simpangan permukaan fluida pada setiap titik berturut-turut untuk F = 0.3, F = 0.6 dan F = 1.5. Untuk beberapa nilai t, plot simpangan permukaan diletakan pada koordinat yang sama dengan menggeser ke atas plot simpangan permukaan untuk level waktu t yang lebih tinggi.

0.1 x

Gambar 4.3 Plot permukaan fluida untuk F = 0.3

Gambar 4.5 Plot permukaan Fluida untuk F = 1.5

Dari pengamatan ketiga plot di atas, mula-mula tidak ada gelombang pada permukaan fluida. Kemudian setelah beberapa saat, tiga buah gelombang terbentuk pada permukaan fluida dengan masing-masing arah perambatannya berbeda. Gelombang sebelah kiri merambat ke kiri, gelombang yang di tengah cenderung diam, dan gelombang sebelah kanan merambat ke kanan

Untuk selanjutnya, kita akan menentukan secara kuantitatif kecepatan dan amplitudo masing-masing gelombang serta membahas bagaimana hubungannya dengan bilangan Froude F.

4.3.1 Analisa Kuantitatif Pengaruh Perubahan Parameter Bilangan

Froude F Terhadap Amplitudo Gelombang

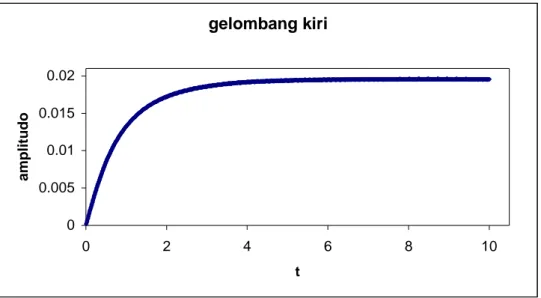
Pada plot solusi sebelumnya, jika kita perhatikan pada awalnya gelombang belum terbentuk. Seiring bertambahnya waktu, masing-masing gelombang terbentuk dengan amplitudo yang berubah-ubah. Gambar 4.6 dan 4.7 berikut ini berturut-turut merupakan plot waktu terhadap amplitudo gelombang kiri dan gelombang tengah untuk nilai F =0.3.

gelombang kiri 0 0.005 0.01 0.015 0.02 0 2 4 6 8 10 t amplitudo

Gambar 4.6 Plot amplitudo gelombang kiri untuk F = 0.3.

gelombang tengah 0.0065 0.007 0.0075 0.008 0.0085 0.009 2 4 6 8 10 12 t amplitudo

Gambar 4.7 Plot amplitudo gelombang tengah untuk F = 0.3.

Dari kedua plot di atas, amplitudo gelombang yang merambat ke kiri asimtotik ke 0.0196, sedangkan amplitudo gelombang yang di tengah asimtotik ke –0.009. Dengan cara yang sama, tabel 4.1 berikut ini merupakan tabel untuk nilai asimtotik dari amplitudo gelombang kiri dan gelombang tengah untuk beberapa nilai F.

Gelombang kiri Gelombang tengah

F Amplitudo F Amplitudo

0.3 0.0196 0.3 0.009

0.5 0.0389 0.5 0.025 0.6 0.0507 0.6 0.036 0.7 0.0641 0.7 0.048 0.8 0.079 0.8 0.063 0.9 0.0956 0.9 0.08 1 0.114 1 0.099 1.1 0.134 1.1 0.119 1.2 0.155 1.2 0.142 1.3 0.179 1.3 0.166 1.4 0.206 1.4 0.192 1.5 0.233 1.5 0.221

Tabel 4.1 Nilai asimtotik dari amplitudo gelombang

kiri dan tengah untuk beberapa nilai F.

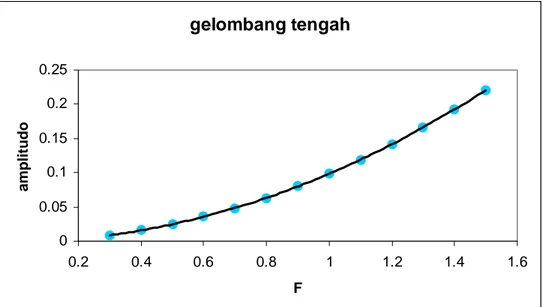
Dari tabel di atas, semakin besar nilai F maka amplitudo gelombang yang merambat ke kiri dan yang berada di tengah akan semakin besar pula. Hal tersebut dapat dilihat juga dari trendline yang terbentuk seperti pada gambar 4.8 dan 4.9 berikut ini.

gelombang kiri 0 0.05 0.1 0.15 0.2 0.25 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 F amplitudo

gelombang tengah 0 0.05 0.1 0.15 0.2 0.25 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 F amplitudo

Gambar 4.9 Trendline amplitudo gelombang tengah.

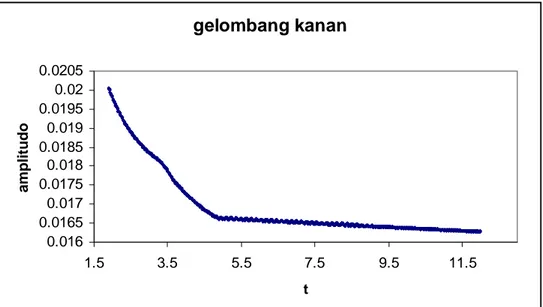
Untuk gelombang yang merambat ke kanan, untuk setiap nilai F, amplitudo gelombang akan semaki kecil seiring dengan berjalannya waktu. Hal ini dapat dilihat dari plot amplitudo terhadap waktu. Sebagai contoh, Gambar 4.10 dan gambar 4.11 berikut ini berturut-turut merupakan plot amplitudo gelombang yang merambat ke kanan terhadap waktu untuk nilai F = 0.4 dan F = 0.8.

gelombang kanan 0.0124 0.0126 0.0128 0.013 0.0132 0.0134 0.0136 0.0138 0.014 0.0142 1.5 3.5 5.5 7.5 9.5 11.5 t amplitudo

gelombang kanan 0.016 0.0165 0.017 0.0175 0.018 0.0185 0.019 0.0195 0.02 0.0205 1.5 3.5 5.5 7.5 9.5 11.5 t amplitudo

Gambar 4.11 Plot amplitudo gelombang kanan untuk F = 0.8.

4.3.2 Analisa Kuantitatif Pengaruh Perubahan Parameter Bilangan

Froude F Terhadap Kecepatan Gelombang

Pada plot solusi numerik sebelumnya, kita misalkan masing-masing gelombang dari ketiga gelombang yang terbentuk adalah kurva dari suatu fungsi. Dengan bertambahnya nilai t, masing-masing kurva bergeser sepanjang sumbu horisontal dari posisi sebelumnya, maka masing-masing kurva tersebut dapat dinyatakan sebagai fungsi terhadap x ct− =k dengan c dan k adalah konstanta sebarang. Secara fisis, c merepresentasikan kecepatan dari masing-masing gelombang.

Sehingga, untuk mencari kecepatan dari masing-masing gelombang, kita akan menggunakan regresi linier untuk menentukan kemiringan garis dari persamaan garis yang menghubungkan posisi amplitudo gelombang x terhadap waktu t. sebagai contoh, Gambar 4.12, 4.13 dan 4.14 berikut ini merupakan plot dari posisi amplitudo masing-masing gelombang terhadap waktu beserta persamaan garis hasil regresi linier untuk . Regresi linier tersebut diperoleh dengan menggunakan perangkat lunak Excel.

0.3

gelombang kiri t = -1.2081x + 33.653 0 2 4 6 8 10 19 21 23 25 27 x t

Gambar 4.12 Plot posisi amplitudo gelombang kiri terhadap waktu.

gelombang tengah t = -30.008x + 847.51 0 2 4 6 8 10 12 14 25 26 27 28 29 30 x t

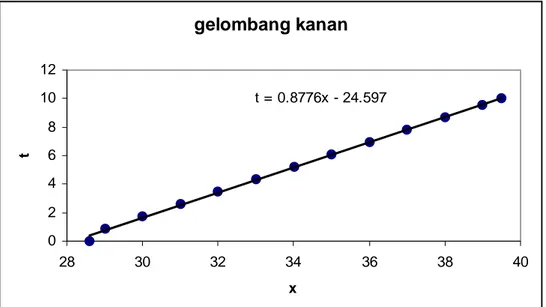
gelombang kanan t = 0.8776x - 24.597 0 2 4 6 8 10 12 28 30 32 34 36 38 40 x t

Gambar 4.14 Plot posisi amplitudo gelombang kanan terhadap waktu.

Dari grafik di atas, kecepatan c masing-masing gelombang diperoleh dari 1

c

gradien

= . Sehingga, kecepatan gelombang kiri c_L, gelombang tengah c , dan _M

gelombang kanan berturut-turut adalah -0.8277, -0.0333, dan 1.1395. Dengan cara yang sama, kita peroleh kecepatan masing-masing gelombang untuk beberapa nilai F seperti pada tabel 4.2 berikut.

R c

Gelombang kiri Gelombang tengah Gelombang kanan F Kecepatan F Kecepatan F Kecepatan

0.1 -0.9211 0.1 -0.0498 0.1 1.0252 0.2 -0.8732 0.2 -0.0405 0.2 1.0808 0.3 -0.8277 0.3 -0.0333 0.3 1.1395 0.4 -0.7849 0.4 -0.0415 0.4 1.2099 0.5 -0.7443 0.5 -0.0469 0.5 1.2726 0.6 -0.7061 0.6 -0.0377 0.6 1.3353 0.7 -0.6703 0.7 -0.1098 0.7 1.4011 0.8 -0.6365 0.8 -0.0951 0.8 1.4682 0.9 -0.6051 0.9 -0.0882 0.9 1.5377 1 -0.5754 1 -0.0847 1 1.6090 1.1 -0.5476 1.1 -0.0808 1.1 1.6818 1.2 -0.5216 1.2 -0.0763 1.2 1.7562 1.3 -0.4969 1.3 -0.0748 1.3 1.8291 1.4 -0.4839 1.4 -0.0616 1.4 1.9077 1.5 -0.4626 1.5 -0.0606 1.5 1.9865

Dari tabel 4.2 dapat kita lihat, kecepatan gelombang yang merambat ke kiri akan semakin kecil dengan bertambahnya nilai F. Kecepatan gelombang yang merambat ke kanan akan semakin besar dengan bertambahnya nilai F. Sedangkan, gelombang yang berada di tengah relatif tidak berubah dengan bertambahnya nilai F. Hal tersebut dapat juga diamati dari trendline yang terbentuk berdasarkan tabel 4.2 seperti pada gambar 4.15, 4.16 dan 4.17 berikut ini.

gelombang kiri -1 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 F c

Gambar 4.15 Trendline kecepatan gelombang kiri terhadap parameter bilangan Froude.

gelombang tengah -1 -0.8 -0.6 -0.4 -0.2 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 F c

Gambar 4.16 Trendline kecepatan gelombang tengah terhadap parameter bilangan Froude.

gelombang kanan 0.9 1.1 1.3 1.5 1.7 1.9 2.1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 F c

Gambar 4.17 Trendline kecepatan gelombang kanan terhadap parameter bilangan Froude.

4.3.3 Analisa Kuantitatif Pengaruh Perubahan Ketinggian

Gundukan Terhadap Amplitudo Gelombang

Analisa kuantitaif pengaruh perubahan ketinggian gundukan terhadap amplitudo gelombang dapat dilakukan dengan terlebih dahulu menentukan nilai asimtotik untuk setiap gelombang. Nilai-nilai asimtotik tersebut dapat kita peroleh

dari plot amplitudo gelombang terhadap waktu untuk setiap ketinggian gundukan dengan bilangan Froude F tertentu. Karena bentuk gundukan yang kita gunakan di sini, yaitu

( )

(

)

(

2

)

0.1 28 1 h x x − =

− + , mempunyai ketinggian 0.1, maka ketinggian

gundukan lainnya diperoleh dengan cara menghitung tinggi maksimum dari kelipatan konstanta positif tertentu bentuk gundukan semula. Sebagai contoh, gambar 4.18 dan 4.19 berikut ini merupakan plot amplitudo gelombang terhadap waktu dengan F = 0.3 untuk ketinggian gundukan 0.15.

gelombang kiri 0 0.005 0.01 0.015 0.02 0.025 0.03 0 2 4 6 8 10 1 t amplitudo 2

Gambar 4.18 Plot amplitudo gelombang kiri terhadap waktu untuk F =0.3 dan ketinggian gundukan 0.15.

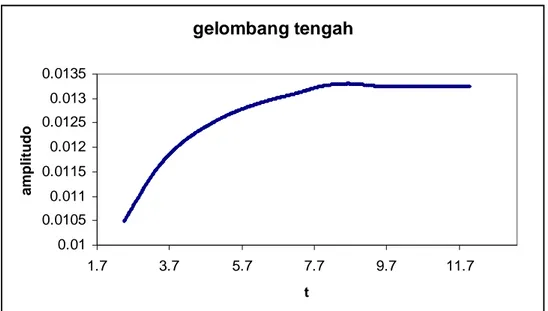
gelombang tengah 0.01 0.0105 0.011 0.0115 0.012 0.0125 0.013 0.0135 1.7 3.7 5.7 7.7 9.7 11.7 t amplitudo

Gambar 4.19 Plot amplitudo gelombang tengah terhadap waktu untuk F = 0.3 dan ketinggian gundukan 0.15.

Dari kedua gambar di atas, amplitudo gelombang kiri asimtotik ke 0.0292, sedangkan amplitudo gelombang tengah asimtotik ke 0.0132. Dengan cara yang sama, tabel 4.3 berikut ini merupakan tabel untuk nilai asimtotik dari amplitudo gelombang kiri dan gelombang tengah, dengan F = 0.3, untuk beberapa ketinggian gundukan.

Gelombang kiri Gelombang tengah

Ketinggian gundukan Amplitudo Ketinggian gundukan Amplitudo 0.1 0.0196 0.1 0.09 0.11 0.0213 0.11 0.097 0.12 0.0233 0.12 0.0106 0.13 0.0253 0.13 0.0115 0.14 0.0292 0.14 0.0133 0.15 0.0292 0.15 0.0133 0.16 0.0312 0.16 0.0141 0.17 0.0332 0.17 0.015 0.18 0.0352 0.18 0.0159 0.19 0.0371 0.19 0.0168 0.2 0.0391 0.2 0.0177

Tabel 4.3 Nilai asimtotik amplitudo gelombang kiri dan tengah, dengan F = 0.3, untuk beberapa ketinggian gundukan.

Dari tabel di atas, semakin tinggi gundukannya maka amplitudo gelombang kiri dan gelombang tengah akan semakin besar pula. Hal ini dapat kita amati juga dari

trendline yang terbentuk berdasarkan tabel 4.3, seperti pada gambar 4.20 dan 4.21

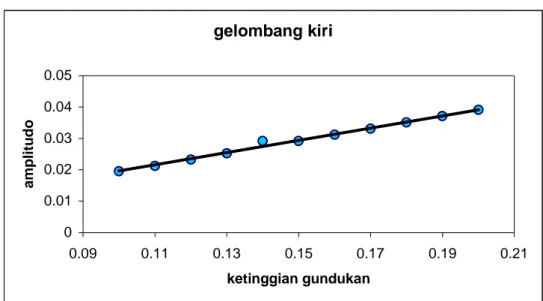
berikut. gelombang kiri 0 0.01 0.02 0.03 0.04 0.05 0.09 0.11 0.13 0.15 0.17 0.19 0.21 ketinggian gundukan amplitudo

Gambar 4.20 Trendline amplitudo gelombang kiri terhadap ketinggian

gundukan untuk F = 0.3. gelombang tengah 0 0.005 0.01 0.015 0.02 0.09 0.11 0.13 0.15 0.17 0.19 0.21 ketinggian gundukan amplitudo

Gambar 4.21 Trendline amplitudo gelombang kanan terhadap ketinggian gundukan untuk F = 0.3.

Untuk gelombang yang merambat ke kanan, untuk setiap ketinggian gundukan, amplitudo gelombang akan semaki kecil seiring dengan berjalannya waktu.

Hal ini dapat dilihat dari plot amplitudo terhadap waktu. Sebagai contoh, gambar 4.22 dan 4.23 berikut ini berturut-turut merupakan plot amplitudo gelombang yang merambat ke kanan terhadap waktu untuk nilai ketinggian gundukan 0.12 dan 0.15.

gelombang kanan 0.0124 0.0126 0.0128 0.013 0.0132 0.0134 0.0136 0.0138 1.7 3.7 5.7 7.7 9.7 t amplitudo

Gambar 4.22 Plot amplitudo gelombang terhadap waktu untuk F = 0.3 dengan ketinggian gundukan 0.12.

gelombang kanan 0.0158 0.016 0.0162 0.0164 0.0166 0.0168 0.017 0.0172 1.7 3.7 5.7 7.7 9.7 t amplitudo

Gambar 4.23 Plot amplitudo gelombang terhadap waktu untuk F = 0.3 dengan ketinggian gundukan 0.15.

4.3.4 Analisa Kuantitatif Pengaruh Perubahan Ketinggian

Gundukan Terhadap Kecepatan Gelombang

Dengan cara yang sama seperti dalam pembahasan sub bab 4.3.2 sebelumnya, kecepatan gelombang dapat kita peroleh dengan terlebih dahulu membuat plot waktu terhadap posisi amplitudo gelombang untuk F tertentu dan ketinggian gundukan tertentu. Sehingga, kecepatan gelombang dapat diperoleh dengan menghitung

1

gradien garis hasil regresi linier dari plot tersebut. Sebagai contoh, gambar 4.24,

4.25 dan 4.26 berikut ini merupakan plot waktu terhadap posisi amplitudo beserta persamaan garis hasil regresi linier berturut-turut untuk gelombang kiri, gelombang tengah dan gelombang kanan, dengan F = 0.3 dan ketinggian gundukan 0.15.

gelombang kiri y = -1.2082x + 33.655 0 2 4 6 8 10 12 19 21 23 25 27 x t

Gambar 4.24 Plot waktu terhadap posisi amplitudo gelombang kiri untuk

gelombang tengah y = -30.008x + 847.51 0 2 4 6 8 10 12 14 20 22 24 26 28 30 x t

Gambar 4.25 Plot waktu terhadap posisi amplitudo gelombang tengah untuk

F = 0.3 dengan ketinggian gundukan 0.15.

gelombang kanan y = 0.869x - 24.288 0 2 4 6 8 10 12 29 31 33 35 37 39 41 x t

Gambar 4.26 Plot waktu terhadap posisi amplitudo gelombang kanan untuk

F = 0.3 dengan ketinggian gundukan 0.15.

Sehingga, dari gambar di atas, kecepatan gelombang kiri adalah –0.8277, kecepatan gelombang kanan adalah –0.0333 dan kecepatan gelombang tengah adalah 1.1507. Dengan cara yang sama, kita peroleh kecepatan masing-masing gelombang untuk beberapa nilai F seperti pada tabel 4.4 berikut.

Ketinggian gundukan Kecepatan gelombang kiri Kecepatan gelombang tengah Kecepatan gelombang kanan 0.1 -0.8277 -0.0333 1.1507 0.11 -0.8277 -0.0333 1.1509 0.12 -0.8277 -0.0333 1.1509 0.13 -0.8277 -0.0333 1.1507 0.14 -0.8277 -0.0333 1.1507 0.15 -0.8277 -0.0333 1.1507 0.16 -0.8277 -0.0333 1.1509 0.17 -0.8277 -0.0333 1.1507 0.18 -0.8277 -0.0333 1.1509 0.19 -0.8277 -0.0333 1.1506 2 -0.8277 -0.0333 1.1507

Tabel 4.4 Kecepatan masing-masing gelombang untuk beberapa ketinggian gundukan, dengan F = 0.3.

Berdasarkan tabel 4.4, kita dapat membentuk trendline yang memperlihatkan hubungan antara pengaruh perubahan ketinggian gundukan dengan kecepatan masing-masing gelombang seperti pada gambar 4.27, 4.28 dan 4.29 berikut.

gelombang kiri -0.828 -0.8275 -0.827 -0.8265 -0.826 -0.8255 -0.825 0 0.05 0.1 0.15 0.2 0.25 ketinggian gundukan kecepatan

Gambar 4.27 Trendline kecepatan gelombang kiri terhadap

gelombang tengah -0.03335 -0.0333 -0.03325 -0.0332 -0.03315 -0.0331 -0.03305 -0.033 0.08 0.1 0.12 0.14 0.16 0.18 0.2 0.22 ketinggian gundukan kecepatan

Gambar 4.28 Trendline kecepatan gelombang tengah terhadap

ketinggian gundukan untuk F = 0.3.

gelombang kanan 0 0.2 0.4 0.6 0.8 1 1.2 1.4 0.09 0.11 0.13 0.15 0.17 0.19 0.21 ketinggian gundukan kecepatan

Gambar 4.29 Trendline kecepatan gelombang kanan terhadap

ketinggian gundukan untuk F = 0.3.

Dari trendline di atas, dapat kita amati, kecepatan masing-masing gelombang tidak berubah seiring dengan berubahnya ketinggian gundukan.