ANALISIS STABILITAS DAN PENAKSIRAN PARAMETER MODEL RENDLEMAN-BARTTER

(1)

ANALISIS STABILITAS DAN PENAKSIRAN PARAMETER MODEL

RENDLEMAN-BARTTER

Murni

1

dan Gatot F. Hertono

2

1,2

Program Magister Matematika, Departemen matematika FMIPA UI e-mail1: murni@ui.ac.id, e-mail2: gatot-f1@ui.ac.id

Abstrak.Model Rendleman-Bartter (RB) merupakan model tingkat bunga ekuilibrium satu faktor dan

diasumsikan memenuhi ukuran risk-neutral. Makalah ini membahas mengenai stabilitas model RB terkait dengan parameter model RB. Stabilitas yang dibahas adalah stabilitas stokastik asimtotik dan stabilitas mean-square. Nilai parameter model RB diestimasi menggunakan data historis tingkat bunga dan model RB terkait data historis berada pada ukuran aktual sehingga perlu dilakukan perubahan ukuran sebelum dilakukan penaksiran parameter model RB. Perubahan ukuran dilakukan dengan menggunakan Teorema Girsanov. Metode Maximum Likelihood Estimation (MLE) dan metode numerik Newton – Raphson digunakan dalam penaksiran parameter. Dengan menggunakan data tingkat bunga bulanan zero-coupon bond dengan maturity time 5 tahun periode Januari tahun 1982 hingga Februari 201 di http://www.bankofengland.co.uk dapat diperoleh nilai taksiran parameter yang memenuhi stabilitas model RB.

Kata Kunci: Rendleman–Bartter, Stabilitas Stokastik Asimtotik, Stabilitas Mean-Square,Teorema Girsanov, Maximum Likelihood Estimation, Newton-Raphson

1. Pendahuluan

Stabilitas Persamaan Diferensial Stokastik (PDS) merupakan suatu sifat yang sangat penting untuk dibahas. Dengan adanya stabilitas maka dapat diketahui kekonsistenan suatu model PDS. Hal ini berarti bahwa jika dilakukan sedikit gangguan pada nilaiawal solusi atau parameter PDS, maka solusi dari PDS akan tetap stabil [3]. Stabilitas model RB yang dibahas adalah stabilitas stokastik asimtotik dan stabilitas mean-square.

Terdapat dua kategori model tingkat bunga, yaitu model equilibrium dan no–arbitrage [8]. Model tingkat bunga yang akan dibahas adalah salah satu model ekuilibrium, yaitu model Rendleman-Bartter (RB). Ada banyak asumsi pada model ekuilibrium, diantaranya adalah asumsi ekonomi (perilaku permintaan, penawaran, dan harga di pasar), asumsi perilaku stokastik dari satu atau lebih variabel atau faktor ekonomi, serta asumsi mengenai preferensi investor terhadap aset yang dipilih. Berdasarkan asumsi-asumsi ini dapat diturunkan model tingkat bunga, salah satunya adalah model RB. Model RB merupakan model ekuilibrium satu faktor yang mendeskripsikan pergerakan tingkat bunga menurut satu sumber resiko, yaitu r(t).

Stabilitas model RB terkait dengan parameter model RB. Nilai parameter model RB tidak diketahui sehingga untuk implementasi model diperlukan penaksiran parameter model RB menggunakan data historis tingkat bunga. Model RB terkait dengan data historis berada pada ukuran aktual (actual

measure). Sedangkan model RB berada pada ukuran risk-neutral. Dengan demikian, sebelum

dilakukan penaksiran parameter dilakukan perubahan ukuran pada model RB. Perubahan ukuran ini diperlukan agar terdapat keterkaitan antara model pada ukuran risk-neutral dengan model pada ukuran aktual [4], dan model RB pada ukuran aktual dapat digunakan untuk penaksiran parameter. Selanjutnya, taksiran parameter dapat diperoleh dengan menggunakan metode Maximum Likelihood

(2)

Pada makalah ini secara berturut-turut akan dibahas mengenai model Rendelman-Bartter, stabilitas model Rendleman-Bartter, dan aproksimasi parameter.

2.

Model Rendleman-Bartter

Model Rendleman-Bartter (RB) pada risk-neutral probability measure

P

didefinisikan sebagai berikut [12],

dr t

 





r t dt

 





r t dW t

 

(1)

dengan

r t

 

adalah tingkat bunga pada waktu t,



parameter ekspektasi laju pengembalian (expected

return),



konstanta positif yang merupakan parameter standar deviasi yang menunjukkan volatilitas tingkat bunga, dan

W t

 

Brownian motion dalam risk-neutral probability measure

P

.

Dengan asumsi solusi analitik model RB unik dan ada untuk setiap

T



0

pada interval

 

0,T

, [12], maka solusi analitik dapat ditentukan dengan menggunakan formula Ito-Doeblin.

Teorema formula Ito-Doeblin:

Misalkan

X t

_t

,



0,

adalah suatu proses Ito, dan misalkan

f t x

 

,

adalah suatu fungsi dengan turunan parsial

f t x

_t

   

,

f

_x

t x

,

dan

f

_xx

 

t x

,

terdefinisi serta kontinu. Maka, untuk setiap

0 T



berlaku









































0 0 ₀ ₀ ₀ 0 0 ₀ ₀ ₀ 1 , 0, , , , , , 2 0, , , , T T T T t t x t t xx t _t T T T t t x t t t x t t t f T X f X f t X dt f t X dX f t X d X X f X f t X dt f t X dW f t X



dW          







2 0 1 , . 2 T xx t t f t X  dt



Dengan menggunakan formula Ito-Doeblin dan dengan memisalkan

f t r t



,

 





ln

r t

 

dapat diperoleh solusi analitik model RB sebagai berikut [6,9],

   

1 2

 

0 exp . 2 r t r __  _tW t _     (2)

Karena

W t

 

berdistribusi normal untuk setiap t [11], maka solusi analitik model RB (1) memiliki distribusi lognormal dengan mean dan variansi beryarat terhadap filtrasi



 

0

sebagai berikut

[9,11]

:

   





 

   

 

2 1 0 0 exp 0 , 2 0 exp . (3) E r t E r t W t r t







       _ __  _  _ _        dan

(3)

   





 



 



 









 

2 2 ₂ 1

var 0 var 0 exp 0 ,

2 0 exp 2 exp 1 . 4 r t r t W t r t t









       _ __  _  _ _          _  _

Oleh karena

r t

 

berdistribusi lognormal maka

r t

 

selalu positif untuk setiap t. Distribusi solusi analitik model RB pada ukuran risk-neutral measure ini akan dibandingkan dengan distribusi solusi analitik model RB pada ukuran aktual pada saat pembahasan estimasi parameter.

3. Stabilitas Model Rendleman -Bartter

Pada persamaan diferensial stokastik, stabilitas merupakan sifat yang sangat penting untuk dibahas. Menurut Arnold [1], stabilitas suatu PDS berarti jika dilakukan sedikit ganggguan pada nilai awal atau parameter PDS tersebut maka solusi PDS tersebut akan tetap stabil. Seperti sudah dijelasakan pada pendahuluan, makalah ini hanya membahas stabilitas stokastik asimtotik dan stabilitas mean-square model RB. Berikut definisi stabilitas stokastik asimtotik dan stabilitas mean-square dengan asumsi

 

0

0 X



[1]:

a. Jika lim

 

0

t X t  dengan probabilitas 1, maka

X

t



0

stabil secara stokastik asimtotik.

b. Jika

lim



 

2



0

t

E X t



, maka

X t

 



0

stabil secara mean-square.

Untuk membuktikan stabilitas model RB, pandang persamaan

dX t

 



aX t dt

 



bX t dW t

 

untuk

0  

t T

,

X

 

0 

x

0

dengan ,

a b C



dan

W t merupakan suatu proses Wiener pada waktu

 

t

dengan

solusi analitik sebagai berikut,

 

1 2

 

0 exp . 2 X t X _a b _tbW t     

Selanjutnya, berdasarkan definisi stabilitas di atas dan asumsikan bahwa

X

 

0 

0

, dan berdasarkan

 

1

2



 



0 exp

exp

,

2 X t



X



at





_



b t



_



bW t





dan

 

2

 

2

 

2

1

₂ 2



 



2

0 exp

exp

,

2 X t



X



at





_



b t



_



bW t





maka dapat diperoleh kriteria stabilitas stokastik asimtotik model RB adalah jika dipenuhi



2



2 

dan kriteria stabilitas mean-square model RB adalah



2  2 .



Penjelasan lebih dalam mengenai pembentukan dua kriteria stabilitas tersebut dapat dilihat pada [9].

Stabilitas stokastik asimtotik dan stabilitas mean-square model RB dapat diilustrasikan dalam daerah stabilitas model RB sebagai berikut:

(4)

Gambar 1. Daerah stabilitas stokastik

asimtotik model RB terkait parameter



dan



berada pada daerah dengan warna biru

Gambar 2. Daerah stabilitas mean-square

model RB terkait parameter



dan



berada pada daerah dengan warna merah

Berdasarkan kedua gambar di atas, yaitu Gambar 1. dan 2., terlihat bahwa daerah stabilitas

mean-square model RB terletak di dalam daerah stabilitas stokastik asimtotik model RB, atau dengan kata

lain solusi model RB yang stabil secara mean-square juga akan stabil secara stokastik asimtotik tetapi belum tentu berlaku sebaliknya.

4. Penaksiran Parameter

Pada pembahasan stabilitas model RB, stabilitas terkait dengan parameter model RB. Dalam implementasi model, nilai parameter model harus ditentukan melalui penaksiran parameter. Berikut akan dibahas mengenai penaksiran parameter model RB.

Penaksiran parameter membutuhkan data historis dan model RB terkait data historis berada pada ukuran aktual (actual measure), sedangkan model RB berada pada ukuran risk-neutral. Agar dapat dilakukan penaksiran parameter, terlebih dahulu dilakukan perubahan ukuran pada model RB menggunakan Teorema Girsanov. Dengan Teorema Girsanov dapat ditunjukkan adanya keterkaitan antara model pada ukuran risk-neutral dengan model pada ukuran aktual, sehingga model pada ukuran aktual dapat digunakan dalam penaksiran parameter. Berikut adalah teorema Girsanov.

Teorema Girsanov:

Misalkan

W t

 

merupakan Brownian motion pada ruang probabilitas



 

, , P



,



 

t

merupakan

filtrasi untuk 0 t T, dan



 

t

merupakan adapted process untuk 0 t T. Definisikan,

 

2

 

0 0

1 exp

,

2

t t

Z t











u dW u





u du











 

0 t

W t



W t







u du

dan asumsikan bahwa

   

2 2 0

.

T

E





u Z

u du

 

2





2





(5)

Tetapkan

Z



Z T

 

. Maka EZ1 dan pada probability measure

P

yang memenuhi

 

   

,

A

P A





Z



dP



untuk semua

A



,proses

W t

 

, 0 t T_{adalah Brownian motion.}

Dengan menggunakan Teorema Girsanov dan memisalkan bahwa



 

u





 

, maka

 

0 0 , , 5 t t W t W t u du W t du







    



atau dalam bentuk diferensial dapat dinyatakan sebagai

 

dW t



dt







(6) sehingga, model RB dalam ukuran aktual dapat ditulis sebagai berikut,

 

,

. (7)

dr t

r t dt

r t dW t

r t dt

r t

dW t

dt

r t dW t





















_



_







Dengan demikian, model RB pada aktual probability measure P adalah

 

.

dr t





r t dW t

(8)

Dengan membandingkan persamaan (1) dan (8), parameter



model RB pada risk-neutral

probability measure

P

_{sama dengan parameter}



model RB pada aktual probability measure P. Model RB (8) memiliki bentuk solusi analitik sebagai berikut [9],

   

1 2

 

0 exp , 9 2 r t r _



_t



W t     

yang berdistribusi lognormal dengan mean dan variansi bersyarat terhadap filtrasi



 

0

sebagai berikut,



   



 

   

 

2 1 0 0 exp 0 , 2 0 . (10) E r t E r t W t r



       _ __ _  _ _        dan

(6)

   





 

   

 





 

2 2 ₂ 1 0 0 exp 0 , 2 0 exp 1 . (11) Var r t Var r b t bW t r b t        _ __ _  _ _          _  _

Berdasarkan (3), (4), (10), dan (11), terlihat bahwa distribusi solusi analitik model RB pada risk-neutral (2) berbeda dengan distribusi solusi analitik model RB pada ukuran aktual (9). Pada [9] juga telah ditunjukkan model RB pada ukuran aktual lainnya, yaitu dengan memisalkan bahwa

 

u





v









 

dan dapat diperoleh persamaan model RB pada ukuran aktual lainnya, yaitu

 

dr t



vr t dt





r t dW t

.

Model RB (9) akan digunakan dalam penaksiran parameter menggunakan metode Maximum

Likelihood Estimation dan dilanjutkan dengan pendekatan numerik menggunakan metode

Newton-Raphson. Data yang digunakan adalah data tingkat bunga bulanan dari zero-coupon bond dengan

maturity time 5 tahun periode Januari tahun 1982 hingga Februari 2011 yang diunduh dari

http://www.bankofengland.co.uk.

5. Hasil Implementasi

Implementasi menggunakan metode Maximum Likelihood Estimation dan metode Newton-Raphson menghasilkan nilai taksiran parameter



ˆ 0.0182



. Karena



_{pada model RB pada risk-neutral}

probability measure

P

_{sama dengan}



pada model RB pada aktual probability measure P maka nilai taksiran parameter



pada model RB pada risk-neutral probability measure

P

adalah juga

ˆ 0.0182





.

Karena model RB dalam ukuran aktual tidak mengandung parameter



, maka nilai taksiran parameter



, yaitu



ˆ pada model RB pada ukuran risk-neutral ditentukan berdasarkan daerah stabilitas (Gambar 1. dan 2.). Pertama dipilih nilai



ˆ yang memenuhi stabilitas stokastik asimtotik dan mean-square (terletak dalam daerah stabilitas stokastik asimtotik dan mean-square), dalam hal ini dipilih



ˆ 0.05. Dengan demikian, nilai taksiran parameter model RB pada risk-neutral adalah

ˆ 0.05 dan ˆ 0.0093.



 





Gambar 3. adalah lintasan-lintasan solusi model RB menggunakan nilai taksiran parameter yang terletak di dalam daerah stabilitas stokastik asimtotik model RB. Sedangkan Gambar 4. jika digunakan parameter-parameter yang terletak di dalam daerah stabilitas mean-square model RB. Pada dua gambar tersebut digunakan beberapa nilai awal yang berbeda.

Gambar 3. Simulasi beberapa solusimodel RB dengan

0.05 dan 0.0093



 



 dan beberapa nilai awal yang

berbeda untuk menguji kestabilan stokastik asimtotik

Gambar 4. Simulasi beberapa solusimodel RB (100 simulasi) dengan



 0.05 dan



0.0093 dan beberapa nilai awal yang berbeda untuk menguji kestabilan

(7)

Pada Gambar 3. diberikan beberapa nilai awal model RB yang berbeda dengan parameter-parameter terletak dalam daerah stabilitas stokastik asimtotik model RB (



 0.05 dan



0.0093). Terlihat bahwa untuk waktu t yang semakin besar nilai absolut solusi model akan menuju nol. Sedangkan pada Gambar 4., setiap lintasan diperoleh dari rata-rata 100 simulasi dan diberikan beberapa nilai awal model RB dengan parameter-parameter yang terletak dalam daerah stabilitas mean-square model RB

(



 0.05 dan



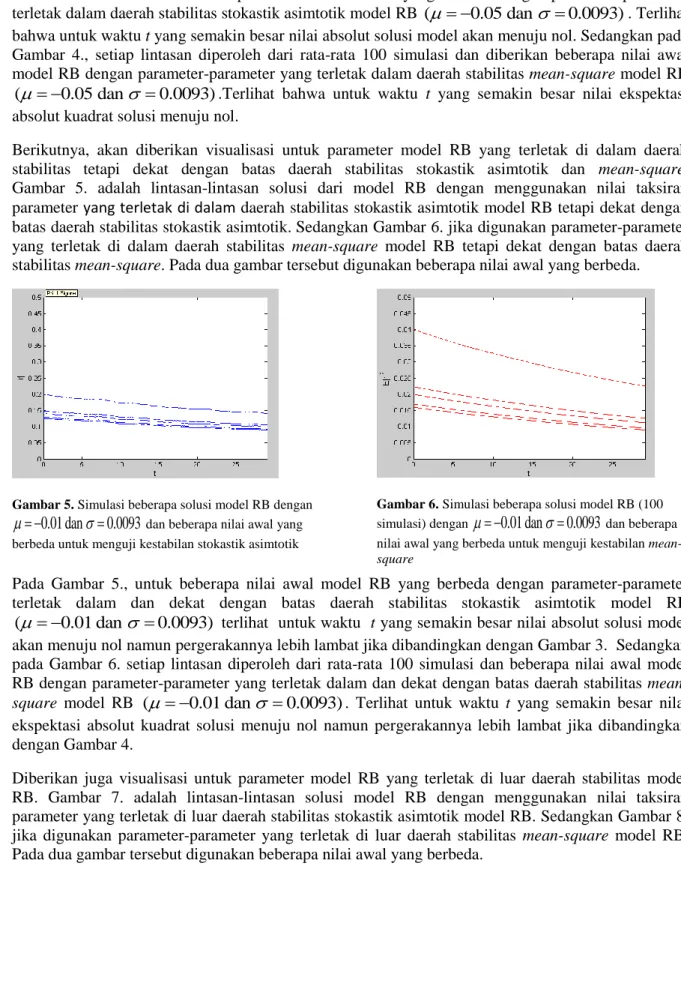
0.0093).Terlihat bahwa untuk waktu t yang semakin besar nilai ekspektasi absolut kuadrat solusi menuju nol.

Berikutnya, akan diberikan visualisasi untuk parameter model RB yang terletak di dalam daerah stabilitas tetapi dekat dengan batas daerah stabilitas stokastik asimtotik dan mean-square. Gambar 5. adalah lintasan-lintasan solusi dari model RB dengan menggunakan nilai taksiran parameter yang terletak di dalam daerah stabilitas stokastik asimtotik model RB tetapi dekat dengan batas daerah stabilitas stokastik asimtotik. Sedangkan Gambar 6. jika digunakan parameter-parameter yang terletak di dalam daerah stabilitas mean-square model RB tetapi dekat dengan batas daerah stabilitas mean-square. Pada dua gambar tersebut digunakan beberapa nilai awal yang berbeda.

0.01 dan 0.0093



 



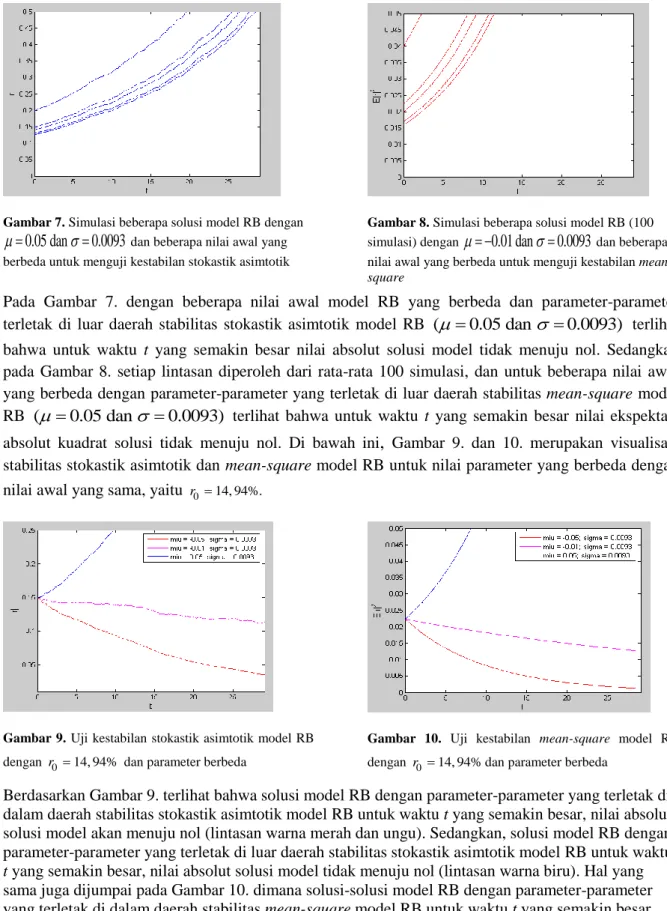
 dan beberapa nilai awal yang berbeda untuk menguji kestabilan stokastik asimtotik



 0.01 dan



mean-square

Pada Gambar 5., untuk beberapa nilai awal model RB yang berbeda dengan parameter-parameter terletak dalam dan dekat dengan batas daerah stabilitas stokastik asimtotik model RB

(



 0.01 dan



0.0093) terlihat untuk waktu t yang semakin besar nilai absolut solusi model akan menuju nol namun pergerakannya lebih lambat jika dibandingkan dengan Gambar 3. Sedangkan pada Gambar 6. setiap lintasan diperoleh dari rata-rata 100 simulasi dan beberapa nilai awal model RB dengan parameter-parameter yang terletak dalam dan dekat dengan batas daerah stabilitas

mean-square model RB (



 0.01 dan



0.0093). Terlihat untuk waktu t yang semakin besar nilai ekspektasi absolut kuadrat solusi menuju nol namun pergerakannya lebih lambat jika dibandingkan dengan Gambar 4.

Diberikan juga visualisasi untuk parameter model RB yang terletak di luar daerah stabilitas model RB. Gambar 7. adalah lintasan-lintasan solusi model RB dengan menggunakan nilai taksiran parameter yang terletak di luar daerah stabilitas stokastik asimtotik model RB. Sedangkan Gambar 8. jika digunakan parameter-parameter yang terletak di luar daerah stabilitas mean-square model RB. Pada dua gambar tersebut digunakan beberapa nilai awal yang berbeda.

(8)

0.05 dan 0.0093







 dan beberapa nilai awal yang berbeda untuk menguji kestabilan stokastik asimtotik



 0.01 dan



mean-square

Pada Gambar 7. dengan beberapa nilai awal model RB yang berbeda dan parameter-parameter terletak di luar daerah stabilitas stokastik asimtotik model RB (



0.05 dan



0.0093) terlihat bahwa untuk waktu t yang semakin besar nilai absolut solusi model tidak menuju nol. Sedangkan pada Gambar 8. setiap lintasan diperoleh dari rata-rata 100 simulasi, dan untuk beberapa nilai awal yang berbeda dengan parameter-parameter yang terletak di luar daerah stabilitas mean-square model RB (



0.05 dan



0.0093) terlihat bahwa untuk waktu t yang semakin besar nilai ekspektasi absolut kuadrat solusi tidak menuju nol. Di bawah ini

,

Gambar 9. dan 10. merupakan visualisasi stabilitas stokastik asimtotik dan mean-square model RB untuk nilai parameter yang berbeda dengan nilai awal yang sama, yaitu r₀ 14, 94%.

Gambar 9. Uji kestabilan stokastik asimtotik model RB

dengan r₀ 14, 94% dan parameter berbeda

Gambar 10. Uji kestabilan mean-square model RB

dengan r₀ 14, 94%dan parameter berbeda

Berdasarkan Gambar 9. terlihat bahwa solusi model RB dengan parameter-parameter yang terletak di dalam daerah stabilitas stokastik asimtotik model RB untuk waktu t yang semakin besar, nilai absolut solusi model akan menuju nol (lintasan warna merah dan ungu). Sedangkan, solusi model RB dengan parameter-parameter yang terletak di luar daerah stabilitas stokastik asimtotik model RB untuk waktu

t yang semakin besar, nilai absolut solusi model tidak menuju nol (lintasan warna biru). Hal yang

sama juga dijumpai pada Gambar 10. dimana solusi-solusi model RB dengan parameter-parameter yang terletak di dalam daerah stabilitas mean-square model RB untuk waktu t yang semakin besar nilai ekspektasi absolut solusi kuadratnya akan menuju nol (lintasan warna merah dan ungu).

Sedangkan, solusi model RB dengan parameter-parameter yang terletak di luar daerah stabilitas

(9)

6. Kesimpulan

Model Rendleman-Bartter (RB) memenuhi stabilitas stokastik asimtotik dan stabilitas mean-square dan dapat ditunjukkan melalui daerah stabilitas parameter model. Pada penaksiran parameter dilakukan perubahan measure menggunakan teorema Girsanov. Parameter model RB dapat diestimasi menggunakan metode Maximum Likelihood Estimation dan metode numerik Newton-Raphson. Berdasarkan data tingkat bunga bulanan yang digunakan dapat diperoleh nilai taksiran parameter yang memenuhi stabilitas model RB.

Daftar Pustaka

[1] Allen, E. (2007). Modeling with Ito Stochastic Differential Equations. Netherland: Springer. [2] Anggono, S. (2004). Kajian Stabilitas pada Masalah dan Metode Numerik untuk Persamaan

Diferensial Stokastik. Depok: Department of Mathematics, University of Indonesia.

[3] Arnold, L. (1974). Stochastic Differential Equations. New York: John Wiley & Sons.

[4] Brigo, D. & Mercurio, F. (2006). Interest Rate Model - Theory and Practice: With Smile,

Inflation, and Credit. New York: Springer.

[5] Dokuchaev, N. (2007). Mathematical Finance Core Theory, Problems, and Statistical

Algorithms. New York: Routledge.

[6] Handhika, T. & Murni. (2010). Kajian Stabilitas Model Tingkat Bunga Rendleman-Bartter.

Science National Seminar Proceeding, Vol. 3, Mathematical Science, No. 1, pp. 382-390.

[7] Higham, D. J. (2001). An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Review, Vol. 43, No. 3, pp. 525-546.

[8] Hull, J.C. (2003). Options, Futures, and Other Derivatives, Prentice Hall, London.

[9] Murni, (2011), Analisis Stabilitas dan Penaksiran Parameter Model Rendleman-Bartter, Depok: Departemen Matematika, Universitas Indonesia.

[10] Kloeden, P. E. & Platen, E. (1992). Numerical Solution of Stochastic Differential Equations. Heidelberg: Springer-Verlag.

[11] Shreve, S. E. (2004). Stochastic Calculus for Finance II Continuous-Time Models. New York: Springer.

[12] Yolcu, Y. (2005). One-Factor Interest Rate Models: Analytic Solutions and Approximations. Turkey: Department of Financial Mathematics, Middle East Technical University.