BAB I
PENDAHULUAN
Model kronig-penney adalah suatu metode aproksimasi untuk meneyederhanakan dan mengidealisasikan sistem mekanika kuantum yang terdiri atas barisan periodis dari energi potensial yang berbentuk segiempat.
Model atom ini juga membahas mengenai elektron dalm kristal zat padat. Di dalam kristal zat padat, atom-atom tersusun secara teratur. Analisis fisika tentang zat padat secara mutlak memerlukan pertimbangan tentang unsur internalnya, yaitu kesetangkupan dan keberkalaan (periodik). Kedudukan atau gugus-gugus atomnya dalam ruang. Oleh karena itu, pengetahuan tentang struktur kristal sangat penting dalam telaah fisika zat padat. Terutama dalam memahami model Kronig-Penney diatas.
Namun untuk analisis secara matematis, model Kronig-Penney dapat diananlisis menggunakan teorema Bloch. Menurut teorema Bloch, maka cukup dicari penyelesaian dari salah satu perioda untuk mengeneralisasi peneyelesaian dari perioda yang lain. Inilah dasar dari penjabaran matematis pada metode Kronig-Penney.
BAB II ISI
Model Kronig-Penney
A. Biografi
Ralph Kronig adalah seorang fisikawan Jerman -Amerika (10 Maret 1904 - 16 November 1995). Ia terkenal karena penemuan partikel berputar dan teori x-ray spektroskopi penyerapan . Teorinya termasuk Kronig-Penney Model , para transisi Coster-Kronig dan hubungan Kramers-Kronig.
Ralph Kronig (1931, 1932), yang diterbitkan teori pertama x-ray struktur penyerapan halus yang berisi beberapa konsep dasar interpretasi modern. The Model Kronig-Penney (1931) adalah model satu-dimensi dari kristal yang menunjukkan bagaimana elektron dalam kristal tersebar ke band diperbolehkan dan dilarang oleh hamburan dari array linier diperpanjang atom. Teori pertama (1931) dari EXAFS adalah setara dengan tiga-dimensi dari model ini. Teori ini menunjukkan bahwa elektron foto melintasi kisi kristal akan mengalami diijinkan dan dilarang zona tergantung pada panjang gelombang dan, bahwa bahkan ketika efek itu rata-rata atas semua arah dalam kisi, struktur sisa harus diamati. Teorinya berhasil dalam memprediksi fitur umumnya diamati banyak struktur halus, termasuk struktur serupa dari kisi yang sama, ketergantungan r2 terbalik, yang benar r vs T ketergantungan dan meningkatkan pemisahan energi fitur struktur halus dengan energi dari tepi. Persamaan yang kembali diturunkan dengan cara yang lebih kuantitatif pada tahun 1932 adalah sederhana untuk menerapkan dan menafsirkan. Setiap eksperimen menemukan kesepakatan perkiraan dengan teori. Selalu ada penyerapan beberapa fitur dekat dengan yang diprediksi oleh pesawat kisi mungkin. Namun, refleksi yang kuat yang diharapkan (misalnya (100), (110), (111), dll) tidak selalu berkorelasi dengan fitur penyerapan yang paling intens sebagai intuitif diharapkan. Namun, kesepakatan itu cukup dekat untuk menjadi menggoda dan semua orang menguji kesepakatan diukur "Struktur Kronig" mereka dengan teori Kronig sederhana. Dalam persamaan Kronig, energi posisi Wn sesuai dengan batas-batas zona, yaitu tidak penyerapan maksimum atau minimum, tetapi kenaikan pertama dalam setiap maksimum struktur halus. abg adalah indeks Miller, adalah kisi-kisi konstan dan q adalah
sudut antara arah elektron dan arah kisi resiprokal. Ketika rata-rata atas semua arah dengan non-terpolarisasi x-ray balok dan penyerap polikristalin, cos2q = 1. Namun, dengan penyerap kristal tunggal dan terpolarisasi x-ray fitur penyerapan harus lebih besar untuk bidang kristal tertentu. Ini adalah variabel lain eksperimental yang mungkin memverifikasi teori dan banyak berusaha untuk menguji itu. Jadi mulai catatan panjang publikasi di mana Kronig struktur ditafsirkan dari segi teori Kronig sederhana. Sampai tahun 1970-an penuh 2% dari makalah yang diterbitkan di Phys. Wahyu yang dikhususkan untuk x-ray spektroskopi penyerapan dan teori Kronig paling dipanggil itu.
Data waktu singkat berbagai HANAWALT (1931b) dirangsang Kronig (1932) untuk mengembangkan teori untuk molekul. Model ini menjabat sebagai titik awal untuk semua teori selanjutnya agar jarak pendek tetapi hanya sedikit berusaha untuk membandingkannya dengan data mereka. Mahasiswa Kronig itu, H. Petersen (1932, 1933) melanjutkan pekerjaan ini. Persamaan Peterson menunjukkan banyak fitur dari teori modern. Teori ini diterapkan untuk GeCl4 oleh Hartree, Kronig dan Petersen (1934). Penjelasan mengenai upaya Hercules yang dibutuhkan untuk melakukan perhitungan dapat ditemukan di Stumm von Bordwehr (1989).
The hubungan Kramers-Kronig untuk dispersi diperoleh oleh Kronig (1926) secara independen dari Kramers (1927).
William George Penney, Baron Penney OM , KBE PhD, DSC,, FRS , [2] FRSE , FIC , Hon FCGI (24 Juni 1909 - 3 Maret 1991), adalah seorang Inggris ahli matematika dan profesor fisika matematika di Imperial College London sebagai serta rektor dari perguruan tinggi kekaisaran. Dia secara luas bertanggung jawab atas perannya terkemuka dan integral dalam pengembangan program nuklir Inggris , sebuah program rahasia mulai mengikuti Perang Dunia II dan keberhasilan program nuklir Soviet .
B. Definisi Model Kronig-Penney
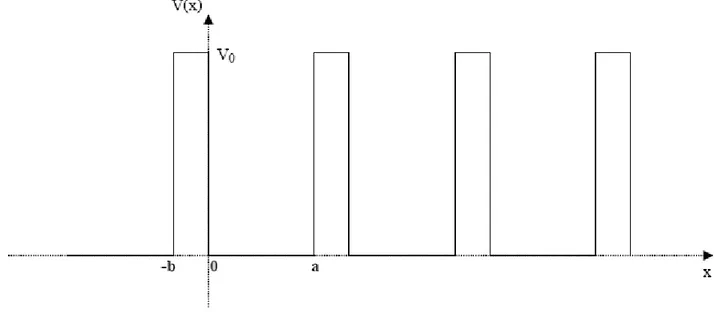
Model Kronig – Penney d alam satu dimensi adalah merupakan suatu deretan sumur potensial persegi dengan lebar a , dipisahkan oleh penghalang energy yang lebarnya b dan tinggi V0 . Luas penghalang bV0,
dan meluruh secara eksponensial. Seperti ditunjukkan dalam Gambar 1.
Gambar 1. Energi potensial periodik satu dimensi yang digunakan oleh Kronig dan Penney. Energi potensial dari sebuah elektron dalam sebuah susunan inti-inti atom yang positif dianggap berbentuk seperti sebuah susunan sumur potensial periodik dengan perioda a + b, seperti ditunjukkan dalam Gambar 1. Di dasar sumur, yaitu untuk 0 < x < a, elektron dianggap berada di sekitar sebuah inti atom (atau di antara dua inti atom) dan energi potensialnya dianggap nol sehingga di daerah ini elektron bertingkah sebagai elektron bebas. Sebaliknya, di luar sumur, yaitu untuk –b < x < 0, energi potensial elektron dianggap sama dengan V0. Meskipun model
Kronig-Penney ini menggunakan pendekatan yang sangat kasar dibandingkan dengan energi potensial yang ada dalam suatu kisi, tetapi model ini sangat berguna untuk menjelaskan berbagai sifat penting dari tingkah laku elektron secara kuantum mekanik dalam sebuah kisi periodik. Fungsi-fungsi gelombang elektron diperoleh dari persamaan Schrodinger untuk kedua daerah yaitu daerah 0 < x < a, dan daerah –b < x < 0) sebagai berikut:
a. untuk 0 < x < a.
𝑑2 𝛹 (𝑥)
𝑑𝑥2 +
2𝑚
b. untuk –b < x < 0.
𝑑2𝛹(𝑥)
𝑑𝑥2 +
2𝑚
ħ2 (𝐸 − 𝑉𝑜)𝛹(𝑥) = 0 [2]
Jika kita misalkan bahwa energi elektron lebih kecil dari pada V0, dan kita difinisikan dua
besaran real 𝛼 dan β sebagai berikut:
𝛼2 = 2𝑚
ħ2 𝐸 𝑑𝑎𝑛 𝛽2 =
2𝑚
ħ2 (𝑉𝑜− 𝐸) [3]
maka persamaan-persamaan (1) dan (2) dapat ditulis menjadi
𝑑2𝛹(𝑥)
𝑑𝑥2 + 𝛼2 𝛹(𝑥) = 0 𝑑𝑎𝑛
𝑑2𝛹(𝑥)
𝑑𝑥2 − 𝛽2𝛹(𝑥) = 0 [4]&[5]
Karena energi potensial dari model Kronig-Penney itu adalah periodik, maka fungsi-fungsi gelombang tersebut haruslah berbentuk fungsi-fungsi Bloch, yaitu:
𝛹(𝑥) = 𝑒±𝑖𝑘𝑥 𝑢
𝑘 (𝑥) [6]
dimana uk(x) sekarang adalah sebuah fungsi periodik dalam x dengan perioda a + b, yaitu
𝑢𝑘(𝑥) = 𝑢𝑘(𝑥 + (𝑎 + 𝑏)) [7]
Sekarang marilah kita hitung turunan kedua terhadap x dari persamaan (6), sebagai berikut: 𝑑2𝛹(𝑥) 𝑑𝑥2 = −𝑘2𝑒𝑖𝑘𝑥𝑢𝑘(𝑥) + 2𝑖𝑘 𝑒𝑖𝑘𝑥 𝑑𝑢𝑘 𝑑𝑥 + 𝑒𝑖𝑘𝑥 𝑑2𝑢 𝑘 𝑑𝑥2 [8]
Selanjutnya coba kita substitusikan persamaan (6) dan (8) ini ke dalam persamaan-persamaan (4) dan (5) di atas. Hasilnya adalah sebagai berikut:
a. untuk 0 < x < a. 𝑑2𝑢 1 𝑑𝑥2 + 2𝑖𝑘 𝑑𝑢𝑖 𝑑𝑥 + (𝛼2− 𝑘2)𝑢1 = 0 [9] b. untuk –b < x < 0. 𝑑2𝑢 2 𝑑𝑥2 + 2𝑖𝑘 𝑑𝑢2 𝑑𝑥 + (𝛽 2+ 𝑘2)𝑢 2 = 0 [10]
yang mana u1dan u2 masing-masing menyatakan nilai uk(x) dalam interval 0 < x < a dan –b < x
<0. Seperti kita ketahui bahwa dari mekanika kuantum atau dari Fisika kuantum, solusi umum untuk persamaan-persamaan (9) dan (10) di atas adalah:
𝑢1 = 𝐴 𝑒𝑖(𝛼−𝑘)𝑥 + 𝐵𝑒−𝑖(𝛼+𝑘)𝑥 [11]
dan 𝑢2 = 𝐶𝑒(𝛽−𝑖𝑘)𝑥+ 𝐷𝑒−(𝛽+𝑖𝑘)𝑥 [12]
yang mana A, B, C, dan D adalah tetapan-tetapan yang biasa ditentukan oleh syarat batas berikut: 𝑢1(0) = 𝑢2(0) ∶ 𝑑𝑢𝑑𝑥1 (𝑢𝑛𝑡𝑢𝑘 𝑥 = 0) = 𝑑𝑢𝑑𝑥2 (𝑢𝑛𝑡𝑢𝑘 𝑥 = 0) [13]
𝑢2 (𝑎) = 𝑢2 (−𝑏) ∶ 𝑑𝑢𝑑𝑥1 (𝑢𝑛𝑡𝑢𝑘 𝑥 = 𝑎) = 𝑑𝑢𝑑𝑥2 (𝑢𝑛𝑡𝑢𝑘 𝑥 = −𝑏) [14]
Syarat batas yang ditunjukkan oleh persamaan (13) sesuai dengan syarat bahwa fungsi gelombang dan turunan pertamanya (d/dx) dan juga u dengan du/dx haruslah kontinyu. Sebaliknya, kondisi yang ditunjukkan oleh persamaan (14) sesuai dengan syarat bahwa uk(x)adalah periodik. Dengan menggunakan syarat-syarat batas ini dan mensubstitusikannya ke dalam persamaan-persamaan (11) dan (12), kita akan memperoleh empat persamaan linier homogen sebagai berikut: 𝐴 + 𝐵 = 𝐶 + 𝐷 [15]
𝐴𝑖 (𝛼 − 𝛽) − 𝐵𝑖(𝛼 + 𝛽) = 𝐶(𝛽 − 𝑖𝑘) − 𝐷(𝛽 + 𝑖𝑘) [16]
𝐴𝑒𝑖(𝛼−𝑘) + 𝐵𝑒−𝑖(𝛼+𝑘) = 𝐶𝑒−(𝛽−𝑖𝑘) + 𝐷𝑒(𝛽+𝑖𝑘) [17]
𝐴𝑖(𝛼 − 𝑘)𝑒𝑖(𝛼−𝑘) − 𝐵𝑖(𝛼 + 𝑘)𝑒−𝑖(𝛼+𝑘) = 𝐶(𝛽 − 𝑖𝑘)𝑒−(𝛽−𝑖𝑘) − 𝐷(𝛽 + 𝑖𝑘)𝑒(𝛽+𝑖𝑘) [18]
Keempat persamaan linier yang homogen ini biasa digunakan untuk menentukan tetapan-tetapan A, B, C, dan D. Solusi yang tidak sama dengan nol untuk keempat persamaan linier tersebut ada jika dan hanya jika determinan dari koefisien-koefisien A, B, C, dan D adalah
sama dengan nol,yaitu:
𝛼2+𝛽2
2𝛼𝛽 sinh(𝛽𝑏) sin(𝛼𝑎) + cos ℎ(𝛽𝑏) cos(𝛼𝑎) − cos 𝑘(𝑎 + 𝑏) = 0 [19]
Untuk menyederhanakan persamaan (19) ini, Kronig dan Penney memilih kasus yang mana nilai V0 cenderung menuju tak hingga dan nilai b menuju nol, tetapi hasil kali V0b tetap
terhingga. Dengan demikian, potensial model Kronig dan Penney menjadi potensial penghalang sebuah fungsi delta. Dalam keadaan seperti ini model Kronig-Penney ini dimodifikasi menjadi sebuah deret sumur potensial yang terpisahkan oleh sebuah potensial penghalang yang sangat-sangat tipis. Karena itu, hasil kali V0b (untuk V0 → ω dan b→ 0) disebut kekuatan penghalang
(barrier strength).
Pada saat b → 0, sinh (βb) → βb, dan cosh (βb)→1. Di samping itu, dari persamaan (3) jika kita menjumlahkan 𝛼2 dan 𝛽2 kemudian membaginya dengan 2𝛼𝛽 maka kita akan
memperoleh hasil sebagai berikut:
𝛼2+ 𝛽2
2𝛼𝛽 = 𝑚𝑉0
𝛼𝛽ħ2 [20]
Dengan menggunakan persamaan (20) ini dan kondisi dimana saat b → 0, sinh (βb) →βb, dan cosh (b) →1, kita akan dapat menulis persamaan (19) menjadi
(𝑚𝑉0
𝛼𝛽ħ2) (𝛽𝑏) sin(𝛼𝑎) + cos(𝛼𝑎) = cos(𝑘𝑎)
(𝑚𝑉0
𝛼𝛽ħ2) sin(𝛼𝑎) + cos(𝛼𝑎) = cos(𝑘𝑎) [21]
Jika kita definisikan besaran P sebagai berikut:
𝑃 = (𝑚𝑉0𝑏𝑎 ħ2 ) , 𝑚𝑎𝑘𝑎 𝑚𝑒𝑛𝑗𝑎𝑑𝑖 𝑃 𝛼𝑎= ( 𝑚𝑉0𝑏 𝛼ħ2 ) [22]
Nilai P ini adalah sama dengan luas energi potensial penghalang V0b. Jadi jika kita meperbesar
coba kita substitusikan persamaan (22) ini ke dalam persamaan (21) di atas. Hasilnya adalah sebagai berikut:
(𝑃
𝛼𝑎) sin(𝛼𝑎) + cos(𝛼𝑎) = cos(𝑘𝑎) [23]
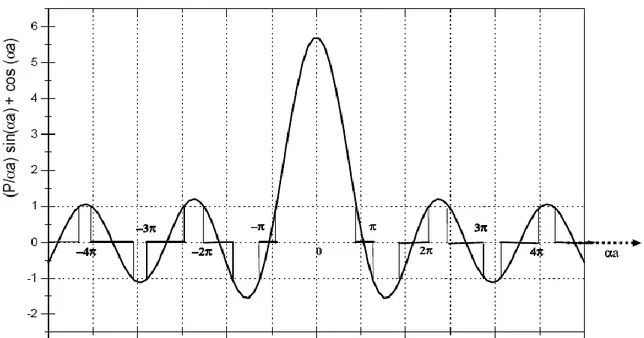
Persamaan (23) ini merupakan syarat agar solusi untuk persamaan gelombang itu ada. Kita ketahui bahwa nilai cos (ka) terletak diantara –1 dan +1 sehingga ruas kiri dari persamaan (23) itu harus memiliki nilai a sedemikian rupa sehingga nilai-nilai ruas kiri persamaan (23) terletak dalam rentang –1 dan +1. Nilai-nilai a yang menghasilkan nilai (P/a) sin (a) + cos (a) berada dalam rentang antara –1 dan +1 ditunjukkan dalam Gambar 2.
Gambar 2. Grafik (P/a) sin (a) + cos (a) sebagai fungsi a untuk P = 3/2. Nilai-nilai a yang menghasilkan nilai (P/a) sin (a) + cos (a) berada dalam rentang –1 dan +1ditunjukkan
oleh potongan (segmen) garis-garis tebal dalam sumbu a.
Karena 2 sebanding dengan energi, maka sumbu horizontal juga secara tidak langsung
menyatakan sumbu energi. Jadi panjang potongan-potangan garis tebal itu menyatakan rentang energi yang diizinkan untuk elektron. Dari Gambar 2 kita dapat melihat bahwa ternyata dengan menggunakan model Kronig-Penney itu sumbu energi (sumbu a) dibagi menjadi daerah-daerah
yang diizinkan dan daerah terlarang bagi elektron. Daerah yang diizinkan untuk elektron adalah sepanjang garis tebal, sedangkan daerah terlarang adalah daerah di antara ujung dua garis tebal yang berdekatan. Panjang segmen garis tebal (yang berarti sebanding dengan rentang energi) itu sebanding dengan nilai a. Artinya, makin besar nilai a makin panjang rentang energi yang diizinkan. Jadi, dengan mengacu pada Gambar 2 di atas kita dapat menarik 3 kesimpulan berikut: 1. Spektrum energi elektron terdiri atas pita-pita energi yang diizinkan dan pita-pita energi
yang terlarang.
2. Lebar pita energi yang diizinkan sebanding dengan nilai a, artinya makin besar nilai a makin besar pula lebar pita energi.
3. Lebar suatu pita energi yang diizinkan berbanding terbalik dengan nilai P, yaitu dengan energi ikat elektron. Makin besar P makin kecil lebar pita energi yang diizinkan.
Jika P →, pita-pita energi yang diizinkan dipersempit sedemikian rupa sehingga menjadi berbentuk garis-garis dan membentuk sebuah spektrum garis. Dalam kasus seperti itu, persamaan (23) akan memiliki solusi hanya jika sin (a) = 0 (sebab jika sin (a) tidak sama dengan nol, persamaan (23) menjadi tak hingga, karena P→). Jadi agar persamaan (23) memiliki solusi maka
sin(𝛼𝑎) = 0
𝛼𝑎 = ± 𝑛𝜋 [24]
dimana n = bilangan bulat. Karena itu, dengan menggunakan persamaan (3) dan (24) energi dapat ditulis sebagai berikut:
𝐸 = 𝛼2ħ2 2𝑚 =
𝜋2ħ2𝑛2
2𝑚𝑎2 [25]
Persamaan (25) ini menyatakan tingkat energi sebuah partikel dalam sebuah energi potensial yang tetap. Sebaliknya, jika P→0, persamaan (23) menjadi:
sehingga dengan menggunakan persamaan (3) dan (26) di atas, energi partikel menjadi:
𝐸 = ħ
2𝑘2
2𝑚 [27]
Persamaan (27) ini menyatakan energi dari elektron bebas. Hal ini memang sesuai dengan harapan kita bahwa jika P → 0, memang elektron menjadi bebas.