BAB 2 LANDASAN TEORI

LANDASAN TEORI

Pada bab ini akan diperlihatkan teori-teori yang berhubungan dengan penelitian ini sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian ini dan akan mempermudah dalam hal pembahasan hasil utama pada bab berikutnya. Teori tersebut mencakup pengertian dari pengenalan pola secara statistika (statistical pattern recognition), contoh statistical pattern recognition, matriks kovarians, contoh matriks kovarians, nilai eigen dan vektor eigen,contoh nilai eigen dan vektor eigen, analisis diskriminan linier, analisis diskriminan linier 2-dimensi dan analisis diskriminan linier 2-dimensi simetris.

2.1 Pengenalan Pola Secara Statistika (Statistical Pattern Recognition)

Pengenalan pola atau dikenal dengan sebutan pattern recognition merupakan salah satu cabang ilmu sains. Pengenalan pola pada dasarnya adalah suatu sistem yang tujuannya adalah mengklasifikasikan objek-objek ke dalam kategori-kategori atau kelas-kelas berdasarkan baik pada apriori pengetahuan atau pada informasi statistik yang diambil dari pola (Theodoridis, 2003).

Fukunaga (1990) menyajikan cara-cara dasar perhitungan matematika untuk proses pembuatan keputusan secara statistik dalam pengenalan pola. Tujuan utama

pattern recognition adalah mengklarifikasikan mekanisasi sulit yang sering

ditemukan dalam dunia sehari-hari seperti langkah dalam permainan catur didasarkan pada pola yang ada di papan catur, pembelian atau persediaan penjualan diputuskan melalui suatu pola informasi yang kompleks. Sebagian besar aplikasi-aplikasi penting

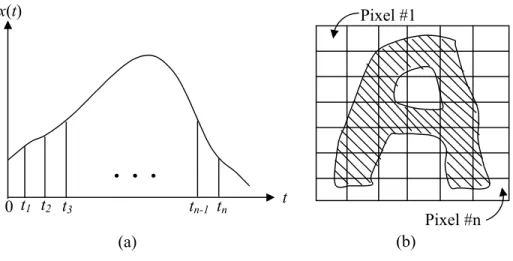
dalam pattern recognition dikarakterkan ke dalam satu bentuk kurva atau pola gambar geometri. Sebagai contoh, pengetesan suatu mesin layak atau tidak menampilkan pola berbentuk kurva. Masalah ini mereduksi untuk pemisahan kurva dari mesin yang bagus dan yang tidak bagus. Pada contoh lain, pengenalan pola huruf hasil cetak tulisan tangan diklasifikasikan dalam bentuk gambar geometri. Dalam proses untuk pengklasifikasiannya, pertama kita ukur karakteristik-karakteristik pengamatan dari sampel. Kemudian, ekstrasi seluruh informasi yang terdapat dalam sampel untuk menghitung nilai sampel-waktu untuk suatu pola berbentuk kurva, x t( ),..., ( )₁ x t_n , dan tingkat kehitaman piksel untuk suatu figur,

(1),..., ( )

x x n seperti yang ditunjukkan dalam gambar 2.1.

Gambar 2.1: Contoh dua pengukuran pola (a) gelombang (b) huruf

Karena input dari pengenalan pola merupakan suatu vektor acak dengan n peubah, maka, baik untuk pola berbentuk gelombang ataupun huruf, keduanya diekspresikan ke dalam bentuk vektor dalam suatu ruang dimensi-n. Sebagai contoh, pengamatan

x(i) bervariasi dari huruf A yang satu ke huruf A yang lainnya dan oleh karena itu, x(i) merupakan suatu variabel acak, dan X merupakan vektor acak.

2.1.1 Vektor Acak dan Distribusinya

Seperti yang telah didiskusikan pada bagian 2.1, input dari jaringan pengenalan pola merupakan suatu vektor acak dengan n peubah sebagai berikut



1 2



X= x x ...x_n T (2.1) 0 t1 t2 t3 x(t) t tn-1 tn (a)

. . .

Pixel #1 Pixel #n (b)

dimana T adalah transpos dari vektor.

Suatu vektor acak dapat dikarakterisasikan oleh suatu fungsi distribusi peluang, yang didefinisikan oleh





1 1 1 ( , . . ., ) Pr x_n , . . ., x_{n n} P x x  x x (2.2) (Fukunaga, 1990)

Selain itu, suatu vektor acak mempunyai suatu paramater distribusi. Parameter distribusi yang akan dibahas dalam penelitian ini adalah matriks kovarians.

2.1.2 Matriks Kovarians

Matriks kovarians S adalah matriks kovarians sampel yang didefinisikan sebagai berikut:

S = E[ Xi– Mi ] [ Xi– Mi]T (Fukunaga, 1990) (2.3)

Xi adalah data pada masing-masing kelas, Mi adalah rata-rata kelas ke-i. Matriks

kovarians S berisi nilai varians pada diagonal utama sebanyak p variabel dan nilai kovarians pada elemen lainnya sebanyak p – 1 kovarians. Suatu matriks  dikatakan matriks kovarians populasi jika matriks tersebut adalah matriks simetris yang diagonalnya harus berisi elemen-elemen nonnegatif sehingga matriks tersebut merupakan matriks definit nonnegatif.

Jika Ai = [ ai1, ai2, . . ., ain]Tmempunyai rata-rata kelas

1 1 n i i i i M a n  



, maka untuk melihat betapa dekatnya korelasi antar kelas, harus diatur agar masing-masing nilai mempunyai jumlah selisih rata-rata sama dengan 0, yaitu dengan cara mengurangi setiap ai dengan rata-rata kelasnya. Kemudian menempatkan nilai-nilai tersebut ke dalam sebuah matriks seperti berikut:

11 1 1 1 1        _{ }  _{ }        n n n nn n a M a M X a M a M

11 1 1 11 1 1 1 1 1 1 1 1 T n n n n n nn n n nn n a M a M a M a M S n a M a M a M a M              _{   }  _{  }  _{   } _         (2.4)

Komponen diagonal dari matriks kovarians adalah varians dari masing-masing kelas peubah acak. Untuk lebih jelasnya tentang matriks kovarians, perhatikan contoh 2.1.2 berikut.

Contoh 2.1.2

Diketahui suatu data nilai 7 mahasiswa meliputi nilai tugas rumah, ujian dan ujian akhir sebagai berikut.

Mahasiswa Nilai Tugas Rumah Ujian Ujian Akhir

MH 1 198 200 196 MH 2 160 165 165 MH 3 158 158 133 MH 4 150 165 91 MH 5 175 182 151 MH 6 134 135 101 MH 7 152 136 80 Rata-rata 161 163 131

Dari data pada contoh 2.1.2 akan diperlihatkan bagaimana kinerja mahasiswa dengan membandingkan antara kelompok ujian atau nilai tugas. Agar terlihat betapa dekatnya dua kelompok nilai saling berkorelasi, harus diatur agar masing-masing nilai tersebut mempunyai rata-rata sama dengan 0, yaitu dengan cara mengurangi setiap nilai dalam kolom dengan rata-rata nilai pada kolom yang sama sehingga nilai yang telah ditranslasikan ini akan mempunyai jumlah selisih atau deviasi terhadap rata-rata sama dengan 0. Kemudian, tempatkan nilai-nilai yang telah ditranslasikan tersebut ke dalam matriks

37 37 65 -1 2 34 -3 -5 2 -11 2 -40 14 19 20 -27 -28 -30 -9 -27 -51                      

Jika terdapat lebih dari dua kelompok data, maka dapat dibentuk sebuah matriks X dimana kolom-kolomnya memperlihatkan simpangan dari rata-rata untuk setiap kelompok dan kemudian membentuk sebuah matriks kovariansi S dengan menetapkan 1 -1 S n  _{X X}T

Matriks kovariansi untuk ketiga kelompok data nilai matematika adalah 37 37 65 1 2 34 37 1 3 11 14 27 9 3 5 2 1 37 2 5 2 19 28 27 11 2 40 6 65 34 2 10 20 30 51 14 19 20 27 28 30 9 27 51 S    _                    _    _  _  _{    }  _{ }       _{  }    417,7 4375,5 725, 7 437,5 546,0 830,0 725, 7 830,0 1814,3      _{ }    

Entri-entri diagonal matriks S adalah variansi untuk ketiga kelompok nilai dan entri-entri di luar diagonal adalah kovariansi-kovariansi.

2.1.3 Nilai Eigen dan Vektor Eigen

Definisi. Anggap A adalah suatu matriks n × n. Skalar  disebut sebagai suatu nilai eigen atau nilai karakteristik dari A jika terdapat suatu vektor tak nol x, sehingga Ax =

x. Vektor x disebut vektor eigen dari A yang berasosiasi dengan  (Horn and Johnson, 1985).

Untuk mengetahui lebih jelas mengenai nilai eigen dan vektor eigen, perhatikan contoh 2.1.3 berikut. Contoh 2.1.3 Misalkan 3 2 dan -1 3 -2 3 A_ _  _{ }   x  . Karena 3 2 -1 3 -3 -1 -3 3 -2 3 -9 3 A _     _{    }   _{ }         x x,

dari penyelesaian contoh soal di atas terlihat bahwa  =-3 adalah nilai eigen dari A

dan x = -1 3    

  merupakan vektor eigen yang berasosiasi dengan  = -3. Hasil Kali dan Jumlah Nilai Eigen

Jika p() adalah polinom karakteristik dari matriks A yang berorde n × n, maka

11 12 1 21 12 2 1 2 ( ) det( ) n n n n nn a a a a a a p A I a a a              (2.5)

Dengan menguraikan determinan sepanjang kolom pertama, diperoleh 1

11 11 1 1

1

det( - ) ( - ) det( ) n (-1) det(i )

i i

i

A I a  M a  M



 



di mana minor-minor Mi1, i = 2, . . ., n tidak mengandung kedua elemen diagonal (a_ii). Dengan menguraikan det(M11) dengan cara yang sama, dapat disimpulkan bahwa

(a11)(a22)...(ann) (2.6) adalah satu-satunya suku dalam ekspansi det(AI)yang menyebabkan suatu hasil kali lebih dari n –2 elemen diagonal. Jika persamaan (2.7) diuraikan, maka koefisien dari n akan menjadi (-1)n. Jadi, koefisien utama dari p() adalah (-1)n dan dengan demikian jika 1, . . .,n adalah nilai-nilai eigen dari A, maka

1 2

( ) ( 1) (n )( )...( ) n

p           (2.7)

untuk menghitung nilai eigen dan vektor eigen, nilai ( )p  harus sama dengan 0, sehingga diperoleh

1 2

( ) ( )( )...( _n )

p         

Dari persamaan (2.5) dan (2.7) maka diperoleh

1. 2 n p(0) det( )A

  _  

Dari persamaan (2.6), juga diperoleh 1 n ii i a 



sebagai koefisien dari (-)n – 1. Jika dengan persamaan (2.7) 1 n i i  



. Dengan demikian, maka 1 n i i  



= 1 n ii i a 



Jumlah elemen diagonal dari (A) dinamakan trace dari A, dan dilambangkan dengan tr(A), catatan bahwa tr(A + B) = tr(A) + tr(B) (Horn and Johnson, 1985).

Contoh 2.1.3.1 Jika 3 2

3 2

A_{ } _

  maka det(A) = (-6) – 6 = -12 dan tr(A) = -3 + 2 = -1 Polinom karakteristik dari A diberikan oleh persamaan

2 3 2 12 3 2          

dan sebagai akibatnya nilai-nilai eigen dari A adalah -4 dan 3. Dapat ditinjau bahwa 1+ 2 = -1 = tr(A) dan 1 . 2 = -12 = det(A).

Dalam penelitian ini digunakan nilai eigen dan vektor eigen. Fungsi nilai eigen pada penelitian ini yakni karena trace = jumlah nilai eigen = jumlah elemen diagonal akan digunakan untuk menentukan nilai fungsi objektif yang berupa skalar bukan dalam bentuk matriks. Vektor eigen digunakan untuk mengetahui kombinasi linier matriks L dan R yang merupakan matriks transformasi kiri dan kanan oleh ADL2-D. Matriks L dan R selanjutnya akan digunakan untuk menentukan matriks sebaran dalam kelas jika L atau R tetap dan matiks sebaran antar kelas jika L atau R

tetap R, , , L R L

w w b b

S S S S . Matriks L dan R tersebut kemudian akan digunakan untuk menghitung transformasi bilinier sehingga diperoleh perbedaan antar kelas dan hasil klasifikasi yang baik.

2.2 Analisis Diskriminan Linier (ADL)

Analisis diskriminan adalah teknik statistik multivariat yang terkait dengan pemisahan (separating) atau alokasi/klasifikasi (classification) sekelompok objek atau observasi ke dalam kelompok (group) yang telah terlebih dahulu didefinisikan. Dalam tujuan pengenalan objek (observasi), metode ini mencoba menemukan suatu

‘discriminant’ yang nilainya secara numeris sedemikian sehingga mampu

memisahkan objek yang karakteristiknya telah diketahui. Sedangkan dalam tujuan klasifikasi objek, metode ini akan mensortir objek (observasi) ke dalam 2 atau lebih kelas (Fukunaga, 1990).

Jika diberikan suatu matriks data _{A R} N n _{, metode ADL klasik bertujuan} menemukan suatu transformasi _{G R} N l _{yang memetakan setiap kolom ai dari} matriks A, untuk 1≤ i ≤ n, dalam ruang dimensi N ke vektor bi dalam ruang dimensi l.

Yakni G : N n T l( )

i i i

a _R  _{b }G a _R l N_{ . Dengan kata lain, ADL bertujuan}

menemukan suatu ruang vektor  direntangkan oleh { }gi il1 di mana G= [g1, g2,

…,gl], sehingga setiap ai diproyeksikan ke  oleh ( . ,...,₁T T. )T l i l i

g a g a R (Ye et. al, 2004).

Asumsikan bahwa data asli dalam A dipartisi ke dalam k kelas sehingga A =

{∏1, ∏2,…, ∏k}, dimana ∏i memuat ni titik data dari kelas ke –i, dan



k_i1n_i n.

ADL klasik bertujuan untuk menemukan transformasi optimal G sehingga struktur kelas dari data ruang berdimensi tinggi yang asli diubah ke dalam ruang berdimensi rendah (Ye et. al, 2004).

Dalam ADL, transformasi ke subruang yang berdimensi lebih rendah yaitu T

i i

y G x (Luo et al, 2007) (2.8) di mana G merupakan transformasi ke subruang. Sering juga dituliskan dengan (y1, ..., yn) = GT(x1, ..., xn) atau Y = GT X. Tujuan utama dari ADL adalah mencari nilai G

sehingga kelas dapat lebih terpisah dalam ruang transformasi dan dengan mudah dapat dibedakan dari yang lainnya.

Dalam metode Analisis Diskriminan Linier, terdapat dua matriks sebaran yaitu matriks sebaran dalam-kelas disimbolkan dengan S_w, dan matriks sebaran antar-kelas disimbolkan dengan S_b, masing-masing didefinisikan sebagai berikut:

1 [ ][ ] k i c T w k i k i i x S x m x m   

 

  (2.9) 1 [ ][ ] c T b i i i i S n m m m m  



  (2.10)

di mana ni adalah jumlah sampel pada kelas

x

i, dan mi adalah image rata-rata dari kelas ke-i dan m adalah rata-rata keseluruhan. Rumus rata-rata kelas dan rata-rata keseluruhan adalah sebagai berikut:

1 i i _x i m x n 





adalah mean (rata-rata) dari kelas ke-i, dan 1 ₁

i k i x m x n   

 

adalah rata-rata keseluruhan (Fukunaga, 1990).

Seperti diutarakan sebelumnya, metode Analisis Diskriminan Linier diharapkan dapat meminimumkan jarak dalam matriks sebaran dalam-kelas ( )S_w sementara jarak matriks sebaran antar-kelas ( )S_b dapat dimaksimumkan sehingga dapat terlihat perbedaan atau pemisahan antar kelas. Dalam hasil ruang dimensi yang lebih rendah dari transformasi linier G (atau proyeksi linier ke dalam ruang vektor ), Sb dan

w S menjadi ( ) T ( ) , b b S Y G S X G (2.11) ( ) T ( ) . w w S Y G S X G (2.12)

Transformasi optimal G akan memaksimumkan trace( L b

S ) dan meminimumkan trace( L

w

S ).

Optimisasi umum dalam Analisis Diskriminan Linier meliputi (lihat Fukunaga, 1990) :

1 1

max{ (( ) )} dan min{ (( ) )}

b w

L L L L

w _G b

G trace S S trace S S

  _(2.13) Hal ini dituliskan dalam fungsi objektif optimum:

( ) ( ) max ( ) tr tr ( ) ( ) T b b T G w w S Y G S X G J G S Y G S X G   (2.14)

Catatan bahwa trace(A/B) = trace(B-1A) = trace (AB-1)

Masalah optimisasi dari persamaan (2.14) di atas ekivalen dengan masalah generalisasi nilai eigen berikut: S x_b S x_w , untuk   0. Penyelesaiannya dapat diperoleh dengan menerapkan eigen-dekomposisi ke matriks 1

w b S S x jika S_w nonsingular, atau 1 b w S S x _jika b

S nonsingular. Terdapat paling banyak k – 1 vektor-vektor eigen yang cocok ke nilai eigen tak nol, karena kedudukan dari matriks S_b

dibatasi oleh k – 1. Oleh karena itu, dimensi yang direduksi oleh ADL klasik terletak pada k – 1.

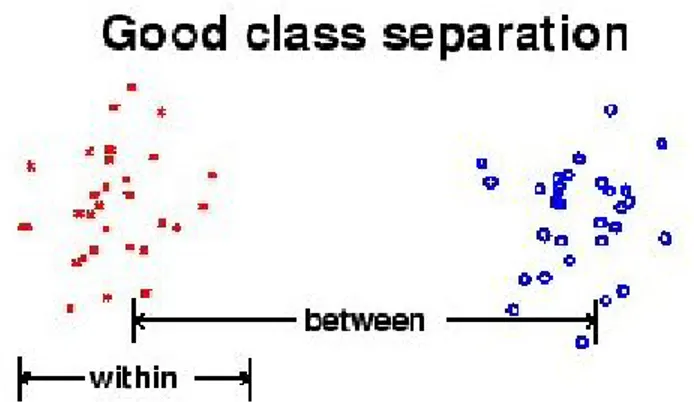
Gambar berikut ini menunjukkan hasil dari penerapan metode Analisis Diskriminan Linier (ADL) dalam pengklasifikasian.

Gambar 2.2 Hasil Klasifikasi dengan Analisis Diskriminan Linier

Dalam hal transformasi setiap data, Fukunaga (1990) mengklasifikasikan himpunan data dan vektor uji ke dalam ruang transformasi melalui dua pendekatan yang berbeda sebagai berikut:

1. Transformasi Class-dependent yaitu pendekatan yang memaksimumkan rasio varians antar-kelas ke varians dalam-kelas.

2. Transformasi Class-independent yaitu memaksimumkan rasio seluruh varians dalam-kelas.

Selain itu, ia juga menyajikan operasi matematika untuk mempermudah klasifikasi sejumlah objek yaitu:

1. Formulasikan himpunan data dan data uji yang akan diklasifikasikan dalam ruang aslinya. Untuk memudahkan pengertian, peneliti menggunakan dua data dan direpresentasikan ke dalam matriks yang berisi fitur dalam bentuk seperti berikut

11 12 21 22 1 2 1 m m a a a a set a a                      11 12 21 22 1 2 1 m m b b b b set b b                     

2. Hitung rata-rata setiap himpunan data dan rata-rata dari seluruh data. Anggap 1 dan 2adalah rata-rata dari himpunan data 1 dan 2, serta 3 sebagai rata-rata dari seluruh data yang diperoleh dari

3 p1 1 p2 2

    

di mana p1 dan p2 adalah peluang dari masing-masing kelas. Pada kasus dua kelas, faktor peluang diasumsikan sebesar 0,5.

3. Matriks sebaran dalam kelas merupakan ekspektasi kovarians dari setiap kelas. dengan perhitungan sebagai berikut

cov

w j j

j

S 



p

Untuk permasalahan dua kelas,

1 2

0,5cov 0,5cov w

S  

Semua matriks kovarians adalah matriks yang simetris. Matriks kovarians dihitung menggunakan persamaan berikut

cov ( )( )T

j  xjj xjj

Matriks sebaran antar-kelas dihitung dengan menggunakan persamaan berikut

3 3

( )( )T

b j j

j

S 



   

Faktor optimisasi dalam tipe dependent-class transformasi dapat dihitung sebagai

( )

j

criterion invcov_j S_b

Faktor optimisasi dalam tipe independent-class transformasi dapat dihitung sebagai

( )

2.3 Analisis Diskriminan Linier 2-Dimensi

Analisis Diskriminan Linier 2-Dimensi (ADL2-D) adalah suatu metode baru yang merupakan perkembangan dari Analisis Diskriminan Linier. Beberapa tahun belakangan ini, metode-metode ADL2-D ini telah diperkenalkan. Li and Yuan (2005), dan Xiong et. al (2005) memformulasikan gambar berdasarkan perhitungan matriks sebaran dalam kelas dan antar kelas. Metode-metode tersebut tidak merepresentasikan gambar ke dalam vektor sehingga tereduksi secara dimensional ke dalam matriks gambar. Song et. al (2005) dan Yang et. al (2003) menggunakan korelasi kolom demi kolom untuk mereduksi sejumlah kolom. Selanjutnya Yang et. al (2005) memperbaiki dan memberikan suatu algoritma untuk mereduksi bilangan-bilangan pada kolom pertama dan mereduksi bilangan-bilangan-bilangan-bilangan pada baris berikutnya. Metode ini merupakan suatu algoritma dependen. Ye et. al (2005) memperkenalkan suatu ADL2-D independen dengan suatu algoritma solusi iteratif.

Untuk Analisis Diskriminan Linier 2 Dimensi, perbedaan utama antara ADL klasik dan ADL2-D yang peneliti usulkan dalam penelitian ini adalah tentang perwakilan (representasi) data. ADL klasik menggunakan representasi vektor, sedangkan ADL2-D bekerja dengan data dalam representasi matriks. Dalam penggunaan metode ADL2-D akan terlihat bahwa representasi mengarah ke eigen-dekomposisi pada matriks dengan ukuran lebih kecil. Lebih khusus, ADL2-D melibatkan eigen-dekomposisi matriks dengan ukuran r × r dan c × c, yang jauh lebih kecil daripada matriks ADL klasik (Ye et. al, 2005).

Dalam ADL2-D telah disepakati bahwa suatu himpunan gambar disimbolkan dengan X=(X1, X2, ..., Xn), Xi _r c _{. Dengan intuisi yang sama dengan ADL klasik,} ADL2-D mencoba untuk mencari suatu transformasi bilinier

 TX

i i

Y L R (2.15)

sehingga kelas-kelas yang berbeda dipisahkan. Kuncinya adalah bagaimana memilih ruang bagian L dan R berdasarkan matriks sebaran dalam kelas dan antar kelas (Luo

Tidak seperti ADL klasik, ADL2-D menganggap hal berikut (l1×l2) - ruang

dimensi L⊗R merupakan perkalian tensor (kronecker product) dua ruang berikut: L

direntang oleh 1

1 { }l

i

i

u dan R direntangkan oleh 2 1 { }l

i

i

v dan didefinisikan sebagai dua

matriks L =[ ] 1 1 l u , ...,u Rr l1 dan R = [ ] 2 1 l v ,..., v Rc l2. Kemudian, himpunan

gambarX_Rr c _{diproyeksikan ke ruang L⊗ Rsehingga hasil proyeksinya adalah L}T_X R Rl l12 (Ye et. al, 2004).

Kronecker product (perkalian tensor) didefinisikan sebagai: anggapL Rr l1, RRc l2 maka Kronecker product (perkalian tensor) L dan R didefinisikan sebagai

matriks 1 1 11 1 1 l r rl l R l R L R l R l R      _{  }         

LR  RLdan apabila L Rr l1 dan RRc l2 simetris maka LRsimetris

(Horn and Johnson, 1985). Sebagai contoh 11 12 21 22 a a L a a        dan R maka 11 12 21 22 a R a R L R a R a R    _{  }  

Jika dimisalkan Ai _r c _{, untuk i = 1, 2, …, n adalah gambar (pola) dalam} dataset, kemudian masing-masing pola dikelompokkan ke dalam ∏1, ∏2,…, ∏k

dimana ∏i memiliki ni gambar (pola). Misalkan 1

i i _x i M X n  



adalah rata-rata dari kelas ke–i, 1 ≤ i ≤ k , dan 1 ₁

i

k i x

M X

n  



 

berarti rata-rata keseluruhan, dalam 2DLDA, peneliti menganggap gambar sebagai sinyal dua dimensi dan bertujuan untuk menemukan dua matriks transformasi Lr l1dan Rc l2yang

memetakan setiap anggota Ai _r c _{untuk 1≤ x≤ n, ke suatu matriks Bi} l l12

sehingga Bi = LT Ai R.

Sama halnya seperti ADL klasik, ADL2D bertujuan untuk mencari transformasi (proyeksi) optimal L dan R sehingga struktur kelas dari ruang

berdimensi tinggi yang asli diubah ke ruang berdimensi rendah. Suatu kesamaan metrik alami antara matriks adalah norma Frobenius (Ye, et. al, 2004). Di bawah metrik ini kuadrat jarak dari within-class (dalam kelas) dan between class (antar kelas) dapat dihitung sebagai berikut:

2 1 i k w i F i x D X M   

 

 , 2 1 k b i i _F i D n M M  



 (2.16) trace (M MT)= M 2_F, untuk suatu matriks M, maka diperoleh

2 1 i k w i F i x D trace X M      _  _ 

 

 (2.17) 2 1 i k b i F i x D trace X M      _  _ 

 

 (2.18)

Dalam ruang berdimensi rendah, hasil dari transformasi linier L dan R, jarak within-class dan between class menjadi:









_ 1 i k T T T w _{i i} i x D trace L X M RR X M L          

 

 (2.19)









_ 1 k T T T b _{i i i} i D trace n L X M RR X M L     _   _ 



 (2.20)

Transformasi optimal L dan R akan memaksimumkan D_bdan meminimumkan

_

w

D , oleh karena kesulitan menghitung optimal Ldan R secara simultan, berikut ini adalah algoritma untuk ADL2D. Lebih khususnya, untuk suatu R tetap, kita dapat menghitung optimal L dengan memecahkan permasalahan optimisasi yang sama dengan persamaan (2.14). Dengan menghitung L, kita kemudian dapat memperbaharui R dengan memecahkan masalah optimisasi lain sebagai satu-satunya penyelesaian dalam persamaan (2.14).

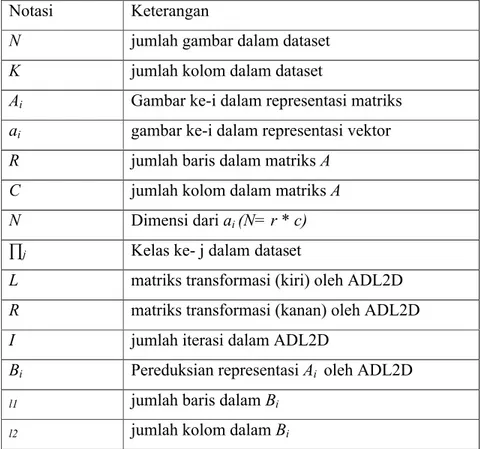
Beberapa notasi penting yang digunakan dalam penelitian ini terdaftar dalam Tabel 2.1 dibawah ini:

Tabel 2.1 Notasi Penting dalam Analisis Diskriminan Linier 2 Dimensi

Perhitungan L

Untuk suatu R tetap, D_wdan

_

b

D dapat ditulis kembali sebagai





_ T R w _w D trace L S L , _



T R



b _b D trace L S L (2.21) di mana 1 1 ( ) ( ) , ( ) ( ) i k k R T T R T T w i i b i i i i X i S M RR M S n M M RR M M    

 

X X 



  (2.22)

Sama seperti masalah yang terdapat pada persamaan (2.14), optimal L dapat dihitung dengan memecahkan masalah optimisasi berikut: maxL trace₍₍ T R _{) (}1 T R ₎₎

w b

L S L  L S L .

Penyelesaiannya dapat diperoleh dengan memecahkan masalah generalisasi nilai Notasi Keterangan

N jumlah gambar dalam dataset

K jumlah kolom dalam dataset

Ai Gambar ke-i dalam representasi matriks

ai gambar ke-i dalam representasi vektor

R jumlah baris dalam matriks A C jumlah kolom dalam matriks A N Dimensi dari ai (N= r * c)

∏j Kelas ke- j dalam dataset

L matriks transformasi (kiri) oleh ADL2D

R matriks transformasi (kanan) oleh ADL2D

I jumlah iterasi dalam ADL2D

Bi Pereduksian representasi Ai oleh ADL2D

l1 jumlah baris dalam Bi l2 jumlah kolom dalam Bi

eigen berikut: R R

w b

S xS x. Karena R w

S secara umum adalah nonsingular, maka L

optimum dapat diperoleh dengan menghitung suatu eigen-dekomposisi pada 1

( R) R

w b

S  S _{. Catatan bahwa ukuran dari matriks} R w

S dan R b

S adalah r r (matriks bujursangkar), yang ukurannya lebih kecil dibandingkan ukuran matriks S_wdan

b

S dalam ADL klasik.

Perhitungan R

Kemudian menghitung R untuk suatu L yang tetap. D_wdan

_

b

D dapat ditulis kembali sebagai





_ T L w _w D trace R S R , _



T L



b _b D trace R S R (2.23) di mana 1 1 ( ) ( ), ( ) ( ) i k k L T T L T T w i i b i i i i X i S X M LL X M S n M M LL M M    

 

  



  (2.24)

Sama seperti masalah yang terdapat pada persamaan (2.14), optimal L dapat dihitung dengan memecahkan masalah optimisasi berikut: maxR trace₍₍ T L _{) (}1 T L ₎₎

w b

R S R  R S R .

Penyelesaiannya dapat diperoleh dengan memecahkan masalah generalisasi nilai eigen berikut: L L

w b

S xS x. Karena L w

S secara umum adalah nonsingular, maka R

optimum dapat diperoleh dengan menghitung suatu eigen-dekomposisi pada 1

( R) R

w b

S  S _{. Catatan bahwa ukuran dari matriks} L w

S dan L b

S adalah r r (matriks bujursangkar), yang ukurannya lebih kecil dibandingkan ukuran matriks S_wdan

b

S dalam ADL klasik.

Algoritma 2.2 ADL2D ( A1,…,An,l1, l2)

Input: A1,…,An, l1, l2

Output: L, R, B1,…, Bn

1. Hitung rata-rata Mi dari kelas ke-i untuk setiap i sebagai

1 i i x i M X n  



2. Hitung rata-rata global 1 ₁

i k i x M X n   

 

3. 





2 0 ,0 T l R I

4. Untuk j dari 1 sampai I

5.





_{1 1}





1 i k T R T w i j j i i x S X M R R_{ } X M   

 

 





1 1





1 k T R T b i i i j j i S 



_ n X M R R   X M

6. Hitung eigen vektor l1 pertama { } dari 11

l L l i   (S ) SR -1w Rb 7. { ,..., }1 ₁ L L j l L    8.









1 i k T L T w i j j i i x S X M L L X M   

 

  SbL 



k_i1n X Mi



 i



T L L X Mj Tj



 i



9. Menghitung eigen vektor l2 pertama { } dari 21

l R l l   (S ) SL -1w Lb 10. 2 1 { ,..., }R R j l R    11. End for 12. LL R_I, R_I 13. B_l L A RT _l , untuk l1, 2,...,n 14. Return (L, R, B1, …,Bn) (Ye, et.al, 2004)

Namun, dalam ADL2-D kita akan melihat ada suatu masalah keraguan yang sangat mendasar yakni ada dua cara untuk mendefinisikan matriks sebaran dalam kelas S_w

1 ( ) ( )( ) i j k T T w j j j x S XX M M    

 

X_i X_i (2.25) 1 ( ) ( ) ( ) i j k T T w j j j x S X X M M    

 

X_i X_i (2.26) dan ada 2 cara untuk mendefinisikan matriks sebaran antar kelas Sb

1 ( T) k ( )( )T b j j j j S XX n M M M M  



  (2.27) 1 ( T ) k ( ) (T ) b j j j j S X X n M M M M  



  (2.28)

Oleh karena itu, dalam ruang transformasi, dapat dituliskan sebagai ( T), ( T ), b b S YY S Y Y ( T), ( T ), w w S YY S Y Y

Pada umumnya, gambar tidak bersifat simetris: XiXiT , maka ( T) ( T ), b b S YY S Y Y ( T) ( T ), w w S YY S Y Y

Karena alasan ini, fungsi objektif ADL menjadi bermakna ganda dan menimbulkan keraguan manakah fungsi objektif yang baik yakni mempunyai sejumlah pilihan sebagai berikut: 1 ( ) tr ( ) T b T w S YY J S YY  (2.29) 2 ( ) tr ( ) T b T w S Y Y J S Y Y  (2.30) 3 ( ) ( ) tr ( ) ( ) T T b b T T w w S YY S Y Y J S YY S Y Y    _  _   (2.31) 4 ( ) ( ) tr , ( ) ( ) T T b b T T w w S Y Y S YY J S Y Y S YY        (2.32) 5 ( ) ( ) tr , ( ) ( ) T T b b T T w w S YY S Y Y J S YY S Y Y    (2.33) dan lain-lain. 2.3.1 Transformasi Bilinier

Suatu transformasi bilinier didefinisikan sebagai: _ _  _ _  , _ _       T i T i T i i X L Y X R Y (Luo, et.al, 2007) (2.34)

Dengan menggunakan transformasi symmetris ini, matriks sebaran menjadi tunggal dan masalah keraguan yang terdapat dalam ADL2-D dapat diselesaikan.

Kemudian, berikut ini ditunjukkan bahwa transformasi bilinier pada persamaan (2.34) ekivalen ke transformasi linier pada persamaan (2.15):

     _{    }     T T i T i T T i i X R X L X L X R (2.35) maka Yi = LT Xi R.

Pada Fukunaga(1990), matriks Γ didefinisikan sebagai:

1 0 0 0 0                n

yakni matriks yang diagonal utamanya merupakan nilai varians dari suatu himpunan data dan elemen lain dalam matriks bernilai 0.