Perancangan Kriptografi
Block Cipher
Menggunakan Pola Tari
Purisari Pati
Artikel Ilmiah
Peneliti :
Ivan Dicky Hendrian (672013049) Magdalena A. Ineke Pakereng, M.Kom.
Program Studi Teknik Informatika Fakultas Teknologi Informasi Universitas Kristen Satya Wacana
Perancangan Kriptografi
Block Cipher
Menggunakan Pola Tari
Purisari Pati
Artikel Ilmiah
Diajukan Kepada Fakultas Teknologi Informasi
Untuk Memperoleh Gelar Sarjana Komputer
Peneliti :
Ivan Dicky Hendrian (672013049) Magdalena A. Ineke Pakereng, M.Kom.
Program Studi Teknik Informatika Fakultas Teknologi Informasi Universitas Kristen Satya Wacana
Perancangan Kriptografi
Block Cipher
Menggunakan Pola Tari
Purisari Pati
Ivan Dicky Hendrian1, Magdalena A. Ineke Pakereng2 Fakultas Teknologi Informasi
Universitas Kristen Satya Wacana Jl. Diponegoro 52-60, Salatiga 50711, Indonesia
E-mail: [email protected], [email protected]2
Abstract
Cryptography is the knowledge that used to secure the data. To increase the security level of the cryptography should be developed. In this study, Block Cipher Cryptographic based at 64 Bit is designed with Dance purisari pati which yield a random Ciphertext. The function cryptography is to make the data in the form of a clear message (plaintext) into an unintelligible message (ciphertext), this pattern is designed using a 64 bit size to create each new block. This cryptography is designed using 4 20-round processes, where the 2nd and 4th processes are transformed using the S-Box table to obtain more random Ciphertext. Testing is also done using Avalanche Effect and Correlation value where character changes reach 49,21875%,so it can be used in securing data.
Keyword : Block Cipher, Cryptography, Dance Purisari Pati, Avalanche Effect, Correlation, S-Box.
Abstrak
Kriptografi merupakan ilmu yang digunakan untuk mengamankan data. Untuk meningkatkan tingkat keamanannya maka kriptografi perlu dikembangkan. Dalam penelitian ini dirancang Kriptografi Block Cipher 64 Bit Berbasis Pola Teknik Tarian purisari pati yang menghasilkan Ciphertext yang acak. Kegunaan kriptografi adalah membuat data berupa pesan yang jelas plaintext menjadi pesan yang tidak dapat dimengerti ciphertext, pola ini dirancang menggunakan ukuran 64 bit untuk membuat setiap blok baru. Kriptografi ini dirancang menggunakan 4 proses 20 putaran, dimana proses ke-2 dan ke-4 ditransformasikan menggunakan tabel S-Box
untuk mendapatkan Ciphertext yang lebih acak. Pengujian juga dilakukan menggunakan Avalanche Effect dan nilai Korelasi dimana terjadi perubahan karakter mencapai 49,21875%, sehingga dapat digunakan dalam mengamankan data.
Kata Kunci : Block Cipher, Kriptografi, Tarian Purisari Pati, Avalanche Effect, Korelasi, S-Box.
1)Mahasiswa Program Studi Teknik Informatika, Fakultas Teknologi Informasi, Universitas Kristen
Satya Wacana
1. Pendahuluan
Kriptografi merupakan sebuah metode yang sering digunakan untuk mengamankan data maupun informasi. Metode ini biasanya dibuat dengan menempatkan berbagai teknik dalam aturan matematika yang membentuk sebuah algoritma. Kegunaan kriptografi adalah membuat data atau informasi berupa pesan yang jelas plaintext menjadi pesan yang tidak dapat dimengerti ciphertext. Block cipher menjadi salah satu kriptografi yang sekarang ini sering digunakan sebagai pengamanan dalam transfer informasi di internet dan sangat berperan penting dalam keamanan informasi saat ini, mulai dari percakapan melalui telepon genggam, transaksi di bank [1]. Kriptografi berasal dari kata Yunani kripto (tersembunyi) dan
grafia (tulisan). Secara harfiah, kriptografi dapat diartikan sebagai tulisan yang tersembunyi atau tulisan yang dirahasiakan. Tujuannya adalah supaya tulisan tersebut tidak dapat dibaca oleh setiap orang, hanya orang tertentu yang mengetahui cara menyembunyikan tulisan tersebut yang dapat membacanya. Di dalam kriptografi itu sendiri memiliki dua proses yaitu proses enkripsi dan proses dekripsi. Proses enkripsi merupakan proses mengkonversikan plaintext ke dalam ciphertext, sedangkan proses dekripsi merupakan kebalikan dari proses enkripsi yaitu mengkonversikan ciphertext kembali ke plaintext [2].
Algoritma pada perancangan kriptografi dalam penelitian ini adalah algoritma berbasis Block Cipher 64 bit dengan pola tari purisari pati yang dikombinasikan dengan tabel substitusi atau S-Box. Block Cipher adalah algoritma enkripsi yang membagi plaintext yang akan dikirimkan dengan jumlah bit tertentu (block), dan setiap block akan dienkripsi dengan proses yang sama untuk menghasilkan ciphertext. Plaintext akan dimasukkan ke dalam blok-blok dimana setiap blok berjumlah 64 bit, terdapat 24 putaran kombinasi dan 20 putaran enkripsi dan dekripsi dimana setiap putaran terdapat 4 proses untuk proses plaintext maupun proses kunci (key). Hasil dari proses plaintext akan di-XOR dengan kunci untuk menghasilkan Ciphertext yang kemudian byte-nya akan dikombinasikan dengan S-Box untuk menghasilkan Avalanche Effect yang besar.
Berdasarkan latar belakang masalah maka dilakukan penelitian yang membahas tentang perancangan kriptografi Block Cipher menggunakan pola tari purisari pati. Penggunaan pola kaki dan gerakan tangan tarian purisari pati ini sesuai dengan kriptografi karena menggunakan pola dari tarian sebagai transposisi pada blok yang ada dan diterapkan sebagai pola pada proses pemasukan dan pengurutan kriptografi Block Cipher 64 bit sehingga menghasilkan teknik kriptografi yang dapat mengacak setiap blok secara unik sesuai dengan pola tarian.
2. Tinjauan Pustaka
Terdapat banyak penelitian tentang kriptografi block cipher. Salah satunya yaitu yang berjudul Perancangan Kriptografi Block Cipher Berbasis pada Teknik Tanam Padi dan Bajak Sawah, membahas tentang implementasi algoritma Block Cipher untuk proses enkripsi dan dekripsi data yang dilakukan sebanyak 8 putaran. Dengan algoritma tanam padi dan bajak sawah dapat membuktikan bahwa teknik tersebut dapat menghasilkan metodologi kriptografi simetris dan dapat memenuhi lima-tuple (Five-tuple). Rata-rata yang dihasilkan enkripsi dan dekripsi pada teknik tanam padi dengan AES-128. Hasilnya adalah teknik tanam padi sebesar 0,00682 ms sedangkan AES-128 sebesar 0,00821 ms maka dapat disimpulkan Teknik Tanam Padi lebih cepat dengan AES1-128 [3].
Penelitian kedua berjudul Perancangan Kriptografi Block Cipher dengan Langkah Kuda, yang membahas tentang proses enkripsi dan dekripsi menggunakan pola langkah kuda yang dilakukan sebanyak 4 putaran. Algoritma langkah kuda lari dan langkah jalan dapat membuktikan bahwa pola ini dapat menghasilkan kriptografi simetris dan dapat memenuhi lima-tuple (Five-tuple). Penelitian ini dapat membandingkan proses keacakan dan proses nilai diferensiasi antara KS dengan AES-128. Hasil perbandingan dengan AES-128, rancangan berbasis langkah kuda lebih cepat 0.94869906 ms [4]. Penelitian ketiga yang berjudul Perancangan Kriptografi Block Cipher Berbasis Pola Ikan Berenang, yang membahas tentang perancangan kriptografi baru menggunakan prinsip s-box, iterated cipher dan jaringan fiestel yang dilakukan sebanyak 15 putaran dan diuji menggunakan avalanche effect dan nilai korelasi. Hasil yang diperoleh dari penelitian ini bahwa penggunaan proses kotak – s, iterated cipher dan jaringan
feistel menghasilkan hasil rata–rata 43% dan korelasi dari 15 putaran menghasilkan nilai 0.21708 [5].
Penelitian-penelitian yang sudah ada terkait perancangan algoritma kriptografi simetris block cipher menjadi acuan dalam membentuk ide untuk merancang penelitian baru tentang perancangan Kriptografi Block Cipher 64 bit
Berbasis Pola Tari Purisari Pati. Pada penelitian ini dilakukan proses kombinasi pola sebanyak 24 putaran, kombinasi pola dengan nilai korelasi menjadi kombinasi pola yang terpilih untuk digunakan dalam proses enkripsi dan dekripsi. Pada proses enkripsi dan dekripsi dilakukan 20 putaran, dimana setiap putaran terdapat 4 proses untuk proses plaintext maupun proses kunci (key). Hasil dari proses plaintext akan di-XOR dengan kunci untuk menghasilkan Ciphertext yang kemudian byte-nya akan dikombinasikan dengan S-Box untuk menghasilkan Avalanche Effect yang besar. S-Box yang digunakan dalam penelitian ini adalah S-Box algoritma AES
(Advanced Encryption Standard). Skema proses enkripsi dan dekripsi block cipher secara umum ditunjukkan
Gambar 1 Skema Proses Enkripsi-Dekripsi Block Cipher [6]
Misalkan blok plaintext (P) yang berukuran bit
p p pn
P 1, 2,, (1)
Blok ciphertext (C) maka blok C adalah
c c cn
C 1, 2,, (2)
Kunci (K) maka kunci adalah
k k kn
K 1, 2,, (3)
Sehingga proses enkripsi adalah
P C
Ek (4)
Proses dekripsi adalah
C PDk (C) = P (5)
Sebuah sistem kriptografi terdiri dari 5-tuple (Five Tuple) (P,C,K,E,D) yang memenuhi kondisi [5] :
1. P adalah himpunan berhingga dari plaintext. 2. C adalah himpunan berhingga dari ciphertext.
3. K merupakan ruang kunci (Keyspace), himpunan berhingga dari kunci. 4. Untuk setiap k K, terdapat aturan enkripsi ek E dan berkorespodensi
dengan aturan dekripsi dk D. Setiap ek : P → C dan dk : C → P adalah
fungsi sedemikian hingga dk(ek(x)) = x untuk setiap plaintext x ∊P.
Tabel 1 Klasifikasi Koefisien Korelasi [8]
Interval Koefisien Tingkat Hubungan
0,00 – 0,199 Sangat Rendah
0,20 – 0,399 Rendah
0,40 – 0,599 Sedang
0,60 – 0,799 Kuat
0,80 – 1,000 Sangat Kuat
3. Metode Penelitian
Perancangan kriptografi ini dilakukan dengan beberapa tahap penyusunan yaitu : identifikasi masalah, pengumpulan data, perancangan kriptografi, pengujian kriptografi, penulisan artikel ilmiah.
Gambar 2 Tahapan Penelitian
Tahapan penelitian berdasarkan Gambar 2, dijelaskan sebagai berikut : Identifikasi masalah : Pada tahapan ini dilakukan analisis terhadap permasalahan yang ada, terkait dengan proses perancangan Kriptografi berbasis tari purisari pati. Pengumpulan Data : Menemukan pola yang akan digunakan dalam proses perancangan kriptografi block cipher dan mengumpulkan data dari penelitian sebelumnya yang dapat dijadikan sebagai pembanding maupun landasan penelitian. Perancangan Kriptografi : Pada tahap ini akan dilakukan perancangan Kriptografi berbasis tari purisari pati, untuk pembuatan kunci, proses enkripsi dan proses dekripsinya yang dikombinasikan dengan XOR dan menggunakan tabel substitusi
Identifikasi Masalah
Pengumpulan Data
Perancangan Kriptografi
Pengujian Kriptografi
S-Box untuk transposisi byte. Uji Kriptografi : Setelah rancangan kriptografi dibuat perlu dilakukan pengujian, melakukan penghitungan mulai dari memasukkan
plaintext, mengubah text ke dalam bit lalu melakukan proses enkripsi-dekripsi. Penulisan Artikel Ilmiah : Penulisan Laporan dilakukan untuk dokumentasi proses tentang perancangan kriptografi block cipher berbasis pada pola Tarian Purisari Pati dalam bentuk jurnal.
Dalam perancangan kriptografi block cipher 64 bit menggunakan pola tari purisari pati ini dilakukan dua proses yaitu proses enkripsi dan proses dekripsi. Enkripsi dan dekripsi itu sendiri dilakukan dalam 20 putaran yang di setiap putarannya terdapat 4 proses.
Putaran ke 1 Hingga Putaran ke 20
Gambar 3 Alur Proses Enkripsi
Gambar 3 menunjukkan alur proses enkripsi, langkah-langkah proses enkripsi, dijelaskan sebagai berikut :
1) Menyiapkan plaintext dan kunci.
2) Mengubah plaintext dan kunci menjadi biner sesuai dalam tabel ASCII. 3) Dalam perancangan enkripsi, plaintext dan kunci akan melewati empat
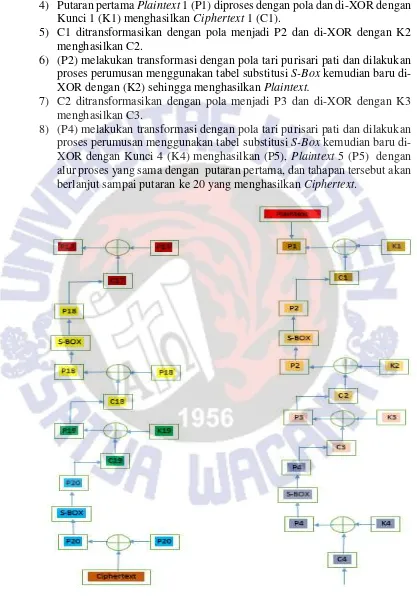
4) Putaran pertama Plaintext 1 (P1) diproses dengan pola dan di-XOR dengan Kunci 1 (K1) menghasilkan Ciphertext 1 (C1).
5) C1 ditransformasikan dengan pola menjadi P2 dan di-XOR dengan K2 menghasilkan C2.
6) (P2) melakukan transformasi dengan pola tari purisari pati dan dilakukan proses perumusan menggunakan tabel substitusi S-Box kemudian baru di-XOR dengan (K2) sehingga menghasilkan Plaintext.
7) C2 ditransformasikan dengan pola menjadi P3 dan di-XOR dengan K3 menghasilkan C3.
8) (P4) melakukan transformasi dengan pola tari purisari pati dan dilakukan proses perumusan menggunakan tabel substitusi S-Box kemudian baru di-XOR dengan Kunci 4 (K4) menghasilkan (P5), Plaintext 5 (P5) dengan alur proses yang sama dengan putaran pertama, dan tahapan tersebut akan berlanjut sampai putaran ke 20 yang menghasilkan Ciphertext.
Gambar 4 menunjukkan alur proses dekripsi, langkah-langkah proses dekripsi tersebut dijelaskan sebagai berikut :
a) Menyiapkan ciphertext dan kunci.
b) Mengubah ciphertext dan kunci menjadi biner.
c) Putaran pertama Ciphertext (C) di S-BOX kemudian dimasukkan ke dalam C20 diproses dengan pola, setelah itu C20 di-XOR dengan Kunci 20 (K20) menghasilkan Plaintext 20 (P20).
d) P20 di S-BOX kemudian dimasukkan ke dalam C19 diproses dengan pola, setelah itu C19 di-XOR dengan K19 menghasilkan P19.
e) P19 ditransformasikan dengan pola menjadi C18 dan di-XOR dengan K18 menghasilkan P18.
f) P18 di S-BOX kemudian dimasukkan ke dalam C17 diproses dengan pola, setelah itu C17 di-XOR dengan K17 menghasilkan P17.
4. Hasil Pembahasan
Dalam bagian ini akan membahas tentang algoritma perancangan kriptografi
block cipter 64 bit menggunakan pola tari purisari pati secara lebih rinci. Teknik proses enkripsi yang melibatkan tabel substitusi untuk memperbesar analisis
avalanche effect. Sedangkan gambar pola tari purisari pati yang digunakan untuk merancang kriptografi dapat ditunjukkan pada Gambar 5.
Dalam algoritma ini pola tari Purisari Pati digunakan sebagai proses pengambilan bit di dalam matriks plaintext. Pola tersebut ditunjukkan pada Gambar 6.
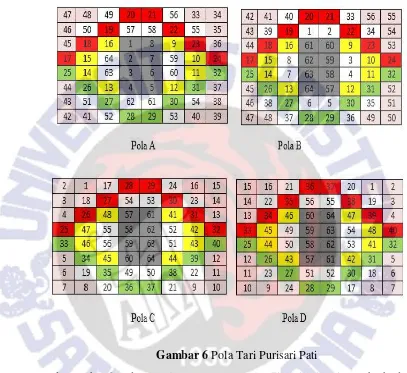
Gambar 6 Pola Tari Purisari Pati
Pada Gambar 6 terdapat pola (A, B, C, D) pola tari purisari pati yang berbeda, pola-pola tersebut menunjukkan cara pengambilan bit yang berbeda-beda berdasarkan yang sudah dirancang, setelah itu dilakukan proses pengujian kolerasi dengan mengkombinasikan urutan pola-pola untuk mendapatkan nilai korelasi yang terbaik. Pengujian menggunakan plaintext “Iv4Nd1KY” dan menggunakan kunci “h3NdR14N”.
Berdasarkan pada Gambar 6 pengambilan bit dilakukan dengan 4 cara yang berbeda-beda yaitu :
pengambilan sesuai rancangan. Selanjutnya pengambilan Pola D dilakukan dari pojok kanan berwarna pink (1, 2, 3,..8) dan selanjutnya mengikuti angka-angka seperti Gambar 6.
Berdasarkan hasil pengujian korelasi, maka hasil terbaiklah yang akan digunakan sebagai acuan perancangan dalam proses enkripsi dan dekripsi.
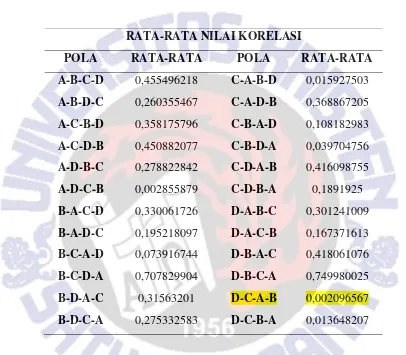
Tabel 2 Tabel Rata Korelasi
RATA-RATA NILAI KORELASI
POLA RATA-RATA POLA RATA-RATA
A-B-C-D 0,455496218 C-A-B-D 0,015927503
A-B-D-C 0,260355467 C-A-D-B 0,368867205
A-C-B-D 0,358175796 C-B-A-D 0,108182983
A-C-D-B 0,450882077 C-B-D-A 0,039704756
A-D-B-C 0,278822842 C-D-A-B 0,416098755
A-D-C-B 0,002855879 C-D-B-A 0,1891925
B-A-C-D 0,330061726 D-A-B-C 0,301241009
B-A-D-C 0,195218097 D-A-C-B 0,167371613
B-C-A-D 0,073916744 D-B-A-C 0,418061076
B-C-D-A 0,707829904 D-B-C-A 0,749980025
B-D-A-C 0,31563201 D-C-A-B 0,002096567
B-D-C-A 0,275332583 D-C-B-A 0,013648207
Tabel 2 menunjukkan hasil kombinasi pola dan mendapatkan nilai korelasi terbaik pada kombinasi pola D-C-A-B sebesar 0,002096567. Tingkat keamanan tergantung pada nilai koefisien korelasi terbaik, dalam kasus ini ditunjukkan bahwa nilai koefisien korelasi yang mendekati 0 adalah kombinasi pola terbaik dalam mengamankan data dibandingkan dengan kombinasi–kombinasi lainnya, yang ditunjukkan dengan warna kuning pada Tabel 2. Kombinasi pola D-C-A-B yang akan digunakan untuk melanjutkan proses enkripsi hingga putaran ke-20 untuk menghasilkan ciphertext.
Perancangan algoritma kriptografi Block Cipher 64 bit berbasis pola tari purisari pati ini dilakukan dengan 20 putaran untuk mendapatkan ciphertext dan dalam setiap putaran terdapat empat proses pola. Proses enkripsi dapat dilihat pada Gambar 3.
Mengubah plaintext dan kunci menjadi biner sesuai dalam tabel ASCII,
(P1) diproses dengan pola dan di-XOR dengan Kunci 1 (K1) menghasilkan
Ciphertext 1 (C1), C1 ditransformasikan dengan pola menjadi P2 dan di-XOR dengan K2 menghasilkan C2, (P2) melakukan transformasi dengan pola tari purisari pati dan dilakukan proses perumusan menggunakan tabel substitusi S-Box
kemudian baru di-XOR dengan (K2) sehingga menghasilkan Plaintext, C2 ditransformasikan dengan pola menjadi P3 dan di-XOR dengan K3 menghasilkan C3, kemudian (P4) melakukan transformasi proses perumusan menggunakan tabel substitusi S-Box lalu di-XOR dengan Kunci 4 (K4) menghasilkan (P5), Plaintext 5 (P5) dengan alur proses yang sama dengan putaran pertama, dan tahapan tersebut akan berlanjut sampai putaran ke 20 yang menghasilkan Ciphertext.
Untuk menjelaskan secara detail proses pemasukan bit dalam matriks maka diambil proses 1 pada putaran 1 sebagai contoh. Misalkan angka 1 merupakan inisialisasi setiap bit yang merupakan hasil konversi plaintext maka urutan bit adalah sebagai berikut 1, 2, 3, 4,..64.
Gambar 7 Pola Pemasukan Bit Plaintext dan Kunci (Key)
Gambar 7 menjelaskan proses pemasukan bit karakter plaintext dan kunci. Setiap 8 bit dari setiap karakter dimasukkan berurutan dengan mengisi blok bagian kiri terlebih dahulu mengikuti garis anak panah berwarna hitam hingga penuh, setelah itu baru blok bagian kanan mengikuti garis anak panah hingga penuh.
Gambar 8 merupakan pola pengambilan dan transpose plaintext dan kunci. Bit diambil setiap 8 bit mengikuti urutan angka. Kemudian dimasukkan kembali ke dalam kolom matriks baris pertama dari kiri ke kanan, dan untuk baris kedua dari kanan ke kiri, selanjutnya mengikuti anak panah dan urutan angka pada Gambar 8. Dari proses tersebut menghasilkan P1 dan K1. Setelah itu P1 dan K1 akan di-XOR kan menghasilkan C1.
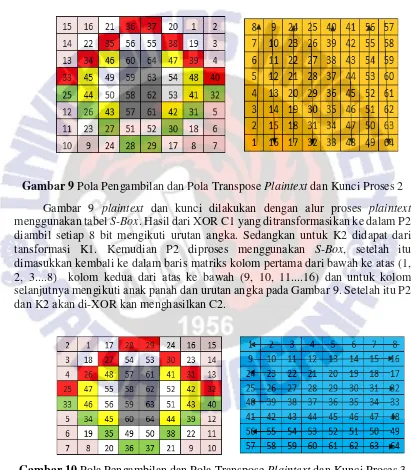
Gambar 9 Pola Pengambilan dan Pola Transpose Plaintext dan Kunci Proses 2
Gambar 9 plaintext dan kunci dilakukan dengan alur proses plaintext
menggunakan tabel S-Box. Hasil dari XOR C1 yang ditransformasikan ke dalam P2 diambil setiap 8 bit mengikuti urutan angka. Sedangkan untuk K2 didapat dari tansformasi K1. Kemudian P2 diproses menggunakan S-Box, setelah itu dimasukkan kembali ke dalam baris matriks kolom pertama dari bawah ke atas (1, 2, 3....8) kolom kedua dari atas ke bawah (9, 10, 11....16) dan untuk kolom selanjutnya mengikuti anak panah dan urutan angka pada Gambar 9. Setelah itu P2 dan K2 akan di-XOR kan menghasilkan C2.
Gambar 10 Pola Pengambilan dan Pola Transpose Plaintext dan Kunci Proses 3
kedua dari kanan ke kiri (9, 10, 11...16) dan untuk baris selanjutnya mengikuti anak panah dan urutan angka pada Gambar 10. Setelah itu P3 dan K3 akan di-XOR kan menghasilkan C3.
Gambar 11 Pola Pengambilan dan Pola Transpose Plaintext dan Kunci Proses 4
Gambar 11 plaintext dan kunci dilakukan dengan alur proses Plaintext
menggunakan tabel S-Box. Hasil dari XOR C3 yang ditransformasikan ke dalam P4 diambil setiap 8 bit mengikuti urutan angka. Sedangkan untuk K4 didapat dari tansformasi K3. Kemudian P4 diproses menggunakan S-Box, setelah itu dimasukkan kembali ke dalam baris matriks kolom pertama dari atas ke bawah (1, 2, 3,...8) kolom kedua dari bawah ke atas (9, 10, 11,..16) dan untuk kolom selanjutnya mengikuti anak panah dan urutan angka pada Gambar 11. Setelah itu P4 dan K4 akan di-XOR kan menghasilkan C4. Proses putaran 1 telah selesai, kemudian dilakukan proses yang sama secara terus-menerus hingga putaran ke 20 untuk mendapatkan ciphertext.
Gambar 12 Tabel Substitusi S-Box AES
nilai S[r, c], maka nilai substitusinya, dinyatakan dengan S’[r, c], adalah elemen di dalam S-Box yang merupakan perpotongan baris x dengan kolom y.
Untuk pengujian algoritma dilakukan dengan mengambil plaintext adalah Iv4Nd1KY dan kunci adalah h3NdR14N. Setelah melewati proses enkripsi yang telah dijabarkan sebelumnya maka mendapatkan ciphertext yang telah dikonversi ke dalam nilai hexadecimal.
Tabel 3 Hasil Ciphertext Setiap Putaran
Putaran Hasil Hexadecimal Putaran Hasil Hexadecimal
1 79E1A1FAC362D735 11 7FDD62ACA9698D
2 630AF59A3D885CFA 12 B1EEE9E9A36AA9C1
3 6EA9DBCF2BC44E26 13 C3B882698BA9113
4 CDB9DC27EC5448E9 14 3DD5E982B296B370
5 46FCEEE43C624913 15 C4FEC93A729939F3
6 72B5968F7B7563D7 16 C6BA17C291FE656
7 29C12679BD7FDC07 17 7750EF6412707953
8 49E2CF0B750E8493 18 C5FBD181446C3DC
9 1E3B2F7911870B96 19 EE8ECB71248CCF
10 D78F3839602BED15 20 61DB81B3AED6CA1F
Tabel 3 merupakan hasil enkripsi dari setiap putaran. Hasil dari putaran 20 merupakan final ciphertext. Proses dekripsi adalah proses merubah ciphertext
menjadi plaintext awal. Dekripsi dilakukan sama seperti enkripsi, tetapi dekripsi dimulai dari putaran ke 20 menuju putaran ke 1 untuk mendapatkan plaintext awal. Pola pengambilan pada proses enkripsi akan menjadi pola pemasukan pada proses dekripsi, sedangkan pola pemasukan pada enkripsi akan digunakan sebagai pola pengambilan pada dekripsi. Proses dekripsi dimulai dari memasukkan ciphertext ke kolom matriks C4 kemudian di-XOR dengan K4 dan pada proses tersebut akan menghasilkan P4. Kemudian P4 ditransformasikan dengan S-Box untuk mendapatkan hasil akhir P4, P4 digunakan sebagai C3, lalu C3 di-XOR dengan K3 dan menghasilkan P3, P3 digunakan sebagai C2, C2 lalu di-XOR dengan K2 dan menghasilkan P2 kemudian ditransformasikan dengan S-Box untuk mendapatkan hasil akhir P2, lalu P2 digunakan sebagai C1, C1 kemudian di-XOR dengan K1 untuk menghasilkan P1, proses itu dilakukan berulang-ulang sebanyak 20 putaran sesuai dengan banyaknya putaran enkripsi dan hasil akhir dari dekripsi putaran ke 20 adalah plaintext awal.
Tabel 4 Algoritma Enkripsi dan Dekripsi
Tabel 4 merupakan algoritma proses enkripsi dan dekripsi. Proses enkripsi menghasilkan C4 dan proses dekripsi menghasilkan P1 awal.
Algoritma proses Kunci (key), dijelaskan sebagai berkut: 1. Masukkan Kunci
2. Kunci diubah ke ASCII 3. ASCII diubah ke BINER
4. Bit BINER dimasukkan ke kolom K1 menggunakan pola masuk Kunci 5. Bit Kunci ditransposisikan dengan pola Kunci D
6. Transposisi K1 = K2
7. K2 ditransposisikan menggunakan pola Kunci C
Proses Enkripsi Proses Dekripsi
1) Masukkan plaintext 1) Masukkan C4
2) Plaintext dirubah ke ASCII 2) C4 dirubah ke ASCII
3) Bit BINER dimasukkan ke kolom matrik P1 dengan pola pemasukan proses 1
4) Bit pada kolom matriks diambil dengan
3) ASCII diubah ke BINER
4) Bit BINER dimasukkan ke kolom matriks C4 dengan pola pemasukan
Proses pengambilan 5) Masukkan bit K4 menggunakan pola pemasukan
5) Bit pengambilan dimasukkan lagi ke dalam matrik untuk mendapatkan hasil akhir P1
6) P1 di XOR dengan K1 menghasilkan C1
7) C1 = P2 diambil menggunakan pola pemasukan
8) BINER diubah menjadi DEC
9) DEC diubah menjadi HEX
10) HEX ditransformasikan menggunakan S-BOX
11) Hasil HEX diubah menjadi BINER
12) Hasil BINER dimasukkan ke blok matriks P2
13) P2 di XOR dengan K2 menghasilkan C2
14) C2 = P3 diambil menggunakan pola pemasukan
15) C3 diubah ke DEC
16) P3 di XOR dengan K3 menghasilkan C3
17) C3 = P4 diambil menggunakan pola pemasukan
18) P4 diproses dengan pola pengambilan proses P4
19) BINER diubah menjadi DEC
20) DEC diubah menjadi HEX
21) HEX ditransformasikan menggunakan S-BOX
22) Hasil HEX diubah menjadi BINER
23) Hasil BINER dimasukkan ke blok matriks P4
24) P4 di XOR dengan K4 menghasilkan C4
25) C4 diubah ke DEC
26) DEC diubah ke HEX, Sebagai Ciphertext
6) C4 di XOR dengan K4 7) Bit P4 diubah ke BINER 8) BINER diubah ke HEX
9) HEX ditransformasikan dengan tabel S-BOX 10) Hasil konversi diubah ke BINER
11) BINER P4 dimasukkan ke kolom matriks dengan pola pengambilan
12) P4 = P3
13) C3 di XOR dengan K3 menghasilkan C3 14) P3 = C2 diambil menggunakan pola pemasukan 15) P2 di XOR dengan K2 menghasilkan C2 16) BINER dimasukkan ke kolom C2 menggunakan
pola masuk
17) Masukkan bit K2 menggunakan pola pemasukan 18) C2 di XOR dengan K2 menghasilkan P2 19) BINEER diubah ke HEX
20) Hasil HEX ditransformasikan dengan tabel S-BOX
21) Hasil konversi diubah menjadi BINNER 22) Bit pengambilan dimasukkan lagi ke dalam
kolom matriks 2 23) P2 = C1
24) C1 di XOR dengan K1 menghasilkan P1 25) P1 diproses dengan pola pengambilan
26) Bit pengambilan dimasukkan lagi ke dalam kolom matriks P1
27) Hasil akhir BINER P1 diubah ke DEC 28) DEC diubah ke HEX
8. Transposisi K2 = K3
9. K3 ditransposisikan menggunakan pola Kunci A 10.Transposisi K3 = K4
11.K4 ditransposisikan menggunakan pola Kunci B
Proses Enkripsi
{Program ini digunakan untuk melakukan proses enkripsi data}
Kamus
Dari BINER = blok matriks P1, masukkan BINER P1 menggunakan Pola pemasukan awal
Dari blok matriks P1 = BINER, ambil bit P1 dengan Pola Tari Purisari Pati D
Dari BINER = blok matriks P1, masukkan BINER P1 dengan pola pemasukan proses 1
Output P1
Input K Read K
K to ASCII ASCII to BINER
Dari BINER = blok matriks K1, masukkan BINER K1 menggunakan Pola pemasukan awal
Dari blok matriks K1 = BINER, ambil bit K1 K1 dengan pola pengambilan D
Dari BINER = blok matriks K1, masukkan BINER K1 dengan pola pemasukan proses 1
Output K1 Print C1
C1 = P2 C2 <- P2 ⊕ K2
Dari C1 = blok matriks P2, masukkan C1 P3 menggunakan Pola pemasukan awal
Dari blok matriks P2 = BINER, ambil bit P2 dengan pola Tari Purisari Pati C
BINER to HEXA
Dari HEXA = Tabel S-box, masukkan HEXA HEXA konversi menggunakan S-box
Print BINER S-box
Dari BINER = blok matriks P2, masukkan BINER P2 menggunakan pola pemasukan proses 2 Output P2
Dari K1 = blok matriks K2, masukkan K2
Dari blok matriks K2 = BINER, ambil bit K2 K2 dengan pola pengambilan C
Dari BINER = blok matriks K2, masukkan BINER K2 K3 menggunakan pola pemasukan proses 2
Output K2 Print C2
C2 = P3 C3 <- P3 ⊕ K3
Dari C2 = blok matriks P3, masukkan C2 P2 menggunakan Pola pemasukan awal
Dari blok matriks P3= BINER, ambil bit P2 dengan pola Tari Purisari Pati A
Dari BINER = blok matriks P3, masukkan BINER P3 dengan pola pemasukan proses 3
Input K Read K
K to ASCII ASCII to BINER
Dari BINER = blok matriks K3, masukkan BINER K1 menggunakan Pola pemasukkan awal
Dari blok matriks K3 = BINER, ambil bit K3 K3 dengan pola pengambilan A
Dari BINER = blok matriks K3, masukkan BINER K3 dengan pola pemasukan proses 3
Output K3 Print C3
C3 = P4
C4 <- P4 ⊕ K4
Dari C3 = blok matriks P4, masukkan C3 P4 menggunakan Pola pemasukan awal
Dari blok matriks P4 = BINER, ambil bit P4 dengan pola Tari Purisari Pati B
BINER to HEXA
Dari HEXA = Tabel S-box, masukkan HEXA HEXA konversi menggunakan S-box
Print BINER S-box
Dari BINER = blok matriks P4, masukkan BINER P3 menggunakan pola pemasukan proses 4 Output P4
N Dari K3 = blok matriks K4, masukkan K3
Dari blok matriks K4 = BINER, ambil bit K4 K4 dengan pola pengambilan B
Dari BINER = blok matriks K4, masukkan BINER K4 K4 menggunakan pola pemasukan proses 4
Output K4 Print C4
Repeat
End
Proses Dekripsi
{Program ini digunakan untuk melakukan proses dekripsi data}
Kamus
Dari BINER = blok matriks K1, masukkan BINER K1 menggunakan Pola pemasukan awal
Dari blok matriks K1 = BINER , ambil bit K1 K1 dengan pola Tari Purisari Pati B
Dari BINER = blok matriks K1, masukkan BINER K1 Output K1
K1 = K2
Dari K1 = blok matriks K2, masukkan Bit K1 dengan pola pemasukan awal
Dari blok matriks K2 = BINER, ambil bit K2 dengan pola pengambilan B
Dari BINER = blok matriks K2, masukkan BINER K2
Output K2 K2 = K3
Dari K2 = blok matriks K3, masukkan Bit K2 K2 dengan pola pemasukan awal
Dari blok matriks K3 = BINER, ambil bit K3 K3 dengan pola pengambilan A
Output K3 K3 = K4
Dari K3 = blok matriks K4, masukkan K3
Dari blok matriks K4 = BINER, ambil bit K4 K4 dengan pola pengambilan A
Dari BINER = blok matriks K4, masukkan BINER K4 Output K4
Dari BINER = blok matriks C4, masukkan BINER C4 ⊕ K4
Print P4
Dari blok matriks P4 = BINER, ambil bit P4
Dari BINER P4 = blok matrik P4, masukkan BINER Menggunakan pola pengambilan C
Output P4 P4 = C3
P3 <- C3 ⊕ K3
Dari P4 = blok matriks C3, masukkan BINER C3 ⊕ K3
Print P3
Dari blok matriks P3 = BINER, ambil bit P3 BINER to HEXA
Dari HEXA = Tabel S-Box, masukkan HEXA HEXA ditranformasi menggunakan S-Box
Dari BINER P3 = blok matriks P3, masukkan BINER Menggunakan pola pengambilan C
Output P3 P3 = C2
P2 <- C2 ⊕ K2
Dari P3 = blok matriks C2, masukkan BINER C2 ⊕ K2
Print P2
Dari blok matriks P2 = BINER, ambil bit P2 Dari BINER P2 = blok matriks P2, masukkan BINER
Menggunakan pola pengambilan D
Output P2 P2 = C1
P1 <- C1 ⊕ K1
Dari P2 = blok matriks C1, masukkan BINER
C1 ⊕ K1
Print P1
Dari blok matriks P1 = BINER, ambil bit P1
BINER to HEXA
Dari HEXA = Tabel S-Box, masukkan HEXA HEXA ditranformasi menggunakan S-Box
Dari BINER P1 = blok matriks P1, masukkan BINER Menggunakan pola pengambilan D
Pengujian korelasi digunakan untuk mengukur perbandingan antara plaintext
Sebaliknya jika mendekati angka 0 maka plaintext dan ciphertext memiliki hubungan yang lemah.
Tabel 5 Nilai Korelasi Setiap Putaran
Tabel 5 setiap putarannya menunjukkan nilai korelasi lemah sehingga dapat disimpulkan bahwa algoritma kriptografi block cipher 64 bit menggunakan Pola Tari Purisari Pati dapat menghasilkan nilai korelasi enkripsi acak yang dapat dibuat dalam bentuk grafik pada Gambar 12.
Gambar 12 Grafik Perbandingan Plaintext dan Ciphertext
Gambar 12 menunjukkan bahwa antara putaran satu dan putaran yang lain memiliki perbedaan yang signifikan antara plaintext dan ciphertext. Pengujian
Avalanche Effect dilakukan untuk mengetahui perubahan bit yang ada ketika
Putaran Korelasi Putaran Korelasi
1 0,354039771 11 0,002922037
2 -0,578739762 12 0,383432036
3 -0,444912572 13 0,211143616
4 0,31913001 14 0,093750068
5 0,047055334 15 0,234170445
6 0,433795044 16 -0,058890056
7 0,400862502 17 -0,695956459
8 0,426132324 18 0,152715404
9 -0,182677669 19 -0,076081575
plaintext diubah. Pengujian dilakukan dengan merubah karakter yang terdapat pada
plaintext awal, sehingga akan menghasilkan perbedaan pada setiap putaran.
Gambar 13 Grafik Avalanche Effect
Pada Gambar 13 yaitu hasil dari pengujian Avalanche Effect, pada penelitian ini plaintext awal adalah Iv4Nd1KY yang kemudian diubah menjadi AnaKPAt1. Pada putaran ke 14 perubahan bitnya terjadi cukup besar yaitu 70,3125%, tetapi juga terjadi perubahan bit yang kecil pada putaran ke 19 yaitu sebesar 29,6875%. Berdasarkan rata-rata hasil pengujian Avalanche Effect ini yaitu sebesar 49,21875%. Presentase setiap putaran dapat dilihat pada Tabel 6.
Tabel 6 Tabel Presentase Avalanche Effect
Jumlah Jumlah Putaran Bit Presentase (%) Putaran Bit Presentase (%)
berubah berubah
1 30 46,875 11 30 46,875 2 36 56,25 12 27 42,1875
3 32 50 13 30 46,875 4 38 59,375 14 45 70,3125
10 34 53,125 20 29 45,3125
Rata-Rata 49,21875%
5. Simpulan
Berdasarkan penelitian yang dilakukan, dapat disimpulkan bahwa kriptografi block cipher 64 bit menggunakan pola Tari Purisari Pati dapat dikatakan sebagai sistem kriptografi. Dalam proses enkripsi, rancangan kriptografi block cipher 64 bit menggunakan pola Tari Purisari Pati ini mengahasilkan output yang acak sehingga dapat digunakan sebagai alternatif dalam pengamanan data. Dalam pengujian avalanche effect yang dilakukan menunjukkan bahwa proses enkripsi di setiap putaran memiliki perubahan yang mencapai 49,21875%.
6. Daftar Pustaka
[1] J. Menezes, P.C. van Oorschot, and S.A. Vanstone, Handbook of Applied Cryptography, CRC Press, 1997.
[2] Pakereng, M. A. I., 2008, “Kriptografi menggunakan Algoritma Genetika
Pada Data Citra”. Salatiga : Fakultas Teknologi Informasi, Universitas Kristen Satya Wacana.
[3] Widodo, A, dkk., 2015 “Perancangan Kriptografi Block Cipher Berbasis
pada Teknik Tanam Padi dan Bajak Sawah”. Teknik Informatika, Fakultas
Teknologi Informasi, Universitas Kristen Satya Wacana.
[4] Bili, D. D. Pakereng, M. A. I., Wowor, A.D., 2015, Perancangan Kriptografi
Block Cipher Dengan Langkah Kuda. Salatiga: Jurusan Teknik Informatika Universitas Kristen Satya Wacana.
[5] Guntoro, Pakereng, M. A. I., 2016 “Perancangan Kriptografi Block Cipher
Berbasis Pola Ikan Berenang”. Teknik Informatika, Fakultas Teknologi
Informasi, Universitas Kristen Satya Wacana. [6] Munir, R., 2006, Kriptografi, Bandung: Informatika.
[7] R. Y. Adiningtyas. https://www.youtube.com/watch?v=oL9sG_DDvQk diambil pada tanggal 1 Agustus 2017 pukul 22:04 WIB.