Perancangan KriptografiBlock Cipher Berbasis Pola Notasi Balok 1/8
Artikel Ilmiah
Peneliti :
Lerry Godwin Andreas Nanariain (672012174) Magdalena A. Ineke Pakereng, M.Kom.
Program Studi Teknik Informatika Fakultas Teknologi Informasi Universitas Kristen Satya Wacana
1. Pendahuluan
Masalah keamanan dan kerahasian data adalah suatu hal yang sangat penting dalam melakukan pengiriman informasi dan komunikasi agar tidak terbaca atau diubah oleh pihak yang tidak berwenang. Dalam menjaga keamanan dalam pengiriman informasi dan komunikasi banyak macam cara atau metode untuk mengamankan suatu file atau data. Salah satunya adalah kriptografi.
Kriptografi merupakan metode untuk mengamankan data, baik data teks, maupun data gambar dengan cara mengubah data ke dalam bentuk data sandi sehingga data tersebut tidak dapat dikenali. Banyak metode kriptografi yang sudah dipecahkan oleh Kriptanalisis (Criptanalisys) dan kriptografi membutuhkan pembaruan, hal ini dikarenakan perkembangan teknologi yang semakin maju sehingga membuat kriptografi tidak bisa digunakan selamanya. Dalam penelitian ini merancang Algoritma Block Cipher 64 Bit dengan pola notasi balok 1/8. Block Cipher merupakan algoritma kriptografi simetris yang mengenkripsi satu block plaintext dengan jumlah bit tertentu dikombinasikan dengan tabel substitusi atauS-Box dan menghasilkan block ciphertext.
Pola Notasi Balok1/8 adalah simbol atau tanda untuk menyatakan tinggi rendahnya suara yang diwujudkan dengan gambar. Notasi balok disebut juga notasi mutlak karena mempunyai patokan tinggi nada yang tetap sehingga sangat efektif digunakan dalam bermain musik. Cara menggambarkan nilai not balok 1/8 yang terdiri dari bendera, tangkai dan kepala, digunakan sebagai pola dalam proses transposisi untuk pengambilan dan pemasukan bit plaintext pada setiap blok matriks. Kelebihan pola notasi balok 1/8 dengan metode yang lain yaitu pola ini diambil sebagai acuan karena memiliki pola yang cukup sederhana tetapi mampu menghasilkan bit yang acak pada kolom matriks.
Plaintext akan dimasukkan ke dalam blok-blok dimana setiap blok berjumlah 64 bit atau 8 Byte, dan terdapat 20 putaran dimana setiap putaran terdapat 4 proses untuk proses plaintext maupun proses kunci (key). Hasil dari proses plaintext akan di-XOR dengan kunci untuk menghasilkan Ciphertext yang kemudian byte-nya akan dikombinasikan dengan S-Box untuk menghasilkanAvalanche Effectyang besar.S-Boxyang digunakan dalam penelitian ini adalah S-BoxalgoritmaAES (Advanced Encryption Standard).
Berdasarkan permasalahan yang ada maka dilakukan penelitian yang membahas tentang perancangan kriptografi simetrisBlock Cipherberbasis pada pola notasi balok 1/8.
2. Tinjauan Pustaka
Penelitian sebelumnya terkait teknik kriptografi block cipher telah banyak dilakukan. Beberapa penelitian ini digunakan sebagai acuan dalam penelitian. Penelitian pertama berjudul
Pengaruh S-Box Advanced Encryption Standard (AES) Terhadap Avalanche Effect, yang membahas tentang Block Cipher256 Bit Berbasis Pola Teknik Tarian Dansa Tali Dari Maluku.
Hasil dari perancangan algoritma kriptografi ini proses enkripsi dimana hasil dari proses ke-2 dan ke-3 ditransformasi menggunakan tabel substitusi S-Box sehingga menghasilkan Ciphertext yang lebih acak pada pengujian Avalanche Effect yang sudah mencapai 50% sehingga dapat digunakan sebagai alternatif dalam pengamanan data [1].
dapat menghasilkan kriptografi simetris dan dapat memenuhi lima-tuple (Five-tuple). Penelitian ini dapat membandingkan proses keacakan dan proses nilai diferensiasi antara KS dengan AES-128. Hasil perbandingan dengan AES-128, rancangan berbasis langkah kuda lebih cepat 0.94869906 ms [2].
Penelitian ketiga berjudul Perancangan Algoritma Kriptografi Block Cipher 256-Bit Berbasis pada Pola Tuangan Air. Dalam penelitian ini, perancangan kriptografi menggunakan pola tuangan air untuk pengambilan dan pemasukan bit yang dikombinasikan dengan tabel substitusi. Hasil dari penelitian ini yaitu algoritma kriptografiblock cipher 256-bit berbasis pola tuangan air menghasilkan hasil enkripsi yang acak [3].
Berdasarkan penelitian-penelitian yang sudah ada terkait perancangan algoritma kriptografi simetris Block Cipher maka dilakukan penelitian yang berjudul Perancangan Kriptografi Simeteris Block Cipher Berbasis Pola Notasi Balok 1/8. Perbedaan penelitian ini dengan penelitian sebelumnya adalah jumlah data yang diproses adalah sebanyak 64-bit kemudian dienkripsi dengan pola notasi balok sebagai pola pengambilan, dan juga dibuat kombinasi sebanyak 24 kombinasi yang memiliki masing-masing kombinasi berbeda dan bertujuan untuk mencari korelasi terendah sebagai pola yang paling optimal.
Kriptografi (cryptography) berasal dari Bahasa Yunani Kriptografi adalah ilmu sekaligus seni untuk menjaga keamanan pesan (message) [4]. Kriptografi adalah ilmu sekaligus seni untuk menjaga kerahasiaan data [5]. Proses menyandikan plaintext menjadiciphertext disebut enkripsi (encryption) atau enciphering, sedangkan proses mengembalikan ciphertext menjadi plaintext disebut dekripsi (decryption) ataudeciphering[6].
Setiap block Cipher memproses text dengan block yang panjangnya 64-bit, untuk mempersulit teknik kriptanalisis dalam membongkar kunci. Block Cipher juga merupakan algoritma kunci simetri atau kriptografi kunciprivate, dimana kunci untuk enkripsi sama dengan kunci untuk dekripsi. Skema proses enkripsi dan dekripsi block ciphersecara umum ditunjukkan pada Gambar 1.
Gambar 1Skema Dasar Proses Enkripsi-Dekripsi PadaBlock Cipher[7]
Misalkanblock plaintext(P) yang berukuran n bit
p
p
p
n
P
1,
2,
,
(1)Block ciphertext(C) makablock Cadalah
c
c
c
n
C
1,
2,
,
(2)Kunci (K) maka kunci adalah
k
k
k
n
Sehingga proses enkripsi adalah
Sebuah kriptografi dapat dikatakan sebagai suatu teknik kriptografi harus melalui uji kriptosistem terlebih dahulu yaitu diuji dengan metode Stinson. Sebuah sistem akan dikatakan sebagai sistem kriptografi jika memenuhi lima-tuple(Five tuple) (P, C, K, E, D) yang memenuhi kondisi [8]:
1. Padalah himpunan berhingga dariplaintext,
2. Cadalah himpunan berhingga dariciphertext,
3. Kmerupakan ruang kunci (keyspace), adalah himpunan berhingga dari kunci,
4. Untuk setiap , terdapat aturan enkripsi dan berkorespodensi dengan aturan
dekripsi t Setiap dan adalah fungsi sedemikian
hingga untuk setiapplaintext t
Untuk menguji nilai algoritma yang dirancang memiliki hasil ciphertext yang acak dari plaintext maka digunakan Persamaan 6, dimana variable X merupakan plaintext dan Y merupakanciphertext.
nΣxy – (Σx) (Σy)
{nΣx² – (Σx)²} {nΣy² – (Σy)²} (6)
Dimana:
n =Banyaknya pasangan data X dan Y Σx =Total jumlah dari variabel X Σy =Total jumlah dari variabel Y
Σx2 =Kuadrat dari total jumlah variabel X Σy2 =Kuadrat dari total jumlah variabel Y
Σxy =Hasil perkalian dari total jumlah variabel X dan variabel Y
Untuk mengetahui nilai keacakan dari hasil enkrispsi antara ciphertext dengan plaintext digunakan diferensiasi data yang dimana perbandingan selisih antara dua titik dalam kalkulus. Metode ini sering disebut sebagai turunan atau kemiringan dari data. Jika diberikan kumpulan data ((x1,y1,), (x2,y2,), (x3,y3,),….(xn,yn)) dengan syarat bahwa xi < xi+1 dimana i = 1,…n. Data
tersebut dapat divisualisasikan kedalam koordinatcarteciusuntuk setiapxsebagai variabel bebas danyatau kadang ditulis sebagai f(x)sebagai variabel tak bebas. Untuk menentukan diferensiasi data pada dua titik maka persamaan yang dapat dibentuk seperti Persamaan 7.
Δ
Δ
=
( ʠ� 钨)
( 钨� ʠ) (7)
korelasi dalam sebuah kriptografi, maka tingkat hubungan koefisien berhubungan dan tergantung dengan pemilihan kunci yang dikombinasikan.
Tabel 1Klasifikasi Koefisien Korelasi [9]
Interval Koefisien Tingkat Hubungan
0,00 – 0,199 Sangat Rendah
0,20 – 0,399 Rendah
0,40 – 0,599 Sedang
0,60 – 0,799 Kuat
0,80 – 1,000 Sangat Kuat
3. Metode dan Perancangan Algoritma
Tahapan yang dilakukan dalam penelitian ini, terdiri dari 5 (lima) tahapan, yaitu: (1) Identifikasi Masalah, (2) Pengumpulan Data, (3) Perancangan Kriptografi, (4) Pengujian Kriptografi, dan (5) Penulisan Artikel Ilmiah.
Gambar 2Tahapan Penelitian
Tahapan penelitian pada Gambar 2 dapat dijelaskan sebagai berikut: Tahap Identifikasi masalah: Merupakan tahapan awal dalam melakukan penelitian untuk melihat masalah-masalah keamanan informasi yang berkaitan dengan kriptografi yaitu pencurian data, baik data teks, maupun data gambar; Tahap Pengumpulan data : Dalam tahapan ini dilakukan pengumpulan referensi dari buku, jurnal, atau sumber lain yang berguna dalam perancangan kriptografi;Tahap Perancangan Kriptografi : Pada tahap ini akan dilakukan perancangan Kriptografi berbasis teknik pola notasi balok 1/8, untuk pembuatan kunci, proses enkripsi dan dekripsinya yang pada plaintext ke-3 disubstitusi dengan tabels-box; Tahap Pengujian Kriptografi: Setelah rancangan kriptografi dibuat dibutuhkan pengujian algoritma. Pengujian dilakukan dengan cara manual dimana plaintext diubah ke dalam bit untuk melakukan proses enkripsi, proses dekripsi dan pengujian avalanche effect; Tahap Penulisan Artikel Ilmiah : Dalam tahap akhir ini dilakukan penulisan artikel tentang Perancangan KriptografiBlock CipherBerbasis 64 Bit Pada Pola Notasi
Identifikasi Masalah
Pengumpulan Data
Perancangan Kriptografi
Pengujian Kriptografi
Balok 1/8. Adapun batasan masalah dalam penelitian ini yaitu: 1) Proses enkripsi dan proses dekripsi dibuat pada data teks; 2) Proses perancangan ini mengunakan teknik pola notasi balok; 3) Jumlah plaintext dan kunci dibatasi yaitu menampung 16 karakter serta proses putaran terdiri dari 5 putaran; 4) Panjangblockadalah 64-bit.
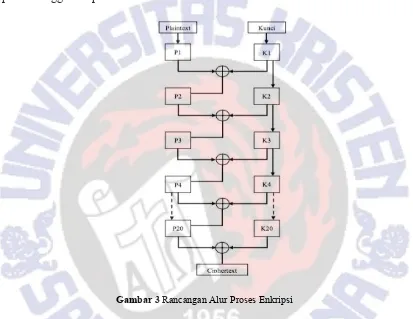
Dalam penelitian ini, perancangan Kriptografi Block Cipher 64 Bit berbasis pola notasi balok 1/8, dilakukan dalam 4 (empat) proses enkripsi ditunjukkan dalam Gambar 3. Plaintext dikonversikan ke dalam bentuk biner sesuai dengan tabel ASCII, kemudian rangkaian bilangan biner dimasukkan pada matriks 8x8 sesuai pola, dan bilangan biner di dalam matriks diambil sesuai pola sehingga didapatkan P1.
Gambar 3Rancangan Alur Proses Enkripsi
Gambar 4Rancangan Alur Proses Dekripsi
Gambar 4 merupakan rancangan alur proses dekripsi. Merupakan kebalikan dari proses enkripsi, sehingga kunci yang digunakan untuk enkripsi sama dengan proses dekripsi. Proses dekripsi pada perancangan dan implementasi algoritma kriptografi block cipher berbasis pada pola notasi balok 1/8.
4. Hasil dan Pembahasan
Dalam bagian ini akan membahas mengenai algoritma perancangan kriptografi block cipher 4 bit berbasis pola teknik notasi balok 1/8 yang ditunjukkan dalam Gambar 5 secara terperinci. Bagian ini juga akan membahas tentang proses enkripsi dan dekripsi.
Gambar 5Notasi Balok 1/8
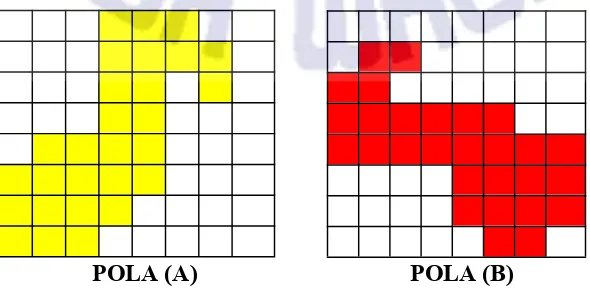
Dalam algoritma ini pola notasi balok 1/8 digunakan untuk proses pengambilan bit di dalam matriksplaintext. Pola notasi balok memiliki pola seperti yang ditunjukkan dalam Gambar 6.
POLA (C) POLA (D)
Gambar 6Pola Berbasis Teknik Notasi Balok
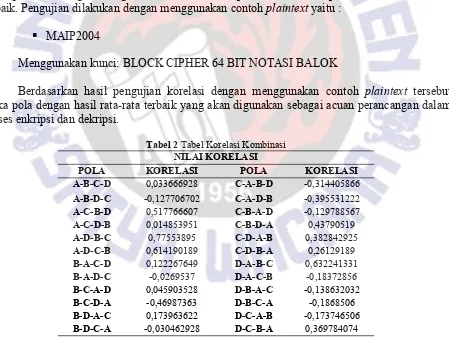
Pada Gambar 6 terdapat 4 (empat) pola yang berbeda dimana pada pola-pola tersebut dapat dijelaskan di dalam notasi balok yang dituangkan dalam bentuk gambar. Berdasarkan pola-pola yang sudah dirancang, dilakukan pengujian korelasi atau nilai keterikatan antara plaintext dan ciphertext dengan mengkombinasikan urutan pola untuk mendapatkan rata-rata korelasi terbaik. Pengujian dilakukan dengan menggunakan contohplaintextyaitu :
MAIP2004
Menggunakan kunci: BLOCK CIPHER 64 BIT NOTASI BALOK
Berdasarkan hasil pengujian korelasi dengan menggunakan contoh plaintext tersebut maka pola dengan hasil rata-rata terbaik yang akan digunakan sebagai acuan perancangan dalam proses enkripsi dan dekripsi.
Tabel 2Tabel Korelasi Kombinasi NILAI KORELASI
POLA KORELASI POLA KORELASI
A-B-C-D 0,033666928 C-A-B-D -0,314405866 A-B-D-C -0,127706702 C-A-D-B -0,395531222 A-C-B-D 0,517766607 C-B-A-D -0,129788567 A-C-D-B 0,014853951 C-B-D-A 0,43790519 A-D-B-C 0,77553895 C-D-A-B 0,382842925 A-D-C-B 0,614190189 C-D-B-A 0,26129189 B-A-C-D 0,122267649 D-A-B-C 0,632241331 B-A-D-C -0,0269537 D-A-C-B -0,18372856 B-C-A-D 0,045903528 D-B-A-C -0,138632032 B-C-D-A -0,46987363 D-B-C-A -0,1868506 B-D-A-C 0,173963622 D-C-A-B -0,173746506 B-D-C-A -0,030462928 D-C-B-A 0,369784074
ciphertext. Kemudian dilanjutkan dengan proses perhitungan nilai korelasi pada setiap putaran menggunakkan pola terbaik A-C-D-B sampai putaran ke-20.
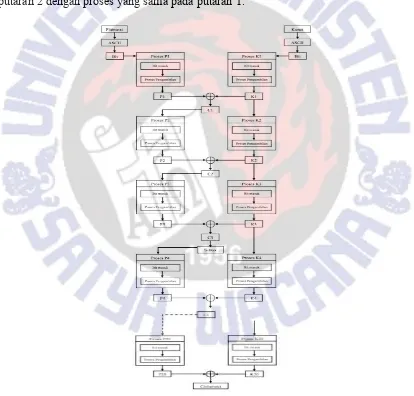
Perancangan algoritma kroptografi Block Cipher 64 bit berbasis pola notasi balok dilakukan dalam 20 putaran untuk mendapatkan ciphertext dan plaintext dalam setiap putaran terdapat 4 (empat) proses. Proses enkripsi secara umum dapat dilihat pada Gambar 7. Pada proses enkripsi plaintext dan kunci dikonversi menjadi ASCII kemudian diubah ke bilangan biner. Plaintext kemudian dimasukkan ke dalam kolom matriks 8x8 menggunakan pola pemasukan bit dan dilakukan pengambilan dengan pola notasi balok yang berbeda-beda pada setiap proses. Putaran 1 proses pertama menghasilkan bit C1 di mana bit C1 didapat dari hasil XOR antara bit P1 yang telah mengalami pengacakan dengan bit K1 dilakukan proses yang sama sampai pada proses ketiga. Setelah proses ketiga diacak menghasilkan bit C3 kemudian dikonversikan ke heksadesimal dan ditransformasikan ke dalam tabel subtitusi S-Box. Kemudian hasil bit C3 dimasukkan ke proses 4 dan menghasilkan C4 kemudian Ciphertext 4 dimasukkan pada putaran 2 dengan proses yang sama pada putaran 1.
Gambar 7Bagan Proses Enkripsi
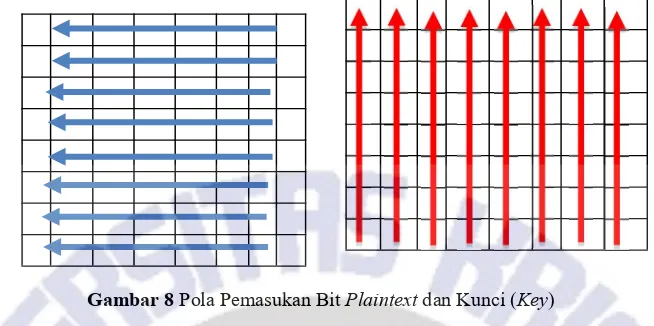
setiap bit yang merupakan hasil konversiplaintextmaka urutan bit adalah sebagai berikut 1, 2, 3, 4, ... 64.
Gambar 8Pola Pemasukan BitPlaintextdan Kunci (Key)
Gambar 8 menjelaskan proses pemasukan bit karakter Plaintext dan Kunci. Setiap pemasukan bit dimasukkan dari arah kanan atas ke kiri bawah, dan untuk pemasukan kunci dimulai dari arah bawah ke atas.
Gambar 9Pola Transposisi BitPlaintextProses 1
Gambar 9 merupakan proses pengambilan dan pemasukan plaintext. Bit diambil mengikuti urutan angka (1, 2, 3, … 28) kemudian dilanjutkan dengan urutan angka (29, … 64) pada gambar yang berwana kuning. Kemudian dimasukkan kembali ke dalam kolom matriks dari kiri bawah ke kanan atas mengikuti anak panah dengan urutan angka dimulai dari (1-8, 9-16, … 57-64) pada Gambar 9.
Gambar 10 menjelaskan tentang proses pengambilan bit pada proses 1. Bit di ambil setiap 8 bit dengan pola pengambilan dari arah kanan atas hingga kiri bawah dari angka (1, 2, 3, ... 64). Kemudian dimasukkan kembali ke dalam kolom matriks dari kiri bawah mengikuti urutan angka (1, 2, 3, ... 64) dan anak panah. Hasil dari transposisi plaintext dan kunci kemudian di-XOR sehingga menghasilkanciphertext1 yang kemudian digunakan sebagai P2 pada proses ke-2.
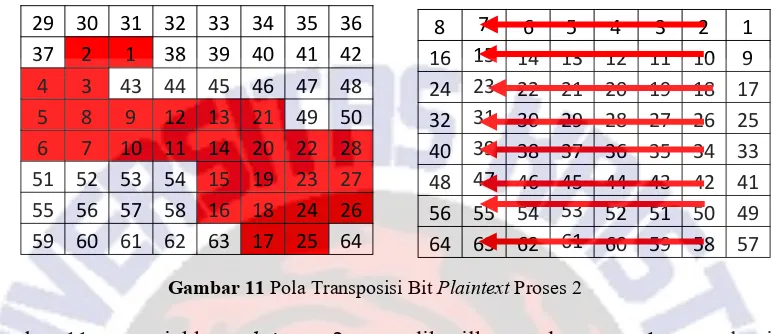
Gambar 11Pola Transposisi BitPlaintextProses 2
Gambar 11 menunjukkan plaintext 2 yang dihasilkan pada proses 1 mengalami proses pengambilan setiap 8 bit mengikuti urutan angka pada gambar dengan urutan angka (1, 2, 3, … 28) Kemudian dimasukkan kembali ke dalam kolom matriks dari kanan atas mengikuti anak panah dan urutan angka hingga berakhir pada angka 64.
Gambar 12Pola Transposisi Bit Kunci Proses 2
Gambar 12 merupakan proses pengambilan dan pemasukan bit kunci pada proses 2. Pengambilan diambil setiap 8 bit mengikuti urutan angka secara horizontal, dimulai dari kanan bawah hingga berakhir pada bagian kiri atas dari angka (1-8, 9-16, … 57-64) pada gambar kiri. Kemudian pada gambar bagian kanan dimasukkan kembali mengikuti anak panah secara vertikal dengan urutan angka (1-8, 9-16, … 57-64) pada gambar kanan. Hasil dari transposisi plaintext dan kunci di-XOR kemudian menghasilkanciphertext2.
Ciphertext3 kemudian diambil setiap 8 bit sesuai dengan pola pemasukan pada P2. Hasil dari pengambilan C2 dikonversi ke bilangan heksadesimal kemudian ditransposisi ke dalam tabel substitusi S-Box. Hasil transposisi kemudian dikonversi kembali ke bilangan biner dan dimasukkan ke dalam kolom matriks yang akan dijadikan sebagai P3 pada proses 3. S-Box sendiri berfungsi untuk TransformasiSubBytes()memetakan setiapbytedariarraystate.
Gambar 13Tabel SubstitusiS-BoxAES
Gambar 13 merupakan tabel substitusiS-boxyang digunakan dalam proses enkripsi. Cara pensubstitusian adalah sebagai berikut: untuk setiapbyte padaarray state, misalkan S[r,c] =xy, yang dalam hal ini xy adalah digit heksadesimal dari nilai S[r, c], maka nilai substitusinya, dinyatakan dengan S’[r,c], adalah elemen di dalam S-box yang merupakan perpotongan baris x dengan kolomy.MisalnyaS[0, 0] = 19, maka S’[0, 0] = d4.
Untuk pengujian algoritma dilakukan dengan mengambil plaintextadalah MAIP2004dan kunci adalah BLOCK CIPHER 64 BIT NOTASI BALOK 1/8. Setelah melewati proses enkripsi dan proses dekripsi yang telah dijabarkan sebelumnya maka mendapatkan ciphertext yang telah dikonversi ke dalam nilaihexadecimal.
Tabel 3HasilCiphertextSetiap Putaran Putaran Plaintext HasilHexadecimal Char
1 MAIP2004 CE31C33148A263 Œ1√1H&
2 Œ1√1H& 904CD2472F523A êL“G/R
3 êL“G/R FAA83A610A0F8CD ˙®¶†¯Õ
4 ˙®¶†¯Õ 5238BDE7D2762C4F R8ΩÁ“v,O
5 R8ΩÁ“v,O 3A768D4A9DDE8AB :vçJùfiä
6 :vçJùfiä D462F4CD8F55BBA ‘bÙÕèU∫
7 ‘bÙÕèU∫ D462F4CD8F55BBA ‘bÙÕèU∫
8 ‘bÙÕèU∫ 9A245BC6A0906DCD ö$[∆†êmÕ
9 ö$[∆†êmÕ 37984679D2E7F544 7òFy“ÁıD
10 7òFy“ÁıD 7A3484CDC3CBE391 z4ÑÕ√À„ë
11 z4ÑÕ√À„ë A244EE2BF6A6895 ¢D‚øjhï
12 ¢D‚øjhï 26C7AD45F9C7AE9A &«≠E˘«Æö
13 &«≠E˘«Æö 4C5EEF1024BC548F L^Ô$ºTè
14 L^Ô$ºTè 5FDD2F49A3014EE _“Ùö0Ó
15 _“Ùö0Ó 232B4E3D52438BB9 #+N=RCãπ
16 #+N=RCãπ 432FBC102A5575CF C/º*Uuœ
17 C/º*Uuœ 61ADB3C2EC5798E a≠≥¬ÏWò
18 a≠≥¬ÏWò 571D32301CE42ED4 W20‰.‘
19 W20‰.‘ 6A271170D1D6A88D j'p—÷®ç
Tabel 3 merupakan hasil enkripsi dari setiap putaran. Hasil dari putaran 20 merupakan final ciphertext.
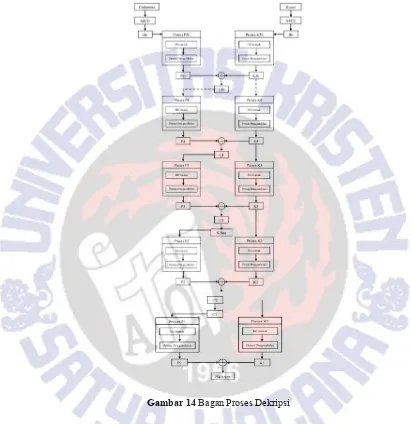
Proses dekripsi merupakan kebalikan dari proses enkripsi. Dekripsi dilakukan dengan memproses kunci sampai putaran ke-20 kemudian ciphertextdimasukkan dengan k4 pada proses keempat.
Gambar 14Bagan Proses Dekripsi
Gambar 14 menunjukkan alur proses pengembalian ciphertext dan plaintext. Pola yang digunakan sebagai pola pengambilan bit pada proses enkripsi akan digunakan sebagai pola pemasukan pada proses dekripsi. Sebaliknya pola pemasukan yang akan digunakan pada proses enkripsi akan digunakan sebagai pola pengambilan proses dekripsi sehingga dapat dikatakan pola notasi balok 1/8 digunakan sebagai pola pemasukan bit pada proses dekripsi.
Gambar 15Pola Transposisi BitPlaintextProses 20
Gambar 15 merupakan pola transposisi dekripsi pada proses 20. Bit hasil XOR C20 dan K20 diambil menggunakan pola pada gambar bagian kanan. Setiap 8 bit diambil dari kanan atas ke kiri bawah mengikuti anak panah pada urutan angka pada kolom matriks. Kemudian bit dimasukkan kembali menggunakan pola notasi balok 1/8 pada gambar bagian kiri mengikuti urutan angka (1, 2, 3, … 28) dengan pola berwarna biru dan dilanjutkan dengan urutan angka (29, 30, … 64). Hasil dari dekripsi proses 20 kemudian dijadikan sebagai ciphertext 19 pada proses 19.
Gambar 16Pola Transposisi BitPlaintextProses 19
Tabel 4Algoritma Proses Enkripsi dan Dekripsi.
Tabel 4 merupakan algoritma proses enkripsi dan dekripsi. Proses enkripsi menghasilkan C4 sedangkan proses dekripsi menghasilkan P1.
Algoritma proses Kunci (Key) dijelaskan sebagai berikut : 1. Masukkan Kunci
2. Kunci diubah ke ASCII
Algoritma Proses Enkripsi Algoritma Proses Dekripsi
1. Masukkanplaintext
2. Plaintextdiubah ke ASCII 3. ASCII diubah ke BINER
4. Bit BINER dimasukkan ke kolom P1 menggunakan pola masukPlaintext 5. Bit P1 ditransposisikan dengan pola Notasi
Balok 1/8 A
6. P1 di-XOR dengan K1 menghasilkan C1 7. C1 = P2
8. Bit P2 ditransposisikan menggunakan pola Notasi Balok 1/8 C
9. P2 di-XOR dengan K2 menghasilkan C2 10. C2 diubah ke BINER
11. BINER diubah ke HEXA
12. Hasil HEXA invers diubah ke BINER 13. BINER dimasukkan ke dalam kolom P3
menggunakan pola masukplaintext 14. Bit P3 ditransposisikan menggunakan pola
Notasi Balok 1/8 D
15. P3 di-XOR dengan K3 menghasilkan C3 16. C3 diubah ke BINER
17. BINER diubah ke HEXA
18. HEXA dimasukkan ke dalam tabel S-BOX 19. Hasil HEXA invers diubah ke BINER 20. BINER dimasukkan ke dalam kolom P4
menggunakan pola masukplaintext 21. Bit P4 ditransposisikan menggunakan pola
Notasi Balok B
22. P4 di-XOR dengan K4 menghasilkan C4 23. C4 diubah ke BINER
24. BINER diubah ke ASCII 25. ASCII diubah ke HEXA
. . .
26. BINER dimasukkan ke dalam kolom P20 menggunakan pola masukplaintext 27. Bit P20 ditransposisikan menggunakan
pola Notasi Balok B
28. P20di-XOR dengan K20 menghasilkan C20
29. C20 diubah ke BINER 30. BINER diubah ke ASCII 31. ASCII diubah ke HEXA
1. Masukkan C20 2. C20 diubah ke ASCII 3. ASCII diubah ke BINER
4. Bit BINER dimasukkan ke kolom P20 menggunakan pola masukPlaintext 5. C20 di-XOR dengan K20
6. Hasil XOR ditransposisikan terbalik dengan pola Notasi Balok 1/8 B menghasilkan P20
7. Bit P20 diubah ke BINER 8. BINER diubah ke HEXA
9. Hasil HEXA invers diubah ke BINER .
. .
10. Masukkan C4 11. C4 diubah ke ASCII 12. ASCII diubah ke BINER
13. Bit BINER dimasukkan ke kolom P4 menggunakan pola masukPlaintext 14. C4 di-XOR dengan K4
15. Hasil XOR ditransposisikan terbalik dengan pola Notasi Balok 1/8 B menghasilkan P4
16. Bit P4 diubah ke BINER 17. BINER diubah ke HEXA
18. Hasil HEXA invers diubah ke BINER 19. BINER dimasukkan ke dalam kolom C3
menggunakan pola masukplaintext 20. C3 diXOR dengan K3
21. Hasil XOR ditransposisikan terbalik dengan pola Notasi Balok 1/8 D menghasilkan P3
22. Bit P3 diubah ke BINER 23. BINER diubah ke HEXA
24. HEXA dimasukkan ke dalam tabel S-BOX 25. Hasil HEXA invers diubah ke BINER 26. BINER dimasukkan ke dalam kolom C2
menggunakan pola masukplaintext 27. C2 di-XOR dengan K2
28. Hasil XOR ditransposisikan terbalik dengan pola Notasi Balok 1/8 C menghasilkan P2
29. P2 = C1
30. C1 di-XOR dengan K1
31. Hasil XOR ditransposisikan terbalik dengan pola Notasi Balok A menghasilkan P1
3. ASCII diubah ke BINER
4. Bit BINER dimasukkan ke kolom K1 menggunakan pola masuk Kunci 5. Bit Kunci ditransposisikan dengan pola Kunci A
6. Transposisi K1 = K2
7. K2 ditransposisikan menggunakan pola Kunci C 8. Transposisi K2 = K3
9. K3 ditransposisikan menggunakan pola Kunci D 10. Transposisi K3 = K4
11. K4 ditransposisikan menggunakan pola Kunci B
Pseudocodeproses enkripsi dan dekripsi dijelaskan sebagai berikut :
Proses Enkripsi
{Program ini digunakan untuk melakukan proses enkripsi data} Kamus
Dari BINER = kolom matriks P1, masukkan BINER
P1 Transposisi mengunakan Pola Notasi Balok 1/8 A Output P1
Input K Read K
K to ASCII ASCII to BINER
Dari BINER = kolom matriks K1, masukkan BINER K1 Transposisi mengunakan Kunci A Output K1
Print C1 C1 = P2 C2 <- P2⨁K2
Dari C1 = kolom matriks P2, masukkan C1
P2 Transposisi menggunakan Pola Notasi Balok 1/8 C Output P2
Dari K1 = kolom matriks K2, masukkan K1
K2 Transposisi menggunakan pola Kunci C Ouput K2
Print C2 C2 = P3 C3 <- P3⨁K3
Dari BINER S-Box = kolom matriks P3, Masukkan BINER S-Box P3 Transposisi menggunakan pola Notasi Balok D Output P3
Dari K2 = kolom matriks K3, masukkan K2
K3 Transposisi menggunakan pola Kunci D Output K3
Print C3
Biner S-Box <- Invers Hexa C3 C3 to BINER BINER to HEXA
Dari HEXA = Tabel S-Box, masukkan HEXA HEXA Substitusi menggunakan S-Box Print BINER S-Box
Return Biner S-Box BINER S-box = P3 C2 <- P2⨁K2
Dari BINER S-BOX = kolom matriks P4, masukkan BINER S-Box P4 Transposisi menggunakan Pola Notasi Balok B Output P4
K4 Transposisi menggunakan pola Kunci B
Biner S-Box <- Invers Hexa C19 C19 to BINER BINER to HEXA
Dari HEXA = Tabel S-Box, masukkan HEXA HEXA Substitusi menggunakan S-Box Print BINER S-Box
Return Biner S-Box BINER S-box = P19 C18 <- P18⨁K18
Dari BINER S-BOX = kolom matriks P20, masukkan BINER S-Box P20 Transposisi menggunakan Pola Notasi Balok B Output P20
Dari K19 = kolom matriks K20, masukkan K19 K20 Transposisi menggunakan pola Kunci B Ouput K
Print C20 Repeat
End
Proses Dekripsi
{Program ini digunakan untuk melakukan proses dekripsi data} Kamus
Dari BINER = kolom matriks K19, masukkan BINER K19 Transposisi menggunakan pola Kunci B Output K20
. . .
K2 <- Traposisi K1 Input K Read K
K to ASCII ASCII to BINER
Dari BINER = kolom matriks K1, masukkan BINER K1 Transposisi menggunakan pola Kunci B Output K2
K3 <- Traposisi K2
K2 Transposisi mengunakan pola Kunci D Output K3
K4 <- Traposisi K3
K3 Transposisi mengunakan pola Kunci C Output K4
K4 Transposisi menggunakan pola Kunci A P20<- Transposisi dari hasil C20⨁K20
Input C Read C
C20 to ASCII ASCII to BINER
Dari BINER = kolom matriks C20, masukkan BINER C20⨁K20
Transposisi terbalik menggunakan Pola Notasi Balok 1/8 B Print P20
. . .
Input C Read C
C4 to ASCII ASCII to BINER
Dari BINER = kolom matriks C4, masukkan BINER C4⨁K4
Transposisi terbalik menggunakan Pola Notasi Balok 1/8 B Print P4
P3 <- Transposisi dari hasil C3⨁K3 Biner S-Box <- Invers Hexa P4 P4 to BINER
BINER to HEXA
Dari HEXA = Tabel S-Box, masukkan HEXA HEXA Substitusi menggunakan S-Box
Dari BINER S-Box = kolom matriks C3, Masukkan BINER S-Box C3⨁K3
Transposisi terbalik menggunakan Pola Notasi Balok 1/8 D Print P3
P2 <- Transposisi dari hasil C3⨁K3 P3⨁K
Transposisi terbalik menggunakan Pola Notasi Balok 1/8 C Print P2
P2=C1
P1<- Transposisi dari hasil C1⨁K1 P2⨁K2
Transposisi terbalik menggunakan Pola Notasi Balok 1/8 A Print P1
Pengujian korelasi digunakan untuk mengukur seberapa acak perbandingan antara hasil enkripsi (ciphertext) dan plaintext. Nilai korelasi sendiri berkisar 1 sampai -1, dimana jika nilai korelasi mendekati 1 maka plaintextdan ciphertext memiliki hubungan yang sangat kuat, tetapi jika mendekati 0 makaplaintextdanciphertextmemiliki hubungan yang tidak kuat.
Tabel 5Nilai Korelasi Putaran
KORELASI
PUTARAN KORELASI PUTARAN KORELASI
1 0,619602687 11 0,04988338
2 -0,298160952 12 -0,346887879
3 -0,125159327 13 0,042299117
4 0,488745578 14 -0,270476923
5 0,074659043 15 0,501202893
6 0,613336628 16 -0,654631272
7 0,613336628 17 0,137061567
8 -0,082491026 18 0,022467997
9 0,652056687 19 -0,073162722
10 -0,798533303 20 -0,187512261
Gambar 17Grafik PerbandinganPlaintextdanCiphertext
Gambar 17 menunjukkan bahwa pada setiap putaran terdapat perbedaan yang signifikan antara bilangan desimal plaintext dan bilangan desimal ciphertext. Pada Gambar 17 juga merupakan grafik hasil korelasi tertinggi dan terendah dimana nilai korelasi yang didapat yaitu korelasi tertinggi -0,798533303 pada putaran ke-10 dan korelasi terendah 0,022467997 pada putaran ke-18.
Hasil Pengujian Avalanche Effect ditunjukkan pada Tabel 6, dan dalam bentuk grafik pada Gambar 18.
Tabel 6Hasil PengujianAvalanche Effect
PUTARAN JUMLAH BIT PRESENTASE
1 29 45,3125
2 34 53,125
3 33 51,5625
4 36 56,25
5 40 62,5
6 37 57,8125
7 37 57,8125
8 32 50
9 33 51,5625
10 41 64,0625
11 31 48,4375
12 37 57,8125
13 26 40,625
14 23 35,9375
15 34 53,125
16 31 48,4375
17 35 54,6875
18 30 46,875
19 30 46,875
20 33 51,5625
Gambar 18Grafik PengujianAvalanche Effect
Pada Gambar 18 plaintext yang digunakan pada grafik Avalanche Effect menunjukkan hasil yang tidak stabil karena terjadi peningkatan paling tertinggi pada putaran ke-10 yaitu 41 bit dengan presentase 64,0625% namun pada putaran ke-14 terjadi penurunan 22 bit dengan presentase 35,9375% dan kembali meningkat pada putaran ke-15 sebanyak 11 bit dengan jumlah presentase 53,125%. Kemudian pada putaran ke-18 dan putaran ke-19 terjadi kestabilan bit dengan presentase yang sama 46,875%, dan pada putaran ke-20 terjadi peningkatan 3 bit dengan jumlah presentase 51,5625%. Berdasarkan hasil tersebut nilai rata-rata Avalanche Effect dari putaran ke-1 sampai putaran ke-20 mencapai 51,71875%.
5. Simpulan
Daftar Pustaka
[1] Tomasoa, L.,Pakereng, M. A. I.,Pengaruh S-Box Advanced Encryption Standard (AES) Terhadap Avalanche Effect Pada Perancangan KriptografiBlock Cipher256 Bit Berbasis Pola Teknik Tarian Dansa Tali Dari Maluku. Salatiga: Jurusan Teknik Informatika Universitas Kristen Satya Wacana.
[2] Bili, D.D. Pakereng, M. A. I., Wowor, A.D., 2015, Perancangan KriptografiBlock Cipher Dengan Langkah Kuda. Salatiga: Jurusan Teknik Informatika Universitas Kristen Satya Wacana.
[3] Frellian Tuhumury., 2016, Perancangan Algoritma Kriptografi Block Cipher 256 bit berbasis pada pola Tuangan Air. Salatiga: Jurusan Teknik Informatika Universitas Kristen Satya Wacana.
[4] Schneier, B., 1996, Applied Cryptography, Secon Editor, New York: John Wiley and Sons.
[5] http://repository.usu.ac.id/bitstream/123456789/55583/5/Chapter%20I.pdf, diakses pada 24 Agustus 2017
[6] Pakereng, M. A. I., 2010,Kriptografi Dengan Algoritma Genetika, Salatiga: Widya Sari. [7] Munir,R., 2006,Kriptografi, Bandung: Informatika.
[8] Stinson, D. R., 1995. Cryptography: Theory and Practice. CRC Press, Boca Raton, London, Tokyo.
![Gambar 1 Skema Dasar Proses Enkripsi-Dekripsi Pada Block Cipher [7]](https://thumb-ap.123doks.com/thumbv2/123dok/3722884.1814014/9.612.82.534.362.603/gambar-skema-dasar-proses-enkripsi-dekripsi-block-cipher.webp)