DIAGRAM LATTICE DAN KONSTRUKSI DYCK PATH DENGAN PANJANG K – UPSTROKES DAN K – DOWNSTROKES DARI TITIK (0,0)
KE (2K,0) DAN PERUBAHAN BENTUK DARI DYCK PATH MENJADI 2 – COLORED MOTZKIN PATH DAN SCHRÖDER PATH
ABSTRAK
Penelitian ini membahas salah satu aplikasi dari bilangan Catalan yaitu ketika menghitung banyaknya cara yang dapat dilakukan oleh seseorang dalam memilih rute perjalanan dari titik awal (0,0) sampai titik Lattice (n,n) dengan cara melangkah setiap satu satuan ke arah kanan atau ke arah atas. Hal ini dikenal sebagai Lattice path. Akan tetapi ketika cara melangkah Lattice path berubah menjadi diagonal maka lintasan yang dihasilkan disebut sebagai Dyck path. Selain itu, Dyck Path dengan panjang K – upstrokes Dan K – downstrokes dari titik (0,0) ke (2k,0) juga dapat berubah bentuk menjadi 2 – colored Motzkin path dan
Schröder path. Dalam penelitian ini juga akan dibuktikan dengan induksi
matematika bahwa bilangan Catalan Cn dapat dinyatakan dalam bentuk
1 ; 1 2 1
n n
n n
Cn atau
n n n
n 2 1
2
2 untuk n ≥ 0.
Kata Kunci : Bilangan Catalan, Dyck path, Lattice path, 2 – colored Motzkin path,
LATTICE DIAGRAM AND DYCK PATH CONSTRUCTION OF LENGTH K – UPSTROKES AND K – DOWNSTROKES FROM (0,0) TO (2K,0) AND
DYCK PATH CHANGING TO 2 – COLORED MOTZKIN PATH AND SCHRÖDER PATH
Abstract
This research discusses about one application of the Catalan numbers which is how to calculate the number of strategies for someone in choosing a travel route from (0,0) to (n,n) using one unit step to the right or above. This is known as the Lattice path. If the Lattice path changes into diagonal path, then the generated path is called as the Dyck path. Moreover, the Dyck path with k – upstrokes and k – downstrokes from (0,0) to (2k,0) also can be changed into 2 – colored Motzkin path and Schroder path. We also prove that the Catalan numbers can be alternatively defined as follow : ; 1
1 2 1
n n
n n
Cn or
n n n
n 2 1
2
2 for n ≥ 0.
DIAGRAM LATTICE DAN KONSTRUKSI DYCK PATH DENGAN PANJANG K – UPSTROKES DAN K – DOWNSTROKES DARI TITIK (0,0) KE(2K,0) DAN PERUBAHAN BENTUK DARI DYCK PATH MENJADI 2 –
COLORED MOTZKIN PATH DAN SCHRÖDER PATH
Oleh :
Cut Nurliana Setia Putri
Tesis
Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Magister Sains
Pada
Jurusan Matematika Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam
MAGISTER MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
IWAYAT HIDUP
Penulis dilahirkan di Tanjung Karang pada tanggal 27 September 1986
merupakan anak pertama dari enam bersaudara pasangan Bapak Teuku M. Nur
dan Ibu Agustina E.
Pendidikan formal yang pernah ditempuh :
1. Sekolah Dasar (SD) di SD Negeri 1 Kampung Baru pada tahun 1991–1997.
2. Sekolah Lanjutan Tingkat Pertama (SLTP) di SLTP Negeri 8 Bandar
Lampung pada tahun 1997–2000.
3. Sekolah Menengah Atas (SMA) di SMA Al –Kautsar Bandar Lampung pada
tahun 2000–2003.
4. S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
Lampung pada tahun 2003–2007.
Pada tahun 2008 sampai dengan Juli 2009 penulis bekerja sebagai salah satu staf
pengajar Universitas Teuku Umar (UTU) Meulaboh Aceh Barat dan pada bulan
Januari 2010 penulis diangkat sebagai CPNS guru matematika Kota Bandar
PERSEMBAHAN
Dengan mengucap alhamdulillah puji syukur atas karunia Allah SWT, atas izin
dan ridha–Nya karya ku ini dapat terselesaikan dan kupersembahkan kepada
orang–orang tercinta :
Ayahanda dan ibunda, Bapak Teuku M. Nur dan Ibu Agustina E atas doa dan
kasih sayang yang diberikan dalam setiap langkahku dalam menggapai semua
impian.
Zaujih al–mahboob, Dedi Syahputra atas cinta, pengertian, semangat dan
dukungan yang selalu diberikan
Adik–adik yang paling kakak sayang, TM Fawaaty HS, Cut Dara Permata Sari,
TM. Robby Mandala, Cut Annisa Intan Keumala, Cut Aziza Tasya Malahayati
MOTTO
Berusaha sebaik dan semaksimal mungkin. Apapun hasilnya, pasrahkan pada
SANWACANA
Puji syukur Alhamdulillah penulis panjatkan kehadirat Allah SWT yang telah
melimpahkan rahmat-Nya sehingga penulis dapat menyelesaikan tesis yang
berjudul “Diagram Lattice dan Konstruksi Dyck Path dengan Panjang
K – Upstrokes dan K – Downstrokes dari Titik (0,0) Ke (2k,0) dan Perubahan
Bentuk dari Dyck Path Menjadi 2 – Colored Motzkin Path dan Schröder Path”.
Shalawat dan salam penulis sanjungkan kepada Nabi Besar Muhammad SAW.
Tesis ini merupakan salah satu syarat yang harus dipenuhi guna memperoleh gelar
Magister Sains di Jurusan Matematika, Fakultas Matematika dan Ilmu
Pengetahuan Alam, Universitas Lampung. Penulis menyadari bahwa penulisan
tesis ini tidak terlepas dari bantuan dan dorongan dari berbagai pihak, baik secara
moril maupun materil. Pada kesempatan ini penulis ingin mengucapkan terima
kasih kepada :
1. Ibu Dra. Wamiliana, M.A, Ph.D, selaku pembimbing I yang telah
memberikan sumbangan pemikiran dalam penyusunan tesis ini.
2. Bapak Dr. Muslim Ansori, S.Si., M.Si, selaku Pembimbing II yang telah
3. Bapak Drs. Tiryono Ruby, M.Sc, Ph.D, selaku Ketua Jurusan Matematika
serta pembahas yang memberikan arahan pada penulis dalam
menyelesaikan tesis ini.
4. Bapak Drs. Mustofa Usman, M.A, Ph.D, selaku Ketua Program Studi
Magister Matemtika sekaligus pembimbing akademik yang telah mendidik
dan memberikan arahan kepada penulis.
5. Seluruh dosen yang telah mendidik dan membimbing penulis selama
menyelesaikan masa studi.
6. Ayahanda dan Ibunda yang telah mendukung penulis dari awal masa studi
ke penulisan tesis ini selesai.
7. Yang selalu mendampingi, suamiku Dedi Syahputra, SP sebagai orang
yang paling mendukung baik doa, moril dan materil demi tercapainya
gelar M.Si ini
8. Teman-teman angkatan 2013 yang telah membantu penulis baik secara
langsung maupun tidak langsung yang telah membantu dan memotivasi
penulis untuk menyelesaikan tesis ini.
Harapan penulis semoga tulisan ini dapat bermanfaat bagi perkembangan ilmu
pengetahuan.
Bandar Lampung, 31 Juli 2015
DAFTAR ISI
Halaman
DAFTAR ISI... i
DAFTAR GAMBAR... iii
DAFTAR TABEL... iv
I PENDAHULUAN 1.1 Latar Belakang Masalah ... 1
1.2 Batasan Penelitian ... 4
1.3 Tujuan Penelitian... 4
1.4 Manfaat Penelitian... 5
II TINJAUAN PUSTAKA 2.1 Koefisien Binomial ... 6
2.2 Segitiga Pascal (Koshy, 2009) ... 7
2.3 Bilangan Catalan (Koshy, 2009)... 8
2.3.1 Relasi Rekurensi (Anderson, 2002)... 8
2.3.2 Definisi Rekursif dari Bilangan Catalan Cn(Davis, 2014) 10 2.4 Konsep Dasar Teori Graf ... 11
III METODE PENELITIAN
3.1 Penelitian Relevan yang Telah Dilakukan... 16
3.2 Waktu dan Tempat Penelitian ... 17
3.3 Metode Penelitian ... 17
IV PEMBAHASAN... 21
DAFTAR TABEL
Halaman Tabel 2.1 Bilangan Catalan ... 8
DAFTAR GAMBAR
Halaman
Gambar 2.1 Segitiga Pascal ... 7
Gambar 2.2 Contoh Graf G dengan 9vertexdan 5edge... 11
Gambar 2.3 Contoh Graf yang memuatwalk... 12
Gambar 2.4 ContohLattice ... 12
Gambar 2.5 ContohDyck pathdenganpeakberjumlah 1 ... 14
Gambar 2.6 ContohDyck pathdenganvalleyberjumlah 1 ... 14
Gambar 2.7 Contohk–colored Motzkin Lattice path dengan k = 2... 15
Gambar 2.8 ContohSchröder pathdari (0,0) sampai (6,0)... 15
Gambar 3.1 Cara mengubahDyck pathmenjadi2–colored Motzkin path 18 Gambar 3.2 Cara mengubahDyck pathmenjadiSchrödder pathtanpapeak 19 Gambar 3.3 Diagram alir penelitian... 20
Gambar 4.1 KonstruksiLattice path, Dyck path, 2–colored Motzkin path, Schrödder pathtanpapeakuntuk k = 1 ... 21
Gambar 4.2 KonstruksiLattice path, Dyck path, 2–colored Motzkin path, Schrödder pathtanpapeakuntuk k = 2 ... 22
Gambar 4.3 KonstruksiLattice path, Dyck path, 2–colored Motzkin path, Schrödder pathtanpapeakuntuk k = 3... 23
Gambar 4.5 KonstruksiLattice path, Dyck path, 2–colored Motzkin path,
Schrödder pathtanpapeakuntuk k = 5 ... 32
Gambar 4.6 Banyaknya cara bersalaman yang mungkin untuk 0≤ n ≤ 3.. 38
Gambar 4.7 Banyaknya cara yang mungkin dapat dilewati semut untuk
I. PENDAHULUAN
1.1. LATAR BELAKANG MASALAH
Eugene C. Catalan adalah seorang matematikawan asal Belgia yang menemukan
bilangan Catalan pada tahun 1838 ketika mempelajari bentuk barisanparentheses
(barisan bentuk kurung). Barisan parentheses dibuat dari semua string seimbang
yang dibentuk dari n tanda kurung sebelah kiri dan n tanda kurung sebelah kanan
dengan jumlah dari tanda kurung sebelah kanan tidak boleh melebihi tanda
kurung sebelah kiri. Catalan menghitung banyaknya cara suatu rantai dari n + 1
simbol yang bisa dibentuk dengan n pasang tanda kurung sehingga setiap
pasangan memiliki 2 simbol, sebuah ekspresi kurung dan sebuah simbol atau dua
ekspresi kurung. Sebagai contoh, untuk n = 3, dapat dibentuk string seperti ()()()
dan (())(), namun tidak diizinkan membentuk string seperti (())) atau ())(()
(Grimaldi, 2012). Akan tetapi, bilangan tersebut tidaklah ditemukan pertama kali
oleh Catalan.
Sekitar tahun 1751 Euler menemukan bilangan Catalan ketika mempelajari
trigonometri dari poligon konveks (Koshy, 2009). Euler menentukan jumlah total
dari cara seseorang bisa menggambarkan n – 3 diagonal dalam suatu poligon
konveks n– sisi ( untuk n≥ 3)sehingga tidak ada dua diagonal beririsan didalam
2
Bilangan Catalan ini dapat diaplikasikan dalam berbagai macam hal. Berbagai
contoh aplikasi bilangan Catalan ini telah dipublikasikan oleh Jiang (2012), antara
lain sebagai berikut :
1. Stacking coinsyaitu jumlah cara mengambil koin pada baris bagian bawah
yang terdiri dari n berurutan dalam sebuah bidang sedemikian sehingga
tidak ada koin yang diijinkan untuk diletakkan pada dua sisi dari koin
bagian terbawah dan setiap koin tambahan harus berada di atas dua koin.
2. Balanced parantheses yaitu jumlah cara mengelompokkan suatu string
dari n pasangan dari tanda kurung sedemikian sehingga setiap kurung buka
berpasangan dengan kurung tutup
3. Mountain ranges yaitu jumlah cara membentuk daerah gunung pada suatu
garis dengan n upstrokes dan n downstrokes sedemikian sehingga setiap
upstroke bersesuaian dengan downstroke dengan lintasan tidak berada di
bawah titik awal.
4. Polygon triangulation yaitu jumlah cara memotong n+2 polygon sisi
konveks dalam sebuah bidang menjadi segitiga dengan menghubungkan
titik–titik dengan garis lurus dan tidak ada garis yang berpotongan.
5. Balanced trees yaitu jumlah dari pohon biner lengkap dengan n titik
dalam. Titik dalam adalah sebuah titik yang menghubungkan titik lain
yang berada diatasnya. Pohon biner lengkap adalah suatu akar pohon yang
setiap titik dalamnya memiliki tepat dua segmen untuk tumbuh.
Salah satu aplikasi lain dari bilangan Catalan adalah ketika menghitung
3
perjalanan dari titik awal (0,0) sampai titik Lattice (n,n) dengan cara melangkah
setiap satu satuan ke arah kanan atau ke arah atas. Hal ini dikenal sebagaiLattice
path. Akan tetapi ketika cara melangkah Lattice path berubah menjadi diagonal
maka lintasan yang dihasilkan disebut sebagaiDyck path.
Sebelumnya sudah banyak peneliti melakukan penelitian mengenai Dyck path,
akan tetapi di Indonesia, sangat jarang sekali peneliti yang meneliti tentang hal
ini. Beberapa penelitian yang telah dilakukan mengenai Dyck pathadalah sebagai
berikut :
1. Heubach and Toufik pada tahun 2006 dalam jurnalnya yang berjudul
Staircase Tilings and Lattice Paths menjelaskan mengenai bagaimana
menentukan suatu struktur kombinatorial, yaitu suatu pengubinan dari tangga
dalam bidang 2
ketika dibatasi dengan cara yang berbeda untuk
menciptakan bijeksi langsung untuk Dyck path dengan panjang 2n, Motzkin
Path dengan panjang n dan n – 1 serta Schröder Paths dan Little Schröder
Pathsdengan panjang n.
2. Dalam jurnal Counting Humps in Motzkin Paths, Ding and Du pada tahun
2011, membahas mengenai jumlah bukit dari Dyck, Motzkin dan Schröder
paths. Sebelumnya, Regev (2010) menyadari bahwa jumlah gunung dari
semuaDyck pathpanjang n adalah satu setengah dari jumlahSuper Dyck path
panjang n.Super Dyck pathadalah suatu Dyck path yang diizinkan berada di
bawah x – axis. Kemudian dihitung jumlah bukit dari Motzkin Path dan
ditemukan relasi yang sama. Dalam jurnal ini, Ding and Du memberikan
4
bahwa jumlah Dyck path dengan panjang n dengan k bukit adalah bilangan
Narayana. Bilangan Narayana N(n,k),n= 1, 2, 3 ..., 1≤k≤n sesuai nama
penemunya seorang matematikawan dari India T.V. Narayana(1930 1987)
didefinisikan dalam bentuk
Dalam penelitian ini akan dibahas mengenai banyaknya cara mengkonstruksi
Dyck path dengan panjang k – upstrokes dan k – downstrokes dari titik (0,0)
sampai (2k,0) dengan syaratpath tidak boleh menyentuh sumbu –x kecuali pada
titik titik ujungnya dan perubahan bentuk dari Dyck path menjadi 2 – colored
Motzkin pathdan menjadiSchröder path.
1.2 Batasan Penelitian
Dalam penelitian ini hanya akan didiskusikan tentang diagram Lattice dan
konstruksiDyck pathdengan panjangk– upstrokesdank–downstrokesdari titik
(0,0) sampai dengan (2k,0) yang dilakukan dibatasi dengan syarat path tidak
boleh menyentuh sumbu – x kecuali pada titik – titik ujung serta perubahan
bentuk menjadi 2 –colored Motzkin path dan menjadi Schröder path tanpapeak.
Hasil konstruksi yang digambarkan dalam penelitian ini hanya sampai k = 5
1.3 Tujuan Penelitian
Tujuan dari penelitian ini adalah sebagai berikut :
1. Mengkonstruksi diagram Lattice dari titik (0,0) sampai (k,k) dan Dyck path
5
(2k,0) dengan syaratpathtidak boleh menyentuh sumbu–x kecuali pada titik
titik ujungnya.
2. Menentukan pola barisan dariDyck pathyang telah dikonstruksi.
3. Mengubah konstruksi dari Dyck path yang telah dibentuk menjadi 2-colored
Motzkin path.
4. Mengubah konstruksi dari Dyck path yang telah dibentuk menjadi Schröder
path.
5. Membuktikan bahwaDyck pathyang terbentuk adalah bilangan Catalan
1.4 Manfaat Penelitian
Manfaat dari penelitian ini adalah untuk memperdalam pengetahuan tentang salah
satu aplikasi bilangan Catalan yaitu diagram Lattice serta Dyck path dan
6
II. TINJAUAN PUSTAKA
Pada bab ini akan diberikan beberapa konsep dasar, istilah – istilah dan definisi
yang erat kaitannya dengan masalah yang harus dibahas yaitu mengenai
banyaknya cara mengkonstruksi Dyck path dengan panjang k – upstrokes dan k –
downstrokes dari titik (0,0) ke (2k,0) dengan syarat path tidak boleh menyentuh
sumbu - x kecuali pada titik titik ujungnya.
2.1Koefisien Binominal
Misalkan n dan r adalah bilangan buat non negatif. Koefisien binomial ��
didefinisikan sebagai berikut :
! !!
r n r
n r
n
Dengan 0 ≤ r ≤ n. Jika r > n, maka �� didefinisikan sebagai 0 (Koshy, 2009).
Teorema 2.1.1 (Koshy, 2009)
Misalkan n dan r adalah bilangan bulat non negatif, maka
7
2.2Segitiga Pascal (Koshy, 2009)
Koefisien binomial �� dengan 0 ≤ r ≤ n dapat disusun dalam bentuk
segitiga. Setelah Pascal pada tahun 1663 menulis buku yang berjudul
Treatise on Arithmetic Triangle kemudian buku tersebut dipublikasikan pada
tahun 1665, maka segitiga yang dibentuk dari koefisien binomial �� disebut
segitiga Pascal. Segitiga Pascal dapat digambarkan sebagai berikut :
8
2.3Bilangan Catalan (Koshy, 2009)
Bilangan Catalan Cn secara umum didefinisikan sebagai berikut :
0
Beberapa bilangan Catalan adalah sebagai berikut :
Tabel 2.1. Tabel bilangan Catalan
n Cn
2.3.1 Relasi Rekurensi (Anderson, 2002)
Ketika mempelajari barisan dari bilangan an, akan didapatkan suatu
hubungan antara an dan an-1 atau antara beberapa nilai sebelum ai, i < n.
9
Contoh 1 : (Menara Hanoi) (Anderson, 2002)
Masalah ini terkenal pada abad ke 19 oleh seorang matematikawan
Perancis yang bernama E. Lucas. Terdapat n piringan, semua
berukuran berbeda yang memiliki lubang ditengahnya dan tiga wadah
vertikal sehingga piringan bisa disusun. Kondisi awalnya adalah semua
piringan berada dalam satu tempat secara berurutan dengan urutan
bagian bawah adalah piringan yang paling besar dan bagian atas adalah
piringan terkecil sehingga membentuk sebuah menara. Piringan akan
dipindahkan satu persatu, sehingga n piringan dapat tersusun dalam
wadah yang lain, dengan syarat tidak ada langkah dimana sembarang
piringan terletak di atas dibagian paling atas dari piringan yang
terkecil. Berapakah jumlah minimum langkah untuk memindahkan
piringan tersebut ?
Misalkan an dinotasikan sebagai jumlah langkah minimum untuk
memindahkan n piringan. Jelas bahwa a1 = 1 dan a2 = 3. Pindahkan
dari bagian atas ke wadah kedua, dan pindahkan bagian berikutnya ke
wadah ketiga. Kemudian pindahkan lagi piringan terkecil di atas
piringan yang lebih besar. Bagaimanakah dengan an ?. Jelas bahwa
untuk memindahkan piringan bagian bawah, harus ada wadah yang
kosong untuk memindahkannya sehingga untuk n -1 piringan yang lain
harus dipindahkan ke wadah ketiga. Untuk memperoleh langkah ini,
an-1 harus dipindahkan. Piringan terbesar harus dipindahkan dalam
wadah yang kosong kemudian piringan an – 1 yang lain dipindahkan
10
2.3.2 Definisi Rekursif Dari Bilangan Catalan Cn (Davis, 2014) Bilangan Catalan Cn didefinisikan sebagai berikut :
0
Diasumsikan telah dihitung bilangan Catalan Cn untuk n = 0,1,2,...,n-1.
Akan dihitung untuk nilai n.
Telah dihitung secara langsung bilangan Catalan Cn untuk n = 0,1,2,3,4
sehingga diperoleh Co = 1, C1 = 1, C2 = 2, C3 = 5, C4 = 14
11
Kondisi Awal : C0 = 1
C1 = C0C0
C2 = C1C0 + C0C1
C3 = C2C0 + C1C1 + C0C2
C4 = C3C0 + C2C1 + C1C2 + C0C3
... ...
Cn = Cn-1C0 + Cn-2C1 + ... + C1Cn-2 + C0Cn-1
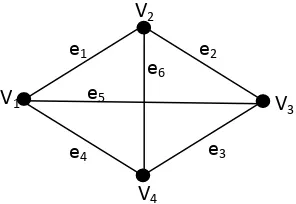
2.4Konsep Dasar Teori Graf
Graf G adalah suatu struktur (V,E) dengan V(G) himpunan tak kosong yang
elemen – elemennya disebut titik / vertex , sedangkan E(G) (mungkin kosong)
adalah himpunan pasangan tak terurut dari elemen – elemen di V(G) yang
anggotanya disebut sisi / edge. (Deo, 1989)
Contoh 2 :
Gambar 2.2. Contoh graf G dengan 9 vertex dan 5 edge
Walk
Deo pada tahun 1989 menyatakan bahwa walk adalah barisan berhingga dari
titik dan garis, dimulai dan diakhiri dengan titik sehingga setiap garis
menempel dengan titik sebelum dan sesudahnya. Tidak ada sisi yang muncul
12
Contoh 3:
Gambar 2.3. Contoh graf yang memuat walk
Contoh walk : v1, e1, v2, e2, v3, e5, v1,e4,v4
Path / Lintasan
Path / lintasan adalah suatu walk yang tidak memiliki pengulangan vertex.
(Hsu and Lin, 2009)
Berdasarkan Gambar 2, contoh path adalah v1, e1, v2, e2, v3, e3, v4
2.5Lattice Path, Dyck Path, 2 – colored Motzkin path dan Schröder Path
Lattice
Lattice (V,E)adalah suatu model matematika dalam ruang diskrit yang
terdiri dari dua himpunan, suatu himpunan vertex n
V dan suatu
himpunan edge n n
E dengan tidak lebih dari dua sisi diantara dua
titik. (Wallner, 2015)
Contoh 4 :
Gambar 2.4. Contoh Lattice
V1
V2
V3
V4
e2
e3
e4
e1
e5
13
Definisi Lattice Path / Lattice Walk
Misalkan (V,E). n – step Lattice path / Lattice walk atau walk dari
V
s menuju xVadalah suatu barisan
(
0,
1,...,
n)dari elemendalam V , sedemikian sehingga :
1.
0 s,
n x2. (
i,
i1)EPanjang dari suatu Lattice path adalah jumlah n langkah (edge) pada
barisan
(
0,
1,...,
n) (Wallner, 2015)Dyck path
Dyck path adalah suatu path dalam kuadran pertama yang dimulai dari titik
asal dan berakhir pada (2n, 0) dan terdiri dari langkah (1,1) (disebut rise ) dan
(1,-1) (disebut fall). (Deutsch, 1999)
Definisi lain dari Dyck path (atau Mountain path) adalah Lattice path dalam
koordinat bidang (x,y) dari (0, 0) to (2n, 0) dengan langkah (1, 1) (Up) dan (1,
-1) (Down) tanpa pernah terletak di bawah sumbu – x. (Došlić and Veljan,
2007)
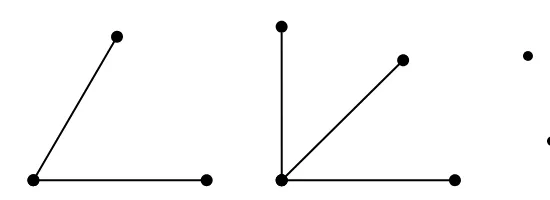
Peak / Puncak
Pada Dyck path, suatu peak dapat terjadi sebagai bagian dari path ketika suatu
14
Contoh 5 :
Gambar 2.5. Contoh Dyck path dengan peak berjumlah 1
Valley / lembah
Suatu valley dalam Dyck path dapat terjadi sebagai bagian dari path ketika
suatu downstroke D*(↘) diikuti dengan langkah upstroke D (↗).(Grimaldi,
2012)
Contoh 6 :
Gambar 2.6. Contoh Dyck path dengan valley berjumlah 1
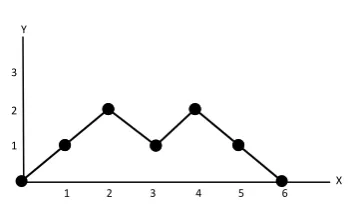
K – Colored Motzkin Lattice Path
Motzkin path dengan panjang n adalah suatu Lattice path dari 2
yang
berjalan dari (0,0) sampai (n,0) tanpa pernah berada di bawah sumbu – x
dengan langkah yang diizinkan adalah langkah diagonal ke atas / rise
(1,1), langkah diagonal ke bawah /fall(1,-1) dan langkah horizontal (1,0).
Jika langkah dilabeli oleh k warna, maka kita menyebutnya K – colored
Motzkin Lattice path. (Tsikouras dan Sapounakis, 2004)
1 2 1
Y
X
1 2 3 4 X 1
2 Y
1 2 3 4 5 6 1
2 3
15
Contoh 7 :
Gambar 2.7. Contoh k – colored Motzkin Lattice path dengan k = 2
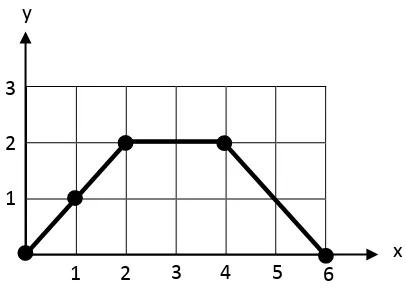
Schröder Path
Schröder path adalah suatu barisan dengan langkah rise yang didefinisikan
oleh (1,1), fall yang didefinisikan oleh (1,-1) dan langkah horizontal yang
didefinisikan oleh (2,0) dimulai dari (0,0) sampai (2n,0) tanpa pernah
berada di bawah sumbu - x. (Pinzani and Pergola,1999)
Contoh 8 :
Gambar 2.8. Contoh Schröder path dari (0,0) sampai (6,0)
1 2 3 4 5 6 1
2 3 y
x 1 2 3 4 5 6
1 y
16
te by Dn the set of allDyck paths of semilength n. We denote by Do the set consisting only of the
III. METODE PENELITIAN
3.1 Penelitian Relevan yang Telah Dilakukan
Adapun beberapa hasil penelitian yang telah dilakukan oleh beberapa peneliti
sebelumnya adalah :
3.1.1 Jiang (2012) mengkonstruksi mountain range untuk n = 0 sampai
n = 3 pada sebuah garis dengan nupstrokes (/) dan ndownstrokes(\)
sehingga setiap upstrokes bersesuaian dengan downstrokes dan path
tidak berada di bawah titik awal. Hasil yang diperoleh adalah
berdasarkan konstruksi tersebut didapat bahwa untuk setiap n dan n
adalah bilangan non negatif, sehingga cara untuk mengkonstruksinya
adalah sebanyak bilangan Catalan Cn.
Tabel 3.1. Konstruksimountain rangesuntuk n = 0,1,2,3
n Bentuk mountain ranges yangdikonstruksi
Banyaknya cara mengkonstruksi
Bilangan Catalan
n= 0 1 cara C0
n = 1 /\ 1 cara C1
n = 2 /\ , /\ / \
2 cara C2
n = 3 /\
/\ /\ /\/\ / \ /\/\/\ , /\/ \ , / \/\ , / \ , / \
17
3.1.2 Peart dan Woan (2001) menghitungDyck pathtanpapeakpada tinggi
k dengan k ≥ 1. Dalam jurnalnya disimpulkan bahwa jumlah dari
Dyck path dengan panjang 2n + 2, untuk n ≥ 0 dengan tanpa peak
pada ketinggian 2 adalah bilangan Catalan Cn.
3.2 Waktu dan Tempat Penelitian
Penelitian ini dilakukan di Program Studi Magister Matematika Jurusan
Matematika Fakultas Matematika dan Ilmu Pengetahuan alam (MIPA)
Universitas Lampung pada semester genap tahun ajaran 2014–2015.
3.3 Metode Penelitian
Langkah – langkah yang dilakukan dalam penelitian ini adalah sebagai
berikut :
1. Mengumpulkan bahan literatur serta studi kepustakaan yang berhubungan
denganDyck pathdan bilangan Catalan
2. Mengkonstruksi Lattice pathdari (0,0) sampai (k,k) untuk k = 1 sampai
dengan k = 5.Lattice pathyang dibentuk adalahLattice path yang berada
pada kuadran pertama pada koordinat Cartesius tanpa pernah melewati
garis y = x dengan langkah yang diizinkan adalah sebagai berikut :
langkah ke kanan : R : (x,y)→ (x +1,y)
langkah ke atas : U : (x,y)↑ (x +1,y)
3. Mengkonstruksi Dyck path dengan panjang k – upstrokes dan k –
downstrokes dari titik (0,0) sampai (2k,0) dengan syarat path tidak boleh
18
Langkah mengkonstruksi Dyck path (Grimaldi, 2012) adalah mengubah
Lattice path yang telah dibentuk menjadi Dyck path dengan cara sebagai
berikut :
Langkah ke kanan diganti menjadiupstroke/ rise
R : (x,y)→ (x +1,y) diubah menjadi D : (x,y) (x +1,y+1)
Langkah ke atas diganti menjadidownstroke / fall
U : (x,y)↑ (x +1,y) diubah menjadi D* : (x,y) (x +1,y-1)
4. Tentukan pola bilangan dariDyck pathyang telah dikonstruksi
5. Susun korespondensi satu – satu dari bentuk Dyck path menjadi 2 –
colored Motzkin path. Empat jenis langkah yang diizinkan dalam 2 –
colored Motzkin pathmenurut Grimaldi (2012)adalah :
1. D : (x,y) (x +1,y+1)
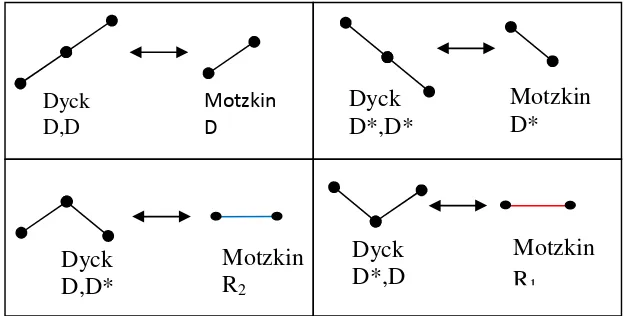
Adapun cara mengubah Dyck path menjadi 2 – colored Motzkin path
adalah sebagai berikut :
19
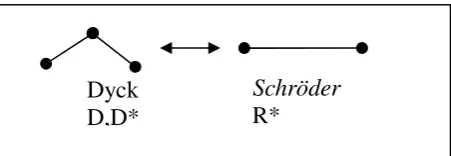
6. Susun korespondensi satu–satu bentukDyck pathmenjadiSchröder path
tanpapeak.
Menurut Grimaldi (2012) tiga langkah yang diizinkan dalam Schröder
pathadalah sebagai berikut :
1. D : (x,y) (x +1,y+1)
2. D* : (x,y) (x +1,y-1)
3. R* : (x,y) (x +2,y)
Cara mengubah bentuk Dyck path menjadi Schröder path tanpa peak
adalah:
Gambar 3.2 Cara mengubah bentuk Dyck path menjadi Schröder path
tanpapeak
7. Membuktikan bahwa jumlah pola bilangan dari Dyck path yang telah
dikonstruksi adalah bilangan Catalan. Dyck
D,D*
Schröder
20
Langkah penelitian ini dapat dinyatakan dalam bentuk diagram alir sebagai
berikut :
Gambar 3.3. Diagram alir penelitian
Start
Tentukan k
1 k 5,
k
GambarkanLattice path
Ubah menjadiDyck path
Tentukan pola bilanganDyck path
Buktikan jumlah pola bilanganDyck
pathadalah Cn
Stop
Ubah menjadi2– colored Motzkin path
Ubah menjadi2– Schröder path
ya
tidak
k<1
k>5
Tidak ada konstruksi
V. KESIMPULAN
Pada penelitian ini telah didiskusikan mengenai diagram Lattice dan konstruksi
Dyck path dengan panjang k – upstrokes dan k – downstrokes dari titik (0,0)
sampai (2k,0) dan perubahan bentuk dari Dyck path menjadi2 –colored Motzkin
path dan Schröder path dengan syarat path tidak boleh menyentuh sumbu – x
kecuali pada titik – titik ujung serta perubahan bentuk menjadi 2 – colored
Motzkin path dan menjadi Schröder path tanpa peak. Hasil konstruksi yang
digambarkan dalam penelitian ini hanya sampai k = 5.
Berdasarkan hasil observasi diperoleh bahwa untuk nk1dengan k ,
menyentuh sumbu–x kecuali pada titik titik ujungnya adalah berjumlah bilangan
Catalan Cn. Selain itu telah dibuktikan bahwa bilangan Catalan Cn dapat
DAFTAR PUSTAKA
Anderson, Ian. 2002.A first Course in Discrete Mathematics. Springer, London.
Davis, Tom. 2014. Catalan Number. http://www.geometer.org/mathcircles, diakses tanggal 20 Mei 2015 pukul 14.00 WIB.
Drake, Dan. 2010. Bijection From Weighted Dyck Paths to Schroder Paths.
Journal Integer Seq. 13 (2010), n0 9, Article 10.9.2, 20pp.
arXiv:1006.1959v2 [math.CO].
Deo, N. 1989. Graph Theory With Application To Engineering and Computer
Science. Prentice Hall, Inc. Engelewood Cliffs, New Jersey.
Deutsch, Emeric. 1998. A Bijection on Dyck Path and Its Cosequences. Discrete Mathematics, Vol 179, pp 253 - 256.
Deutsch, Emeric. 1999. An Involution on Dyck paths and its consequences.
Discrete Mathematics, Vol 204,pp 163–166.
Došlić, Tomislav and Veljan, Darko. 2007. Secondary Structures, Plane Tree and Motzkin Number.Mathematical Communication, Vol 12, pp 163–169.
Ding,Yun and Du, Rosena R.X. 2011. Counting Humps in Motzkin Paths.Departement of mathematics. Shanghai. arXiv:1 109.2661v1 [math.CO]13 Sep 2011.
Grimaldi, Ralph P. 2012. Fibonacci and Catalan Numbers: An Introduction. Hoboken, NJ: John Wiley & Sons,. Print.
Heubach, Silvia and Mansour, Toufik. 2006. Staircase Tilings and Lattice Paths. CA 90032–8204 USA.Congressus Numerantium, Vol 182, 97–109.
Hsu, Lih-Sing and lin, Cheng-Kuan.2009. Graph Theory and Interconnection
Network. Taylor & francis Group, Boca Raton.
Jiang, Xiaotong. 2012. Aplication of Catalan Numbers.
Koshy, Thomas. 2009. Catalan Numbers with Applications. Oxford: Oxford UP,Print.
Peart , Paul and Woan, Wen Jin. 2001. Dyck Path With No Peaks at Height k.
Journal of Integer Sequences, Vol. 4, Article 01.1.3
Pinzani, R and Pergola, E. 1999. A combinatorial Interpretation of area of Schröder Paths.The Electronic Journal of Combinatorics Vol 6, #R40
Regev, A. 2010. Humps For Dyck And For Motzkin Paths. arXiv: 1002. 4504 v1 [math.CO] 24 Feb 2010
Tsikouras, P and Sapounakis, A. 2004. On k –colored Motzkin Word.Journal of Integer Sequences, Vol. 7, Article 04.2.5