Penyelesaian Masalah Pelangsiran Unit Kereta Penumpang pada Stasiun Kereta Api dengan Menggunakan Teknik Pembangkitan Kolom

PENYELESAIAN MASALAH PELANGSIRAN UNIT KERETA

PENUMPANG PADA STASIUN KERETA API DENGAN

MENGGUNAKAN TEKNIK PEMBANGKITAN KOLOM

Oleh:

DINA LIANITA SARI

G54102025

PROGRAM STUDI MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

DINA LIANITA SARI. Penyelesaian Masalah Pelangsiran Unit Kereta Penumpang pada Stasiun Kereta Api dengan Menggunakan Teknik Pembangkitan Kolom. Dibimbing oleh FARIDA HANUM dan DONNY CITRA LESMANA.

Dalam suatu stasiun kereta api, pada jam-jam tertentu terdapat kereta api penumpang yang tidak dioperasikan untuk mengangkut penumpang. Perusahaan kereta api harus melakukan kegiatan pelangsiran dengan biaya minimum agar kereta api dapat beroperasi dengan baik. Dalam praktiknya, masalah pelangsiran adalah suatu masalah yang sangat kompleks yang harus dihadapi oleh perusahaan kereta api.

Dua proses penting dalam masalah pelangsiran adalah pendataan unit kereta api yang harus diparkir di tempat pelangsiran menjadi unit kereta api yang harus diberangkatkan dari tempat pelangsiran serta pemarkiran unit -unit kereta api pada rel pelangsiran.

Pada proses pendataan kereta-api-datang menjadi kereta-api-berangkat, didefinisikan part sebagai subset dari himpunan unit kereta yang berdampingan pada suatu kereta api. Dalam proses ini akan dicari suatu kombinasi part dari kereta-api-datang yang akan meminimumkan biaya untuk ditetapkan menjadi kereta-api-berangkat. Solusi dari masalah ini dicari dengan menggunakan LINDO 6.1. Dari proses ini diperoleh himpunan part dari kereta-api-datang yang ditetapkan menjadi himpunan part dari kereta-api-berangkat yang disebut dengan blok. Blok-blok ini akan digunakan dalam proses pemarkiran unit-unit kereta pada rel pelangsiran. Assignment fisibel adalah cara menyusun blok-blok pada suatu rel pelangsiran yang tidak boleh melebihi panjang rel dan tidak mengandung crossing. Crossing terjadi jika suatu blok menghalangi blok yang lain pada suatu rel pelangsiran.

PENYELESAIAN MASALAH PELANGSIRAN UNIT KERETA

PENUMPANG PADA STASIUN KERETA API DENGAN

MENGGUNAKAN TEKNIK PEMBANGKITAN KOLOM

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

DINA LIANITA SARI

G54102025

PROGRAM STUDI MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Dengan segala ketulusan hati, kupersembahkan

karya kecilku kepada

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 25 November 1984 sebagai anak pertama dari pasangan bapak Fahmi D.S dan ibu Ermina Zaenah.

Pada tahun 2002 penulis lulus dari SMUN 3 Depok dan berhasil menjadi mahasiswa Departemen Matematika, Fakultas Matematika dan Ilmu pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI (Undangan Seleksi Masuk IPB).

PRAKATA

Bismillahhirrahmanirrahim,

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia, rahmat tak terhingga dan kekuatan yang mengisi relung jiwa sehingga penulis dapat menyelesaikan karya ilmiah ini. Dengan segala kerendahan hati, penulis ingin berterima kasih kepada segala cinta yang telah menggenapkan karya ilmiah ini:

1. Ibu Farida Hanum selaku pembimbing 1 yang telah memberikan saran dan masukan serta bantuan yang tak terbalaskan.

2. Bapak Donny Citra Lesmana selaku pembimbing 2 yang telah banyak membantu dalam penulisan karya ilmiah ini.

3. Bapak I Gusti Putu Purnaba atas bimbingan dan kesediaannya menjadi penguji.

4. Papa dan mama tercinta yang tiada hentinya memberikan nasihat, do’a dan dukungan. Terima kasih atas segenap kasih sayang yang tak terbalaskan. Kedua adik, Ira yang telah banyak membantu dala m pengetikan dan seminar dan Andi yang telah banyak memberi senyum lewat tingkah lakunya.

5. Nanang Siswanto yang telah memberikan warna baru dalam kehidupan pada tiga tahun terakhir. Selalu untuk semangat, kesabaran dan support yang tak berujung yang menjadikan hari ini ada.

6. Sepupu-sepupu tersayang, ayuk Rian, ayuk Dika, Riska, dan semua keluarga besar Yusuf Basir atas segala nasihat, do’a, dan semua cerita pengalamannya.

7. Sahabat-sahabat terbaikku, nonoy (teman sekamarku yang baik), desi (teman se-kosan yang bijak), tami (teman se-kosan yang kritis), nita (teman se-kosan yang lucu), eryt (temanku yang gemar makan), mere (temanku yang dewasa), tika (temanku yang selalu ceria), ade atas segala kebersamaan dalam mengerjakan skripsi serta kisah-kisah seru bersama sampah. 8. Arif, Febi, Ardhi, dan Avie, kalian selalu aku anggap sebagai sahabat-sahabat terindahku. 9. Teman-teman Math ’39 yang tidak bisa aku sebutkan satu persatu, terima kasih atas segala

kebersamaan serta momen-momen terindah dalam setiap detiknya.

10. Dosen-dosen Departemen Matematika atas segala ilmu yang telah diberikan tanpa lelah. 11. Staf-staf Departemen Matematika ibu Susi (atas segala nasihat dan ceritanya), ibu Ade, mas

Deni, mas Yono, mas Bono, ibu Marisi, pak Juanda, dan mbak Yanti.

12. Teman-teman Math ’38 dan Math ’40 serta seluruh civitas Matematika yang membuat kisah hidup lebih lengkap.

13. Serta semua pihak yang telah membantu terselesaikannya skripsi ini.

Akhir kata, semoga karya ilmiah ini menjadi amal saleh bagi penulis dan bagi orang-orang yang terlibat di dalamnya serta dapat bermanfa’at bagi siapapun yang tertarik terhadap karya ilmiah ini. Amin.

Bogor, Januari 2006

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

I PENDAHULUAN Latar Belakang ... 1

Tujuan ... 1

II LANDASAN TEORI Pemrograman Linear ... 1

Masalah Dual ... 3

Pemrograman Linear Bilangan Bulat ... 5

Graf ... 6

III DESKRIPSI DAN FORMULASI MASALAH PELANGSIRAN UNIT KERETA PENUMPANG PADA STASIUN KERETA Masalah Pelangsiran Unit Kereta Penumpang pada Stasiun Kereta ... 8

Pendekatan Solusi ... 10

IV MENYELESAIKAN MASALAH PENETAPAN BLOK PADA REL PELANGSIRAN DENGAN MENGGUNAKAN TEKNIK PEMBANGKITAN KOLOM (COLUMN GENERATION) Representasi Network dan Masalah Penetapan Blok pada Rel Pelangsiran ... 15

Memeriksa Kefisibelan Suatu Assignment dengan Menggunakan Algoritme Pemrograman Dinamik ... 17

Teknik Pembangkitan Kolom untuk Optimisasi Penetapan Blok pada Rel Pelangsiran.. 17

V CONTOH KASUS PELANGSIRAN UNIT KERETA PENUMPANG PADA STASIUN KERETA Penyelesaian Masalah Pemadanan Kereta-api-datang Menjadi Kereta-api-berangkat dengan Menggunakan LINDO 6.1 ... 19

Penyelesaian Masalah Penetapan Blok pada Rel Pelangsiran dengan Menggunakan Teknik Pembangkitan Kolom ... 21

VI SIMPULAN DAN SARAN Simpulan ... 31

Saran ... 32

DAFTAR PUSTAKA ... 32

DAFTAR TABEL

Halaman

1 Contoh tabel waktu untuk sebuah jalur-bebas ... 9

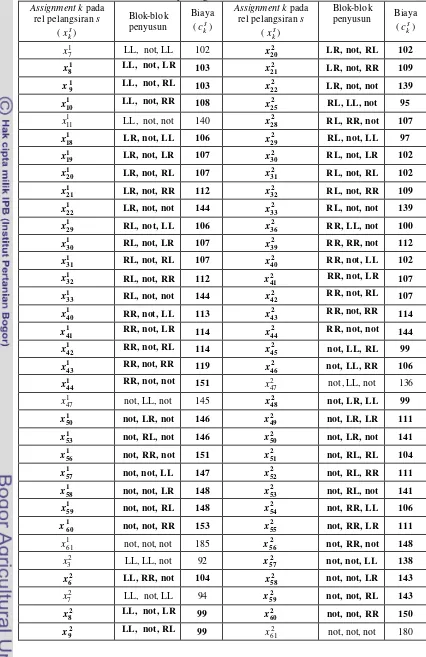
2 Daftar biaya pemarkiran blok ke rel pelangsiran 1, 2, dan 3 ... 23

3 Daftar assignment yang tidak mengandung crossing serta biayanya masing-masing ... 23

4 Daftar assignment fisibel yang diperoleh dengan menggunakan Algoritme Pemrograman Dinamik... 27

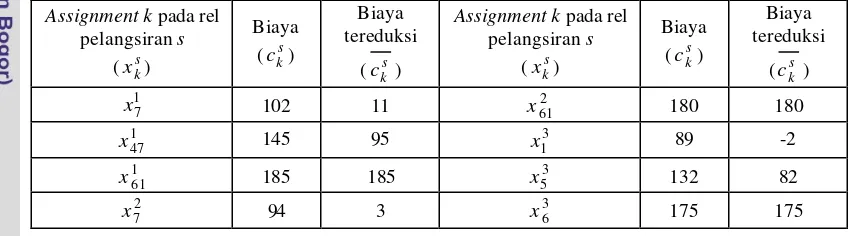
5 Biaya tereduksi dari assignment fisibel k pada rel pelangsiran s untuk RP0 ... 30

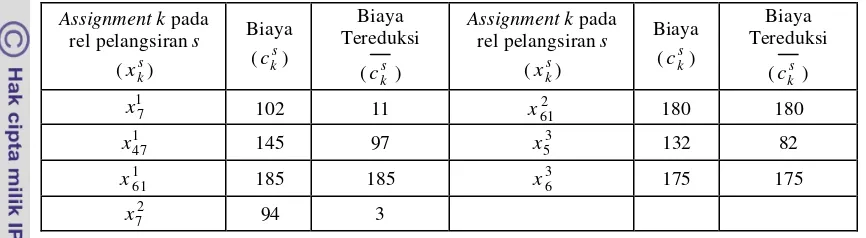
6 Biaya tereduksi dari assignment fisibel k pada rel pelangsiran s untuk RP1 ... 31

DAFTAR GAMBAR

Halaman 1 Graf G = (V,E) ... 6

2 Digraf G’ = (V,A) ... 7

3 Sisi berarah menjauhi atau mendekati, suksesor dan predesesor ... 7

4 Situasi di rel pelangsiran pada Selasa pukul 06.00 ... 10

5 Situasi di rel pelangsiran pada Selasa pukul 06.00 jika Kereta 561 dan Kereta 3678 memasuki rel pelangsiran melalui sisi yang sama ... 10

6 Network dari Kereta 3629 pada Tabel 1 ... 11

7 Network dari Kereta 3629 pada Tabel 1 tanpa simpul rekaan ... 12

8 Contoh dari sebuah network untuk jalur-bebas dengan 3 blok ... 16

9 Network dari Kereta 3628 pada Tabel 1 ... 19

10 Network dari Kereta 561 pada Tabel 1 ... 19

11 Network dari Kereta 3678 pada Tabel 1 ... 19

12 Network dari Kereta 3629 pada Tabel 1 ... 19

13 Network dari Kereta 520 pada Tabel 1 ... 19

14 Keadaan di stasiun yang sesuai dengan Tabel 1 dan memiliki 2 jalur-bebas dan 1 jalur-satu-arah ... 22

15 Network yang terbentuk dari assignment yang tidak mengandung crossing pada rel pelangsiran 3 ... 22

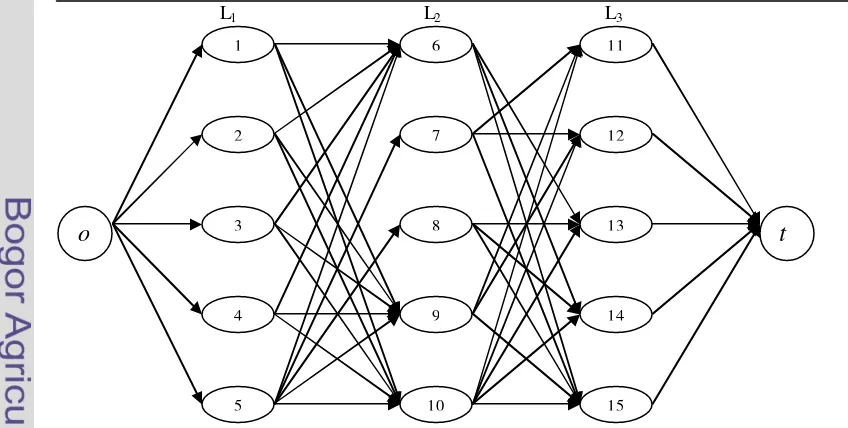
16 Graf G yang terbentuk dari assignment yang tidak mengandung crossing pada rel pelangsiran 1 dan 2 dengan notasi i = 1,2,…,15 untuk masing-masing simpul-antara ... 25

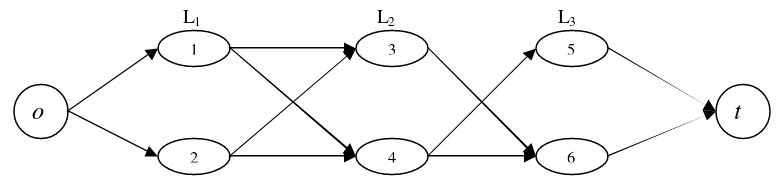
17 Graf G yang terbentuk dari assignment yang tidak mengandung crossing pada rel pelangsiran 3 dengan notasi i = 1,2,…,6 untuk masing-masing simpul-antara ... 26

DAFTAR LAMPIRAN

Halaman 1 Contoh penyelesaian suatu pemrograman linear dengan algoritme simpleks ... 33

2 Hasil penghitungan Contoh 3 dengan menggunakan LINDO 6.1 ... 34

3 Hasil penghitungan masalah pemadanan kereta-api-datang menjadi kereta-api-berangkat dengan menggunakan LINDO 6.1 ... 35

4 Prosedur pemeriksaan kefisibelan dan kedominanan assignment di graf G dengan menggunakan Algoritme Pemrograman Dinamik ... 36

I PENDAHULUAN

1.1 Latar Belakang

Pada jam-jam tertentu, dalam suatu stasiun kereta api terdapat kereta api penumpang yang tidak dioperasikan untuk mengangkut penumpang. Perusahaan kereta api harus melakukan kegiatan pelangsiran agar kereta api dapat beroperasi dengan baik. Kegiatan pelangsiran ini meliputi pendataan kereta api yang datang ke stasiun kereta api menjadi kereta api yang berangkat dari stasiun kereta api, pemarkiran kereta-api-datang pada rel-rel pelangsiran, pemeliharaan kereta, serta perencanaan pekerja yang akan melakukan kegiatan pelangsiran.

Dua proses penting dalam masalah pelangsiran adalah pendataan unit kereta-api-datang (arriving shunt unit) yang harus diparkir di tempat pelangsiran menjadi unit kereta-api-berangkat (departing shunt unit) yang harus diberangkatkan dari tempat pelangsiran, serta pemarkiran unit-unit kereta api pada rel pelangsiran.

Dalam praktiknya, kegiatan pelangsiran adalah suatu masalah yang sangat kompleks yang harus dihadapi oleh perusahaan kereta api. Masalah pelangsiran ini telah banyak dibahas dan dipelajari, di antaranya dalam

(Freling et al., 2000) dan (Lentink et al., 2003).

Penyelesaian dari masalah pelangsiran ini dapat menggunakan algoritme simpleks, namun akan membutuhkan waktu yang lama karena banyaknya variabel yang harus diselesaikan. Pada tulisan ini digunakan teknik pembangkitan kolom. Teknik pembangkitan kolom merupakan teknik yang telah banyak digunakan untuk menyelesaikan masalah dalam bidang transportasi dan penjadwalan. Salah satunya dikenalkan dalam (Barnhart et al., 1998) yang menggunakan teknik pembangkitan kolom dalam konteks pemrograman bilangan bulat. Tulisan ini merupakan rekonstruksi dari tulisan Richard Frelling, Ramon M. Lentink, Leo G. Kroon & Dennis Huisman (2002) yang berjudul “ Shunting of passenger train units in a railway station”.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah mempelajari penyelesaian masalah pelangsiran unit kereta penumpang pada stasiun kereta api dengan menggunakan teknik pembangkitan kolom (column generation).

II LANDASAN TEORI

2.1 Pemrograman Linear

Pemrograman linear adalah kegiatan merencanakan untuk mendapatkan hasil yang optimal. Model Pemrograman Linear (PL) meliputi pengoptimuman suatu fungsi linear terhadap kendala linear (Hillier & Lieberman, 1990).

Pada tulisan ini, suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut:

Definisi 1 (Bentuk Standar Suatu PL) Suatu pemrogra man linear dalam bentuk standar didefinisikan sebagai: Minimumkan z=cTx

terhadap Ax =b 0

≥

x (1)

dengan x dan c berupa vektor berukuran n, vektor b berukuran m, sedangkan A berupa

matriks berukuran m×n yang disebut juga sebagai matriks kendala.

(Nash & Sofer, 1996)

2.1.1 Solusi suatu Pemrograman Linear Untuk menyelesaikan suatu masalah Pemrograman Linear (PL), metode simpleks merupakan salah satu metode yang dapat menghasilkan solusi optimum. Metode ini mulai dikembangkan oleh Dantzig tahun 1947. Sejak perkembangannya, metode ini adalah metode yang paling umum digunakan untuk menyelesaikan PL, yaitu berupa metode iteratif untuk menyelesaikan masalah PL dalam bentuk standar.

taksingular yang elemennya berupa koefisien variabel basis dan N adalah matriks yang elemennya berupa koefisien variabel nonbasis pada matriks kendala . Matriks B disebut matriks basis untuk PL.

Misalkan x dapat dinyatakan sebagai

vektor     = N B x x

x , dengan xBadalah vektor

variabel basis dan xN adalah vektor variabel nonbasis. Maka Ax =b dapat dinyatakan sebagai

(

)

_ _ = N B x x

x B N

A

=Bx_B +Nx_N =b. (2) Karena B adalah matriks taksingular, maka Bmemiliki invers, sehingga dari (2) xBdapat dinyatakan sebagai:

x_B =B−1b−B−1Nx_N (3)

Definisi 2 (Solusi Basis)

Vektor x disebut solusi basis dari suatu pemrograman linear jika :

1. x memenuhi kendala dari PL, dan 2. kolom-kolom pada matriks kendala

yang berkorespondensi dengan komponen taknol dari x adalah bebas linear.

(Nash & Sofer, 1996)

Definisi 3 (Solusi Basis Fisibel)

Vektorx disebut solusi basis fisibel jika x merupakan solusi bas is dan x ≥0.

(Nash & Sofer, 1996)

Ilustrasi solusi basis dan solusi basis fisibel dapat dilihat dalam contoh berikut:

Contoh 1

Misalkan diberikan pemrograman linear berikut:

Minimumkan z=−2x₁−3x₂ terhadap −2x₁+x₂+x₃ =4

−x₁ +2x₂+x₄ =11 x₁+x₅ =5

x₁,x₂,x₃,x₄,x₅≥0 (4)

Dari pemrograman linear tersebut didapatkan:

A =

          − − 1 0 0 0 1 0 1 0 2 1 0 0 1 1 2

, b =

          5 11 4 . Misalkan dipilih

(

)

T

x x

x_{3 4 5}

=

B

x dan x_N =

(

x₁ x₂

)

T maka matriks basis

          = 1 0 0 0 1 0 0 0 1 B .

Dengan menggunakan matriks basis tersebut diperoleh

(

)

T

B b

x =B−1 = 4 11 5 ,

(

)

T

0 0

=

N

x . (5) Solusi (5) merupakan solusi basis, karena solusi tersebut memenuhi kendala pada PL (4) dan kolom-kolom pada matriks kendala yang berkorespondens i dengan komponen taknol dari (5) yaitu B adalah bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (5) juga merupakan solusi basis fisibel, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

PL (1) dapat dinyatakan dalam xB dan xN sebagai berikut:

Minimumkan z=c_BTx_B+c_NTx_N (6) terhadap Bx_B +Nx_N =b

0

≥

x

dengan c_Badalah koefisien variabel basis pada fungsi objektif, c_N adalah koefisien variabel nonbasis pada fungsi objektif.

Jika Persamaan (3) dis ubstitusikan ke Persamaan (6) maka akan didapat:

(

N

)

N N

B b x c x

c T T

z= B−1 −B−1N +

=c_BTB−1b+

(

c_NT −c_BTB−1N

)

x_N. Jika didefinisikan

(

cB

)

cB

y= TB−1 T =B−T

maka z dapat dinyatakan dalam y:

z= yTb+

(

c_NT −yTN

)

x_N. (7) Vektor y disebut vektor pengali simpleks (simplex multiplier).

Untuk suatu solusi basis x_N =0 dan b

b

x_B =ˆ=B−1 , maka: b c_B 1 ˆ= TB−

z .

Notasi zˆadalah notasi untuk z optimal. Koefisien cˆ_j disebut biaya tereduksi (reduced cost) dari xj dengan cˆj adalah

elemen dari ˆ T =

(

T − TB−1N

)

B N

N c c

c .

dijadikan variabel basis (artinya menjadi solusi taknol) pada suatu pemrograman linear.

2.1.2 Penyelesaian Pemrograman Linear dengan Algoritme Simpleks

Solusi suatu pemrograman linear dapat diketahui optimal atau tidak untuk PL tersebut melalui algoritme sebagai berikut:

• Tes Keoptimalan

Vektor y=c_BTB−1 dihitung, kemudian dapat dihitung pula nilai biaya tereduksi cˆ_NT =

(

c_NT −yTN

)

.

Jika cˆ_NT ≥0 maka solusi yang diperoleh adalah solusi optimal.

Jika cˆ_NT <0 maka dipilih variabel xt

yang memenuhi cˆ_t <0sebagai variabel-masuk yaitu variabel xt yang akan masuk

ke dalam basis.

• Langkah tertentu t

Hitung Aˆ _t =B−1A_t, yaitu koefisien kendala yang berhubungan dengan variabel-masuk ke t. Indeks s ditentukan pada kolom kendala yang berhubungan dengan variabel-masuk yang memenuhi

= t s

s

a b

,

ˆ

m i≤

≤

1 min

    

  

>0 ; ˆ

, ,

t i t i

i _a

a b

.

Memilih indeks dengan cara tersebut disebut dengan uji nisbah minimum (minimum ratio test).

Variabel yang menjadi variabel-keluar (variabel yang akan keluar dari basis dan digantikan oleh variabel-masuk) dan pivot entry adalah variabel yang berpadanan dengan aˆs,t.

Jika aˆ_i,t ≤0, 1≤i≤m untuk semua i, maka masalah PL disebut takterbatas.

• Pivot

Matriks basis B dan vektor basis xB diperbaiki, kemudian dilanjutkan ke tes keoptimalan.

Berikut contoh penggunaan algoritme simpleks:

Contoh 2

Misalkan diberikan PL (4) seperti pada Contoh 1, maka dengan menggunakan algoritme simpleks akan diperoleh solusi:

0 ,

6 , 8 ,

5 _{2 3 4 5}

1= x = x = x =x =

x

dengan z=−34(lihat Lampiran 1).

2.2 Masalah Dual

Setiap masalah pemrograman linear memiliki padanan, yaitu masalah lain yang disebut pemrograman linear dual. Pemrograman linearnya sendiri disebut masalah primal. Misalkan diberikan masalah primal:

Minimumkan z=cTx

terhadap Ax ≥b 0

≥

x . (8)

Masalah dual dari (8) adalah Maksimumkan w=bTy

terhadap ATy≤c

0 ≥

y . (9)

Jika masalah primal memiliki n variabel dan m kendala, maka masalah dual akan memiliki m variabel dan n kendala. Koefisien fungsi objektif masalah primal merupakan nilai sisi kanan pada masalah dual, begitu pula sebaliknya. Jika masalah primal merupakan masalah minimisasi maka masalah dual merupakan masalah maksimisasi.

Solusi optimal dari masalah dual merupakan pengali simpleks pada masalah primal. Pada kondisi optimal, solusi dari masalah dual dan masalah primal akan menghasilkan nilai fungsi objektif yang sama. Hal ini disebutkan dalam Teorema Dualitas Kuat, namun sebelumnya perlu diperkenalkan pula Teorema Dualitas Lemah yang akan digunakan untuk membuktikan Teorema Dualitas Kuat.

Teorema 1 (Teorema Dualitas Lemah) Misalkan diberikan pemrograman linear primal dan masalah dualnya. Misalkan x adalah solusi fisibel untuk masalah primal dalam bentuk standarnya dan misalkan y solusi fisibel untuk masalah dual, maka nilai fungsi objektif dari masalah primal selalu lebih besar atau sama dengan nilai fungsi objektif dari masalah dual.

Bukti: lihat (Nash & Sofer, 1996).

Akibat 1

Jika x adalah solusi fisibel untuk masalah primal, y adalah solusi fisibel untuk masalah dual, dan bTy=cTx, maka x dan y adalah solusi optimal berturut-turut untuk masalah primal dan dual.

Teorema 2 (Teorema Dualitas Kuat) Misalkan diberikan pemrograman linear primal dan masalah dualnya. Jika salah satu dari masalah primal atau masalah dual tersebut memiliki solusi optimal, maka masalah lainnya juga memiliki solusi optimal dan nilai fungsi objektif optimalnya adalah sama.

Bukti:

Misalkan diasumsikan bahwa masalah primal dalam bentuk standar dan mempunyai solusix yang merupakan solusi basis fisibel optimal. Misalkan x dapat

dinyatakan sebagai vektor

    = N B x x x ,

dengan xB adalah vektor variabel basis dan xN adalah vektor variabel nonbasis.

Selain itu, seperti telah dijelaskan sebelumnya matriks A dapat dinyatakan sebagai A=

(

B N

)

dan matriks koefisien pada fungsi objektif c dapat dinyatakan

sebagai     = N B c c

c . Karena B adalah matriks

taksingular, maka B memiliki invers sehingga xB dapat dinyatakan sebagai

b x_B =B−1 .

Dari tes keoptimalan pada algoritme simpleks diketahui pula, jika solusi x optimal maka biaya tereduksinya adalah

0 N

B ≥

− T −1 B T

N c

c ataucT_BB−1N≤cT_N (*) Misalkan y adalah vektor dari pengali simpleks yang berhubungan dengan solusi basis fisibel, dengan y=B−Tc_B atau

.

1

−

= T_BB

T _c

y Akan ditunjukkan bahwa: 1) Nilai dari fungsi objektif masalah

primal dan dual adalah sama, yaitu

x c y

bT = T , dan

2) yadalah optimal untuk masalah dual.

Bukti:

1) Sebelumnya akan diperiksa terlebih dahulu kefisibelan dari y :

A T

y =cT_BB−1

(

B N

)

(

B−1N

)

= T

B T

B c

c ≤

(

cT_B cT_N

)

..dari (*) = cT.

Sehingga ATy≤cdan y fisibel untuk masalah dual, kemudian dihitung nilai objektif untuk masalah primal (z) dan dual (w): b c x c x

cT = T_{B B} = T_B −1

= B

z

z

w=bTy=yTb=cT_BB−1b= .

Jadi y adalah fisibel untuk masalah dual dan nilai fungsi objektif solusi optimal dari masalah primal dan dual mempunyai nilai yang sama.

2) Berdasarkan Akibat 1 dan bTy=cTx

maka y adalah solusi optimal untuk masalah dual. <

Bukti dari Teorema Dualitas Kuat menghasilkan solusi optimal dual. Misalkan

    = N B x x

x , A=

(

B N

)

, dan

    = N B c c c

maka nilai optimal dari variabel dual diberikan oleh vektor pengali simpleks

B

c y=B−T .

Dari bukti teorema dualitas kuat terlihat bahwa kondisi primal optimal

0 N

B ≥

− T −1 B T

N c

c

adalah ekivalen dengan kondisi fisibel dual

c y≤

T

A atau c−ATy≥0. Jadi vektor dari biaya tereduksi cˆ adalah variabel slack dual

y c

cˆ= −AT . Contoh 3

Misalkan diberikan pemrograman linear primal sebagai berikut:

Minimumkan

5 4 3 2

1 7 9 7 5

5x x x x x

z= + + + +

terhadap x₁+x₂ ≥1 1

4 3

1+x +x ≥

x

1

4 3

2+x +x ≥

x

1

5 1+x ≥

x

1

3

2+x ≥

x

1

5 4

3+x +x ≥

x 1 4≥ x 0 ≥ i

x , untuk i=

{

1,2,3,4,5

}

.

Maksimumkan 7 6 5 4 3 2

1 y y y y y y

y

w= + + + + + +

terhadap y₁+y₂+y₄ ≤5 7

5 3

1+y + y ≤

y

9

6 5 3

2+y +y +y ≤

y

7

7 6 3

2+y +y +y ≤

y

5

6

4+y ≤

y 0

≥ i

y , untuk i=

{

1,2,3,4,5,6,7

}

.

Dengan menggunakan LINDO 6.1, diperoleh solusi dari masalah primal sebagai berikut:

, 1

4 2

1= x =x =

x x₃= x₅ =0

dengan nilai fungsi objektifnya z=19(lihat Lampiran 2). Nilai pengali simpleks untuk masing-masing kendala adalah sebagai berikut:

7 ,

5 ,

0 _{4 5 7}

6 3 2

1 =y = y =y = y = y =y =

y

dengan yi adalah nilai pengali simpleks

kendala ke -i.

Solusi dari masalah dual tersebut juga dapat dicari menggunakan LINDO 6.1 yang menghasilkan solusi:

7 ,

5 ,

0 _{4 5 7}

6 3 2

1= y =y = y = y = y =y =

y

dengan nilai fungsi objektif w = 19 (lihat Lampiran 2).

Dari penghitungan tersebut, nilai pengali simpleks masalah primal sama dengan optimal dari masalah dual dan fungsi objektif dari masalah primal dan dual mempunyai nilai yang sama seperti yang dinyatakan Teorema 2.

2.3 Pemrograman Linear Bilangan Bulat (PLBB)

Model pemrograman linear bilangan bulat atau disebut juga pemrograman bilangan bulat adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat. Jika semua variabel harus berupa bilangan bulat maka masalah tersebut disebut pemrograman bilangan bulat alami . Jika hanya sebagian yang harus bilangan bulat maka disebut Pemrograman bilangan bulat campuran. Pemrograman bilangan bulat dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 PLBB.

Definisi 4 (P L-Relaksasi)

PL-Relaksasi dari suatu PLBB merupakan pemrograman linear yang diperoleh dari PLBB tersebut dengan menghilangkan kendala bilangan bulat atau kendala 0-1 pada variabelnya.

(Winston, 1995)

Model yang digunakan pada tulisan ini yang berkaitan dengan masalah PLBB adalah masalah pemartisian himpunan (set partitioning problem).

2.3.1 Masalah Pemartisian Himpunan (Set PartitioningProblem)

Definisi 5 (Partisi)

Misalkan diberikan himpunan I=

{

1,2,...,m

}

dan himp unan P=

{

P₁,P₂,...,P_n

}

dengan Pj

adalah himpunan bagian dari I, j∈J=

{

1,2,...,n

}

.

Himpunan P_j dengan j∈J*⊆J

adalah partisi dari I jika :

= ∩ ⇒ ≠

∈J j k Pj Pk

k

j, *,

ø

dan

U

* J j j I P ∈ =

(Garfikel & Nemhauser, 1972)

Ilustrasi dari suatu partisi dapat dilihat pada Contoh 4 berikut:

Contoh 4

Misalkan diberikan himpunan

{

1,2,3,4,5,6

}

=

I dan kelas-kelas P₁=

{ }

1,6 ,

{ }

3,4

2 =

P , P₃=

{ }

1,4,5 , P₄ =

{ }

2,5 ,

{

2,3,5,6

}

5=

P .

Partisi dari I di antaranya adalah

{

P1,P2,P4

}

, karena untuk

{ }

1,2,4

* ₌ J berlaku = ∩ ⇒ ≠

∈J j k Pj Pk

k

j, *, ø

dan

U

* J j j I P ∈ =

Masalah pemartisian himpunan (set partitioning problem/SPP) adalah masalah menentukan partisi dari himpunan I yang mempunyai biaya minimum. Untuk mendapatkan partisi tersebut, misalkan didefinisikan variabel 0-1 sebagai berikut:

1, jika Pj termasuk dalam partisi

xj =

0, selainnya

Bentuk umum SPP:

Minimumkan

∑

=

n

j j jx

c

1

terhadap

∑

( )

= =

j n

j

x j

1

A 1

xj =0 atau 1

dengan cj adalah biaya Pj, A(j) adalah

matriks koefisien kendala, dan 1 adalah vektor dengan dimensi n dengan semua komponennya sama dengan 1.

Model ini memiliki beberapa sifat penting, yaitu:

Sifat 1 Masalah pada model merupakan masalah minimisasi dan semu a kendalanya berupa persamaan. Sifat 2 Nilai sisi kanan

semua kendala adalah 1.

Sifat 3 Semua elemen matriks koefisien A(j) adalah 0 atau 1.

Contoh 5 (Masalah Pemartisian Himpunan)

Misalkan diberikan himpunan I beserta kelas-kelas P seperti pada Contoh 4. Misalkan diketahui biaya dari masing-masing kelas Pj, yaitu cj, dengan

7 , 8 , 9 , 10 ,

5 _{2 3 4 5}

1= c = c = c = c =

c .

Diinginkan himpunan dari Pj yang dapat

memartisi I dengan biaya minimum. Masalah tersebut dapat dimodelkan sebagai masalah pemartisian himpunan. Misalkan didefinisikan variabel 0-1 sebagai berikut:

1, jika Pj termasuk dalam partisi

xj =

0, selainnya

1, jika elemen ke-i di I merupakan elemen Pj, dengan j=1,2,...,5

A(j) =

0, selainnya

Masalah tersebut dapat dimodelkan sebagai berikut:

SPP : Minimumkan

∑

=

5

1

j j jx

c

terhadap x₁+x₃ =1 1

5

4+x =

x

1

5

2+x =

x

1

3

2+x =

x

1

5 4

3+x +x =

x

1

5 1+x =

x

0

=

j

x atau 1, untuk j=

{

1,2,3,4,5

}

. Dengan mengunakan LINDO 6.1 diperoleh solusi untuk masalah SPP tersebut sebagai berikut:

0 ,

1 _{3 5}

4 2

1=x =x = x =x =

x , dan nilai

fungsi objektif sebesar 23.

Pada tulisan ini, model matematika dalam penetapan unit kereta pada rel pelangsiran diformulasikan sebagai masalah pemartisian himpunan dengan kendala tambahan.

masalah pemartisian himpunan dengan kendala tambahan adalah masalah pemartisian himpunan dengan beberapa kendala tambahan yang berbeda den gan kendala yang berada pada SPP itu sendiri.

Dalam tulisan ini juga diperlukan konsep tentang graf. Berikut uraian tentang teori graf yang berhubungan dengan masalah pelangsiran unit kereta pada stasiun kereta api dan algoritme pembangkitan kolom.

2.4 Graf

Definisi 6 (Graf)

Suatu graf adalah pasangan terurut (V,E) dengan V himpunan takkosong dan hingga dan E adalah himpunan pasangan takterurut yang menghubungkan elemen-elemen V dan dinotasikan dengan

( )

V E G= , .

Elemen V dinamakan simpul (node), dan elemen E dinamakan sisi (edge), dinotasikan sebagai

{ }

i,j , yaitu sisi yang menghubungkan simpul i dengan simpul j, dengan i,j∈V .

(Foulds, 1992)

Ilustrasi graf dapat dilihat pada Contoh 6 berikut:

Contoh 6 G :

Gambar 1. Graf G = (V, E).

v1 v5

v4

Pada Gambar 1, V =

{

v₁,v₂,v₃,v₄,v₅

}

dan

{

} {

} {

} {

} {

}

{

v1,v2 , v1,v5 , v2,v3 , v2,v5 , v3,v4

E=

{

v₃,v₅

} {

, v₄,v₅

}}

.

Definisi 7 (Walk)

Suatu walk pada graf G=

( )

V,E adalah suatu barisan simpul dan sisi dari G dengan bentuk:

{

v v

} {

v v v

} {

vn vn

}

vn

v1, 1, 2 , 2, 2, 3 ,..., −1, , ,

atau ditulis dengan ringkas:

n

v v

v1, 2,..., atau (v1,v2,...,vn). Walk

tersebut menghubungkan simpul v₁ dengan

n

v .

(Foulds, 1992)

Definisi 8 (Path)

Path pada suatu graf G adalah suatu walk dengan semua simpulnya berbeda.

(Foulds, 1992)

Berikut diberikan ilustrasi dari walk dan path. Pada graf G yang terdapat pada Gambar 1 salah satu contoh walk adalah

) , , , , , ,

(v₁ v₂ v₅ v₄ v₃ v₂ v₅ , sedangkan salah satu contoh path adalah (v₁,v₂,v₅,v₄).

Definisi 9 (Digraf)

Digraf (directed graf/graf berarah) adalah pasangan terurut (V, A) dengan V adalah himpunan takkosong dan hingga, dan A adalah himpunan pasangan terurut dari elemen-elemen di V.

Elemen dari A disebut sisi berarah (arc) dan dituliskan sebagai

( )

i,j dengan

V j

i, ∈ .

(Foulds, 1992)

Ilustrasi digraf dapat dilihat pada Contoh 7 berikut:

Contoh 7

Gambar 2. Digraf G'=(V,A).

Pada Gambar 2, digraf G’ memiliki himpunan simpul V =

{

v₁,v₂,v₃,v₄,v₅

}

dan

{

(v₁,v₂),(v₁,v₅),(v₂,v₃),(v₅,v₃),(v₃,v₄), A=

(

v₅,v₄

)}

.

Definisi 10 (Sisi Berarah Menjauhi atau Mendekati, Suksesor dan Predesesor)

Misalkan diberikan digraf D=

(

V,A

)

. Jika a=

( )

vi,vj ∈A maka sisi berarah ini

dikatakan menjauhi v_i dan mendekati v_j. Simpul v_i disebut predesesor bagi simpul

j

v , simpul v_j disebut suksesor bagi simpul

i

v .

(Foulds, 1992)

Definisi tersebut dapat digambarkan dalam digraf seperti berikut:

Gambar 3. Sisi berarah menjauhi atau mendekati, suksesor, dan predesesor.

Definisi 11 (Graf Berbobot)

Suatu graf G=

( )

V,E atau digraf

(

V A

)

D= , dikatakan berbobot jika terdapat fungsi w:E→ℜatau ϑ:A→ℜ (dengan

ℜ

himpunan bilangan real) yang memberikan bobot pada setiap elemen E atau A.

(Foulds, 1992)

Terdapat kasus khusus dari graf berbobot yaitu network. Beberapa definisi yang digunakan dalam network adalah sebagai berikut:

Definisi 12 (Simpul sumber)

Simpul sumber (source) adalah suatu simpul dengan tidak ada sisi berarah yang mendekati simpul tersebut.

(Foulds, 1992)

Definisi 13 (Simpul tujuan)

Simpul tujuan (sink) adalah suatu simpul sehingga tidak ada sisi berarah yang menjauhi simpul tersebut.

(Foulds, 1992)

Definisi 14 (Network)

Network adalah suatu digraf yang mempunyai tepat satu simpul sumber dan satu simpul tujuan.

(Foulds, 1992)

i

v

v1 v5

v4

v2 v3

j

Contoh 8

Graf G’ pada Gambar 2 merupakan network dengan v1 sebagai simpul sumber

dan v4 sebagai simpul tujuan.

Masalah graf berbobot ini biasanya untuk suatu kasus tertentu diinginkan bobot yang terkecil, salah satunya adalah masalah path terpendek (shortest path problem).

Definisi 15 (Shortest Path Problem) Masalah path terpendek adalah masalah untuk menemukan path terpendek (path dengan biaya minimum) dari suatu simpul ke suatu simpul lain dalam suatu network.

(Foulds, 1992)

III DESKRIPSI DAN FORMULASI MASALAH

3.1 Masalah Pelangsiran Unit Kereta Penumpang pada Stasiun Kereta

Dalam jam-jam sibuk, kereta api penumpang khusus dioperasikan untuk mengangkut penumpang, sedangkan di luar jam sibuk, terdapat kelebihan kereta api yang tidak dioperasikan. Kelebihan kereta api tersebut dapat diparkir di rel-rel tertentu pada stasiun kereta api. Proses dari pendataan, pemarkiran, dan pemeliharaan unit kereta api beserta proses lain yang berhubungan disebut pelangsiran (shunting). Namun dalam tulisan ini hanya akan dibahas mengenai pendataan dan pemarkiran unit kereta api saja.

Pelangsiran dari unit kereta biasanya dilakukan di stasiun kereta yang memiliki jumlah rel yang banyak. Unit kereta-api-datang yang akan dilangsir (unit pelangsiran) dapat diletakkan pada rel-rel di depan peron ataupun rel-rel di sekitar peron. Ada dua jenis peron pada stasiun kereta, yaitu peron kedatangan dan peron keberangkatan. Unit kereta yang diparkir di depan peron adalah unit kereta dari kereta-api-terus. Kereta-api-terus adalah jenis kereta yang memiliki jangka waktu yang cukup dekat antara kedatangan ke stasiun dan keberangkatan dari stasiun. Rel yang jarang digunakan untuk memarkir unit pelangsiran adalah rel yang sering digunakan oleh kereta-api-terus. Hal ini bertujuan agar aktivitas kereta-api-terus tidak terganggu karena pelangsiran biasanya memerlukan waktu yang tidak singkat.

Unit kereta api yang harus diparkir di tempat pelangsiran disebut unit keretaapi -datang (arriving shunt unit), sedangkan unit kereta-api -berangkat (departing shunt unit) didefinisikan sebagai unit kereta api yang harus diberangkatkan dari tempat pelangsiran. Unit kereta-api-datang dapat berasal dari kereta api yang telah selesai

dioperasikan dalam jangka waktu tertentu, sedangkan unit kereta-api-berangkat membentuk suatu rangkaian kereta yang akan dioperasikan untuk melayani penumpang.

Sebagian besar kereta api dapat bergerak dalam dua arah dan tidak membutuhkan lokomotif. Dalam masalah ini, unit kereta diklasifikasikan berdasarkan tipe dan subtipe. Tipe dari suatu unit kereta api merupakan kelas kereta api, misalkan kereta api tipe (kelas) bisnis, ekonomi atau eksekutif. Pada masalah ini diasumsikan bahwa hanya unit kereta dari tipe yang sama yang dapat dikombinasikan untuk membentuk suatu rangkaian kereta api. Sedangkan subtipe dari suatu unit kereta didasarkan atas banyaknya gerbong per unit kereta. Sebagai contoh, kereta api dengan subtipe MAT1_3 terdiri atas 1 unit kereta tipe MAT1 dengan banyaknya gerbong 3 buah. Kereta api dengan subtipe MAT1_3 MAT1_4 terdiri atas 2 unit kereta MAT1 dengan banyaknya gerbong 7 buah, di mana unit pertama terdiri atas 3 gerbong dan unit kedua dengan 4 gerbong. Dalam penggunaannya, unit kereta dari subtipe yang sama dapat dipertukarkan urutannya.

Secara umum, masalah pelangsiran unit kereta terdiri atas dua submasalah. Pertama adalah pendataan unit kereta-api-datang menjadi unit kereta-api-berangkat. Kedua berhubungan dengan pemarkiran unit-unit kereta pada rel pelangsiran. Selanjutnya, akan diminimumkan ongkos dari sebuah rencana pelangsiran sehingga kapasitas dari rel pelangsiran tidak terlebihi.

Kendala dari masalah pelangsiran unit kereta secara umum terdiri atas empat hal, yaitu:

datang di stasiun tidak harus yang pertama kali berangkat dari stasiun. 2. Rel-rel pelangsiran dapat memiliki tipe

serta panjang yang berbeda. Tipe dari sebuah rel menentukan bagaimana suatu unit pelangsiran dapat memasuki rel. Dalam hal ini, rel pelangsiran dibagi menjadi dua tipe, yaitu jalur-satu-arah (Last In First Out track) yang dapat dimasuki hanya dari salah satu sisi rel dan jalur-bebas (free track) yang dapat dimasuki dari dua sisi.

3. Unit pelangsiran dapat memiliki subtipe (banyaknya gerbong) yang berbeda. Hal ini membatasi himpunan rel pelangsiran di mana unit pelangsiran dapat diparkir karena rel-rel pelangsiran memiliki ukuran panjang yang berbeda.

4. Kereta api mempunyai waktu yang tetap untuk kedatangan dan keberangkatan dari peron, namun

mempunyai waktu kedatangan dan keberangkatan dari rel pelangsiran yang fleksibel. Sebagai contoh, waktu keberangkatan sebuah unit kereta-api-datang dari sebuah peron kekereta-api-datangan ke tempat pelangsiran dapat fleksibel dalam suatu interval waktu. Keberangkatan dapat dimulai dari waktu kedatangan dari unit tersebut ke peron dan berakhir pada sebuah kedatangan selanjutnya dari sebuah unit kereta pada peron kedatangan yang sama.

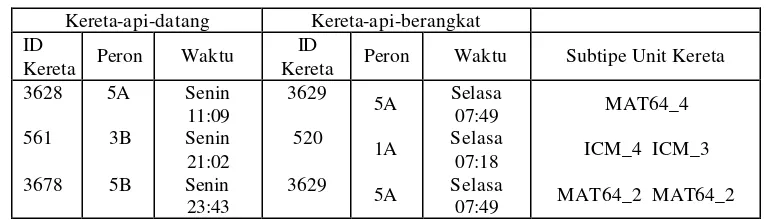
Tabel 1 adalah sebuah contoh dari tabel waktu (time table) untuk sebuah rel pelangsiran bertipe jalur-bebas . Tabel waktu ini berisi identitas (ID) kereta, subtipe dari kereta, dan waktu kedatangan dan/atau keberangkatan kereta serta peron stasiun yang digunakan.

Tabel 1. Contoh tabel waktu untuk sebuah jalur-bebas

Kereta-api-datang Kereta-api-berangkat ID

Kereta Peron Waktu

ID

Kereta Peron Waktu Subtipe Unit Kereta 3628

561

3678

5A

3B

5B

Senin 11:09 Senin 21:02 Senin 23:43

3629

520

3629

5A

1A

5A

Selasa 07:49 Selasa 07:18 Selasa 07:49

MAT64_4

ICM_4 ICM_3

MAT64_2 MAT64_2

Tabel 1 menjelaskan sebuah rencana pelangsiran dari 5 unit kereta pada sebuah jalur-bebas . Setiap baris menunjukkan pendataan dari unit kereta-api-datang menjadi unit-kereta-api-berangkat. Dalam contoh ini, satu unit subtipe MAT64_4 dari kereta dengan ID 3628 tiba di peron 5A pada Senin pukul 11:09 dan unit ini akan meninggalkan stasiun dengan Kereta 3629 dari peron 5A pada Selasa pukul 07:49. Selanjutnya, baris ketiga menjelaskan bahwa

dua unit kereta dengan subtipe MAT64_2 tiba dengan Kereta 3678 di peron 5B pada Senin pukul 23:43 dan akan berangkat juga dengan Kereta 3629 dari peron 5A pada Selasa 07:49. Jadi unit-unit dari Kereta 3628 dan Kereta 3678 dipasangkan berdekatan pada rel pelangsiran yang sama.

Kereta-api- datang

Gambar 4. Situasi di rel pelangsiran pada Selasa pukul 06:00.

Pada Gambar 4, Kereta 3628 berangkat dari peron 5A ke rel pelangsiran melalui salah satu sisi rel. Kemudian dari peron 3B Kereta 561 memasuki rel pelangsiran melalui sisi kiri rel, sedangkan Kereta 3678 berangkat dari peron 5A ke rel pelangsiran melalui sisi kanan rel. Kereta 561 dan 3678

tidak dapat memasuki rel pelangsiran dari sisi yang sama baik kiri maupun kanan.

Gamb ar 5 menggambarkan situasi di rel pelangsiran Selasa pukul 06:00 jika unit-unit dari Kereta 561 dan 3678 memasuki rel pelangsiran melalui sisi yang sama (dalam contoh ini melalui sisi kanan rel).

Gambar 5. Situasi di rel pelangsiran pada Selasa pukul 06:00 jika Kereta 561 dan Kereta 3678 memasuki rel pelangsiran melalui sisi yang sama.

Pada Gambar 5, Kereta 520 yang harus berangkat lebih dulu daripada Kereta 3629 akan tertutup dari kedua sisi rel oleh Kereta 3628 dan Kereta 3678. Hal ini disebut crossing dan tidak diperbolehkan karena akan menyulitkan proses pemberangkatan kereta. Selanjutnya, dalam kasus ini Kereta 3628 dan Kereta 3678 yang akan membentuk Kereta-api-berangkat 3629 tidak dapat diparkir berdekatan pada rel pelangsiran yang sama. Hal ini juga akan menyulitkan proses pelangsiran pada pagi hari. Jika rel berupa jalur-bebas , crossing hanya dapat dihindari dengan memarkir beberapa unit pada rel yang berbeda.

3.2 Pendekatan Solusi

Untuk mencari solusi dari masalah pelangsiran secara utuh adalah hal yang rumit. Oleh karena itu, untuk memudahkan pencarian solusi dari masalah pelangsiran, pendekatan solusi dipecah ke dalam dua submasalah.

Langkah pertama adalah proses pemadanan dari sejumlah unit kereta-api-datang menjadi unit kereta-api-berangkat. Setiap unit kereta-api-datang ditetapkan menjadi unit kereta-api-berangkat.

Misalkan berdasarkan tabel waktu pada Tabel 1, unit kereta-api-datang dengan subtipe MAT64_4 dari Kereta 3628 ditetapkan menjadi unit kereta-api-berangkat

Kereta 3629 Kereta 520

MAT 64_2 MAT

64_2 MAT

64_4 ICM_3

ICM_4

Kereta 561 Kereta 3628 Kereta 3678

MAT 64_2 MAT

64_2 ICM_3

ICM_4

Kereta 3629

Kereta 3628 Kereta 561 Kereta 3678

MAT 64_4

Kereta 520

Kereta-api-berangkat

Kereta-api-datang

dengan subtipe yang sama dari Kereta 3629. Hal yang perlu diperhatikan bahwa unit kereta-api-datang dan unit kereta-api-berangkat dari suatu kereta tertentu adalah dua unit kereta dari subtipe yang sama, hanya saja penamaan keretanya yang berbeda. Pada contoh ini kereta yang datang dinamakan Kereta 3628, sedangkan kereta yang berangkat dinamakan Kereta 3629.

Hasil dari langkah ini adalah himpunan gabungan dari satu atau lebih unit kereta yang digunakan secara bersama-sama selama periode tertentu yang didefinisikan sebagai blok. Sebagai contoh, unit kereta ICM_4 dan ICM_3 dalam Gambar 4 membentuk sebuah blok karena kedua unit ini digunakan secara bersama-sama pada Kereta 561. Unit kereta ICM_3 dan MAT64_4 tidak membentuk blok karena kedua unit ini tidak digunakan secara bersama-sama dalam pembentukan suatu kereta.

Langkah kedua berkaitan dengan pemarkiran unit-unit pelangsiran pada rel-rel pelangsiran. Dalam hal ini, setiap blok diparkir di suatu rel pelangsiran sedemikian sehingga kapasitas rel tidak terlebihi dan crossing tidak terjadi.

3.2.1 Formulasi Masalah Pemadanan api-datang menjadi kereta-api -berangkat

Untuk setiap kereta-api-datang dan kereta-api-berangkat didefinisikan sebuah network. Simp ul-simpul dari network menyatakan unit-unit kereta dan sebuah simpul rekaan (dummy/simpul 0). Simpul-simpul tersebut dapat mewakili tempat-tempat di mana unit kereta dapat dibagi ke dalam beberapa part. Part adalah himpunan bagian dari unit-unit kereta yang berdampingan pada suatu kereta api. Sisi berarah pada network mewakili part yang mungkin terbentuk dari suatu kereta. Secara matematis, banyaknya part yang dapat dibentuk dari suatu kereta dapat dinyatakan sebagai kombinasi _mC_n, dengan m adalah banyaknya simpul dari suatu kereta dan n adalah banyaknya simpul yang berada di antara simpul sumber dan simpul tujuan pada suatu network dari kereta.

Gambar 6 menggambarkan suatu network untuk Kereta-api-berangkat 3629 pada Tabel 1.

Gambar 6. Network dari Kereta 3629 pada Tabel 1.

Simpul 0 adalah simpul rekaan, sedangkan simpul 1, 2, 3 adalah unit kereta dari Kereta 3629, yang secara berurutan memiliki subtipe MAT64_4, MAT64_2, MAT64_2.

Setiap sisi berarah bersesuaian dengan satu part dan terdapat 6 part yang berbeda yang mungkin pada contoh ini. Himpunan part yang terbentuk pada network di Gambar 6 diperoleh dari kombinasi yang mungkin semua subtipe unit kereta dari Kereta 3629 pada Tabel 1 dan sebuah simpul rekaan. Sebagai contoh sisi berarah (0,1) pada network menyatakan bahwa subtipe MAT64_4 dari Kereta 3629 membentuk suatu part, sedangkan sisi berarah (0,2) menyatakan bahwa subtipe MAT64_4 dan

MAT64_2 dari Kereta 3629 membentuk suatu part. Sebuah path dari simpul pertama sampai yang terakhir pada network ini bersesuaian dengan pembagian kereta ke dalam beberapa part. Sebagai contoh, path 0-2-3 pada Gambar 6 menyatakan bahwa unit kereta 1 dan 2 membentuk satu part dan unit kereta 3 membentuk part yang lain. Sebuah blok merupakan suatu kombinasi dari part-part pada kereta api.

Simpul rekaan pada network dari Kereta 3629 dibutuhkan karena terdapat kemungkinan bahwa dua unit kereta membentuk satu part dan unit kereta lainnya membentuk part yang berbeda.

Gambar 7 adalah network dari Kereta 3629 pada Tabel 1 tanpa simpul rekaan.

Gambar 7. Network dari Kereta 3629 pada Tabel 1 tanpa simpul rekaan.

Jika tidak ada simpul rekaan pada network ini, maka hanya ada 3 part yang mungkin terbentuk. Dalam hal ini path yang dapat dibentuk hanya ada dua. Pertama, path 1-2-3 pada Gambar 7 yang menyatakan bahwa ketiga unit kereta membentuk part yang berbeda, sedangkan yang kedua, path 1-3 pada Gambar 7 yang menyatakan bahwa ketiga unit kereta hanya membentuk 1 part.

Misalkan diberikan I sebagai himpunan dari semua part yang mungkin untuk kereta-api-datang dan J sebagai himpunan dari semua part yang mungkin untuk kereta-api-berangkat. Secara formal diperkenalkan sebuah formulasi matematika dengan variabel biner sebagai berikut:

1, jika part i

∈

I digunakan pada suatu kereta-api-datang

ui =

0, selainnya

1, jika part j

∈

J digunakan pada suatu kereta-api-berangkat vj=

0, selainnya

1, jika part i

∈

I ditetapkan menjadi part j

∈

J

zij =

0, selainnya

Misalkan:

a

T : himpunan dari kereta-api-datang dengan unit pelangsirannya,

d

T : himpunan dari kereta-api-berangkat dengan unit pelangsirannya,

t

A : himpunan sisi berarah pada network dari kereta t,

+

t h

A : himpunan sisi berarah yang menjauhi simpul h untuk kereta t, −

t h

A : himpunan sisi berarah yang mendekati simpul h pada network kereta t,

−

t

C : himpunan dari semua simpul-antara di network pada kereta t; simpul-antara adalah simpul-simpul yang berada di antara simpul sumber dan simpul tujuan pada suatu network,

i

J : himpunan part dari kereta-api-berangkat dengan konfigurasi pemadanan yang sama sebagai part dari kereta-api-datang i,

j

I : himpunan part dari kereta-api-datang dengan konfigurasi pemadanan yang sama sebagai part dari kereta-api-berangkat j.

Misalkan Q menyatakan penalti untuk setiap part dari kereta-api-datang yang ada di rel pelangsiran tetapi tidak ditetapkan menjadi part dari kereta-api-berangkat. Misalkan pula wij menyatakan ongkos dari

penetapan part dari kereta-api-datang i menjadi part dari kereta-api-berangkat j. Dalam tulisan ini ongkos didefinisikan sebagai perbedaan antara waktu datang dan berangkat dari part i dan j.

Model matematikanya: Minimumkan

∑

∈ + I i i u Q

∑∑

∈ ∈I i j J

ij ij

i z

w (10)

terhadap

∑

₊ ∈ = t A i i u 0

1 ∀t∈Ta (11)

∑

₊ ∈ − t h A i i u

∑

− ∈ = t h A i i

u 0,∀t∈Ta,∀h∈C_t− (12)

1

0

=

∑

₊ ∈_At

j j

v ∀t∈Td (13)

∑

₊ ∈ − t h A j j

v

∑

=0

− ∈t h A j j

v , ∀t∈Td,∀h∈C_t− (14)

i J j ij u z i =

∑

∈

∀i∈I (15)

j I i ij v z j =

∑

∈

∀j∈J (16)

{ }

0,1 ,

, i j∈ ij u v

z ∀i∈I,∀j∈J (17) Tujuan dari fungsi objektif (10) adalah meminimumkan jumlah terboboti dari banyaknya part dan ongkos penetapan part dari kereta-api-datang menjadi part dari kereta-api-berangkat sehingga unit -unit kereta dapat dikelompokkan sebanyak mungkin ke dalam suatu part. Kendala (11) dan (12) menjamin tercovernya setiap unit kereta-api-datang oleh sebuah part, sedangkan kendala (13) dan (14) menjamin

tercovernya setiap unit kereta-api-berangkat oleh sebuah part. Kendala (15) menjamin bahwa untuk setiap part dari kereta-api-datang ditetapkan menjadi suatu part pada kereta-api-berangkat jika dan hanya jika part dari kereta-api-datang adalah hasil dari pemecahan kereta. Kendala (16) memodelkan hal yang sama untuk setiap part dari kereta-api-berangkat. Kendala (17) menyatakan bahwa variabel yang digunakan adalah variabel 0-1 yang telah didefinisikan.

Hasil dari langkah ini adalah himpunan part dari kereta-api-datang yang ditetapkan menjadi part dari kereta-api-berangkat, yang sebelumnya kita sebut dengan blok. Blok-blok ini akan digunakan dalam langkah 2.

3.2.2 Formulasi Masalah Penetapan Unit Kereta pada Rel Pelangsiran Seperti telah dijelaskan sebelumnya, pemadanan dari sejumlah unit kereta-api-datang menjadi unit kereta-api-berangkat dari unit pelangsiran menghasilkan sebuah himpunan blok B. Blo k yang tidak perlu diparkir di rel pelangsiran tidak dimasukkan dalam himpunan B ini.

Untuk setiap blok diberikan waktu kedatangan dan keberangkatan serta peron kedatangan dan keberangkatan. Selain itu diberikan pula ongkos rute antara rel-rel di depan peron dan semua rel pelangsiran yang fisibel untuk setiap blok. Rel pelangsiran yang fisibel untuk suatu blok adalah rel pelangsiran yang memiliki tipe serta panjang yang sesuai untuk suatu blok.

Ongkos rute untuk jalur-bebas dapat berbeda antara sisi kanan dan kirinya. Hal ini disebabkan antara lain karena jarak yang berbeda antara rel-rel di depan peron dengan rel-rel pelangsiran jika dimasuki dari sisi kiri atau kanan.

Berdasarkan informasi-informasi di atas, langkah kedua dari pendekatan solusi masalah pelangsiran terdiri dari penetapan blok pada rel pelangsiran dengan ongkos yang minimum sehingga kapasitas dari rel pelangsiran tidak terlebihi dan tidak terjadi crossing antarblok. Crossing terjadi jika suatu blok menghalangi blok yang datang ke rel pelangsiran atau blok yang berangkat dari rel pelangsiran.

Submasalah dari penetapan blok pada rel pelangsiran ini disebut sebagai Track Assignment Problem (TAP). TAP diformulasikan sebagai sebuah masalah pemartisian hinpunan dengan kendala tambahan.

Untuk formulasi ini, didefinisikan suatu track assignment, yang disingkat dengan assignment, sebagai sebuah penyusunan dari blok-blok pada rel pelangsiran yang fisibel dalam suatu periode perencanaan.

Sebuah assignment dikatakan fisibel jika memenuhi kondisi-kondisi berikut:

§ assignment tidak mengandung crossing.

§ panjang total dari unit kereta pelangsiran pada rel tidak melebihi panjang rel.

§ semua blok mempunyai kesempatan yang sama untuk parkir pada rel. Tabel 1 dan Gambar 1 memuat sebuah contoh assignment yang tidak mengandung crossing dari blok terhadap sebuah rel pelangsiran.

Misalkan S adalah himpunan dari rel pelangsiran dan misalkan pula Ks adalah himpunan assignment fisibelpada rel s

∈

S dan K_bs adalah himpunan assignment fisibel pada rel s

∈

S yang mengandung blok b

∈

B.

Kemudian didefinisikan variabel-variabel biner berikut:

1, jika assignment fisibel k

∈

Ks digunakan pada rel pelangsiran s

∈

S

=

s k

x

0, selainnya

1, jika blok b

∈

B tidak diparkir pada rel pelangsiran s

∈

S

= b

y

0, selainnya

Misalkan cs_k menyatakan ongkos dari suatu assignment k pada rel s. Ongkos ini merupakan jumlah ongkos rute pelangsiran dari blok-b lok yang berbeda pada suatu assignment.

Misalkan d menyatakan penalti jika sebuah blok tidak diparkir pada sebuah rel. TAP kemudian diformulasikan sebagai berikut:

Minimumkan

∑ ∑

∑

∈ ∈ ∈

+ B b

b S

s k K s k s

kx d y

c s

(18)

terhadap

∑ ∑

+ =1

∈ ∈

b S

s k K s

k y

x

s b

, ∀b∈B (19)

1

≤

∑

∈_Ks

k s k

{ }

0,1

∈

s k

x , ∀s∈S,∀k∈Ks (21)

{ }

0,1

∈ b

y , ∀b∈B (22)

Tujuan dari fungsi objektif (18) adalah meminimumkan ongkos dari assignment-assignment yang fisibel serta meminimumkan banyaknya blok yang tidak diparkir pada rel pelangsiran. Kendala (19) menyatakan bahwa setiap blok dicover oleh tepat satu assignment pada satu rel pelangsiran atau tidak diparkir sama sekali. Selanjutnya, kendala (20) menyatakan bahwa setiap rel pelangsiran dapat

mempunyai paling banyak satu assignment. Kendala (21) dan (22) menyatakan bahwa variabel yang digunakan adalah variabel 0-1 yang telah didefinisikan.

Kolom pada matriks kendala dari masalah TAP tersebut menunjukkan assignment pada rel pelangsiran tertentu dan baris pada matriks menunjukkan blok dan rel pelangsiran. Jika blok b tercover dalam assignment k pada suatu rel s, maka elemen matriks pada baris b dan kolom ks memiliki nilai 1, dan 0 jika blok b tidak tercover dalam assignment tersebut.

IV PENYELESAIAN MASALAH PENETAPAN BLOK PADA REL

PELANGSIRAN DENGAN MENGGUNAKAN TEKNIK

PEMBANGKITAN KOLOM

Penyelesaian masalah pelangsiran secara utuh dengan menggunakan algoritme simpleks adalah hal yang rumit. Hal ini disebabkan banyaknya assignment yang terbentuk pada masalah penetapan blok di rel pelangsiran.

Karena banyaknya variabel yang besar, menyelesaikan masalah minimisasi penetapan blok pada rel pelangsiran dengan menggunakan metode simpleks akan menghabiskan banyak waktu dalam pengerjaannya. Di sini akan dibahas salah satu teknik yang dapat digunakan untuk menyelesaikan masalah penetapan blok pada rel pelangsiran, yaitu teknik pembangkitan kolom atau column generation.

Teknik pembangkitan kolom adalah salah satu teknik untuk menyelesaikan suatu pemrograman linear dengan hanya menggunakan sebagian variabel dari masalah keseluruhan. Jika solusi PL tersebut belum mencapai kondisi optimal pada masalah secara keseluruhan, maka dengan kriteria tertentu ditambahkan variabel pada PL tersebut. Setelah itu diselesaikan kembali PL yang telah ditambah tersebut sampai diperoleh suatu kriteria pemberhentian.

Masalah induk (master problem/MP) dari masalah ini merupakan masalah pemilihan himpunan assignment yang sesuai dengan model (18) – (22), yaitu:

Minimumkan

∑ ∑

∑

∈ ∈ ∈

+ B b

b S

s k K s k s

kx d y

c s

terhadap

∑ ∑

+ =1

∈ ∈

b S

s k K s

k y

x

s b

, ∀b∈B

1

≤

∑

∈_Ks

k s k

x , ∀s∈S

0

≥

s k

x , ∀s∈S,∀k∈Ks 0

≥ b

y , ∀b∈B

Masalah induk merupakan masalah PL-relaksasi. Dalam teknik pembangkitan kolom digunakan pemrograman linear masalah induk terbatas (Restricted Master Problem/RMP), yaitu pemrograman linear yang hanya menggunakan sebagian variabel dari MP. Variabel (kolom) yang belum digunakan dalam RMP dibangkitkan berdasarkan nilai variabel dual yang diperoleh dari masalah induk. Oleh karena itu, diperkenalkan variabel dual λ_b(b∈B) dan µ_s(s∈S) berturut-turut untuk kendala (19) dan (20).

Biaya tereduksi dari suatu PL dapat diperoleh dari masalah dual PL tersebut. Misalkan B_ks adalah himpunan blok dari assignment k yang diparkir pada rel s.

Dengan informasi ini, masalah dual dari masalah induk (23) adalah:

Maksimumkan

∑ ∑

∈ ∈ + s k B

b s S

s b µ λ terhadap s k s B b b c s k ≤ +

∑

∈ µ

λ , ∀s∈S,k∈Ks (24)

b λ λ

λ₁, ₂,..., takterbatas 0 ,..., , ₂

1 µ µs ≤

µ

Berdasarkan pemaparan bukti dari Teorema Dualitas Kuat (Nash & Sofer, 1996), kondisi optimal primal yang merupakan biaya tereduksi adalah ekivalen dengan kondisi fisibel pada masalah dual. Sehingga kendala (24) merupakan biaya tereduksi dari masalah induk (23).

Misalkan biaya tereduksi tersebut dinotasikan dengan c_ks , maka sesuai dengan kendala (24) :

s s B b b s k s

k c s S k K

c s k ∈ ∈ ∀ − − =

∑

∈ , , µ

λ (25)

Persamaan (25) mewakili biaya tereduksi dari assignment k pada rel pelangsiran s.

Selanjutnya akan didiskusikan representasi network untuk masalah penetapan blok pada rel pelangsiran dan akan diberikan teknik pembangkitan kolom untuk optimisasi penetapan blok pada rel pelangsiran.

Hasil dari algoritme ini adalah sebuah himpunan kolom atau himpunan assignment untuk suatu rel pelangsiran.

4.1 Representasi Network dari Masalah Penetapan Blok pada Rel Pelangsiran Representasi network digunakan untuk membangkitkan assignment-assignment pada satu rel pelangsiran. Misalkan F adalah himpunan tipe pendekatan yang berbeda dari dan ke suatu rel pelangsiran. Untuk suatu jalur-satu-arah, F hanya mengandung satu elemen, yaitu datang dari dan berangkat ke arah yang sama, baik kiri (LL) atau kanan (RR). Sedangkan untuk suatu jalur-bebas , F mengandung 4 elemen:

§ Datang dari kiri dan berangkat ke kiri (LL)

§ Datang dari kiri dan berangkat ke kanan (LR)

§ Datang dari kanan dan berangkat ke kiri (RL)

§ Datang dari kanan dan berangkat ke kanan (RR)

Untuk memudahkan pembentukan assignment pada tulisan ini diasumsikan

bahwa himpunan blok B yang perlu diparkir disusun secara berurutan berdasarkan waktu kedatangan.

Setiap blok b∈B diwakili oleh suatu lapisan ke -b dalam suatu rel pelangsiran atau disebut juga sebagai lapisan L_b yang terdiri dari simpul-simpul nbf dengan

F

f∈ dan simpul n_notb yang berpadanan dengan tidak diparkirnya suatu blok b pada rel.

Simpul-simpul pada network memuat sebuah simpul sumber o, sebuah simpul tujuan t dan untuk setiap blok b terdapat lapisan L_b. Karena blok-blok disusun secara berurutan berdasarkan waktu kedatangan, maka blok yang pertama kali harus diparkir di rel pelangsiran diwakili oleh lapisan L1,

blok yang kedua datang diwakili oleh lapisan L2, dan seterusnya.

Sisi-sisi berarah pada network ini diarahkan dari simpul sumber ke setiap simpul pada lapisan pertama, dari setiap simpul di lapisan terakhir ke simpul tujuan, dan antara dua simpul pada lapisan-lapisan yang berturutan antara simpul sumber dan simpul tujuan jika blok-blok yang berhubungan dapat diparkir pada suatu rel tanpa terjadi crossing. Sisi yang menghasilkan crossing dikatakan sisi yang takfisibel.

Misalkan didefinisikan B− sebagai himpunan dari blok tanpa adanya crossing, kemudian didefinisikan sebuah network

) , (N A

G= yang telah dijelaskan di atas sebagai :

{ }

U

B b

b

o

t

L

N

∈

∪

=

,

(26)

(

)

{

1 1 , , : , + ∈ − ∈ ∈ ₊

= b b

b j b

i n b B i L j L

n

A dan

(

1

)

, bj+ b i n

n adalah fisibel

}

∪

(27)

( )

{

_o,n1 _:i∈_L1

}

∪

i _  ∈ B_ B

j t j L

n , :

(28)

dengan B adalah banyaknya anggota

(kardinalitas) himpunan B.

G :

L1 L2 L3

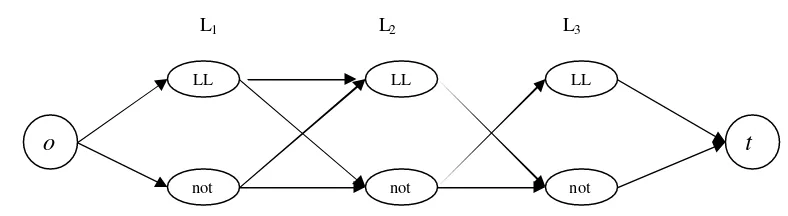
Gambar 8. Contoh dari sebuah network untuk jalur-bebas dengan 3 blok.

Pada Gambar 8, berdasarkan waktu kedatangan seperti yang telah diberikan pada Tabel 1 lapisan L1 mewakili blo k 1 yaitu

Kereta 3628, lapisan L2 mewakili blok 2

yaitu Kereta 561, dan lapisan L3 mewakili

blok 3 yaitu Kereta 3678. Sisi-sisi berarah yang dicetak tebal dalam gambar ini mewakili sebuah path dalam network ini. Path ini membentuk sebuah asssignment di mana semua blok diparkir di rel. Dalam hal ini assignment yang terbentuk adalah blok pertama datang dari kiri dan berangkat dari sisi kanan, sedangkan blok ke