PENGGUNAAN METODE ANALISIS HOMOTOPI PADA
PENYELESAIAN PERSAMAAN SCHRODINGER-KdV
DINI FITRI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penggunaan Metode Analisis Homotopi pada Penyelesaian Persamaan Schrodinger-KdV adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
DINI FITRI. Penggunaan Metode Analisis Homotopi pada Penyelesaian Persamaan Schrodinger-KdV. Dibimbing oleh JAHARUDDIN dan SISWANDI.
Persamaan Schrodinger-KdV adalah model matematika yang dapat diterapkan dalam menentukan tinggi maksimum selubung paket gelombang bikromatik. Persamaan ini berbentuk persamaan diferensial parsial yang taklinear. Penyelesaian dari persamaan Schrodinger-KdV dilakukan dengan menggunakan metode analisis homotopi. Penggunaan metode analisis homotopi dilakukan dengan mendefinisikan suatu fungsi homotopi. Fungsi homotopi memerlukan parameter bantu yang dapat digunakan untuk mengontrol daerah kekonvergenan dari penyelesaian persamaan Schrodinger-KdV. Penyelesaian yang diperoleh berbentuk rumus rekursif dengan pendekatan awal yang diberikan berbentuk fungsi hiperbolik. Penggunaan metode analisis homotopi sangat efisien dan efektif untuk menyelesaikan persamaan Schrodinger-KdV, dan galat yang dihasilkan sangat kecil.
Kata kunci: gelombang bikromatik, metode analisis homotopi, persamaan diferensial parsial, persamaan Schrodinger-KdV
ABSTRACT
DINI FITRI. The Use of Homotopy Analysis Method on Solution of Schrodinger-KdV Equations. Supervised by JAHARUDDIN and SISWANDI.
Schrodinger-KdV equations are mathematical model that can be applied in determining the maximum height of the bichromatic wave packet wrapper. These equations form nonlinear partial differential equations. Solution of Schrodinger-KdV equations are done by using homotopy analysis method. The use of homotopy analysis method is done by defining a homotopy function. Homotopy function requires auxiliary parameter that can be used to control the convergence area of the solution of Schrodinger-KdV equations. The obtained solution is in the form of recursive formula with given initial approach in the form of hyperbolic function. The use of homotopy analysis method is highly efficient and effective to solve Schrodinger-KdV equations, and the resulting error is very small.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PENGGUNAAN METODE ANALISIS HOMOTOPI PADA
PENYELESAIAN PERSAMAAN SCHRODINGER-KdV
DINI FITRI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PRAKATA
Puji syukur penulis panjatkan kepada Allah swt atas segala rahmat dan karunia-Nya sehingga karya ilmiah ini bisa diselesaikan. Tema yang dipilih adalah Persamaan Schrodinger-KdV pada masalah gelombang, dengan judul Penggunaan Metode Analisis Homotopi pada Penyelesaian Persamaan Schrodinger-KdV.
Penulis mengucapkan terima kasih kepada
1 Ayah, Ibu, Rafiq, sanak saudara dan seluruh keluarga yang senantiasa memberikan doa, kasih sayang serta dukungan,
2 Bapak Dr Jaharuddin, MS selaku Pembimbing I dan Bapak Drs Siswandi, MSi selaku Pembimbing II atas semua ilmu, dukungan, motivasi, serta bimbingannya selama penulisan karya ilmiah ini,
3 Bapak Drs Ali Kusnanto, MSi selaku dosen penguji atas kritik dan sarannya selama penyelesaian karya ilmiah ini,
4 Seluruh staf pengajar Departemen Matematika yang telah memberikan ilmunya,
5 Seluruh staf tata usaha Departemen Matematika atas bantuannya,
6 Direktorat Pendidikan Tinggi (Dikti) yang telah memberikan bantuan biaya kuliah selama empat tahun melalui pemberian Beasiswa Bidik Misi,
7 Teman-teman departemen Matematika, teman-teman kost, dan semua pihak yang telah terlibat dalam penyelesaian karya ilmiah ini.
Semoga karya ilmiah ini bermanfaat.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Perumusan Masalah 1
Tujuan Penelitian 2
TINJAUAN PUSTAKA 2
Persamaan Schrodinger 2
Persamaan KdV 3
Model Persamaan Schrodinger-KdV 5
Metode Analisis Homotopi 6
HASIL DAN PEMBAHASAN 9
Aplikasi 9
SIMPULAN DAN SARAN 14
Simpulan 14
Saran 15
DAFTAR PUSTAKA 15
LAMPIRAN 16
DAFTAR TABEL
1 Galat dan dengan penyelesaian eksak 9 2 Galat dan dengan penyelesaian eksak 13
DAFTAR GAMBAR
1 Kurva dan terhadap 8
2 (a) Kurva dan (b) kurva 8
3 (a) Kurva terhadap dan (b) kurva terhadap 12 4 (a) Kurva terhadap dan (b) kurva terhadap 12 5 (a) Penyelesaian eksak ( , ) dan (b) penyelesaian eksak ( , ) 14
DAFTAR LAMPIRAN
1 Penurunan persamaan (20) 16
2 Penurunan persamaan (22) dan (23) 17
3 Penurunan persamaan (24) 18
4 Penurunan persamaan (25) 20
5 Penurunan persamaan (36) 21
6 Penentuan persamaan deformasi orde ke- 22
7 Penyelesaian persamaan deformasi orde ke- 25
PENDAHULUAN
Latar Belakang
Banyak fenomena yang ada di alam semesta seperti masalah getaran dan gerak gelombang dapat dideskripsikan ke dalam bentuk model matematika. Salah satu model matematika yang sering muncul untuk menjelaskan masalah tersebut adalah persamaan Schrodinger-Korteweg de Vries (Schrodinger-KdV). Persamaan Schrodinger-KdV merupakan persamaan diferensial yang dapat diterapkan dalam menentukan tinggi maksimum selubung paket gelombang bikromatik (Kusumawinahyu dan Andonowati 2003), model dinamika taklinear Langmuir satu dimensi dan gelombang ion-akustik dalam suatu sistem atau koordinat bergerak dengan kecepatan ion-akustik (Golbabai dan Vaighani 2011). Persamaan Schrodinger-KdV berbentuk persamaan diferensial parsial yang taklinear. Model-model taklinear dari masalah nyata biasanya sulit diselesaikan secara analitik.
Fan dan Hon (2003) menentukan penyelesaian eksplisit dari persamaan Schrodinger-KdV menggunakan metode extended tanh. Abdou dan Soliman (2005) menggunakan metode iterasi variasional untuk mendapatkan hampiran penyelesaian dari persamaan tersebut. Metode dekomposisi telah digunakan oleh Ray (2008) untuk menyelesaikan persamaan Klein-Gordon-Schrodinger. Khuri (1998) menggunakan teknik dekomposisi untuk mendapatkan penyelesaian persamaan taklinear Schrodinger orde tiga.
Persamaan Schrodinger-KdV dapat diselesaikan dengan menggunakan beberapa metode. Metode-metode yang digunakan antara lain, metode dekomposisi Adomian, metode Perturbasi, dan metode analisis homotopi. Metode dekomposisi Adomian adalah metode untuk menyelesaikan masalah taklinear yang dinyatakan dalam suatu deret pangkat yang hanya terdefinisi pada daerah kekonvergenannya. Metode Perturbasi adalah metode yang mengandung parameter ketaklinearan yang kecil. Metode analisis homotopi adalah suatu pendekatan analitik yang memanfaatkan suatu fungsi homotopi dan parameter bantu.
Dalam penelitian ini akan dibahas mengenai penyelesaian dari persamaan Schrodinger-KdV dengan menggunakan metode analisis homotopi. Metode analisis homotopi diperkenalkan pertama kali oleh Liao (1992). Metode ini telah digunakan untuk menyelesaikan beberapa persamaan, seperti persamaan Blasius takhomogen (Allan dan Syam 2005), gabungan persamaan KdV dan persamaan Hirota-Satsuma (Abbasbandy 2007) dan beberapa sistem persamaan diferensial biasa (Bataineh et al. 2008).
Perumusan Masalah
Berdasarkan latar belakang di atas, maka beberapa masalah yang akan ditinjau adalah sebagai berikut:
1. Bagaimana aplikasi metode analisis homotopi untuk menyelesaikan persamaan Schrodinger-KdV.
2
Tujuan Penelitian
Tujuan dari penelitian ini adalah:
1. Menggunakan metode analisis homotopi untuk menyelesaikan persamaan Schrodinger-KdV.
2. Mengkaji akurasi penyelesaian persamaan Schrodinger-KdV dengan menggunakan metode analisis homotopi terhadap penyelesaian eksaknya.
TINJAUAN PUSTAKA
Persamaan Schrodinger
Dalam penurunan persamaan Schrodinger (Cresser 2009), diperiksa suatu gelombang monokromatik yang dinyatakan dalam bentuk
, (1)
yang merepresentasikan gelombang yang bergerak dalam arah positif dan waktu . Misalkan momentum dan energi kinetik dengan
J s sebagai konstanta Planck, bilangan gelombang , serta
frekuensi gelombang . Jika persamaan (1) diturunkan dua kali terhadap , maka diperoleh
. (2)
Jika ⁄ ⁄ digunakan, dengan sebagai massa, maka persamaaan (2) menjadi
. (3)
Hal yang sama, jika persamaan (1) diturunkan terhadap , maka diperoleh
, (4)
Jika kedua ruas pada persamaan (4) dikalikan dengan , maka diperoleh
. (5)
Karena energi total merupakan penjumlahan dari energi kinetik dan energi potensial , maka energi total yang diperoleh ⁄ , sehingga
. (6)
Berdasarkan persamaan (3) dan (5), maka persamaan (6) menjadi
,
atau
,
3 Persamaan KdV
Tinjau persamaan dasar fluida ideal sebagai berikut
, di ,
, di ,
, di ,
, di ,
dengan sebagai suatu fungsi yang disebut sebagai kecepatan potensial, , , berturut-turut menyatakan koordinat horizontal, vertikal, dan waktu dengan
{ } sebagai gaya gravitasi, menyatakan kurva yang membatasi air dan udara, serta sebagai kedalaman air (Ramayanti 1999). Untuk mendapatkan persamaan KdV terlebih dahulu dilakukan penskalaan peubah sebagai berikut
̂ , ̂
√ , ̂ √ , ̂ √ . (8)
Jika persamaan (8) disubstitusikan ke dalam persamaan-persamaan (7) dengan
, maka diperoleh persamaan-persamaan sebagai berikut
̂ ̂ ̂ ̂ , pada ̂ ,
̂ ̂ ̂ ̂ , di ̂ ,
̂ ̂ ( ̂ ̂) ( ̂ ) ̂ , di ̂, (10)
̂ ̂ ̂ ̂ ̂ ̂ ̂ , di ̂. (11)
Untuk penyederhanaan, tanda ‘topi’ dapat dihilangkan.
Misalkan penyelesaian dari persamaan-persamaan (9), (10), dan (11) berbentuk
. (12) Jika persamaan (12) disubstitusikan ke persamaan (9), maka diperoleh persamaan-persamaan sebagai berikut
, (13)
, di . (14)
Berdasarkan persamaan (13), diperoleh
, , .
Kemudian berdasarkan persamaan (14), karena , maka diperoleh
, di , (15)
, di , (16)
, di . (17)
Untuk memperoleh , persamaan diintegralkan dari ke , maka didapat
.
Berdasarkan persamaan (15), maka
(7)
4
, ,
sehingga fungsi tidak bergantung pada . Jadi dapat dimisalkan
. (18)
Untuk memperoleh , digunakan persamaan dan persamaan (18) sehingga diperoleh
.
Jika persamaan diintegralkan dari ke , maka diperoleh
.
Berdasarkan persamaan (16), maka
.
Selanjutnya persamaan diintegralkan lagi dari ke , maka diperoleh
. (19) Sedangkan untuk memperoleh dilakukan dengan cara yang sama, sehingga diperoleh
, (20)
(lihat Lampiran 1).
Jadi bila persamaan (18), (19), dan (20) disubstitusikan ke dalam persamaan (12), maka diperoleh
. (21)
Kemudian dengan memisalkan pada persamaan (21), sehingga persamaan (10) dan (11) berturut-turut menjadi
, (22) dan
, (23)
(lihat Lampiran 2).
Selanjutnya perhatikan peubah berikut
, dan , dengan
, √ .
Lalu fungsi dinyatakan dalam peubah dan sebagai berikut
.
Jika fungsi disubstitusikan ke persamaan (22) dan (23), maka diperoleh ⁄
⁄ , (24)
(lihat Lampiran 3).
5
dan ∫ ⁄ ,
diperoleh persamaan
, (25)
(lihat Lampiran 4).
Persamaan (22) dan (23) untuk memberikan
dan . Persamaan dapat diubah menjadi
.
Jika persamaan diintegralkan terhadap , maka , atau , atau ,
sehingga persamaan (25) menjadi
.
Jika , maka diperoleh persamaan
,
yang merupakan bentuk persamaan KdV.
Model Persamaan Schrodinger-KdV
Dalam penelitian ini akan ditinjau persamaan Schrodinger-KdV sebagai berikut
,
,
dengan syarat awal
Penyelesaian eksak dari model persamaan (26) dengan syarat awal
2 2
1
, 0 6 2 i x sech
u x g x e k kx ,
2
2 2
2
16
, 0 6 tanh ,
3 k
v x g x k kx
berbentuk
2 2 2 2
2
2 2
, 6 2exp / 3 10 / 3 sech 2 ,
16
, 16 tanh 2 ,
3
u x t i t t k t x k k x t
k
v x t k k x t
(Alomari et al. 2009).
6
Metode Analisis Homotopi
Berikut ini diberikan ilustrasi konsep dasar metode analisis homotopi yang disajikan dari Liao (2004). Misalkan diberikan persamaan diferensial sebagai berikut:
[ ] , (27)
dengan suatu operator taklinear dan fungsi yang akan ditentukan dan bergantung pada peubah . Misalkan merupakan hampiran awal dari dan suatu parameter bantu dengan . Didefinisikan suatu operator linear yang memenuhi
[ ] , sehingga . (28) Kemudian dengan menambahkan parameter dengan [ ] didefinisikan suatu fungsi , dan suatu fungsi homotopi , yaitu
[ ] [ ]. Jika maka diperoleh persamaan deformasi orde nol
[ ] [ ]. (29)
Untuk persamaan (29) menjadi [ ] sehingga berdasarkan persamaan (28), diperoleh
. (30)
Sedangkan untuk persamaan (29) menjadi [ ] sehingga berdasarkan persamaan (27), diperoleh
. (31)
Persamaan deformasi orde nol merupakan persamaan yang mengalami deformasi atau perubahan bentuk, di mana berdasarkan persamaan (30) dan (31), ketika nilai parameter meningkat dari 0 sampai 1, maka berubah bentuk secara kontinu dari penduga awal ke penyelesaian eksak . Perubahan kontinu itulah yang disebut sebagai deformasi dalam homotopi. Oleh karena itu persamaan (29) disebut dengan persamaan deformasi orde nol.
Penyelesaian eksak ditentukan dengan menggunakan deret Taylor. Deret Taylor dari fungsi di sekitar , diperoleh
∑ .
Jika persamaan (30) digunakan, maka
∑
,
dengan
.
Jika , maka , sehingga diperoleh penyelesaian berbentuk
∑
.
Selanjutnya metode analisis homotopi akan diterapkan pada masalah nilai awal sebagai berikut
, ,
t
t x
u u x
v xu
7 dengan nilai awal
, .
Penyelesaian eksak dari persamaan (32) adalah sebagai berikut
,
.
Untuk menentukan penyelesaian persamaan (32) dengan metode analisis homotopi, terlebih dahulu ditentukan hampiran awal sebagai berikut
, .
Berdasarkan persamaan (29), diperoleh persamaan sebagai berikut
[ ] ,
[ ] .
Jika metode analisis homotopi digunakan, maka diperoleh penyelesaian dari persamaan (32) sebagai berikut
∫[ ] ,
∫[ ] ,
dengan
dan
dengan nilai awal
, .
Jika nilai awal tersebut digunakan, maka diperoleh penyelesaian hampiran dan sebagai berikut
,
, dengan
,
,
,
,
,
,
,
.
Gambar 1 menunjukkan pemilihan nilai untuk mendapatkan penyelesaian hampiran dengan daerah kekonvergenan yang luas, artinya penyelesaian hampiran yang diperoleh menggunakan metode analisis homotopi akan tepat pada daerah yang lebih luas.
8
[image:18.595.55.479.67.290.2]
Gambar 1 Kurva dan terhadap
Gambar 1 menunjukkan grafik turunan pertama untuk fungsi dan di (2,1). Nilai yang akan dipilih ialah nilai yang berada di sekitar atau dekat dengan titik belok dari setiap gambar. Berdasarkan Gambar 1, nilai yang dipilih yaitu di .
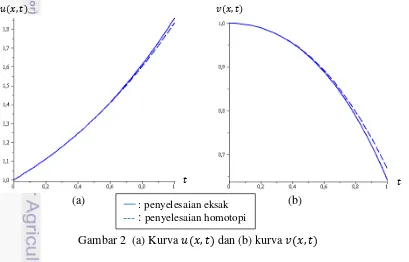
Selanjutnya pada Gambar 2 terlihat perbedaan kurva antara penyelesaian eksak dan kurva dengan penyelesaian metode homotopi, dengan parameter h yang dipilih yaitu . Hal ini terjadi karena penyelesaian hampiran (33) akan tepat mendekati penyelesaian eksaknya, sehingga kurva penyelesaian hampiran yang dihasilkan terlihat hampir sama dengan kurva penyelesaian eksaknya. Perbedaan antara kedua kurva inilah kemudian menimbulkan galat.
(a) (b)
Gambar 2 (a) Kurva dan (b) kurva : penyelesaian eksak
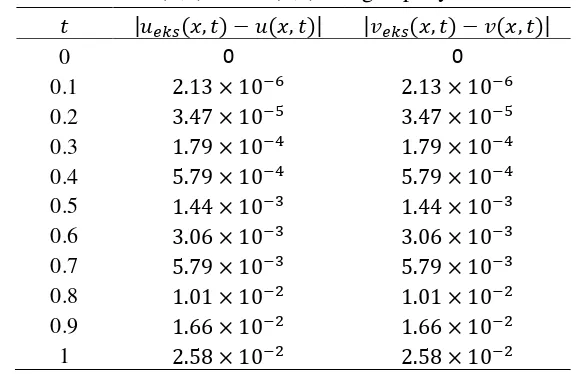
[image:18.595.40.487.70.791.2] [image:18.595.85.494.439.701.2]9 Tabel 1 Galat u x t( , ) dan v x t( , ) dengan penyelesaian eksak
0 0 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
Tabel 1 menunjukkan galat untuk h 1 dengan . Berdasarkan Tabel 1, galat yang dihasilkan pada fungsi sama dengan galat yang dihasilkan pada fungsi . Rata-rata galat yang dihasilkan pada selang yang diberikan pada Tabel 1 sebesar . Dengan demikian, metode analisis homotopi dapat digunakan untuk menentukan hampiran penyelesaian eksak dari persamaan diferensial parsial dengan nilai awal yang diberikan.
HASIL DAN PEMBAHASAN
Aplikasi
Dalam menemukan penyelesaian persamaan (26), terlebih dahulu dimisalkan hampiran awalnya, yaitu
, .
Berdasarkan persamaaan (26), didefinisikan operator taklinear sebagai berikut
[ ] ,
[ ] . Fungsi dan yang bergantung pada dan merupakan fungsi yang akan ditentukan sekaligus sebagai penyelesaian dari persamaan (26). Kemudian didefinisikan operator linear
,
.
Misal dan masing-masing merupakan hampiran awal dari
dan Dengan menambahkan parameter dengan [ ] dan parameter bantu dengan , kemudian didefinisikan fungsi dan
yang memenuhi persamaan deformasi orde nol yang memenuhi persamaan dan , dengan
10
[ ] [ ]. Jadi diperoleh persamaan deformasi orde nol
[ ] [ ], (34)
[ ] [ ], (35) dengan syarat awal
. Untuk dan diperoleh
, ,
, , (lihat Lampiran 5).
Karena nilai parameter meningkat dari 0 sampai 1, maka nilai dan
bervariasi dari penduga awal dan hingga ke penyelesaian eksak dan . Dengan menggunakan teorema Taylor dan persamaan (36), fungsi dan dapat diuraikan seperti berikut
∑ , ∑ ,
dengan
|
,
| .
Jika , maka dan sehingga fungsi
dan menjadi
∑
∑ (37)
Persamaan (37) merupakan penyelesaian dari persamaan taklinear (26).
Selanjutnya akan ditentukan persamaan deformasi orde ke- Persamaan deformasi orde ke- merupakan persamaan deformasi yang diturunkan dari persamaan deformasi orde nol. Persamaan deformasi orde ke- digunakan untuk menentukan dan yang merupakan bagian dari fungsi (37). Untuk mendapatkan persamaan deformasi orde ke turunkan persamaan deformasi orde nol pada persamaan (34) dan (35) terhadap sebanyak kali, kemudian dibagi dengan dan masukkan nilai parameter , sehingga didapat persamaan sebagai berikut
[ ] , (38)
[ ] , (39)
dengan
∑
∑
(∑
)
dan
11
(lihat Lampiran 6).
Selanjutnya dengan menggunakan operator linear dan diperoleh penyelesaian dari persamaan deformasi orde ke- (38) dan (39) sebagai berikut
∫[ ] ,
∫[ ] ,
(lihat Lampiran 7).
Jika diketahui nilai awal sebagai berikut
, , (40)
maka dapat ditentukan nilai hampiran untuk dan sebagai berikut
,
,
( )
( ( ) )
1
4
2
1
2 , 2(1 ) 2 2 4 1
1
2ht i h g x g x g x h
x g x
u t x t x
1 2 1
2 2
2 2 1 2 2
2ht g x g
x x
x x g x g x htg x x g x
2
2
1 2 1 3 2 1 1
3
6ihtg x g x ihtg x g x 2ihtg x
x x g x x
2
1 2
htg x g x
,
3
2 2(1 ) 6 1 2 3 2 1 1
1
1 ,
2 4
v x t ht h g x g x g
x x x h g x xg x
1 1 2 1 1 2
2 2
1
2 2
36htg x g x g x 12htg x g 3
x x x x g x x g x
2
2 1 1 1 2
4 2
4 g x g x 2iht g x 2g x g x 2 g x1
x x x x
3 2 2
3 1 2 2 1 2 2
6ht g x g x 3 g x
x
x x x g x
22 1 2 1
3 6 2
3 6 2
3 6
x g x xg x ht x g x x g x
1 1 1 1 1
3 4
3 1 3
3 4
8 g x g x 2g x g x 2
x x ihtg x g x
x x
2
2 2 1 1 1
2 2
2iht g x 3g x g x g x 3 g x
12
dan seterusnya, sehingga diperoleh
(41)
(lihat Lampiran 8).
Diberikan syarat awal sebagai berikut
2 2
1
2
2 2
2
, 0 6 2 sech ,
16
, 0 6 tanh .
3 i x
u x g x e k kx
k
v x g x k kx
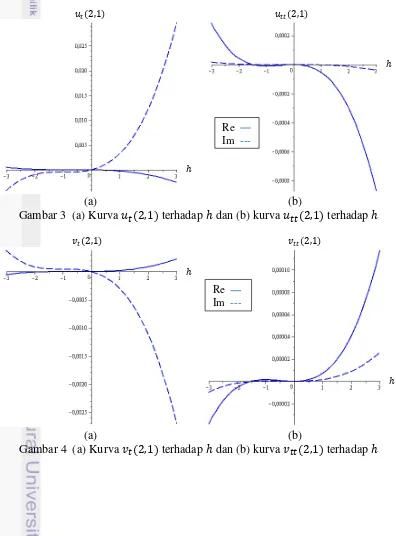
Jika syarat awal (42) disubstitusikan ke dalam persamaan (41) dengan dan , maka diperoleh penyelesaian untuk dan . Gambar 3 dan Gambar 4 menunjukkan pemilihan nilai untuk mendapatkan penyelesaian hampiran dengan daerah kekonvergenan yang luas.
(a) (b)
Gambar 3 (a) Kurva terhadap dan (b) kurva terhadap
(a) (b)
Gambar 4 (a) Kurva terhadap dan (b) kurva terhadap
Re Im
---Re Im
13 Gambar 3 dan Gambar 4 menampilkan turunan pertama dan turunan kedua untuk
dan dengan memisahkan bagian real dan imajiner dari setiap persamaannya. Nilai yang dipilih ialah nilai yang berada di sekitar atau dekat dengan titik belok dari setiap gambar. Jika masing-masing gambar ditampilkan dengan sumbu yang semakin panjang, maka semakin terlihat bahwa pergantian kecekungan berada pada sekitar .
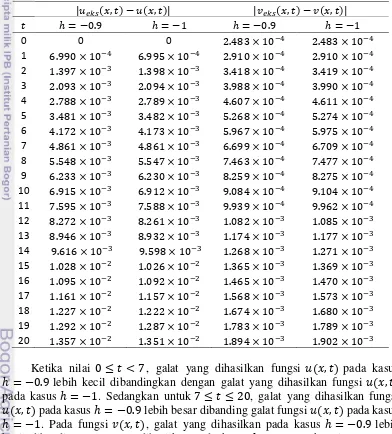
Selanjutnya pada Tabel 2 akan ditunjukkan galat penyelesaian antara penyelesaian eksak dan penyelesaian homotopinya untuk fungsi dan
Parameter h yang dipilih yaitu dan Tabel 2 menunjukkan galat untuk dan dengan .
Tabel 2 Galat u x t( , ) dan v x t( , ) dengan penyelesaian eksak
0 0 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Ketika nilai , galat yang dihasilkan fungsi pada kasus
lebih kecil dibandingkan dengan galat yang dihasilkan fungsi pada kasus . Sedangkan untuk , galat yang dihasilkan fungsi
pada kasus lebih besar dibanding galat fungsi pada kasus
14
yang tidak terlalu besar tidak berpengaruh terhadap penyelesaian yang diperoleh. Berdasarkan Tabel 2, galat yang dihasilkan akan semakin bertambah ketika nilai meningkat.
(a) (b)
Gambar 5 (a) Penyelesaian eksak dan (b) penyelesaian eksak Pada Gambar 5 menunjukkan penyelesaian eksak persamaan dan dengan nilai dan . Gambar 5 (a) menjelaskan bahwa nilai maksimum yang diperoleh sebesar 0.02 satuan ketika untuk . Sedangkan pada Gambar 5 (b), nilai maksimum yang diperoleh sebesar 0.03 satuan saat untuk .
SIMPULAN DAN SARAN
Simpulan
Metode analisis homotopi dapat digunakan untuk menyelesaikan persamaan Schrodinger-KdV. Persamaan Schrodinger dan KdV merupakan persamaan yang menggambarkan gerak gelombang yang bergantung pada posisi horizontal dan waktu.
Penggunaan metode analisis homotopi memerlukan operator linear dan taklinear. Operator taklinear ditentukan berdasarkan bentuk fungsi yang dimiliki persamaan Schrodinger dan KdV. Dengan operator yang telah didefinisikan sebelumnya, diperoleh rumus rekursif untuk mendapatkan penyelesaian dari persamaan Schrodinger-KdV. Metode ini sangat efisien dalam penyelesaian persamaan Schrodinger-KdV.
Nilai galat diperoleh dari selisih antara penyelesaian analitik dengan penyelesaian eksak. Penyelesaian analitik yang diperoleh menggunakan metode analisis homotopi hampir akurat mendekati penyelesaian eksaknya dengan rata-rata galat yang cukup kecil yaitu . Galat yang diperoleh akan semakin bertambah ketika nilai meningkat, sehingga metode analisis homotopi lebih bagus digunakan untuk selang waktu yang kecil.
15 Saran
Penyelesaian dari persamaan Schrodinger-KdV memerlukan beberapa orde penyelesaian. Dalam karya ilmiah ini, orde yang digunakan sampai orde tiga. Perlu adanya kajian lebih lanjut dengan menggunakan orde yang lebih tinggi.
DAFTAR PUSTAKA
Abbasbandy S. 2007. The application of homotopy analysis method to solve a generalized Hirota-Satsuma coupled KdV equation. Phys. Lett. A. 361: 478-483.doi:10.1016/j.physleta.2006.09.105.
Abdou MA, Soliman AA. 2005. New application of variational iteration method. Physica. D. 211:1-8.doi:10.1016/j.physd.2005.08.002.
Allan FM, Syam MI. 2005. On the analytic solution of non-homogeneous Blasius problem. J. Comput. Appl. Math. 182:362-371.doi:10.1016/j.cam.2004.12. 017.
Alomari AK, Noorani MSM, Nazar R. 2009. Comparison between the homotopy analysis method and homotopy perturbation method to solve coupled Schrodinger-KdV equation. J. Appl. Math. Comput. 31:1-12.doi:10.1007/ s12190-008-0187-4.
Bataineh AS, Noorani MSM, Hashim I. 2008. Solving system of ODEs by homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 13: 2060-2070.doi:10.1016/j.cnsns.2007.05.026.
Cresser JD. 2009. PHYS201: Wave Mechanics. Sydney (AU): Macquarie University.
Fan E, Hon YC. 2003. Applications of extended tanh method to ‘special’ types of nonlinear equations. Appl. Math. Comput. 141:351-358.doi:10.1016/ S0096-3003(02)00260-6.
Golbabai A, Vaighani AS. 2011. A meshless method for numerical solution of the coupled Schrodinger-KdV equations. Computing. 92:225-242.doi:10.1007/ s00607-010-0138-4.
Khuri SA. 1998. A new approach to the Cubic Schrodinger equation: An application of the decomposition technique. Appl. Math. Comput. 97: 251-254.doi:10.1016/S0096-3003(97)10147-3.
Kusumawinahyu WM, Andonowati. 2003. Tinggi maksimum selubung paket gelombang bikromatik [catatan penelitian]. Sains. 35A(1):51-63.
Liao SJ. 1992. Homotopy Analysis Method and its Application [disertasi]. Shanghai (CN): Shanghai Jiao Tong University.
Liao SJ. 2004. Beyond Perturbation : Introduction to the Homotopy Analysis Method. New York (US) : Boca Raton.
Ramayanti T. 1999. Data Hamburan pada Persamaan Korteweg-de Vries (KdV) dengan Perturbasi [Skripsi]. Bogor (ID): Fakultas MIPA, Institut Pertanian Bogor.
16
Lampiran 1 Penurunan persamaan (20)
.
.
.
Karena , maka 0, dan 0, sehingga
. (43) Jika persamaan (43) disubstitusikan ke dalam persamaan , maka diperoleh
. (44) Persamaan (44) diintegralkan dari ke , sehingga didapat
.
Berdasarkan persamaan (17) dan (18), maka , sehingga
. (45) Kemudian persamaan (45) diintegralkan lagi dari ke , sehingga diperoleh
17 Lampiran 2 Penurunan persamaan (22) dan (23)
Persamaan (10) diturunkan terhadap , menghasilkan
, di . (46) Karena
, (47)
dan , maka
, sehingga
,
,
,
, (48)
,
, atau
,
.
Bila persamaan-persamaan pada (48) disubstitusikan ke dalam persamaan (46), maka diperoleh
, atau
.
Sedangkan jika persamaan-persamaan pada (48) disubstitusikan ke persamaan (11), diperoleh
,
Karena berorde , maka , sehingga
18
Lampiran 3 Penurunan persamaan (24) Diketahui
, dengan
,
,
, √ dengan ,
maka dihasilkan
⁄ ,
,
sehingga
⁄ ,
,
⁄ ⁄ ⁄ ⁄ ,
⁄ ⁄ ,
⁄ , ⁄ ,
⁄ ⁄ ,
⁄ ,
,
, .
Karena , dan , maka
⁄ ⁄ ,
⁄ ⁄ ⁄ ⁄
⁄
⁄ ⁄ ⁄
,
⁄ ⁄ ⁄
⁄ ⁄ ,
⁄ ,
⁄
⁄
⁄
⁄
,
19
⁄ ⁄ ⁄ ⁄
⁄ ⁄
⁄ ,
⁄ .
Persamaan (22) diturunkan terhadap , sedangkan persamaan (23) diturunkan terhadap . Selanjutnya kedua persamaan digabung dengan cara eliminasi, sehingga diperoleh
2 2 3
1 1 1
( ) ( )
2 2 6
tt h xx xxtth t x xt xxxh hx xxxxh xx
. (49)
Ruas kiri dari persamaan (49) berupa
,
⁄
⁄ ⁄
⁄ ,
. (50)
Sedangkan ruas kanan dari persamaan (49) yaitu
⁄ ⁄
⁄ ⁄
⁄ ⁄
⁄
⁄
⁄
⁄
⁄ ⁄
⁄ ⁄
⁄
⁄
⁄ ⁄ . (51)
Kemudian penyetaraan persamaan (50) dan (51) menghasilkan
⁄ ⁄ ⁄ ,
atau
20
Lampiran 4 Penurunan persamaan (25) Dengan mengambil peubah
, dan ∫ ⁄ , maka
,
, (52)
.
⁄ ,
⁄ ,
⁄ ,
sehingga
⁄ ⁄
⁄ ⁄ . (53)
Jika persamaan (52) dan (53) disubstitusikan ke dalam persamaan (24), maka diperoleh
⁄ ⁄ ⁄
⁄ ⁄
, atau
. (54)
Kedua ruas persamaan (54) dibagi dengan
,
,
,
21
Lampiran 5 Penurunan persamaan (36)
Untuk , dari persamaan (34) diperoleh
[ ]
sehingga menurut persamaan (28) diperoleh . Dengan cara yang sama, persamaan (35) menghasilkan
[ ]
sehingga .
Untuk , dari persamaan (34) diperoleh
[ ]
sehingga menurut persamaan [ ] diperoleh . Dengan cara yang sama, persamaan (35) menghasilkan
[ ]
22
Lampiran 6 Penentuan persamaan deformasi orde ke-
Untuk mendapatkan persamaan deformasi orde ke- , kedua ruas pada persamaan deformasi orde nol (34) dan (35) diturunkan terhadap sebanyak kali, kemudian dibagi dengan dan masukkan nilai .
a. [ ] [ ] Turunan pertama
, ;
0
, 1
, ;
u x t q u x t q u x t q
q L L
1 , ; 1 , ;
h x t q qh x t q
q
N N
Untuk , maka
[ ] [ ]. Turunan kedua
22
2 u x t q, ; 1 q u x t q, ;
q q
L L
2
1 2 1
2h x t q, ; qh x t q, ;
q q
N N
Untuk , maka [ ]
[ ]| , atau
[ ] [ ]| . Turunan ketiga
2 3 2 33 u x t q, ; 1 q u x t q, ;
q q
L L
2 3 1 1 2 33h x t q, ; qh x t q, ;
q q
N N
Untuk , maka [ ]
[ ] , atau
[ ] [ ]| . Turunan keempat
3 4 3 44 u x t q, ; 1 q u x t q, ;
q q
L L
3 4 1 1 3 44h x t q, ; qh x t q, ;
q q
23 Untuk , maka [ ]
[ ] , atau
[ ] [ ]|
.
Untuk turunan ke- dengan , diperoleh
1
1 , ; (1 ) , ;
m m
u m u m
m x t q q x t q
q q
L L
1 1 11 , ; , ;
m m
m m
mh x t q qh x t q
q q
N N .
Untuk maka
[ ]
[ ]|
, atau
[ ] dengan [ ]| (55) dan
b. [ ] [ ]
Dengan cara yang sama, untuk persamaan deformasi orde ke- dari persamaan di atas diperoleh seperti berikut
[ ]
dengan
[ ]| , (56)
dan
Kemudian didefinisikan operator taklinear sebagai berikut
[ ] ,
[ ] . Subtitusikan operator taklinear dan masing-masing ke dalam persamaan (55) dan (56)
1
2
1 1 1 2
0 , ; , ; 1 , ; , ; 1 ! m
m m m
q
x t q x t q
R u i x t q x t q
m q t x
1
3
2 1 1 3
, ; , ; , ;
1
6 , ; 1 !
m
m m m
x t q x t q x t q
R x t
x
v q
m q t x
24
0 , ; 2 , ;
q
x t q x t q
x
0 0 0 011 t xx 0
R u iu u u v
0 0 0 021 t 6 x 0xxx 2 0 0x
R v v u v v u u
12 1 1t 1xx 1 0 0 1
R u iu u u v u v
0 0 122 1 1t 6 1 x 6 x 1xxx 2 0 1x 2 1 0x
R v v u v u v v u u u u
2
2 0 1 1
13 2 2 2 0 2
2 2 2 2 2
1
t xx v v
R u iu u u u u v
2 0 1 1 0 2
2t 2xx v v
iu u u u u v
2
2 0 0 2 1 1 2 0 2 2 0
23 2 2 12 12 12 4 1 1
2 4
1
2 4
x x x x x
t xx x x
v v u v u v u v v u u u u
R u u
2 0 1 1 0 2 2 0 2 1 1 2 0
2t 6 x 6 x 6 x xxx 2 x 2 x 2 x
v u v u v u v v u u u u u u
3
3 0 2 1
14 3 3! 3 3! 1 2 0 3
1 3!
3! t xx v 6 v 6 v 3!
R u iu u u u u u v
3 0 2 1 1 3
3t 3xx v v v2 0v
iu u u u u u
3
3 0 2 1 1 224 3! 3 (3!)6 36 36 ( 0 3 3
1
3! t x x x 3!)6 x 3! x xx
v v u v u v
R u v u v v
(3!)2u u0 3x 12u u1 2x 12u u2 1x (3!)2u u3 0x
v3t 6u v3 0x 6u v2 1x 6u v1 2x 6u v0 3x v3xxx 2u u0 3x 2u u1 2x 2u u2 1x
2u u3 0x
.Maka untuk diperoleh
11 1 1 1 1
0
m
m m m t m xx i m i
i
R u i u u u v
,
1
12 1 1 1 1 1
0 0
6 ( ) 2 ( )
m m
m m m t i m i x m xxx i m i x
i i
R v v u v v u u
25
Lampiran 7 Penyelesaian persamaan deformasi orde ke- Didefinisikan operator linear yaitu
, dan
.
Subtitusikan operator dan ke dalam persamaan (38) dan (39), sehingga untuk persamaan (38) didapat
[ ] ,
sehingga
∫[ ] .
Sedangkan untuk persamaan (39) menjadi
[ ] ,
sehingga diperoleh
26
Lampiran 8 Penentuan nilai hampiran dan
dan sebagai hampiran inisial. Orde 1
∫[ ] ,
( ) .
Berdasarkan nilai awal (40), diperoleh , sehingga
( ).
1 , 0t 6 0 0x 0xxx 2 0 0x 2 v x t h
v u v v u u dtC x
1 1 1
3
2 3 2 2
6 2
ht g x g x g x g g
x x x x x C x
.
Dengan cara yang sama, diperoleh , sehingga
3
1 , 6g1 g2 3g2 2g1 g1
x x x
v x t ht x x x x x
. Orde 2 ∫[ ] ,
2
2 , 2 1 1 2 1t 1xx 0 1 1 0 1
u x t iht g x g x g x ih iu u u v u v dt C x
x
22 1
1
2 44 1
2 2 )
1 (1 ,
2ht i h x g x g x g x ht x g x
u x t
2 21 2 1 2 1 2
2 2
2ht g x g x g x g x htg x g x
x x x x
2
3
2
1 2 1 3 2 1 1
6ihtg x g x ihtg x g x 2ihtg x g x
x x x
2
1 2 1
htg x g x C x
Karena , maka , sehingga
22 1
1
2 44 1
2 2 )
1 (1 ,
2ht i h x g x g x g x ht x g x
u x t
2 21 2 1 2 1 2
2 2
2ht g x g x g x g x htg x g x
27
2
3
2
1 2 1 3 2 1 1
6ihtg x g x ihtg x g x 2ihtg x g x
x x x
2
1 2
htg x g x
.
∫[ ]
3
2 , 6 1 2 3 2 2 1 1
v x t ht g x g x g x g x g x
x x x
1t 6 0 1x 6 1 0x 1xxx 2 0x 1 2 1x 0
2
.h v u v u v v u u u u dt C x
Berdasarkan nilai awal (40), diperoleh , sehingga
2
33
1
2 2(1 ) 6 1 2 4 1 1
1 ,
2
v ht h g x g x g x h g x g x
x x
x x
t
2
2
1 1 2 1 1 2 2 2 1
36htg x g x g x 12htg x g x 3 g x g x
x x x x
2
4 2
2 1 1 1 2 1
4 g x xg x 2iht xg x 2g x g x 2 g x
x x
3 2 2
1 2 1 2
3 2 2
6ht g x g x 3 g x g x
x
x x x
23 6 2
2 1 2 1
3 6 2
3 g x g x ht g x 6 g x
x
x x x
3
4
3
1 3 1 1 4 1 1 3 1
8 g x g x 2g x g x 2ihtg x g x
x x x x
2 2
2 2 1 1 2 1
2iht g x 3g x g x g x 3 g x
x x . Orde 3 ∫[ ] ,
2 2t 2xx 0 2 1 1 2 0 1 ,
u ih iu u u v u v u v dt C x
∫[ ]
2
2 2t 6 0 2x 6 1 1x 6 2 0x 2xxx 2 0 2 1 x 2 .
v h v u v u v u v v u u u dt C x
Dengan menggunakan nilai awal (40), maka diperoleh dan , sehingga
2
2 2 0 2 1 1
3 , u ih iu t u xx u v u v u v dt2 0 ,
u x t
2
2 2 0 2 1 1 2 0 2 0
3 , v h vt 6u v x 6u vx 6u v x v xxx 2u u2 u1 x .
29
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 24 September 1992 dari pasangan Bapak Netrazan dan Ibu Sarinah. Penulis adalah putri pertama dari dua bersaudara. Pendidikan formal yang ditempuh penulis yaitu di SMAN 99 Jakarta lulus pada tahun 2010 dan pada tahun yang sama penulis diterima di Institut Pertanian Bogor melalui jalur USMI di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama menuntut ilmu di IPB, penulis pernah berkecimpung dalam himpunan profesi Gugus Mahasiswa Matematika (GUMATIKA) sebagai bendahara divisi keilmuan pada periode 2011-2012 dan sebagai staf keilmuan periode 2012-2013. Penulis juga aktif dalam kepanitiaan berbagai acara, di antaranya adalah Try Out Gumatika 2012 sebagai staf divisi konsumsi, Try Out Gumatika 2013 sebagai staf divisi konsumsi, Gumatika Calculus Competition 2012 sebagai staf desain, dekorasi, dan dokumentasi, Masa Perkenalan Fakultas 2012 sebagai staf Logistik dan Transportasi, Masa Perkenalan Departemen 2012 sebagai staf Medis, IPB Mathematics Challenge 2012 sebagai staf Logistik dan Transportasi, IPB Mathematics Challenge 2013 sebagai staf Tim Khusus, Matematika Ria 2012 sebagai bendahara umum, dan Matematika Ria 2013 sebagai ketua divisi konsumsi.