Mekanika bahan

S

TRESS

!

Stress

!

Average Normal Stress in an Axially Loaded

Bar

!

Average Shear Stress

!

Allowable Stress

Equilibrium of a Deformable Body

A

D

w(s) _C

F_R

.

w

s

• Body Force

• Support Reaction

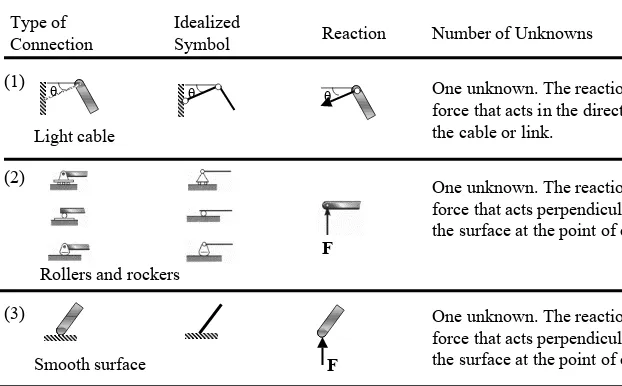
Dy

Type of Connection

Idealized

[image:3.842.83.705.76.462.2]

Symbol Reaction Number of Unknowns Table 1 Supports for Coplanar Structures

(1) _θ

Light cable

One unknown. The reaction is a force that acts in the direction of the cable or link.

θ _θ

One unknown. The reaction is a force that acts perpendicular to the surface at the point of contact. F

Rollers and rockers (2)

One unknown. The reaction is a force that acts perpendicular to the surface at the point of contact. (3)

Type of Connection

Idealized

Symbol Reaction Number of Unknowns

Three unknowns. The reactions are the moment and the two force components.

M Fy F_x

(6)

Fixed support

Two unknowns. The reactions are two force components. F_y

F_x (4)

Smooth pin or hinge

Two unknowns. The reactions are a force and moment.

(5)

Internal pin

• Equation of Equilibrium

Σ

Σ

Σ

Σ F = 0

Σ

Σ

Σ

Σ M

_O

= 0

Σ

Σ

Σ

Σ F

_x

= 0

Σ

Σ

Σ F

Σ

_y

= 0

Σ

Σ

Σ F

Σ

_z

= 0

Σ

Σ

Σ

• Internal Resultant Loadings

F

₂

F

₁

F

₃

F

₄

section

F

₂

F

₁

x

y

F

₃

F

₄

V

N

M

_O

V

N

Example 1

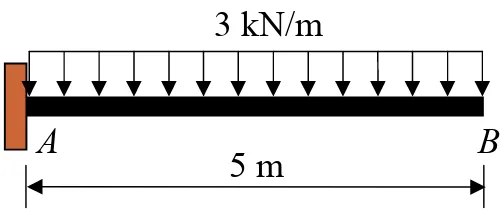
Determine the resultant internal loadings acting on the cross section at C of the beam shown.

270 N/m

3 m 6 m

A B

• Support Reactions

(1/2)(9)(270) = 1215 N

3 m 6 m

A

B C

270 N/m

540 N

4 m

B

2 m 180 N/m

C

540 N =

V

_C

N

_C

M

_C

0 = -540(2) = -1080 N•m =

540 N 135 N

90 N/m

M_A = 3645 N•m

3 m

A _C

A = 1215 N 270 N/m

180 N/m

540 N

1080 N•m

0

• Internal Loading

M_A = 3645 N•m

9

b

h t_w

(1/2)(9)(270) = 1215 N

3 m 6 m

A

B C

270 N/m

• Shear and bending moment diagram

3645 N•m

1215 N

V (N) 1215

M (N•m)

+

3645

-540

1080

1080 N•m

C

540 N

web flanges

Example 2

Determine the resultant internal loadings acting on the cross section at C of the machine shaft shown. The shaft is supported by bearings at A and B, which exert only vertical forces on the shaft.

225 N 800 N/m

200 mm

50 mm

100 mm 100 mm

50 mm A

C

B

11

(800 N/m)(0.15 m) = 120 N/m 225 N

0.275 m 0.125 0.1 m

A B

D • Support Reactions

0.2 m

0.025 m A

C

800(0.05) = 40 N

18.75 N

V_C M_C

N_C • Internal Loading

+ Σ M

A = 0: -(120)(0.275) + By(0.4) - (225)(0.5) = 0, By = 363.75 N

+ ΣM

A = 0:

18.75(0.25) + 40(0.025) + M_C = 0 M = -5.69 N•m ΣF_x = 0: N_C = 0

+

ΣF_y = 0:

-18.75 - 40 - V_C = 0,

V_C = -58.75 N

+

Σ F_y = 0: A_y - 120 +363.75 - 225 = 0 A_y = -18.75 N,

+

B_y A_y

A_x

Σ F_x = 0: A_x = 0 A_x = 0,

58.75 N 5.69 N•m

0

0.2 m

0.025 m A

C

800(0.05) = 40 N

18.75 N

V_C = -58.75 N

M_C = -5.69 N•m

N_C = 0

0.2 m

0.025 m A

C

800(0.05) = 40 N

18.75 N

Example 3

The hoist consists of the beam AB and attached pulleys, the cable, and the motor. Determine the resultant internal loadings acting on the cross section at C if the motor is lifting the 2 kN load W with constant velocity. Neglect the weight of the pulleys and beam.

1 m 2 m 0.5 m

W 0.15 m

0.15 m C

A D

1 m 2 m 0.5 m

W 0.15 m

0.15 m C

A D

B

W = 2 kN

1 m 0.15 m

C A

W = 2 kN

V_C MC N_C T_{C = 2 kN}

+ Σ M

C = 0:

M_C - 2(0.15) + 2(1.15) = 0

M_C = -2 kN•m Σ F_x = 0:

2 + N_C = 0 N_C = -2 kN

+

Σ F_y = 0:

-2 - V_C = 0, V_C = -2 kN

Example 4

Determine the resultant internal loadings acting on the cross section at G of the wooden beam shown . Assume the joints at A, B, C, D, and E are pin-connected.

6.5 kN

0.6 m 0.6 m 2 m

1 m

A

B C

D

E G

6.5 kN

0.6 m 0.6 m (2/3)(2) = 4/3 m

1 m

A

B _C

D

E G

4 kN/m (1/2)(2)(4) = 4 kN

2/3 m

F_BC

E_x E_y • Support Reactions

+ Σ M

E = 0: 4(4/3) + 6.5(3.2) - FBC(1) = 0, FBC = 26.1 kN

Σ F_y = 0: -6.5 - 4 + E_y = 0 E_y = 10.5 kN

+

Two - force

Σ F_x = 0: 26.13 + E_x = 0 E_x = -26.1 kN,

• Internal loadings acting on the cross section at G

+ ΣM

G = 0: MG -34.02 sin39.81o(0.6) + 6.5(0.6) = 0 MG = 9.17 kN•m

ΣF_y = 0: -6.5 + 34.02 sin39.81o _{- V}

G = 0 VG = 15.3 kN

+

ΣF_x = 0: 34.02 cos39.81o _{+ N}

G = 0 NG = -26.1 kN

+

V_C

M_C N_C 0.6 m

6.5 kN

A

G

B

F_BC = 26.13 kN

50.19o

39.81o

FBD FBA

F_AB

Joint B ΣF_x = 0:

-F_BA sin50.19o _{+ 26.13 = 0}

F_BA = 34.0 kN, (T)

+

ΣF_y = 0:

-F_BA cos50.19o _-F

BD = 0

F_BD = -21.8 kN, (C)

+

= -21.78 kN 34.02 kN =

= 34.02 kN

Example 5

Determine the resultant internal loadings acting on the cross section at B of the pipe shown. The pipe has a mass of 2 kg/m and is subjected to both a vertical force of 50 N and a couple moment of 70 N•m at its end A. It is fixed to the wall at C.

50 N

1.25 m 0.75 m

0.5 m

70 N•m _A

B C

D x

(M_B)_y

50 N

70 N•m _A

B

D

x _y

z

(F_B)_y (F_B)_x

(F_B)_z

0.25 m

WBD= 9.81 N W

BD = (2 kg/m)(0.5 m)(9.81 N/kg) = 9.81 N

0.625 m

0.625 m W_AD

W_AD = (2 kg/m)(1.25 m)(9.81 N/kg) = 24.52 N

• Free-Body Diagram

• Equilibrium of Equilibrium

Σ

F_y = 0: (F_B)_y = 0

Σ

F_z = 0: (F_B)_z - 9.81 -24.525 -50 = 0, (F_B)_z = 84.3 N

Σ

(M_B)_x = 0: (M_B)_x + 70 - 50(0.5) - 24.525(0.5) - 9.81(0.25) = 0, (M_B)_x = -30.3 N•m

Σ

(M_B)_y = 0: (M_B)_y + 24.525(0.625) + 50(1.25) = 0, (M_B)_y = -77.8 N•m

Σ

(M_B)_x = 0: (M_B)_z = 0

(M_B)_x

(M_B)_z

(M_B)_y

(M_B)_x

(M_B)_z

Σ

F_x = 0: (F_B)_x = 0

• Free-Body Diagram

50 N

70 N•m _A

B

D

x _y

z

0.25 m 9.81 N

0.625 m

0.625 m 24.5 N

70 N•m

(F_B)_x = 0

(F_B)_y = 0

(F_B)_z = 84.3 N

(M_B)_x = -30.3 N•m

(M_B)_y = -77.8 N•m

(M_B)_z = 0

84.3 N

30.3 N•m

+

z

Face

+

x

Face

x

y

z

Stress

22

x

y

z

-

x

Face

τ

_yz

τ

_yx

σ

y

τ

_zy

τ

_zx

σ

_z

σ

'

_x

τ

'

_xz

τ

'

_xy

-

y

Face

σ

'

_y

τ

'

_yz

τ

'

_yx

-

z

Face

τ

'

_zy

τ

'

zx

σ

'

_z

x

y

Top View

τ

_xy

∆

y

∆

z

σ

_x

∆

y

∆

z

τ

_yx

∆

x

∆

z

σ

_y

∆

x

∆

z

σ'

_x

∆

y

∆

z

τ'

_xy

∆

y

∆

z

σ'

_y

∆

x

∆

z

τ'

_yx

∆

x

∆

z

σ

_x

=

σ

'

x

σ

_y

=

σ

'

y

σ

_z

=

σ

’

z

τ

_xy

=

τ

'

xy

τ

_yx

=

τ

'

yx

τ

_zx

=

τ

’

xz

By compatibility,

τ

_xz

τ

_xy

ΣF_y = 0: - σ'_y

∆

x

∆

z +

σ

_y

∆

x

∆

z

= 0

+

σ'

_y

=

σ

_y

ΣF_x = 0:

σ

_x

∆

y

∆

z -

σ'

_x

∆

y

∆

z

= 0

+

σ

_x

=

σ'

_x

+ ΣM

O´ = 0: (τxy

∆

y

∆

z

)(∆

x

) - (τ

yx

∆

x

∆

z

)(∆

y

) = 0

τ

_xy

= τ

_yx

x

y

τ

_xy

∆

y

∆

z

σ

_x

∆

y

∆

z

τ

_yx

∆

x

∆

z

σ

_y

∆

x

∆

z

σ'

_x

∆

y

∆

z

τ'

_xy

∆

y

∆

z

σ'

_y

∆

x

∆

z

τ'

_yx

∆

x

∆

z

O

σ

_x

∆

y

∆

z

σ'

_x

∆

y

∆

z

τ

_xy

∆

y

∆

z

τ'

_xy

∆

y

∆

z

σ

_y

∆

x

∆

z

σ'

_y

∆

x

∆

z

τ

_yx

∆

x

∆

z

τ'

_yx

∆

x

∆

z

z

x

y

∆

x

∆

y

τ

_yz

∆

x

∆

z

σ

_y

∆

x

∆

z

τ

_yx

∆

x

∆

z

σ

_z

∆

x

∆

y

τ

zy

∆

x

∆

y

τ

_zx

∆

x

∆

y

∆

z

τ

_xz

∆

y

∆

z

τ

_xy

∆

y

∆

z

σ

_x

∆

y

∆

z

σ

'

_z

∆

x

∆

y

σ

'

_x

∆

y

∆

z

σ

'

_y

∆

x

∆

z

z

x

y

σ

_y

∆

x

∆

z

σ

_z

∆

x

∆

y

σ

_x

∆

y

∆

z

z

x

y

τ

_zx

∆

x

∆

y

τ

_xz

∆

y

∆

z

τ

'

_xz

∆

y

∆

z

τ

'

_zx

∆

x

∆

y

z

x

y

τ

_yz

∆

x

∆

z

τ

_zy

∆

x

∆

y

τ

'

_yz

∆

x

∆

z

τ

'

_zy

∆

x

∆

y

z

x

y

τ

_xy

∆

y

∆

z

τ

_yx

∆

x

∆

z

τ

'

_yx

∆

x

∆

z

Average Normal Stress in an Axially Loaded Bar

• Assumptions

The material must be

- Homogeneous material

- Isotropic material

P

P

P

External force

Internal force

P

P x

y z

P

x

y

σ

∆F = σ∆A

P

σ _σ

∫

=

∫

Σ = ↑

+

A z

Rz F dF dA

F ;

σ

A P =

σ

A P =

σ

Example 6

The bar shown has a constant width of 35 mm and a thickness of 10 mm.

Determine the maximum average normal stress in the bar when it is subjected to the loading shown.

9 kN

9 kN

4 kN

4 kN

A B C _D

35 mm

9 kN

9 kN

4 kN

4 kN

A B C _D

35 mm

22 kN 12 kN

12

22 30

P (kN)

x

10 mm

35 mm

30 kN

σ

MPa 7

. 85 )

m 01 . 0 )( m 035 . 0 (

kN 30

max = = = =

A P

σ

σ BC

9 kN

9 kN

4 kN

4 kN

A B C _D

35 mm

22 kN 12 kN

34.3

62.9 85.7

σ

(MPa)

x

10 mm

35 mm

30 kN

σ

MPa 7

. 85 )

m 01 . 0 )( m 035 . 0 (

kN 30

max = = = =

A P

σ

σ BC

Example 7

The 80 kg lamp is supported b two rods AB and BC as shown . If AB has a diameter of 10 mm and BC has a diameter of 8 mm, determine which rod is subjected to the greater average normal stress.

60o

A

B

C

B

x y

• Internal Loading

0 60 cos ) 5 4 ( ;

0 − =

= Σ →

+ o

BA BC

x F F

F 0 8 . 784 60 sin ) 5 3 ( ;

0 + − =

= Σ ↑ + o BA BC

y F F

F

FBC = 395.2 N, FBA = 632.4 N

• Average Normal Stress

60o A B C 3 4 5 d = 10 mm

d = 8 mm

MPa 86 . 7 ) m 004 . 0 ( N 2 . 395 2 = = = π A F σ BC BC BC MPa 05 . 8 ) m 005 . 0 ( N 4 . 632 2 = = = π A F σ BA BA BA

The average normal stress distribution acting over a cross section of rod AB.

632.4 N 8.05 MPa 8.05 MPa 8.05 MPa 60o F_BA 3 4 5 F_BC

Example 8

Member AC shown is subjected to a vertical force of 3 kN. Determine the

position x of this force so that the average compressive stress at C is equal to the average tensile stress in the tie rod AB. The rod has a cross-sectional area of 400 mm2 _{and the contact area at C is 650 mm}2_.

200 mm 3 kN

A B

200 mm 3 kN

A

C x

F_AB

F_C ) 1 ( 0

3 ;

0 + − = −−−−

= Σ ↑

+ F_y F_AB F_C

+ Σ M

A = 0: -3(x) + FC(200) = 0 ---(2)

• Internal Loading

• Average Normal Stress

650 400

C

AB F

F = =

σ

) 3 ( 625

.

1 −−−−

= _AB

C F

F

Substituting (3) into (1), solving for F_AB, the solving for F_C, we obtain

V

V

P

Connections

P

A

B

C

D

ττττ

_avg

A V

avg =

τ

P

A

A

V

• Single Shear

P

P

P

V = P

P

P

Top View

P

P

Side View

P

P

P

V = P

P

P

Top View

P

P

• Double Shear

P

P

Top View

P

/2

P

P

/2

P

P

Side View

V = P/2

P

V = P/2

P

P

Top View

P

/2

P

P

/2

P

P

Side View

V = P/2

P

Normal Stress: Compression and Tension Load

P

P

P

P´

b

d t a

a b

b

bt P

a a− = @

σ

b

t

A

=

bt

P

Section a-a

t d b

P

b b

) (

@

− =

−

σ

b

t

d

A = (b-d)t

P

t

b

d

P

P

b´

b´

t

d Abearing = dt

Bearing Stress

dt P

bearing =

σ

P/2

P/2

P

39

dθ

d b

t t

d b

P

normal

) ( − =

σ

ΣF_x = 0:

+ _{) cos 0}

2 (

90

90 =

−

∫

°

°

−

σ

t

θ

d

θ

d

P _b

P d

t d

b =

°

° − 90

90

sin )

2

(

σ

θ

θ

o bearing

td P

90 sin =

σ

* − − − − − = P

bearing

σ

θ

dt P

bearing =

P

d

P

b

t

Tension

Compression

• Axial Force Diagram for Compression Load on Plate

-P

-P

dt P Stress

Bearing _bearing =

−

σ

n compressio t

bd P Stress

Normal ,

) (

: = −

41

b

t

Tension

Compression

• Axial Force Diagram for Tension Load on Plate

tension t

d b

P Stress

Normal ,

) (

max :

− + =

−

σ

at P Stress

Shearing

2 =

−

τ

dt P Stress

Bearing _bearing =

−

σ

P

P

d

P

a

P/2

P/2

t

a

P

P

τ

• Shearing Stress on pin

P

P

P

P

P

P

P

P

P

P

P

P

A P =

τ

Double Shear

P/

2

P

P/

2

P

/2

P

P

/2

P/

2

P/

2

P

P/

2

P/2

P/

2

P/2

P

P/2

P/2

P/

2

P/

2

P

A P

τ = / 2

A P

z

x

y

∆

y

∆

x

∆

z

Section plane

Pure shear

τ

_yz

τ

_zy

τ

_yz

τ

_zy

Pure Shear

Example 9

The bar shown a square cross section for which the depth and thickness are 40 mm. If an axial force of 800 N is applied along the centroidal axis of the bar’s cross-sectional area, determine the average normal stress and average shear stress acting on the material along (a) section plane a-a and (b) section plane b-b.

800 N

a

a

b

b

30o

N = 800 N

(a) section plane a-a

800 N

a

a

kPa 500 )

m 04 . 0 )( m 04 . 0 (

N 800

= =

= A N

σ

0 =

avg

τ

500 kPa 800 N

a

a

b

b

30o

(b) section plane b-b 800 N b b 30o 800 N 30o

N = 800sin30o _{= 400 N} V = 800 cos30o _{= 692.82 N}

kPa 125 ) m 08 . 0 )( m 04 . 0 ( N 400 = = = A N σ kPa 51 . 216 ) m 08 . 0 )( m 04 . 0 ( N 82 . 692 = = = A V τ avg 30o x 40 mm mm 80 ; 40 30

sin = x =

Example 10

The wooden strut shown is suspended form a 10 mm diameter steel rod, which is fastened to the wall. If the strut supports a vertical load of 5 kN, compute the average shear stress in the rod at the wall and along the two shaded planes of the strut, one of which is indicated as abcd.

5 kN a b

c

d

20 mm

5 kN

63.7 MPa

V = 5 kN

• Average shear stress in the rod at the wall

5 kN

d = 10 mm

MPa 7 . 63 ) m 005 . 0 ( kN 5 2 = = = π A V τ avg

• Average shear stress along the two shaded plane

MPa 12 . 3 ) m 02 . 0 )( m 04 . 0 ( kN 5 . 2 = = = A V τ avg 5 kN 3.12 MPa 5 kN a b c d 20 mm 40 mm

V = 2.5 kN

a b

c

d

5 kN

Example 11

The inclined member show is subjected to a compressive force of 3 kN.

Determine the average compressive stress along the areas of contact defined by AB and BC, and the average shear stress along the horizontal plane defined by EDB.

25 mm

40 mm _{80 mm} 50 mm

3 kN 4

F_BC= 3(4/5) = 2.4 kN V = 1.8 kN

1. 2 MPa

3 kN 4 5 3 3 kN 4 5 3 MPa 8 . 1 kPa 1800 ) m 040 . 0 )( m 025 . 0 ( kN 8 . 1 = = = = AB AB AB A F σ MPa 2 . 1 kPa 1200 ) m 040 . 0 )( m 050 . 0 ( kN 4 . 2 = = = = BC BC A F σ

• The average compressive stress along the areas of contact defined by AB and BC :

1.8 MPa

25 mm

40 mm _{80 mm} 50 mm

3 kN 4

5 3

V = 1.8 kN

F_BC= 3(4/5) = 2.4 kN

3 kN

4 5

3

F_AB = 3(3/5) = 1.8 kN

• The average shear stress along the horizontal plane defined by EDB :

25 mm

40 mm _{80 mm} 50 mm

3 kN 4

5 3

MPa 562

. 0

kPa 5 . 562 )

m 08 . 0 )( m 04 . 0 (

kN 8 . 1

=

= =

= A V

τ avg

1.8 kN

Allowable Stress

allow fail

P P S

F. =

allow fail

S F

σ

σ

= .

allow fail

S F

τ

τ

= .

6. Design of Simple Connections

allow

P A

σ

=

allow

V A

τ

=

• Cross-Sectional Area of a Tension Member

P

P

a

a

P

τ

_allow

allow

P A

σ

(σ

_b

)

_allow

P

V = P

P

• Cross-Sectional Area of a Connector Subjected to Shear

allow

P A

σ

=

P

P

ττττ

_allow

• Required Area to Resist Bearing

allow b

P A

• Required Area to Resist Shear by Axial Load

P

d P l

allow

π

τ

=

P

d

Example 12a

The control arm is subjected to the loading shown. (a) Determine the shear stress for the steel at all pin (b) Determine normal stress in rod AB, plate D and E. The thickness of plate D and E is 10 mm.

pin C 13 kN 25 kN

3 4

5

75 mm 50 mm 200 mm

A B

C D E

φ

= 10 mm

φ

= 20 mm

D E

φ

= 25 mm

13 kN 50 mm

25 kN 50 mm

25 kN 13 kN

3 4

5

75 mm 50 mm 200 mm

• Reaction C

0 ) 125 . 0 ( 87 . 36 sin 25 ) 075 . 0 ( 13 ) 2 . 0 ( + − = AB F + ΣM

C = 0:

F_AB = 4.5 kN , ←

ΣF_y = 0:

+ _C

y + 13 - 25sin36.87o = 0 C_y = 2 kN, ↑ ΣF_x = 0:

+

-4.5 - C_x + 25cos36.87o _{= 0}

C_x = 15.5 kN, ←

kN 63 . 15 ) 2 ( ) 5 . 15

( 2 + 2 =

= C

25 kN 13 kN

25 kN 13 kN

75 mm 50 mm 200 mm

4.5 kN

(a) Shear stress

15.63 kN

15.63 kN

Pin C (Double shear)

7.815 kN

7.815 kN

Pin D and E (Single shear)

pin C 13 kN 25 kN

3 4

5

75 mm 50 mm 200 mm

A B

C D E

φ

= 35 mm

φ

= 20 mm

φ

= 25 mm

φ

= 25 mm

⇐ =

=

= 24.88 MPa

) 02 . 0 )( 4 / ( kN 815 . 7 2 π A V τ C C ⇐ = =

= 26.48 MPa

) 025 . 0 )( 4 / ( kN 13 2 π A V τ D D D ⇐ = =

= 50.93 MPa

59

25 kN 13 kN

75 mm 50 mm 200 mm

4.5 kN

(b) Normal stress

15.63 kN

Cale AB Plate D

φ

_rod = 10 mm A

C D E σ ⇐ = =

= 56.7 MPa

) 010 . 0 )( 4 / ( kN 5 . 4 2

π

σ

AB AB A P D E

φ

= 25 mm

13 kN 50 mm

25 kN 50 mm

φ = 25 mm

13 kN

σ_D 13 kN

13 kN

t = 0.01 m

25 kN 13 kN

75 mm 50 mm 200 mm

4.5 kN

15.63 kN

φ

_rod = 35 mm A

C

D E

Plate E

⇐ =

− =

=

MPa 100

) 01 . 0 )( 025 . 0 05 . 0 (

kN 25 A

P

E

σ

D E

φ

= 25 mm

13 kN 50 mm

25 kN 50 mm

φ

= 25 mm

25 kN 50 mm

25 kN

25 kN 50 mm

σ_E

0.05 m

0.02 5 m t = 0

Example 12b

The control arm is subjected to the loading shown. Determine the required diameter of the steel pin at C if the allowable shear stress for the steel is τ_allow = 55 MPa. Note in the figure that the pin is subjected to double shear.

22 kN 13 kN

3 4

5

75 mm 50 mm 200 mm

A B

• Internal Shear Force 0 ) 125 . 0 ( 87 . 36 sin 22 ) 075 . 0 ( 13 ) 2 . 0 ( − − = AB F + ΣM

C = 0:

F_AB = 13.125 kN

ΣF_y = 0:

+ _C

y - 13 - 22sin36.87o = 0

C_y = 26.2 kN ΣF_x = 0:

+

-13.125 - C_x + 22cos36.87o _{= 0}

C_x = 4.47 kN

kN 58 . 26 ) 2 . 26 ( ) 47 . 4

( 2 + 2 =

= C

22 kN 13 kN

75 mm 50 mm 200 mm F_AB C_y C_x 22 kN 13 kN 3 4 5

• Required Area

2 2

6 6

3

mm 242

m 10 6

. 241 10

55

10 29

. 13

= ×

= ×

× =

= −

allow τ

V A

2 2

mm 242

) 2

(d =

π

d = 17.55 mm

Use d = 20 mm 22 kN

13 kN 3

4 5

75 mm 50 mm 200 mm

A B

C

22 kN 13 kN

75 mm 50 mm 200 mm

13.125 kN

26.58 kN

26.58 kN

13.29 kN

Example 13a

The two members are pinned together at B as shown below. Top views of the pin connections at A and B are also given. If the pins have an allowable shear stress of

τ

_allow = 86 MPa , the allowable tensile stress of rod CB is (

σ

_t)_allow = 112 MPa and the allowable bearing stress is (

σ

_b)_allow = 150 MPa, determine to the smallest diameter of pins A and B ,the diameter of rod CB and the thickness of AB

necessary to support the load.

13 kN

A

B

C

1 m 0.6 m

3 4 5 Top view

A

• Internal Force

13 kN

A B

F_BC

1 m 0.6 m

36.87o

A_y

A_x

+ Σ M

A = 0: −13(1)+ FBC sin36.87(1.6) =0 F_BC = 13.54 kN Σ F_y = 0:

+ A_y −13+13.54sin36.87 =0

A_y = 4.88 kN Σ F_x = 0:

+ − +_{13.54cos36.87} =₀

x

A

• Diameter of the Pins

13 kN

A B

F_BC = 13.54 kN

1 m 0.6 m

36.87o

A_y = 4.88 kN

A_x = 10.83 kN

Top view A B 11.88 kN Pin A 11.88 kN

V_A = 5.94 kN

V_A = 5.94 kN

2 2

3 69.07 mm

m / kN 10 86 kN 94 . 5 = × = = allow A A τ V A 2 2 mm 07 . 69 ) (

4 d A =

π

d = 9.38 mm, Use d = 10 mm

Pin B

F_BC = 13.54 kN

V_B= 13.54 kN

2 2

3 157.4 mm

m / kN 10 86 kN 54 . 13 = × = = allow B B V A

τ

2 2 mm 4 . 157 ) (

4 dB =

π

• Diameter of Rod

13.54 kN

13.54 kN

2 2

3 120.9 mm

m / kN 10

112

kN 54 . 13 )

( = × =

=

allow t

BC

σ

P A

2 2

mm 9 . 120 )

(

4 dBC =

π

d_BC = 12.4 mm, Use d_BC = 15 mm 13 kN

A B

F_BC = 13.54 kN

1 m 0.6 m

36.87o

A_y = 4.88 kN

t_AB

φ

_B = 15 mm 20 kN

A B

13.54 kN 11.88 kN

t_AB

φ

_A = 10 mm

A B

(

σ

_b )_A (

σ

_b )_B

m 00792 . 0 ) 010 . 0 ( 10 88 . 11 10 150 ) ( 3 6 = × = × = AB AB allow b t t A P σ • Thickness 13 kN A B

F_BC = 13.54 kN

1 m 0.6 m

36.87o

A_y = 4.88 kN

Example 13b

The two members are pinned together at B as shown below. Top views of the pin connections at A and B are also given. If the pins have an allowable shear stress of

τ

_allow = 86 MPa, the allowable tensile stress of rod CB is (

σ

_t)_allow = 112 MPa and the allowable bearing stress is (

σ

_b)_allow = 150 MPa, determine to the

maximum load P that the beam can supported.

P A

B

C

1 m 0.6 m

3 4 5 Top view

A

B

φ

= 15 mm

φ

= 10 mm

t = 8 mm

φ

= 15 mm

• Internal Force

P

A B

F_BC

1 m 0.6 m

36.87o

A_y

A_x

+ Σ _M

A = 0: −P(1)+ FBC sin36.87(1.6) = 0

FBC = 1.042P (T) 0

87 . 36 sin 042

. 1 ;

0 − + =

= Σ ↑

+ F_y A_y P P

A_y = 0.375P 0

87 . 36 cos 042

. 1 ;

0 − + =

= Σ → +

P A

F_{x x}

Pin A (double shear) 0.914P

V_A = 0.457P

V_A = 0.457P

kN 78 . 14 ) 01 . 0 )( 4 / ( 457 . 0 kPa 10

86 3 ₂

= = × = P π P A V τ A A allow

Pin B (single shear)

F_BC = 1.042P

V_B= 1.042P

kN 58 . 14 ) 015 . 0 )( 4 / ( 042 . 1 kPa 10

86 3 ₂

= = × = P π P A V τ B B allow P A B

F_BC = 1.042P

1 m 0.6 m

36.87o

A_y = 0.375P

0.834P

Top view A

B

0.914P

φ

= 10 mm

1.042P

1.042P Rod AB

P

A B

F_BC = 1.042P

1 m 0.6 m

36.87o

A_y = 0.375P

0.834P

0.914P

kN 19

) 015 . 0 )( 4 / (

042 . 1 kPa

10

112 3 ₂

= = ×

=

P

π

P A

P

σ

BC allow

t_AB = 10 mm

φ

_B = 15 mm 20 kN

A B

F_BC = 1.042P

0.914P

t_AB = 10 mm

φ

_A = 10 mm

A B

(

σ

_b )_A (

σ

_b )_B

kN 41 . 16 ) 010 . 0 )( 010 . 0 ( 914 . 0 10 150 ) ( 6 = = × = P P A P σ allow b kN 60 . 21 ) 01 . 0 )( 015 . 0 ( 042 . 1 10 150 ) ( 6 = = × = P P A P σ allow b P A B

F_BC = 1.042P

1 m 0.6 m

36.87o

A_y = 0.375P

0.834P

Top view A

B

0.914P

φ

= 10 mm

φ

= 15 mm

t = 10 mm

t = 10 mm

⇐ =14.58 kN P

Example 14

The suspender rod is supported at its end by a fixed-connected circular disk as shown. If the rod passes through a 40-mm diameter hole, determine the minimum required diameter of the rod and the minimum thickness of the disk needed to support the 20 kN load. The allowable normal stress for the rod is σ_allow = 60 MPa, and the allowable shear stress for the disk is τ_allow = 35 MPa.

d

40 mm t

20 kN 20 kN

40 mm

d

40 mm t

20 kN 20 kN

40 mm

τ_allow

• Diameter of Rod

2 3 m / kN 10 60 kN 20 × = = allow σ P A 2 3 2 m / kN 10 60 kN 20

4 = ×

= π d A

d = 0.0206 m = 20.6 mm

• Thickness of Disk

2 3 m / kN 10 35 kN 20 × = = allow τ V A 2 3 m / kN 10 35 kN 20 ) m 02 . 0 ( 2 × = t π

Example 15

An axial load on the shaft shown is resisted by the collar at C, which is attached to the shaft and located on the right side of the bearing at B. Determine the largest value of P for the two axial forces at E and F so that the stress in the collar does not exceed an allowable bearing stress at C of (σ_b)_allow = 75 MPa and allowable shearing stress of the adhesive at C of τ_allow = 100 MPa , and the average normal stress in the shaft does not exceed an allowable tensile stress of (σ_t)_allow = 55 MPa.

A B

P

C E

F 2P

60 mm _{20 mm}

A B P C E F 2P

60 mm _{20 mm}

80 mm 3P Position Load 3P 2P

• Axial Stress

3P P 2P A P allow

t) =

(

σ

2 2 3 ) m 03 . 0 ( 3 m / kN 10 55 π P = ×

P₁ = 51.8 kN

• Bearing Stress

A P

allow

b) =

(

σ

] ) m 03 . 0 ( ) m 04 . 0 ( [ 3 m / kN 10

75 3 2 _{2 2}

π π P − = × B C 60 mm 80 mm 3P

A B P

C E

F 2P

60 mm _{20 mm}

80 mm 3P

Position Load

3P 2P

The largest load that can be applied to the shaft is P = 51.8 kN.

shear allow

A P =

τ

)] 020 )(. m 04 . 0 ( 2 [

3 m

/ kN 10

100 3 2

π

P =

×

P₃ = 55 kN • Shearing Stress

B

C

60 mm

80 mm 3P

20 mm

• Axial Stress

• Shearing Stress • Bearing Stress

P₃ = 55 kN P₁ = 51.8 kN

Example 16

The rigid bar AB shown supported by a steel rod AC having a diameter of 20 mm and an aluminum block having a cross-sectional area of 1800 mm2 _.

The18-mm-diameter pins at A and C are subjected to single shear. If the failure stress for the steel and aluminum is (σ_st)_fail = 680 Mpa and (σ_al)_fail = 70 MPa, respectively, and the failure shear stress for each pin is τ_fail = 900 MPa, determine the largest load P that can be applied to the bar. Apply a factor of safety of F.S = 2.0.

P Steel

0.75 m

2 m

Aluminum

A B

+ ΣM

B = 0: P(1.25 m) - FAC(2 m) = 0 ---> FAC = 0.625P 1.25 m P A B F_AC F_B 0.75 m + ΣM

A = 0: P(0.75 m) - FB(2 m) = 0 ---> FB = 0.375P P Steel 0.75 m 2 m Aluminum A B C

• Rod AC

AC AC fail st allow st A F S F = = . ) ( ) (

σ

σ

2 3 m) π_(0.01 0.625 2 kPa 10 680 P = ×

P₁ = 171 kN

• Block B

B B fail al allow al A F S F = = . ) ( ) (

σ

σ

2 6 3 m 10 1800 0.375 2 kPa 10 70 − × = × P

P Steel

0.75 m

2 m

Aluminum

A B

C

• Pin A or C

pin AC fail

allow

A F S

F =

= .

τ

τ

2 3

m)

π_(0.009

0.625 2

kPa 10

900 P

= ×

P₃ = 183 kN

Largest load P = 168 kN

1.25 m P

A B

F_AC= 0.625P

F_B= 0.375P 0.75 m

• Pin A or C P₃ = 183 kN Summary

• Rod AC P1 = 171 kN

STRAIN

!

Deformation

!

Strain

!

Normal Strain

!

Shear Strain

Deformation

Deformed body

θ

A B C

Undeformed body u(A)

A´

B´ C´

Strain

x y

z

x y

z

x y

1 ε_x 1

x y

1

1

ε_y

x y

x y

2

π x

y

xy

γ

xy

γ

ε_y

1

1 εx

Example 1

The slender rod shown subjected to an increase of temperature along its axis, which creates a normal strain in the rod of

ε

_z = 40(10-3_)z1/2_{, where z is given in} meters. Determine (a) the displacement of the end B of the rod due to the

temperature increase, and (b) the average normal strain in the rod.

200 mm z

dz

A

200 mm z

dz

A

B

(a) the displacement of the end B of the rod due to the temperature increase

dz z

dz'=[40(10−3) 1/2]

∫

−

=

∆ 0.2m

0 2 / 1 3 ] ) 10 ( 40

[ z dz

B

↓ =

= −

m z ) 0.00239 3 2 )( 10 ( 40 m 2 . 0 0 2 / 3 3

(b) the average normal strain in the rod.

Example 2

A force acting on the grip of the lever arm shown causes the arm to rotate clockwise through an angle of θ = 0.002 rad. Determine the average normal strain developed in the wire BC.

B

A

L 2L

B

A

L 2L

C B´

2L

B

A

L 2L

C

Lcos

θ

Lsin θ

θ

• Solution

001 . 0 2

002 . 0 2 2

'

= =

= =

−

=

θ

θ

ε

L L CB

CB CB

avg

Since θ is small, the stretch in wire CB, is using Eq.2-6. The average normal strain in the wire is then

, sinθ Lθ

Example 3

The plate is deformed into the dashed shape shown. If in this deformed shape horizontal lines on the plate remain horizontal and do not change their length, determine (a) the average normal strain along the side AB, and (b) the average shear strain in the plate relative to the x and y axes.

250 mm

300 mm

3 mm

2 mm B

C x

y

250 mm 3 mm 2 mm B y A B´ mm 018 . 248 ) 3 ( ) 2 250 (

'= − 2 + 2 = AB

(a) the average normal strain along the side AB

250 250 018 . 248 ' ) ( = − = − AB AB AB avg AB

ε

mm/mm ) 10 ( 93 .

7 −3

− =

(b) the average shear strain in the plate relative to the x and y axes.

250 mm

300 mm 3 mm

2 mmB

C x y A B´

γ

_xy θ´ rad 0121 . 0 ) 2 250 3 (

tan 1 =

Example 4

The plate shown is held in the rigid horizontal guides at its top and bottom, AD and BC. If its right side CD is given a uniform horizontal displacement of 2 mm, determine (a) the average normal strain along the diagonal AC, and (b) the shear strain at E relative to the x, y axes.

150 mm

150 mm A

B _C

D

E

A B 75 mm C´ D´ E´ 75 mm

76 mm 76 mm

(a) the average normal strain along the diagonal AC

m 21213 . 0 ) 150 . 0 ( ) 150 . 0

( 2 + 2 =

= AC m 21355 . 0 ) 152 . 0 ( ) 150 . 0 (

'= 2 + 2 =

A

B 75 mm

C´ D´

E´ 75 mm

76 mm 76 mm

θ

´

(b) the shear strain at E relative to the x, y axes.

75 76 )

2 ' tan(

θ

= 150 mm

150 mm A

B _C

D

E

2 mm x y

rad 58404 .

1 ) 759 . 90 ( 180 759

. 90

'= o = π _o o =

θ

rad 0132 .

0 58404

. 1

2 − = −

= π

1

M

ECHANICAL

P

ROPERTIES OF

M

ATERIALS

!

Simple Tension Test

!

The Stress-Strain Diagram

!

Stress-Strain Behavior of Ductile and Brittle

Materials

!

Hooke’s Law

!

Strain Energy

!

Poisson’s Ratio

!

The Shear Stress-Strain Diagram

2

400

350

300

250

200

150

100

50

0

εεεε

(mm/mm)

σ

σ

σ

σ

(MPa)

0.10 0.20 0.30 0.40 Upper scale

0.00

0.0020 0.0030

0.0010 0.0040 Lower scale

0.0000

Stress Strain Relationship

L₀ d₀

3

necking

strain

hardening

yielding

elastic

region

The Stress-Strain Diagram

εεεε

σ

σ

σ

σ

σ

_pl

proportional limit

elastic limit

σ

_f

σ

_u

σ

_{f ´}

fracture stress

ultimate stress

elastic

behavior

plastic behavior

true fracture stress

yield stress

4

σ_Y

0.002 (0.2% offset) 300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.005 0.010

5

(

σ

_y)_u= 230 MPa

(

σ

_y)_l= 220 MPa

0

A P =

σ

0

L

δ

ε

=

400

350

300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.10 0.20 0.30 0.40 Upper scale

0.00

0.0020 0.0030

0.0010 0.0040 Lower scale

0.0000

E = _{= 200x10}3 _{MPa= 200 GPa}

0.001

σ

_fail = 295 MPa

σ_pl = 200 MPa

σ

_u = 390 MPa

200

L₀ d₀

6

400

350

300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.10 0.20 0.30 0.40 Upper scale

0.00

0.0020 0.0030

0.0010 0.0040 Lower scale

0.0000

σ

_pl= 180 MPa

σ

_y= 250 MPa

σ

_u= 360 MPa

σ

_fail= 310 MPa

E = _{= 200x10}3 _{MPa = 200 GPa}

7

Stress-Strain Behavior of Ductile and Brittle Materials

0.02 0.04 0.06

100 200 300 400

σ (MPa)

ε (mm/mm)

σ−ε

σ−ε

σ−ε

σ−ε

diagrams for a methacrylate plastic Brittle material

8

• Elongation

%) 100 ( 0

0

L L L

elongation

Percent = f −

%) 100 ( 0 0

A A A

area of

reduction

9

• Temperature Effects:

0.02 0.04 0.06

100 200 300 400

σ (MPa)

ε (mm/mm)

σ−ε σ−ε σ−ε

σ−ε diagrams for a methacrylate plastic

10 o_C

40 o_C

70 o_C

10

σ

ε

Hooke’s Law

σ

_pl

ε

_pl

= =

pl pl E

ε

σ

11

- Apply load to failure

• Elastic and Plastic Behavior of Materials

1

σ

ε

PL

EL

12

- Apply and release load

σ

ε

PL

EL

(a) Load is less than proportional limit

1

2

σ

ε

PL

EL

(b) Load is more than proportional limit, but less than elastic limit

1

13

2

3

1

2

3

4

Mechanical

hysteresis

1

σ

ε

PL

EL

(c) Load is more than elastic limit, and reaply

σ

ε

PL

EL

14

2

σ

ε

PL

EL

Repeated loading

3

4

mechanical

hysteresis

1

σ

εεεε

O

1

15

E

E

elastic

region

plastic

region

O´

unload

ε

σ

A

O

load

A´

B

permanent

set

elastic

region

plastic

region

elastic

recovery

ε

σ

O´

A´

16

u

_t

u

_r

Strain Energy

• Modulus of Resilience

σ

_pl

ε

_pl

ε

σ

Modulus of resilience

u

_r

• Modulus of Toughness

ε

σ

Modulus of toughness

u

_t

E pl u_{r pl pl}

2

2 1 2

1

σ

ε

σ

=

17

Modulus of resiliency(u_r)= Area under curve @ proportional limit

u_r= (1/2)(0.001)(180 MPa) = 90 kPa = 90 kN/m2 _{= 90 kN•m/m}3 _{= 90 kJ/m}3

Upper scale

Lower scale

400

350

300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.10 0.20 0.30 0.40

0.00

0.0020 0.0030

0.0010 0.0040

0.0000

Energy per unit volume = (90 kN/m2_{)(1 m}3_{) = 90 kN•m = 90 kJ}

σ σσ

σ_pl= 180 MPa

18

400

350

300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.10 0.20 0.30 0.40

0.00

0.0020 0.0030 0.0010

Upper scale

Lower scale

0.0040

0.0000

Modulus of hyper-resiliency EL

2

1

19

400

350

300

250

200

150

100

50

0

εεεε

(mm/mm)

σ

σ

σ

σ

(MPa)

0.10 0.20 0.30 0.40 Upper scale 0.00

0.0020 0.0030

0.0010 0.0040

Lower scale

0.0000

Failure

20

Example 1

A tension test for a steel alloy results in the stress-strain diagram shown.

Calculate the modulus of elasticity and the yield strength based on a 0.2% offset. Identify on the graph the proportional limit, elastic limit, ultimate stress and the fracture stress.

400

350

300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.10 0.20 0.30 0.40 Upper scale

0.00

0.0020 0.0030

0.0010 0.0040 Lower scale

21

400

350

300

250

200

150

100

50

0

ε

(mm/mm)

σ

(MPa)

0.10 0.20 0.30 0.40 Upper scale

0.00

0.0020 0.0030

0.0010 0.0040 Lower scale

0.0000

σ σ σ σ_y

E

• Modulus of Elasticity

GPa mm

mm MPa

E 200

/ 0005

. 0

100

= =

• Yield Strength

σ_y = 250 MPa

σ σ σ

σ_pl • Proportional Limit

σ_pl = 180 MPa

σ σ σ σ_EL

• Elastic Limit

σ

_pl = 220 MPa

σ σσ σ_u

• Ultimate Stress

σ

_u = 365 MPa

• Fracture Stress

σ

= 310 MPa

22

Example 2

An aluminum specimen shown has a diameter of d₀ = 25 mm, a gauge length of L₀ = 250 mm and is subjected to an axial load of 294.5 kN. If a portion of the stress-strain diagram for the material is shown, determine the approximate elongation of the rod when the load is applied. If the load is removed, does the rod return to its original length? Also, compute the modulus of resilience both before and after the load application.

0.01 0.02 0.04

150 300 450

σ (MPa)

ε (mm/mm)

0.03

750

600

L₀ d₀

23

0.01 0.02 0.04

150 300 450

σ (MPa)

ε (mm/mm)

0.03

750

600

F

O

294.5 kN 294.5 kN

L₀ = 250 mm

294.5 kN 294.5 kN

L₀ = 250 mm

d₀ = 25 mm • The Load is Applied

- Normal Stress

MPa m

N A

P

600 )

025 . 0 )( 4 / (

10 5 . 294

2 3

0

= ×

= =

π

σ

- The Strain

ε

= 0.023 mm/mm

- The Elongation

δ

=

ε

L = (0.023 mm/mm)(250 mm) = 5.75 mm

D

0.023

(5.75 mm)/2 (5.75 mm)/2

A

24

294.5 kN 294.5 kN

• The Load is Removed

0.01 0.02 0.04

150 300 450

σ (MPa)

ε (mm/mm)

0.03 750 600 F O D 0.023 A B

L₀ = 250 mm

d₀ = 25 mm

- Permanent Strain

CD MPa GPa mm mm MPa

E 75.0 600

/ 006 . 0 450 = = =

CD = 0.008 mm/mm

The permanent strain, ε_OC = 0.023 - CD

ε_OC = 0.023 - 0.008 = 0.015 mm/mm - Normal Stress

MPa m N A P 600 ) 025 . 0 )( 4 / ( 10 5 . 294 2 3 0 = × = =

π

σ

- The Permanent Elongation

δ

=

ε

L = (0.015 mm/mm)(250 mm) = 3.75 mm

ε_pl=0.006

ε_OC

σ_pl =

E _CDE C

294.5 kN 294.5 kN

L = 250 mm

25

(u_r)_initial

(u_r)_final

0.01 0.02 0.04

150 300 450

σ (MPa)

ε (mm/mm)

0.03 750 600 F O D 0.023 A B

L₀ = 250 mm

d₀ = 25 mm

294.5 kN 294.5 kN

- Normal Stress

MPa m N A P 600 ) 025 . 0 )( 4 / ( 10 5 . 294 2 3 0 = × = =

π

σ

ε_pl=0.006

σ_pl =

CD = 0.008

C

• Modulus of Resilience

- Modulus of Resilience

3 / 40 . 2 ) / 008 . 0 )( 600 ( 2 1 2 1 ) ( m MJ mm mm MPa u_{r final pl pl}

= = =

σ

ε

3 / 35 . 1 ) / 006 . 0 )( 450 ( 2 1 2 1 ) ( m MJ mm mm MPa u_{r initial pl pl}

= =