APLIKASI METODE RESPON SPEKTRUM DENGAN METODE
TEORITIS DENGAN EXCEL DIBANDINGKAN DENGAN
PROGRAM SOFTWARE
Tugas Akhir
Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil
Disusun oleh:
AGUS PRONOTO 080404041
SUB JURUSAN STRUKTUR DEPARTEMEN TEKNIK SIPIL
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA MEDAN
LEMBAR PENGESAHAN
APLIKASI METODE RESPON SPEKTRUM DENGAN METODE TEORITIS DENGAN EXCEL DIBANDINGKAN DENGAN PROGRAM SOFTWARE
Tugas Akhir
Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil
Disusun oleh:
NIP.19561224 198103 1 002
DEPARTEMEN TEKNIK SIPIL FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA MEDAN
KATA PENGANTAR
Puji syukur penulis ucapkan atas kehadirat Tuhan Yang Maha Esa yang telah memberikan anugrah, berkat dan karunia-Nya hingga terselesaikannya tugas akhir ini dengan judul “Aplikasi Metode Respon Spektrum Dengan Metode Teoritis Dengan Excel Dibandingkan Dengan Program Software”.
Tugas akhir ini disusun untuk diajukan sebagai syarat dalam ujian sarjana teknik sipil bidang studi struktur pada fakultas teknik Universitas Sumatera Utara Medan.Penulis menyadari bahwa isi dari tugas akhir ini masih banyak kekurangannya.Hal ini disebabkan keterbatasan pengetahuan dan kurangnya pemahaman penulis.Untuk penyempurnaannya, saran dan kritik dari bapak dan ibu dosen serta rekan mahasiswa sangatlah penulis harapkan.
Penulis juga menyadari bahwa tanpa bimbingan, bantuan dan dorongan dari berbagai pihak, tugas akhir ini tidak mungkin dapat diselesaikan dengan baik.Oleh karena itu pada kesempatan ini penulis menyampaikan rasa terima kasih yang sebesar-besarnya kepada kedua orang tua yang senantiasa penulis cintai yang dalam keadaan sulit telah memperjuangkan hingga penulis dapat menyelesaikan perkuliahan ini.
Ucapan terima kasih juga penulis ucapkan kepada :
1. Bapak Prof. Dr. Ing. Johannes Tarigan selaku dosen pembimbing yang telah bersedia meluangkan waktu untuk memberikan saran dan bimbingan serta selaku ketua Departemen Teknik Sipil Fakultas Teknik
3. Ibu Ir. Chainul Mahni selaku dosen pembanding yang telah memberikan kritikan dan nasehat yang membangun
4. Bapak Ir. Torang Sitorus, MT selaku dosen pembanding yang telah memberikan kritikan dan nasehat yang membangun.
5. Bapak Ir. Syahrizal, MT selaku sekretaris Departemen Teknik Sipil Fakultas Teknik USU
6. Kedua orang tua penulis yang turut mendukung segala kegiatan akademis penulis
7. Teman-teman yang telah memberikan semangat kepada penulis, khususnya Pratiwi Nawawi, dan Felix Winardi, serta, Handiman, Wira, Hendry, Edward, Randy, Iskandar, senior stambuk 06, 07 dan adik-adik stambuk 09 yang memberikan dukungan serta info mengenai kegiatan sipil.
8. Para pegawai Departemen Teknik Sipil Fakultas Teknik USU atas ketersediannya untuk mengurus administrasi Tugas akhir ini.
Walaupun dalam menyusun Tugas akhir ini penulis telah berusaha untuk mengkaji dan menyampaikan materi secara sistematis dan terstruktur, tetapi tentunya Tugas Akhir ini masih jauh dari sempurna.Kritik dan saran yang membangun tentulah sangat penulis harapkan di kemudian hari.
Medan, Juni 2012
Penyusunan tugas akhir ini bertujuan untuk memperlihatkan langkah-langkah atau prosedur dalam menganalisis permasalahan dinamik khususnya gempa bumi dengan metode respon spektrum untuk pendekatan gaya gempa serta mengverifikasi hasil dari perhitungan teoritis dengan hasil keluaran program.
ABSTRAK
Umumnya gaya gempa dapat dilakukan pendekatan dengan beberapa cara yaitu ekivalen statik, respon spektrum, dan analisis riwayat waktu. Metode-metode tersebut memiliki keunggulan dan kekurangannya masing-masing.Metode respon spektrum merupakan salah satu metode yang dapat diandalkan dalam menganalisis permasalahan dinamik khususnya gempa bumi.
Pembahasan dalam tugas akhir ini, memberikan penjabaran rumus-rumus dalam menganalisis untuk mendapatkan pendekatan gaya gempa. Hasil pendekatan gaya gempa dari metode respon spektrum kemudian dianalisis dengan metode elemen hingga untuk didapatkan perpindahan, reaksi tumpuan dan gaya dalam pada struktur kemudian diverifikasi dengan program dan membuktikan bahwa hasil perhitungan teoritis dan program memberikan hasil yang sama.
Lembar Pengesahan ...
2.2 Perbedaan Antara Beban Statik dan Beban Dinamik ... 7
2.3 Pengaruh Beban Gempa Terhadap Struktur ... 8
2.4 Derajat Kebebasan (Degree of Freedom, DOF) ... 12
2.5 Prinsip Bangunan Geser (Shear Building) ... 13
2.6 Persamaan Diferensial Pada Struktur SDOF ... 16
2.7 Dinamik Karakteristik Struktur Bangunan ... 22
2.9 Getaran Bebas Pada Struktur MDOF ... 31
2.10 Metode Respon Spektrum ... 42
2.11 Metode Elemen Hingga Untuk Plane Frame Element ... 54
BAB III APLIKASI METODE RESPON SPEKTRUM ... 59
3.1 Pemodelan Struktur ... 59
3.2 Penyelesaian Perhitungan Pemodelan Struktur ... 60
3.3 Perhitungan Analisis Dengan Metode Elemen Hingga (FEM) .... 80
3.4 Perhitungan Dengan Program (Software) ... 93
3.5 Verifikasi Perhitungan Teoritis Dengan Program (Software) ... 99
BAB IV KESIMPULAN DAN SARAN ... 104
4.1 Kesimpulan ... 104
4.2 Saran ... 105
Tabel 3.1 : Nilai-nilai ω, dan Ø pada tiap-tiap mode ... 74
DAFTAR TABEL
Tabel 3.2 : Penomoran Simpul ... 81Tabel 3.3 : Hasil Perhitungan Perpindahan Simpul dari FEM ... 88
Tabel 3.4 : Hasil Perhitungan Reaksi Tumpuan dari FEM ... 88
Tabel 3.5 : Hasil Perhitungan Gaya Batang Elemen dari FEM ... 89
Tabel 3.6 : Perpindahan simpul pada program FEM ... 94
Tabel 3.7 : Reaksi tumpuan pada program FEM ... 94
Tabel 3.8 : Gaya dalam tiap elemen pada program FEM ... 95
Tabel 3.9 : Selisih nilai perpindahan simpul ... 100
Tabel 3.10 : Selisih nilai reaksi tumpuan ... 101
Gambar.2.1 : Gaya Inersia ... 9
DAFTAR GAMBAR
Gambar.2.2 : Gerakan akibat gempa pada bangunan bertingkat banyak ... 10Gambar.2.3 : Pola Goyangan Struktur Bertingkat Banyak ... 13
Gambar.2.4 : Pemodelan Struktur SDOF ... 16
Gambar.2.5 : Momen Kolom dan Balok akibat Simpangan y(t) ... 18
Gambar.2.6 : Kekakuan Kolom Jepit-jepit dan Jepit-sendi ... 24
Gambar.2.7 : Pegas Paralel dan Pegas Seri ... 25
Gambar.2.8 : Struktur 3-DOF, Model Matematik dan Free Body Diagram .... 29
Gambar.2.9 : Bangunan 2-DOF dan Model Matematik ... 33
Gambar.2.10 : Normal Modes ... 38
Gambar.2.11 : Struktur dengan Derajat Kebebasan Tunggal (SDOF) ... 43
Gambar.2.12 : Sejarah Simpangan (Displacement History) Struktur SDOF ... 45
Gambar.2.13 : Respon Spektrum Gempa Rencana SNI 03-1726-2002 ... 48
Gambar.2.14 : DOF Element Frame Sebagai Portal Bidang (Plane Frame) ... 54
Gambar.3.6 : Gaya Horisontal Mode dan Gaya Horisontal Tingkat ... 80
Gambar.3.7 : Penomoran Simpul dan Penamaan Elemen ... 81
Gambar.3.8 : Gaya Normal (N) dengan perhitungan teoritis ... 91
Gambar.3.10 : Momen (M) dengan perhitungan teoritis ... 92
Gambar.3.11 : Tampilan Pemodelan Pada Program... 91
Gambar.3.12 : Gaya Normal Hasil Keluaran Program ... 97
Gambar.3.13 : Gaya Lintang Hasil Keluaran Program ... 98
FI = Gaya Inersia (N)
[D] = Matriks Dinamik Fleksibilitas [S] = Sweeping Out Matrix
θ = Rotasi (rad) Γ = Partisipasi Mode
Penyusunan tugas akhir ini bertujuan untuk memperlihatkan langkah-langkah atau prosedur dalam menganalisis permasalahan dinamik khususnya gempa bumi dengan metode respon spektrum untuk pendekatan gaya gempa serta mengverifikasi hasil dari perhitungan teoritis dengan hasil keluaran program.
ABSTRAK
Umumnya gaya gempa dapat dilakukan pendekatan dengan beberapa cara yaitu ekivalen statik, respon spektrum, dan analisis riwayat waktu. Metode-metode tersebut memiliki keunggulan dan kekurangannya masing-masing.Metode respon spektrum merupakan salah satu metode yang dapat diandalkan dalam menganalisis permasalahan dinamik khususnya gempa bumi.
Pembahasan dalam tugas akhir ini, memberikan penjabaran rumus-rumus dalam menganalisis untuk mendapatkan pendekatan gaya gempa. Hasil pendekatan gaya gempa dari metode respon spektrum kemudian dianalisis dengan metode elemen hingga untuk didapatkan perpindahan, reaksi tumpuan dan gaya dalam pada struktur kemudian diverifikasi dengan program dan membuktikan bahwa hasil perhitungan teoritis dan program memberikan hasil yang sama.
BAB I
PENDAHULUAN
1.1 Latar Belakang Masalah
Pada umumnya dalam menyelesaikan permasalahan beban dinamik yang diakibatkan oleh gempa bumi, gaya gempa dapat didekati dengan beberapa metode antara lain metode beban statik ekivalen, metode respon spektrum (Response Spectrum Method), dan analisis riwayat waktu (Time History Analysis). Pada umumnya beberapa building code, memberikan batasan pada konstruksi yang bagaimana yang diperbolehkan dipakai metode ekivalen statik, metode respon spektrum, atau metode analisis riwayat waktu.
Gempa bumi, walaupun tidak terjadi sehari-hari namun dapat berakibat fatal pada kerusakan struktur bangunan apabila perencanaan beban gempa tidak dilakukan dengan tepat atau asal-asal.Metode statik ekivalen merupakan metode paling sederhana dari ketiga metode, namun metode ini terbatas hanya untuk bangunan yang sederhana dan tidak bertingkat banyak. Sedangkan metode time history
analysisakan relatif menyita waktu yang banyak dalam menyelesaikan permasalahantersebut namun akurat, maka diperlukan suatu metode yang lebih praktis dan lebih cepat.
Metode respon spektrum merupakan salah satu metode yang cukup dapat diandalkan dalam melakukan pendekatan gaya gempa dimana metode ini menggunakan nilai-nilai maksimum pada spektrum respon. Walaupun tidak berupa
langsung. Pada tugas akhir ini akan dijelaskan dari awal langkah-langkah dalam menganalisis pembebanan dinamik dengan metode respon spektrum.
1.2 Perumusan Masalah
Penyebab utama kerusakan struktur sewaktu gempa bumi adalah pengaruh dari pergerakan tanah dasar struktur.Oleh karena itu, menganalisis perilaku struktur akibat tipe pembebanan seperti ini menghendaki penerapan analisis dinamik struktur akibat pengaruh gempa tersebut.
Sebutan dinamik dapat didefinisikan sebagai perubahan waktu.Oleh karena itu beban dinamik merupakan beban yang mempunyai magnitud, arah atau tempat yang berubah dengan waktu. Begitu juga untuk struktur apabila dikenakan beban dinamik, maka akan menghasilkan tegangan dan deformasi yang berubah dengan waktu.
Berdasarkan latar belakang masalah tersebut, maka perumusan masalah dalam skripsi ini adalah :
1. Bagaimana cara melakukan perhitungan pendekatan gaya gempa dengan metode responspektrum secara teoritis?
2. Bagaimanacara menganalisisstruktur denganFinite Element Methodakibat pendekatan gaya gempa yang didapat?
1.3 Pembatasan Masalah
Agar hasil analisa dapat diterima dengan validitas seperti yang diharapkan, maka ditentukan batasan-batasan masalah sebagai berikut :
1. Metode pendekatan yang digunakan adalah metode respon spektrum 2. Struktur bangunan yang digunakan dalam perhitungan merupakan
struktur portal sederhana bertingkat 4 secara 2 dimensi
3. Kurva pembebanan dinamik digunakan kurva spektrum SNI 03-1726-2002
4. Struktur diasumsi berada pada wilayah gempa 3 dengan keadaan tanah lunak
5. Hasil yang dibandingkan berupa perpindahan simpul, reaksi tumpuan, dan gaya dalam berdasarkan perhitungan teoritis (finite element method) dan programakibat hasil pendekatan gaya gempa yang didapat
1.4 Tujuan Penulisan
Adapun tujuan dari penulisan tugas akhir ini adalah :
1. Untuk memahami konsep analisis pembebanan dinamik akibat beban gempa dengan metode respon spektrum
3. Untukmengetahui tingkat keakuratan dari hasil akibat pembebanan pendekatan gaya gempa dengan perhitungan teoritis (Finite Element Method) yang mana hasilnya akan dibandingkan dengan program
1.5 Metode Penulisan
Metodologi penulisan yang akan digunakan pada penulisan tugas akhir ini yaitu berupa kajian literatur dengan mencari solusi untuk permasalahan dengan mengumpulkan data-data dan keterangan dari buku-buku, jurnal-jurnal serta masukan dari dosen pembimbing.
1.6 Sistematika Penulisan
Sistematika penulisan tugas akhir ini akan diselesaikan dalam empat bab yaitu :
BAB I : PENDAHULUAN
Pada bab ini akan disajikan mengenai latar belakang masalah, perumusan masalah, batasan masalah, tujuan penulisan, metodologi penulisan dan sistematika penulisan pada laporan tugas akhir ini.
BAB II : TINJAUAN PUSTAKA
BAB III : APLIKASI METODE RESPON SPEKTRUM
Pada bab ini akan disajikan mengenai aplikasi pendekatan gaya gempa dengan menggunakan metode respon spektrum pada bangunan portal sederhana bertingkat 4 dan kemudian analisis dilanjutkan dengan metode elemen hingga setelah gaya gempa didapatkan untuk memperhitungkan perpindahan, reaksi tumpuan dan gaya dalam.
BAB IV : KESIMPULAN DAN SARAN
BAB II
TINJAUAN PUSTAKA
2.1Defenisi Beban Dinamik
Menurut Widodo (2001), Beban dinamik merupakan beban yang berubah-ubah menurut waktu (time varying) sehingga beban dinamik merupakan fungsi dari waktu.
Menurut Clough dan Penzien (1993), “Dynamic load is any load of which its magnitude, direction, and/or position varies with time” yang dapat diartikan beban dinamik merupakan beban yang mempunyai magnitud, arah atau tempat yang berubah dengan waktu.
Beban dinamik adalah berupa getaran-getaran yang dihasilkan oleh sumber getaran. Getaran-getaran tersebut dapat berupa getaran yang diakibatkan oleh mesin yang beroperasi, kereta api yang melintas di atas rel, gempa bumi dan lain-lain. Pada pembahasan tugas akhir ini adalah mengenai beban dinamik yang disebabkan oleh gempa bumi.
akibat peristiwa gempa bumi tersebut khususnya pada daerah-daerah rawan gempa. Kerusakan pada struktur akan terjadi apabila getaran tanah yang terjadi cukup besar, berulang-ulang dan terjadi dalam waktu yang relatif lama.
2.2 Perbedaan Antara Beban Statik dan Beban Dinamik
Pada ilmu statika keseimbangan gaya-gaya didasarkan atas kondisi statik, dimana gaya-gaya tersebut tetap intensitasnya, tetap tempatnya, dan tetap arah/garis kerjanya.Gaya-gaya tersebut dikategorikan sebagai beban statik.Menurut Widodo (2001), kondisi tersebut akan berbeda dengan beban dinamik dengan pokok-pokok perbedaan sebagai berikut :
1. Beban dinamik merupakan beban yang berubah-ubah menurut waktu dan merupakan fungsi dari waktu.
2. Beban dinamik umumnya hanya bekerja pada rentang waktu tertentu. Untuk beban gempa bumi maka rentang waktu tersebut kadang-kadang hanya beberapa detik. Walaupun hanya beberapa detik namun dapat merusak stuktur dengan kerugian yang sangat besar.
3. Beban dinamik dapat menyebabkan timbulnya gaya inersia pada pusat massa yang arahnya berlawanan dengan arah gerakan. Tumpukan barang yang terguling kebelakang ketika kendaraan dijalankan dan terguling ke depan ketika direm merupakan salah satu contoh adanya gaya inersia pada pembebanan dinamik.
kadang-kadang perlu diambil untuk mengatasi ketidakpastian yang mungkin ada pada beban dinamik.
5. Karena beban dinamik berubah-ubah intensitasnya menurut waktu, maka pengaruhnya terhadap struktur juga akan berubah-ubah menurut waktu, oleh karena itu penyelesaian problem dinamik harus dilakukan secara berulang-ulang menyertai sejarah pembebanan yang ada. Berbeda dengan penyelesaian problem statik yang bersifat penyelesaian tunggal (single solution), maka penyelesaian problem dinamik bersifat penyelesaian berulang-ulang (multiple solutions).
2.3 Pengaruh Beban Gempa Terhadap Struktur
Peristiwa gempa merupakan salah satu aspek yang sangat menentukan dalam merencanakan struktur.Struktur yang direncanakan harus mempunyai ketahanan terhadap gempa dengan tingkat keamanan yang dapat diterima. Aspek penting dari pengaruh gerakan tanah akibat gempa bumi adalah tegangan dan deformasi atau banyaknya kerusakan yang akan terjadi. Hal tersebut bergantung kepada kekuatan gempa bumi.
Kekuatan dari gerakan tanah yang ditinjau pada beberapa tempat disebut intensitas gempa.Tiga komponen dari gerakan tanah yang dicatat oleh alat pencatat gempa accelerograph untuk respon struktur adalah amplitudo, frekuensi dan durasi.
arah vertikal maupun horisontal akan timbul di node-node pada massa struktur. Dari kedua gaya ini, gaya dalam arah vertikal hanya sedikit mengubah gaya gravitasi yang bekerja pada struktur, sedangkan struktur biasanya dirancang terhadap gaya vertikal dengan faktor keamanan yang mencukupi.
Sebaliknya gaya gempa horisontal bekerja pada node-node lemah pada struktur yang kekuatannya tidak mencukupi dan akan menyebabkan keruntuhan (failure). Dikarenakan keadaan tersebut, prinsip utama dalam perancangan tahan gempa (earthquake resistant design) adalah meningkatkan kekuatan struktur terhadap gaya horisontal yang umumnya tidak mencukupi. Gerakan permukaan bumi menimbulkan gaya inersia pada struktur bangunan karena adanya kecenderungan massa bangunan (struktur) untuk mempertahankan dirinya. Besar gaya inersia mendatar F tergantung dari massa bangunan M, percepatan (acceleration) permukaan A dan sifat struktur. Apabila bangunan dan pondasinya kaku (stiff), maka menurut rumus Newton; F= M.A.
Dalam kenyataannya hal tersebut tidaklah demikian, semua struktur tidaklah benar-benar sebagai massa yang kaku melainkan fleksibel. Suatu bangunan bertingkat banyak (multi storey building) dapat bergetar dengan berbagai bentuk karena gaya gempa yang dapat menyebabkan lantai pada berbagai tingkat mempunyai percepatan dalam arah yang berbeda-beda.
Gambar 2.2. Gerakan akibat gempa pada bangunan bertingkat banyak
Salah satu hal penting pengaruh gempa pada struktur adalah periode alami getar struktur. Gedung yang sangat kaku pada umumnya mengalami gaya gempa yang lebih kecil apabila gerakan tanah yang mempunyai periode getaran yang panjang dibandingkan dengan gedung yang fleksibel, begitu pula sebaliknya.
periode alami getaran yang relatif panjang apabila mengalami osilasi (gerak bolak-balik) dalam waktu yang relatif lama, dan sebaliknya.
Untuk itu maka diperlukan analisis dinamik untuk menentukan pembagian gaya geser tingkat akibat gerakan tanah oleh gempa dapat dilakukan dengan cara analisis respon spektrum. Cara ini adalah menggantikan gaya geser yang didapat sebagaimana analisis beban statik ekivalen untuk bangunan-bangunan yang tidak memerlukan analisis dinamik.
Modal analisis pada umumnya dapat digunakan dalam analisis responspektrum untuk menentukan respon elastis pada struktur-struktur dengan banyak derajat kebebasan (MDOF) yang didasarkan kepada kenyataan bahwa respon sesuatu struktur merupakan superposisi dari respon masing-masing ragam getaran.Masing-masing ragam memberikan respon dengan sifat-sifatnya tersendiri, seperti yang ditentukan oleh bentuk lenturan, frekuensi getaran dari redaman yang bersangkutan.Karena itu, respon dari sesuatu struktur yang dimodelkan sebagai pendulum majemuk, dapat dianggap sebagai superposisi dari sejumlah pendulum sederhana (pendulum oscillator) dengan satu derajat kebebasan (SDOF).
2.4 Derajat Kebebasan (Degree of Freedom, DOF)
Apabila suatu struktur sebagai contoh portal sederhana dibebani secara dinamik maka massa struktur akan bergoyang baik ke kanan (simpangan bernilai positif) atau ke kiri (simpangan bernilai negatif). Sesungguhnya goyangan akan terjadi secara 3 dimensi, yaitu apabila terdapat deformasi aksial kolom ataupun adanya puntiran. Menurut Widodo (2001), Derajat kebebasan (degree of freedom) adalah derajat independensi yang diperlukan untuk menyatakan suatu posisi suatu sistim pada setiap saat. Apabila suatu titik yang ditinjau mengalami perpindahan tempat secara horisontal, vertikal dan ke samping, maka sistim tersebut mempunyai 3 derajat kebebasan.Hal ini terjadi karena titik yang bersangkutan dapat berpindah secara bebas dalam 3 arah.
Namun demikian, dari persoalan tersebut dapat dilakukan penyederhanaan dimana dapat dianggap hanya terjadi dalam satu bidang saja (tanpa puntiran).Hal ini dimaksudkan agar penyelesaian persoalan menjadi sedikit berkurang baik secara kualitas maupun kuantitas.Penyelesaian yang dahulunya sangat banyak menjadi berkurang banyak.Hal ini terjadi karena penyelesaian dinamik merupakan penyelesaian berulang-ulang dalam ratusan bahkan ribuan kali.
SDOF) dan struktur yang mempunyai n-tingkat akan mempunyai n-derajat kebebasan atau struktur dengan derajat kebebasan banyak (multi degree of freedom, MDOF). Maka dapat disimpulkan bahwa, jumlah derajat kebebasan adalah jumlah koordinat yang diperlukan untuk menyatakan posisi suatu massa pada saat tertentu.
2.5 Prinsip Bangunan Geser (Shear Building)
Apabila suatu struktur bangunan bertingkat banyak bergoyang ke arah horisontal, maka umumnya terdapat 3 macam pola goyangan yang terjadi. Kombinasi antara kelangsingan struktur, jenis struktur utama penahan beban dan jenis bahan yang dipakai akan berpengaruh terhadap pola goyangan yang dimaksud. Misalnya, struktur dengan bangunan core cantilever concrete wallakan mempunyai pola goyangan yang berbeda dengan struktur portal terbuka beton bertulang (open moment resisting concrete frame).
Pola goyangan yang pertama adalah bangunan yang bergoyang dengan dominasi geser (shear mode) atau pola goyangan geser. Pola goyangan seperti ini akan terjadi pada bangunan bertingkat banyak dengan portal terbuka sebagai struktur utama. Secara keseluruhan bangunan seperti ini akan relatif fleksibel, sementara pelat-pelat lantai relatif kaku terhadap arah horisontal.
Pola goyangan yang kedua adalah pola goyangan bangunan yang didominasi oleh lentur (flexible mode). Bangunan yang mempunyai pola goyangan tersebut adalah bangunan yang mempunyai struktur dinding yang kaku baik pada frame walls
atau cantilever wall yang kedua-duanya dijepit secara kaku pada pondasinya. Struktur dinding yang kaku dan anggapan jepit pada pondasi akan membuat struktur dinding berprilaku seperti struktur dinding kantilever. Sebagaimana sifat-sifat kantilever, maka struktur akan berdeformasi menurut prinsip lentur.
Pola goyangan yang ketiga adalah kombinasi diantara dua pola goyangan
shear mode dengan flextural mode. Struktur portal terbuka yang dikombinasikan dengan struktur dinding (structural walls) yang tidak terlalu kaku berkemungkinan mempunyai perilaku goyangan kombinasi.
Pada analisis dinamika struktur pola goyangan pertamalah yang umumnya diadopsi, dimana struktur dianggap cukup fleksibel dengan lantai-lantai tingkat yang relatif kaku.Untuk sampai pada anggapan hanya terdapat satu derajat kebebasan pada setiap tingkat, maka terdapat beberapa penyederhanaan/anggapan-anggapan. Anggapan-anggapan tersebut adalah :
beban berguna, beban hidup dan berat kolom pada ½ tingkat dibawah dan diatas tingkat yang bersangkutan. Massa itu semua kemudian dianggap terkonsentrasi pada satu titik (lumped mass) pada elevasi tingkat yang bersangkutan. Hal ini bertujuan agar struktur yang terdiri atas derajat kebebasan tak terhingga berkurang menjadi hanya satu derajat kebebasan.
2. Lantai-lantai tingkat dianggap sangat kaku dibanding dengan kolom-kolomnya karena balok-balok portal disatukan secara monolit oleh plat lantai. Hal ini berarti bahwa beam column joint dianggap tidak berotasi sehingga lantai tingkat tetap horisontal sebelum dan sesudah terjadi penggoyangan.
3. Simpangan massa dianggap tidak dipengaruhi oleh beban aksial kolom atau deformasi aksial kolom diabaikan. Disamping itu pengaruh P-delta terhadap momen kolom juga diabaikan. Oleh karena itu dengan anggapan ini dan anggapan sebelumnya lantai tingkat tetap pada elevasinya dan tetap horisontal baik sebelum maupun setelah terjadi penggoyangan.
2.6 Persamaan Diferensial Pada Struktur SDOF
Dengan anggapan struktur berderajat kebebasan tunggal (SDOF) hanya akan mempunyai satu koordinat yang diperlukan untuk menyatakan posisi massa pada saat tertentu yang ditinjau.
Gambar 2.4. Pemodelan Struktur SDOF
Pada gambar diatas dapat dilihat bahwa P(t) merupakan beban dinamik yaitu beban yang intensitasnya merupakan fungsi dari waktu. Notasi m, c, dan k berturut-turut adalah massa, redaman, dan kekakuan kolom. Apabila beban dinamik P(t) bekerja ke arah kanan, maka akan terdapat perlawanan pegas, damper dan gaya inersia. Berdasarkan prinsip keseimbangan dinamik pada free body diagram tersebut, maka dapat diperoleh hubungan,
(2.1)
(2.2)
FI, FD, FS adalah gaya inersia, gaya redam, dan gaya pegas, sedangkan ӱ, ẏ , y adalah percepatan, kecepatan, dan simpangan.
Apabila persamaan 2.2) disubstitusikan pada persamaan 2.1) maka akan diperoleh,
(2.3)
atau,
(2.4)
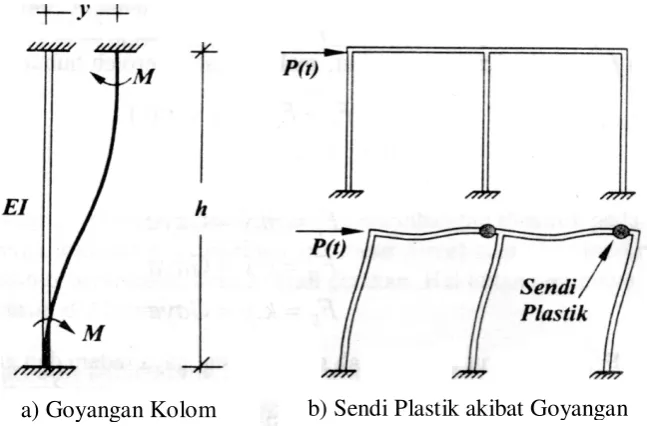
Gambar 2.5. Momen Kolom dan Balok akibat Simpangan y(t)
Gambar 2.5.a) merupakan simpangan horisontal suatu ujung kolom sebesar y(t). berdasarkan prinsip mekanika maka pada ujung-ujung kolom tersebut akan timbul momen lentur sebesar,
(2.5)
Dengan Mc adalah momen ujung kolom, E adalah modulus elastik bahan, I adalah momen inersia potongan, h adalah panjang kolom dan y(t) adalah simpangan horisontal. Berdasarkan persamaan 2.5) maka tampak bahwa semakin besar simpangan horisontal y(t) maka momen lentur yang terjadi pada ujung-ujung kolom akan semakin besar. Oleh karena itu penyelesaian persamaan 2.3) atau 2.4) yang terpenting adalah mencari simpangan horisontal y(t). penyelesaian yang lain yaitu kecepatan dan percepatan masa hanya penting pada permasalahan yang lain misalnya pada permasalahan respon lapisan-lapisan tanah akibat gempa.
Simpangan horisontal tingkat yang terjadi selanjutnya akan berpengaruh terhadap momen balok. Semakin besar simpangan horisontal tingkat maka semakin besar momen pada ujung kolom dan ujung balok. Pada desain bangunan yang memakai prinsip strong column and weak beam, terjadinya simpangan tingkat yang melebihi batas tertentu akan mengakibatkan terjadinya sendi plastik pada ujung-ujung balok. Hal seperti itu diperbolehkan karena kolom masih cukup kuat menahan beban.
2.6.1 Persamaan Diferensial Pada Tiap Tipe Getaran
Secara umum gerakan massa suatu struktur dapat disebabkan baik oleh adanya gangguan luar maupun adanya suatu nilai awal (initial conditions). Sebagai contoh, massa yang berada diujung atas tiang bendera yang ditarik sedemikian rupa sehingga mempunyai simpangan awal sebesar yo dan apabila gaya tarik tersebut dilepas maka tiang bendera akan bergoyang/bergetar ke kanan dan ke kiri. Peristiwa gerakan massa akibat adanya simpangan awal yo (dapat juga kecepatan awal) seperti itu biasa disebut dengan getaran bebas (free vibration systems). Sebaliknya apabila goyangan suatu struktur disebabkan oleh gangguan luar, maka peristiwa seperti itu biasanya disebut getaran dipaksa (forced vibration systems).
1. Persamaan diferensial pada getaran bebas
Pada tipe getaran ini, getaran bukan disebabkan oleh beban luar atau gerakan tanah akibat gempa tetapi adanya nilai awal (initial
conditions), misalnya simpangan awal yo atau kecepatan awal yo. Pada tipe getaran ini maka yo, P(t) = 0, maka persamaan diferensial untuk
a. Getaran bebas tanpa redaman (undamped free vibrations)
Pada getaran bebas tanpa redaman ini, maka nilai c = 0, sehingga persamaan diferensial gerakan massa akan menjadi,
(2.6) b. Getaran bebas yang diredam (damped free vibrations)
Pada getaran bebas yang diredam, maka struktur yang bersangkutan mempunyai sistim peredam energi, atau koefisien redaman (c) 0, sehingga persamaan diferensialnya menjadi,
(2.7) 2. Persamaan diferensial pada getaran dipaksa
Getaran dipaksa adalah suatu getaran yang diakibatkan oleh adanya gaya luar ataupun adanya getaran tanah akibat gempa. Dalam hal ini nilai P(t) 0. Getaran dipaksa dapat dikategorikan dalam dua golongan yaitu :
a. Getaran dipaksa yang tidak diredam (undamped forced vibration). Persamaan diferensial untuk getaran dipaksa yang tidak diredam adalah,
(2.8)
b. Getaran dipaksa yang diredam (damped forced vibration) Persamaan diferensial untuk jenis ini adalah,
2.6.2 Periode Getar (T), Frekuensi Sudut (ω), dan Frekuensi Alami (f)
Pada kondisi getaran bebas tanpa redaman (undamped free vibration systems) maka persamaan diferensial gerakannya adalah,
(2.10) Persamaan 2.10) merupakan persamaan diferensial linear homogen dengan koefisien konstan yang ditunjukkan oleh konstanta m dan k. disebut persamaan homogen karena suku sebelah kanan sama dengan nol. Persamaan tersebut juga akan menghasilkan gerakan yang periodik dan harmonik. Berdasarkan respon tersebut maka penyelesaian persamaan 2.10) dinyatakan dalam bentuk,
(2.11)
A merupakan suatu amplitude atau koefisien yang nilainya bergantung pada kondisi awal (initial value). Dari persamaan tersebut dapat diperoleh,
(2.12) (2.13) Persamaan 2.13) kemudian disubstitusi ke dalam persamaan 2.10) akan didapat,
(2.14)
Nilai A dan sin( ) tidak selalu sama dengan nol, maka nilai yang sama dengan nol adalah,
(2.15)
Maka akan diperoleh,
(2.17)
(2.18)
Dimana adalah frekuensi sudut (angular frequency) dalam rad/s, T adalah periode getar struktur dalam sekon, dan f adalah natural frequency dalam cps (cycles per second) atau Hertz.
2.7 Dinamik Karakteristik Struktur Bangunan
Pada persamaan diferensial struktur berderajat tunggal (SDOF) melibatkan tiga properti utama suatu struktur yaitu, massa, kekakuan, dan redaman. Ketiga properti struktur tersebut disebut dinamik karakteristik struktur.Properti-properti tersebut sangat penting dalam penyelesaian analisa dinamik.
2.7.1 Massa
Terdapat dua pendekatan yang secara umum digunakan untuk mendeskripsikan massa struktur yaitu :
1. Model Lumped Mass
terkonsentrasi pada tiap-tiap tingkat bangunan, maka penggunaan model ini masih cukup akurat dan akan mempermudah proses perhitungan.
2. Model Consistent Mass Matrix
Pada pemodelan ini, elemen struktur akan berdeformasi menurut bentuk fungsi (shape function) tertentu. Pemodelan massaseperti ini akan sangat bermanfaat pada struktur yang distribusi massanya adalah kontinu, seperti balok yang membentang cukup panjang, struktur cerobong dan sejenisnya. Pada prinsip ini, diperhitungkan tiga derajat kebebasan (horisontal, vertikal, dan rotasi) pada setiap node, yang nantinya akan menghasilkan full populated consistent matrix artinya suatu matriks yang diagonal matriksnya tidak sama dengan nol. Melalui pendekatan finite element, maka untuk setiap elemen balok lurus dan degree of freedom yang ditinjau akan menghasilkan konsisten matriks yang sudah standar.
2.7.2 Kekakuan
Kekakuan adalah salah satu dinamik karakteristik struktur bangunan yang sangat penting disamping massa bangunan. Antara massa dan kekakuan struktur akan mempunyai hubungan yang unik yang umumnya disebut karakteristik diri atau
linear dengan kekakuannya. Dengan prinsip shear building maka dimungkinkan pemakaian lumped mass model. Pada prinsip ini, kekakuan setiap kolom dapat dihitung berdasarkan rumus standar.
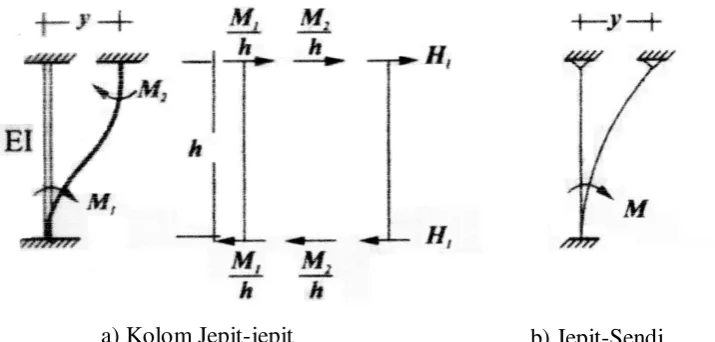
Gambar 2.6 Kekakuan Kolom Jepit-jepit dan Jepit-sendi
Menurut prinsip mekanika, suatu kolom jepit-jepit panjang h dengan kekakuan lentur (flextural rigidity) EI yang salah satu ujungnya mengalami perpindahan tempat sebesar y, maka pada ujung-ujung elemen tersebut akan timbul momen sebesar,
, dan (2.19)
Karena elemen tersebut mempunyai potongan yang prismatik maka M1, akan sama dengan M2. Adanya momen akan menimbulkan gaya geser yang bekerja pada masing-masing join sebesar,
(2.20)
Pada hakikatnya gaya horisontal yang bekerja pada join atas P = H1 = H2, maka kekakuan kolom dapat dihitung dengan,
(2.21)
Persamaan 2.21) adalah kekakuan kolom prismatik jepit-jepit dengan mengabaikan efek P-delta. Untuk kolom jepit-sendi maka kekakuannya dapat dicari dengan cara yang sama dan dapat dihitung dengan,
(2.22)
Gambar 2.7 Pegas Paralel dan Pegas Seri
Struktur yang umumnya didukung oleh beberapa kolom, kolom tersebut memiliki fungsi utama menahan beban baik beban vertikal maupun beban horisontal. Kolom-kolom tersebut akan memperkuat satu sama lain dalam hal menahan beban. Pemodelan kekakuan kolom dimodelkan sebagai serangkaian pegas paralel yang bekerja secara bersama-sama. Kolom-kolom/pegas-pegas tersebut akan berhubungan dengan massa secara bersamaan. Pegas yang tersusun secara paralel menganut prinsip persamaan regangan artinya seluruh pegas memiliki regangan yang sama, sehingga kekakuan total yang merupakan kekakuan ekivalen dihitung dengan rumus,
Dimana i = 1, 2, 3,…n adalah jumlah kolom, Ki adalah kekakuan kolom i menurut persamaan 2.21) atau persamaan 2.22).
Pada rangkaian pegas seri, kondisinya sedikit berbeda. Pada rangkaian ini sebelum bertemu dengan massa, maka pegas yang satu saling bertemu/berhubungan dengan pegas lain. Oleh karena itu pegas-pegas tersebut tidak saling memperkuat sebagaimana rangkaian paralel tetapi justru saling memperlemah.Pembebanan vertikal pada lapisan-lapisan tanah yang mana tiap-tiap lapis mempunyai kekakuan masing-masing adalah salah satu contoh dari pemodelan kekakuan tanah dengan pegas seri. Pada rangkaian tersebut perpendekan pegas merupakan jumlah dari perpendekan masing-masing pegas dan menganut prinsip persamaan tegangan/beban sepanjang pegas sehingga,
(2.24)
Dimana y adalah perpendekan yang dialami oleh masing-masing pegas.
Total perpendekan yang dialami pegas seri adalah jumlah dari perpendekan yang dialami oleh masing-masing pegas sehingga,
(2.25)
Dengan demikian kekakuan ekivalen rangkaian pegas seri dapat dihitung dengan rumus,
2.7.3 Redaman
Redaman merupakan peristiwa pelepasan energi (energy dissipation) oleh struktur akibat adanya berbagai macam sebab.Beberapa penyebab itu diantaranya adalah pelepasan energi oleh adanya gerakan antar molekul di dalam material, pelepasan energi oleh gesekan alat penyambung maupun sistim dukungan, pelepasan energi akibat gesekan dengan udara dan pada respon inelastik pelepasan energi juga terjadi akibat adanya rotasi sendi plastik. Karena redaman berfungsi melepaskan energi maka hal tersebut akan mengurangi respon struktur.
Terdapat dua sistim disipasi energy yaitu : 1. Damping Klasik (Classical Damping)
Apabila di dalam struktur memakai bahan yang sama bahannya akan mempunyai rasio redaman (damping ratio) yang relatif kecil dan struktur damping dijepit didasarnya maka sistim struktur tersebut mempunyai damping yang bersifat klasik (classical damping). Damping dengan sistim ini akan memenuhi kaidah kondisi ortogonal (orthogonal condition).
2. Damping Non-klasik (Non Classical Damping)
non-klasik, karena tanah mempunyai redaman yang cukup besar misalnya antara 10 – 25 %, sedangkan struktur atasnya mempunyai rasio redaman yang relatif kecil, misalnya 4 – 7 %.
2.8 Persamaan Diferensial Gerakan Struktur MDOF
Secara umum struktur bangunan gedung tidaklah selalu dapat dinyatakan di dalam suatu sistim yang mempunyai derajat kebebasan tunggal (SDOF).Struktur bangunan gedung banyak yang mempunyai derajat kebebasan banyak (multi degree of freedom, MDOF). Pada struktur bangunan gedung bertingkat banyak umumnya massa struktur dapat digumpalkan pada tempat-tempat tertentu (lumped mass) yang umumnya pada tiap-tiap lantai tingkat. Dengan anggapan berprilaku sebagai shear
building maka struktur yang semula mempunyai derajat kebebasan tidak terhingga akan menjadi struktur dengan derajat kebebasan terbatas.
2.8.1 Matriks Massa, Matriks Kekakuan, dan Matriks Redaman
Untuk menyatakan persamaan diferensial gerakan pada struktur dengan derajat kebebasan banya maka dipakai anggapan dan pendekatan seperti pada struktur dengan derajat kebebasan tunggal. Anggapan seperti prinsip shear building
Gambar 2.8 Struktur 3-DOF, Model Matematik dan Free Body Diagram
Struktur bangunan gedung bertingkat 3 pada gambar tersebut akan mempunyai 3 derajat kebebasan. Persamaan diferensial disusun berdasarkan atas goyangan struktur menurut first mode atau mode pertama. Berdasarkan pada keseimbangan dinamik pada free body diagram maka akan diperoleh,
(2.27)
(2.28)
(2.29)
Pada persamaan-persamaan tersebut tampak bahwa keseimbangan dinamik suatu massa yang ditinjau dipengaruhi oleh kekakuan, redaman dan simpangan massa sebelum dan sesudahnya. Persamaan dengan sifat-sifat seperti itu umumnya disebut coupled equation karena persamaan-persamaan tersebut akan bergantungan satu sama lain. Penyelesaian persamaan coupled harus dilakukan secara simultan artinya dengan melibatkan semua persamaan yang ada. Pada struktur dengan derajat
kebebasan banyak, persamaan diferensial gerakannya merupakan persamaan yang
dependent atau coupled antara satu dengan yang lain.
Dengan menyusun persamaan-persamaan tersebut menurut parameter yang sama (percepatan, kecepatan, dan simangan) selanjutnya akan diperoleh,
(2.30)
(2.31)
(2.32)
Persamaan-persamaan diatas dapat ditulis dalam bentuk matriks sebagai berikut,
(2.33)
Persamaan 2.33) dapat ditulis dalam matriks yang lebih kompak,
(2.34)
Dimana [m], [c] dan [k] berturut-turut adalah matriks massa, matriks redaman, dan matriks kekakuan yang dapat ditulis menjadi,
(2.35)
dan (2.36)
2.9 Getaran Bebas Pada Struktur MDOF
2.9.1 Nilai Karakteristik
Pada kenyataannya getaran bebas (free vibration system) jarang terjadi pada struktur MDOF, tetapi dengan menganalisis jenis getaran ini akan diperoleh suatu besaran/karakteristik dari struktur yang akan berguna berupa frekuensi sudut (ω), periode getar (T), frekuensi alami (f) dan normal modes.
Pada getaran bebas di struktur yang mempunyai derajat kebebasan banyak (MDOF), maka matriks persamaan diferensial gerakannya adalah,
(2.37)
Pada struktur dengan redaman, frekuensi sudut yang dihasilkan hampir sama dengan frekuensi sudut pada struktur yang dianggap tanpa redaman. Hal ini akaan diperoleh apabila nilai rasio redaman relatif kecil. Apabila prinsip ini digunakan untuk struktur dengan derajat kebebasan banyak, maka nilai C = 0, persamaan 2.37) akan menjadi,
(2.38)
Karena persamaan 2.38) adalah persamaan diferensial pada struktur MDOF yang dianggap tidak mempunyai redaman, maka penyelesaian persamaan diferensial tersebut diharapkan dalam fungsi harmonik menurut bentuk,
(2.39)
dimana, {Ø}i adalah suatu ordinat massa pada mode yang ke-i.persamaan 2.39) disubstitusikan ke dalam persamaan 2.38) maka akan diperoleh,
(2.40)
(2.41)
Persamaan 2.41) merupakan persamaan yang sangat penting dan biasa disebut persamaan eigenproblem atau karakteristik problem atau eigenvalue problem.Persamaan 2.41) tersebut adalah persamaan simultan yang harus dicari penyelesaiannya. Salah satu cara yang dapat dipakai adalah dengan memakai dalil Cramer (1704-1752). Gabriel Cramer adalah salah satu ahli matematika dari Swiss. Dalil tersebut menyatakan bahwa penyelesaian persamaan simultan yang homogen akan ada nilainya apabila determinan dari matriks yang merupakan koefisien dari vektor {Ø}i adalah nol, sehingga,
(2.42)
modenya. Apabila jumlah derajat kebebasan adalah n, maka persamaan 2.42) akan
menghasilkan suatu polinomial pangkat n yang selanjutnya akan menghasilkan
untuk i = 1, 2, 3, …n. selanjutnya substitusi masing-masing frekuensi ωi ke dalam persamaan 2.41) akan diperoleh nilai Ø1, Ø2, …Øn.
2.9.2 Frekuensi Sudut (ω) dan Normal Modes
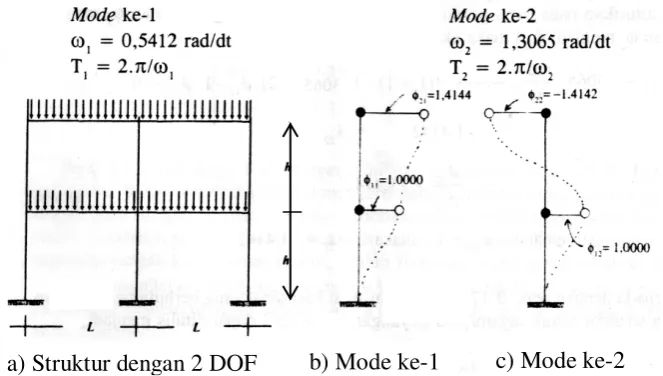
Pada struktur yang mempunyai derajat kebebasan banyak (MDOF) dalam menghitung frekuensi sudut, diambil suatu anggapan bahwa struktur tersebut dianggap tidak mempunyai redaman atau C = 0. Dalam menghitung dan menggambarkan normal modes, maka diambil suatu model struktur seperti pada gambar berikut.
Gambar 2.9 Bangunan 2-DOF dan Model Matematik
Setiap struktur yang dibebani dengan beban dinamik akan mengalami goyangan, untuk struktur derajat kebebasan banyak, maka struktur yang bersangkutan akan mempunyai banyak ragam/pola goyangan. Normal modes adalah suatu istilah yang dipakai pada problem dinamika struktur, yang diterjemahkan sebagai ragam/pola
Suatu persamaan diferensial gerakan dapat diperoleh dengan memperhatikan
free body diagram pada gambar 2.9 dan diperoleh,
(2.43)
Persamaan 2.43) dapat ditulis dalam bentuk yang sederhana yaitu,
(2.44)
Persamaan 2.44) dapat ditulis ke dalam bentuk matriks yaitu,
(2.45)
Selanjutnya persamaan eigenproblem pada persamaan 2.45) adalah,
(2.46)
Dengan Øi adalah suatu nilai/ordinat yang berhubungan dengan massa ke-i pada ragam/pola goyangan massa ke-i. persamaan 2.46) akan mempunyai penyelesaian apabila dipenuhi nilai determinan,
(2.47)
Apabila persamaan 2.47) tersebut diteruskan maka nilai determinannya adalah,
Agar pembahasan tersebut memiliki nilai, maka perlu diberikan nilai m1, m2, k1, dan k2. Misalnya nilai-nilai tersebut diberikan (menurut unitnya masing-masing) m1 = 2, m2 = 1, k1 = k2 = 1, maka diperoleh,
(2.49)
Nilai yang akan dicari adalah nilai-nilai percepatan sudut ω. Dengan memakai rumus abc, maka nilai-nilai tersebut adalah,
(2.50)
Persamaan 2.50) umumnya disebut eigenvalue dari eigenproblem persamaan 2.42). Berdasarkan pada persamaan 2.50), maka dapat dimengerti bahwa struktur yang mempunyai dua tingkat atau struktur degan 2-derajat kebebasan akan mempunyai 2 nilai frekuensi sudut. Frekuensi sudut ω1 adalah frekuensi sudut untuk mode ke-1 atau untuk pola/ragam goyangan ke-1, sedangkan ω2 adalah frekuensi sudut untuk mode ke-2.
Substitusi nilai ω1 ke dalam persamaan 2.46), misalnya substitusi baris pertama persamaan tersebut (dengan catatan bahwa Ø1 menjadi Ø11 dan Ø2 menjadi Ø21) maka akan diperoleh,
Secara umum nilai-nilai penyelesaian persamaan simultan homogen tidak akan memberikan suatu nilai yang pasti/tetap tetapi nilai-nilai tersebut hanya akan sebanding antara satu dengan yang lain (persamaan 2.51). dengan memperhatikan sifat tersebut maka umumnya diambil nilai Ø11=1, maka akan diperoleh,
, maka (2.52)
Nilai/koordinat yang berhubungan dengan suatu massa pada setiap pola goyangan umumnya dapat ditulis dalam bentuk baku,
(2.53)
Dimana indeks i menunjukkan massa dan indeks j menunjukkan nomor ragam/pola goyangan. Dengan demikian Øij adalah suatu koordinat yang berhubungan dengan massa ke-i pada ragam/pola goyangan ke-j.
Nilai-nilai koordinat yang berhubungan dengan massa struktur untuk pola goyangan ke-1 seperti persamaan 2.53) dapat ditulis menjadi,
(2.54)
Persamaan 2.54) umumnya disebut sebagai eigenvector untuk ragam/pola goyangan atau mode shape untuk mode ke-1. Nilai-nilai koordinat untuk ragam/pola
(2.55)
Apabila , maka
Sesuai dengan persamaan 2.54), maka nilai-nilai koordinat yang berhubungan dengan massa struktur untuk ragam/pola goyangan/mode ke-2 dapat ditulis menjadi,
(2.56)
Sesuai dengan persamaan 2.54) maka persamaan 2.56) juga disebut dengan
eigenvector untuk ragam/pola goyangan mode ke-2. Dengan mengingat persamaan 2.50), persamaan 2.54) dan persamaan 2.56) maka dapat dipahami bahwa struktur dengan n-derajat kebebasan akan mempunyai n-frekuensi sudut dan n-modes.
Antara persamaan 2.54) dan persamaan 2.56) dapat ditulis menjadi suatu matriks yang umumnya disebut modal matrix yaitu,
(2.57)
Dengan diperolehnya nilai-nilai frekuensi sudut untuk tiap-tiap mode seperti pada persamaan 2.50), maka akan diperoleh juga nilai periode getar T tiap-tiap mode yaitu,
dan (2.58)
Nilai T1 umumnya disebut periode getar dasar atau undamped fundamental
koefisien gempa dasar C seperti yang tercantum pada spektrum respon. Nilai ordinat mode shape pada tiap-tiap massa untuk semua ragam/pola goyangan digambar seperti berikut,
Gambar 2.10 Normal Modes
Nilai-nilai ordinat mode shapes pada gambar 2.10) tidak tergantung pada beban luar, melainkan hanya tergantung pada properti fisik struktur, misalnya massa mi dan kekakuan ki. Struktur dianggap tidak mempunyai redaman sehingga periode getar yang dicari adalah merupakan undamped free vibration periods. Nilai-nilai mode
shapes tidak dipengaruhi oleh waktu, artinya nilai tersebut akan tetap jika nilai-nilai massa dan kekakuan tidak berubah. Karena nilai-nilai kekauan ki tidak berubah-ubah maka mode shapes merupakan nilai untuk struktur yang bersifat elastik, atau hanya struktur yang elastiklah yang mempunyai nilai mode shapes. Nilai mode shapes juga tidak dipengaruhi oleh frekuensi beban. Dengan demikian menurut Widodo (2001), dapat disimpulkan bahwa nilai-nilai mode shapesadalah :
1. Bebas dari pengaruh redaman, 2. Bebas dari pengaruh waktu
3. Bebas dari pengaruh frekuensi beban 4. Hanya untuk struktur yang elastik
2.9.3 Metode Stodola (Matriks Iterasi)
Metode Stodola atau matriks iterasi merupakan alternatif lain dalam mencari nilai-nilai koordinat mode shapes. Pada metode ini lebih banyak menggunakan perhitungan matriks, namun metode ini memberikan keuntungan bahwa vibration modes yang dicari selalu berurut dari mode yang paling rendah hingga ke mode yang lebih tinggi.
a. Mode – 1
Dari persamaan eigenproblem {K – ω2M}Ø = 0. Apabila persamaan tersebut dikalikan awalnya (premultiply) dengan 1/ω2.K-1 maka persamaan tersebut menjadi (K-1 adalah nilai invers atas matriks kekakuan),
atau (2.59)
Dengan I adalah matriks identitas, persamaan 2.59) dapat ditulis menjadi,
atau (2.60)
dibawa kedalam bentuk perkalian skala r dengan modal vektor untuk iterasi pertama Ø1 atau,
(2.61)
Langkah selanjutnya adalah dibandingkan apakah nilai Ø1sama atau dekat dengan Ø0. Jika nilai tersebut belum sama , maka iterasi berikutnya diteruskan, sehingga diperoleh hubungan baru,
(2.62) Iterasi akan terus berlanjut hingga diperoleh,
(2.63) Apabila pada iterasi ke-n hubungan pada persamaan 2.63) tersebut telah dipenuhi maka sesuai dengan hubungan pada persamaan 2.60) dan persamaan 2.61) maka akan diperoleh,
, maka (2.64)
b. Mode yang lebih tinggi
Vektor simpangan dapat diperoleh dengan memperhatikan kontribusi setiap mode atau,
diperoleh dengan mengalikan awal persamaan 2.65) dengan {Ø1}T.[M] maka akan diperoleh (Berg, 1988),
(2.66)
Dengan memperhatikan hubungan ortogonalitas maka perkalian pada persamaan 2.66) akan sama dengan nol untuk subskrip yang tidak sama, oleh karena itu persamaan 2.66) akan menjadi,
maka
(2.67)
Vektor simpangan seperti pada persamaan 2.65) setelah dilakukan
sweeping out, mode pertama akan menjadi,
(2.68)
Kemudian apabila diambil suatu notasi bahwa sweeping matrix [S1] adalah,
(2.69)
Maka matriks dinamik fleksibilitas yang baru adalah,
(2.70)
dalam mencari mode ke-1 akan berpengaruh kepada mode ke-2. Kesalahan dalam mencari mode ke-2 akan berpengaruh terhadap mode ke-3 dan seterusnya, sehingga akhirnya terjadi akumulasi kesalahan. Apabila hal tersebut terjadi, maka mode-mode terakhir sudah tidak benar lagi.
2.10 Metode Respon Spektrum
Menurut Widodo (2001), spektrum respon merupakan suatu spektrum yang disajikan dalam bentuk grafik/plot antara periode getar struktur T, lawan respon-respon maksimum berdasarkan rasio redaman dan gempa tertentu. Respon-respon-respon yang dimaksud dapat berupa simpangan maksmum (spectrum displacement, SD), kecepatan maksimum (spectrum velocity, SV), atau spektrum percepatan (spectrum acceleration, SA) dari massa struktur SDOF.
a. Pseudo Spektrum Simpangan (PSD)
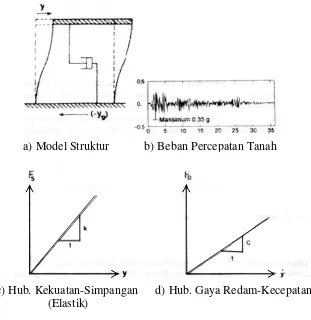
Spektrum respon adalah suatu plot antara nilai-nilai respon maksimum lawan periode getar struktur atas struktur dengan derajat kebebasan tunggal (SDOF) dengan redaman dan beban gempa tertentu. Dalam pembuatan suatu respon spektrum diambil model struktur SDOF seperti gambar 2.11.
berbanding lurus dengan kecepatan. Persamaan diferensial gerakan struktur SDOF akibat gerakan tanah/gempa adalah,
(2.71) Dengan m, c, k masing-masing adalah massa, koefisien redaman dan kekakuan struktur, ӱ, ẏ, dan y masing-masing adalah percepatan, kecepatan dan simpangan massa dan yt adalah percepatan tanah akibat gempa.
Gambar 2.11 Struktur dengan Derajat Kebebasan Tunggal (SDOF) Persamaan 2.71) dapat ditulis menjadi,
(2.72)
terdapat hubungan bahwa,
dan (2.73)
a) Model Struktur b) Beban Percepatan Tanah
c) Hub. Kekuatan-Simpangan (Elastik)
Deng an ξ ad alah damping rasio (damping ratio) struktur dan ω adalah
frekuensi sudut struktur.Apabila k dan m diketahui maka frekuensi sudut ω struktur dapat dihitung. Dengan demikian maka periode getar struktur T adalah,
(2.74)
Dengan demikian persamaan 2.72) akan menjadi,
(2.75)
persamaan 2.75) adalah persamaan diferensial gerakan struktur dengan derajat kebebasan tunggal (SDOF). Penyelesaian pertama persamaan 2.75) yang dicari umumnya adalah simpangan y, kemudian dapat dihitung kecepatan maupun percepatan massa. Penyelesaian persamaan 2.75) umumnya dapat dilakukan dengan cara numerik. Penyelesaian persamaan diferensial struktur SDOF akibat beban dinamik F(t) dengan prinsip Duhamel’s Integral dengan persamaan sebagai berikut,
(2.76)
Dengan ωd adalah damped frequency yang mempnyai hubungan,
(2.77)
Antara percepatan, massa dan gaya mempunyai hubungan yang linear yaitu a = F/m. oleh karena itu untuk struktur SDOF dibebani dengan beban gempa yang mempunyai percepatan tanah ӱ t, maka persamaan diatas akan menjadi,
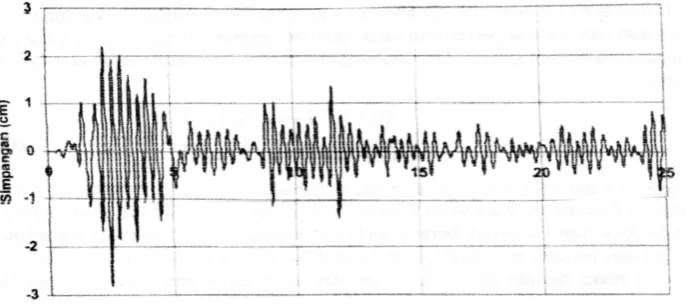
Penyelesaian persamaan 2.78) dilakukan secara numerik dengan memakai prinsip Duhamel’s Integral. Apabila tidak terjadi kesalahan pada proses numerik, maka hasil penyelesaian persamaan 2.78) akan bersifat eksak. Contoh riwayat simpangan (displacement history) struktur SDOF akibat gempa adalah seperti pada gambar 2.12.
Velocity waves umumnya mempunyai kandungan frekuensi yang lebih tinggi daripada displacement waves, sedangkan acceleration waves mempunyai kandungan frekuensi yang lebih tinggi daripada velocity waves. Berdasarkan riwayat kecepatan dan percepatan massa tersebut selanjutnya dapat dipilih kecepatan dan percepatan maksimum dengan program. Hasilnya akan diperoleh spektrum kecepatan (SV) dan spektrum percepatan (SA) yang ditulis dalam bentuk,
(2.79)
Pada gambar 2.12 dapat dilihat bahwa simpangan suatu massa akan berubah-ubah menurut fungsi waktu. Pada saat tertentu akan mencapai simpangan maksimum, dan simpangan maksimum inilah yang diperlukan. Spektrum simpangan biasa ditulis dalam bentuk,
(2.80)
Setelah riwayat simpangan (displacement waves) diperoleh maka integrasi numerik juga dapat diteruskan dengan menghitung riwayat kecepatan (velocity waves) dan percepatan (acceleration waves) dengan gambar yang mirip dengan gambar 2.12
b. Pseudo Spektrum Kecepatan (PSV) dan Percepatan (PSA)
Nilai-nilai kecepatan maksimum dan percepatan maksimum sebenarnya dapat dicari dengan integrasi numerik sebagaimana dilakukan untuk mencari simpangan maksimum. Namun demikian integrasi numerik seperti itu umumnya diperlukan waktu yang cukup lama sehingga ada terkesan time consuming sedangkan nilai yang akan dicari hanyalah nilai-nilai maksimum saja. Oleh karena itu terdapat cara yang lebih praktis yang dapat digunakan yang pada prinsipnya merupakan penyederhanaan.
Terdapat beberapa cara penyederhanaan, namun beberapa cara tersebut akhirnya akan bermuara pada suatu hasil bahwa terdapat hubungan,
fase yang sama dengan riwayat simpangan. Dari hubungan tersebut kemudian dapat dianalogikan bahwa,
(2.82) Dengan PSV dan PSA berturut-turut adalah pseudo spektrum kecepatan dan pseudo spektrum percepatan.Pseudo itu sendiri mempunyai arti maya/tidak nyata sehingga pseudo spektrum kecepatan berarti spektrum kecepatan yang sifatnya pendekatan. Beberapa literatur mengatakan bahwa apabila struktur tidak mempunyai redaman (c = 0) maka pseudo spektrum kecepatan akan sama persis dengan spektrum percepatan.
Uang dan Bertero (1990) membuat studi bahwa untuk struktur yang mempunyai periode getar 0,20< T < 5,0 s, maka nilai-nilai pseudo spektrum kecepatan dan pseudo spektrum percepatan sangat dekat dengan nilai eksak dari spektrum kecepatan dan spektrum percepatan. Struktur bangunan gedung umumnya mempunyai periode getar dalam rentang tersebut sehingga hubungan pada persamaan 2.82) dapat dipakai.
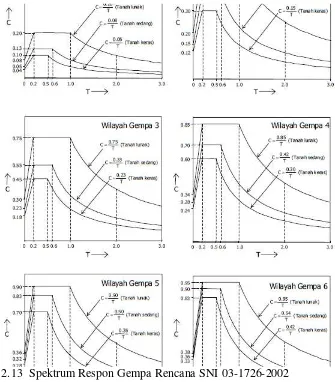
yang disajikan juga pengaruh kondisi tanah, yaitu spectrum untuk tanah keras, tanah sedang, dan tanah lunak.Definisi tanah keras, sedang dan lunak ini dapat didekati menurut beberapa kriteria. Kriteria yang dapat dipakai untuk menentukan jenis tanah diantaranya adalah jenis dan kedalaman endapan, nilai SPT, nilai undrain shear strength, cu, atau kecepatan gelombang geser VS.
Gambar 2.13 Spektrum Respon Gempa Rencana SNI 03-1726-2002
Dalam metode spektrum respon terdapat beberapa elemen-elemen yang digunakan. Salah satu elemen yang digunakan pada metode spektrum respon adalah
tingkat struktur SDOF yang dicari dengan Duhamel’s Integral dengan persamaan yang diredam dan dibebani dengan beban gempa yaitu,
(2.83)
Dengan ωd adalah damped frequency. Hal demikian terjadi karena terdapat hubungan,
(2.84)
Pada struktur MDOF, kontribusi setiap mode ditunjukkan oleh besaran partisipasi setiap mode yang dinyatakan dalam persamaan,
(2.85)
Mengingat matriks massa merupakan matriks diagonal, maka persamaan 2.85) dapat ditulis dalam bentuk,
(2.86)
Partisipasi setiap mode juga berhubungan dengan simpangan atas kontribusi suatu mode gj dengan modal amplitude Zj,
(2.87)
Modal amplitude Zj dapat diperoleh dengan mengikutkan partisipasi setiap mode pada persamaan 2.85), sehingga struktur MDOF diperoleh hubungan,
Nilai integral persamaan 2.88) akan menghasilkan suatu kecepatan yang merupakan fungsi dari waktu. Dengan memakai kecepatan tersebut, maka akan memperoleh kecepatan maksimum untuk mode yang ke-j, ẏ j.maks, dengan demikian persamaan 2.88) akan menjadi,
(2.89)
Dalam metode respon spektrum diperoleh suatu hubungan bahwa,
, atau
Maka (2.90)
Nilai-nilai kecepatan maupun percepatan maksimum pada persamaan 2.90) merupakan nilai-nilai kecepatan dan percepatan pada spektrum respon. Dengan
menganggap bahwa ωd nilainya sama dengan ω, maka modal amplitude Zj pada persamaan 2.89) akan menjadi,
(2.91)
Disain spektrum respon yang seperti yang disajikan dalam buku Peraturan Perencanaan Bangungan Tahan Gempa Untuk Gedung adalah plot antara koefisien gempa dasar C lawan periode getar T. Koefisien C tersebut adalah suatu koefisien yang dapat dihubungkan dengan SA, sehingga C.g = SA, dengan demikian modal amplitude Zj dari persamaan 2.91) menjadi (g = percepatan gravitasi),
SA pada persamaan 2.92) adalah pseudo spectral acceleration dan nilai koefisien gempa dasar C dapat diketahui dengan memakai desain spektrum respon menurut daerah gempa, jenis tanah dasar dan periode getar struktur T. Nilai modal amplitude
persamaan 2.92) dapat dihitung dengan menggunakan disain spektrum respon yang menunjukkan bahwa simpangan total suatu massa adalah produk antara modal matriks dengan faktor amplitudo Zj. dengan demikian modal displacement massa ke-i kontrke-ibuske-i mode ke-j, Yij adalah,
(2.93)
Setelah modal displacement Yij diperoleh, maka simpangan horisontal tingkat dapat dihitung. Pada prinsip SRSS, simpangan horisontal massa ke-i dapat dihitung dengan,
(2.94)
Pada analisis dinamik struktur, gaya horisontal tingkat (modal seismic force) adalah respon penting yang selalu dicari. Dengan menggunakan prinsip sebelumnya dimana simpangan horisontal massa ke-i kontribusi mode ke-j adalah,
(2.95)
Dengan menggunakan persamaan 2.90) percepatan massa ke-i sebagai kontribusi mode ke-j, ӱij menjadi,
Dengan demikian gaya horisontal tingkat atau gaya horisontal yang bekerja pada massa ke-i akibat kontribusi mode ke-j, Fij adalah,
(2.97)
Karena matriks massa adalah matriks diagonal maka persamaan 2.97) dapat ditulis menjadi,
(2.98)
Dengan prinsip SRSS maka gaya horisontal tingkat (storey seismic force) Fi dapat dihitung dengan,
(2.99)
Modal seismic force pada persamaan 2.99) juga dapat dicari dari hubungan antara kekakuan dan simpangan,
(2.100)
(2.101)
Persamaan 2.101) dapat diolah menjadi,
(2.102)
Persamaana 2.102) dapat ditulis menjadi,
(2.103)
Dengan catatan,
(2.104)
(2.105)
Persamaan 2.105) adalah modal base shear. Pada pembahasan eigenproblem
diperoleh suatu hubungan bahwa,
(2.106)
Dengan hubungan seperti pada persamaan 2.99), maka persamaan 2.106) dapat ditulis menjadi,
atau, (2.107)
2.11 Metode Elemen Hingga Untuk Plane Frame Element
Portal bidang (plane frame) merupakan gabungan antara truss element dengan
Gambar 2.14 DOF Element Frame Sebagai Portal Bidang (Plane Frame)
Matriks Kekakuan lokal untuk portal bidang (plane frame) adalah,
(2.108)
Sedangkan matriks kekakuan global untuk portal bidang dicari dengan,
(2.109)
Dimana [Te] merupakan matriks transformasi,
(2.110)
Matriks kekakuan struktur global mengikuti persamaan,
(2.111)
Dimana,
, dan , (2.112)
Boundary condition untuk setiap perletakan adalah sebagai berikut, - Perletakan jepit
(2.113) - Perletakan sendi
(2.114)
- Perletakan rol
(2.115)
Untuk mencari gaya dalam elemen, maka digunakan persamaan matriks kekakuan struktur lokal yaitu,
(2.116)
Dengan ,
BAB III
APLIKASI METODE RESPON SPEKTRUM
3.1 Pemodelan Struktur
Pada bab ini akan diberikan sebuah contoh perhitungan struktur 4 lantai dimana struktur tersebut merupakan struktur portal bertingkat biasa. Struktur tersebut akan dianalisis dengan metode respon spektrum secara analisis secara 2 dimensi. Hasil yang didapatkan salah satunya adalah gaya gempa horisontal yang akan dibebani pada struktur, kemudian akan dianalisis dengan mengunakan Metode Elemen Hingga (Finite Element Method) untuk mendapatkan gaya dalam dan perpindahan dari struktur tersebut.
Data-data strukur portal 4 lantai tersebut adalah sebagai berikut :
- Kurva spektrum yang digunakan sebagai contoh dalam perhitungan adalah kurva spektrum wilayah gempa 3 tanah lunak berdasarkan SNI 03-1726-2002.
3.2 Penyelesaian Perhitungan Pemodelan Struktur
Pada pemodelan struktur 4 lantai ini akan menggunakan prinsip bangunan geser (shear building) dan massa tergumpal (lumped mass) pada tiap lantai. Dengan anggapan seperti ini, maka massa akan terkumpul pada satu titik dan hanya mempunyai 1 derajat kebebasan serta akan menghasilkan 4 mode shapes. Untuk
Free Vibration System) dan dianalisis dengan menggunakan metode stodola atau matriks iterasi.
Gambar 3.2 Pemodelan Lumped Mass struktur 4 lantai
Dalam memulai menganalisis pemodelan struktur tersebut, hal pertama yang perlu dilakukan adalah menggambarkan free body diagram dari pemodelan struktur 4 lantai tersebut berdasarkan prinsip getaran bebas tanpa redaman.
Berdasarkan gambar free body diagram pada gambar 3.3, dapat disusun persamaan diferensial simultan gerakan massa yaitu,
(3.1) Persamaan 3.1) di atas dapat ditulis juga menjadi,
(3.2)
Persamaan 3.2) selanjutnya dapat ditulis ke dalam bentuk matriks sebagai berikut,
(3.3)
Dari persamaan 3.3) maka dapat ditulis matriks massa dan matriks kekakuannya adalah sebagai berikut,
(3.4)
(3.5)
Sedangkan untuk matriks kekakuannya adalah, - Kolom tepi berukuran 30 x 40 cm
- Kolom tepi berukuran 30 x 50 cm
- Kolom tepi berukuran 30 x 60 cm
- Kekakuan kolom lantai 1 (K1) adalah
- Kekakuan kolom lantai 2 (K2) adalah
- Kekakuan kolom lantai 4 (K4) adalah
Maka matriks kekakuannya dapat ditulis sebagai berikut,
Nilai K = 442.969 kN/cm merupakan nilai yang ditarik keluar dan ditinggalkan untuk sementara waktu dari matriks kekakuan kolom agar angka dalam matriks kekakuan lebih sederhana dan nantinya nilai tersebut akan digunakan dalam perhitungan frekuensi sudut.
a) Mode ke-1
Nilai invers dari matriks kekakuan diatas adalah,
Apabila koefisien 1/442.969 ditinggalkan untuk sementara agar angka perhitungan menjadi lebih sederhana maka,
Dengan cara coba-coba, diambil modal vektor untuk mode ke-1 misalnya,
Dengan demikian maka ,
Maka,
Maka,
Dengan nilai = 1.149 dan masih belum sama dengan . Maka proses iterasi diteruskan pada iterasi ke-3,
Maka,
Dengan nilai = 1.156 dan masih belum sama dengan . Maka proses iterasi diteruskan dan pada iterasi ke-4 diperoleh,
Maka,
442.969 kN/cm yang ditinggalkan sementara pada perhitungan sebelumnya digunakan dalam menghitung frekuensi sudut. Maka nilai frekuensi sudut yang dihasilkan adalah,
rad/s
b) Mode ke-2
Maka,
Setelah [S1] didapatkan maka matriks dinamik fleksibilitas yang baru adalah,
Dengan cara coba-coba, diambil modal vektor untuk mode ke-2 misalnya,
Maka,
Dengan nilai = 0.164. Terlihat bahwa nilai belum sama dengan , maka iterasi dilanjutkan berikutnya iterasi ke-2,
Maka,
Dengan nilai = 0.167 dan masih belum sama dengan . Maka proses iterasi diteruskan pada iterasi ke-3,
Maka,
Maka,
Pada iterasi ke-4 , nilai = 0.169 sama dengan nilai = 0.169, dan nilai
mendekati nilai maka proses iterasi sudah dapat dihentikan. Maka nilai frekuensi sudut yang dihasilkan adalah,
rad/s
c) Mode ke-3
Maka,
Setelah [S2] didapatkan maka matriks dinamik fleksibilitas yang baru adalah,
Dengan cara coba-coba, diambil modal vektor untuk mode ke-3 misalnya,
Maka,
Dengan nilai = 0.068. Terlihat bahwa nilai belum sama dengan , maka
iterasi dilanjutkan berikutnya iterasi ke-2,
Maka,
Dengan nilai = 0.072 dan masih belum sama dengan . Maka proses iterasi diteruskan pada iterasi ke-3,
Pada iterasi ke-3 , nilai = 0.072 sama dengan nilai = 0.072, dan nilai
mendekati nilai maka proses iterasi sudah dapat dihentikan. Maka nilai frekuensi sudut yang dihasilkan adalah,
rad/s
d) Mode ke-4
Pada mode ke-4, nilai sweeping matrix [S3] dihitungan dengan persamaan,
Setelah [S3] didapatkan maka matriks dinamik fleksibilitas yang baru adalah,
Dengan cara coba-coba, diambil modal vektor untuk mode ke-4 misalnya,
Dengan demikian maka ,
Dengan nilai = 0.002. Terlihat bahwa nilai belum sama dengan , maka iterasi dilanjutkan berikutnya iterasi ke-2,
Maka,
Dengan nilai = 0.053 dan masih belum sama dengan . Maka proses iterasi diteruskan pada iterasi ke-3,
Maka,
Pada iterasi ke-3 , nilai = 0.053 sama dengan nilai = 0.053, dan nilai sama dengan nilai maka proses iterasi sudah dapat dihentikan. Maka nilai frekuensi sudut yang dihasilkan adalah,
rad/s
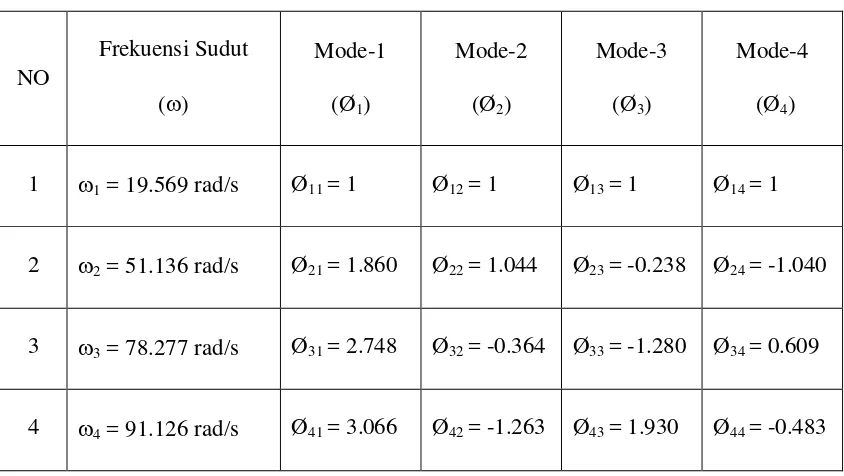
Tabel 3.1 Nilai-nilai ω, dan Ø pada tiap-tiap mode
Untuk menggambarkan nilai Ø tiap mode, maka untuk lantai teratas dianggap nilai Ø4 = 1, maka nilai-nilai Ø yang digunakan dalam penggambaran tiap koordinat mode adalah,
Ø41 = 1 Ø42 = 1 Ø43 = 1 Ø44 = 1
Ø31 = 0.896 Ø32 = 0.291 Ø33 = -0.663 Ø34 = -1.262
Ø21 = 0.607 Ø22 = -0.827 Ø23 = -0.123 Ø24 = 2.155
Gambar 3.4 Mode shapes struktur 4 lantai
Setelah nilai ordinat tiap-tiap mode didapat, maka perhitungan dapat dilanjutkan ke tahapan berikutnya yaitu analisis pembebanan gempa dengan metode respon spektrum. Namun sebelumnya terlebih dahulu dicari nilai-nilai periode getar struktur
(T) dari masing-masing mode dengan menggunakan rumus T = .
ω4 = 91.126 rad/s , T4 = 0,069 s
Setelah nilai-nilai periode getar (T) masing-masing mode didapat, maka nilai koefisien gempa dasar (C) bisa didapatkan berdasarkan kurva spectrum gempa wilayah 3, dengan kondisi tanah lunak.
Gambar 3.5 Kurva Spektrum Wilayah Gempa 3 (SNI 03-1726-2002)
Berdasarkan kurva spektrum tanah lunak wilayah gempa 3, maka nilai koefisien gempa dasar (C) berdasarkan tiap-tiap mode adalah,
T1 = 0,321 s C1 = 0.75
T2 = 0,123 s C2 = 0.58
T4 = 0,069 s C4 = 0.46
1. Partisipasi Mode
a) Mode -1
Partisipasi mode -1, Γ1 adalah,
b) Mode -2
c) Mode -3
Partisipasi mode -3, Γ3 adalah,
Partisipasi mode -4, Γ4 adalah,
Sebagai control, partisipasi semua mode harus sama dengan 1 maka,
2. Gaya Horisontal Mode atau Modal Seimic Force (Fij)
Gaya horisontal mode yang bekerja pada setiap massa akibat kontribusi setiap mode dapat dihitung dengan menggunakan persamaan,
a) Mode – 1,
b) Mode – 2,
c) Mode – 3,
Dengan memakai prinsip SRSS, maka gaya horisontal tingkat (storey seismic force) adalah,
Gambar 3.6 Gaya Horisontal Mode dan Gaya Horisontal Tingkat
3.3 Perhitungan Analisis dengan Metode Elemen Hingga (FEM)