TRANFORMASI
DAN
INVERS LAPLACE
Didalam perancangan dan analisa sistem pengaturan akan banyak dijumpai persamaan-persamaan diferensial dimana ia merupakan pemodelan dari suatu sistem. Untuk mengetahui sifat-sifat dari suatu sistem, persamaan-persamaan tersebut harus dipecahkan, dan salah satu teknik untuk memecahkan persamaan diferensial adalah menggunakan metode transformasi Laplace.
Teknik pengalih bentuk yang menghubungkan fungsi-fungsi waktu ke fungsi-fungsi tergantung frekuensi dari suatu variabel kompleks. Teknik ini disebut Transformasi Laplace atau alih bentuk Laplace.
Dalam bab ini akan dibahas tentang metode transformasi Laplace, dan transformasi baliknya.
Tujuan Instruksional khusus:
Mahasiswa mendapat pengetahuan tentang dasar matematis yang diperlukan dalam sistem kendali.
Mahasiswa dapat menggunakan metode transformasi Laplace untuk menyelesaikan persamaan sistem kendali.
Mahasiswa dapat menggunakan tabel transformasi Laplace untuk menyelesaikan persamaan sistem kendali.
2.1. TRANSFORMASI LAPLACE
Transformasi Laplace adalah suatu metode operasional yang dapat digunakan secara mudah untuk menyelesaikan persamaan diferensial linier. Dengan menggunakan transformasi Laplace, dapat diubah beberapa fungsi umum seperti fungsi sinusoida, fungsi sinusoida teredam, dan fungsi eksponensial menjadi fungsi-fungsi aljabar variabel kompleks s. Bila persamaan aljabar dalam s dipecahkan, maka penyelesaian dari persamaan diferensial (transformasi Laplace balik dari variabel tidak bebas) dapat diperoleh dengan menggunakan tabel transformasi Laplace.
Secara sederhana prosedur dasar pemecahan menggunakan metode transformasi Laplace adalah:
Persamaan diferensial yang berada dalam kawasan waktu (t), ditransformasikan ke kawasan frekuensi (s) dengan transformasi Laplace. Untuk mempermudah proses transformasi dapat digunakan Tabel 2-1.
Persamaan yang diperoleh dalam kawasan s tersebut adalah persamaan aljabar dari variabel s yang merupakan operator Laplace.
Penyelesaian yang diperoleh kemudian ditransformasi-balikkan ke dalam kawasan waktu.
Hasil transformasi balik ini menghasilkan penyelesaian persamaan dalam kawasan waktu.
Gambar 2.1 Prosedur penyelesaian persamaan diferensial menggunakan metode transformasi Laplace.
Persamaan diferensial
variabel x(t). Penyelesaian x(t).
Persamaan Aljabar
operator s Penyelesaian Aljabar X(s) TransformasiLaplace Transformasi Balik
Laplace
PerhitunganAljabar
Penyelesaian Langsung (analitik) Kawasan
waktu (t)
1. Definisi transformasi Laplace
L
0 [ ( )] 0 ( )
) ( )] (
[f t F s e stdt f t f t e stdt (2-1)
)
(
t
f
= fungsi waktut
sedemikian rupa sehinggaf
(
t
)
0
untuk t 0s = variabel kompleks (operator Laplace) = + j (dengan j = satuan imajiner)
L = simbol operasional yang menunjukkan bahwa besaran yang didahuluinya ditransformasikan dengan integral Laplace
0 e dt st
)
(
s
F
= tranformasi Laplace darif
(
t
)
2.2. TRANSFORMASI LAPLACE BALIK (INVERS-LAPLACE)
Proses kebalikan dari penemuan fungsi waktu
f
(
t
)
dari transformasi LaplaceF
(
s
)
dinamakan transformasi balik Laplace. Notasi untuk transformasi balik Laplace adalah L-1. JadiL-1
[
F
(
s
)]
f
(
t
)
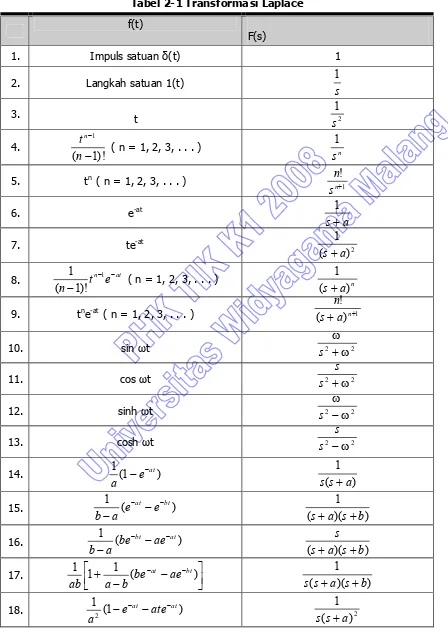
(2-2)Tabel 2-1Transformasi Laplace
f(t)
F(s)
1. Impuls satuan δ(t) 1
2. Langkah satuan 1(t)
s
1
3. t
1
2s
4.
)! 1 (
1
n tn
( n = 1, 2, 3, . . . ) n
s
1
5. tn ( n = 1, 2, 3, . . . )
1
!
n
s
n
6. e-at
a
s
1
7. te-at
2
)
(
1
a
s
8.
t
ne
atn
1
)!
1 (
1
( n = 1, 2, 3, . . . )n
a
s
)
(
1
9. tne-at ( n = 1, 2, 3, . . . ) 1
)
(
!
a
ns
n
10. sin ωt
s
2
211. cos ωt
s
2
2s
12. sinh ωt
s
2
213. cosh ωt
s
2
2s
14.
1
(
1
e
at)
a
(
)
1
a
s
s
15.
1
(
e
ate
bt)
a
b
(
)(
)
1
b
s
a
s
16.
1
(
be
btae
at)
a
b
(
s
a
)(
s
b
)
s
17.
1
(
)
1
1
be
atae
btb
a
ab
(
)(
)
1
b
s
a
s
s
18.
1
2(
1
e
atate
at)
a
(
)
21
f(t)
F(s)
19.
1
2(
at
1
e
at)
a
(
)
1
2
s
a
s
20.
e
atsin
t
2 2
)
(
s
a
21.
e
atcos
t
2 2
)
(
s
a
a
s
22. n 2 e ntsin n 1 2t
1
2 2 2
2
n nn
s
s
23. ) 1 sin( 1 2
2
e t
n t
n n
tan1 1 2
2 2
2
n ns
s
s
24. ) 1 sin( 1 1 22
e t
n t
n n
tan1 1 2
(
2
)
2 2 2 n n n
s
s
s
25. 1 - cos ωt
)
(
2 22
s
s
26. ωt - sin ωt
)
(
2 2 2 3
s
s
27. sin ωt - ωt cos ωt 2 2 2
3
)
(
2
s
28.
t
t
sin
2
1
2 2 2)
(
s
s
29. t cos ωt 2 2 2
2 2
)
(
s
s
30.
1
2(cos
1cos
2)
1 2 2t
t
(
12
22)
(
)(
2)
2 2 2 1
2
s
s
s
31.
(sin
cos
)
2
1
t
t
t
2 2 22
)
(
s
Sekarang akan dibahas beberapa sifat dari transformasi Laplace Perkalian dengan konstanta
L
0
0 ( ) ( )
)
(t Af t e dt A f t e dt
Af st st
AF
(
s
)
(2-3)Penjumlahan dan pengurangan
L
f1(t) f2(t)
0 1 0 2
0 [f1(t) f2(t)]e dt f (t)e dt f (t)e dt st st
st
F1(s)F2(s) (2-4)
Diferensiasi
L
0 00
(
)
[
(
)
]
(
)(
)
)
(
f
t
e
dt
f
t
e
f
t
se
dt
dt
d
t
f
dt
d
st st st0 (0) ( ) ( ) (0)
0 f t e dt sF s f
s
f st
(2-5)Mirip dengan itu, untuk turunan ke-n dari
f
(
t
)
diperolehL ( ) ( ) 1 (0) 2 .(0)... ( 2)(0)( 1)(0)
n n
n n n n n f f s f s f s s F s t f dt d
n r r r n nF
s
s
f
s
1 ) 1 ()
0
(
)
(
(2-6)Integrasi
L
0 0
0
(
)
(
)
t t
st t
t
f
d
f
d
e
dt
0 10
1
)
(
)(
)
(
)
(
0
f
d
e
f
t
e
dt
st s st
s t
t
0 1(
)
1 0(
)
0
f
d
f
t
e
dt
st s
t s
1 1 00
(
)
)
(
s ts
F
s
f
d
(2-7)Diferensiasi dan Integrasi pada kawasan s
)
(
s
F
ds
d
0(
)
0f
(
t
)
e
dt
ds
d
dt
e
t
f
ds
0 tf(t)e stdt = L[-t f(t)] = -L[tf(t)]
sF(s)ds
s f t e stdtds
0 ( )
0 ( )
s
stdsdt
e t f
s st s
t s
st
t f t e dt 0 1 f t e dt
1 ( ) 0 ( )
L
1f
(
t
)
t
(2-8)Perubahan skala waktu
L
f
t
f
t
e
stdt
0
(2-9)Dengan mengganti t/ t1 ; sehingga tt1, dan dt dt1, diperoleh
L
0
(
1)
(
1)
1
1
d
t
e
t
f
t
f
s t
0 f(t1)e s1t1dt1
)
(
s
F
(2-10)Harga awal
)
(
lim
)
(
lim
0
f
t
ssF
s
t
(2-11)Untuk interval waktu 0t , jika s mendekati tak hingga,
e
stmendekati nol.
(
)
(
0
)
lim
(
)
(
0
)
0
lim
)
(
lim
0
dt
f
t
e
dt
sF
s
sF
s
f
d
s s
st s
atau
)
0
(
)
(
lim
sF
s
f
s
karena
(
0
)
lim
(
)
0
f
t
f
t
maka)
(
lim
)
(
lim
0
f
t
s
sF
t
s
(2-12)Harga akhir
)
(
lim
)
(
lim
0
sF
s
t
f
s
Untuk membuktikan teorema ini, ambil s mendekati nol pada persamaan transformasi Laplace untuk turunan fungsi
f
(
t
)
atau
(
)
(
0
)
lim
)
(
lim
0 0
0
dt
f
t
e
dt
sF
s
d
s st
s (2-14)
Karena lim 1
0
st
s e , diperoleh
)
0
(
)
(
)
(
)
(
00
dt
f
t
dt
f
t
f
f
d
lim
(
)
(
0
)
0
sF
s
f
s
sehingga
)
(
lim
)
((
lim
)
(
0
sF
s
t
f
f
s t
(2-15)Translasi pada kawasan t
L
f t t
f t t estdt
0) 0 ( 0)
( dimana
f
(
t
)
0
untuk t0, dant
0
0
misal
t
1
t
t
0, makat
t
1
t
0 dan dt = dt1, makadt e t t
f st
0 ( 0) 0 f(t1)es(t1t0)dt1
1
0 1
1
0 f(t )e dt
est st
)
(
0
F
s
e
st
(2-16)Translasi pada kawasan s
L
eatf t
e at f t estdt
0 ( )
) (
dt e
t f (s a)t 0 ( )
)
(
s
a
F
(2-17)Konvolusi
Tinjau transformasi Laplace berikut:
f d
t f
t
0 1( ) 2( ) (2-18)) ( )
( 2
1 t f t
f
Operasi matematik f1(t) f2(t) disebut konvolusi. Jika dinyatakan
t
,maka
f d f f t d
t
f t
t
0 1( ) 2( ) 0 1( ) 2( )
t f f t d0 1( ) 2( )
Oleh karena itu
( )
)
( 2
1 t f t
f
0t f1(t)f2()d
t f f t d0 1( ) 2( )
f2(t) f1(t) (2-19)
Bila f1(t) dan f2(t) adalah kontinyu sepotong-sepotong (piecewise) dan mempunyai orde eksponensial, maka
L
(
)
(
)
1(
)
2(
)
0
f
1t
f
2d
F
s
F
s
t
(2-20)
Dengan
f t e dt sF st
0 1
1( ) ( ) L
f1(t) (2-21)
f t e dt sF st
0 2
2( ) ( ) L
f2(t)
(2-22)Untuk membuktikan persamaan (3-9), perhatikan bahwa f1(t)1(t)0
untuk
t
. Oleh karena itu
f d f t t f d
t f
t
0 1( ) 2( ) 0 1( )1( ) 2( ) (2-23)Selanjutnya
L
tf
t
f
d
0 1
(
)
2(
)
L
t
f
d
t
f
e
stf
t
t
f
d
dt
0
0 1(
)
1
(
)
2(
)
(2-24)Dengan substitusi t dalam persamaan terakhir ini dengan mengubah urutan integrasi, yang diperbolehkan dalam kasus ini karena f1(t) dan f2(t)
dapat ditransformasi dengan integral Laplace, diperoleh
L
tf
t
f
d
0 1
(
)
2(
)
f t t e dt f d st
0 2
0 1( )1( ) ( )
f e s d f d
0 1( ) ( ) 0 2( )
f e sd f e sd
0 1( ) 0 2( )
F1(s)F2(s) (2-25)
Persamaan terakhir ini memberi transformasi Laplace dari integral konvolusi. Sebaliknya, jika transformasi Laplace dari suatu fungsi diberikan oleh perkalian dua fungsi transformasi Laplace, F1(s)F2(s), maka fungsi waktu yang berkaitan (transformasi Laplace balik) diberikan oleh integral konvolusi
) ( )
( 2
1 t f t
Tabel 3-2. Sifat-sifat Transformasi Laplace
1. L [Af(t)] = AF(s)
2. L [f1(t) f2(t)] = F1(s) F2(s)
3. L
dtdf
(
t
)
= sF(s) – f(0 )4. L
2(
)
2
t
f
dt
d = s2F(s) – sf (0
) –
f
(0)5. L
nf
(
t
)
n
dtd = s
nF(s) – ( 1)
(
0
)
1
kns
n k kf
dengan(
)
(
)
1 1
) 1 (
t
f
t
f
kk
dtd k
6.
L
f
(
t
)
dt
=s
s
F
(
)
+
sdt t f t
( ) 07. L
f
(
t
)
dt
dt
=2
)
(
s
s
F
+
2 0) (
s dt t f
t
+
s dtdt t f
t
( ) 08. L
...
f
(
t
)
(
dt
)
n
= ns
s
F
(
)
+
n
k t
k k
n
f
t
dt
s
1 1 0
)
)(
(
...
1
9. L
tdt
t
f
0
(
)
=s
s
F
(
)
10.
0 f(t)dt =
lim
s0F
(
s
)
jika
0 f(t)dt ada
11. L
e
atf
(
t
)
= F(s + a)12. L
f(t)1(t)
= e-s F(s) 013. L
tf(t) =ds
s
dF
(
)
14. L
t
2f
(
t
)
=(
)
2 2
s
F
ds
d
15. L
t
nf
(
t
)
=(
1
)
F
(
s
)
ds
d
n n n
n = 1, 2, 3, . . .16. L
1f
(
t
)
t =
0 F(s)ds
17. L
f
(
at)
= aF(as)1. Metode ekspansi pecahan parsial untuk memperoleh transformasi Laplace balik
Masalah dalam analisis sistem kendali,
F
(
s
)
, transformasi Laplace darif
(
t
)
lebih sering dijumpai dalam bentuk)
(
)
(
)
(
s
A
s
B
s
F
(2-26)Dengan
A
(
s
)
danB
(
s
)
adalah polinomial dalam s dan derajatB
(
s
)
lebih kecil dariA
(
s
)
. BilaF
(
s
)
dipotong dalam komponen)
(
...
)
(
)
(
)
(
s
F
1s
F
2s
F
s
F
n (2-27)Dan bila transformasi Laplace balik dari
F
1(
s
),
F
2(
s
),...,
F
n(
s
)
memungkinkan, makaL -1
F(s) L -1
( )
1 s
F L -1
( )
2 s
F . . . + L -1
F
(
s
)
n
f
1(
t
)
f
2(
t
)
...
f
n(
t
)
(2-28)Dengan
f
1(
t
),
f
2(
t
),...,
f
n(
t
)
adalah transformasi Laplace balik dari)
(
),...,
(
),
(
21
s
F
s
F
s
F
n . Transformasi Laplace balikF
(
s
)
diperoleh secara unik kecualimungkin pada titik-titik dengan fungsi waktu tak kontinyu. Apabila fungsi waktu kontinyu, maka fungsi waktu
f
(
t
)
dan transformasi Laplace baliknyaF
(
s
)
mempunyai hubungan korespondensi satu-satu.Keuntungan dari pendekatan ekspansi pecahan parsial adalah masing-masing suku dari
F
(
s
)
akibat dari ekspansi dalam bentuk pecahan parsial, merupakan fungsi dalam s yang sangat sederhana, sehingga tidak diperlukan tabel transformasi Laplace lagi bila kita ingat beberapa pasangan transformasi Laplace sederhana. Harus diperhatikan bahwa menerapkan teknik ekspansi pecahan parsial dalam mencari transformasi Laplace balik dariF
(
s
)
B
(
s
)
/
A
(
s
)
akar dari penyebut polinomialA
(
s
)
harus diketahui. Jadi metode ini tidak dapat diterapkan bila polinomial penyebut telah difaktorkan.2. Ekspansi pecahan parsial bila
F
(
s
)
hanya melibatkan kutub-kutub (pole).Perhatikan fungsi
F
(
s
)
yang ditulis dalam bentuk faktor) )...( )( ( ) )...( )( ( ) ( ) ( ) ( 2 1 2 1 n m p s p s p s z s z s z s K s A s B s F
(
m
n
)
(2-29)Dengan p1, p2, . . ., pn dan z1, z2, . . ., zm masing-masing besaran real atau
kompleks, tetapi untuk masing-masing bilangan kompleks pi atau zi mempunyai
konjugat kompleks pi dan zi . Jika
F
(
s
)
hanya terdiri dari kutub-kutub (pole)maka dapat diekspansikan dalam jumlah pecahan parsial sederhana sebagai berikut: n n p s a p s a p s a s A s B s F ... ) ( ) ( ) ( 2 2 1 1 (2-30)
Dengan
a
k (k = 1, 2, . . .,n ) adalah konstanta, koefisiena
k disebut residu pada kutub dis
p
k. Nilaia
k dapat diperoleh dengan mengalikan kedua sisi persamaan (2-30) dengan(
s
p
k)
dan menggantis
p
k yang memberikan
)
(
)
(
)
(
)
(
)
(
2 2 1 1 k k p sk
B
A
s
s
s
a
p
s
p
s
a
p
s
p
p
s
k . . . ( k)
k k s p
p s
a . . .
k
p s k n
n
s
p
p
s
a
(
)
= ak (2-31)
Dapat dilihat bahwa semua suku ekspansi dapat dihilangkan kecuali yang mengandung ak, sehingga residu ak diperoleh
k
p s k
k
s
p
B
A
s
s
a
)
(
)
(
)
(
(2-32)Perhatikan bahwa
f
(
t
)
adalah fungsi real dari waktu, bila p1 dan p2 konjugat kompleks, maka residu a1 dan a2 juga konjugat kompleks. Hanya satu dari konjugat a1 atau a2 yang diperlukan karena yang lain dapat diketahui dengan sendirinya.Karena
L -1 pt
k k
k a e k
p s
a
)
(
t
f
Diperoleh sebagai)
(
t
f
= L -1
ptn t
p t
p
a
e
a
e
ne
a
s
F
(
)
1
2
...
2
1
(
t
0
)
(2-33)Contoh
Tentukan transformasi Laplace balik dari
F(s) =
)
2
)(
1
(
3
s
s
s
Ekspansi pecahan parsial dari F(s) adalah F(s) =
)
2
)(
1
(
3
s
s
s
=2 1 2 1 s a s a
Dengan a1 dan a2 diperoleh dari persamaan di atas
a1 =
2
2
3
)
2
)(
1
(
3
1
1 1
s ss
s
s
s
s
s
a2 =
1
1
3
)
2
)(
1
(
3
1
2 2
s ss
s
s
s
s
s
Jadi,f(t) = L -1[F(s)]
= L -1
1
2
s
+ L -1
2
1
s
= 2e-t – e-2t (t 0)
3. Ekspansi pecahan parsial bila
F
(
s
)
melibatkan banyak kutub.Berikut ini ditampilkan contoh untuk menunjukkan bagaimana mendapatkan ekspansi pecahan parsial dari
F
(
s
)
.Contoh :
Perhatikan persamaan berikut:
Ekspansi pecahan parsial dari
F
(
s
)
ini melibatkan 3 bagian, 1 ) 1 ( ) 1 ( ) ( ) ( ) ( 1 2 2 3 3 s b s b s b s A s B s FDengan b3, b2 dan b1 ditentukan sebagai berikut. Dengan mengalikan kedua sisi dari persamaan terakhir ini dengan (s + 1)3 , diperoleh
2 1
2 3
3
(
1
)
(
1
)
)
(
)
(
)
1
(
b
b
s
b
s
s
A
s
B
s
Dengan menjadikan s = –1 , persamaan menjadi
3 1 3
)
(
)
(
)
1
(
b
s
A
s
B
s
s
Juga, diferensiasi kedua sisi dan dengan mengacu pada s dihasilkan
)
1
(
2
)
(
)
(
)
1
(
3
2
1
b
b
s
s
A
s
B
s
ds
d
Jika s = –1 , maka
2 1 3
)
(
)
(
)
1
(
b
s
A
s
B
s
ds
d
s
Dengan mendeferensiasi kedua sisi dan dengan mengacu pada s, hasilnya adalah
1 3 2 2
2
)
(
)
(
)
1
(
b
s
A
s
B
s
ds
d
Dari analisis sebelum ini terlihat bahwa nilai b1, b2 dan b3 ditemukan secara sistem sebagai berikut
1 3 3
)
(
)
(
)
1
(
ss
A
s
B
s
b
(
s
2
2
s
3
)
s11 3
2
(
1
)
(
(
)
)
s
s
A
s
B
s
ds
d
b
1 2 2 3)
(
s
s s ds
d
(
2
s
2
)
s1 01 3
2 2
1
2
1
!
(
1
)
(
(
)
)
s
s
A
s
B
s
ds
d
b
1 2
2 2
) 3 2 ( ! 2 1
s
s s ds
d
(
2
)
1
2
1
Selanjutnya, diperoleh
)
(
t
f
L -1
F(s)= L -1
1)3
( 2
s L
-1
1)2
( 0
s L
-1
1
1
s
t
2e
t
0
e
tTransformasi Laplace menggunakan MATLAB
• Transformasi Laplace F (s) dari suatu fungsi f (t) adalah cukup sederhana dalam Matlab. Pertama perlu menentukan variabel simbolis t dan s menggunakan perintah
>> syms t s
• Selanjutnya menentukan fungsi f (t) dengan perintah >> F=laplace(f,t,s)
Contoh :
Untuk membuat ekspresi lebih enak dibaca menggunakan perintah, simplify dan pretty. di sini diberikan contoh untuk fungsi f (t),
Invers Transformasi Laplace menggunakan Matlab
• Perintah Transformasi Laplace balik (invers) menggunakan perintah >> F=ilaplace(f,t,s)
2.3. Ringkasan
SOAL-SOAL
1. Dapatkan Transformasi Laplace fungsi yang didefinisikan oleh a. f1(t)0 (t0)
0)
(t
45
5
sin
3
)
(
1
t
(
t
)
f
b. f2(t)0 (t0) 0) (t 2
cos 1 03 . 0 ) (
2 t ( t)
f
2. Bagaimana Transformasi Laplace, fungsi f(t) pada gambar berikut :
3. Tentukan Transformasi Laplace balik dari fungsi berikut: a. 1
(
)
6
23
s
s
s
F
b. 2 2
)
2
)(
1
(
2
5
)
(
s
s
s
s
F
4. Sederhanakan diagram blok yang ditunjukkan dalam gambar di bawah dan dapatkan fungsi alih loop tertutup C(s)/ R(s).
5. Andaikan sistem yang diberikan oleh
2 1
2 1 2
1
0
1
1
1
1
3
1
4
x
x
y
u
x
x
x
x
Dapatkan fungsi alih sistem
f
(
t
)
b
0 a a + b t
G
1G
2G
3G
4+ _
+
+
_ +