The Role of the Average Tax Rate in the (1)
Teks penuh
Gambar
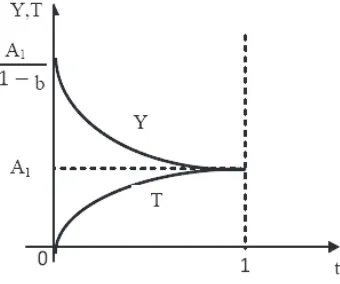
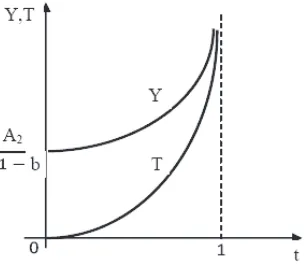
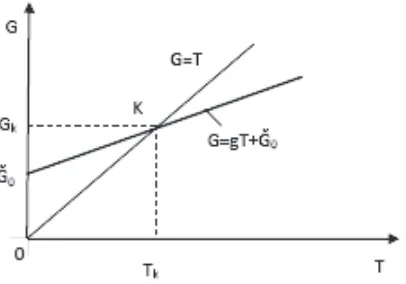
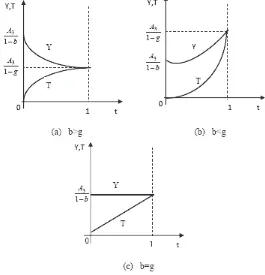
Garis besar
Dokumen terkait
However, based on an extrapolation of the regression for tem- perature increase, and assuming the high-elevation trees had been measured at an ambient temperature of 25 °
Pokja BLPBJ Provinsi Papua mengundang saudara untuk dapat hadir pada. Klarifikasi dan Negosiasi Teknis dan Biaya yang akan dilaksanakan
[r]
Telah dilakukan percobaan penentuan kadar air dan kadar asam lemak bebas pada minyak sawit mentah ( crude palm oil ).. Dimana pada penentuan kadar air dilakukan
Asusindo Servistama dan Medan Selular yang merupakan perjanjian baku dan merupakan akta di bawah tangan (bukan akta notariil).Skripsi ini diangkat dari permasalahan kesesuaian
Hal tersebut kembali dipertegas dalam konsiderans Undang-Undang Perindustrian (Undang-Undang Nomor 5 Th. 1984) yang menyatakan bahwa untuk mencapai sasaran pembangunan di
Siswa pada tingkat 3 mampu membuat suatu jawaban yang baru dengan fasih, tetapi tidak dapat menyususn cara berbeda (fleksibel) untuk mendapatkannya atau siswa dapat
Penelitian ini dilakukan untuk meningkatkan ketetapan hasil perhitungan balas jasa dalam pembayaran gaji yang sesuai pada PT. Varia Usaha Beton. Metode analisis