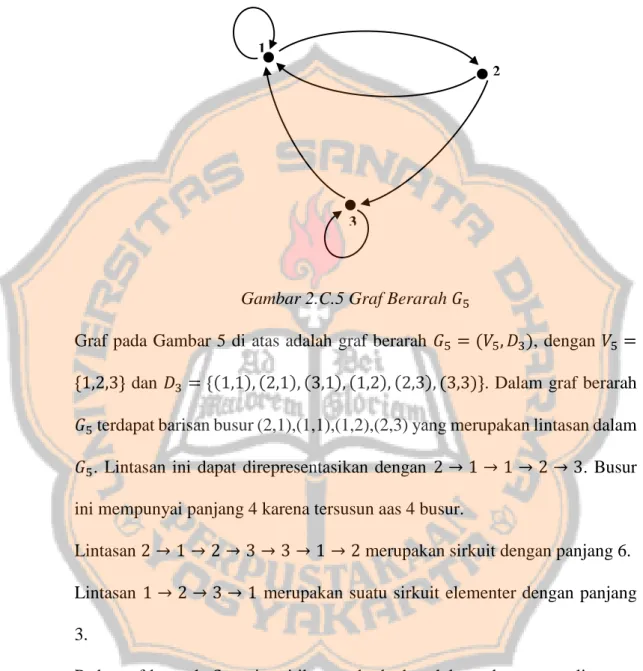
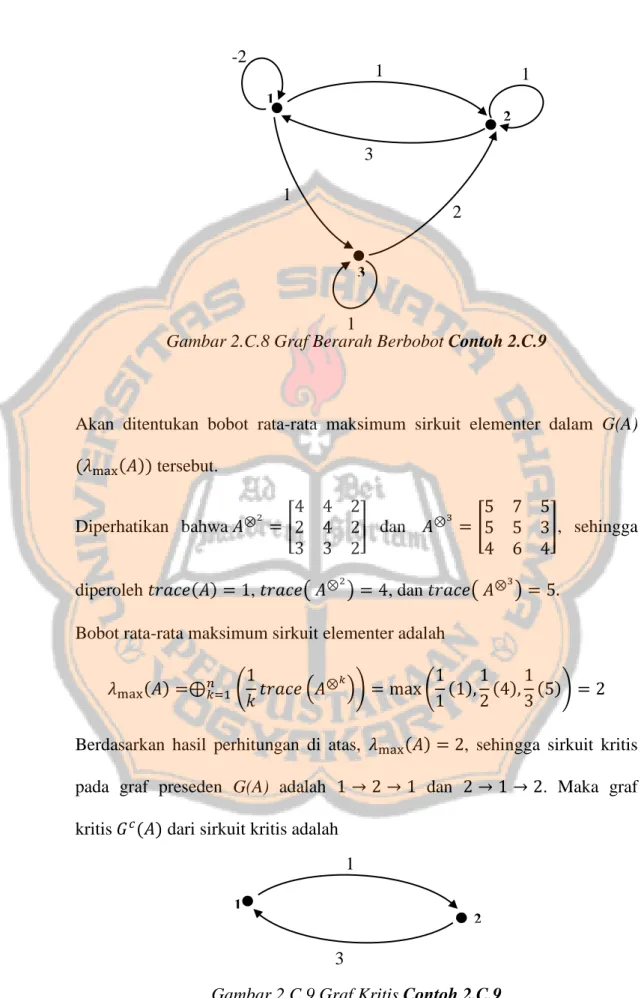
Pemodelan jaringan dan analisa penjadwalan kereta api komuter di DAOP VI Yogyakarta dengan menggunakan aljabar max-plus

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PEMODELAN JARINGAN DAN ANALISA PENJADWALAN KERETA API KOMUTER DI DAOP VI YOGYAKARTA DENGAN MENGGUNAKAN ALJABAR MAX-PLUS. SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika. Oleh : SCOLASTIKA LINTANG RENGGANIS RADITYANI NIM : 121414047. PROGRAM STUDI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSTAS SANATA DHARMA YOGYAKARTA 2016.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PEMODELAN JARINGAN DAN ANALISA PENJADWALAN KERETA API KOMUTER DI DAOP VI YOGYAKARTA DENGAN MENGGUNAKAN ALJABAR MAX-PLUS. SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika. Oleh : SCOLASTIKA LINTANG RENGGANIS RADITYANI NIM : 121414047. PROGRAM STUDI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSTAS SANATA DHARMA YOGYAKARTA 2016. i.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. HALAMAN PERSEMBAHAN. Iman tanpa perbuatan pada hakekatnya adalah mati. (Yakobus 2:14-26). Be thankful for what you have, you’ll having more. If you concentrate on what you don’t have, you will never, ever have enough. (Oprah Winfrey). Karya ini kupersembahkan kepada: Tuhan Yesus Kristus dan Bunda Maria yang senantiasa memberkatiku Papa Donatus dan Mama Paula Mbak Raras, Adik Bela, dan Adik Theo Mami Tun, Mbak Galuh, dan Om Tarigan Laurensius Andi Saputra Teman-temanku tercinta Almamaterku Universitas Sanata Dharma, Yogyakarta. iv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRAK. Scolastika Lintang Rengganis Radityani, 2016. Pemodelan Jaringan dan Analisa Penjadwalan Kereta Api Komuter di DAOP VI Yogyakarta dengan Menggunakan Aljabar Max-Plus. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta. Saat ini, penjadwalan kereta api komuter di Daerah Operasi VI (DAOP VI) Yogyakarta dibuat berdasarkan kebutuhan penumpang (konsumen), sehingga belum terjadi proses sinkronisasi. Proses sinkronisasi dalam jaringan transportasi penting untuk dilakukan guna menjamin tersedianya sarana transportasi, dalam hal ini kereta api komuter, pada saat penumpang dari suatu kereta api dengan rute tertentu ingin berpindah ke kereta api lainnya dengan rute yang berbeda. Oleh karena itu, pada penelitian ini dibuat suatu desain penjadwalan untuk keberangkatan kereta api komuter di DAOP VI Yogyakarta dengan memperhatikan proses sinkronisasi. Salah satu cara untuk memudahkan penyusunan jadwal berdasarkan aturan sinkronisasi adalah menggunakan aljabar max-plus. Penelitian ini bertujuan untuk menyusun suatu model jaringan dan menganalisa penjadwalan kereta api komuter di DAOP VI Yogyakarta menggunakan aljabar max-plus. Metode penelitian yang digunakan adalah metode studi pustaka yang didukung dengan data lapangan dan proses komputasi dengan program MATLAB. Hasil penelitian menunjukkan bahwa matriks dari model jaringan kereta api komuter di DAOP VI Yogyakarta dinyatakan sebagai matriks yang tidak irreducible (tereduksi). Hal ini diduga karena tidak semua lintasan terdapat kereta api komuter yang siap melayani sehingga lintasan tersebut seperti dianggap tidak ada. Berdasarkan hasil perhitungan dengan program MATLAB, didapatkan nilai eigen maksimum yaitu 𝜆(𝐴) = 786 dan vektor eigen yang berupa bilangan real, sehingga dapat dibuat penjadwalan kereta api komuter yang tersinkronisasi. Nilai eigen tersebut menyatakan periode keberangkatan kereta api komuter dari masingmasing stasiun, yaitu setiap 786 menit sekali atau setiap 13 jam 6 menit sekali. Sedangkan waktu keberangkatan awal kereta api komuter di setiap stasiun diperoleh dari vektor eigen. Kata Kunci: aljabar max-plus, nilai eigen, vektor eigen, jadwal, kereta api komuter. vii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRACT. Scolastika Lintang Rengganis Radityani, 2016. Network Modelling and Analyze Scheduling of Commuter Train in DAOP VI Yogyakarta using Max-Plus Algebra. Thesis. Mathematics Education Study Program, Mathematics and Science Education Department, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta. Scheduling of commuter train in the Daerah Operasi VI (DAOP VI) Yogyakarta currently made based on the needs of passengers (consumers), so the synchronization process has not happened yet. The synchronization process in the transportation network is important to be done to ensure the availability of transportation means, in this case is commuter train, when the passengers of a train with a particular route want to move to other train with different route. Therefore, this research is made a scheduling design for commuter train departure in DAOP VI Yogyakarta by considering the synchronization process. One way to make it easier is to use max-plus algebra. This research aims to made a network modelling and analyze the scheduling of commuter train in DAOP VI Yogyakarta using max-plus algebra. The research method used is literature method which is supported by field data and computation process with MATLAB program. The result showed that the matrix of the network model of commuter train in DAOP VI Yogyakarta isn’t irreducible (reduced). It is suspected because not all of the line has commuter train that is ready to serve so that the line is like considered doesn’t exist. Based on the calculation result with MATLAB program obtained that the eigenvalues maximum is 𝜆(𝐴) = 786 and eigenvectors is form of real numbers, so it can be made for synchronize scheduling of commuter train. The eigenvalues stated the period of commuter train departures from each station every 786 minutes or every 13 hour 6 minutes. Then, the first departures of commuter train in each station is obtained from eigenvectors. Keyword: max-plus algebra, eigenvalues, eigenvectors, schedule, commuter train. viii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. KATA PENGANTAR Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa karena berkat penyertaan-Nya penulis dapat menyelesaikan skripsi yang berjudul “Pemodelan Jaringan dan Analisa Penjadwalan Kereta Api Komuter di DAOP VI Yogyakarta dengan Menggunakan Aljabar Max-Plus”. Skripsi ini disusun dalam rangka memenuhi salah satu syarat untuk memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma. Penulis menyadari bahwa tanpa dukungan dan bantuan dari berbagai pihak, penelitian dan penyusunan skripsi ini tidak dapat berjalan dengan baik dan lancar. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih kepada: 1.. Bapak Rohandi, Ph.D., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma.. 2.. Bapak Dr. M. Andy Rudhito, S.Pd., selaku Ketua Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas Sanata Dharma sekaligus dosen pembimbing skripsi yang telah membimbing, memberikan dukungan, kritikan, dan masukan yang membangun selama penyusunan skripsi ini.. 3.. Bapak Dr. Hongki Julie, M.Si., selaku Ketua Program Studi Pendidikan Matematika Universitas Sanata Dharma.. 4.. Ibu Dra. Haniek Sri Pratini, M.Pd. dan Bapak Antonius Yudhi Anggoro, M.Si., selaku dosen penguji skripsi yang telah memberikan kritik dan saran untuk perbaikan skripsi ini.. 5.. Bapak dan Ibu Dosen Program Studi Pendidikan Matematika Universitas Sanata Dharma yang telah membimbing dan mendidik penulis selama menuntut ilmu di Program Studi Pendidikan Matematika Universitas Sanata Dharma.. 6.. Segenap karyawan PT KAI DAOP VI Yogyakarta, yang telah membantu penulis dalam proses perizinan dan pengumpulan data-data yang diperlukan untuk penelitian dan penyusunan skripsi ini.. ix.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. 7.. Bapak Allexander Gumawang, S.Pd., M.Si., yang telah bersedia meluangkan waktunya untuk membimbing penulis selama penyusunan skripsi ini.. 8.. Orangtua penulis, Bapak Donatus Purwanto Mekomana dan Ibu Paula Elisabeth Sri Kunthi Himawan Purbabatari yang selalu mendoakan, menyemangati, dan memberikan dukungan secara moril maupun materi.. 9.. Kakak dan adik-adikku terkasih, serta Mami Tun, Mbak Galuh, dan Om Tarigan, yang juga selalu mendoakan, memberikan semangat dan dukungan untuk menyelesaikan skripsi ini.. 10. Laurensius Andi Saputra, yang selalu memberikan semangat, bantuan, dan meluangkan waktunya untuk menemani penulis saat mengumpulkan data penelitian dan selama proses penyusunan skripsi ini. 11. Sahabat-sahabatku, Arinta Yudhi Laksito, Valentina Rina, Stania Mirandai Putri, Cindy, Natalia Ika Eristaria, dan Yohana Kristin Anggraeni yang telah menemani penulis berbagi suka dan duka selama menempuh kuliah di Universitas Sanata Dharma dan selama proses penyusunan skripsi ini. 12. Teman-teman Program Studi Pendidikan Matematika Universitas Sanata Dharma angkatan 2012 yang telah bersama-sama berbagi pengalaman dan membantu penulis selama menuntut ilmu di Universitas Sanata Dharma. 13. Semua pihak yang tidak dapat disebutkan satu per satu, yang telah membantu penulis secara langsung maupun tidak langsung dalam menyelesaikan penyusunan skripsi ini. Penulis menyadari bahwa masih banyak kekurangan yang perlu ditingkatkan oleh penulis dalam penulisan skripsi ini. Oleh karena itu, penulis mengharapkan kritik dan saran yang membangun bagi sempurnanya tulisan ini. Semoga skripsi ini dapat memberikan manfaat bagi para pembaca dan pihak-pihak yang terkait.. Penulis. x.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR ISI JUDUL HALAMAN JUDUL ....................................................................................... i. HALAMAN PERSETUJUAN PEMBIMBING ........................................... ii. HALAMAN PENGESAHAN ......................................................................... iii. HALAMAN PERSEMBAHAN ..................................................................... iv. PERNYATAAN KEASLIAN KARYA ......................................................... v. LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIIAH.......................................................................................................... vi. ABSTRAK ...................................................................................................... vii ABSTRACT .................................................................................................... viii KATA PENGANTAR ..................................................................................... ix. DAFTAR ISI .................................................................................................... xi. DAFTAR TABEL .......................................................................................... xiii DAFTAR GAMBAR ...................................................................................... xiv DAFTAR NOTASI .......................................................................................... xv. BAB I PENDAHULUAN ................................................................................ 1. A. Latar Belakang Masalah ........................................................................ 1. B. Tinjauan Pustaka ................................................................................... 4. C. Rumusan Masalah ................................................................................. 8. D. Batasan Masalah.................................................................................... 9. E. Asumsi .................................................................................................. 9. F. Tujuan Penelitian .................................................................................. 9. G. Penjelasan Istilah ................................................................................... 9. H. Manfaat Penelitian ................................................................................ 10. I. Metode Penelitian.................................................................................. 11. J. Sistematika Penulisan ........................................................................... 12. BAB II LANDASAN TEORI ......................................................................... 15. A. Definisi dan Sifat dasar Aljabar Max-Plus............................................ 16. B. Matriks dan Vektor di ℝmax .................................................................. 21. Matriks di ℝmax .............................................................................. 21. 1.. xi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. Vektor di ℝmax ............................................................................... 32. C. Matriks dan Graf di ℝmax ...................................................................... 34. D. Nilai Eigen dan Vektor Eigen Matriks di ℝmax .................................... 49. BAB III PEMODELAN JARINGAN KERETA API .................................. 57. A. Sistem Transportasi Kereta Api di DAOP VI Yogyakarta ................... 57. B. Rute Pilihan ........................................................................................... 60. C. Graf Rute Pilihan................................................................................... 62. D. Sinkronisasi ........................................................................................... 70. E. Model Aljabar Max-Plus ....................................................................... 81. 2.. BAB VI ANALISIS PENJADWALAN KERETA API .............................. 100 A. Menghitung Nilai Eigen dan Vektor Eigen .......................................... 100 B. Desain Penjadwalan ............................................................................. 102 C. Pembahasan .......................................................................................... 126 BAB V PENUTUP .......................................................................................... 129 A. Kesimpulan .......................................................................................... 129 B. Saran ..................................................................................................... 129 DAFTAR PUSTAKA ..................................................................................... 131 LAMPIRAN. xii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR TABEL Tabel 2.1 Contoh Pengoperasian dalam ℝmax .................................................. 20. Tabel 3.C.1 Waktu Tempuh Kereta Api Komuter ............................................ 67. Tabel 3.E.1 Definisi Variabel Kereta Api Komuter .......................................... 81. Tabel 4.B.1 Jadwal Keberangkatan Kereta Api Komuter Rute 1: Kutoarjo – Solo Balapan PP .................................................................................... 103 Tabel 4.B.2 Jadwal Keberangkatan Kereta Api Komuter Rute 2: Yogyakarta – Solo Balapan PP ............................................................................ 107 Tabel 4.B.3 Jadwal Keberangkatan Kereta Api Komuter Rute 3: Madiun Yogyakarta PP ............................................................................... 109 Tabel 4.B.4 Jadwal Keberangkatan Kereta Api Komuter Rute 4: Solo Balapan Purwokerto PP ............................................................................... 113 Tabel 4.B.5 Jadwal Keberangkatan Kereta Api Komuter Rute 5: Purwosari – Semarang Poncol PP ..................................................................... 118 Tabel 4.B.6 Jadwal Keberangkatan Kereta Api Komuter Rute 6: Purwosari Wonogiri PP .................................................................................. 120 Tabel 4.B.7 Pilihan Desain Jadwal Keberangkatan Rute 1: Kutoarjo – Solo Balapan PP .................................................................................... 121 Tabel 4.B.8 Pilihan Desain Jadwal Keberangkatan Rute 2: Yogyakarta – Solo Balapan PP .................................................................................... 122 Tabel 4.B.9 Pilihan Desain Jadwal Keberangkatan Rute 3: Madiun – Yogyakarta PP .................................................................................................. 122 Tabel 4.B.10 Pilihan Desain Jadwal Keberangkatan Rute 4: Solo Balapan Purwokerto PP ............................................................................... 123 Tabel 4.B.11 Pilihan Desain Jadwal Keberangkatan Rute 5: Purwosari – Semarang Poncol PP ..................................................................... 123 Tabel 4.B.12 Pilihan Desain Jadwal Keberangkatan Rute 6: Purwosari – Wonogiri PP .................................................................................................. 124. xiii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR GAMBAR. Gambar 2.C.1 Graf Secara Umum .................................................................... 34. Gambar 2.C.2 Graf Berarah .............................................................................. 35. Gambar 2.C.3 Graf Berbobot ............................................................................ 37. Gambar 2.C.4 Graf Berarah Berbobot .............................................................. 38. Gambar 2.C.5 Graf Berarah G5 ............................................................................... 40. Gambar 2.C.6 Graf Berarah Berbobot Contoh 2.C.6 ........................................ 42. Gambar 2.C.7 Graf Berarah Berbobot Contoh 2.C.6 ........................................ 43. Gambar 2.C.8 Graf Berarah Berbobot Contoh 2.C.9 ........................................ 47. Gambar 2.C.9 Graf Kritis Contoh 2.C.9 ........................................................... 47. Gambar 3.A.1 Denah Lintas DAOP VI Yogyakarta ......................................... 60. Gambar 3.C.1 Rute 1 ......................................................................................... 62. Gambar 3.C.2 Rute 2 ......................................................................................... 63. Gambar 3.C.3 Rute 3 ......................................................................................... 63. Gambar 3.C.4 Rute 4 ......................................................................................... 64. Gambar 3.C.5 Rute 5 ......................................................................................... 64. Gambar 3.C.6 Rute 6 ......................................................................................... 65. Gambar 3.C.7 Graf Rute Kereta Api Komuter di DAOP VI Yogyakarta......... 66. Gambar 3.C.8 Graf Rute Sistem Kereta Api Komuter di DAOP VI Yogyakarta Pada Waktu Acuan .................................................................... xiv. 69.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR NOTASI ℝ. : himpunan bilangan real.. 𝑵. : himpunan bilangan asli.. ⨁. : operasi biner maksimum.. ⨂. : operasi biner penjumlahan.. (𝑺, +, ×) : himpunan tak kosong 𝑺 yang dilengkapi dengan dua operasi biner + dan × ∀. : semua anggota himpunan.. ∃. : beberapa (ada) anggota himpunan.. ∈. : elemen himpunan.. ℝ𝜀. : ℝ ∪ {𝜀}.. 𝜀. : elemen identitas untuk operasi ⨁ (𝜀 = −∞).. 𝑒. : elemen identitas untuk operasi ⨂ (𝑒 = 0).. ℝ𝑚𝑎𝑥. : (ℝ𝜀 , ⨁, ⨂).. ℝ𝑚×𝑛 𝑚𝑎𝑥. : himpunan matriks berukuran 𝑚 × 𝑛 dalam aljabar max-plus.. ℝ𝑛𝑚𝑎𝑥. : himpunan vektor berukuran 𝑛 × 1 dalam aljabar max-plus.. 𝐴. : matriks 𝐴. 𝑎𝑖𝑗. : elemen matriks 𝐴 pada baris ke−𝑖 dan kolom ke−𝑗.. 𝐴𝑇. : matriks 𝐴 transpose.. 𝐺(𝐴). :graf berarah dari matriks 𝐴.. 𝑉. : himpunan vertices dari graf berarah.. 𝐸. : himpunan edges dari graf berarah.. |𝜌|𝑙. : panjang suatu lintasan 𝜌.. |𝜌|𝑤. : bobot suatu lintasan 𝜌.. 𝜆. : nilai eigen mariks 𝐴.. 𝑣. : vektor eigen matriks 𝐴.. 𝑥(𝑘 − 1). : vektor waktu keberangkatan yang ke−(𝑘 − 1) dari semua kereta api komuter.. xv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB I PENDAHULUAN. A. Latar Belakang Sarana transportasi merupakan sesuatu yang berperan penting dalam membantu perpindahan manusia maupun perpindahan barang dari satu tempat ke tempat lainnya. Selain itu, sarana tranportasi berperan untuk meningkatkan keterjangkauan suatu wilayah, yaitu membantu daerah-daerah terpencil menjadi lebih maju dan berkembang. Sarana transportasi di Indonesia terdiri dari tiga jenis, yaitu sarana transportasi darat, laut, dan udara. Sarana transportasi yang digunakan pada suatu daerah, dipilih berdasarkan kondisi geografis masing-masing daerah. Oleh karena itu di daerah Sumatera dan Jawa, masyarakatnya lebih dominan menggunakan sarana transportasi darat, sedangkan di daerah lain yang kondisi geografisnya tidak memungkinkan dilalui oleh sarana transportasi darat, masyarakatnya lebih dominan menggunakan sarana transportasi laut dan udara. Sarana transportasi darat yang digunakan di Yogyakarta memiliki banyak jenis, salah satunya adalah kereta api komuter. Kereta api komuter adalah sebuah sarana transportasi kereta api penumpang yang menghubungkan antara pusat kota atau daerah perkotaan dan pinggiran kota dimana setiap harinya menarik sejumlah besar orang untuk melakukan perjalanan. Kereta api komuter disebut juga sebagai kereta api lokal. Kereta api komuter yang dioperasikan oleh Daerah Operasi VI (DAOP VI) Yogyakarta, antara lain. 1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 2. kereta api Prambanan Ekspres dengan rute Kutoarjo – Solo Balapan PP dan Yogyakarta – Solo Balapan PP, kereta api Sidomukti dengan rute Yogyakarta – Solo Balapan PP, kereta api Kalijaga dengan rute Purwosari – Semarang Poncol PP, kereta api Madiun Jaya dengan rute Madiun – Yogyakarta PP, kereta api Joglo Kerto dengan rute Solo Balapan – Purwokerto PP, dan kereta api Bathara Kresna dengan rute Purwosari – Wonogiri PP. Setiap harinya, banyak penumpang yang menggunakan transportasi kereta api komuter ini untuk melakukan perjalanan, terutama pada rute Yogyakarta – Solo Balapan PP. Penumpang tersebut terdiri dari para pelaju yang berprofesi sebagai dosen, dokter, pegawai pemerintah atau pegawai swasta, mahasiswa atau pelajar, para pedagang, dan para wisatawan baik wisatawan dalam negeri maupun wisatawan asing (http://id.m.wikipedia.org/ wiki/Kereta_api_Prambanan_Ekspres). Dengan adanya perbedaan kepadatan atau intensitas yang terjadi pada rute Yogyakarta – Solo PP dibandingkan dengan rute lainnya, mengakibatkan operator DAOP VI Yogyakarta meningkatkan jumlah perjalanan untuk rute ini menjadi 10 kali perjalanan PP setiap harinya menggunakan kereta api Prambanan Ekspres. Selain itu, untuk rute Yogyakarta – Solo Balapan PP juga dibantu oleh kereta komuter lainnya yang dioperasikan oleh DAOP VI Yogyakarta, yaitu kereta api Sidomukti (beroperasi pada hari Minggu dan hari libur), kereta api Madiun Jaya, dan kereta api Joglo Kerto. Berdasarkan paparan di atas, terlihat bahwa pembuatan jadwal keberangkatan kereta api komuter di DAOP VI Yogyakarta bergantung pada.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 3. kebutuhan. penumpang. (konsumen),. sehingga. belum. terjadi. proses. sinkronisasi. Proses sinkronisasi dalam jaringan transportasi penting untuk dilakukan guna menjamin tersedianya sarana transportasi pada saat penumpang ingin berpindah rute. Menurut Subiono (2015: 1), sinkronisasi memerlukan ketersediaan beberapa sumber pada saat yang bersamaan, dalam hal ini memerlukan ketersediaan kereta api untuk menjamin terjadinya perpindahan penumpang dari suatu kereta api dengan rute tertentu ke kereta api lainnya dengan rute yang berbeda. Melihat pentingnya sinkronisasi dalam jaringan transportasi, maka pada penelitian ini dibuat suatu desain penjadwalan untuk keberangkatan kereta api komuter di DAOP VI Yogyakarta dengan memperhatikan proses sinkronisasi. Salah satu cara untuk memudahkan penyusunan jadwal berdasarkan aturan sinkronisasi adalah menggunakan aljabar max-plus. Langkah awal dalam melakukan penelitian ini adalah mengumpulkan data yang diperlukan seperti rute, jadwal keberangkatan, dan waktu tempuh antar stasiun yang dilewati oleh kereta api komuter tersebut. Selanjutnya, dibuat aturan sinkronisasi yang menjamin terjadinya perpindahan penumpang dari suatu kereta api dengan rute tertentu ke kereta api lainnya dengan rute yang berbeda. Kemudian, dibentuk suatu model matematika berdasarkan aturan sinkronisasi tersebut. Dengan model ini, sistem dianalisis untuk membuat suatu desain penjadwalan yang memperhatikan sinkronisasi dan menentukan kesesuaiannya dengan kondisi real..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 4. Berdasarkan uraian di atas, penulis tertarik untuk membuat pemodelan jaringan dan analisa penjadwalan kereta api komuter di DAOP VI Yogyakarta dengan menggunakan aljabar max-plus.. B. Tinjauan Pustaka Penelitian yang pernah dilakukan berhubungan dengan aplikasi aljabar max-plus pada sistem jaringan kereta api, antara lain: 1.. Penelitian yang dilakukan oleh Geert Jan Olsder, Subiono, dan Michael Mc Gettrick (2000) dengan judul “On Large Scale Max-Plus Algebra Models in Railway System”. Penelitian ini membentuk sebuah model dari seluruh sistem kereta api di Belanda menggunakan aljabar max-plus. Pemodelan dilakukan dengan mempertimbangkan gabungan dari tiga jenis kereta api yang berbeda dari sistem kereta api ini, yaitu kereta antar kota (intercity train), kereta semi-cepat (sneltrein), dan kereta lambat (stoptrein). Dalam penelitian ini terdapat 61 lintasan, dimana 11 lintasan merupakan lintasan kereta antar kota (diberi nomor 1 – 11) dan sisanya yaitu 50 lintasan merupakan lintasan kereta semi-cepat dan kereta lambat. Penelitian ini menggunakan waktu acuan 11:40. Pada waktu acuan ini terdapat minimal satu kereta dan maksimal dua kereta pada 61 lintasan tersebut. Berdasarkan hasil pemodelan, didapatkan matriks 𝐴 yang berukuran 441 × 441. Setelah dilakukan proses reduksi didapatkan matriks 𝐴 yang berukuran 214 × 214, dimana matriks 𝐴 tersebut dideskripsikan. sebagai. 𝐴𝑟𝑒𝑑 .. Berdasarkan. hasil. perhitungan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 5. menggunakan algoritma power, didapatkan nilai eigen yaitu 𝜆𝐴𝑟𝑒𝑑 = 53,4 menit. Kemudian, dari hasil penelitian juga diketahui bahwa terdapat 5 sirkuit kritis dalam sistem kereta api di Belanda yang nilai sirkuit kritis tersebut sama dengan 53,4 menit. Sirkuit kritis ini adalah ukuran untuk kinerja keseluruhan sistem. Peneliti mendeskripsikan struktur dari 𝐴 𝐴12 matriks 𝐴𝑟𝑒𝑑 sebagai 𝐴𝑟𝑒𝑑 = ( 11 ), dimana matriks 𝐴11 dan 𝐴22 𝐴21 𝐴22 masing-masing mereprentasikan sub sistem dari kereta antar kota dan kereta semi-cepat serta kereta lambat. Matriks 𝐴11 merepresentasikan sub sistem dari kereta antar kota yang mempunyai ukuran matriks 67 × 67. Sedangkan, untuk matriks 𝐴22 merepresentasikan sub sistem kereta semicepat dan kereta lambat yang mempunyai ukuran matriks 147 × 147. Peneliti tidak membagi total sistem menjadi tiga sub sistem untuk kereta antar kota, kereta semi-cepat, dan kereta lambat karena beberapa kereta semi-cepat yang berangkat dari suatu stasiun ke stasiun yang lain berganti menjadi kereta lambat, begitu sebaliknya. Nilai eigen pada setiap sub matriks digunakan untuk memberikan informasi tentang seberapa cepat jaringan dapat beroperasi jika hanya dilakukan sinkronisasi untuk masing-masing kereta pada sub sistem. 2.. Penelitian yang dilakukan oleh Ahmad Afif (2015), dengan judul tesis “Aplikasi Petri Net dan Aljabar Max-Plus pada Sistem Jaringan Kereta Api di Jawa Timur”. Penelitian ini dilakukan untuk membuat penjadwalan kereta api yang tepat demi mengurangi kelemahan kereta api dalam melayani ketepatan waktu kedatangan dan keberangkatan..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 6. Pada penelitian dibuat model dan analisa jaringan kereta api di Jawa Timur menggunakan petri net dan aljabar max-plus. Pada penelitian, penentuan waktu tempuh antar stasiun didasarkan pada waktu tempuh semua kereta api yang beroperasi setiap hari dalam bentuk interval waktu, dimana penentuan batas bawah adalah waktu tempuh tercepat sedangkan batas atas adalah waktu tempuh rata-rata pada setiap lintasan. Dalam penelitian ini, jumlah kereta api yang beroperasi pada setiap lintasan ditentukan dengan menggunakan dua waktu acuan, yaitu pukul 5:00 – 8:00 WIB dan pukul 10:00 – 13:00 WIB. Waktu acuan pukul 5:00 – 8:00 WIB digunakan untuk menentukan jumlah kereta api yang beroperasi di setiap jalur menuju Surabaya dengan jadwal keberangkatan kereta api pukul 3:00 – 9:00 WIB dan waktu acuan pukul 10:00 – 13:00 WIB digunakan untuk menentukan jumlah kereta api yang beroperasi di setiap jalur meninggalkan Surabaya dengan jadwal keberangkatan kereta api pukul 9:00 – 15:00 WIB. Pada waktu acuan ini terdapat minimal satu kereta api dan maksimal empat kereta api pada setiap lintasan. Oleh karena itu, diperoleh 4 buah matriks 𝐴𝑝 , dengan 𝑝 = {1,2,3,4} dan masing-masing matriks berukuran 42 × 42. Matriks 𝐴𝑝 adalah matriks ̃ yang berkaitan dengan 𝑥(𝑘 + 1 − 𝑝). Kemudian, diperoleh matriks 𝐴. 𝐴1 𝐴2 𝐴3 𝐴4 𝐼 ℇ ℇ ℇ ̃ = 𝑚𝑎𝑥 yang berukuran 168 × 168, yaitu 𝐴 , dimana ℇ 𝐼𝑚𝑎𝑥 ℇ ℇ [ ℇ ℇ 𝐼𝑚𝑎𝑥 ℇ ] matriks 𝐴1 bersesuaian dengan keberangkatan kereta api ke-k, matriks 𝐴2 bersesuaian dengan keberangkatan kereta api ke-(𝑘 − 1), matriks 𝐴3.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 7. bersesuaian dengan keberangkatan kereta api ke-(𝑘 − 2), matriks 𝐴4 bersesuaian dengan keberangkatan kereta api ke-(𝑘 − 3), dan 𝐼𝑚𝑎𝑥 adalah matriks identitas berukuran 𝑛 × 𝑛 dengan elemen diagonalnya sama dengan 𝑒 = 0 dan elemen lainnya sama dengan 𝜀 = −∞. Sedangkan ℇ adalah matriks berukuran 𝑛 × 𝑛 yang semua elemennya sama dengan 𝜀. Penelitian ini memperoleh model dan desain jadwal keberangkatan kereta api di Jawa Timur yang stabil dan realistik (dilakukan uji coverability tree, uji kerealistikan, dan uji kestabilan model sistem jaringan kereta api di Jawa Timur) dengan periode keberangkatan setiap 𝜆 menit, yaitu 93,625 ≤ 𝜆 ≤ 101,25. Dalam penelitian ini nilai eigen dan vektor eigen dihitung menggunakan algoritma power. Berdasarkan paparan di atas, terlihat bahwa kedua penelitian tersebut memiliki persamaan yaitu terdapat minimal satu kereta api pada setiap lintasan dan tidak terdapat perbedaan intensitas pada suatu lintasan tertentu. Hal ini yang nantinya menjadi perbedaan dengan penelitian yang akan penulis lakukan. Dalam penelitian, penulis mencoba untuk memodelkan jaringan dan membuat analisa penjadwalan kereta api komuter di DAOP VI Yogyakarta menggunakan aljabar max-plus. Penelitian ini nantinya memiliki perbedaan kepadatan atau intensitas pada suatu lintasan tertentu, yaitu pada rute Yogyakarta – Solo Balapan PP. Hal ini terlihat dari penjadwalan yang telah dibuat oleh DAOP VI Yogyakarta, bahwa rute tersebut dilalui oleh beberapa.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 8. kereta api komuter, yaitu kereta api Prambanan Ekspres dengan rute Kutoarjo – Solo Balapan PP dan Yogyakarta – Solo Balapan PP, kereta api Madiun Jaya dengan rute Madiun – Yogyakarta PP, dan kereta api Joglo Kerto dengan rute Solo Balapan – Purwokerto PP. Selain itu, berdasarkan jadwal yang telah ada, terlihat pula bahwa penggunaan waktu acuan pukul berapa saja, masih menyebabkan perbedaan kerapatan di setiap lintasan. Perbedaan kerapatan yang dimaksud adalah tidak semua lintasan yang dimodelkan dilewati oleh kereta api komuter. Adanya perbedaan intensitas suatu lintasan tertentu dan perbedaan kerapatan inilah yang membedakan penelitian ini dari penelitian – penelitian sejenis sebelumnya. Oleh karena itu, penelitian ini perlu dilakukan untuk memberikan alternatif pemodelan apabila pada penelitian selanjutnya ditemukan masalah yang serupa.. C. Rumusan Masalah Berdasarkan uraian di atas, maka penulis dapat merumuskan masalah dalam penelitian ini sebagai berikut: 1.. Bagaimana pemodelan jaringan kereta api komuter di DAOP VI Yogyakarta menggunakan aljabar max-plus?. 2.. Bagaimana analisa penjadwalan kereta api komuter di DAOP VI Yogyakarta menggunakan aljabar max-plus?.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 9. D. Batasan Masalah Masalah yang dibahas dalam penelitian ini dibatasi pada pemodelan jaringan dan analisa mengenai penjadwalan kereta api komuter yang beroperasi pada hari efektif di DAOP VI Yogyakarta menggunakan aljabar max-plus.. E. Asumsi Dalam penelitian ini diberikan asumsi sebagai berikut. 1.. Kecepatan kereta api komuter dianggap tetap.. 2.. Distribusi jumlah kereta api pada setiap lintasan dianggap tetap.. 3.. Jenis kereta api komuter yang digunakan dalam model tidak dibedakan.. F. Tujuan Penelitian Adapun tujuan yang diharapkan dapat tercapai dari penelitian ini, yaitu: 1.. Menyusun model jaringan kereta api komuter di DAOP VI Yogyakarta menggunakan aljabar max-plus.. 2.. Menganalisa penjadwalan kereta api komuter di DAOP VI Yogyakarta menggunakan aljabar max-plus.. G. Penjelasan Istilah 1.. Pemodelan Jaringan Pemodelan jaringan adalah suatu usaha merumuskan persoalanpersoalan nyata, dalam hal ini adalah suatu jaringan kereta api komuter,.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 10. ke dalam persoalan matematika untuk mendapatkan penyelesaian atau solusi dari persoalan tersebut. 2.. Aljabar Max-Plus Aljabar max-plus didefinisikan sebagai himpunan semua bilangan real ℝ ∪ {−∞}, dilengkapi dengan operasi maksimum (disingkat max) yang dinotasikan dengan ⊕ (dibaca o-plus) dan operasi penjumlahan (atau plus) yang dinotasikan dengan ⊗ (dibaca o-times), serta membentuk semilapangan idempoten.. H. Manfaat Penelitian Manfaat yang diperoleh melalui hasil penelitian ini, antara lain: a.. Memberikan sumbangan pada dunia matematika dalam pemodelan jaringan transportasi kereta api dan analisa penjadwalan kereta api komuter di DAOP VI Yogyakarta dengan menggunakan aljabar maxplus.. b.. Memberikan alternatif pemodelan jaringan transportasi kereta api yang memiliki perbedaan intensitas dan kerapatan pada setiap lintasan dengan menggunakan aljabar max-plus.. c.. Memberikan rekomendasi penjadwalan bagi PT Kereta Api Indonesia (PT KAI) yang memperhatikan sinkronisasi..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 11. I.. Metode Penelitian Metode penelitian yang digunakan adalah metode studi pustaka yang didukung dengan data lapangan dan komputasi dengan program MATLAB. Adapun langkah-langkah yang dilakukan dalam penelitian ini, yaitu: 1.. Mengumpulkan dan membaca buku-buku, artikel-artikel, dan tesis-tesis untuk menjelaskan landasan teori pada Bab II, menyusun model jaringan kereta api komuter di DAOP VI Yogyakarta pada Bab III, dan menganalisa penjadwalan yang dimodelkan dengan aljabar max-plus, dengan kondisi real jadwal keberangkatan kereta api komuter di DAOP VI Yogyakarta pada bab IV.. 2.. Mengumpulkan data tentang kereta api komuter di DAOP VI Yogyakarta menggunakan instrumen penelitian berupa dokumen, yang meliputi denah lintas DAOP VI Yogyakarta, jadwal keberangkatan, dan rute yang dilewati oleh kereta api komuter. Instrumen penelitian tersebut dapat dijamin kevalidannya karena dikeluarkan langsung oleh PT KAI DAOP VI Yogyakarta.. 3.. Menentukan suatu rute pilihan dan membuat graf dari rute pilihan tersebut.. 4.. Menyusun aturan sinkronisasi untuk graf rute pilihan.. 5.. Membuat model matematika berdasarkan aturan sinkronisasi yang dibuat.. 6.. Menentukan matriks 𝐴 berdasarkan model matematika yang diperoleh.. 7.. Menentukan nilai eigen dan vektor eigen matriks 𝐴..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 12. 8.. Membuat suatu desain penjadwalan kereta api komuter di DAOP VI Yogyakarta yang telah tersinkronisasi.. 9.. Menganalisa kesesuaian antara jadwal keberangkatan yang diperoleh dengan kondisi real.. 10. Membandingkan hasil penelitian yang telah dilakukan dengan hasil penelitian sejenis yang sudah ada.. J.. Sistematika Penulisan Secara garis besar, skripsi ini dibagi menjadi lima pokok bahasan, yaitu: 1.. Bab I Pendahuluan Bab ini menjelaskan tentang latar belakang masalah, tinjauan pustaka, rumusan masalah, batasan masalah, asumsi penelitian, tujuan penelitian, manfaat penelitian, metode penelitian, dan sistematika penulisan.. 2.. Bab II Landasan Teori Bab ini menjelaskan tentang konsep dasar aljabar max-plus yang meliputi definisi aljabar max-plus, operasi dan sifat operasi aljabar maxplus, matriks dan vektor dalam aljabar max-plus, graf dalam aljabar maxplus, dan konsep nilai eigen dan vektor eigen dalam aljabar max-plus. Selain itu, dijelaskan pula mengenai eksistensi dan ketunggalan nilai eigen pada aljabar max-plus..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 13. 3.. Bab III Pemodelan Jaringan Kereta Api Bab ini menjelaskan tentang aplikasi aljabar max-plus pada penjadwalan kereta api komuter di DAOP VI Yogyakarta. Penjelasan diawali dengan memberikan gambaran mengenai sistem transportasi kereta api komuter di DAOP VI Yogyakarta secara umum. Kemudian, dibuat pemodelan jaringan penjadwalan kereta api komuter tersebut menggunakan aljabar max-plus. Pemodelan yang dimaksud meliputi penentuan rute pilihan, pembuatan graf rute pilihan, penyusunan sinkronisasi graf rute pilihan, penyusunan model matematika berdasarkan aturan sinkronisasi yang dibuat, dan penentuan matriks 𝐴 berdasarkan model matematika yang diperoleh.. 4.. Bab IV Analisa Penjadwalan Kereta Api Bab ini menganalisa matriks 𝐴 yang telah dibuat pada bab III. Analisa ini dilakukan dengan cara mengitung nilai eigen dan vektor eigen dari matriks 𝐴. Kemudian, berdasarkan nilai eigen dan vektor eigen tersebut dibuat suatu desain penjadwalan kereta api komuter di DAOP VI Yogyakarta yang telah tersinkronisasi. Desain penjawalan yang diperoleh, dianalisa kesesuaiannya dengan kondisi real. Setelah itu, dibuat suatu pembahasan untuk membandingkan hasil penelitian yang diperoleh dengan penelitian sejenis lainnya yang dipaparkan dalam tinjauan pustaka di bab I..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 14. 5.. Bab V Penutup Bab ini merupakan bab terakhir dalam skripsi ini. Bab ini menjelaskan tentang kesimpulan dari pembahasan pada Bab III dan Bab IV, serta saran-saran yang dapat digunakan untuk penelitian selanjutnya..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB II LANDASAN TEORI. Bab ini menjelaskan tentang konsep dasar aljabar max-plus yang diperlukan sebagai landasan teori untuk pemodelan jaringan dan analisa penjadwalan kereta api komuter di DAOP VI Yogyakarta. Sebelum menjelaskan konsep dasar aljabar max-plus, dijelaskan dahulu mengenai pemodelan jaringan. Menurut Iswanto (2012: 16), secara umum pemodelan matematika merupakan usaha perancangan rumusan matematika yang secara potensial menggambarkan bagaimana mendapatkan penyelesaian masalah matematika yang digeneralisasikan untuk diterapkan pada perilaku atau kejadian alam. Menurut. Anggoro (2015),. pemodelan matematika. adalah. usaha. merepresentasikan persoalan-persoalan nyata dalam persoalan matematika untuk mendapatkan solusi dari permasalahan tersebut. Berdasarkan dua definisi tersebut, dapat disimpulkan bahwa pemodelan dalam bidang matematika adalah suatu usaha merumuskan persoalan-persoalan nyata (perilaku atau kejadian alam) dalam persoalan matematika untuk mendapatkan penyelesaian atau solusi dari persoalan tersebut. Sedangkan, jaringan adalah serangkaian komponen atau simpul-simpul yang terhubung secara fungsional untuk mencapai suatu tujuan tertentu (http://kbbi.web.id/jaring), sehingga dapat didefinisikan jaringan kereta api komuter adalah serangkaian komponen atau simpul-simpul, dalam hal ini berupa stasiun, yang dihubungkan dengan kereta api komuter yang berjalan di atas rel untuk memudahkan perpindahan manusia atau barang dari satu tempat ke tempat. 15.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 16. lainnya. Berdasarkan uraian di atas, dapat ditarik kesimpulan bahwa pemodelan jaringan adalah suatu usaha merumuskan persoalan-persoalan nyata, dalam hal ini adalah suatu jaringan kereta api komuter, ke dalam persoalan matematika untuk mendapatkan penyelesaian atau solusi dari persoalan tersebut. Selanjutnya, dijelaskan mengenai konsep dasar aljabar max-plus yang meliputi definisi aljabar max-plus, operasi dan sifat operasi aljabar max-plus, matriks dan vektor dalam aljabar max-plus, graf dalam aljabar max-plus, serta nilai eigen dan vektor eigen dalam aljabar max-plus. Secara umum konsep dasar aljabar max-plus ini dirangkum dari buku yang ditulis oleh Rudhito (2016) dan Subiono (2015).. A. Definisi dan Sifat Dasar Aljabar Max-Plus Secara singkat, aljabar max-plus dapat didefinisikan sebagai himpunan semua bilangan real ℝ ∪ {−∞}, dilengkapi dengan operasi maksimum (disingkat max) yang dinotasikan dengan ⊕ (dibaca o-plus) dan operasi penjumlahan (atau plus) yang dinotasikan dengan ⊗ (dibaca o-times), serta membentuk semilapangan idempoten. Berikut akan dijelaskan lebih lanjut mengenai definisi dan sifat-sifat dasar aljabar max-plus. Pembahasan diawali dengan meninjau suatu struktur aljabar yang lebih umum. Definisi 2.A.1 Suatu semiring (𝑺, +, ×) adalah suatu himpunan tak kosong S yang dilengkapi dengan dua operasi biner + dan ×, dan memenuhi aksioma berikut:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 17. 1. (𝑺, +) adalah semigrup komutatif dengan elemen netral 0, yaitu ∀𝑥, 𝑦, 𝑧 ∈ 𝑺 memenuhi 𝑥+𝑦 =𝑦+𝑥. (Sifat komutatif). (𝑥 + 𝑦) + 𝑧 = 𝑥 + (𝑦 + 𝑧). (Sifat asosiatif). 𝑥+𝟎=𝟎+𝑥 =𝑥. (Memiliki elemen netral 0). 2. (𝑺, ×) adalah semigrup dengan elemen satuan 1, yaitu ∀𝑥, 𝑦, 𝑧 ∈ 𝑺 memenuhi (𝑥 × 𝑦) × 𝑧 = 𝑥 × (𝑦 × 𝑧). (Sifat asosiatif). 𝑥×𝟏= 𝟏×𝑥 = 𝑥. (Memiliki elemen satuan 1). 3. Elemen netral 0 merupakan elemen penyerap terhadap operasi ×, yaitu ∀𝑥 ∈ 𝑺 memenuhi 𝑥×𝟎 = 𝟎×𝑥 = 𝟎 4. Operasi × distributif terhadap +, yaitu ∀𝑥, 𝑦, 𝑧 ∈ 𝑺 berlaku (𝑥 + 𝑦) × 𝑧 = (𝑥 × 𝑧) + (𝑦 × 𝑧). (distributif kanan). 𝑥 × (𝑦 + 𝑧) = (𝑥 × 𝑦) + (𝑥 × 𝑧). (distributif kiri). Contoh 2.A.1 Diberikan ℝ𝜀 ≔ ℝ ∪ {ε} dengan ℝ adalah himpunan semua bilangan real dan 𝜀 ≔ −∞. Pada ℝ𝜀 didefinisikan operasi ⊕ dan ⊗ yaitu ∀𝑥, 𝑦 ∈ ℝ𝜀 berlaku: 𝑥 ⊕ 𝑦 ≔ max(𝑥, 𝑦). dan. Misalnya: −8 ⊕ 7 = max(−8,7) = 7 7 ⊗ −15 = 7 + (−15) = −8. 𝑥⊗𝑦 ≔𝑥+𝑦.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 18. Selanjutnya, ditunjukkan bahwa (ℝ𝜀 , ⊕, ⊗) merupakan semiring dengan elemen netral 𝜀 = −∞ dan elemen satuan 𝑒 = 0. Bukti: 1. (ℝ𝜀 , ⊕) adalah semigrup komutatif dengan elemen netral 𝜺 = −∞, yaitu ∀𝑥, 𝑦, 𝑧 ∈ ℝ𝜀 memenuhi a. 𝑥 ⊕ 𝑦 = max(𝑥, 𝑦) = max(𝑦, 𝑥) = 𝑦 ⊕ 𝑥, b. (𝑥 ⊕ 𝑦) ⊕ 𝑧 = max(max(𝑥, 𝑦), 𝑧) = max(𝑥, 𝑦, 𝑧) = max(𝑥, max(𝑦, 𝑧)) = 𝑥 ⊕ (𝑦 ⊕ 𝑧), c. 𝑥 ⊕ 𝜺 = max(𝑥, −∞) = max(−∞, 𝑥) = 𝜺 ⊕ 𝑥 = 𝑥. 2. (ℝ𝜀 , ⊗) adalah semigrup dengan elemen satuan 𝒆 = 𝟎, yaitu ∀𝑥, 𝑦, 𝑧 ∈ ℝ𝜀 memenuhi a. (𝑥 ⊗ 𝑦) ⊗ 𝑧 = (𝑥 + 𝑦) + 𝑧 = 𝑥 + (𝑦 + 𝑧) = 𝑥 ⊗ (𝑦 ⊗ 𝑧), b. 𝑥 ⊗ 𝒆 = 𝑥 + 𝟎 = 𝟎 + 𝑥 = 𝒆 ⊗ 𝑥 = 𝑥. 3. Elemen netral 𝜺 merupakan elemen penyerap terhadap operasi ⊗, yaitu ∀𝑥 ∈ ℝ𝜀 memenuhi 𝑥 ⊗ 𝜺 = 𝑥 + (−∞) = −∞ = −∞ + 𝑥 = 𝜺 ⊗ 𝑥. 4. Operasi ⊗ distributif terhadap ⊕, yaitu ∀𝑥, 𝑦, 𝑧 ∈ ℝ𝜀 berlaku a. Distributif kanan (𝑥 ⊕ y) ⊗ 𝑧 = max(𝑥, 𝑦) + 𝑧 = max(𝑥 + 𝑧, 𝑦 + 𝑧) = (𝑥 ⊗ 𝑧) ⊕ (𝑦 ⊗ 𝑧), b. Distributif kiri 𝑥 ⊗ (𝑦 ⊕ 𝑧) = 𝑥 + max(𝑦, 𝑧) = max(𝑥 + 𝑦, 𝑥 + 𝑧) = (𝑥 ⊗ 𝑦) ⊕ (𝑥 ⊗ 𝑦)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 19. Selanjutnya, dalam skripsi ini penulisan semiring (ℝ𝜀 , ⊕, ⊗) ditulis sebagai ℝmax .. Definisi 2.A.2 Suatu semiring (𝑺, +, ×) dikatakan semiring komutatif jika terhadap operasi × berlaku sifat komutatif, yaitu ∀𝑥, 𝑦 ∈ 𝑺, 𝑥 × 𝑦 = 𝑦 × 𝑥.. Definisi 2.A.3 Suatu semiring (𝑺, +, ×) dikatakan semiring idempoten jika terhadap operasi + berlaku sifat idempoten, yaitu ∀𝑥 ∈ 𝑺, 𝑥 + 𝑥 = 𝑥.. Dalam Subiono (2015: 3) istilah semiring indempoten disebut juga sebagai dioid.. Contoh 2.A.2 Semiring ℝmax merupakan suatu semiring komutatif yang sekaligus idempoten, karena untuk setiap 𝑥, 𝑦 ∈ ℝmax berlaku: 𝑥⊗𝑦 =𝑥+𝑦 =𝑦+𝑥 =𝑦⊗𝑥. dan. 𝑥 ⊕ 𝑥 = max(𝑥, 𝑥) = 𝑥. Definisi 2.A.4 Suatu semiring komutatif (𝑺, +, ×), disebut semifield jika setiap elemen tak netralnya mempunyai invers terhadap operasi ×, yaitu (∀𝑥 ∈ 𝑺\{𝟎})(∃𝑥 −1 ∈ 𝑺): 𝑥 × 𝑥 −1 = 𝑥 −1 × 𝑥 = 𝟏..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 20. Contoh 2.A.3 Semiring komutatif ℝmax merupakan semifield, karena untuk setiap 𝑥 ∈ ℝmax terdapat −𝑥, sehingga berlaku 𝑥 ⊗ (−𝑥) = 𝑥 + (−𝑥) = 𝟎. Dari Contoh 2.A.2 dan 2.A.3 di atas, terlihat bahwa ℝmax merupakan semifield idempoten. Elemen-elemen ℝmax akan disebut juga dengan skalar (Subiono, 2015: 4). Seperti dalam aljabar biasa, prioritas urutan operasi dalam ℝmax juga penting untuk diperhatikan. Apabila tidak diberikan tanda kurung, maka operasi ⊗ mempunyai prioritas yang lebih tinggi daripada operasi ⊕. Operasi lainnya dalam ℝmax yang memiliki prioritas tertinggi dibandingkan dengan operasi ⊕ dan ⊗ adalah operasi pangkat. Pangkat 𝑛 ∈ 𝐍 ∪ {0} dengan N adalah himpunan semua bilangan asli, dari elemen 𝑥 ∈ 𝑛. 𝑛. ℝmax yang dinotasikan dengan 𝑥 ⊗ . Notasi 𝑥 ⊗ kemudian didefinisikan 0. 𝑛. 𝑥 ⊗ ≔ 0 dan 𝑥 ⊗ ≔ 𝑥 ⊗ 𝑥 ⊗. sebagai berikut:. 0. 𝑛−1. , untuk 𝑛 = 1, 2, … .. 𝑛. Didefinisikan juga 𝜀 ⊗ ≔ 0 dan 𝜀 ⊗ ≔ 𝜀, untuk 𝑛 = 1, 2, … . 𝑘. Diperhatikan bahwa 𝑥 ⊗ ≔ 𝑥 ⊗ 𝑥 ⊗ … ⊗ 𝑥 = 𝑥 + 𝑥 + ⋯ + 𝑥 = 𝑘𝑥, 𝑘. 𝑘. dengan operasi perkalian pada bilangan real. Berikut diberikan beberapa contoh penggunaan operasi dalam ℝmax . Tabel 2.1 Contoh Pengoperasian dalam ℝ𝑚𝑎𝑥 ℝ𝐦𝐚𝐱. Aljabar Biasa. =. 8⊕6. max(8,6). 8. 1⊕3⊕5⊕7⊕9. max(1,3,5,7,9). 9.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 21. ɛ⊕1. max(−∞, 1). 1. 3⊗7. 3+7. 10. 3⊗ɛ. 3 + (−∞). −∞. −2 ⊗ 5. −2 + 5. 3. 12 ⊗ 𝑒. 12 + 0. 12. 4⊗ = 4 ⊗ 4. 2×4=4+4. 8. 2⊗ = 2 ⊗ 2 ⊗ 2 ⊗ 2. 4×2= 2+2+2+2. 8. 3×0= 0×3. 0. 2. 4. 3. 0. 2. 2. 𝑒 ⊗ = 3⊗. (3 ⊕ 5)⊗ = 3⊗ ⊕ 5⊗. 2. 2 × max(3,5) atau max(2 × 3, 2 × 5). 10. B. Matriks dan Vektor di ℝ𝐦𝐚𝐱 Bagian ini menjelaskan tentang matriks dan vektor dalam ℝmax , yang meliputi definisi matriks di ℝmax , operasi matriks di ℝmax beserta sifatsifatnya, dan definisi vektor di ℝmax . 1.. Matriks di ℝ𝐦𝐚𝐱 Himpunan matriks 𝑚 × 𝑛 dalam ℝmax untuk 𝑚, 𝑛 ∈ 𝐍, dimana N adalah himpunan semua bilangan asli, dinotasikan dengan ℝ𝑚×𝑛 max . Operasi ⊕ dan ⊗ yang telah dijelaskan sebelumnya dapat diperluas untuk operasioperasi dalam ℝ𝑚×𝑛 max . Seperti pada matriks real, operasi matriks atas ℝmax meliputi tiga operasi dasar, yaitu penjumlahan matriks, perkalian matriks, dan perkalian matriks dengan skalar, yang akan dijelaskan menggunakan definisi berikut..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 22. Definisi 2.B.1.1 Diberikan ℝ𝑚×𝑛 max ≔ {𝐴 = (𝑎𝑖𝑗 ) | 𝑎𝑖𝑗 ∈ ℝmax , i = 1, 2, … , m dan j = 1, 2, …, n}. 𝑚×𝑛 a. Diketahui 𝐴 ∈ ℝ𝑚×𝑛 max , 𝐵 ∈ ℝmax , didefinisikan. 𝐴 ⊕ 𝐵 adalah matriks yang unsur ke-ij-nya: (𝐴 ⊕ 𝐵)𝑖𝑗 = 𝑎𝑖𝑗 ⊕ 𝑏𝑖𝑗 untuk i = 1, 2, … , m dan j = 1, 2, …, n b. Diketahui 𝛼 ∈ ℝmax , 𝐴 ∈ ℝ𝑚×𝑛 max , didefinisikan 𝛼 ⊗ 𝐴 adalah matriks yang unsur ke-ij-nya: (𝛼 ⊗ 𝐴)𝑖𝑗 = 𝛼 ⊗ 𝑎𝑖𝑗. untuk i = 1, 2, … , m dan j = 1, 2, …, n. 𝑚×𝑛 c. Diketahui 𝐴 ∈ ℝ𝑚×𝑛 max , 𝐵 ∈ ℝmax , didefinisikan. 𝐴 ⊗ 𝐵 adalah matriks yang unsur ke-ij-nya: (𝐴 ⊗ 𝐵)𝑖𝑗 =⊕𝑝𝑘=1 𝑎𝑖𝑘 ⊗ 𝑏𝑘𝑗 untuk i = 1, 2, … , m dan j = 1, 2, …, n. Berikut diberikan contoh cara pengoperasian matriks berdasarkan definisi operasi matriks di atas. Contoh 2.B.1.1 9 7 3 a. [−4 6 ] ⊕ [2 𝜀 −8 6. 9⊕3 9 −3] = [(−4 ⊕ 2) 𝜀⊕6 7. 7⊕9 6 ⊕ (−3)] (−8) ⊕ 7. max(9,3) max(7,9) = [max(−4,2) max(6, −3)] max(𝜀, 6) max(−8,7) 9 9 = [2 6 ] 6 7.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 23. 0 b. 7 ⊗ [ 4. 7⊗0 1 6 ]=[ 7⊗4 𝜀 5. 7⊗1 7⊗ε. 7⊗6 ] 7⊗5. =[. 7+0 7+1 7+6 ] 7+4 7+𝜀 7+5. =[. 7 8 11 𝜀. 𝜀 −1 2 0 c. [ ] ⊗ [1 𝜀 1 3 4. 13 ] 12. 2 0] −3. =[. −1 ⊗ ε ⊕ 2 ⊗ 1 ⊕ 0 ⊗ 4 𝜀⊗𝜀⊕1⊗1⊕3⊗4. =[. max(−1 + ε, 2 + 1, 0 + 4) max(−1 + 2, 2 + 0, 0 + (−3)) ] max(ε + ε, 1 + 1, 3 + 4) max(ε + 2, 1 + 0, 3 + (−3)). =[. max(ε, 3, 4) max(ε, 2, 7). =[. −1 ⊗ 2 ⊕ 2 ⊗ 0 ⊕ 0 ⊗ −3 ] 𝜀 ⊗ 2 ⊕ 1 ⊗ 0 ⊕ 3 ⊗ −3. max(1, 2, −3) ] max(ε, 1, 0). 4 2 ] 7 1. Definisi 2.B.1.2 Matriks 𝐴, 𝐵 ∈ ℝ𝑚×𝑛 𝑚𝑎𝑥 dikatakan sama jika 𝑎𝑖𝑗 = 𝑏𝑖𝑗 , untuk setiap i dan j.. Selanjutnya, dijelaskan mengenai sifat-sifat operasi ⊕ dan ⊗ pada matriks. Teorema 2.B.1.1 (Rudhito, 2016) Pernyataan-pernyatan berikut berlaku untuk sebarang skalar α dan β, dan sebarang matriks A, B, dan C, asalkan operasi yang dimaksud terdefinisi. a. (𝐴 ⊕ 𝐵) ⊕ 𝐶 = 𝐴 ⊕ (𝐵 ⊕ 𝐶) b. 𝐴 ⊕ 𝐵 = 𝐵 ⊕ 𝐴 c. (𝐴 ⊗ 𝐵) ⊗ 𝐶 = 𝐴 ⊗ (𝐵 ⊗ 𝐶).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 24. d. 𝐴 ⊗ (𝐵 ⊕ 𝐶) = (𝐴 ⊗ 𝐵) ⊕ (𝐴 ⊗ 𝐶) e. (𝐴 ⊕ 𝐵) ⊗ 𝐶 = (𝐴 ⊗ 𝐶) ⊕ (𝐵 ⊗ 𝐶) f. 𝛼 ⊗ 𝐴 = 𝐴 ⊗ 𝛼 g. 𝛼 ⊗ (𝛽 ⊗ 𝐴) = (𝛼 ⊗ 𝛽) ⊗ 𝐴 h. 𝛼 ⊗ (𝐴 ⊗ 𝐵) = (𝛼 ⊗ 𝐴) ⊗ 𝐵 = 𝐴 ⊗ (𝛼 ⊗ 𝐵) i. (𝛼 ⊕ 𝛽) ⊗ 𝐴 = (𝛼 ⊗ 𝐴) ⊕ (𝛽 ⊗ 𝐴) j. 𝛼 ⊗ (𝐴 ⊕ 𝐵) = (𝛼 ⊗ 𝐴) ⊕ (𝛼 ⊗ 𝐵) k. 𝐴 ⊕ 𝐴 = 𝐴. Berikut ini diberikan pembuktian untuk sifat c dan d, sedangkan untuk pembuktian sifat yang lain langsung mengikuti definisi operasi dan sifat-sifat operasi pada ℝ𝐦𝐚𝐱 . a. Akan dibuktikan bahwa: (𝐴 ⊗ 𝐵) ⊗ 𝐶 = 𝐴 ⊗ (𝐵 ⊗ 𝐶) Bukti: 𝑝×𝑟 𝑟×𝑛 Ambil sebarang matriks 𝐴 ∈ ℝ𝑚×𝑝 𝑚𝑎𝑥 , 𝐵 ∈ ℝ𝑚𝑎𝑥 , 𝐶 ∈ ℝ𝑚𝑎𝑥 .. Untuk setiap elemen baris ke-i dan kolom ke-j matriks (𝐴 ⊗ 𝐵) ⊗ 𝐶, berlaku ((𝐴 ⊗ 𝐵) ⊗ 𝐶)𝑖𝑗 = ⊕𝑟𝑘=1 (⊕𝑝𝑘=1 𝑎𝑖𝑙 ⊗ 𝑏𝑙𝑘 ) ⊗ 𝑐𝑘𝑗 = ⊕𝑟𝑘=1 ⊕𝑝𝑘=1 𝑎𝑖𝑙 ⊗ 𝑏𝑙𝑘 ⊗ 𝑐𝑘𝑗 = ⊕𝑟𝑘=1 𝑎𝑖𝑙 ⊗ (⊕𝑝𝑘=1 𝑏𝑙𝑘 ⊗ 𝑐𝑘𝑗 ) = (𝐴 ⊗ (𝐵 ⊗ 𝐶))𝑖𝑗 ; untuk 𝑖 ∈ 𝑚 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa (𝐴 ⊗ 𝐵) ⊗ 𝐶 = 𝐴 ⊗ (𝐵 ⊗ 𝐶)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 25. b. Akan dibuktikan bahwa: 𝐴 ⊗ (𝐵 ⊕ 𝐶) = (𝐴 ⊗ 𝐵) ⊕ (𝐴 ⊗ 𝐶) Bukti: 𝑝×𝑛 Ambil sebarang matriks 𝐴 ∈ ℝ𝑚×𝑝 𝑚𝑎𝑥 , 𝐵, 𝐶 ∈ ℝ𝑚𝑎𝑥 .. Untuk setiap elemen baris ke-i dan kolom ke-j matriks 𝐴 ⊗ (𝐵 ⊕ 𝐶), berlaku (𝐴 ⊗ (𝐵 ⊕ 𝐶))𝑖𝑗 = ⊕𝑝𝑘=1 𝑎𝑖𝑘 ⊗ (𝑏𝑘𝑗 ⊕ 𝑐𝑘𝑗 ) = ⊕𝑝𝑘=1 (𝑎𝑖𝑘 ⊗ 𝑏𝑘𝑗 ⊕ 𝑎𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) = (⊕𝑝𝑘=1 𝑎𝑖𝑘 ⊗ 𝑏𝑘𝑗 ) ⊕ (⊕𝑝𝑘=1 𝑎𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) = (𝐴 ⊗ 𝐵)𝑖𝑗 ⊕ (𝐴 ⊗ 𝐶)𝑖𝑗 ; untuk 𝑖 ∈ 𝑚 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa 𝐴 ⊗ (𝐵 ⊕ 𝐶) = (𝐴 ⊗ 𝐵) ⊕ (𝐴 ⊗ 𝐶).. Definisi 2.B.1.3 Transpose matriks dalam ℝ𝑚𝑎𝑥 dinotasikan dengan 𝐴𝑇 dan didefinisikan sama dengan matriks transpose dalam aljabar biasa, yaitu [𝐴𝑇 ]𝑖𝑗 = [𝐴]𝑗𝑖. Definisi 2.B.1.4 (Rudhito, 2016) 0 𝑗𝑖𝑘𝑎 𝑖 = 𝑗 Didefinisikan matriks 𝐸 ∈ ℝ𝑛×𝑛 𝑚𝑎𝑥 dengan (𝐸)𝑖𝑗 ∶= { ɛ 𝑗𝑖𝑘𝑎 𝑖 ≠ 𝑗 Didefinisikan matriks Ԑ ∈ ℝ𝑚×𝑛 𝑚𝑎𝑥 dengan (Ԑ)𝑖𝑗 ∶= ɛ untuk setiap baris kei dan kolom ke-j..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 26. Contoh 2.B.1.2 (ℝ𝑛×𝑛 max , ⊕, ⊗) merupakan semiring idempoten dengan elemen netral adalah matriks Ԑ dan elemen satuan adalah matriks 𝐸. Matriks 𝐸 disebut juga sebagai matriks identitas max-plus dan matriks Ԑ disebut sebagai matriks nol max-plus.. Selanjutnya, ditunjukkan bahwa (ℝ𝑛×𝑛 max , ⊕, ⊗) merupakan semiring dengan elemen netral adalah matriks Ԑ dan elemen satuan adalah matriks 𝐸. Bukti: 1.. (ℝ𝑛×𝑛 max , ⊕) adalah semigrup komutatif dengan elemen netral matriks Ԑ, yaitu untuk sebarang 𝐴, 𝐵, 𝐶 ∈ ℝ𝑛×𝑛 max memenuhi a.. Sifat komutatif Untuk setiap elemen baris ke-i dan kolom ke-j matriks 𝐴 ⊕ 𝐵, berlaku (𝐴 ⊕ 𝐵)𝑖𝑗 = max(𝑎𝑖𝑗 , 𝑏𝑖𝑗 ) = max(𝑏𝑖𝑗 , 𝑎𝑖𝑗 ) = (𝐵 ⊕ 𝐴)𝑖𝑗 ; untuk 𝑖 ∈ 𝑛 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa (𝐴 ⊕ 𝐵) = (𝐵 ⊕ 𝐴).. b.. Sifat asosiatif Untuk setiap elemen baris ke-i dan kolom ke-j matriks (𝐴 ⊕ 𝐵) ⊕ 𝐶, berlaku ((𝐴 ⊕ 𝐵) ⊕ 𝐶)𝑖𝑗 = max(max(𝑎𝑖𝑗 , 𝑏𝑖𝑗 ), 𝑐𝑖𝑗 ) = max(𝑎𝑖𝑗 , 𝑏𝑖𝑗 , 𝑐𝑖𝑗 ).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 27. = max(𝑎𝑖𝑗 , max(𝑏𝑖𝑗 , 𝑐𝑖𝑗 )) = (𝐴 ⊕ (𝐵 ⊕ 𝐶))𝑖𝑗 ; untuk 𝑖 ∈ 𝑛 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa (𝐴 ⊕ 𝐵) ⊕ 𝐶 = 𝐴 ⊕ (𝐵 ⊕ 𝐶). c.. Memiliki elemen netral matriks Ԑ(𝑛, 𝑛) Untuk setiap elemen baris ke-i dan kolom ke-j matriks 𝐴 ⊕ Ԑ, berlaku (A ⊕ Ԑ)𝑖𝑗 = max(𝑎𝑖𝑗 , Ԑ𝑖𝑗 ) = max(Ԑ𝑖𝑗 , 𝑎𝑖𝑗 ) = (Ԑ ⊕ 𝐴)𝑖𝑗 = 𝐴; untuk 𝑖 ∈ 𝑛 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa A ⊕ Ԑ = Ԑ ⊕ 𝐴 = 𝐴.. 2.. (ℝ𝑛×𝑛 max , ⊗) adalah semigrup dengan elemen satuan matriks 𝐸, yaitu untuk sebarang 𝐴, 𝐵, 𝐶 ∈ ℝ𝑛×𝑛 max memenuhi a.. Sifat asosiatif Untuk setiap elemen baris ke-i dan kolom ke-j matriks (𝐴 ⊗ 𝐵) ⊗ 𝐶, berlaku ((𝐴 ⊗ 𝐵) ⊗ 𝐶)𝑖𝑗 = ⊕𝑛𝑘=1 (⊕𝑛𝑘=1 𝑎𝑖𝑙 ⊗ 𝑏𝑙𝑘 ) ⊗ 𝑐𝑘𝑗 = ⊕𝑛𝑘=1 ⊕𝑛𝑘=1 𝑎𝑖𝑙 ⊗ 𝑏𝑙𝑘 ⊗ 𝑐𝑘𝑗 = ⊕𝑛𝑘=1 𝑎𝑖𝑙 ⊗ (⊕𝑛𝑘=1 𝑏𝑙𝑘 ⊗ 𝑐𝑘𝑗 ) = (𝐴 ⊗ (𝐵 ⊗ 𝐶))𝑖𝑗 ; untuk 𝑖 ∈ 𝑛 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa (𝐴 ⊗ 𝐵) ⊗ 𝐶 = 𝐴 ⊗ (𝐵 ⊗ 𝐶).. b.. Memiliki elemen satuan matriks 𝐸(𝑛, 𝑛) Untuk setiap elemen baris ke-i dan kolom ke-j matriks 𝐴 ⊗ 𝐸, berlaku.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 28. (A ⊗ 𝐸)𝑖𝑗 =⊕𝑛𝑘=1 𝑎𝑖𝑘 ⊗ 𝐸𝑘𝑗 =⊕𝑛𝑘=1 𝐸𝑖𝑘 ⊗ 𝑎𝑘𝑗 = (𝐸 ⊗ 𝐴)𝑖𝑗 = 𝐴; untuk 𝑖 ∈ 𝑛 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa A ⊗ 𝐸 = 𝐸 ⊗ 𝐴 = 𝐴. 3.. Elemen netral matriks Ԑ merupakan elemen penyerap terhadap operasi ⊗, yaitu untuk sebarang 𝐴 ∈ ℝ𝑛×𝑛 max memenuhi (A ⊗ Ԑ )𝑖𝑗 =⊕𝑛𝑘=1 𝑎𝑖𝑘 ⊗ Ԑ 𝑘𝑗 =⊕𝑛𝑘=1 Ԑ 𝑖𝑘 ⊗ 𝑎𝑘𝑗 = (Ԑ ⊗ 𝐴)𝑖𝑗 = Ԑ ; untuk 𝑖 ∈ 𝑛 dan 𝑗 ∈ 𝑛 Jadi terbukti bahwa A ⊗ Ԑ = Ԑ ⊗ 𝐴 = Ԑ.. 4.. Operasi ⊗ distributif terhadap ⊕, yaitu untuk sebarang 𝐴, 𝐵, 𝐶 ∈ ℝ𝑛×𝑛 max berlaku a.. Distributif kanan Untuk setiap elemen baris ke-i dan kolom ke-j matriks (𝐴 ⊕ 𝐵) ⊗ 𝐶, berlaku ((𝐴 ⊕ 𝐵) ⊗ 𝐶)𝑖𝑗 = ⊕𝑛𝑘=1 (𝑎𝑖𝑘 ⊕ 𝑏𝑖𝑘 ) ⊗ 𝑐𝑘𝑗 = ⊕𝑛𝑘=1 (𝑎𝑖𝑘 ⊗ 𝑐𝑘𝑗 ⊕ 𝑏𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) = (⊕𝑛𝑘=1 𝑎𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) ⊕ (⊕𝑛𝑘=1 𝑏𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) = (𝐴 ⊗ 𝐶)𝑖𝑗 ⊕ (𝐵 ⊗ 𝐶)𝑖𝑗 ; untuk 𝑖 ∈ 𝑛 dan 𝑗∈𝑛.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 29. Jadi, (𝐴 ⊕ 𝐵) ⊗ 𝐶 = (𝐴 ⊗ 𝐶) ⊕ (𝐵 ⊗ 𝐶). b.. Distributif kiri Untuk setiap elemen baris ke-i dan kolom ke-j matriks 𝐴 ⊗ (𝐵 ⊕ 𝐶), berlaku (𝐴 ⊗ (𝐵 ⊕ 𝐶))𝑖𝑗 = ⊕𝑛𝑘=1 𝑎𝑖𝑘 ⊗ (𝑏𝑘𝑗 ⊕ 𝑐𝑘𝑗 ) = ⊕𝑛𝑘=1 (𝑎𝑖𝑘 ⊗ 𝑏𝑘𝑗 ⊕ 𝑎𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) = (⊕𝑛𝑘=1 𝑎𝑖𝑘 ⊗ 𝑏𝑘𝑗 ) ⊕ (⊕𝑛𝑘=1 𝑎𝑖𝑘 ⊗ 𝑐𝑘𝑗 ) = (𝐴 ⊗ 𝐵)𝑖𝑗 ⊕ (𝐴 ⊗ 𝐶)𝑖𝑗 ; untuk 𝑖 ∈ 𝑛 dan 𝑗∈𝑛 Jadi, 𝐴 ⊗ (𝐵 ⊕ 𝐶) = (𝐴 ⊗ 𝐵) ⊕ (𝐴 ⊗ 𝐶).. Kemudian, ditunjukkan bahwa (ℝ𝑛×𝑛 max , ⊕, ⊗) merupakan semiring idempoten. Bukti: Semiring ℝ𝑛×𝑛 max merupakan suatu semiring idempoten karena untuk sebarang 𝐴 ∈ ℝ𝑛×𝑛 max , yaitu untuk setiap elemen baris ke-i dan kolom ke-j matriks 𝐴 ⊕ 𝐴, berlaku: (𝐴 ⊕ 𝐴)𝑖𝑗 = max(𝑎𝑖𝑗 , 𝑎𝑖𝑗 ) = (𝐴)𝑖𝑗 Jadi terbukti bahwa semiring ℝ𝑛×𝑛 max , terhadap operasi ⊕, berlaku sifat idempoten, yaitu 𝐴 ⊕ 𝐴 = 𝐴, sehingga (ℝ𝑛×𝑛 max , ⊕, ⊗) disebut sebagai semiring idempoten (Definisi 2.A.3)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 30. (ℝ𝑛×𝑛 max , ⊕, ⊗) bukan semiring komutatif (Rudhito, 2016), karena terdapat matriks 𝐴 = [ 𝐴⊗B=[. 0 2 0 ] dan 𝐵 = [ 1 ɛ ɛ. 1 ] dengan 4. max(0, ε) max(1,6) 0 2 0 1 0 6 ]⊗[ ]=[ ]=[ ] max(1, ɛ) max(2, ɛ) 1 ɛ ɛ 4 1 2. 𝐵⊗A=[. max(0,2) 0 1 0 2 ]⊗[ ]=[ max(ɛ, 5) ɛ 4 1 ɛ. max(2, ɛ) 2 2 ]=[ ] max(ɛ, ɛ) 5 ɛ. Sehingga terlihat bahwa 𝐴 ⊗ B ≠ 𝐵 ⊗ A. Jadi dapat disimpulkan bahwa sifat komutatif pada operasi matriks hanya berlaku untuk operasi ⊕ dan tidak berlaku untuk operasi ⊗.. Definisi 2.B.1.5 Pangkat 𝑛 ∈ 𝑵 ∪ {0} dengan N adalah himpunan semua 𝑘. ⊗ bilangan asli, dari matriks 𝐴 ∈ ℝ𝑛×𝑛 . Notasi max dinotasikan dengan 𝐴 𝑛. 𝐴⊗ kemudian didefinisikan sebagai berikut: 0. 𝑘. 𝐴⊗ ≔ 𝐸𝑛 dan 𝐴⊗ ≔ 𝐴 ⊗ 𝐴⊗. 𝑘−1. , untuk 𝑘 = 1, 2, … .. Berdasarkan definisi tersebut, maka dapat dijelaskan unsur ke-st matriks berpangkat, sebagai berikut: 2. Unsur ke-st matriks 𝐴⊗ adalah 2. (𝐴⊗ )𝑠𝑡 = (𝐴 ⊗ 𝐴)𝑠𝑡 = (𝑎𝑠1 ⊗ 𝑎1𝑡 ) ⊕ (𝑎𝑠2 ⊗ 𝑎2𝑡 ) ⊕ … ⊕ (𝑎𝑠𝑛 ⊗ 𝑎𝑛𝑡 ) = ⊕𝑛𝑖1 =1 (𝑎𝑠,𝑖1 ⊗ 𝑎𝑖1 ,𝑡 ) = max1≤𝑖1 ≤𝑛 (𝑎𝑠,𝑖1 + 𝑎𝑖1 ,𝑡 ) 3. Unsur ke-st matriks 𝐴⊗ adalah 3. 2. (𝐴⊗ )𝑠𝑡 = (𝐴 ⊗ 𝐴⊗ )𝑠𝑡.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 31. = ⊕𝑛𝑖2 =1 (𝑎𝑠,𝑖2 (⊕𝑛𝑖1 =1 (𝑎𝑖2 ,𝑖1 ⊗ 𝑎𝑖1 ,𝑡 ))) = ⊕𝑛𝑖2=1 (⊕𝑛𝑖1 =1 (𝑎𝑠,𝑖2 ⊗ 𝑎𝑖2 ,𝑖1 ⊗ 𝑎𝑖1 ,𝑡 )) = max1≤𝑖1 ,𝑖2 ≤𝑛 (𝑎𝑠,𝑖2 + 𝑎𝑖2 ,𝑖1 + 𝑎𝑖1 ,𝑡 ) 𝑘. Secara umum, unsur ke-st matriks 𝐴⊗ adalah 𝑘. (𝐴⊗ ) = ⊕𝑛𝑖𝑘−1 =1 (𝑎𝑠,𝑖𝑘−1 … (⊕𝑛𝑖1 =1 (𝑎𝑖2 ,𝑖1 ⊗ 𝑎𝑖1 ,𝑡 ))) 𝑠𝑡. = ⊕𝑛𝑖2=1 … (⊕𝑛𝑖1 =1 (𝑎𝑠,𝑖𝑘−1 ⊗ … ⊗ 𝑎𝑖2 ,𝑖1 ⊗ 𝑎𝑖1 ,𝑡 )) = max1≤𝑖1 ,𝑖2 ,…,𝑖𝑘−1 ≤𝑛 (𝑎𝑠,𝑖𝑘−1 + ⋯ + 𝑎𝑖2 ,𝑖1 + 𝑎𝑖1 ,𝑡 ) Berdasarkan persamaan terakhir, untuk sebarang 𝛼 ∈ ℝmax dan 𝐴 ∈ ℝ𝑛×𝑛 max 𝑘. unsur ke-st (𝛼 ⊕ 𝐴)⊗ adalah 𝑘. ((𝛼 ⊕ 𝐴)⊗ ). 𝑠𝑡. = max1≤𝑖1 ,𝑖2 ,…,𝑖𝑘−1 ≤𝑛 ((𝛼 + 𝑎𝑠,𝑖𝑘−1 ) + ⋯ + (𝛼 + 𝑎𝑖2 ,𝑖1 ) + (𝛼 + 𝑎𝑖1 ,𝑡 )) = (𝛼 + 𝛼 + ⋯ + 𝛼) + max1≤𝑖1 ,𝑖2,…,𝑖𝑘−1 ≤𝑛 (𝑎𝑠,𝑖𝑘−1 + ⋯ + 𝑎𝑖2 ,𝑖1 + 𝑎𝑖1 ,𝑡 ) 𝑘 𝑘. 𝑘. = 𝛼 ⊗ ⊗ (𝐴⊗ ) ; untuk 𝑘 = 1, 2, … . 𝑠𝑡. Jadi, untuk sebarang skalar 𝛼 ∈ ℝmax dan 𝐴 ∈ ℝ𝑛×𝑛 max berlaku : 𝑘. 𝑘. 𝑘. (𝛼 ⊕ 𝐴)⊗ = 𝛼 ⊗ ⊗ 𝐴⊗ ; untuk 𝑘 = 1, 2, … .. 𝑛 Untuk sebarang 𝐴 ∈ ℝ𝑛×𝑛 max didefinisikan 𝑡𝑟𝑎𝑐𝑒(𝐴) ≔⊕𝑖=1 𝑎𝑖𝑖 ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 32. Contoh 2.B.1.3 1 0 Diberikan 𝐴 = [2 3 ɛ ɛ. −2 ɛ ] 0. maka, 𝐴. ⊗2. 𝐴. ⊗3. 1 = 𝐴 ⊗ 𝐴 = [2 ɛ =𝐴⊗𝐴. ⊗2. 0 −2 1 0 −2 2 3 −1 3 ɛ ] ⊗ [2 3 ɛ ] = [5 6 0 ] ɛ 0 ɛ ɛ 0 ɛ ɛ 0. 1 = [2 ɛ. 0 −2 2 3 3 ɛ ] ⊗ [5 6 ɛ 0 ɛ ɛ. −1 5 6 0 ] = [8 9 0 ɛ ɛ. 0 3] 0. 𝑡𝑟𝑎𝑐𝑒(𝐴) =⊕𝑛𝑖=1 𝑎𝑖𝑖 = max(1,3,0) = 3 2. 𝑡𝑟𝑎𝑐𝑒(𝐴⊗ ) = max(2,6,0) = 6 3. 𝑡𝑟𝑎𝑐𝑒(𝐴⊗ ) = max(5,9,0) = 9 2.. Vektor di ℝ𝐦𝐚𝐱 Bagian ini membahas semimodul atas ℝmax yang melandasi pembahasan konsep vektor di ℝmax .. Definisi 2.B.2.1 Diberikan semiring komutatif (𝑺, +, ×) dengan elemen netral 0 dan elemen identitas 1. Semimodul M atas S adalah semigrup komutatif (M, +) bersama operasi perkalian skalar • : 𝑺 × 𝑴 → 𝑴, yang dituliskan dengan (𝛼, 𝑥) ↦ 𝛼 • 𝑥, yang memenuhi aksioma berikut: ∀𝛼, 𝛽 𝜖 𝑺 dan ∀𝑥, 𝑦 ∈ 𝑴 berlaku: a. 𝛼 • (𝑥 + 𝑦) = 𝛼 • 𝑥 + 𝛼 • 𝑦 b. (𝛼 + 𝛽) • 𝑥 = 𝛼 • 𝑥 + 𝛽 • 𝑥 c. 𝛼 • (𝛽 • 𝑥) = (𝛼 • 𝛽) • 𝑥.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 33. d. 1 • 𝑥 = 𝑥 e. 0 • 𝑥 = 0 Suatu elemen dalam semimodul disebut vektor.. Contoh 2.B.2.1 𝑛×1 ℝ𝑛×1 𝑚𝑎𝑥 adalah semimodul atas ℝmax . Selanjutnya, ℝ𝑚𝑎𝑥 cukup ditulis. sebagai ℝ𝑛𝑚𝑎𝑥 , dimana ℝ𝑛𝑚𝑎𝑥 ≔ {𝑥 = [𝑥1 , 𝑥2 , … , 𝑥𝑛 ]𝑇 |𝑥𝑖 ∈ ℝmax , 𝑖 = 1, 2, … , 𝑛} Untuk setiap 𝑥, 𝑦 ∈ ℝ𝑛𝑚𝑎𝑥 dan untuk setiap 𝛼 ∈ ℝmax didefinisikan operasi ⊕ dengan 𝑥 ⊕ y = [𝑥1 ⊕ 𝑦1 , 𝑥2 ⊕ 𝑦2 , … , 𝑥𝑛 ⊕ 𝑦𝑛 ]𝑇 dan operasi perkalian skalar • dengan 𝛼 • 𝑥 = 𝛼 ⊗ 𝑥 = [𝛼 ⊗ 𝑥1 , 𝛼 ⊗ 𝑥2 , … , 𝛼 ⊗ 𝑥𝑛 ]𝑇 .. Berdasarkan Teorema 2.B.1.1 a dan b, maka dapat disimpulkan bahwa (ℝ𝑛𝑚𝑎𝑥 ,⊕) adalah semigrup komutatif dengan elemen netral ɛ = [ɛ, ɛ, … , ɛ]𝑇 . Kemudian, berdasarkan Teorema 2.B.1.1 j, i, dan g, maka dapat disimpulkan pula bahwa ℝ𝑛𝑚𝑎𝑥 adalah semimodul atas ℝmax . Diberikan vektor-vektor 𝑥1 , 𝑥2 , … , 𝑥𝑛 di dalam semimodul M dan skalar-skalar 𝛼1 , 𝛼2 , … , 𝛼𝑛 di dalam semiring komutatif S. Didefinisikan kombinasi linear dari vektor-vektor 𝑥1 , 𝑥2 , … , 𝑥𝑛 adalah suatu bentuk aljabar 𝛼1 • 𝑥1 + 𝛼2 • 𝑥2 + … + 𝛼𝑛 • 𝑥𝑛 ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 34. C. Matriks dan Graf di ℝ𝐦𝐚𝐱 Bagian ini memberikan penjelasan secara singkat mengenai teori graf dan interpretasi beberapa operasi dan konsep dasar aljabar max-plus dalam teori graf. Konsep ini menjadi dasar pembahasan nilai eigen dan vektor eigen dalam aljabar max-plus. Definisi 2.C.1 Suatu graf 𝐺 didefinisikan sebagai pasangan himpunan (𝑉, 𝐸) dengan 𝑉 adalah suatu himpunan berhingga tak kosong yang anggotanya disebut titik (vertices) dan 𝐸 adalah suatu himpunan pasangan (tak terurut dan boleh merupakan himpunan kosong) titik-titik yang anggotanya disebut rusuk (edges).. Contoh 2.C.1 Perhatikan graf 𝐺1 di bawah ini. 1 2. 3. Gambar 2.C.1 Graf Secara Umum Graf pada Gambar 2.C.1 di atas adalah graf 𝐺1 = (𝑉1 , 𝐸1 ), dengan 𝑉1 = {1,2,3} dan 𝐸1 = {(1,2), (1,3), (2,3)}..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 35. Definisi 2.C.2 Suatu graf berarah 𝐺 didefinisikan sebagai pasangan himpunan (𝑉, 𝐷) dengan 𝑉 adalah suatu himpunan berhingga tak kosong yang anggotanya disebut titik (vertices) dan 𝐷 adalah suatu himpunan pasangan terurut titik-titik yang anggotanya disebut busur (arc).. Definisi 2.C.3 Untuk busur (𝑖, 𝑗) ∈ 𝐷, i disebut sebagai titik awal busur dan j disebut sebagai titik akhir busur. Suatu loop adalah busur (𝑖, 𝑖) ∈ 𝐷.. Kedua definisi di atas menjelaskan bahwa graf berarah 𝐺 adalah graf yang setiap busurnya mempunyai arah. Secara geometri dinyatakan suatu anak panah yang arahnya dari 𝑖 ke 𝑗.. Contoh 2.C.2 Perhatikan graf 𝐺2 di bawah ini. 1 2. 3. Gambar 2.C.2 Graf Berarah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 36. Graf pada Gambar 2.C.2 di atas adalah graf berarah 𝐺2 = (𝑉2 , 𝐷1 ), dengan 𝑉2 = {1,2,3} dan 𝐷1 = {(1,2), (2,3), (3,1)}, yang merupakan himpunan pasangan terurut. Berdasarkan Definisi 2.C.1 dan Definisi 2.C.2, serta Contoh 2.C.1 dan Contoh 2.C.2 dapat dijelaskan cara menggambar suatu graf adalah sebagai berikut: jika suatu graf disajikan dalam bentuk gambar, maka titik digambarkan sebagai noktah yang diberi label dengan nama titik yang diwakilinya. Rusuk digambarkan sebagai kurva atau ruas garis yang menghubungkan noktahnoktah yang bersesuaian pada rusuk atau loop. Sedangkan busur digambarkan sebagai kurva atau ruas garis berarah yang menghubungkan noktah-noktah yang bersesuaian dengan titik awal dan titik akhir busur, dengan tanda panah yang ujungnya menandakan arah busur.. Definisi 2.C.4 Suatu graf berbobot 𝐺 adalah graf yang memiliki bobot pada setiap rusuknya, dinotasikan dengan 𝑤(𝑗, 𝑖) ∈ ℝ, untuk (𝑗, 𝑖) ∈ 𝐸, dimana 𝐸 adalah suatu himpunan pasangan (tak terurut dan boleh merupakan himpunan kosong) titik-titik yang anggotanya disebut rusuk (edges), 𝑗 dan 𝑖 adalah titiktitik (vertices)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 37. Contoh 2.C.3 Perhatikan graf 𝐺3 di bawah ini a 1 2. c b. 3. Gambar 2.C.3 Graf Berbobot Graf pada Gambar 2.C.3 di atas adalah graf berbobot 𝐺3 = (𝑉3 , 𝐸2 ), dengan 𝑉3 = {1,2,3} dan 𝐸2 = {(1,2), (1,3), (2,3)}, serta bobot-bobot dari setiap rusuknya yang dinyatakan dengan 𝑤(1,2) = 𝑎, 𝑤(1,3) = 𝑏, dan 𝑤(2,3) = 𝑐, dimana 𝑎, 𝑏, 𝑐 ∈ ℝ.. Definisi 2.C.5 Suatu graf berarah 𝐺 disebut berbobot jika setiap busur (𝑗, 𝑖) ∈ 𝐷 dapat dikawankan dengan suatu bilangan real 𝑎𝑖𝑗 ≠ ɛ yang merupakan bobot busur (𝑗, 𝑖), dinotasikan. dengan 𝑤(𝑗, 𝑖), dimana 𝐷 adalah suatu. himpunan pasangan terurut titik-titik yang anggotanya disebut busur (arc), 𝑗 adalah titik awal busur, dan 𝑖 adalah titik akhir busur..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 38. Contoh 2.C.4 Perhatikan graf 𝐺4 di bawah ini a 1 2. c b. 3. Gambar 2.C.4 Graf Berarah Berbobot Graf pada Gambar 2.C.4 di atas adalah graf berarah 𝐺4 = (𝑉4 , 𝐷2 ), dengan 𝑉4 = {1,2,3} dan 𝐷2 = {(1,2), (2,3), (3,1)}, serta bobot-bobot dari setiap busurnya adalah 𝑤(1,2) = 𝑎; 𝑤(2,3) = 𝑏; 𝑤(3,1) = 𝑐.. Selanjutnya, dijelaskan tentang definisi lintasan dalam graf dan beberapa konsep yang berhubungan dengan lintasan, untuk mendefinisikan graf terhubung kuat.. Definisi 2.C.6 Diberikan 𝐺 = (𝑉, 𝐷) yang merupakan graf berarah dengan 𝑉 = {1, 2, … , 𝑛}. Suatu lintasan 𝜌 dalam 𝐺 adalah suatu barisan berhingga busur (𝑖1 , 𝑖2 ), (𝑖2 , 𝑖3 ), … , (𝑖𝑙−1 , 𝑖𝑙 ) dengan (𝑖𝑘 , 𝑖𝑘+1 ) ∈ 𝐷 untuk suatu 𝑙 ∈ 𝑵 dan 𝑘 = 1,2, … , 𝑙 − 1..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 39. Lintasan 𝜌 yang dimaksudkan dalam Definisi 2.C.6 dapat direpresentasikan dengan 𝑖1 → 𝑖2 → ⋯ → 𝑖𝑙 . Titik 𝑖1 disebut sebagai titik awal lintasan dan titik 𝑖𝑙 disebut sebagai titik akhir lintasan.. Definisi 2.C.7 Untuk suatu lintasan 𝜌 pada suatu graf berarah berbobot 𝐺, panjang lintasan didefinisikan sebagai banyaknya busur yang menyusun 𝜌 dan dinotasikan dengan |𝜌|𝑙 .. Definisi 2.C.8 (Rudhito, 2016) Suatu lintasan disebut sirkuit jika titik awal dan titik akhirnya sama. Sirkuit elementer adalah sirkuit yang titik-titiknya muncul tidak lebih dari sekali, kecuali titik awal yang muncul tepat dua kali.. Definisi. 2.C.9. Suatu. graf. berarah. 𝐺 = (𝑉, 𝐷). dengan. 𝑉=. {1,2, … , 𝑛} dikatakan terhubung kuat jika untuk setiap 𝑖, 𝑗 ∈ 𝑉, 𝑖 ≠ 𝑗 terdapat suatu lintasan dari i ke j.. Definisi 2.C.10 (Rudhito, 2016) Suatu graf yang memuat sirkuit disebut graf siklik, sedangkan suatu graf yang tidak memuat sirkuit disebut graf taksiklik..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 40. Contoh 2.C.5 Perhatikan graf 𝐺5 di bawah ini. 1 2. 3. Gambar 2.C.5 Graf Berarah 𝐺5 Graf pada Gambar 5 di atas adalah graf berarah 𝐺5 = (𝑉5 , 𝐷3 ), dengan 𝑉5 = {1,2,3} dan 𝐷3 = {(1,1), (2,1), (3,1), (1,2), (2,3), (3,3)}. Dalam graf berarah 𝐺5 terdapat barisan busur (2,1),(1,1),(1,2),(2,3) yang merupakan lintasan dalam 𝐺5 . Lintasan ini dapat direpresentasikan dengan 2 → 1 → 1 → 2 → 3. Busur ini mempunyai panjang 4 karena tersusun aas 4 busur. Lintasan 2 → 1 → 2 → 3 → 3 → 1 → 2 merupakan sirkuit dengan panjang 6. Lintasan 1 → 2 → 3 → 1 merupakan suatu sirkuit elementer dengan panjang 3. Pada graf berarah 𝐺5 setiap titik yang berbeda selalu terdapat suatu lintasan, sehingga graf berarah 𝐺5 terhubung kuat. Selanjutnya, dijelaskan mengenai hubungan antara matriks dan graf berarah berbobot yang terhubung kuat di ℝmax . Penjelasan diawali dengan.

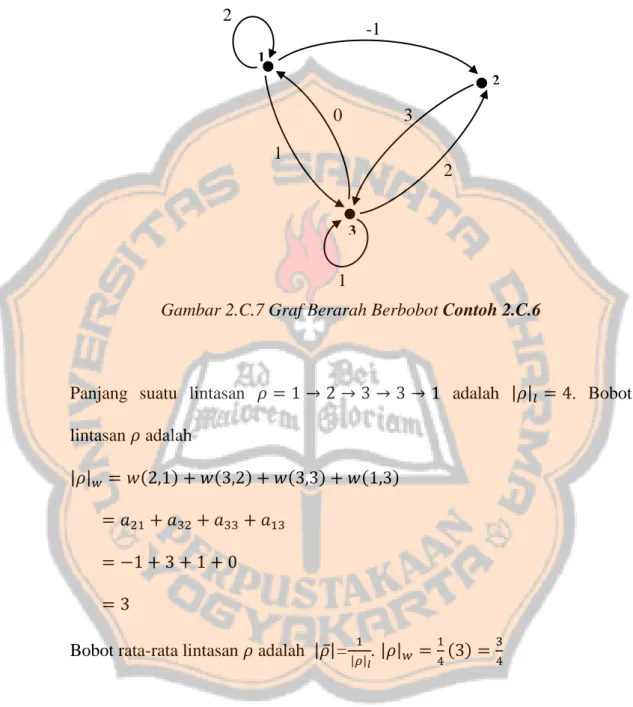
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 41. definisi graf bobot atau graf preseden, yang merupakan graf dari suatu matriks dalam ℝmax .. Definisi 2.C.11 (Graf Bobot (Precedence Graph), Schutter, 1996 dalam Rudhito, 2016) Diberikan 𝐴 ∈ ℝ𝑛×𝑛 𝑚𝑎𝑥 . Graf bobot atau preseden dari A adalah graf berarah berbobot 𝐺(𝐴) = (𝑉, 𝐷) dengan 𝑉 = {1, 2, … , 𝑛} dan 𝐷 = {(𝑗, 𝑖)|𝑤(𝑖, 𝑗) = 𝑎𝑖𝑗 ≠ ɛ}.. Contoh 2.C.6 2 ɛ 0 Diberikan matriks 𝐴 = [−1 ɛ 2] 1 3 1 Graf bobot dari matriks 𝐴 merupakan graf berarah berbobot 𝐺(𝐴) = (𝑉, 𝐷) dengan himpunan titik 𝑉 = {1,2,3} dan himpunan busur 𝐷 = {(1,1), (3,1), (1,2), (3,2), (1,3), (2,3), (3,3)}, seperti yang disajikan dalam Gambar 2.C.6. Perhatikan sebaliknya bahwa untuk setiap graf berarah berbobot 𝐺(𝐴) = (𝑉, 𝐷) selalu dapat didefinisikan suatu matriks 𝐴 ∈ ℝ𝑛×𝑛 𝑚𝑎𝑥 dengan 𝑎𝑖𝑗 = {. 𝑤(𝑗, 𝑖), 𝑗𝑖𝑘𝑎(𝑗, 𝑖) ∈ 𝐴 ɛ, 𝑗𝑖𝑘𝑎(𝑗, 𝑖) ∉ 𝐴. Matriks 𝐴 ini disebut sebagai matriks bobot dari graf 𝐺(𝐴) dan graf berarah berbobot tersebut merupakan graf bobot dari 𝐴. Berikut disajikan gambar graf berarah berbobot yang bersesuaian dengan matriks 𝐴 pada contoh yang diberikan di atas..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 42. 2. -1 1 2. 0. 3. 1 2. 3. 1 Gambar 2.C.6 Graf Berarah Berbobot Contoh 2.C.6. Selanjutnya, dijelaskan pula mengenai konsep lintasan dan sirkuit pada graf preseden.. Definisi 2.C.12 Diberikan graf berarah berbobot 𝐺(𝐴) = (𝑉, 𝐷) dengan 𝑉 = {1, 2, … , 𝑛}. Bobot suatu lintasan 𝜌 = 𝑖1 → 𝑖2 → ⋯ → 𝑖𝑙 didefinisikan sebagai jumlahan bobot busur-busur yang menyusun 𝜌 dan dinotasikan dengan |𝜌|𝑤 .. Definisi 2.C.13 (Rudhito, 2016) Untuk matriks 𝐴 ∈ ℝ𝑛×𝑛 𝑚𝑎𝑥 , 𝑏obot suatu lintasan 𝜌 = 𝑖1 → 𝑖2 → ⋯ → 𝑖𝑙 dalam graf bobot 𝐺(𝐴) adalah |𝜌|𝑤 = 𝑎𝑖2 ,𝑖1 + 𝑎𝑖3 ,𝑖2 + ⋯ + 𝑎𝑖𝑙,𝑖𝑙−1 . Bobot rata-rata lintasan 𝜌, dinotasikan dengan |𝜌̅ |, didefinisikan sebagai operasi perkalian dan pembagian pada bilangan real).. 1 . |𝜌|𝑙. |𝜌|𝑤 (dengan.